轧机垂扭耦合振动控制模型的建立与优化

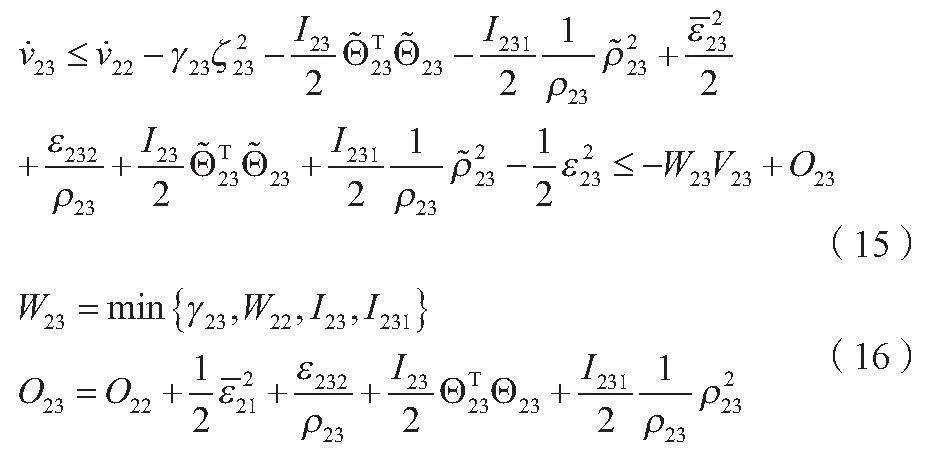
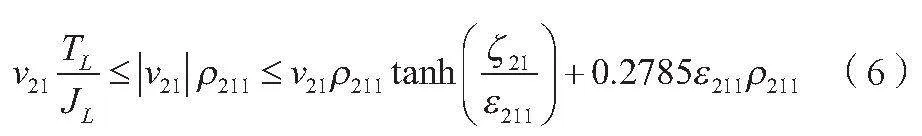
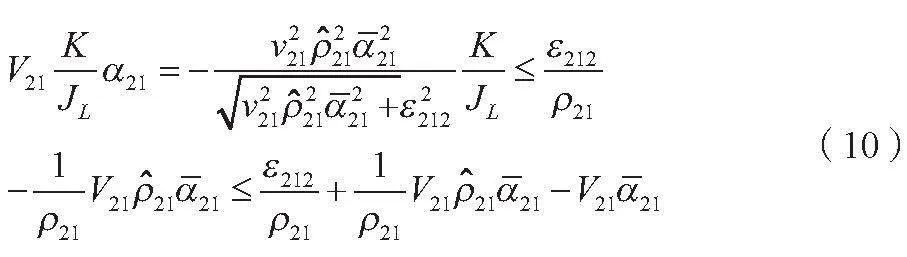
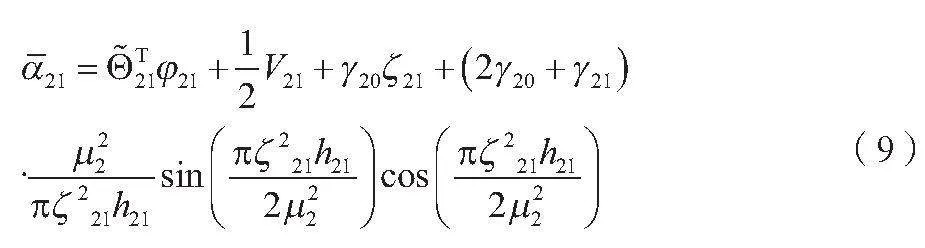
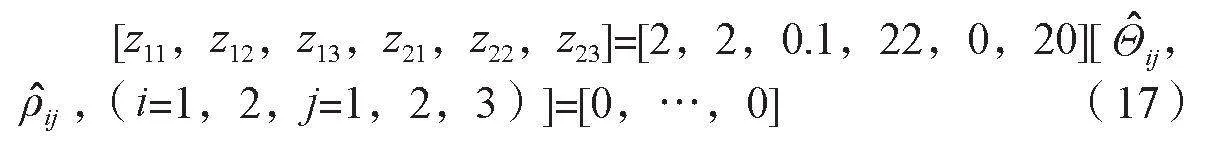
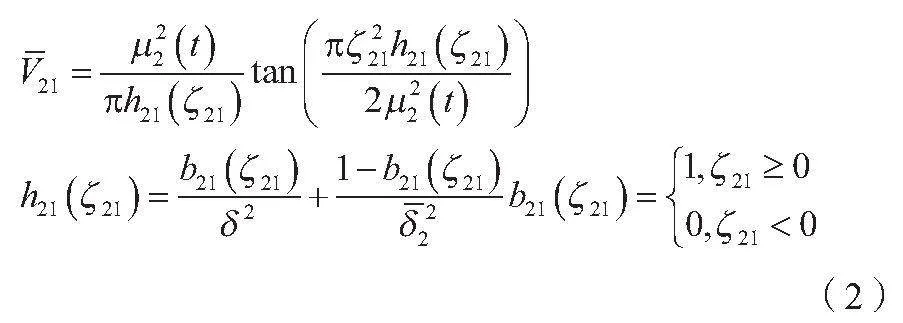
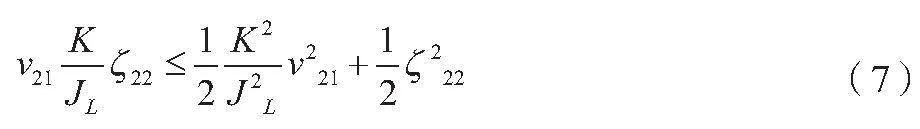
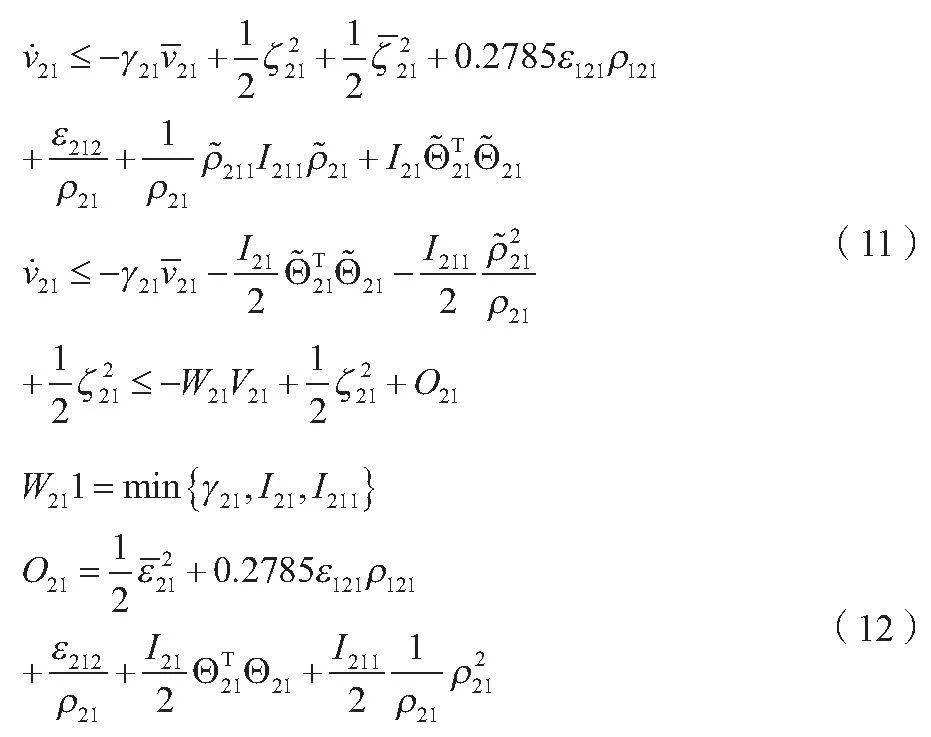
摘 要：本文针对轧机垂扭耦合振动问题，建立了相应的控制模型，并提出了一种优化方法。首先，分析轧机系统的动力学特性，建立垂扭耦合振动的数学模型。其次，基于该模型提出一种基于控制理论的优化方法，以有效控制轧机振动。最后，通过仿真试验验证所提方法的有效性和优越性。本文算法引入了输出性能约束，建立了合理的控制策略，能够使系统的状态变量始终保持在有界范围内，从而提高了系统的稳定性。

关键词：轧机；耦合振动；控制模型

中图分类号：TG 333" " 文献标志码：A

轧机是一种重要的金属加工设备，广泛应用于钢铁、有色金属等行业。但是轧机结构复杂并具有一定的工作特性，经常会出现垂扭耦合振动问题，严重影响了轧机的工作效率和产品质量[1]。因此，对轧机垂扭耦合振动进行控制和优化具有重要的理论和实际意义。本文旨在建立相应的控制模型和优化方法，提供一种有效的解决方案。

1 轧机垂扭耦合振动控制模型的建立

1.1 整体设计思路

本文针对扭振系统，设计了一个扭振控制器来抑制扭转振动。该控制器可测量扭转振动的反馈信号，并结合系统模型和控制算法生成相应的控制信号来抑制扭转振动[2]。并优化控制器参数和调节算法，对扭转振动进行有效控制。

1.2 具体设计算法

本文建立了轧机主传动扭振系统的数学模型，该系统包括轧机主传动系统和扭振系统，本文主要探讨扭振系统。扭振系统由轧机辊和轧机辊间的弹簧、阻尼器组成。反步坐标变换是一种将系统的输入和输出变量进行转换的方法，能更好地描述系统的动态特性[3]。本文将扭振系统的扭转角度和扭转角速度作为反步坐标。针对轧机主传动扭振系统，引入反步坐标变换，如公式（1）所示。

式中：z21为电机转动角速度；z22为电机转动角度-电机转动角速度；z23为电机转动角度；α21、α22分别为虚拟控制器；ζ21、ζ22和ζ23分别为输出变量。

在轧机垂扭耦合振动控制模型的建立中，本文引入正切障碍李雅普诺夫函数，将其作为描述系统稳定性的函数，定义一个障碍函数来限制系统的输出变量可以有效控制系统的性能。在耦合垂振问题中，本文构造了一个非对称的正切障碍李雅普诺夫函数来限制输出变量的性能。非对称是指障碍函数的上界和下界不对称，这样可以使系统对输出变量的上界和下界具有不同响应，从而更好地控制系统的振动行为。当建立轧机垂扭耦合振动控制模型时，本文将正切障碍李雅普诺夫函数引入系统的控制策略中。合理选择障碍函数的形式和参数可以限制系统输出变量在一定范围内波动，从而有效控制系统的振动幅度和稳定性。特别是在耦合振动问题中，正切障碍李雅普诺夫函数的非对称性可以更好地适应系统的复杂性，提高系统的控制性能和稳定性[4]。为了限制输出变量ζ21的性能，需要构造非对称的正切障碍李雅普诺夫函数，如公式（2）所示。

1.2.1 构建第一部分的李雅普诺夫函数

为了使输出变量ζ21趋于稳定，构建第一部分的李雅普诺夫函数，分别如公式（3）、公式（4）所示。

在轧制过程中，轧机会施加一定压力和扭矩，将金属坯料压制成所需形状和尺寸。不同厚度和规格的产品需要不同的轧制参数和工艺调整，这就需要在切换不同产品过程中进行相应调整和适应[5]。然而，在切换过程中，产品的厚度和规格的变化会导致轧机主传动系统的负载转矩发生变化。这种变化是突变的、不确定的，甚至会产生冲击和振动。这样的不确定干扰会对轧机的稳定性和轧制质量产生负面影响，因此负载转矩表示为公式（5）。

TL=TL1+TLD " " " " " " " " " " " " （5）

式中：TL1为稳定轧制时的负载转矩；TLD为轧制过程存在干扰导致的干扰转矩。

公式（5）的引理如公式（6）所示。

式中：v21为控制输入或控制信号的增益；ρ211为物理参数或系统参数；tanh为双曲正切函数；ε211为小的正数。

根据定义的状态变换z22=ζ22+α21，由杨氏不等式可得公式（7）。

杨氏不等式的意义在于它给出了组合数的一个上界估计。利用RBF神经网络来逼近未知的非线性函数，将输入值输入网络中，经过隐藏层计算和输出层计算得到网络的输出值。这个输出值就是对未知函数在该输入值下的逼近值。利用RBF神经网络来逼近未知的非线性函数，如公式（8）所示。

式中：K为系统的增益系数；JL为系统的转动惯量；c3、c4分别为常数系数；aRFz为RBF神经网络的权重；φ21（Z21）为RBF神经网络的基函数。

PID控制器是最常用的虚拟控制器之一，包括比例、积分和微分3个控制分量。调节这些分量的参数，可实现系统的稳定性和响应速度的折衷。PID控制器适用于许多线性和部分非线性系统。模型参考自适应控制（MRAC）利用在线辨识系统模型，并根据模型误差来调整控制器参数，从而实现对系统的自适应控制。MRAC适用于系统参数变化较快或不确定的情况。本文选取的虚拟控制器和自适应律分别如公式（9）、公式（10）所示。

将公式（9）带入公式（10）可得公式（11）、公式（12）。

1.2.2 构建第二部分的李雅普诺夫函数

计算方式与第1.2.1节的第一部分相似，得到第二部分的李雅普诺夫函数，分别如公式（13）所示。

1.2.3 构建第三部分的李雅普诺夫函数

计算方式与第1.2.1节的第一部分相似，得到第三部分的李雅普诺夫函数，分别如公式（15）、公式（16）所示。

2 模型仿真验证

2.1 仿真设置

本文选取650mm轧机为仿真对象，轧机机电液垂扭耦合系统的仿真参数如下：m1为（8.9357×104）kg，kv为（1.25×10-4）m/v，k11为（7.2×1010）N/m，βe为（7×108）Pa，c11为（1.2×106）（N·s）/m，V为0.0732m3，Ps为（2×107）Pa，

Jm为1552kg·m2，P2为（1×106）Pa，JL为1542kg·m2，A1为（1.9635×10-1）m2，A2为（3.015×10-2）m2，TL1为14500N·m，Ct为（5×10-16）N·m，TLD为（2190×sinπt）N·m，Cd为0.62，R为0.4，w为0.119，c1为0.2，c2为0.1，c3为0.1，c4为0.2，a为0.13，B为0.002，c为0.2。

轧机垂扭耦合系统状态初始值选取如公式（17）所示。

2.2 仿真结果

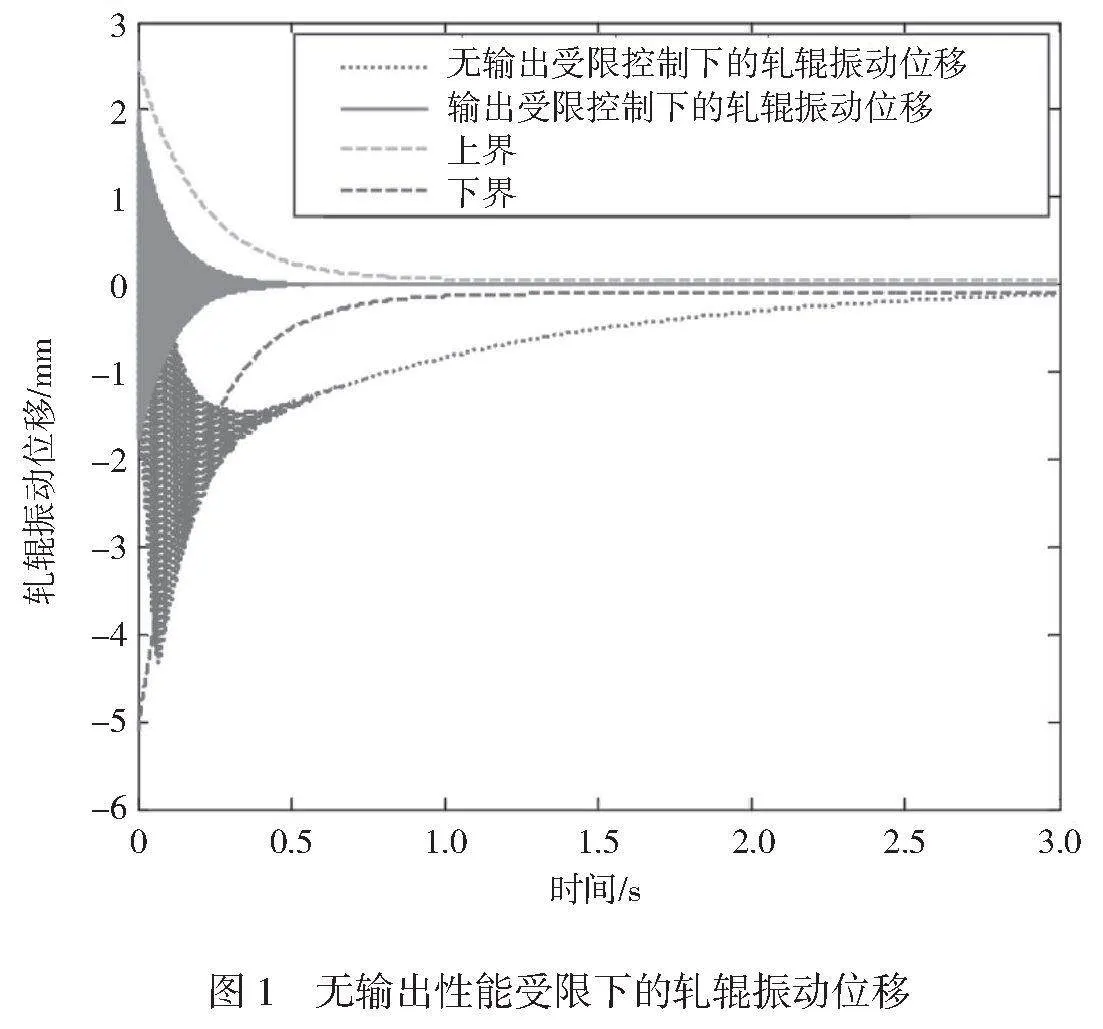
利用本文提出的控制算法，轧辊振动位移的衰减速度得到了显著提高。传统的无输出性能约束控制方法无法有效抑制振动的衰减速度，导致系统的响应时间较长。而本文算法能够合理控制策略和参数调节，快速减少振动位移，使系统的衰减速度更快，从而提高了系统的动态性能。在稳态误差方面，本文的控制算法也取得了良好效果。传统的无输出性能约束控制方法无法消除系统的稳态误差，导致系统无法达到期望的稳定状态。而本文算法引入额输出性能约束，能够有效减少稳态误差，使系统能够达到期望的稳定状态。超调量是衡量系统控制性能的重要指标之一。传统的无输出性能约束控制方法在控制过程中存在较大超调量，导致系统的响应过程不够平滑。而本文算法能够优化控制策略和参数调节，有效减少超调量，使系统的响应过程更平滑、稳定。

无输出性能受限下的轧辊振动位移、无输出性能受限下的负载转速跟踪误差分别如图1、图2所示。利用本文提出的控制算法，负载转速的跟踪误差趋于稳定。传统的无输出性能约束控制方法无法有效控制负载转速的误差，导致系统的跟踪性能较差。而本文算法引入了输出性能约束和合理的控制策略，能够快速减少跟踪误差，使其稳定在规定的上、下界内，从而提高了系统的动态性能。在稳态性能方面，本文的控制算法也取得了良好效果。传统的无输出性能约束控制方法无法严格限制负载转速的跟踪误差，导致系统无法达到期望的稳定状态。而本文算法优化了控制策略和参数调节，能够将跟踪误差严格限制在规定的上、下界内，使系统能够更好地达到期望的稳定状态。

负载转速与电机转速差的响应曲线和电机转速响应曲线分别如图3、图4所示。传统的无输出性能约束控制方法无法有效控制振动速度，导致系统的振动速度波动较大。而本文算法引入了输出性能约束和合理的控制策略，能够快速减少振动速度的波动，并使其趋于稳定。传统的无输出性能约束控制方法无法严格限制液压缸无杆腔工作压力的波动，导致系统的压力不稳定。而本文算法优化了控制策略和参数调节，能够有效控制液压缸无杆腔工作压力的波动。传统的无输出性能约束控制方法无法保证系统的状态变量不超出规定范围，影响系统的稳定性。而本文算法引入了输出性能约束和合理的控制策略，能够将系统的状态变量始终保持在有界范围内，从而提高了系统的稳定性。

3 结语

本文对轧机垂扭耦合振动问题进行建模和优化，提出了一种基于控制理论的优化方法仿真试验表明，该方法能够有效控制轧机的振动，提高轧机的工作效率和产品质量。本文的研究成果对轧机行业的发展具有重要意义，也为其他领域的振动控制问题提供了借鉴和参考。未来的研究进一步探索更高效的优化方法，以进一步提升轧机垂扭耦合振动控制的效果和性能。

参考文献

[1]侯东晓，陈善平，方成，等.万向接轴附加动态弯矩下板带轧机垂扭耦合振动特性研究[J].振动与冲击，2022，41（19）：48-54，63.

[2]李苗苗，王卫，李英民.锚杆-围岩结构的耦合振动和减振[J].土木与环境工程学报（中英文），2024（2）：51-59.

[3]张宗素，王婷，谭帅，等.基于Galerkin截断的薄膜-床面耦合振动响应分析[J].噪声与振动控制，2024，44（2）：22-26.

[4]王少钦，马仕杰，郭明浩，等.风荷载对车桥耦合振动及行车舒适性影响[J].公路交通科技，2024，41（4）：51-64.

[5]吴志渊，闫寒，吴林潮，等.旋转裂纹叶片-弹性轮盘耦合系统振动特性[J].航空学报，2022，43（9）：101-114.