对一道轻杆关联物体试题的深度探讨

摘 要：详细探讨了一道轻杆关联物体试题情境和解析的自洽性，同时借助计算机数值模拟和仿真实验等方式，对如何将绳杆关联问题可视化进行了探索尝试，以期为试题命制和教学备考提供参考。

关键词：轻杆关联；深度探讨；可视化研究

中图分类号：G633.7 文献标识码：A 文章编号：1003-6148（2024）11-0068-4

１ 问题的提出

高中阶段涉及绳杆关联物体运动规律的问题，分析时常用到动力学、能量和动量等知识，综合考查学生的必备知识和关键能力，因而是试题命制的热点和教学的重难点。有关绳杆关联物体的创新试题层出不穷，但这类问题复杂多样且隐蔽抽象，导致试题容易出现情境或解析不自洽的情形，在教学备考中也经常陷入困惑或误区。下面选取在教学中遇到的一道轻杆关联物体试题，详细探讨情境和解析的自洽性，并尝试将物体的运动规律进行可视化以方便直观研究。

２ 轻杆关联试题的深度探讨

例１ 如图１所示，Ａ、Ｂ两小球质量均为ｍ。Ａ球穿过半径为Ｒ的竖直光滑圆轨道，Ｂ球穿过光滑竖直长杆，杆和圆轨道均固定在同一竖直平面内，杆的延长线过轨道圆心Ｏ，两球用轻质铰链与长为ｌ（ｌ＞２Ｒ）的轻杆连接，连接两球的轻杆能随小球自由移动，其中Ｍ、Ｎ和Ｐ三点分别为圆轨道上最低点、圆心的等高点和最高点，重力加速度为ｇ。某时刻Ａ球在Ｍ点获得水平向右的初速度，并能做完整的圆周运动，下列说法正确的是（ ）

Ａ．A球在Ｍ点的初速度大于5

Ｂ．当A球到达Ｐ点时，Ｂ球的加速度为０

Ｃ．A球运动到Ｐ点的过程中，Ａ球的速度一直减小

Ｄ．当A球经过杆与圆轨道相切的Ｑ点（图中未画出）时，Ｂ球的速度达到最大值

本题考查轻杆关联问题，巧妙设计两小球分别做圆周运动和直线运动，增强了情境的复杂性和考查的综合性，类似本题情境的问题曾在笔者执教学校以及网络上各大物理交流群引起热烈讨论。本题的参考答案为Ｂ、Ｄ选项，解析为：若Ａ球恰能过Ｐ点，则Ａ球在Ｐ点的速度须大于０，又此时Ｂ球的速度为０，根据机械能守恒定律有mv>2mg2R，联立解得v0>2，Ａ选项错误；因为Ａ球在Ｐ点时Ｂ球的速度为０，此时Ｂ球受力平衡，故aB=0，Ｂ选9b1b1e7352054464c797d3ca470e7189项正确；在Ａ球从M运动到Ｐ的过程中，Ｂ球的速度先增后减，故Ａ球的速度也先增后减，Ｃ选项错误；A球运动到Ｑ点时，设轻杆与竖直方向的夹角为θ，有vA=vBcosθ，根据数学知识可知此时θ最大，即cosθ最小，vB最大，Ｄ选项正确。

我们不妨类比做竖直上抛的物体运动到最高点的情境，可知Ｂ选项认为Ｂ球的速度为０时其受力平衡并不严谨。有观点认为，此时Ａ、Ｂ球加速度aA、aB沿杆分量应相等，因此aB=aA=，这种说法也不对，因为Ａ球也在绕Ｂ球做圆周运动，由加速度关联有aA=-+aB，故应为aB=v（+）。而Ａ、Ｂ球的速度只是沿杆分量相等，不一定是正相关，Ｃ选项有待商榷。Ｄ选项中虽然cosθ最小，但由于vA也在变化，因此并不能确定是否vB在该处最小。

显然，在讨论本题时，需要关注Ａ、Ｂ球的速度和加速度随Ａ球在圆轨道不同位置处的变化规律，可用Ａ球转过的角度来描述位置，并做如下分析：设初始时Ａ球的速度为v0，ＡＯ连线转过α角时，轻杆与竖直方向的夹角为θ，此时Ａ、Ｂ球的速度分别为vA和vB，整体位形如图２所示。由几何关系有

=（１）

在地面系中，Ｂ球的加速度aB=沿轻杆方向，Ａ球的加速度可分解为沿圆轨道切向aAt=和径向a=，设轻杆对Ａ、Ｂ球的作用力大小为Ｔ，由动力学规律有

-mAaAt=mAgsinα+Tsin（α－θ）（２）

mBaB=-Tcosθ-mBg（３）

联立（２）（３）式可得

-mAaAt=mAgsinα+mB（aB+g）（４）

根据运动关联有

vBcosθ=vAsin（α-θ）（５）

由系统能量守恒得

mv=mv+mv+mgh+mgh（６）

其中，hA=R（1-cosα），hB=lcosθ+hA-l。联立（５）（６）式可解得

vA=（７）

vB=（８）

接下来，分别将（１）（５）式两边对时间求导得

Rcosα=lcosθ（９）

acosθ-vsinθ=

asin（α-θ）+vcos（α-θ）（-）（１０）

其中，= （１１）

联立（４）（９）（10）（１１）式，可解得

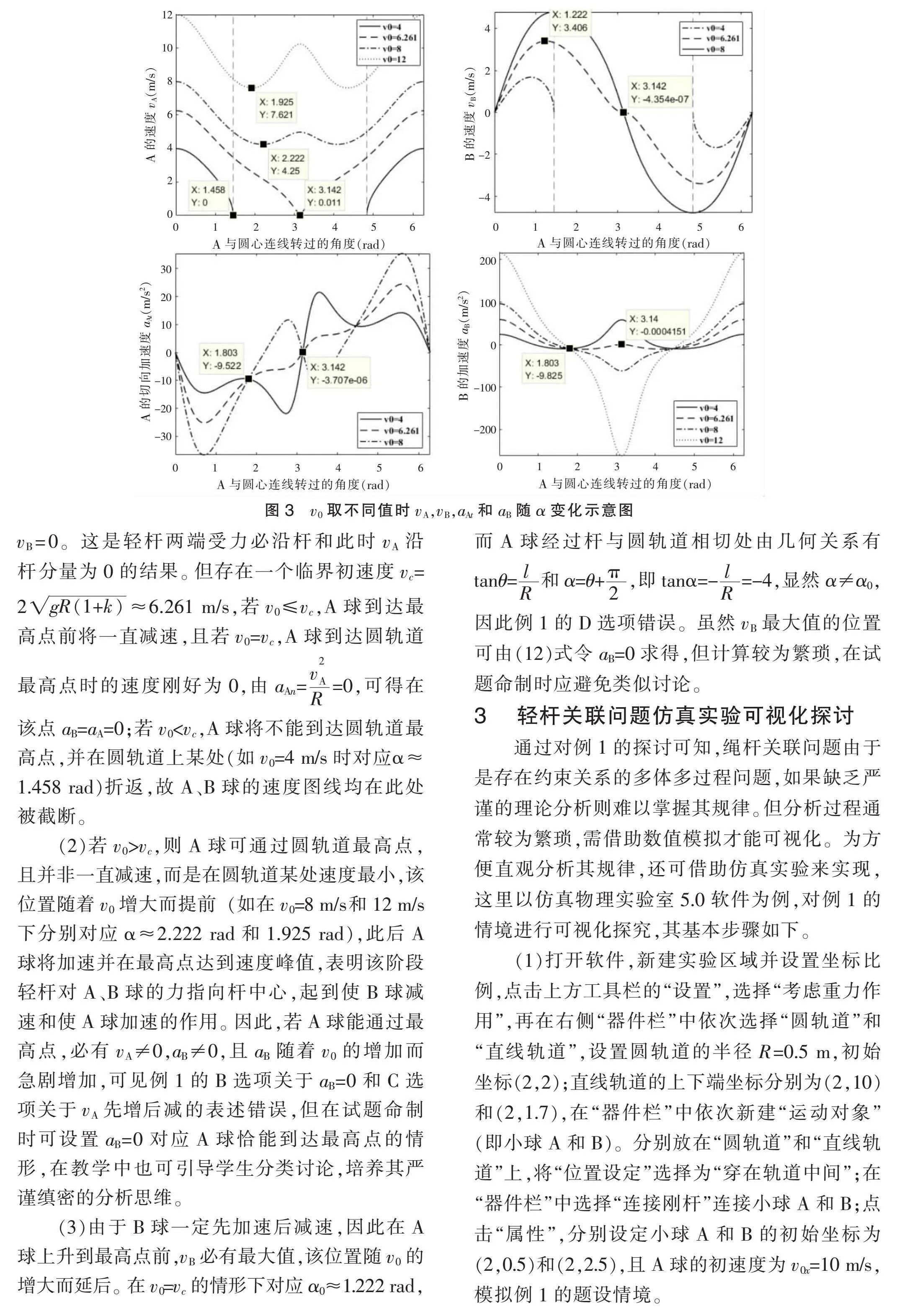
注意到（７）（８）（１２）（１３）式中的θ和α并不独立，而是满足（１）式的约束，若再将上述各式和（１）式联立便可推出vA（α）、vB（α）、aAt（α）和aB（α）的表达式，由于表达式均较为冗长，故此处不列出，借助计算机软件可视化可方便、直观地研究各量随α的变化规律。令l=2 m，R=0.5 m，g=9.8 m/s2，并依次令v0=４ ｍ/ｓ、６．２６１ ｍ/ｓ、８ m/ｓ和１２ ｍ/ｓ，借助Ｍａｔｌａｂ软件分别绘制出vA、vB、aAt和aB随α从０到2π变化的图线如图３所示，观察图３可得到以下规律和启示。

（１）不论v0如何，初始时必有aAt=0，且若Ａ球能到达圆轨道最高点，则在该点必有aAt=0和vB=0。这是轻杆两端受力必沿杆和此时vA沿杆分量为０的结果。但存在一个临界初速度vc=2≈6.261 m/s，若v0≤vc，Ａ球到达最高点前将一直减速，且若v0=vc，Ａ球到达圆轨道最高点时的速度刚好为０，由aAn==0，可得在该点aB=aA=0；若v0<vc，Ａ球将不能到达圆轨道最高点，并在圆轨道上某处（如v0=4 m/s时对应α≈1.458 rad）折返，故Ａ、Ｂ球的速度图线均在此处被截断。

（２）若v0>vc，则Ａ球可通过圆轨道最高点，且并非一直减速，而是在圆轨道某处速度最小，该位置随着v0增大而提前（如在v0=8 m/s和12 m/s下分别对应α≈2.222 rad和1.925 rad），此后Ａ球将加速并在最高点达到速度峰值，表明该阶段轻杆对Ａ、Ｂ球的力指向杆中心，起到使Ｂ球减速和使Ａ球加速的作用。因此，若Ａ球能通过最高点，必有vA≠0，aB≠0，且aB随着v0的增加而急剧增加，可见例1的Ｂ选项关于aB=0和Ｃ选项关于vA先增后减的表述错误，但在试题命制时可设置aB=0对应Ａ球恰能到达最高点的情形，在教学中也可引导学生分类讨论，培养其严谨缜密的分析思维。

（３）由于Ｂ球一定先加速后减速，因此在Ａ球上升到最高点前，vB必有最大值，该位置随v0的增大而延后。在v0=vc的情形下对应α0≈1.222 rad，而Ａ球经过杆与圆轨道相切处由几何关系有tanθ=和α=θ+，即tanα=-=-4，显然α≠α0，因此例１的Ｄ选项错误。虽然vB最大值的位置可由（１２）式令aB=0求得，但计算较为繁琐，在试题命制时应避免类似讨论。

３ 轻杆关联问题仿真实验可视化探讨

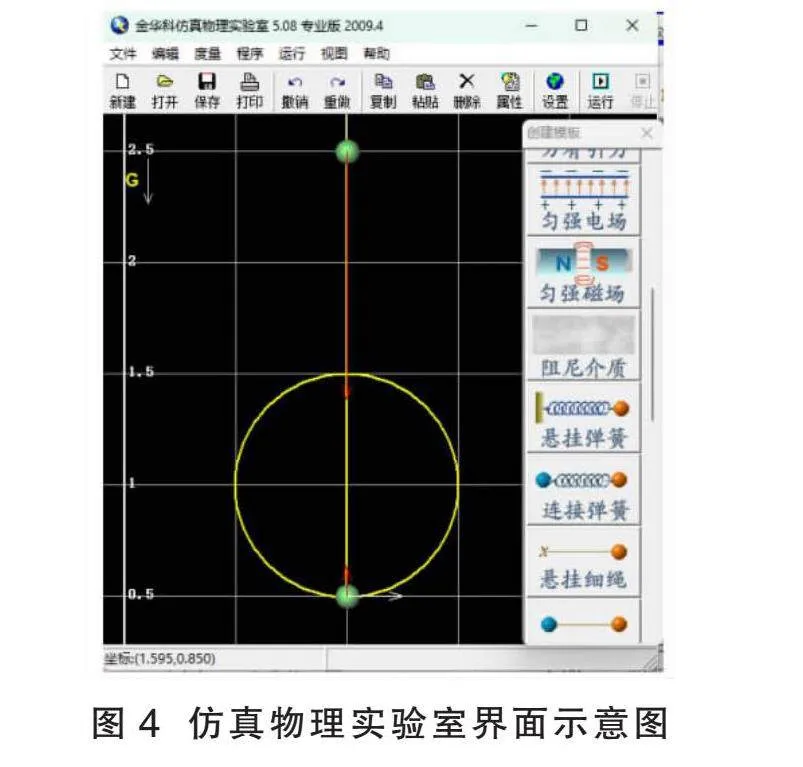
通过对例１的探讨可知，绳杆关联问题由于是存在约束关系的多体多过程问题，如果缺乏严谨的理论分析则难以掌握其规律。但分析过程通常较为繁琐，需借助数值模拟才能可视化。为方便直观分析其规律，还可借助仿真实验来实现，这里以仿真物理实验室５．０软件为例，对例１的情境进行可视化探究，其基本步骤如下。

（１）打开软件，新建实验区域并设置坐标比例，点击上方工具栏的“设置”，选择“考虑重力作用”，再在右侧“器件栏”中依次选择“圆轨道”和“直线轨道”，设置圆轨道的半径Ｒ＝０．５ ｍ，初始坐标（２，２）；直线轨道的上下端坐标分别为（２，１０）和（２，１．７），在“器件栏”中依次新建“运动对象”（即小球Ａ和Ｂ）。分别放在“圆轨道”和“直线轨道”上，将“位置设定”选择为“穿在轨道中间”；在“器件栏”中选择“连接刚杆”连接小球Ａ和Ｂ；点击“属性”，分别设定小球Ａ和Ｂ的初始坐标为（２，０．５）和（２，２．５），且Ａ球的初速度为v0x=10 m/s，模拟例1的题设情境。

（２）在“属性”的“动态显示”中选择“显示速度矢量”和“显示加速度矢量”，如图４所示。画面中的箭头定性表示小球Ａ和Ｂ的速度和加速度，点击“运行”，可发现当Ａ球运动到圆轨道的最高点时，小球Ａ和Ｂ均具有竖直向下且不等的加速度。

（３）为了更具体地观察小球Ａ和Ｂ各物理量的变化，点击“属性”并选择“实验数据曲线”，可以选择不同的运动参量进行绘图。如果实验进行太快，不方便观察和采集数据，可以点击“设置”，将“实验最小扫描时间”修改得小一些即可。这里分别输出Ａ球的v-t图和Ｂ球的a-t图，在合理设置坐标分度后得到图５，可见vA-t图与图３中的vA-α图相似，aB-t图与图３中的aB-α图相似，实现了理论推导数值模拟和仿真实验的相互验证。

参考文献

［１］彭芳麟．计算物理基础［Ｍ］．北京：高等教育出版社，２００９：２１１－２１３．

［２］曾祥军，黄致新．利用“减心法”处理加速度关联问题［Ｊ］．物理教学，２０２４，４６（３）：６２－６５．

［３］蒋邦勇．可视化角度深度分析绳牵连物体的运动规律［Ｊ］．物理教学，２０２４，４６（５）：１５－１９．

（栏目编辑 蒋小平）