渐省样例对物理综合问题解决的影响研究

摘 要：通过对比普通样例，探讨了渐省样例如何逐步减少解题步骤，引导学生主动建构知识，并提升问题解决能力。以初二学生为被试，采用密度和浮力综合问题为学习材料和测试材料，结果显示渐省样例组学生的测试成绩显著高于普通样例组。这表明渐省样例有助于促进物理综合问题解决的学习效果，为教育者和学习者提供了新的教学策略和学习方法。

关键词：渐省样例；初中物理；物理综合问题

中图分类号：G633.7 文献标识码：A 文章编号：1003-6148（2024）11-0013-3

根据Ａｎｄｅｒｓｏｎ的认知技能获得的四阶段模型，学习者的技能获取确实是一个渐进、动态的过程。这一模型为理解学习者如何从样例学习中逐渐提升问题解决能力提供了有力的理论框架［１］。在第一阶段，学习者通过接触具体的样例，尝试将样例与问题解决策略相联系；到了第二阶段，学习者开始形成抽象的规则，这些规则可以帮助他们运用书面知识来解决问题；进入第三阶段，学习者的问题解决速度显著提高，他们不再需要严格按照书面知识的步骤来解题，而是能够自动、快速地解决问题，且不需要过多注意资源；到了第四阶段，学习者通过大量的练习，积累了丰富的样例解法，可以直接从记忆中提取正确的解法，并表现出灵活性，不再受顺序的限制。此时，学习者已经具备了高水平的问题解决能力。在这一过程中，样例学习在初始阶段起着关键作用，但随着学习者技能的提升，样例学习的重要性逐渐降低。然而，我们的目标是促进学习者问题解决能力的获得，因此，需要一种更为有效的样例呈现思路来支持学习者的学习。

渐省样例正是一种符合Ａｎｄｅｒｓｏｎ认知技能获得过程的样例设计思路。它通过从完整样例到简化步骤的逐渐过渡，帮助学习者逐步建构新的知识图式。这一呈现过程不仅符合建构主义的学习观，即学习者通过主动建构知识来理解和掌握知识，而且能够有效地促进学习者从依赖样例到独立解决问题的转变［２］。

１ 研究目的

物理综合问题是指那些涉及两个或两个以上来自不同章节的物理概念、规律的问题。这类问题要求学生不仅理解每个物理概念，还要能够将这些概念综合起来，深入分析物理情境，并通过一定量的数学运算来得到答案［３］。相较单一物理问题，物理综合问题更能检验学生对物理知识的全面掌握程度和应用能力，从而促使学生在学习中更深入地理解和运用物理知识。因此，在中学物理教学过程中，讲解物理综合问题对提升学生的物理学习能力和分析问题能力具有重要意义。尽管学者们在问题解决领域进行了广泛而深入的中学物理教育研究，但大部分的研究聚焦于单一概念物理问题上，对于物理综合问题的学习方法的研究显得相对匮乏［４］。

样例学习作为一种提升问题解决效率的有效策略，其成效往往受到样例呈现方式的影响［５］。自２００２年渐省样例这种独特的呈现形式被提出，受到学者的广泛关注。这种方法的核心思想是从完整的样例出发，逐步减少其中的解题步骤，直至最后仅留下一个待解决的问题。学者经过深入研究后发现，渐省样例能够帮助学生动态地将问题和样例结合在一起，通过逐步减少样例中的解题步骤，引导学生逐步深入思考，从而加深对学习材料的理解［６］。渐省样例作为一种创新的样例呈现形式，对于提高学生的学习效果，培养他们的独立思考和问题解决能力具有重要意义。由此，本文将研究使用渐省样例是否有助于物理综合问题解决。

２ 研究设计

２．１ 研究目的

以初二学生为被试，选取难度适宜的包含密度和浮力概念知识的物理综合问题为学习材料，考察渐省样例对物理综合问题学习效果的影响，即学习渐省样例的被试后测成绩是否优于学习普通样例的被试。

２．２ 研究假设

本研究假设在物理综合问题的学习中，渐省样例组学生的测试成绩显著高于普通样例组学生的测试成绩。

２．３ 选择被试

选取广东省东莞市属初级中学两个班８４名学生作为被试，女生４１人，男生４３人。渐省样例组被试人数４１人，普通样例组被试人数４３人。被试的平均年龄在１３周岁左右。两组的前测平均成绩相当，在此之前被试已经学习了密度和浮力的相关知识。

２．４ 实验设计

本实验为单因素被试间设计。自变量为样例类型，包括两个水平，普通样例和渐省样例。因变量是测试成绩。

２．５ 实验材料

（１）渐省样例学习材料

由４道关于密度和浮力的综合样例题组成，并且每道样例的解题步骤都是３步。样例的呈现方式是先呈现解题步骤完整的样例，下一样例的呈现步骤缺少倒数第一步，以此类推，直至呈现第四道样例时完全无解题步骤。具体呈现形式如表 １所示。

下面是其中一道样例题。

例１ 如图 １所示，用细绳系住体积为3×10-4 m3的物体Ａ，使它竖直下垂且全部浸入水中静止，此时绳子的拉力是1.5 N，容器和水的总质量是0.7 kg，容器与水平桌面的接触面积是100 m2。（ρ=1.0×103 kg/m3，g取10 N/kg）求：物体的密度。

解：

因为物体Ａ完全浸没在水中，所以

V=V=3×10-4 m3

第一步（阿基米德原理）：

物体所受的浮力为

F=ρgV=1.0×103 kg/m3·10 N/kg·3×10-4 m3=3 N

第二步（受力分析）：

由于物体处于静止状态，受到竖直向上的浮力和绳子拉力及竖直向下的重力。

由力的平衡条件得

G=F+F=3 N+1.5 N=4.5 N

第三步：

物体质量mA===0.45 kg

物体密度ρA===1.5×103 kg/m3

（２）普通样例学习材料

与渐省样例学习材料的例题相同且呈现顺序相同，但是每道例题都呈现完整的解题步骤。

（３）测试材料

由３道关于密度和浮力的综合题组成，满分为９分。每道题的解题步骤分３步，每步１分，每题满分３分。题型和解题思路与所学样例一致。下面是其中一道测试题。

测试题 如图 ２所示，用弹簧测力计吊起体积为300 cm3的物体，物体浸没在圆柱形容器的酒精中，已知容器底面积200 cm2。求：物体的密度。（ρ=0.8×103 kg/m3，g取10 N/kg）

２．６ 实验程序

实验地点为被试平时上课的教室。主试由研究者担任。

（１）样例学习阶段

①渐省样例组的指导语为“下面有4道例题，请同学们认真学习例题１的解题步骤，并参照例题１完成例题２、３、４的解题步骤，每完成一道例题，可将答案与教室前希沃平板上的标准答案相对照。总共的学习时间为２０分钟，学习结束后由老师统一收回学习材料（本次学习不会记录你的成绩，请认真作答）。”

②普通样例组的指导语为“下面有4道例题，请同学们认真学习例题解题步骤。总共的学习时间为２０分钟，学习结束后，由老师统一收回学习材料。”

（２）测试阶段

在收回学习材料后，给被试发放测试材料。指导语为“请同学们根据前面学习材料中的解题步骤，认真完成下面3道练习题。本次作答需独立完成，勿相互交流。作答时长为２０分钟，练习结束后，由老师统一收回测试卷。”

３ 结果与分析

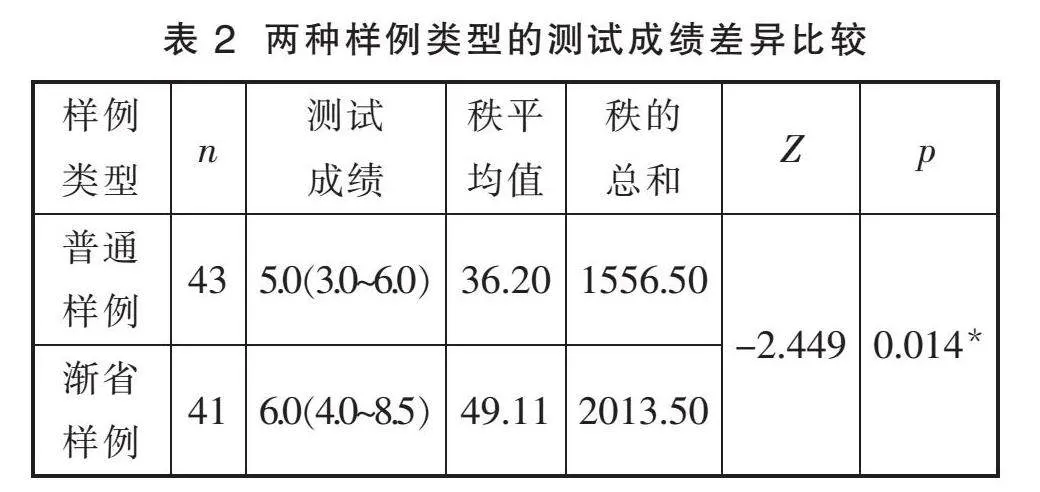
使用ＩＢＭ ＳＰＳＳ Ｓｔａｔｉｓｔｉｃｓ ２７对实验数据进行统计分析。因为实验数据呈非正态分布，所以本研究采用非参数检验方法。以样例类型为自变量，测试成绩为因变量，进行Ｍａｎｎ－Ｗｈｉｔｎｅｙ Ｕ检验，结果如表 ２所示。

表 ２结果显示，两组被试的测试成绩差异显著（Ｚ＝－２．４４９，ｐ＜０．０５）。并且渐省样例组被试的测试成绩中位数（２５％～７５％）为６．０（４．０～８．５），显著高于普通样例组被试的测试成绩５．０（３．０～６．０），符合研究假设，说明相比于普通样例，渐省样例可以更有效地促进学生对物理综合问题的学习和掌握。

４ 讨 论

上面的实验结果表明，在物理综合问题的学习中，渐省样例的学习效果要好于普通样例。相比于普通样例，渐省样例对学生解决物理综合问题具有更大的促进作用，更有助于学生进行学习迁移。本研究分析具体原因如下。

物理综合问题解决学习的核心在于深入理解和把握其深层的结构特征。这种深层结构特征通常指的是物理概念、原理以及它们之间的内在联系和逻辑关系。在实际学习过程中，学生往往过于关注问题的表面特征，如具体的数值、表述方式等，而忽视了更为重要的结构信息。这种倾向在解决简单的单概念问题时可能影响不大，因为这类问题通常可以直接通过表面特征找到答案。但是，当面对复杂的综合问题时，过于关注表面特征就会导致学生无法深入理解和解决问题，从而影响了学习效果。

渐省样例作为一种有效的教学策略，通过提供从认知模型到支架问题再到剩余问题的渐进式引导，帮助学生逐步深入理解和掌握物理知识。在初始阶段，通过提供完整的认知模型，学生可以初步了解物理概念和原理；随着学习的深入，逐渐减少提示信息，通过支架问题引导学生自主思考和探索；最后，在剩余问题阶段，学生需要独立解决问题，从而实现对所学知识的建构和内化。通过渐省样例的引导，学生可以逐渐从依赖表面特征转向关注深层结构，不断提升对物理问题的理解和解决能力。这种教学方法不仅有助于提高学生的认知水平，还能够培养他们的自主学习能力和问题解决能力，使他们能够进行更高水平的认知活动。

因此，在物理综合问题解决学习中，教育者应充分利用渐省样例等有效教学策略，引导学生逐步掌握问题解决技能，帮助学生深入理解和掌握物理知识的深层结构特征，从而实现更好的学习效果。

参考文献：

［１］王淼．安德森认知技能获得理论及其对教学的启示作用［Ｊ］．内蒙古教育，２０１７（２４）：４－５．

［２］邢强，莫雷．渐减提示法呈现样例对学习迁移的作用［Ｊ］．心理与行为研究，２００３（４）：２７４－２７７．

［３］邓磊，简鑫，张杨，等．数学复杂度对物理综合问题解决的影响［Ｊ］．中国考试，２０２１（１）：７５－８２．

［４］杨立娜． 类比比较样例对物理综合问题解决迁移效果的影响［Ｄ］．大连：辽宁师范大学，２０２３．

［５］杜雪娇，林洪新．解释的呈现方式对小学生数学样例学习的影响［Ｊ］．数学教育学报，２０１８，２７（５）：５２－５６．

［６］万梦婷． 渐省样例中自我解释提示类型对高中生问题解决能力的影响［Ｄ］．南京：南京师范大学，２０２0．

（栏目编辑 赵保钢）