基于Stacking模型融合下的HPC抗压强度预测

摘 要：为了实现高性能混凝土（HPC）抗压强度快速、准确地预测，基于58组HPC配合比数据，选取9个可解释特征作为模型输入变量，采用 Stacking 集成学习模型对HPC抗压强度进行预测，并与其他4种单一模型进行对比。结果表明：相较于传统的基模型，Stacking 集成学习模型的误差值最小，相关系数最大，对HPC抗压强度预测的MAPE、MAE、RMSE、R²分别为11.40%、3.72、5.04、0.91，该模型对HPC抗压强度的预测具有更高的准确性。

关键词：高性能混凝土；抗压强度；基模型；Stacking

中图分类号：TU528.01"" 文献标识码：A"" 文章编号：1673-1794（2024）05-0001-04

作者简介：徐玲，合肥城市学院土木工程学院讲师，研究方向：市政基础设施理论与技术（合肥 238076）；景楠，陕西省引汉济渭工程建设有限公司工程师（西安 710000）；石光，国家能源集团国能宝日希勒能源有限公司工程师（内蒙古 呼伦贝尔 021000）；通信作者：郭治龙，中国科学院西北生态环境资源研究院高级工程师，研究方向：时间序列预测研究（北京 100049）；景向楠，合肥城市学院经济与管理学院学生（合肥 238076）；袁瑞，滁州学院土木与建筑工程学院讲师，研究方向：市政基础设施理论与技术（安徽 滁州 239000）。

1 引言

随着我国基础设施建设投资规模的增加，高性能混凝土（High Performance Concrete，HPC）被广泛用于道路和桥梁等基础设施建设工程中。高性能混凝土又被称为绿色混凝土，具有高强度、优性能和强稳定等多方面优点^[1-2]。由于高性能混凝土中一般掺入外加剂和矿物掺合料，组成成分复杂，常规的经验公式无法对其强度指标进行有效预测，因此如何快速准确地预测混凝土抗压强度具有重要的实际工程意义。

近年来人工智能技术被广泛应用于工程科技、信息技术等领域^[3-4]。常见的机器学习方法有支持向量机回归（Support Vector Regression，SVR）、人工神经网络（Artificial Neural Netwroks，ANN）、随机森林（Random Forest，RF）等。且已有诸多学者将机器学习应用于混凝土性能的研究。Pham^[5]等采用改进的最小二乘支持向量机对239组混凝土强度指标进行预测，预测结果较为理想。Cui^[6]等提出一种改进的卷积神经网络，通过重构语义、有效提取混凝土裂缝的特征值，使得Att-Unet模型的裂缝分割能力得到显著提高。Chun^[7]等利用RF模型对钢筋腐蚀导致混凝土内部结构损伤的程度进行预测，最终获得了准确度较高的预测结果。徐潇航^[8]等采用人工神经网络、决策树与支持向量机3种回归基模型对三峡大坝的混凝土28d抗压强度进行预测，结果表明水泥用量、温度、水灰比是标签值的主要影响因素；经过参数调优后模型的预测拟合性能有所提升，Epsilon-SVR模型的预测效果最好。Shen^[9]等人采用XGBoost、AdaBoost和Bagging 3种深度学习算法构建了超高强度混凝土强度的预测模型，结果表明XGBoost模型的相关系数最高、误差最小，较其他算法更为准确。

上述单一模型对混凝土的样本数量及分布特征都具有较强的依赖性，且样本假设空间的随机性较大，样本数据的不稳定性以及空间信息利用的不充分性均可降低模型的泛化能力，导致预测效果不佳。Stacking集成学习算法是由两层学习器组成的一种融合算法，相比上述单一算法，Stacking算法泛化能力和抗过拟合能力均较强，可有效提高模型预测的准确性。目前该算法已经广泛应用于深基坑地面沉降预测^[10]、电力负荷预测^[11]、贷前风控^[12]等领域。但关于Stacking算法在HPC抗压强度预测问题中的应用鲜有报道。

基于此，本研究融合SVR、神经网络多层感知器（Multi-Layer Perceptron，MLP）、RF和极端随机树XGBoost 4种机器学习算法构建HPC抗压强度预测的Stacking集成算法，并与单个模型抗压强度的预测结果进行对比。以期获得HPC抗压强度预测的最优模型，为其抗压强度预测提供借鉴和参考。

2 实验

2.1 实验原材料

HPC的主要组成成分为水泥、水、骨料、矿物掺合料和外加剂。胶凝材料选用P·O 42.5级水泥；矿物掺合料选用F类Ⅱ级粉煤灰和S95级矿粉；粗、细骨料分别为连续粒级为5～20 mm的碎石和150～400 um的石英砂；减水剂采用聚羧酸系高效减水剂；根据规范《普通混凝土配合比设计规程》（JGJ 55-2011 ）和《高性能混凝土技术条件》（GB/T 41054-2021）进行试块制备，模具尺寸为100mm×100mm×100 mm。搅拌、振捣、养护均依据《高性能混凝土评价标准》（JGJT 385-2015 ）的评价要求进行操作，试样养护28d后拆模，实测坍落度符合实验要求。

2.2 试验方案设计

采用自带力传感系统的YAW-3000 电液伺服万能试验机对混凝土试块进行等应力速度加载。

加载过程：将试件中心对准试验机下压板中心；调整球座，使接触面受压均衡；均匀施加竖向荷载，直至试件破坏。当混凝土强度等级小于C30时，竖向加荷速度为0.3～0.5MPa/s；当混凝土强度等级大于C30时，竖向加荷速度为0.5～ 0.8MPa/s。

2.3 实验结果

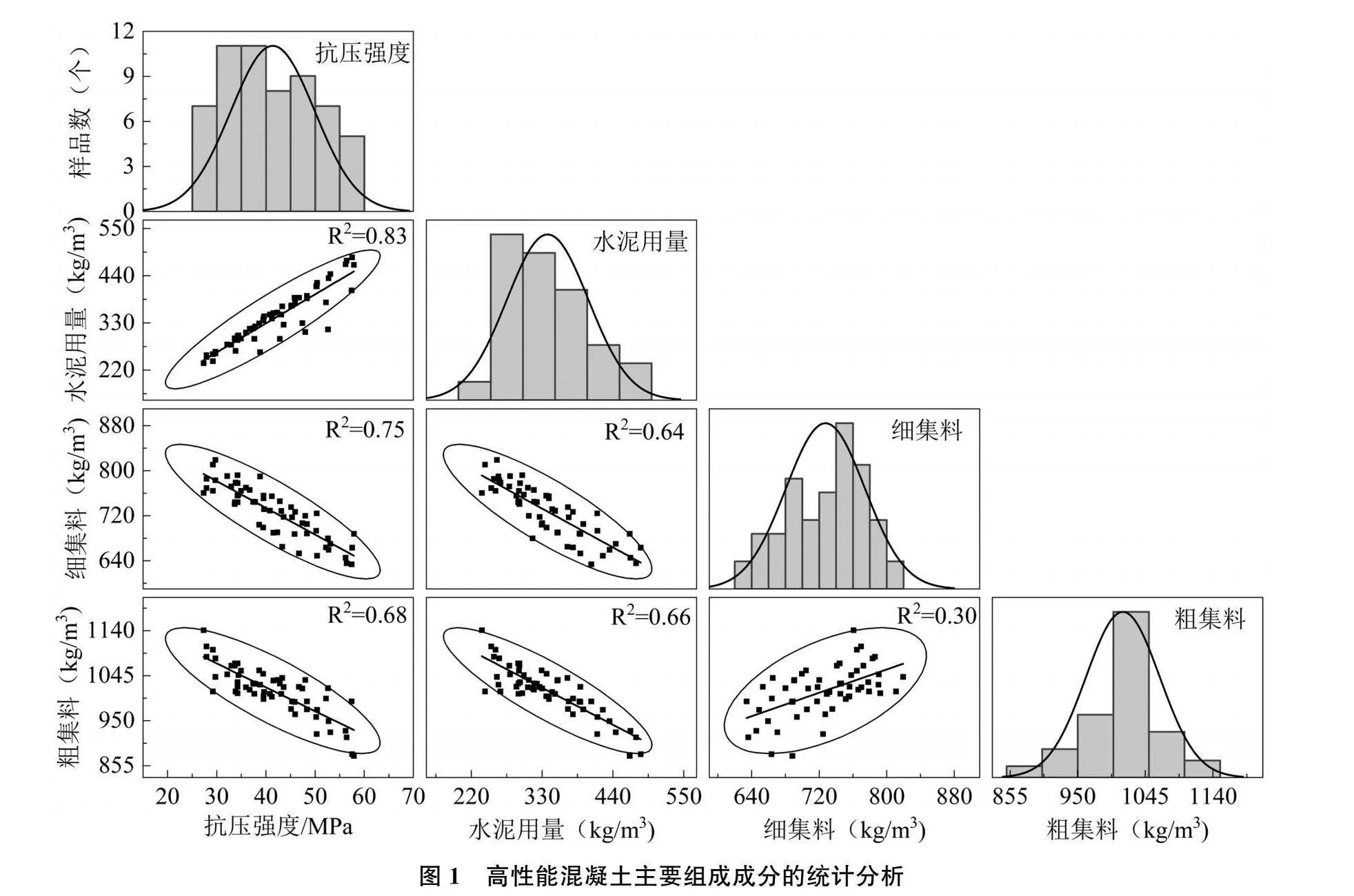
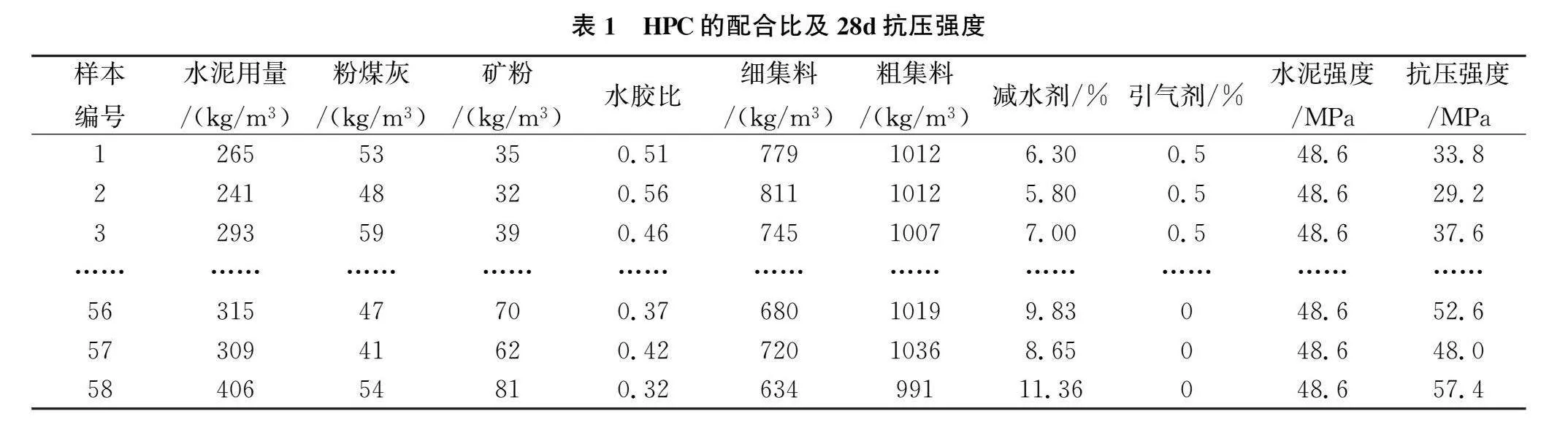
试件养护至28d龄期后进行抗压强度试验，共获得 58 组数据样本，每个样本包括9个输入相关变量，分别为水泥用量、水泥强度、粉煤灰、矿粉、水胶比、粗集料、细集料、高效减水剂、引气剂。HPC的配合比及28 d抗压强度如表1所示。为了进一步了解高性能混凝土样本数据的分布特征，对上述58组混凝土主要组成成分的实验数据进行统计分析，结果见图1。由图1可知，水泥、细集料和粗集料的取值离散度较高、分布范围广，有利于增强建模的鲁棒性和稳定性；此外，水泥、细集料和粗集料与HPC抗压强度相关性较大，相关系数R²均大于0.65，宜作为模型的输入指标。

3 HPC强度预测模型

3.1 模型构建

3.1.1 基于Stacking的集成学习模型

Stacking集成学习算法共包括两层学习器，第一层多个基学习器的输出可作为第二层元学习器的输入特征，最终由第二层输出预测结果^[10-11]。具体的训练过程如下（以4个基学习器为例）：

（1）确定第一层的基学习器M1、M2、M3、M4和第二层的元学习器M5，将数据集划分为训练集D和测试集T，且切分训练集，将训练集划分为5等份；

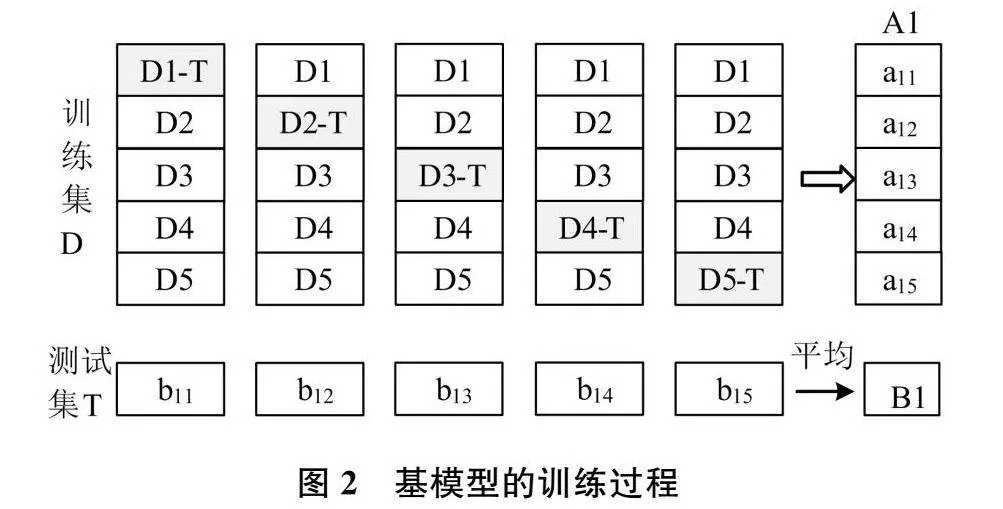
（2）依次选择训练集中的4个子数据集作为M1的训练集，剩余一个作为M1的验证集，采用5折交叉验证对M1进行训练，训练集的预测值为A1=（a11，a12，a13，a14，a15）^T，训练后的模型M1分别对测试集进行预测，预测结果为B1=Average（b11，b12，b13，b14，b15）；

（3）重复步骤2，对其他3个基学习器进行训练，得到各学习器训练集的预测值A2、A3、A4和测试集的预测值B2、B3、B4；

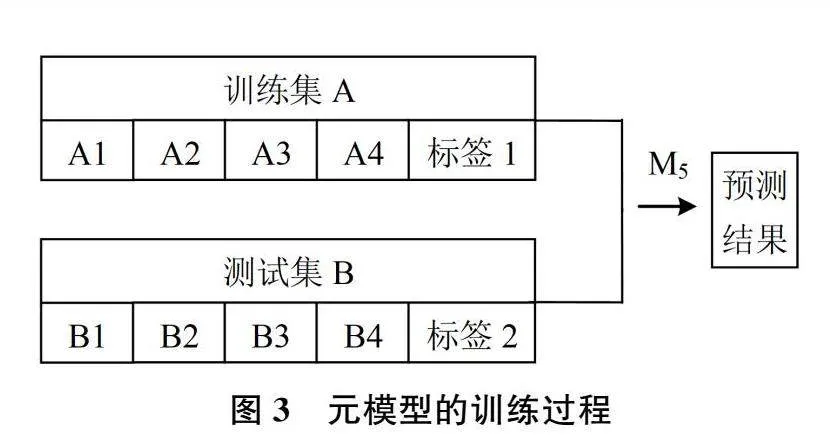
（4）以A=（A1，A2，A3，A4）作为M5训练集的输入特征，以原始训练集的标签值作为M5训练集的新标签值进行M5的训练建模，最后以B=（B1，B2，B3，B4）作为M5的测试集进行预测。基模型与元模型的训练过程如图2和图3所示。

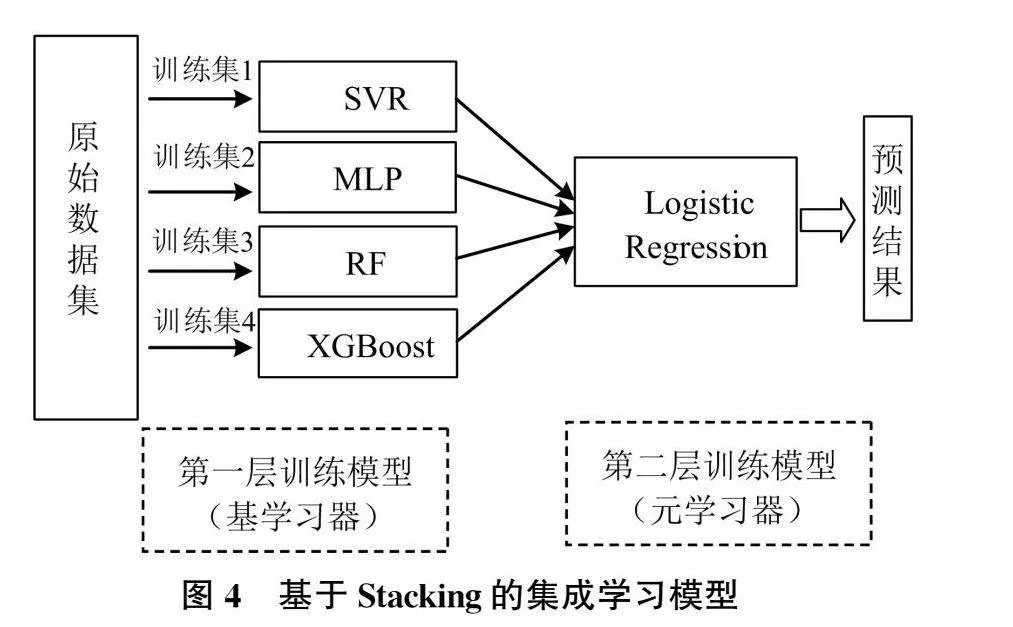
本研究采用SVR、MLP、RF和XGBoost作为Stacking算法的第一层基学习器，采用回归分析作为元学习器，Stacking 集成学习框架如下图4所示：

3.1.2 支持向量机回归模型（SVR）

SVR算法是利用核函数将低维特征空间的样本数据集映射到高维特征空间，并构建高维空间的线性决策函数从而实现数据回归^[13]。

对于样本数据集：

D=（xi，yi），i=1，2，…，n，yi∈（－1，1）

构建目标决策函数：

f（x）=w·φ（x）+b（1）

其中φ（x）为非线性变换函数。以f（x）为中心，构建一个分类间距为2∈的间隔带，训练样本落入其间隔带则预测正确。

3.1.3 神经网络多层感知器模型（MLP）

MLP的运算单元主要由输入层、隐藏层、输出层三部分组成，主要通过隐藏层和输出层的非线性激励函数对输入信息进行反复训练，实现对前一层人工神经元输入信号的加权整合，反复迭代直至算法收敛，得模型最终的阈值及权重^[14]。本次MLP建模的输入层数为9，隐藏层数为4，阈值为0.5，迭代次数达200左右。

3.1.4 随机森林模型（RF）

RF是一种改进的Bagging算法，是决策树的集成模型。Bagging 算法通过对有N个样本的原始数据集进行n次有放回抽样，每次可得到样本量为n的一个子数据集，重复K次，共获得K个独立的、同质化的训练集。对所有训练集的预测结果加权整合得到模型最终的预测值。

RF算法先通过Bootstrap自助法从原始数据集中重复抽样产生决策树的训练数据，再使用CART函数建立若干独立决策树h（X，θk），k=1，2，…，K，最终每棵决策树输出结果的均值即为RF算法的预测值^[15]。

3.1.5 极端随机树模型（XGBoost）

XGBoost是一种改进的梯度提升决策树（Gradient Boosting Decision Tree，GDBT）算法^[16]，该算法通过贪心算法进行2次循环优化，以获得每个特征增益最大的分割点以及收益最大的特征。

XGBoost模型结构：用XGBRegressor库来构建该模型，用前向分布算法对其训练集进行贪婪优化。树的最大深度为6，调学习率为0.2，最大迭代次数为50。

3.2 模型评价标准

选取相关系数（coefficient of determination，R²）、平均绝对误差（Mean Absolute Error，MAE）、平均绝对百分比误差（Mean Absolute Percentage Error，MAPE）、均方根误差（Root Mean Square Error，RMSE）作为模型的评价指标，数学表达式分别为：

R2=1－∑ni=1（yi－y′）2∑ni=1（yi－y）2，∈[0，1]（2）

MAE=1n∑ni=1y′i－yi，∈[0，+∞]（3）

MAPE=1n∑ni=1y′i－yiyi，∈[0，+∞）（4）

RMSE=1n∑ni=1（y′i－yi）2，∈[0，+∞]（5）

式中：yi为第i个试块抗压强度的实测值，y′i第i个试块抗压强度的预测值，y为试块抗压强度的平均值，i=1，2，3，…，n。

采用均方误差增量（IncMSE）评价输入特征的重要度排序。IncMSE越大，表明特征变量对预测值的影响度越大。

IncMSEi=∑ntreei=1（MSE^OOBi1－MSE^OOBi2）ntree（6）

式中MSE^OOBi1和MSE^OOBi2分别代表未受扰动和随机扰动后的袋外数据的均方误差。

4 研究结果与分析

将58 组数据样本按3∶1划分为训练集和测试集，然后将影响HPC抗压强度的相关变量及抗压强度分别作为特征值和标签值输入各模型中进行训练与验证。

4.1 变量的重要性分析和特征选择

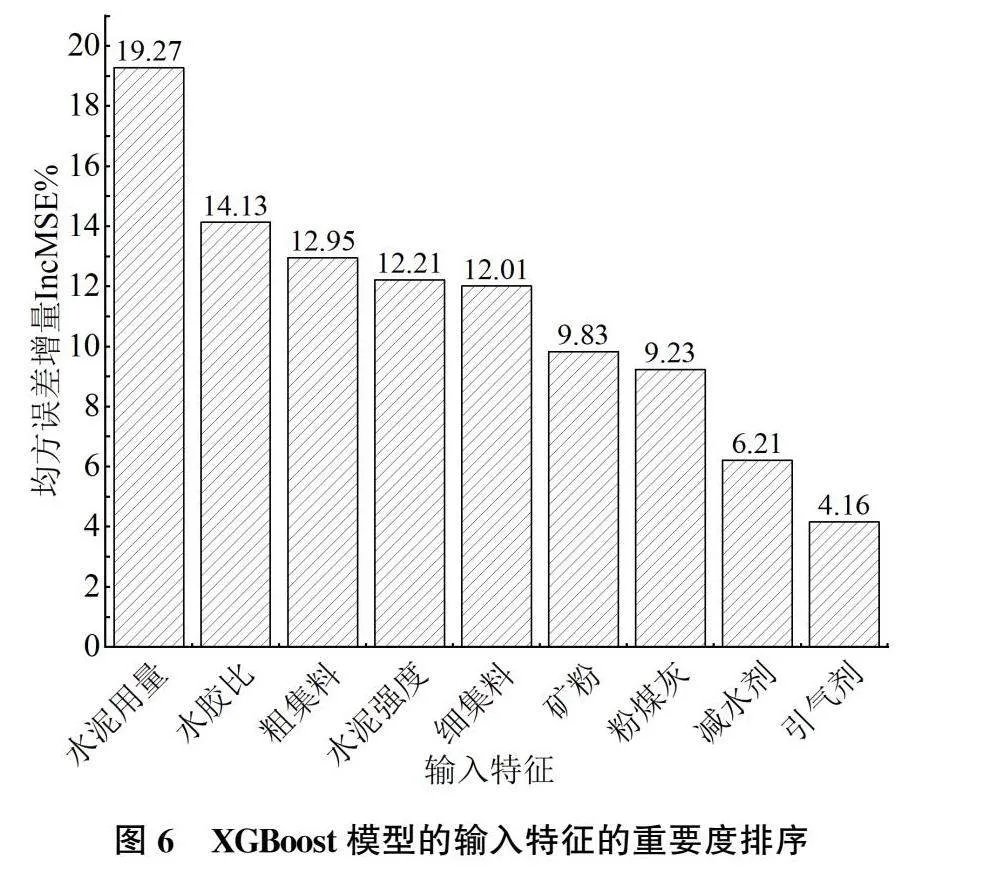
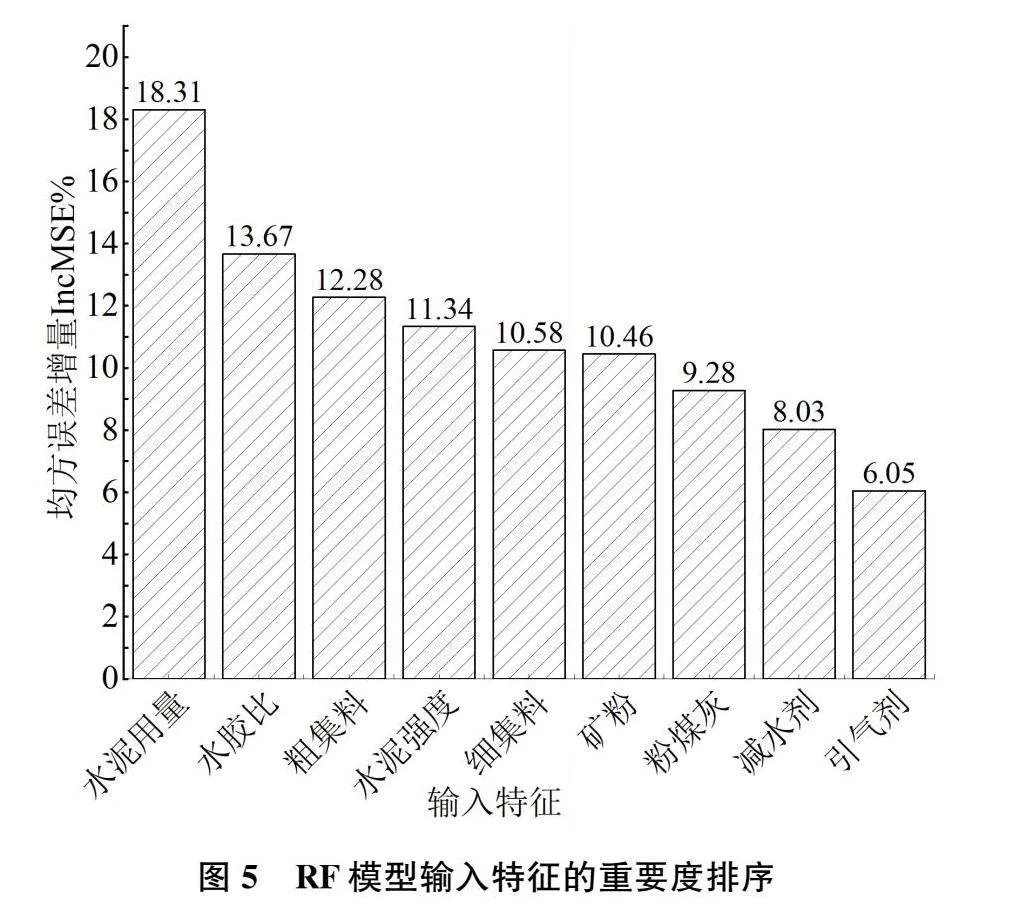
混凝土抗压强度的影响因素较多，定量分析每个特征对HPC抗压强度的重要度，剔除影响度小的输入变量，选择与HPC抗压强度相关性较高的特征变量作为模型的训练值可大幅度提高模型的预测精度和泛化能力，加快模型的运算速度。基于RF和XGBoost模型下的特征重要度排序如图5、图6所示：

由图 5、图 6可知，在RF和XGBoost模型中，水泥用量的IncMSE值均大于18%，水泥强度的IncMSE值均大于11%，说明作为混凝土的重要组成部分水泥的用量、强度与HPC抗压强度密切相关。水胶比的IncMSE值均大于13%，作为混凝土配合比的重要参数，在一定范围内水胶比越低，HPC的强度越高^[17]。粗、细集料的重要程度与水胶比基本相当。前7种指标的IncMSE值之和均大于85.5%，表明这7种特征在HPC抗压强度预测建模中起关键作用。外加剂（减水剂和引气剂）的IncMSE值均低8.5%，这是由于外加剂对HPC抗压强度的提高主要起到一定的辅助作用。故剔除减水剂和引气剂2个变量指标，保留其他7个特征作为模型的最终输入指标。

4.2 建模预测结果

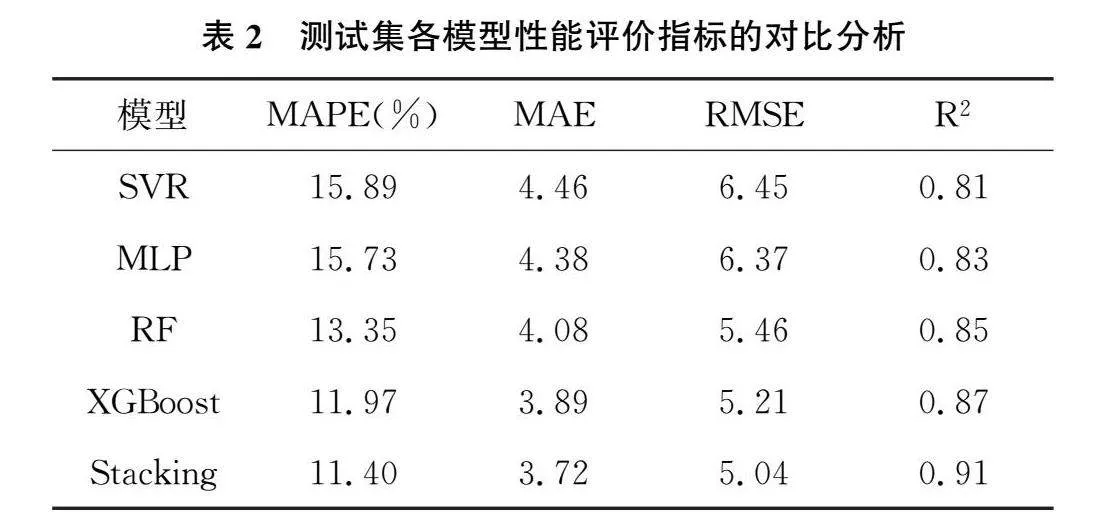
4.2.1 各模型性能评价指标的对比

测试集中各模型的性能评价指标对比分析见表2。由下表可知Stacking、XGBoost模型的MAPE、MAE及RMSE值均小于其他三种模型，相关系数R²均达0.85以上，误差较小，拟合度较高，预测效果较理想。RF预测精度仅次之，MAPE和MAE分别为13.35%和4.08。SVR、MLP模型的表现相对较差，R²值均小于0.85，且其MAPE、MAE值也较高。总体来看，Stacking集成学习模型的误差离散程度最低，相关系数最高，模型的预测性能优于单个模型。

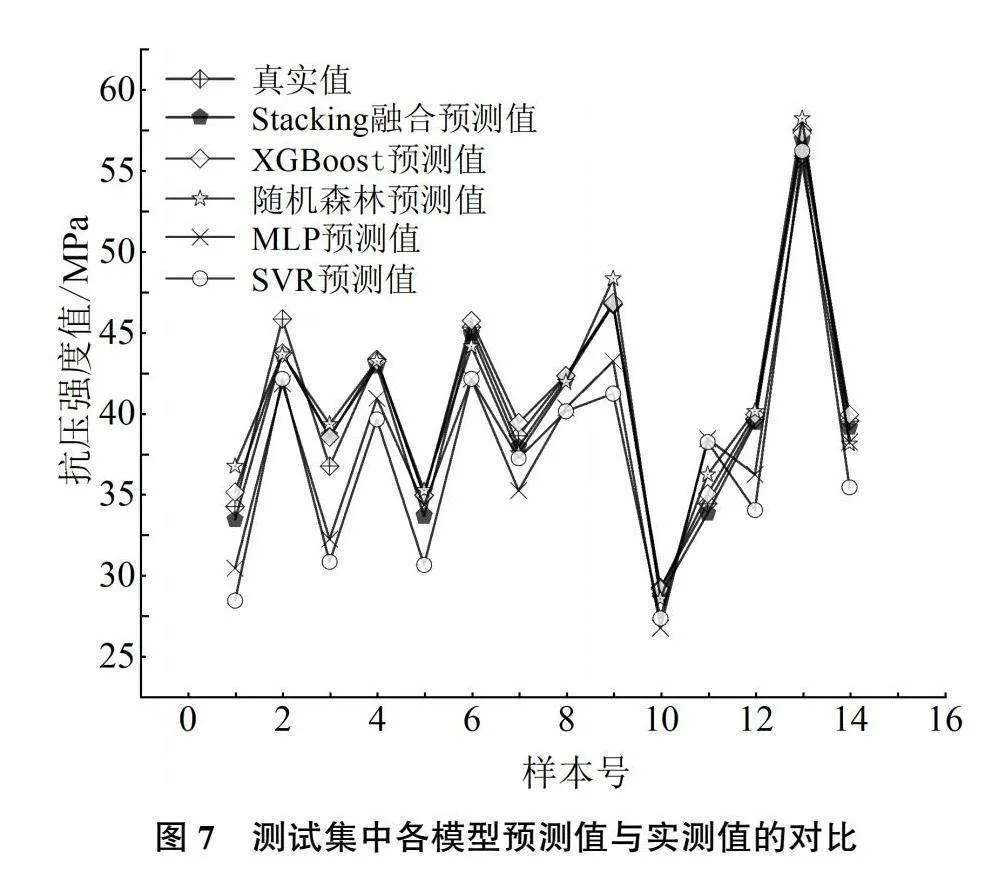
4.2.2 各模型预测值与实测值的对比

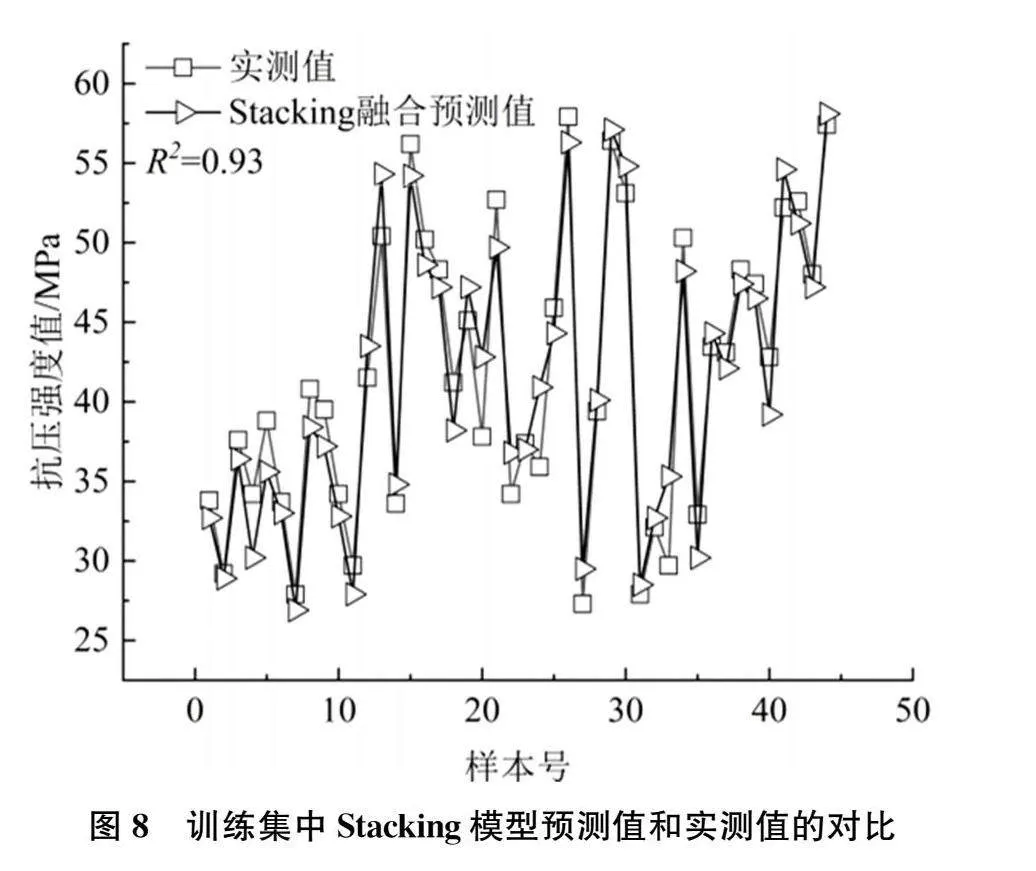
测试集中各模型对HPC抗压强度预测值与实测值的拟合效果如图7所示。MLP、SVR模型的预测值略偏离实测值，预测的实际效果略差。RF、XGBoost模型的预测值与实测值较为接近。Stacking模型的预测结果最为理想，预测值与实测值极为贴近。此外，Stacking模型在训练集中同样取得较好的表现，模型对HPC抗压强度预测值和实测值的拟合效果如图8所示。训练集中预测值和实测值也十分接近，相关系数R²达0.93，MAPE、MAE和RMSE值分别为10.60%、3.32、4.72，误差较小。综上所述，Stacking融合建模表现较好，可实现对HPC抗压强度的有效预测。

5 结论

本研究以9种可解释特征作为输入变量，共构建5种HPC抗压强度预测模型，结果表明，水泥用量、水泥强度、水胶比、粗、细集料、粉煤灰、矿粉7种特征是HPC抗压强度的主要影响因素。RF、XGBoost、Stacking 3种机器学习算法

对HPC抗压强度预测的表现均较好，利用机器学习算法对HPC抗压强度进行预测具有可行性。对比5种模型对HPC强度预测的结果，Stacking集成学习模型的MAPE、MAE值最小，预测值与实测值最贴近，对HPC强度的预测表现出更好的适应性和优越性，可准确预测HPC抗压强度。

6 展望

本研究仅考虑9种变量对HPC抗压强度的影响，在后续的研究中可将表观密度、坍落度、实验龄期、温度等因素纳入特征范围内，以进一步提高模型对HPC抗压强度的预测精度，为今后的实际生产提供有效的理论指导，有效保障混凝土工程的进度、质量、安全。

［参 考 文 献］

［1］

住房和城乡建设部标准定额司，工业和信息化部原材料工业司.高性能混凝土应用技术指南[M].北京：中国建筑工业出版社，2015：1-4.

[2] 惠勇.浅谈高性能混凝土在高原寒旱地区的施工质量控制[J]. 兰州交通大学学报，2015，34（3）：10-14.

[3] 赵嵩颖，王梦娜，陈雷.神经网络下能量桩桩基混凝土强度及导热预测[J].混凝土，2023（7）：24-27.

[4] 陈浩，刘荣桂，闫乾勋.基于GA-BP神经网络的SAP内养护机制砂混凝土抗压强度预测[J].混凝土，2023（5）：72-76.

[5] PHAM A D，HOANG N D，NGUYEN Q T.Predicting compressive strength of high-performance concrete using metaheuristic-optimized least squares support vector regression[J].Journal of Computing in Civil Engineering， 2016，30（3）：06015002.

[6] CUI X N，WANG Q C，DAI J P，et al.Intelligent crack detection based on attention mechanism in convolution neural network[J].Advances in Structural Engineering，2021，24（9）：1859-1868.

[7] CHUN P J，UJIKE I，MISHIMA K，et al.Random forest-based evaluation technique for internal damage in reinforced concrete featuring multiple nondestructive testing results[J].Construction and Building Materials，2020，253：119238.

[8] 徐潇航，胡张莉，刘加平，等.基于机器学习回归模型的三峡大坝混凝土强度预测[J].材料导报，2023，37（2）：22010068.

[9] SHEN Z J，DEIFALLA A F，KAMINSKI P，et al.Compressive streng the valuation of ultra-high-strength concrete by machine learning[J].Materials，2022，15（10）：3523.

[10] 秦胜伍，张延庆，张领帅，等.基于Stacking模型融合的深基坑地面沉降预测[J].吉林大学学报（地球科学版），2021，51（5）：1316-1323.

[11] 史佳琪，张建华.基于多模型融合Stacking集成学习方式的负荷预测方法[J].中国电机工程学报，2019，39（14）：4032-4041.

[12] 刘允.基于不平衡样本下Stacking集成方法的贷前风控研究[D].武汉：华中师范大学，2022：37-50.

[13] 卢纯义，于津，余忠东，等.基于改进灰狼算法优化SVR的混凝土中钢筋直径检测方法[J].计算机科学，2022，49（11）：228-233.

[14] 陈湘州， 陶李红. 基于MLP神经网络的中小企业供应链金融信用风险评估[J]. 湖南科技大学学报（自然科学版），2021，36 （4）：91-99.

[15] 吴贤国，刘鹏程，陈虹宇，等.基于随机森林的高性能混凝土抗压强度预测[J].混凝土， 2022（1）：17-24.

[16] 赵楠，卢毅敏.基于XGBoost算法的近地面臭氧浓度遥感估算[J].环境科学学报，2022，42（5）：95-108.

[17] 王利红.高性能混凝土配合比的优化设计[D].济南：山东大学，2014：8-9+33.

Prediction of High Performance Concrete Compressive Strength based on Stacking

Xu Ling， Jing Nan， Shi Guang， Guo Zhilong， Jing Xiangnan， Yuan Rui

Abstract： In order to achieve rapid and accurate prediction of the compressive strength of high performance concrete （HPC），the study is based on the dataset of 58 HPC mix proportions ， utilizing Stacking ensemble learning model with nine interpretable features as input variables to predict the compressive" strength of" HPC compared with the other four single models.The results showed that compared with the traditional base models，the Stacking ensemble learning model had the smallest error values and the largest determination coefficient . The mean absolute percentage error， mean absolute error， root mean square error and correlation coefficients for compressive strength prediction of the high performance concrete" were 11.40%、3.72、5.04、0.91， respectively， The proposed model had higher accuracy in predicting HPC compressive strength.

Key words：high performance concrete; compressive strength; base model; Stacking

责任编辑：陈星宇