基于神经网络的永磁同步电机模型预测电流控制
2024-12-03李耀华刘东梅陈桂鑫刘子焜王孝宇童瑞齐
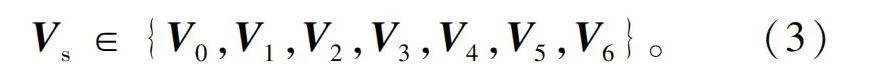

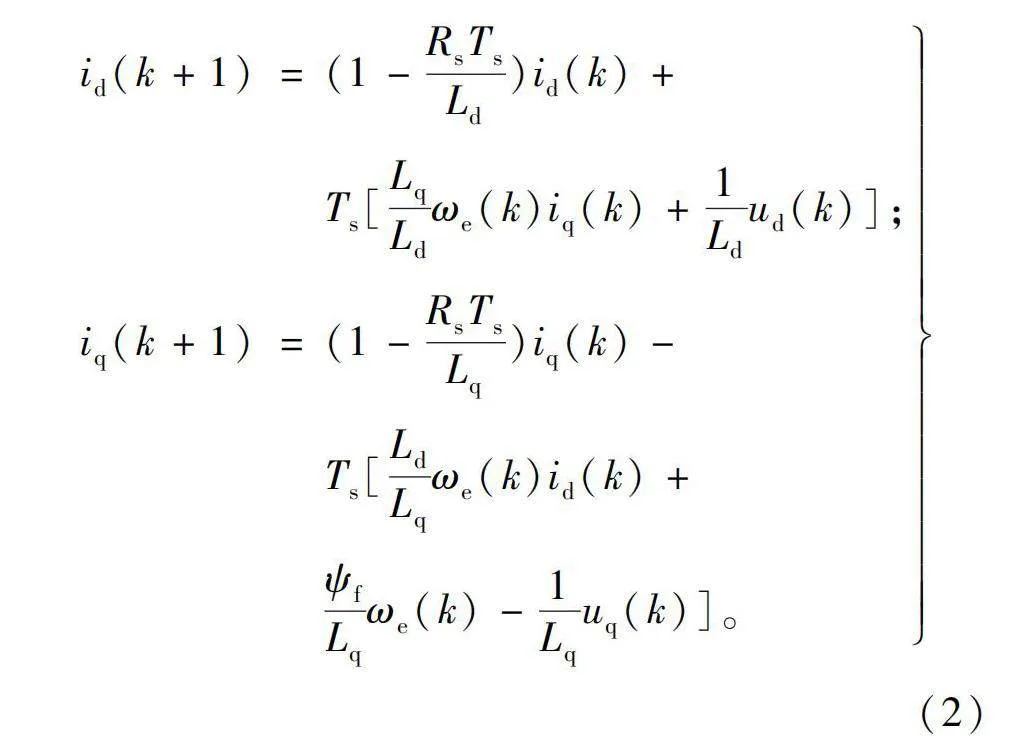
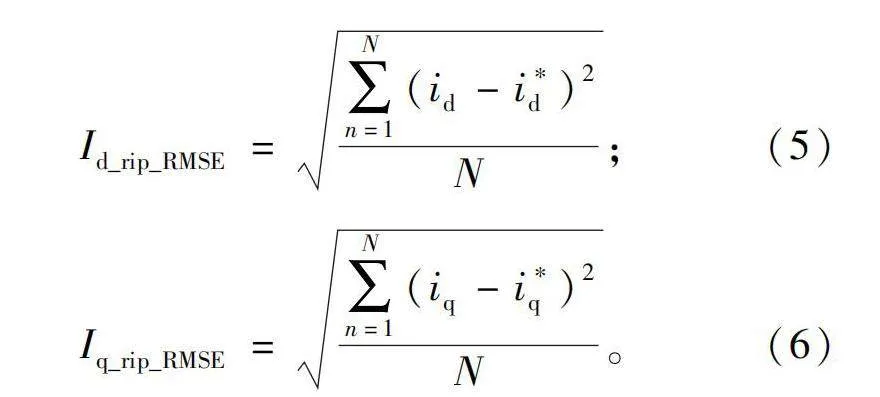
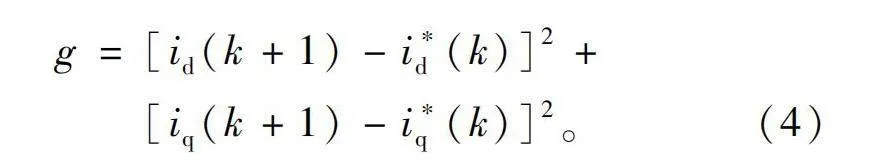
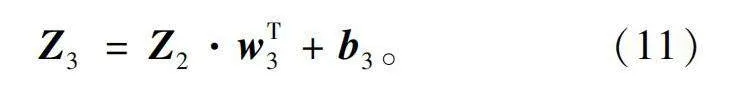
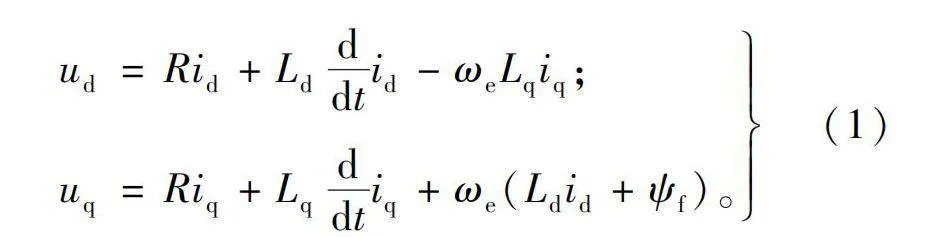
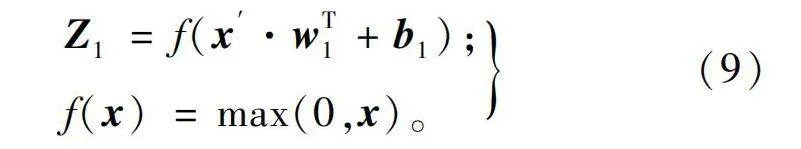
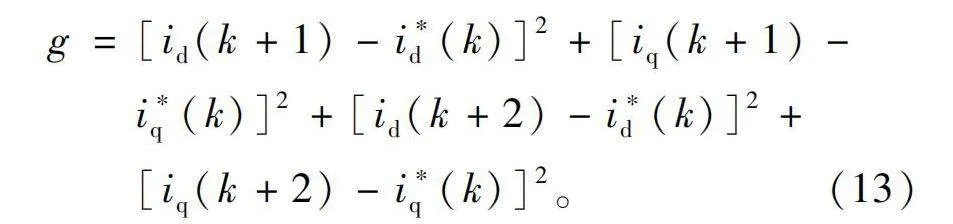


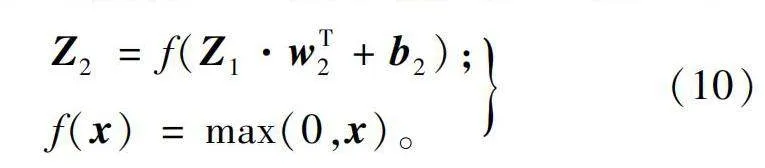
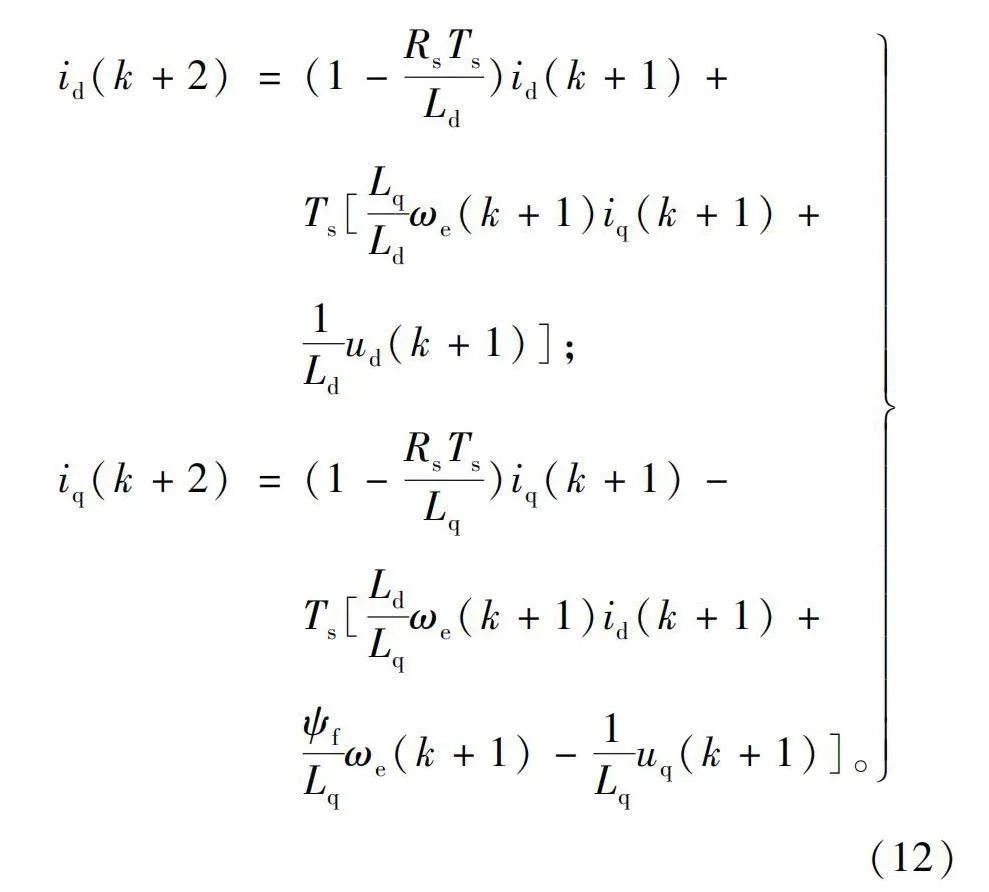
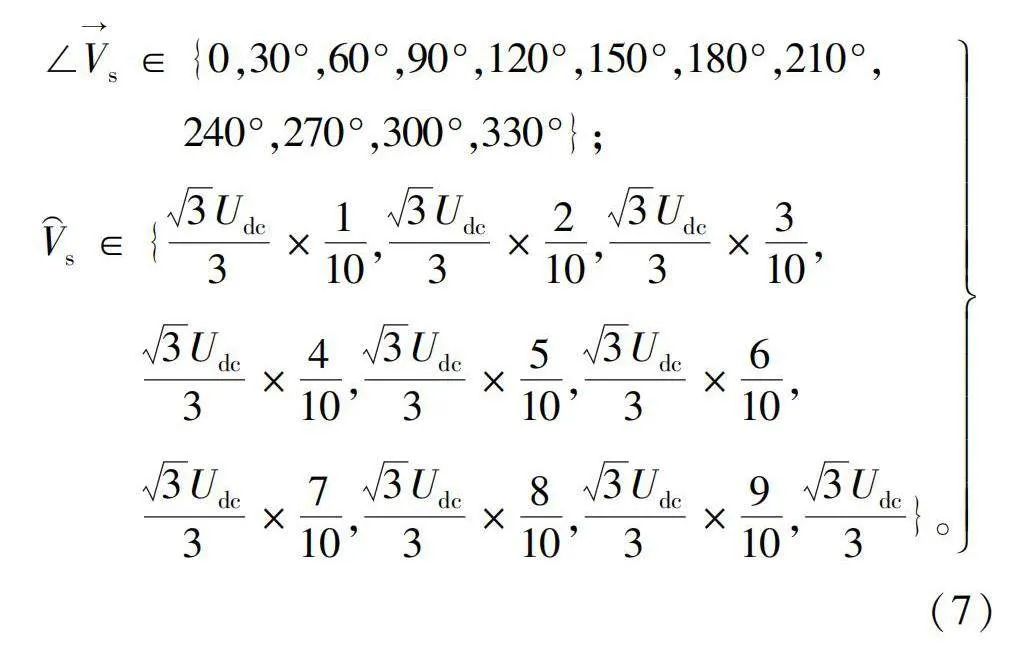
摘 要:针对备选电压矢量有限导致永磁同步电机有限集模型预测电流控制性能较差及计算量较大的问题,提出基于神经网络的永磁同步电机模型预测电流控制。基于7个基本电压矢量和121个扩展电压矢量的永磁同步电机模型预测电流控制分别建立7分类和121分类神经网络。随着备选电压矢量的增加,模型预测电流控制性能提升,对应的神经网络控制性能也得到改善,但分类任务数也随之增加。对于多步模型预测控制,计算量随步长呈指数上升,但输出电压矢量不变。因此,基于两步模型预测电流控制建立7分类神经网络。仿真结果表明:以上神经网络控制均可行,性能与相对应的模型预测电流控制基本相当。实时性实验结果表明相较于单步模型预测电流控制,神经网络控制并不占优势,但相较于两步模型预测电流控制,神经网络实时性有明显优势,计算耗时减小29.58%,表明神经网络控制更适于多步模型预测电流控制。
关键词:永磁同步电机;模型预测电流控制;神经网络;备选电压矢量;实时性;多步预测
DOI:10.15938/j.emc.2024.10.011
中图分类号:TM351
文献标志码:A
文章编号:1007-449X(2024)10-0109-14
收稿日期: 2023-01-03
基金项目:陕西省自然科学基金(2021JM-163);西安市碑林区科技计划项目(GX2252)
作者简介:
李耀华(1980—),男,博士,副教授,研究方向为电机电控与新能源汽车技术;
刘东梅(1997—),女,硕士研究生,研究方向为新能源汽车电机电控;
陈桂鑫(1997—),男,硕士研究生,研究方向为新能源汽车电机电控;
刘子焜(1997—),男,硕士研究生,研究方向为新能源汽车电机电控;
王孝宇(1997—),男,硕士研究生,研究方向为新能源汽车电机电控;
童瑞齐(1999—),男,硕士研究生,研究方向为新能源汽车电机电控。
通信作者:李耀华
Neural-network-based model predictive current control for permanent magnet synchronous motor
LI Yaohua, LIU Dongmei, CHEN Guixin, LIU Zikun, WANG Xiaoyu, TONG Ruiqi
(School of Automobile,Chang’an University, Xi’an 710064, China)
Abstract:Aiming at the problems of poor performance of finite-control-ser model predictive current control (MPCC) for permanent magnet synchronous motor (PMSM) caused by limited candidate voltage vectors and large calculation burden, a neural-network-based MPCC for PMSM was proposed. Based on the MPCC for PMSM with 7 basic voltage vectors and 121 extended candidate voltage vectors, the neural networks with 7 and 121 classification tasks were established. With the increase in candidate voltage vectors, the control performances of MPCC and the corresponding neural network were improved, but classification tasks were increased, too. For multi-step control, calculation burden will increase exponentially with the increase of steps, but output voltage vectors will not change. Therefore, a neural-network with 7 classification tasks was established based on two-step MPCC. Simulation results show all proposed neural networks operate well. And neural networks’ control performances are almost the same as the corresponding MPCC. Real-time experiments show that compared with one-step MPCC, the real-time performance of neural network is worse. But compared with two-step MPCC, the real-time performance of neural network is better and its calculation time is decreased by 29.58%. Thus, neural network is more suitable for multi-step MPCC.
Keywords:permanent magnet synchronous motor; model predictive current control; neural network; candidate voltage vectors; real-time performance; multi-step prediction
0 引 言
有限控制集模型预测控制(finite control set-model predictive control, FCS-MPC)遍历逆变器所有可能开关状态,代入至预测模型计算变量的预测值,并通过反映控制性能的成本函数输出令成本函数最小的开关状态,近年来在电力电子与电力传动领域得到高度关注[1-5]。
模型预测控制需要遍历所有备选开关状态,导致计算量大和实时性差[6]。对于采用空间矢量调制拓展备选电压矢量集合、多电平逆变器或矩阵变换器供电的系统及多步预测系统,这一问题更为严重[7-11]。文献[12-16]分别从精简备选电压矢量个数、简化预测模型、采用无差拍控制改变模型预测控制形式及硬件提升等角度提高系统实时性。
近年来,随着人工智能技术的高速发展,其在电机控制领域得到广泛应用[17]。神经网络(neural network)通过对数据学习和训练,可逼近复杂的非线性映射关系,具有快速大量运算能力和线上推理速度,具有一定的实时性优势[18]。文献[19-21]将神经网络用于电机参数在线辨识、无差拍控制规律替代和模型预测控制的成本函数参数确定。有限状态集模型预测控制基于成本函数在备选电压集合中选择最优矢量,可将其视为非线性映射的多分类任务,采用数据驱动的思想,建立并训练神经网络去学习多任务分类规律。当网络训练成熟后,可采用神经网络取代原有的模型预测控制策略。文献[22]采用神经网络取代三相逆变器原有的模型预测控制策略。文献[23]采用深度神经网络代替模型预测转矩控制策略,验证神经网络代替原有模型预测控制用于驱动电机的可行性。为解决神经网络控制出现的失控问题,文献[24-25]分别提出基于直接转矩控制切换策略和混合决策策略。以上研究验证神经网络可取代单步模型预测控制,但并未对比神经网络和原有模型预测控制的实时性。
本文建立永磁同步电机模型预测电流控制系统,采用空间矢量调制拓展备选电压矢量至性能饱和,建立和训练基于7个基本电压矢量和121个拓展电压矢量单步模型预测电流控制及两步模型预测电流控制的神经网络,验证神经网络代替两步模型预测电流控制的可行性,并实验对比神经网络控制与模型预测电流控制的实时性。
1 永磁同步电机模型预测电流控制
转子旋转坐标坐标系下,永磁同步电机数学模型为:
ud=Rid+Ldddtid-ωeLqiq;
uq=Riq+Lqddtiq+ωe(Ldid+ψf)。(1)
其中:ud和uq为电机dq轴定子电压;id和iq为电机dq轴定子电流;Rs为电机定子电阻;Ld和Lq为电机定子dq轴电感;ωe为转子电角速度;ψf为转子永磁体。
基于一阶前向欧拉法将式(1)离散化,可得到下一时刻定子d轴和q轴电流的预测模型,即:
id(k+1)=(1-RsTsLd)id(k)+
Ts[LqLdωe(k)iq(k)+1Ldud(k)];
iq(k+1)=(1-RsTsLq)iq(k)-
Ts[LdLqωe(k)id(k)+ψfLqωe(k)-1Lquq(k)]。(2)
将下式所示的备选电压矢量遍历代入至式(2),则可得到下一时刻的预测电流。备选电压矢量,其中零电压矢量V0可由开关状态000或111生成,具体以开关次数最小原则选择[26],即
Vs∈{V0,V1,V2,V3,V4,V5,V6}。(3)
定义成本函数为
g=[id(k+1)-i*d(k)]2+[iq(k+1)-i*q(k)]2。(4)
其中由于采样时间很短,近似认为当前时刻的参考值与未来时刻的参考值相同。
将下一时刻预测电流代入至成本函数,并选择令成本函数最小的电压矢量输出,从而实现永磁同步电机无模型预测电流控制。
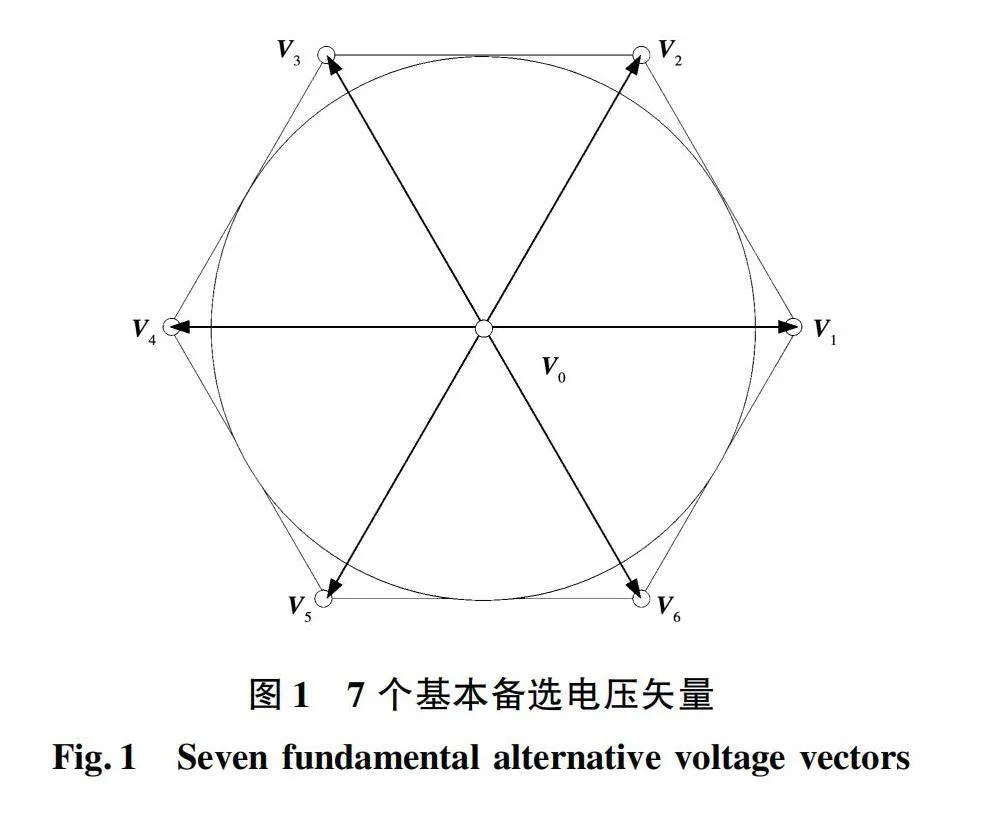
逆变器可产生7个基本电压矢量,如图1所示。为了提升系统控制性能,可对备选电压矢量进行扩展,通过空间矢量调制生成更多的备选电压矢量[27]。
理论上,备选电压矢量可为图1所示的六边形内任意点,并且备选电压矢量越多,模型预测控制所选择的电压矢量越优,系统控制性能也越好。通过角度和幅值拓展备选电压矢量集合,可使得备选电压矢量在六边形尽可能密集均匀分布。当电压矢量密度达到一定数量时,则可认为此时选择得到的局部最优解近似为全局最优解,即电压矢量数量达到饱和。此时,再增大电压矢量数量,对性能的提升极为有限,达到饱和。
为确定达到饱和的备选电压矢量,从电压矢量的角度和幅值2个维度对电压矢量六边形进行切分。为了便于计算,将切分平面缩小为电压矢量六边形的内切圆。将电压矢量幅值[0,3Udc/3]进行x等分,将角度[0, 360°]进行y等分,再加上零电压矢量,则可得到(xy+1)个备选电压矢量。
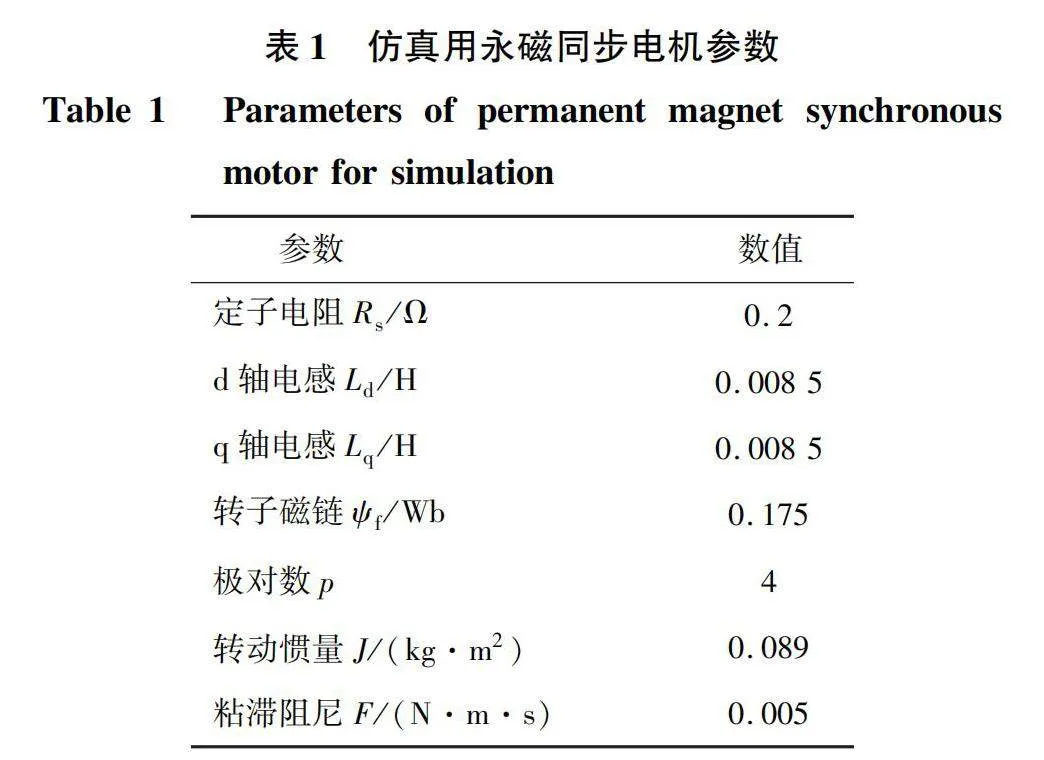
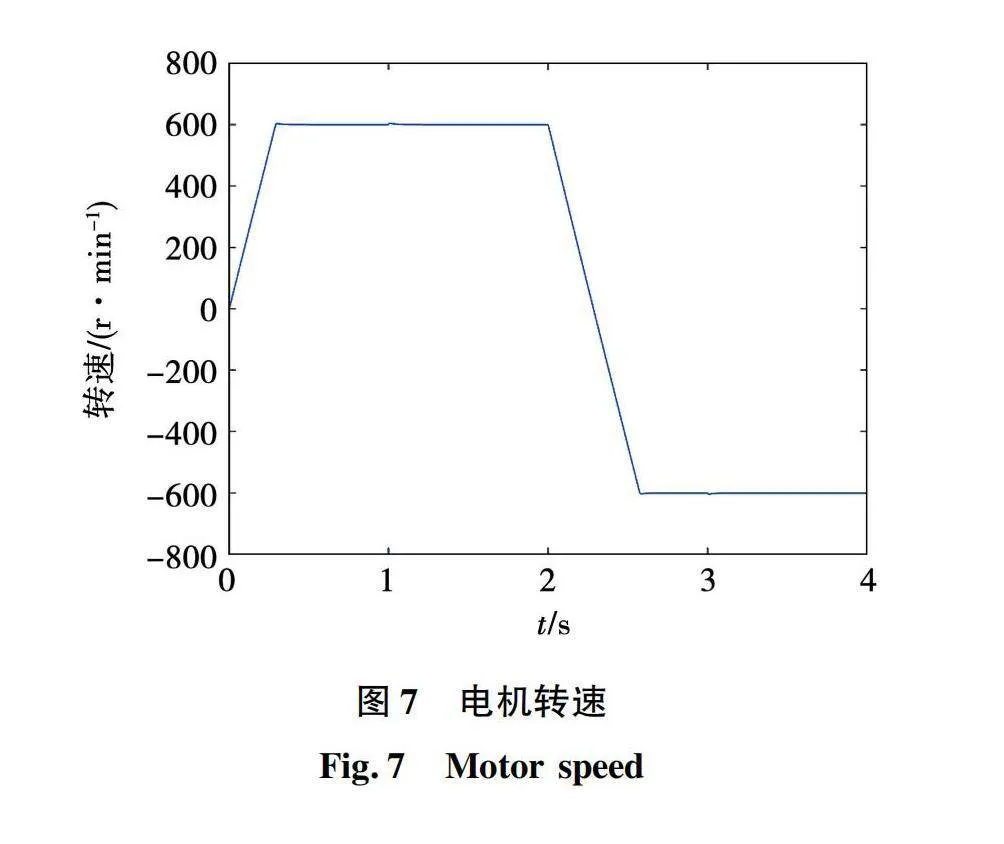
基于MATLAB/Simulink建立永磁同步电机模型预测电流控制系统仿真模型。仿真模型为离散模型,采样周期为5×10-5 s。直流母线电压为312 V。仿真条件设置如下:参考转速初始为600 r/min,2 s时阶跃为-600 r/min,负载转矩初始为12 N·m,1 s时阶跃至-12 N·m,3 s时阶跃至12 N·m。仿真总时长为4 s。仿真用永磁同步电机参数如表1所示。
定义定子d轴和q轴电流脉动均方根误差(root mean square error,RMSE)为:
其中N为采样点个数。
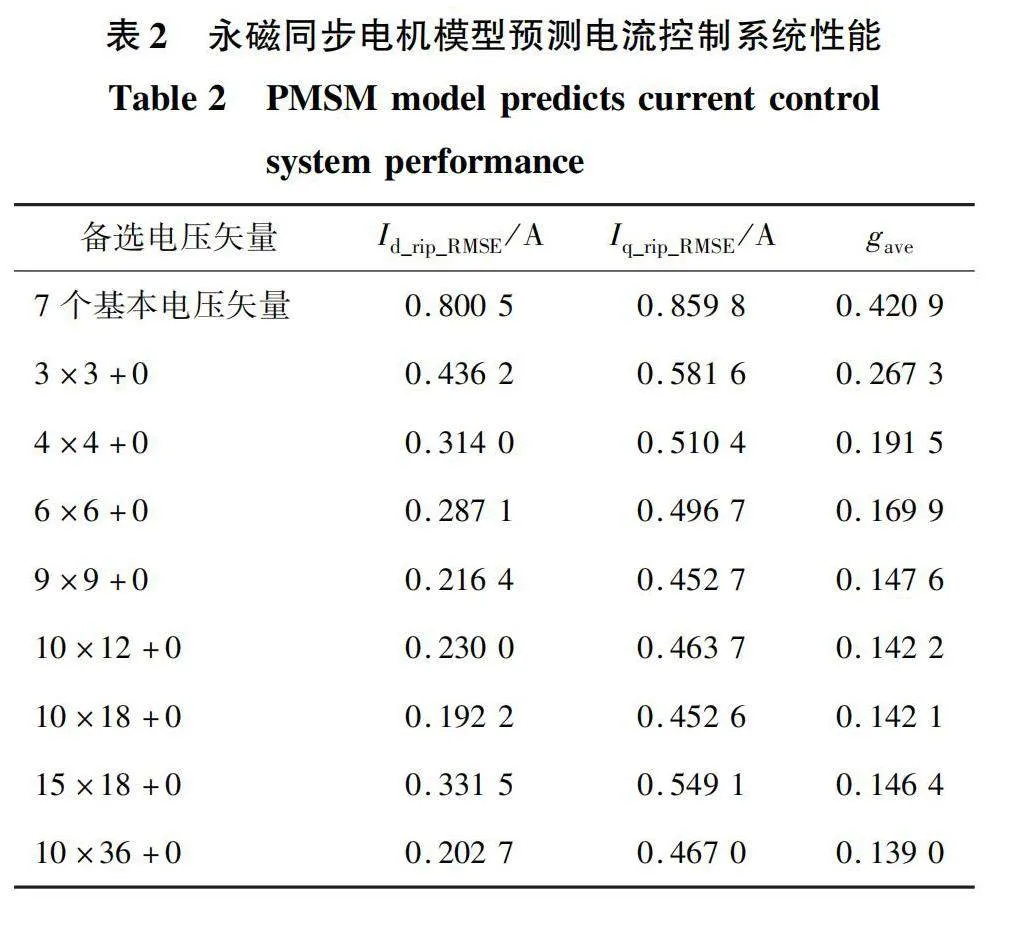
7个基本电压矢量和不同等分方式下,永磁同步电机模型预测电流控制系统性能如表2所示,其中(3×3+0)表示将幅值3等分、角度3等分得到的9个备选电压矢量再加上零电压矢量组成的备选电压矢量集,gave为预测成本函数的平均值。
随着备选电压矢量数量的增大,系统控制性能得到优化,但当备选电压矢量分布程度达到一定密度时,理想电压矢量距离备选电压矢量距离趋近为0,性能提升变缓,趋于饱和。此时,备选电压矢量数量的增加对系统性能的提升影响较小。表2中的数据也验证了这一理论规律。
由表2可知,将幅值[0,3Udc/3]进行10等分,将角度[0,360°]进行12等分,再加上零电压矢量的方式,系统性能饱和。此时,共计121个备选电压矢量,平面布局如图2所示,其中120个非零电压的角度和幅值为:
2 基于神经网络的模型预测电流控制
永磁同步电机模型预测电流控制根据成本函数从备选电压矢量中选择最优电压矢量,将该过程视为一个非线性映射下的多分类任务。因此,可以基于数据驱动建立和训练神经网络来学习并逼近该多任务分类规律,从而替代模型预测电流控制。
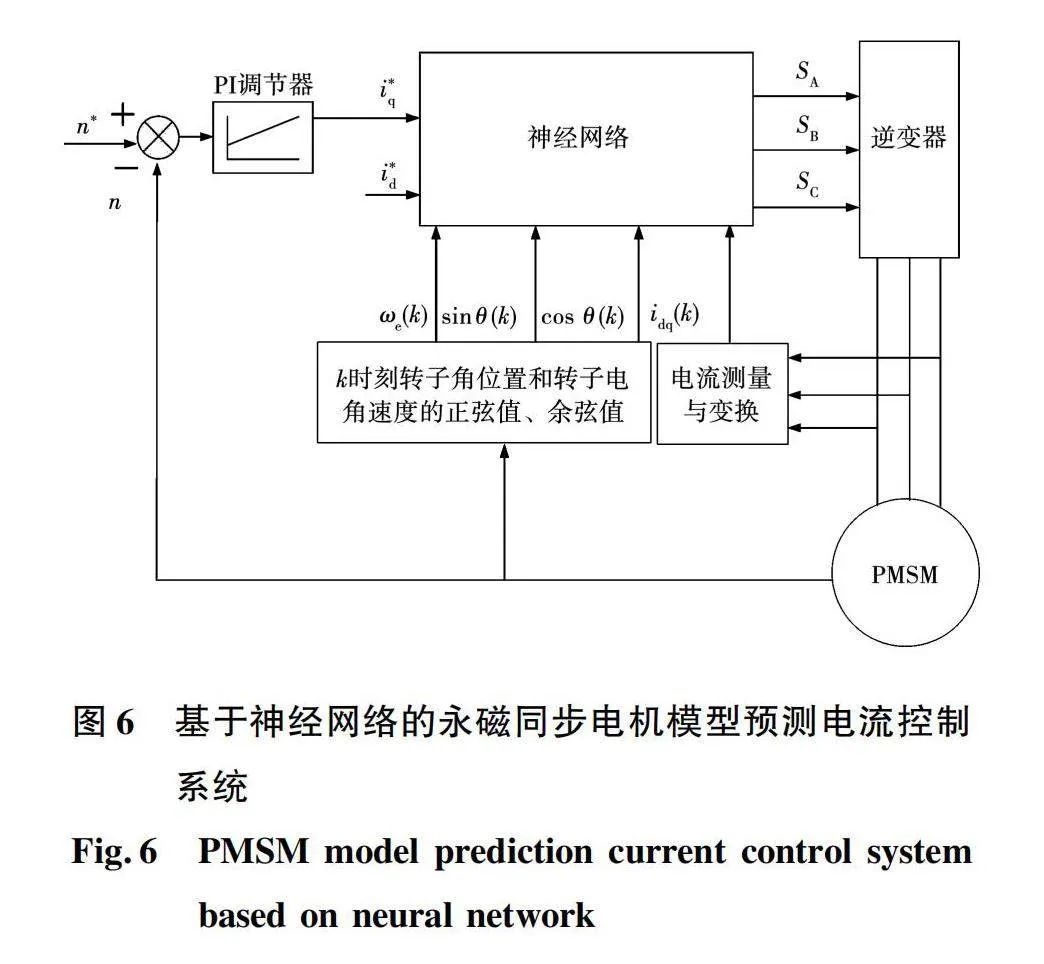
根据模型预测电流控制的预测模型和成本函数,选取k时刻的q轴参考电流、d轴电流和q轴电流、电角速度及转子坐标系d轴与静止坐标系α轴的夹角的正弦值和余弦值这6个数据作为神经网络的输入,神经网络输出为备选电压矢量之一。
2.1 7分类神经网络
神经网络学习基于7个基本电压矢量的模型预测电流控制分类规律,分类任务数为7。基于上文仿真模型收集训练数据集,实验条件如下:设置参考转速分别保持-500、-400、-300、-200、-100、100、200、300、400和500 r/min恒定,在每种参考转速设置下分别设置负载转矩为-30、-25、-20、-15、-10、-5、5、10、15、20、25和30 N·m,每次实验仿真时间均设置为1 s,共进行120组实验。删去重复的数据,共得到2 057 439组包含6个输入特征和1个输出量的运行训练数据。
由于收集到的训练数据包含的6个特征并不属于同一量纲,训练样本在梯度下降的过程中容易受到数量级较大数据的影响,从而影响训练效率和效果,导致训练时间过长甚至无法收敛。因此,需对数据进行标准化处理,即
x′=x-x-S。(8)
其中x-为特征均值,S为特征标准差,均为数据自身决定的定值。标准化后的数据按照95∶5比例随机划分为训练集和测试集。
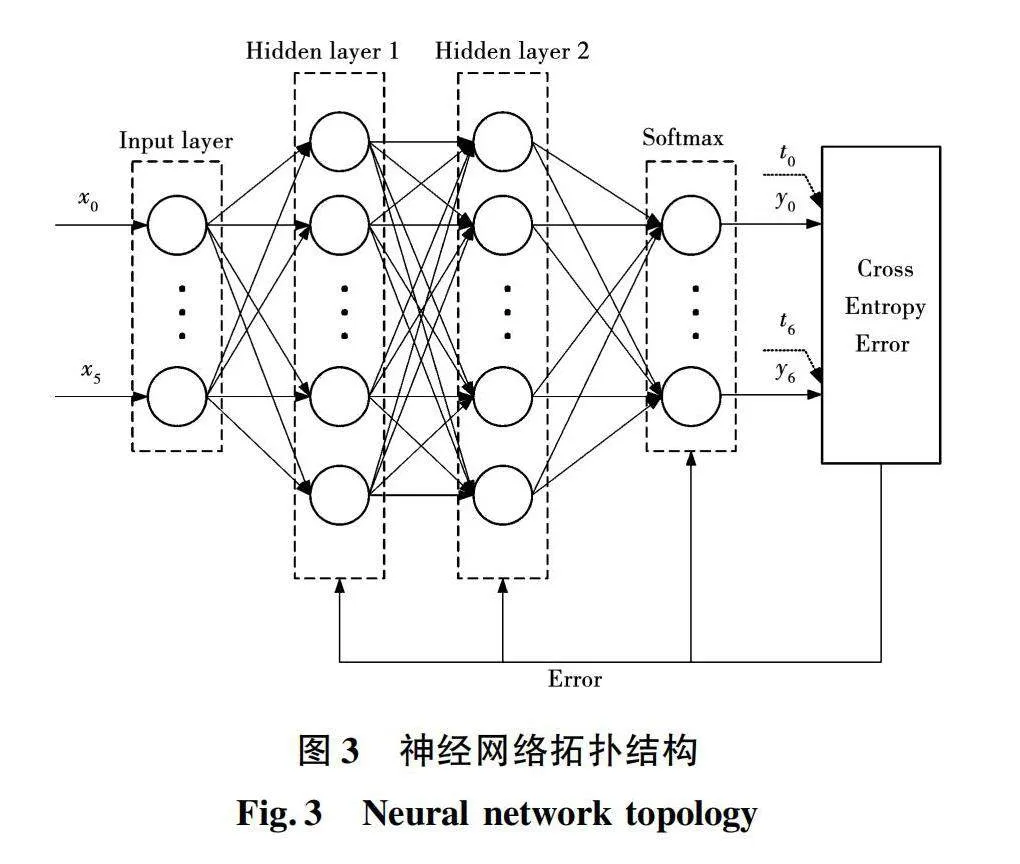
神经网络采用2个隐藏层的网络结构,输入层、隐藏层一、隐藏层二和输出层各层神经元数目分别为6、10、15和7,网络拓扑结构如图3所示,其中神经元激活函数选择ReLU函数,损失函数选择交叉熵函数,迭代优化器选择Adam,各个层的连接权重和偏重的初始值采用随机生成,学习率设置为0.01,设置训练次数为100个epoch,其中batch size设置为3 000。
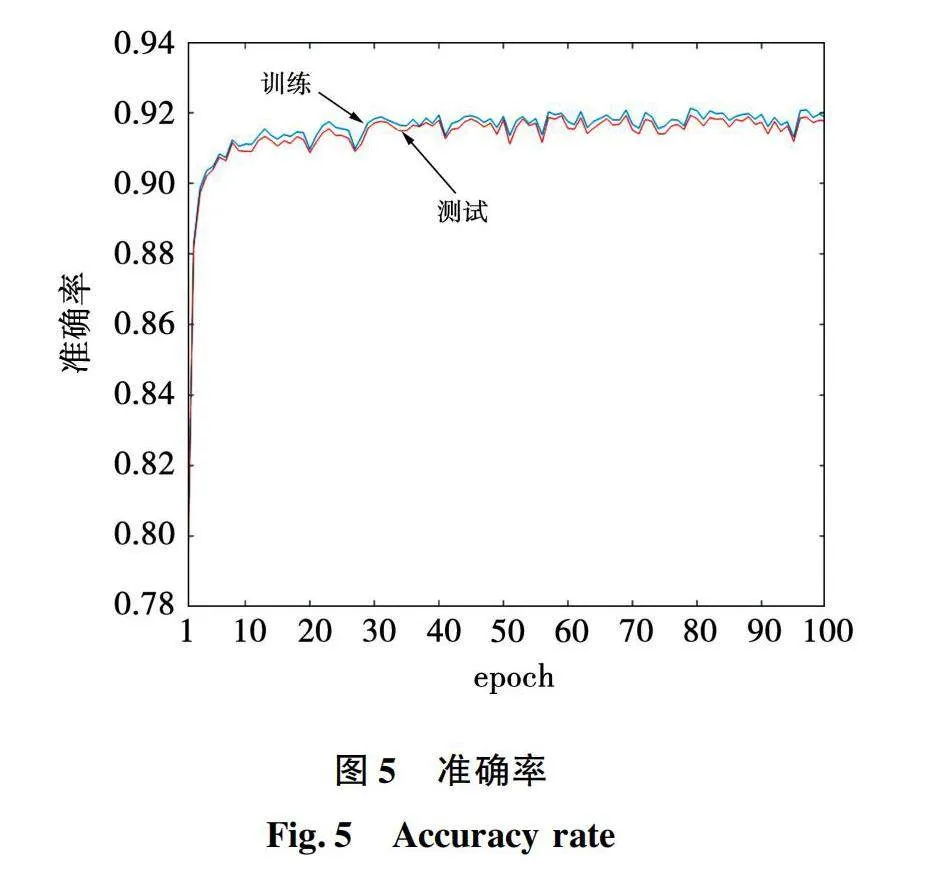
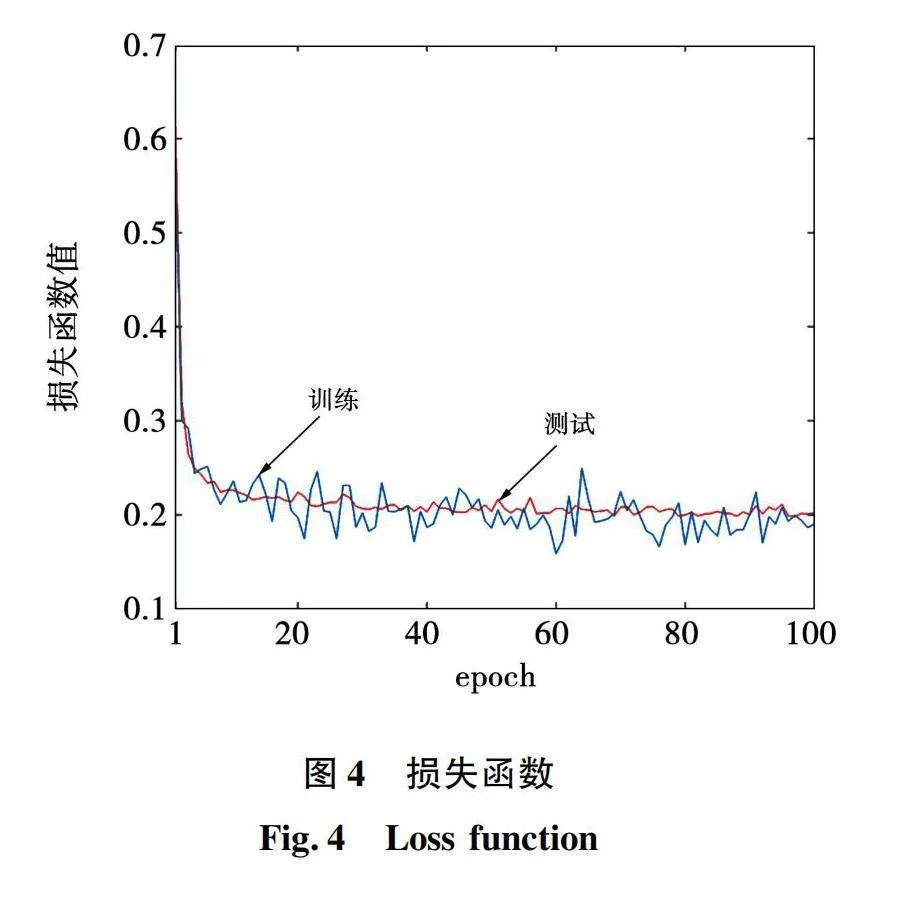
通过重复前向推理和误差反向传播过程,网络参数迭代更新,损失函数值随之减小,神经网络也逐步逼近模型预测电流的分类规律。经过100次训练,神经网络训练结果如图4和图5所示。
图4和图5表明随着训练过程的进行,损失函数值随之减小,训练集和测试集的准确率同步上升并稳定,同时无明显过拟合和欠拟合现象,网络在未知新样本上的分类性能和可用性得到保障。经过100个epoch的训练,训练集和测试集的准确率均接近92%,说明神经网络的分类性能较好,较充分逼近模型预测电流控制的电压矢量分类规律。
将训练成熟的神经网络取代原有的模型预测电流控制,即可实现基于神经网络的永磁同步电机模型预测电流控制系统,如图6所示,其中神经网络输入为特征工程的6个变量,输出为施加的电压矢量。当神经网络训练成熟时,网络的权重和偏置等参数已经整定完毕。运行过程中,神经网络仅需执行前向推理过程即可得到所需的电压矢量。在前向推理之前,输入信号需要标准化处理,标准化的参数使用训练集的均值与标准差参数。
采用Python和Simulink建立基于神经网络的永磁同步电机模型预测电流控制系统联合仿真模型,其中Python接受来自Simulink的特征工程输入,运行神经网络,并将神经网络确定的电压矢量输入给Simulink模型,Simulink模型施加神经网络确定的电压矢量,产生特征工程下一时刻的输入。仿真参数与仿真条件设置均与上文相同。这里需要指出,该仿真条件并未出现在训练数据搜集过程中,对于神经网络是全新的输入数据。
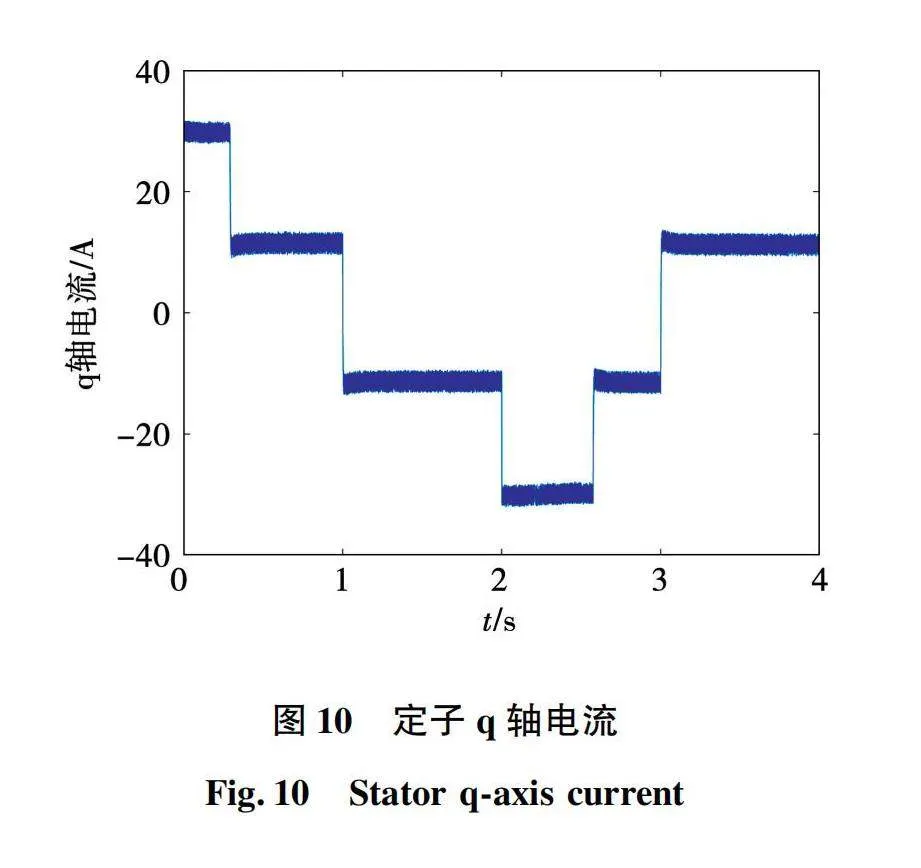
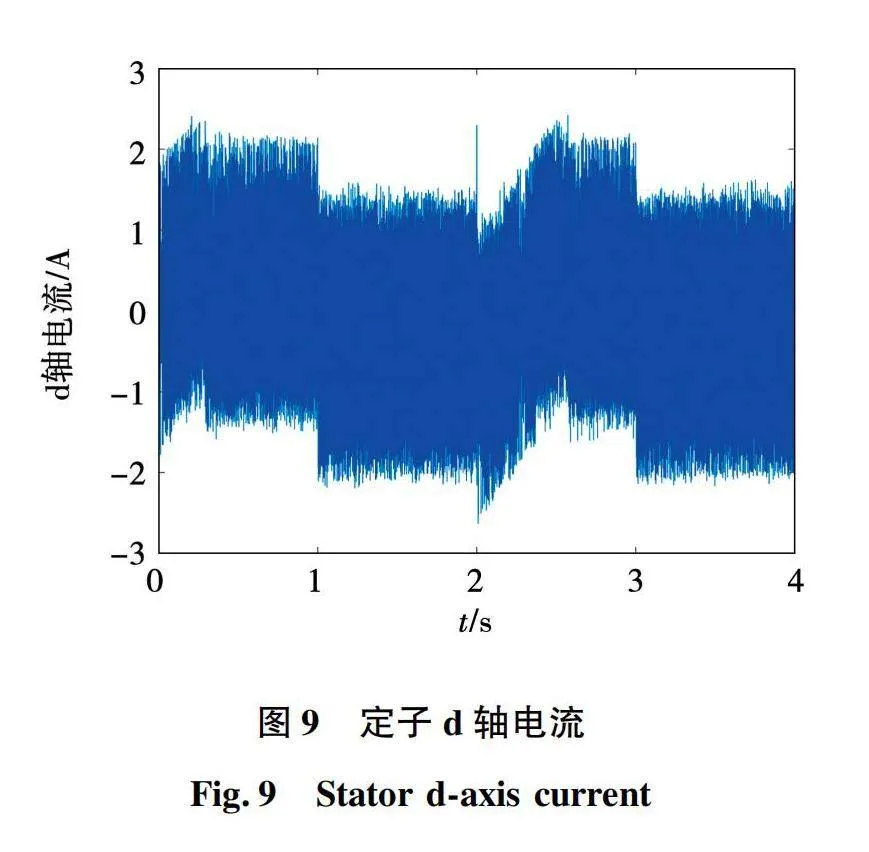
基于7分类神经网络的永磁同步电机模型预测电流控制仿真波形如图7~图10所示。
2.2 121分类神经网络
神经网络学习基于121个基本电压矢量的模型预测电流控制分类规律,分类任务数为121。同样基于上文仿真模型收集训练数据集,由于121个备选电压矢量数目较多,训练数据搜集应尽可能多遍历工况,避免出现数据不均衡[28]。训练数据收集的实验条件如下:设置初始转速为-500 r/min第2 s时阶跃至500 r/min;初始转速为-300 r/min第2 s时阶跃至300 r/min;初始转速为-100 r/min第2 s时阶跃至100 r/min;初始转速为100 r/min第2 s时阶跃至-100 r/min;初始转速为300 r/min第2 s时阶跃至-300 r/min;初始转速为500 r/min第2 s时阶跃至-500 r/min。在每种参考转速设置下分别设置负载转矩为-30、-25、-20、-15、-10、-5、5、10、15、20、25、30 N·m,每次实验仿真时间为4 s,共有72组实验。在删去重复数据后,共收集到5 578 738组包含6个输入特征和1个输出量的运行数据。将收集到的训练数据标准化处理后,按照95∶5比例随机抽取,划分为训练集和测试集。
基于121个备选电压矢量的神经网络依然2个隐藏层的网络结构,但由于分类任务数增多,分类规律更加复杂。为了更好学习分类规律,神经网络的隐藏一和隐藏层二的神经元个数有所增多。同时由于分类任务数为121,输出层神经元个数也为121个。因此,神经网络的输入层、隐藏层一、隐藏层二和输出层各层神经元数目分别为6、15、30和121。
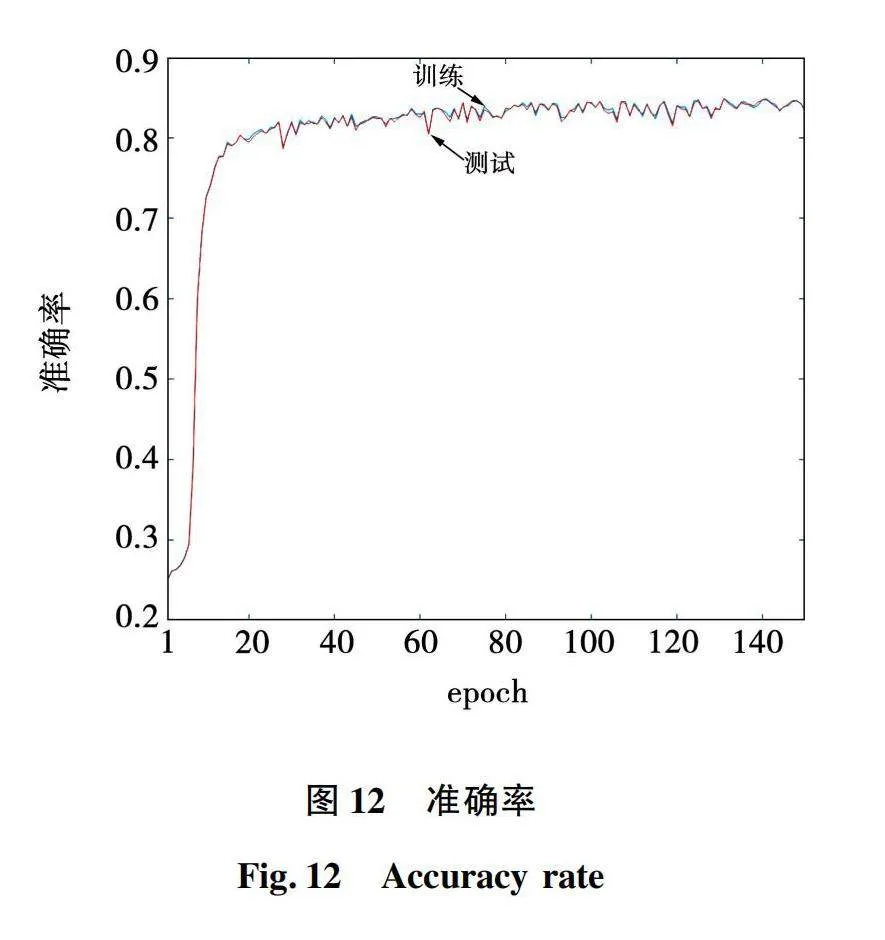
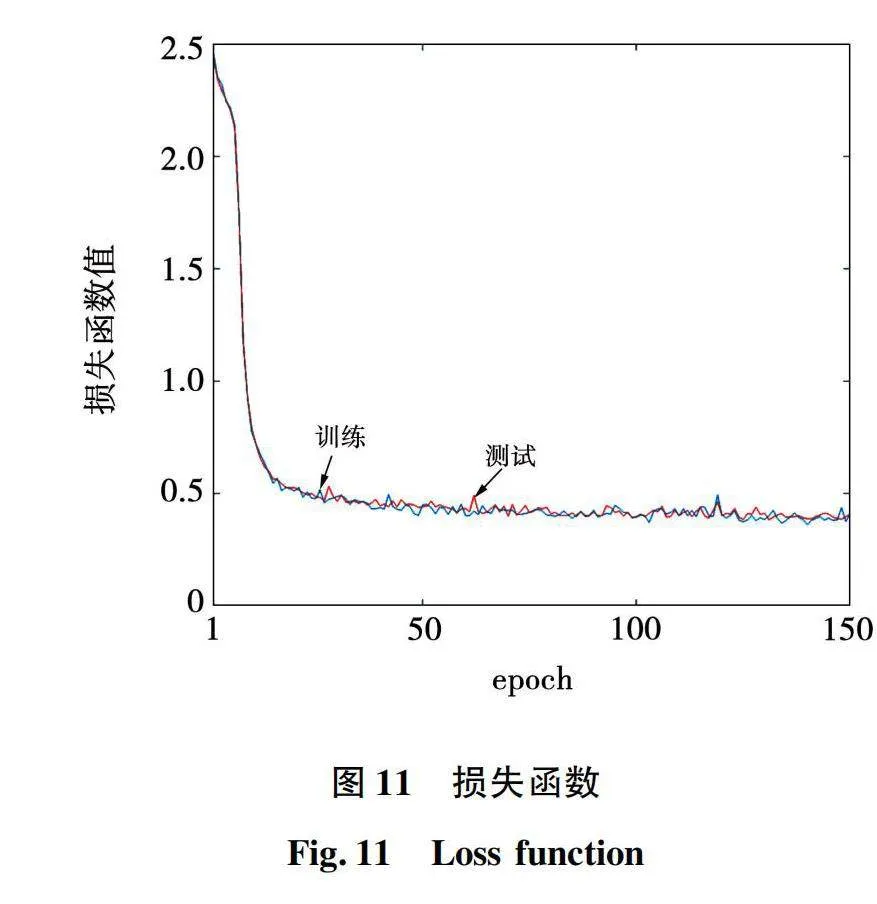
神经网络训练的超参数除训练次数设置为150个epoch和batch size设置为5 000以外,其余均与上文设置相同。经过迭代训练,基于121个备选电压矢量的神经网络训练结果如图11和图12所示。
图11和图12也表明随着训练过程的进行,损失函数值随之减小,训练集和测试集的准确率同步上升并稳定,同时无明显过拟合和欠拟合现象,网络在未知新样本上的分类性能和可用性得到保障。经过150个epoch的训练,训练集和测试集的准确率均超过84%,网络分类效果较好。同样将训练成熟的神经网络取代原有的模型预测电流控制,则可实现基于神经网络的永磁同步电机模型预测电流控制。
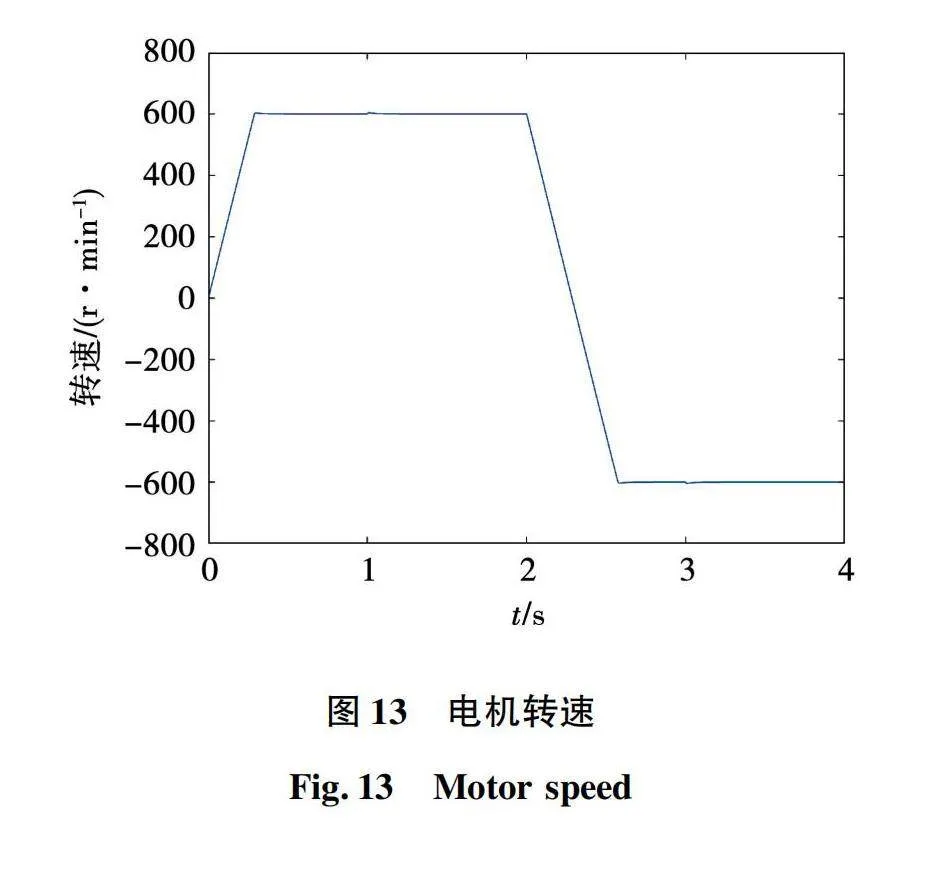
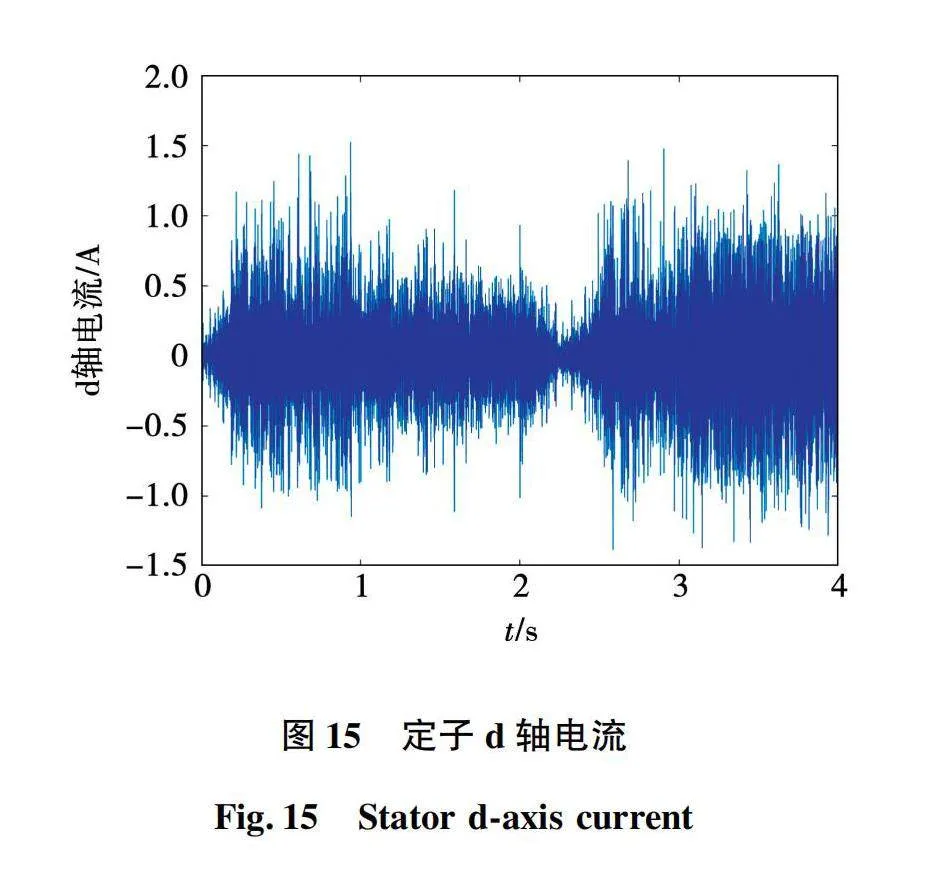
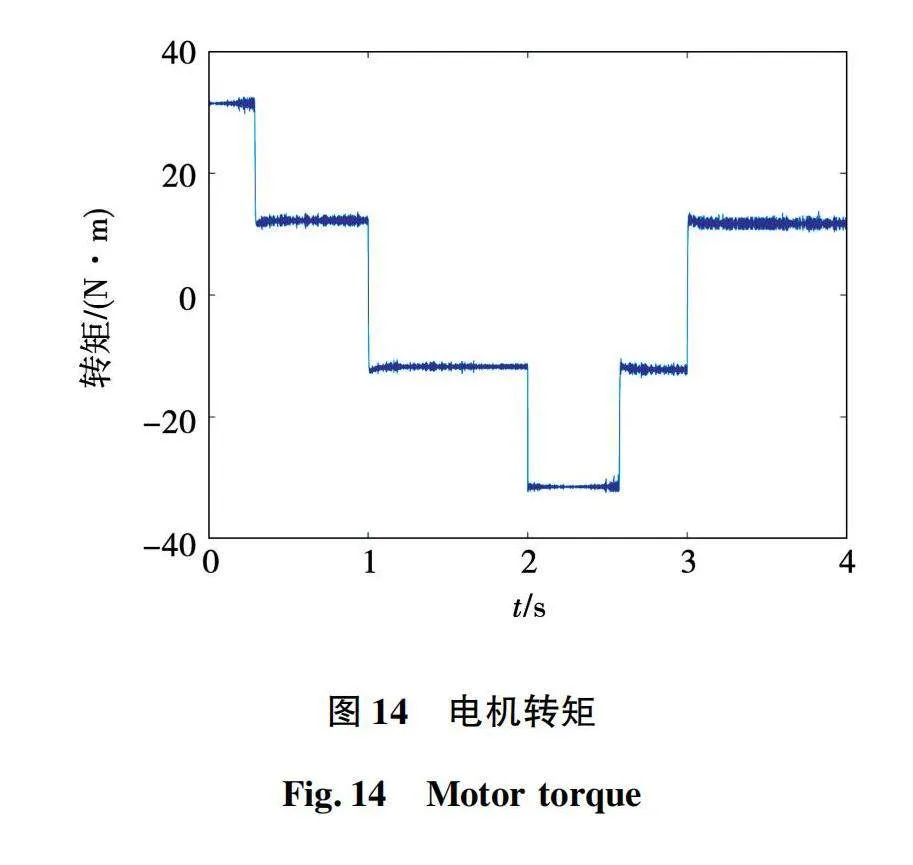
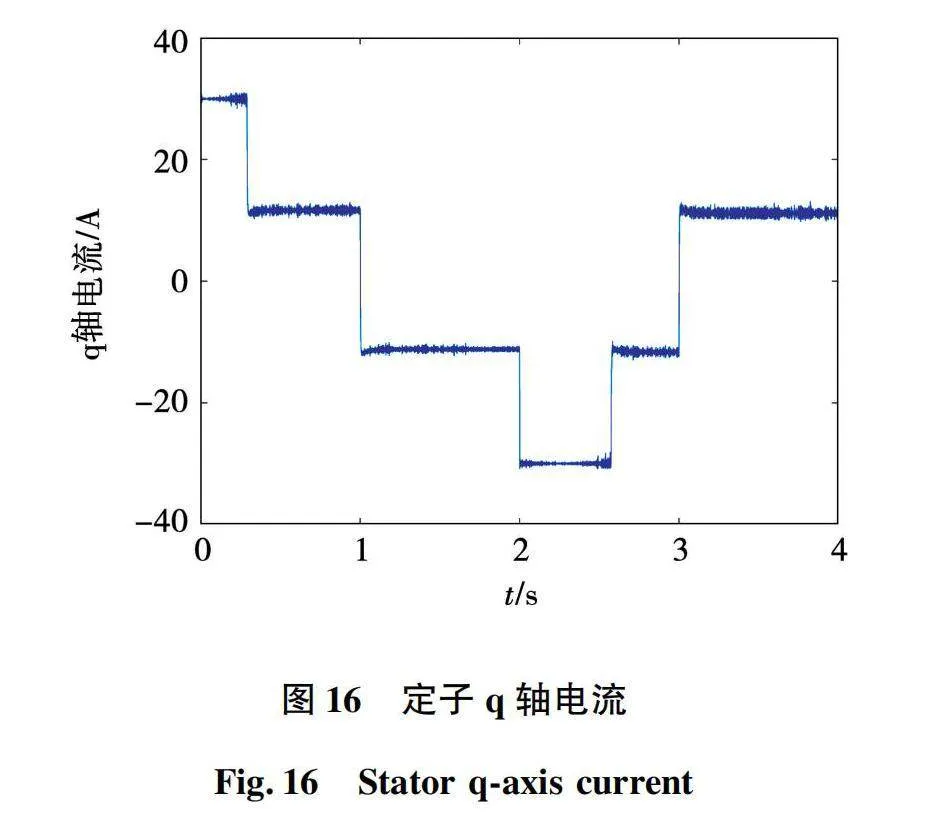
同样建立基于Python和Simulink永磁同步电机神经网控制系统联合仿真模型,仿真条件与上文相同,对于神经网络也是全新的输入数据。基于121分类神经网络的永磁同步电机模型预测电流控制系统仿真波形如图13~图16所示。
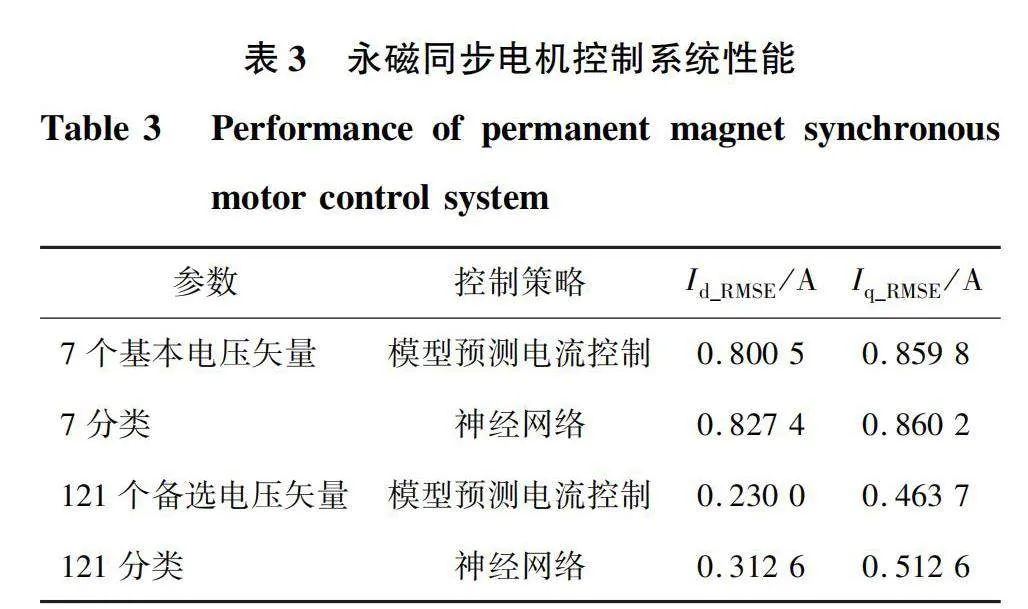
基于7个和121个备选电压矢量的模型预测电流控制及相对应的7分类和121分类的神经网络控制系统性能如表3所示。
仿真结果表明:基于神经网络的永磁同步电机模型预测电流控制可行,控制性能略差于相应的模型预测电流控制,但两者基本相当。通过学习基于121个备选电压矢量的模型预测电流控制分类规律,121分类的神经网络控制性能优于基于7个基本电压矢量的模型预测电流控制和7分类神经网络控制。
3 实时性实验
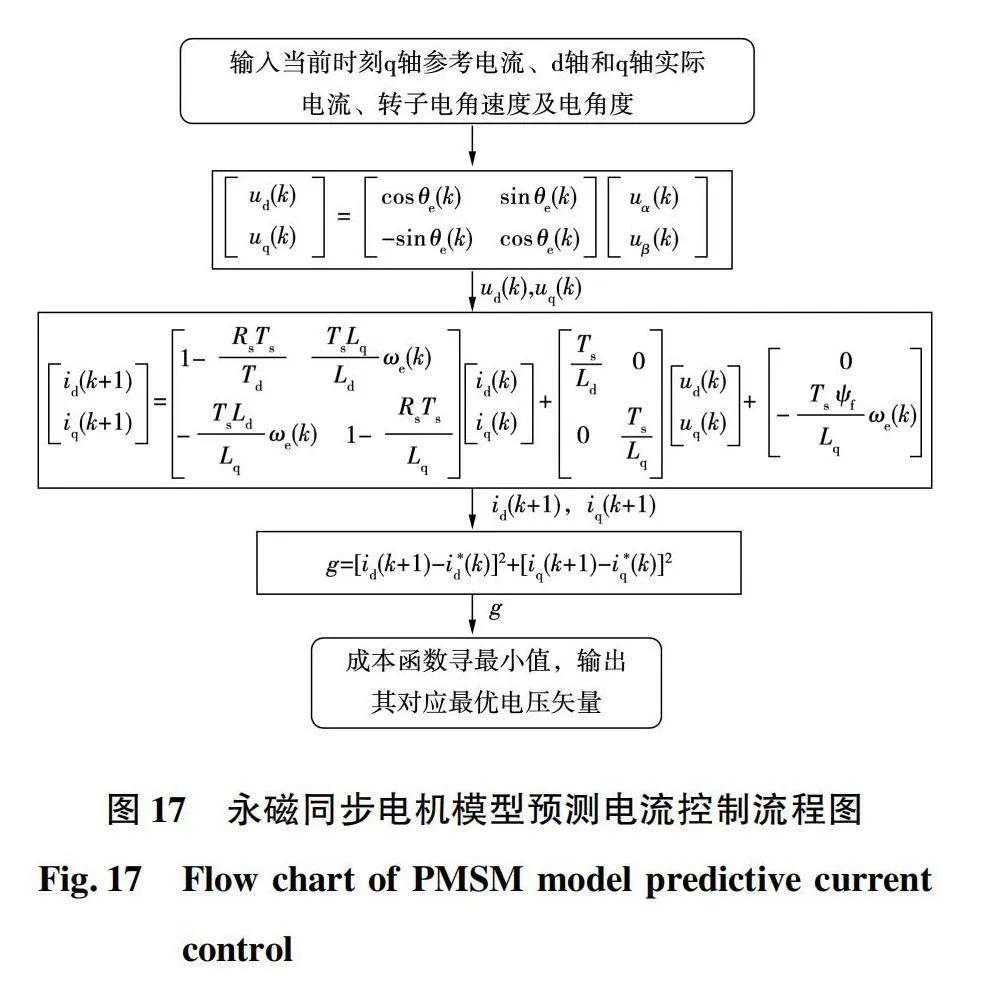
永磁同步电机模型预测电流模型预测控制流程图如图17所示。
由图17可知,永磁同步电机模型预测电流控制计算过程如下:
1)步骤一:备选电压矢量坐标变换。将备选电压矢量在静止坐标系的αβ轴分量转换为在转子坐标系的dq轴分量。
2)步骤二:预测电流计算。遍历备选电压矢量dq轴分量代入至电流模型,得到下一时刻定子电流dq轴分量。
3)步骤三:成本函数计算。将下一时刻的定子电流dq轴分量代入至成本函数,计算得到所有成本函数。
4)步骤四:最优电压矢量确定。对成本函数寻最小值,并输出对应电压矢量。
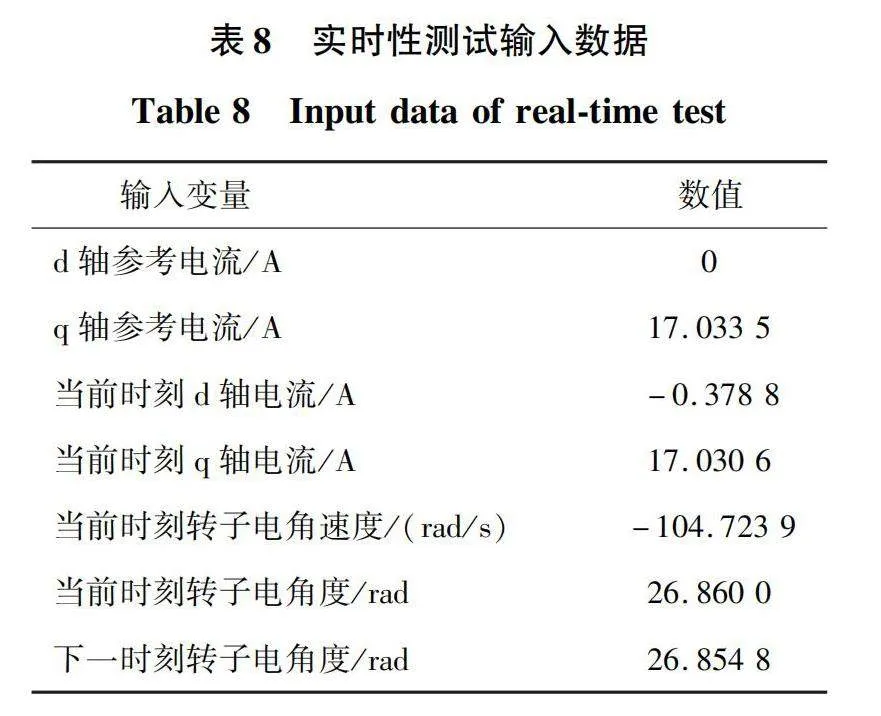
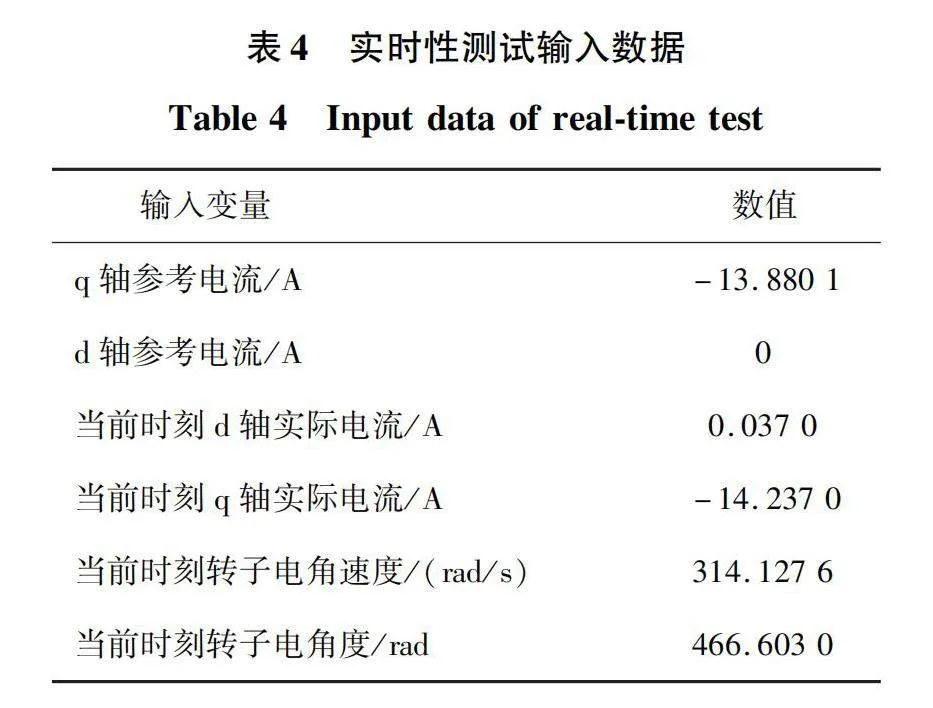
基于STM32平台,对基于7个和121个备选电压矢量的模型预测电流控制进行实时性验证。实时性测试输入数据如表4所示。
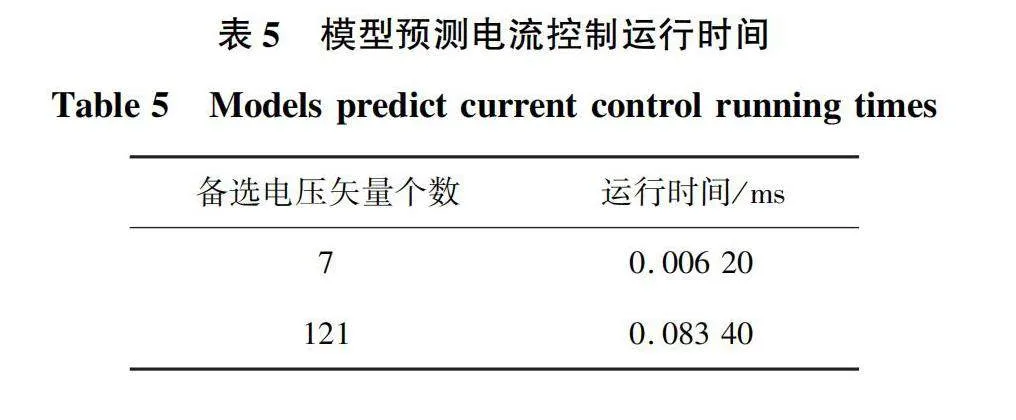
将永磁同步电机模型预测电流控制算法单步循环10次,共进行3组实验,并取平均值,可得永磁同步电机模型预测电流控制单次运行时间如表5所示。
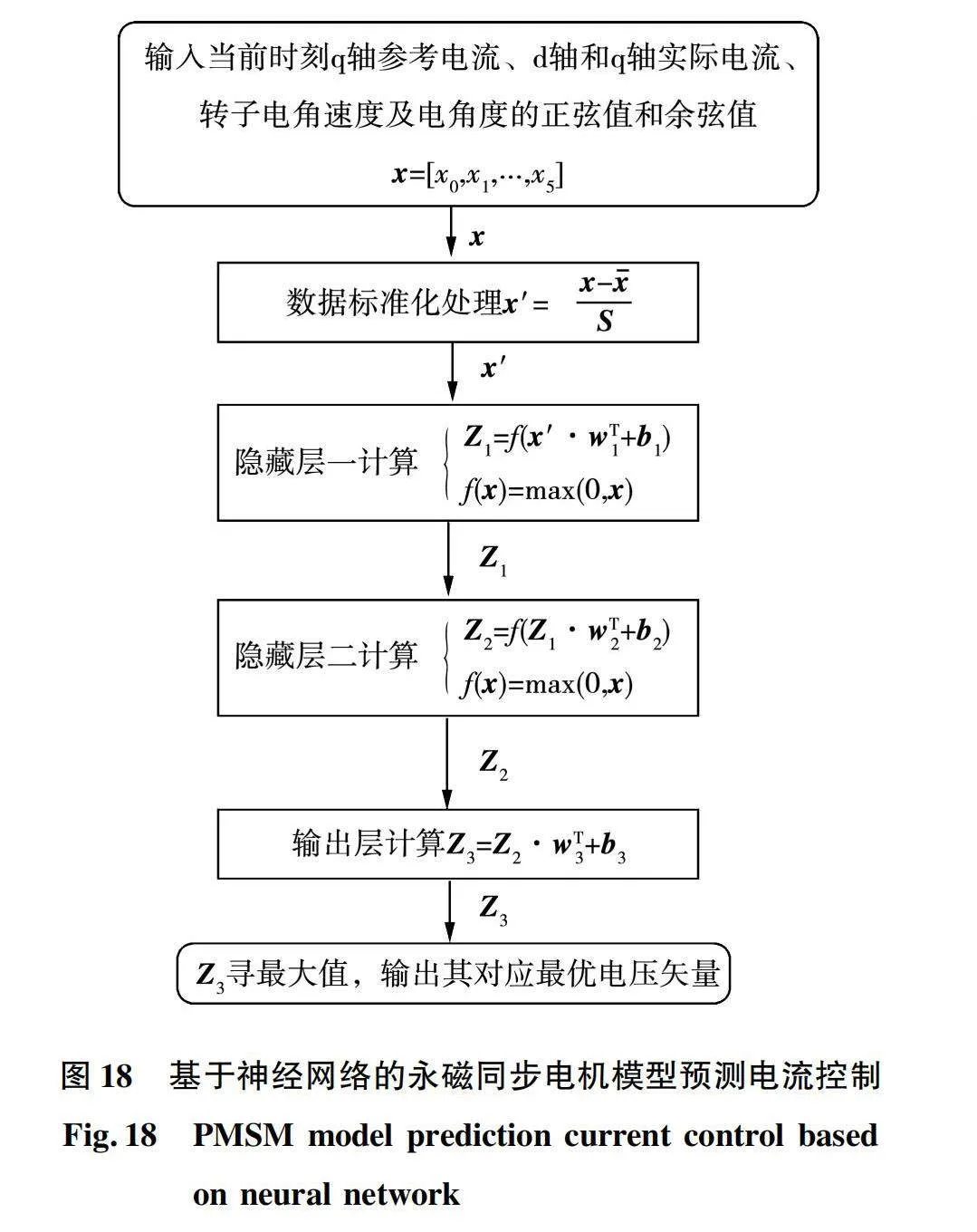
对于神经网络控制,当网络训练成熟后,则网络无需再进行反馈迭代,仅执行前向推理运算。基于神经网络的永磁同步电机模型预测电流控制流程图如图18所示。
由图18可知,基于7分类神经网络的永磁同步电机模型预测电流控制的前向推理运算过程如下:
1)步骤一:输入层标准化计算。对特征工程的6个输入x进行标准化处理,输出为1×6的矩阵x′。
2)步骤二:隐藏层一计算。隐藏层一计算为:
Z1=f(x′·wT1+b1);
f(x)=max(0,x)。(9)
输入层标准化后输出的1×6矩阵x′乘以6×10矩阵wT1,加上1×10矩阵b1,采用ReLU函数激活,输出1×10的矩阵Z1。
3)步骤三:隐藏层二计算。隐藏层二计算为:
Z2=f(Z1·wT2+b2);
f(x)=max(0,x)。(10)
隐藏层一输出的1×10矩阵Z1乘以10×15矩阵wT2,加上1×15矩阵b2,采用ReLU函数激活,最终输出1×15的矩阵Z2。
4)步骤四:输出层计算。输出层计算为
Z3=Z2·wT3+b3。(11)
隐藏层二输出的1×15矩阵Z2乘以15×7矩阵wT3,加上1×7矩阵b3,最终输出1×7的矩阵Z3。
5)步骤五:最优电压矢量确定。对1×7的矩阵Z3寻最大值,将其对应电压矢量作为最优电压矢量输出。
基于STM32平台,对7分类和121分类的神经网络控制进行实时性验证,采用如表5所示的模型预测电流控制输入数据。神经网络的矩阵参数w1、b1、w2、b2、w3和b3以随机值替代。特征均值x~=[-0.252 037 39,0.001 653 408 64,-0.251 804 687,-0.000 469 957 935,0.018 942 222 5,-0.544 795 659],特征标准差S=[19.462 507 31,0.135 410 79,19.443 786 39,0.702 655 43,0.711 277 95,130.811 632]。
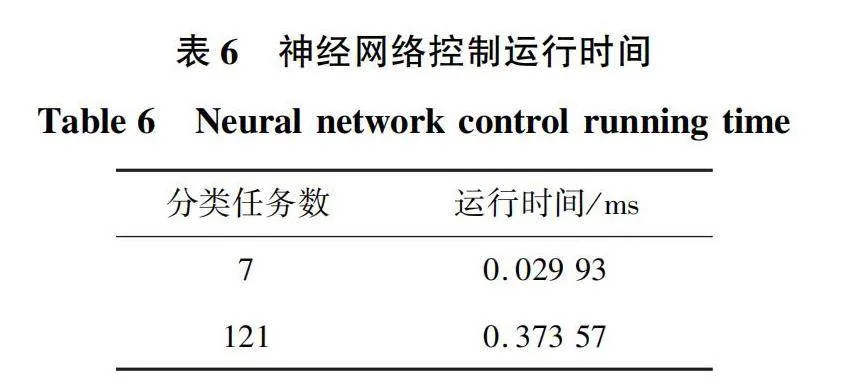
将神经网络控制算法单步循环10次,共进行3组实验,并取平均值,可得基于神经网络永磁同步电机模型预测电流控制单次运行时间如表6所示。
由表5和表6可知,相较于模型预测电流控制,神经网络控制并不占实时性优势。由模型预测电流控制算法流程可知,预测计算次数与计算量基本呈线性关系。对于神经网络控制,计算量与特征工程个数、网络拓扑结构、网络节点个数及分类任务个数有关。对于7分类神经网络控制,输入层标准化计算量约为6个乘积累加运算(multiply accumulate,MAC),隐藏层一计算量约为6×10=60个MAC,隐藏层二计算量约为10×15=150个MAC,输出层计算量为15×7=105个MAC,总计算量为321个MAC。对于121分类神经网络控制,输入层标准化计算量为6个MAC,隐藏层一计算量约为6×15=90个MAC。隐藏层二计算量约为15×30=450个MAC,输出层计算量为30×121=3 630个MAC,计算量约为4 176个MAC。因此,与模型预测控制相比,神经网络控制的乘加计算量更大,运行时间更长,实时性更差。
4 基于神经网络的两步预测电流控制
由上文可知,通过扩展备选电压矢量,可有效提升模型预测电流控制性能,并改善与其对应的神经网络控制性能,但增加分类任务个数,使得神经网络控制计算量较大,实时性变差。因此,神经网络控制不太适用于分类任务数较多的场合。
对于多步预测控制,计算量将随步长呈指数上升。虽然多步预测控制得到最优多步电压矢量序列,但只作用序列的第一个电压矢量[29-31]。因此,对于模型预测电流控制,步长的增加引起计算量呈指数级上升,但对于神经网络控制,由于多步预测的最终输出电压矢量依然仅为备选电压矢量之一,分类任务数没有发生变化,计算量并不增加。因此,神经网络控制适用于取代多步预测控制。
下文以永磁同步电机两步模型预测电流控制为例,研究基于神经网络取代多步预测控制。
对于永磁同步电机两步模型预测电流控制,需要在第一步预测电流基础上,预测第二步电流如下[32-33]:
id(k+2)=(1-RsTsLd)id(k+1)+Ts[LqLdωe(k+1)iq(k+1)+
1Ldud(k+1)];
iq(k+2)=(1-RsTsLq)iq(k+1)-
Ts[LdLqωe(k+1)id(k+1)+
ψfLqωe(k+1)-1Lquq(k+1)]。(12)
在得到第一步和第二步的预测电流后,将其代入至成本函数,即
g=[id(k+1)-i*d(k)]2+[iq(k+1)-
i*q(k)]2+[id(k+2)-i*d(k)]2+
[iq(k+2)-i*q(k)]2。(13)
对成本函数寻最小值,并将其对应的电压矢量序列的第一个电压矢量作为下一时刻输出电压矢量。
备选电压矢量为7个基本电压矢量,永磁同步电机两步模型预测电流模型控制流程如下:
1)步骤一:第一步模型预测电流控制。遍历7个电压矢量,代入至第一步模型预测电流控制模型,得到7个(k+1)时刻定子dq轴电流预测值。
2)步骤二:第二步模型预测电流控制。基于第一步模型预测电流控制得到的7个(k+1)时刻的定子dq轴电流预测值,每一个再遍历7个电压矢量,代入式(12),得到49个确定(k+2)时刻定子dq轴电流预测值。
3)步骤三: 成本函数计算。将7个(k+1)时刻的定子dq轴电流预测值和49个(k+2)时刻的定子dq轴电流预测值代入至式(13),则可得49个电压矢量序列对应的49个成本函数。
4)步骤四:最优电压矢量确定。对49个成本函数寻最小值,并将其对应的电压矢量序列的第一个电压矢量作为下一时刻输出电压矢量。
因此,对于永磁同步电机两步模型预测电流控制,预测计算次数为(7+49)=56次,但输出电压矢量与单步预测相同,为7个基本电压矢量之一。
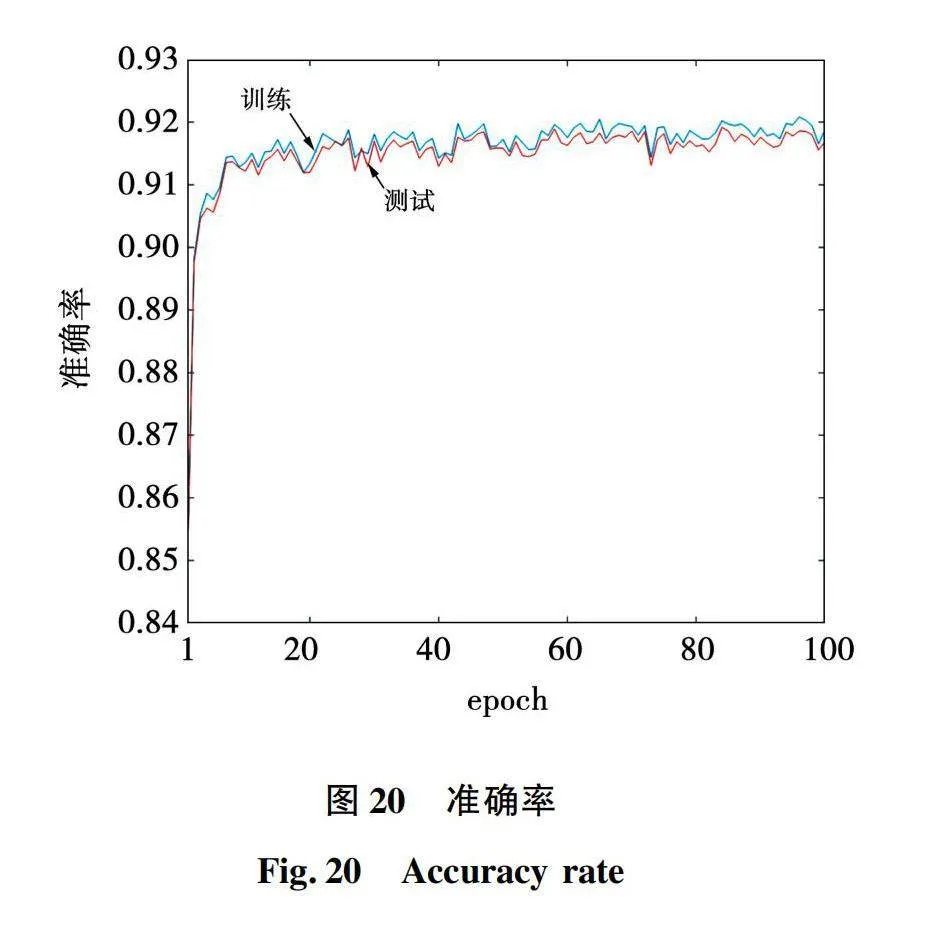
与上文相同,将永磁同步电机多步模型预测电流控制也视为一个多分类任务,采用端到端的神经网络控制学习分类规律,输入端和输出端与单步预测相同,神经网络的特征工程、分类任务数也与单步预测均相同。因此,采用与上文7分类神经网络拓扑结构完全相同的网络,输入层、隐藏层一、隐藏层二和输出层的神经元数目为6、10、15和7。神经网络的训练数据收集和训练也与上文基于7个基本电压矢量的单步模型预测电流控制相同,共收集到2 048 623组数据。经过迭代训练,基于两步模型预测电流控制的神经网络训练结果如图19和图20所示。
图19和图20表明随着训练过程的进行,损失函数值随之减小,训练集和测试集的准确率同步上升并稳定。经过100个epoch的训练,训练集和测试集的准确率均超过91%,说明网络较充分逼近两步模型预测电流控制的电压矢量选择规律。
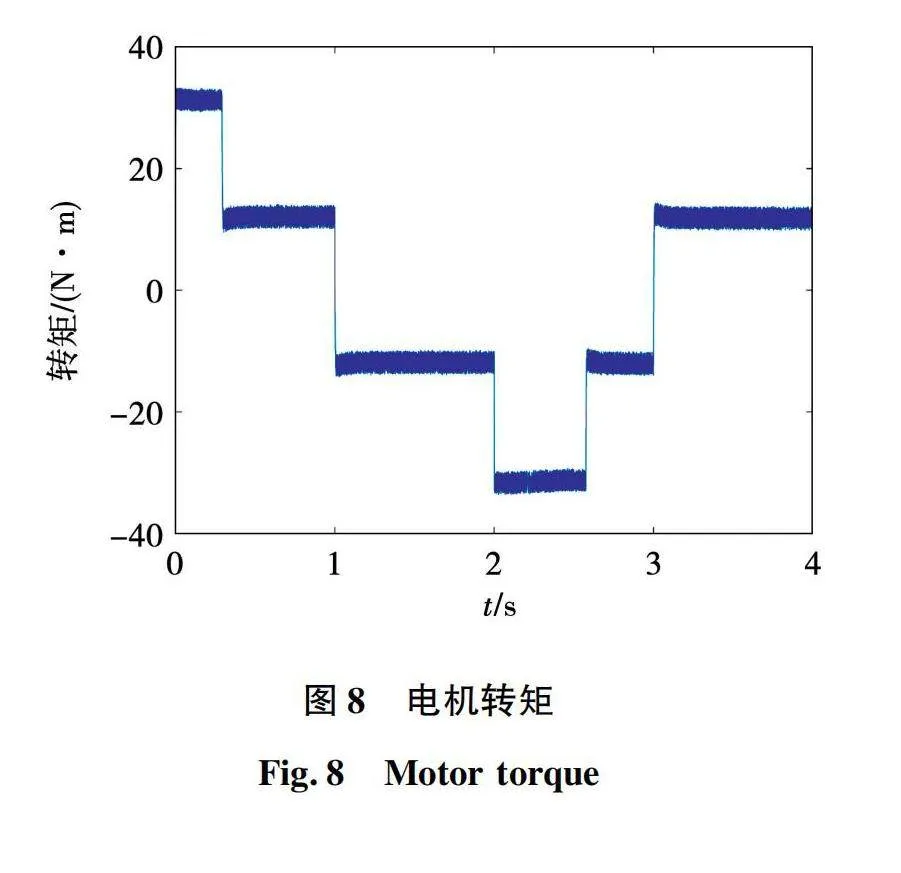
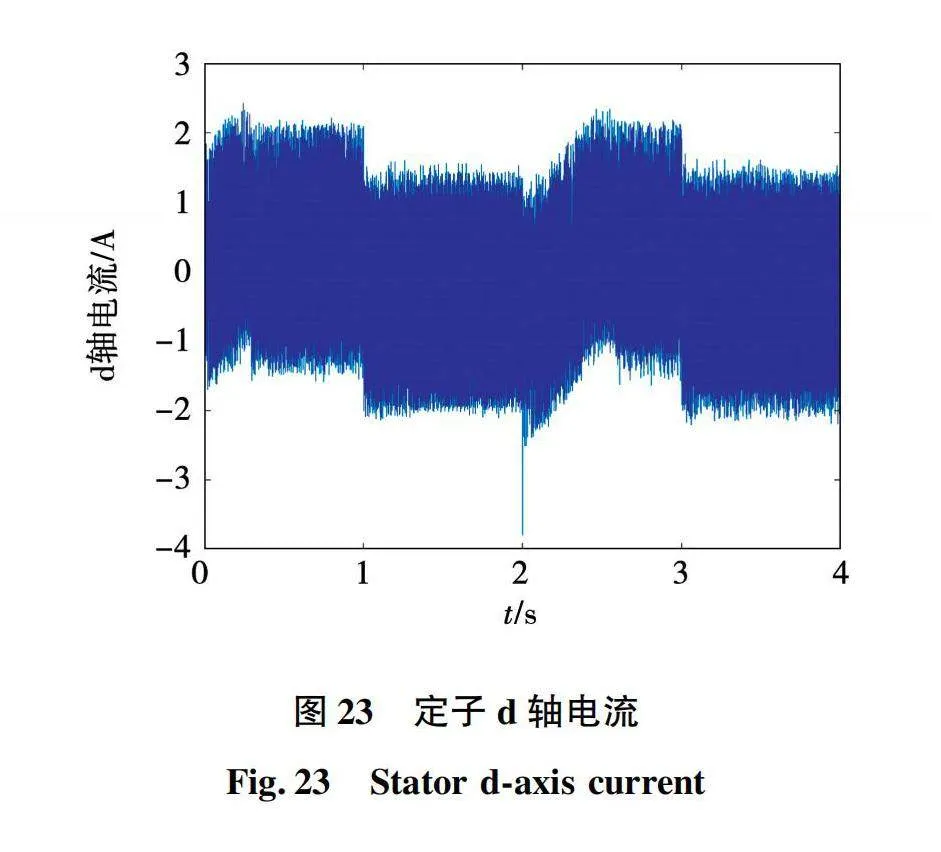
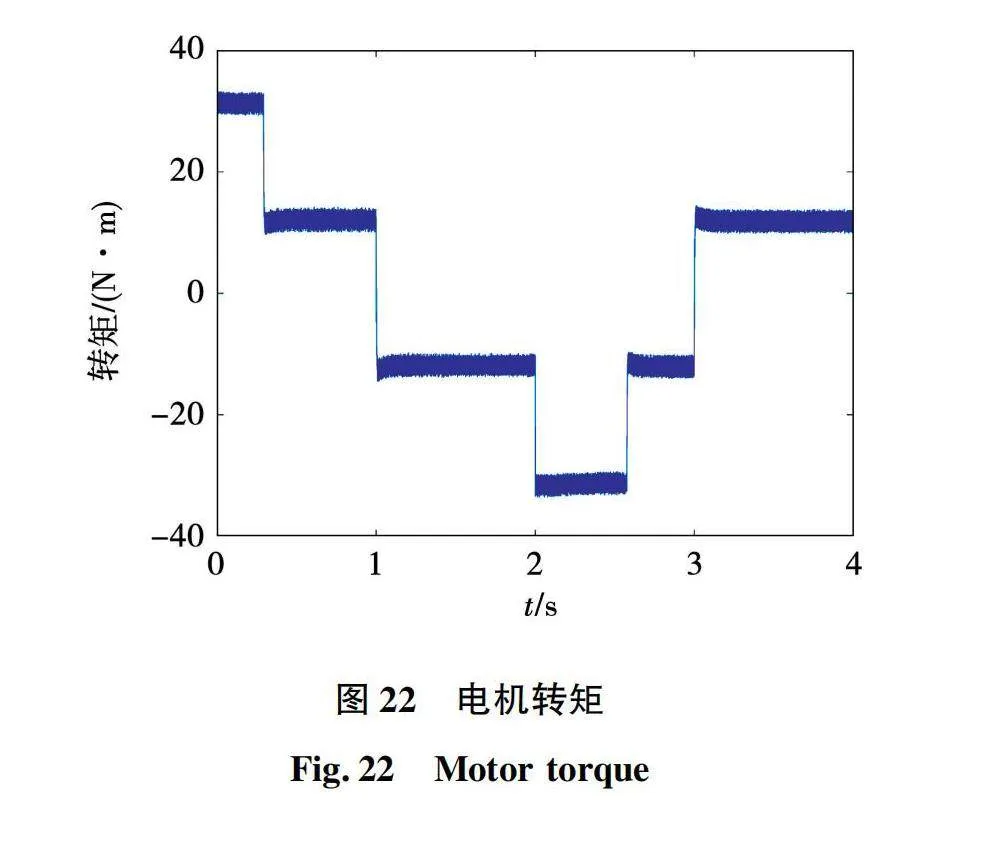
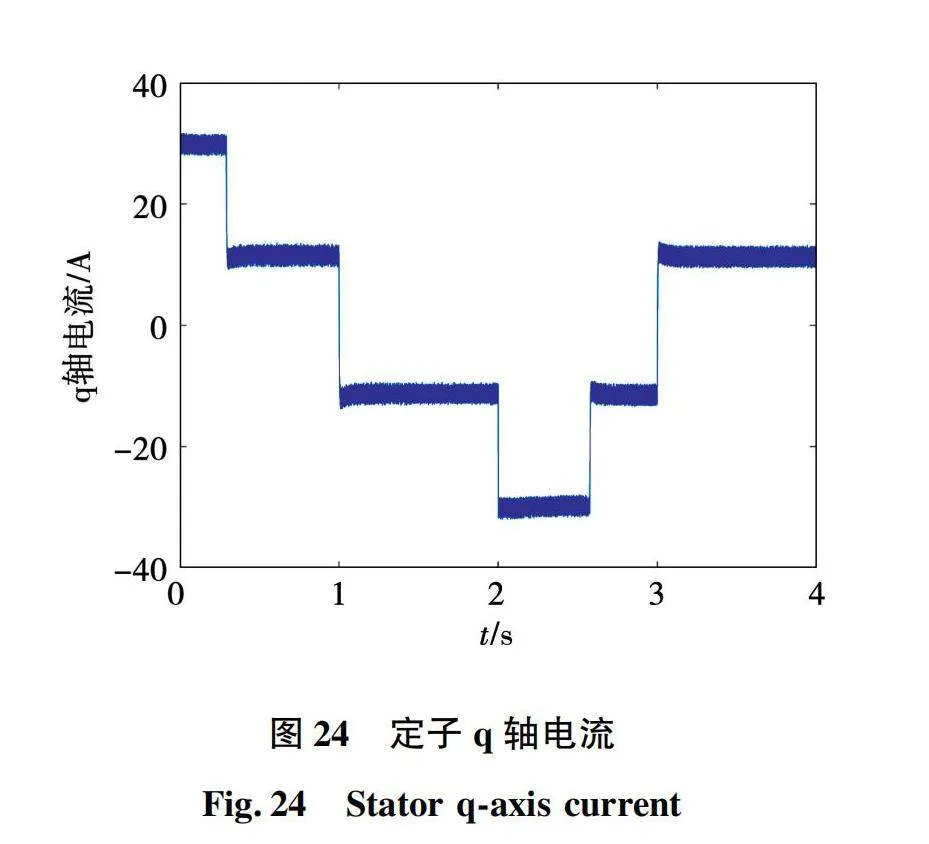
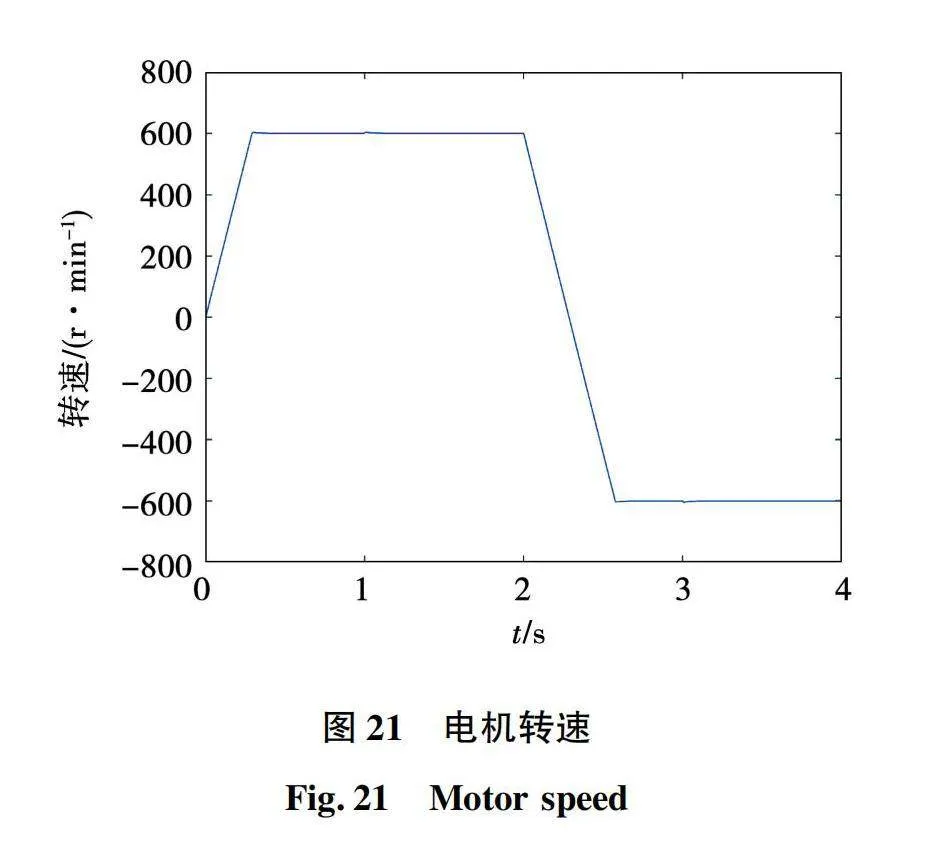
同样建立基于Python和Simulink永磁同步电机神经网控制系统联合仿真模型,仿真条件与上文相同,对于神经网络也是全新的输入数据。基于神经网络的永磁同步电机两步模型预测电流控制系统仿真波形如图21~图24所示。
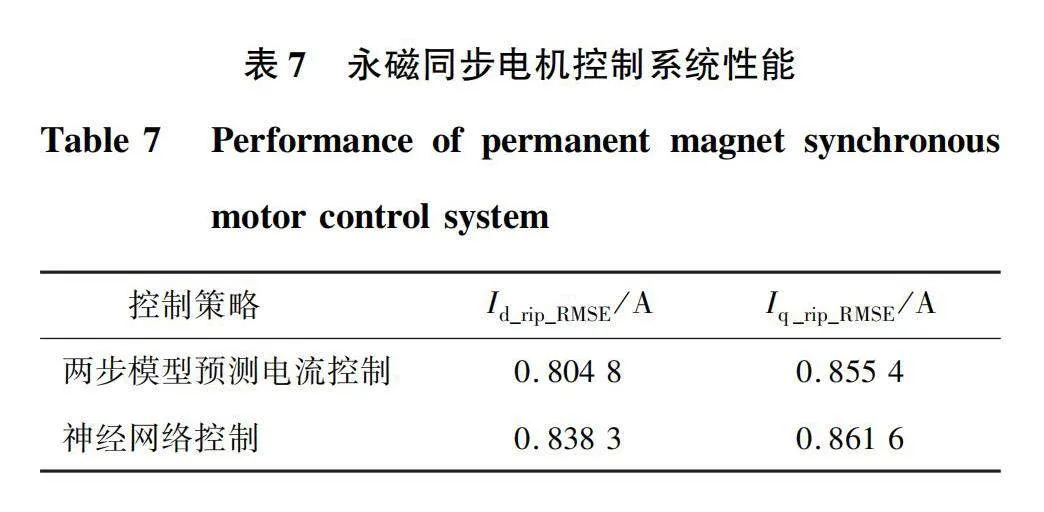
永磁同步电机两步模型预测电流控制系统和神经网络控制系统性能如表7所示。
仿真结果表明:基于神经网络的永磁同步电机两步模型预测电流控制可行,控制性能略差于模型预测电流控制,但两者基本相当。
基于STM32平台,对永磁同步电机两步模型预测电流控制系统和神经网络控制进行实时性验证,实时性测试输入数据如表8所示。两步神经网络的特征均值x~=[0.377 414 86,-0.005 153 65,0.375 505 05,0.000 736 92,0.030 065 69,-0.603 933 76],特征标准差S=[19.858 732 1,0.819 365 81,19.831 652 97,0.698 474 74,0.715 002 48,127.596 767 2]。
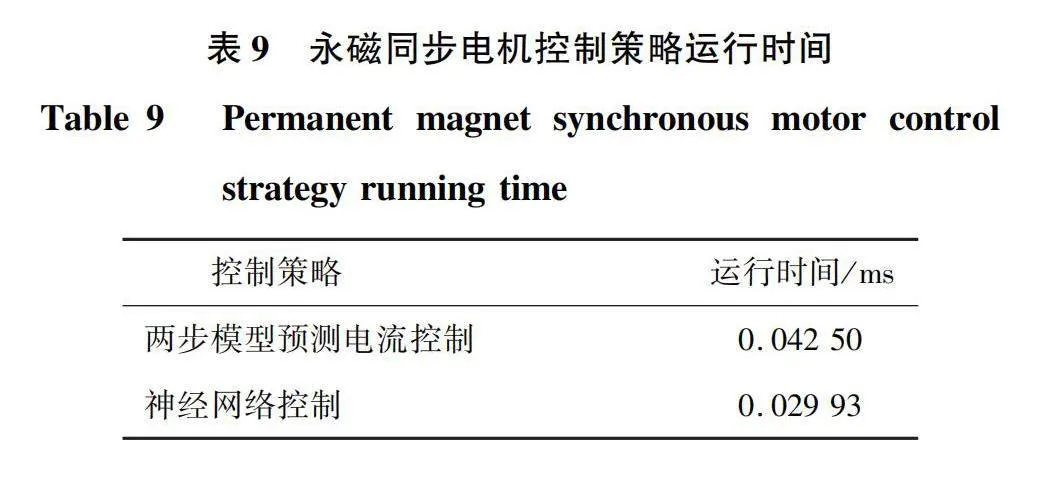
将两步模型预测电流控制和神经网络控制算法分别单步循环10次,共进行3组实验,并取平均值,可得两者的单次运行时间如表9所示。
对于多步预测,模型预测电流控制的预测计算次数呈现指数上升,达到56次,而神经网络控制输出层分类个数不变,计算量依然为321个MAC,计算耗时与上文基于单步预测的神经网络控制相同。表9表明,神经网络控制的实时性优于两步模型预测电流控制,计算耗时减小29.58%。
5 结 论
1)基于神经网络的永磁同步电机单步和两步模型预测电流控制可行,电机运行良好,可实现四象限运行,系统性能与对应的模型预测电流控制基本相当。
2)对于模型预测电流控制,计算量基本与预测计算次数成正比。假设n个备选电压矢量,m步预测控制,则预测计算次数为(n+n2+n3+…+nm)。对于神经网络控制,计算量与网络拓扑结构、网络节点个数有关。假设神经网络输入层有a个输入,有m层隐藏层,隐藏层一有b1个节点,隐藏层二有b2个节点,……,隐藏层m有bm个节点,输出层分类任务个数为n,则神经网络控制计算量为(a+ab1+b1b2+…+nbm)个MAC。
3)对于单步模型预测电流控制,神经网络控制并不占实时性优势。通过扩展备选电压矢量,可有效提升模型预测电流控制性能,改善与其对应的神经网络控制性能,但增加分类任务个数,使得神经网络控制计算量较大,实时性变差。
4)对于多步预测,模型预测电流控制的预测计算次数随步长数呈指数级别上升,但神经网络的输出层分类个数不变。因此,对于端对端的神经网络控制而言,输入和输出与步长无关,使得神经网络控制具有实时性优势,更适用于多步模型预测控制系统。
5)后期计划将从仿真模型数据中得到的神经网络预测模型应用于实际永磁同步电机系统,从仿真数据得到网络模型,减小实际系统的实验,降低应用的成本。
参 考 文 献:
[1]RODRIGUEZ J, GARICA C, MORA A, et al. Latest advances of model predictive control in electrical drives-part I: Basic concepts and advanced strategies[J]. IEEE Transactions on Power Electronics, 2022, 37(4): 3927.
[2]RODRIGUEZ J, GARICA C, MORA A, et al. Latest advances of model predictive control in electrical drives-part II: Applications and benchmarking with classical control methods[J]. IEEE Transactions on Power Electronics, 2022, 37(5): 5047.
[3]ELMORSHEDY M F, XU Wei, EL-SOUSY F F M, et al. Recent achievements in model predictive control techniques for industrial motor: a comprehensive state-of-the-art[J]. IEEE Access, 2021, 9: 58170.
[4]KARAMANAKOS P, GEYER T. Guidelines for the design of finite control set model predictive controllers[J]. IEEE Transactions on Power Electronics, 2020, 35(7): 7434.
[5]王治国,郑泽东,李永东. 交流电机模型预测控制综述[J]. 电机与控制学报, 2022, 26(11): 14.
WANG Zhiguo, ZHENG Zedong, LI Yongdong. A review of model predictive control for AC motor [J]. Electric Machines and Control, 2012, 26(11):14.
[6]VAZQUEZ S, RODRIGUEZ J, RIVERA M, et al. Model predictive control for power converters and drives: advances and trends[J]. IEEE Transactions on Industrial Electronics, 2017, 64(2): 935.
[7]李耀华,刘洋,孟祥臻. 一种表面式永磁同步电机有限状态集模型预测直接转矩控制[J]. 电机与控制学报,2020,24(8):33.
LI Yaohua, LIU Yang, MENG Xiangzhen. Finite control set model predictive direct torque control of surface permanent magnet synchronous motor [J]. Electric Machines and Control, 2019, 24(8):33.
[8]张珍睿,刘彦呈,陈九霖,等. 永磁同步电机幅值控制集模型预测控制策略[J]. 电工技术学报,2022,37(23):6127.
ZHANG Zhenrui, LIU Yancheng, CHEN Jiulin, et al. Amplitude control set model predictive control strategy for permanent magnet synchronous motor [J]. Transactions of China Electrotechnical Society, 2022,37(23):6127.
[9]周汉斌,杨建,陈晓娇,等. 考虑死区电压矢量的三电平变换器模型预测控制[J]. 电工技术学报,2022,37(20):5290.
ZHOU Hanbin, YANG Jian, CHEN Xiaojiao, et al. Model predictive control of three-level converter considering dead-zone voltage vector [J]. Transactions of China Electrotechnical Society, 2022, 37(20):5290.
[10]VARGAS R, AMMANN U, RODRIGUEZ J. Predictive approach to increase efficiency and reduce switching lossed on matrix converters[J]. IEEE Transactions on Power Electronics, 2009, 24(4): 894.
[11]李耀华,苏锦仕,秦辉. 表贴式永磁同步电机多步预测控制简化算法[J]. 电机与控制学报,2022,26(11):122.
LI Yaohua, SU Jinshi, QIN Hui. Simplified multi-step predictive control for surface permanent magnet synchronous motor [J]. Electric Machines and Control, 2012, 26(11):122.
[12]HABIBULLAH M, LU D D, XIAO Dan, et al. A simplified finite-state predictive direct torque control for induction motor drive[J]. IEEE Transactions on Industrial Electronics, 2016, 63(6): 3964.
[13]李耀华,刘子焜,王孝宇,等. 永磁同步电机模型预测转矩控制简化控制策略[J]. 控制理论与应用,2023,40(10):1793.
LI Yaohua, LIU Zikun, WANG Xiaoyu, et al. Simplified control strategies of model predictive torque control for permanent magnet synchronous motor [J]. Control Theory amp; Applications, 2023,40(10):1793.
[14]李耀华,师浩浩,孟祥臻. 表面式永磁同步电机直接转矩控制系统简化预测控制策略[J]. 电机与控制学报, 2020, 24(4): 96.
LI Yaohua, SHI Haohao, MENG Xiangzhen. Simplified predictive control for direct torque control of surface permanent magnet synchronous motor [J]. Electric Machines and Control, 2020, 24(4): 96.
[15]SIAMI M, KHABURI D A, RODRIGUEZ J. Simplified finite control set-model predictive control for matrix converer-fed PMSM drives[J]. IEEE Transactions on Power Electronics, 2018, 33(3): 2438.
[16]刘涛,习金生,宋战锋,等. 基于多核并行计算的永磁同步电机有限集模型预测控制策略 [J]. 电工技术学报, 2021, 36(1): 107.
LIU Tao, XI Jinsheng, SONG Zhanfeng, et al. Finite control set model predictive control of permanent magnet synchronous motor based on multi-core parallel computing [J]. Transactions of China Electrotechnical Society, 2021,36(1):107.
[17]ZHAO Shuai, BLAABJERG F, WANG Huai. An overview of artificial intelligence applications for power electronics[J]. IEEE Transactions on Power Electronics, 2021, 36(4): 4633.
[18]戴文战,娄海川,杨爱萍. 非线性系统神经网络预测控制研究进展[J]. 控制理论与应用,2009,26(5):521.
DAI Wenzhan, LOU Haichuan, YANG Aiping. An overview of neural network predictive control for nonlinear systems [J]. Control Theory amp; Applications, 2009,26(5):521.
[19]谷鑫,胡升,史婷娜,等. 基于神经网络的永磁同步电机多参数解耦在线辨识[J]. 电工技术学报,2015,30(6):114.
GU Xin, HU Sheng, SHI Tingna, et al. Muti-parameter decoupling online identification of permanent magnet synchronous motor based on neural network [J]. Transactions of China Electrotechnical Society,2015,30(6): 114.
[20]李耀华,王孝宇,周逸凡,等. 双BP神经网络的永磁同步电机磁链转矩无差拍控制[J]. 电机与控制应用,2022,49(4):16.
LI Yaohua, WANG Xiaoyu, ZHOU Yifan, et al. Deadbeat control of stator flux and torque for permanent magnet synchronous motor with dual BP neural networks [J]. Electric Machines amp; Control Application, 2022,49(4):16.
[21]NOVAK M, XIE Haotian, DRAGICEVIC T, et al. Preditive torque control (PTC) using artificial neural networks (ANN)[J]. IEEE Transactions on Industrial Electronics, 2021, 68(8): 7309.
[22]MOHAMED I S, ROVETTA S, DO T D, et al. A neural-network-based model predictive control of three-phase inverter with an output LC filter[J]. IEEE Access, 2019(7): 124737.
[23]李耀华,赵承辉,周逸凡,等. 基于数据驱动的永磁同步电机深度神经网络控制[J]. 电机与控制学报,2022,26(1):115.
LI Yaohua, ZHAO Chenghui, ZHOU Yifan, et al. Deep neural network control for PMSM based on data drive [J]. Electric Machines and Control, 2012, 26(1) : 115.
[24]李耀华,刘东梅,赵承辉,等. 基于CNN的MPTC与DTC自适应切换的表贴式永磁同步电机控制策略[J]. 电机与控制应用,2022,49(5):8.
LI Yaohua, LIU Dongmei, ZHAO Chenghui, et al. Adaptive switching control strategy between MPTC based on CNN and DTC for surface-mounted PMSM [J]. Electric Machines amp; Control Application, 2012, 49(5):8.
[25]LI Yaohua, WU Tingxu, ZHAI Dengwang, et al. Hybrid decision based on DNN and DTC for model predictive torque control of PMSM[J]. Symmetry, 2022,14(4):693.
[26]李耀华,杨启东, 曲亚飞. 自适应变电压矢量PMSM直接转矩控制开关表[J]. 电机与控制学报, 2019, 23(9): 75.
LI Yaohua, YANG Qidong, QU Yafei. Adaptive variable voltage vectors switching table in direct torque control for PMSM [J]. Electric Machines and Control, 2019, 23(9): 75.
[27]刘珅,高琳. 永磁同步电机的改进模型预测直接转矩控制[J]. 电机与控制学报,2020,24(1):10.
LIU Shen, GAO Lin. Improved model of predictive direct torque control for permanent magnet synchronous motor [J]. Electric Machines and Control, 2019, 24(1):10.
[28]王乐,韩萌,李小娟,等. 不平衡数据集分类方法综述[J]. 计算机工程与应用,2021,57(22):42.
WANG Le, HAN Meng, LI Xiaojuan, et al. Review of classification methods for unbalanced data sets [J]. Computer Engineering and Applications, 2021, 57(22):42.
[29]GEYER T, QUEVED D E. Performance of multistep finite control set model predictive control for power electronics[J]. IEEE Transactions on Power Electronics, 2015, 30(3): 1633.
[30]李耀华,王孝宇,陈桂鑫,等. 永磁同步电机多步模型预测电流控制球形编码研究[J]. 控制理论与应用,2023,40(9):1683.
LI Yaohua, WANG Xiaoyu, CHEN Guixin, et al. Multi-step model predictive current control of permanent magnet synchronous motor based on sphere decoding [J]. Control Theory amp; Applications, 2023,40(9):1683.
[31]李耀华,王孝宇,刘子焜,等. 表贴式永磁同步电机多步模型预测电流控制简化策略[J]. 电机与控制学报,2023,27(6):85.
LI Yaohua, WANG Xiaoyu, LIU Zikun, et al. Simplified multi-step predictive current control for surface permanent magnet synchronous motor [J]. Electric Machines and Control, 2023,27(6):85.
[32]沈坤, 章兢, 王坚. 一种多步预测的变流器有限控制集模型预测控制算法[J]. 中国电机工程学报, 2012, 32(33):37.
SHEN Kun, ZHANG Jing, WANG Jian. A model predictive control scheme of multi-step prediction finite control set for converters[J]. Proceedings of the CSEE, 2012, 32(33): 37.
[33]XU Yanping, SUN Yifei, HOU Yongle. Multi-step model predictive current control of permanent-magnet synchronous motor[J]. Journal of Power Electronics, 2020, 20(1): 176.
(编辑:刘琳琳)
