基于残差生成器的Buck双向变换器改进模型预测控制
2024-12-03李劲松沈琦丰李国锋吕敬华浩杨庆新李永建

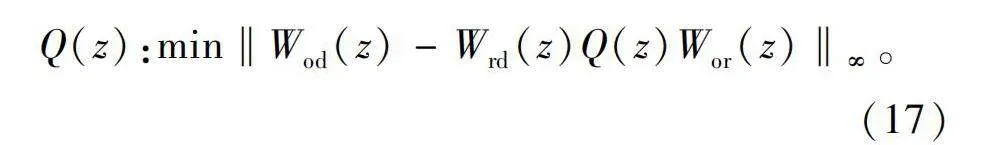
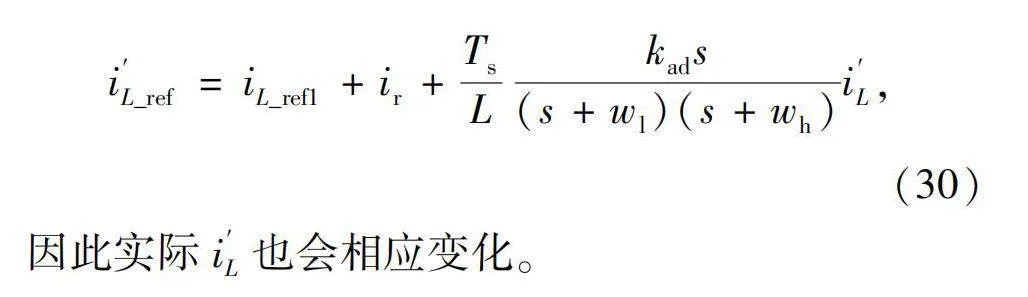
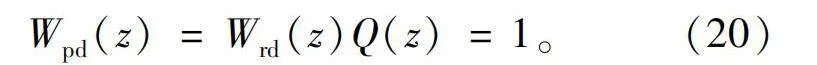

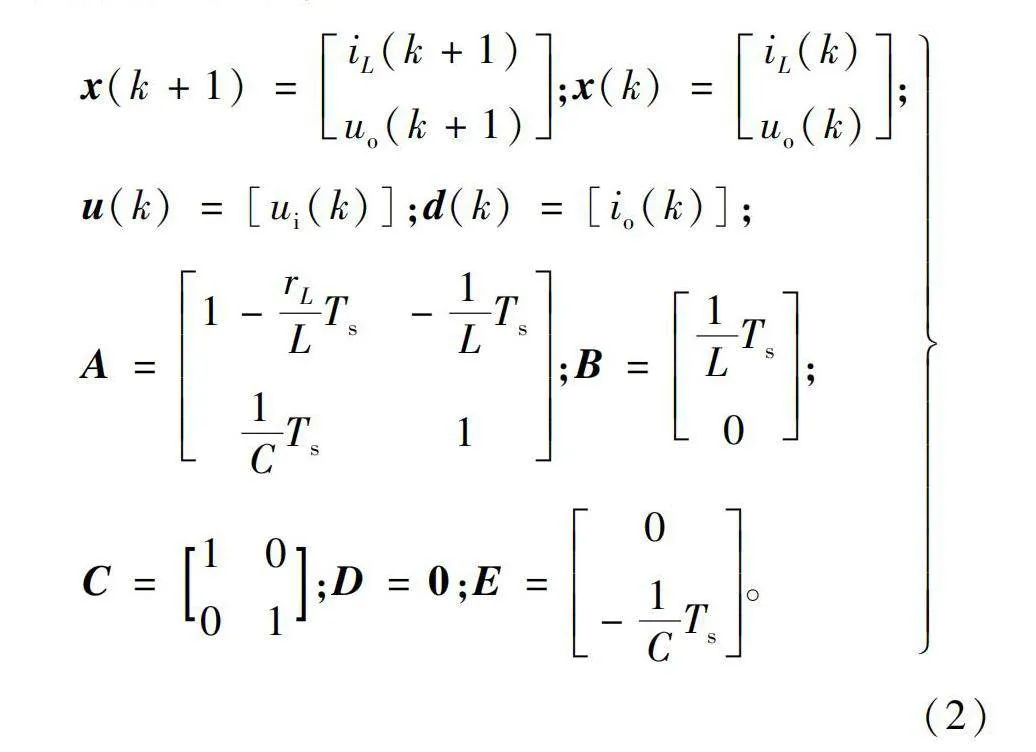
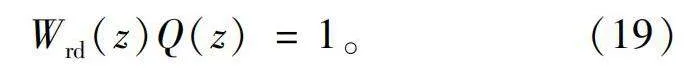

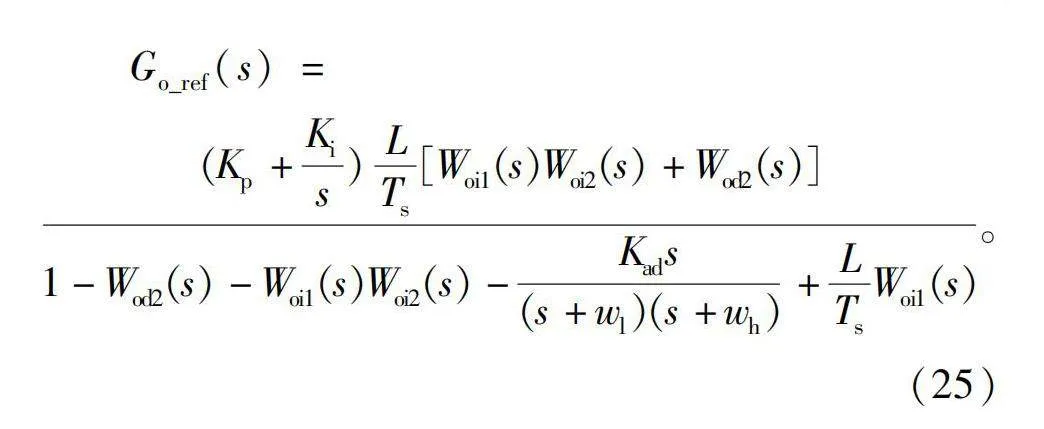
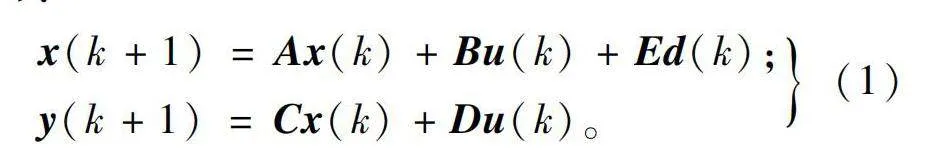
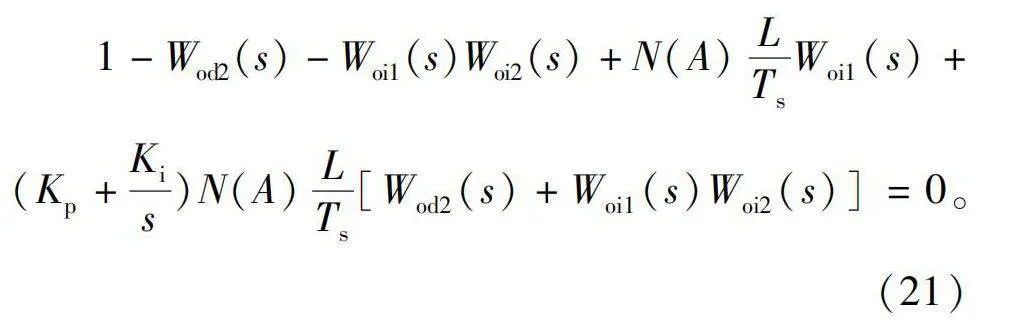
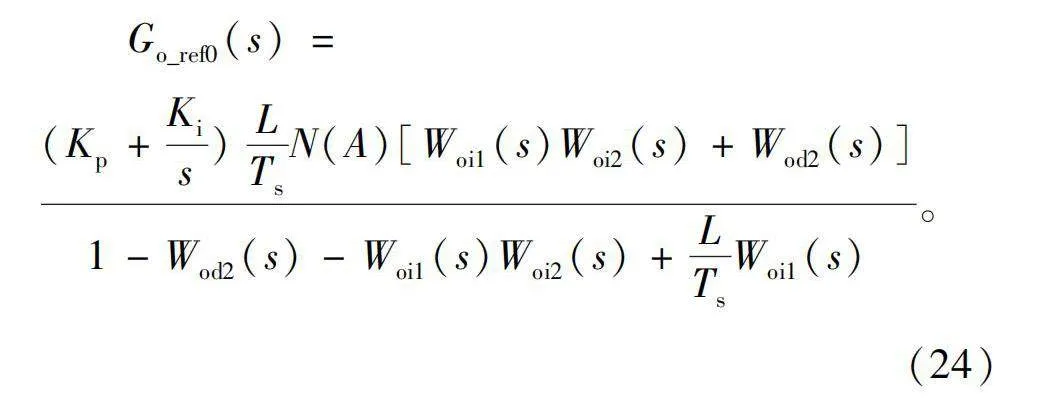
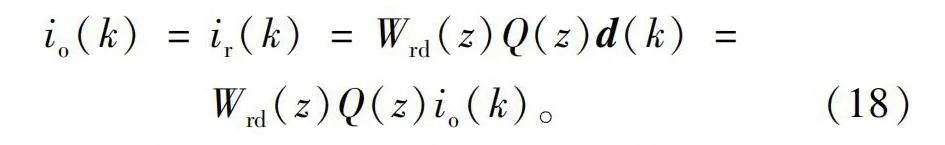



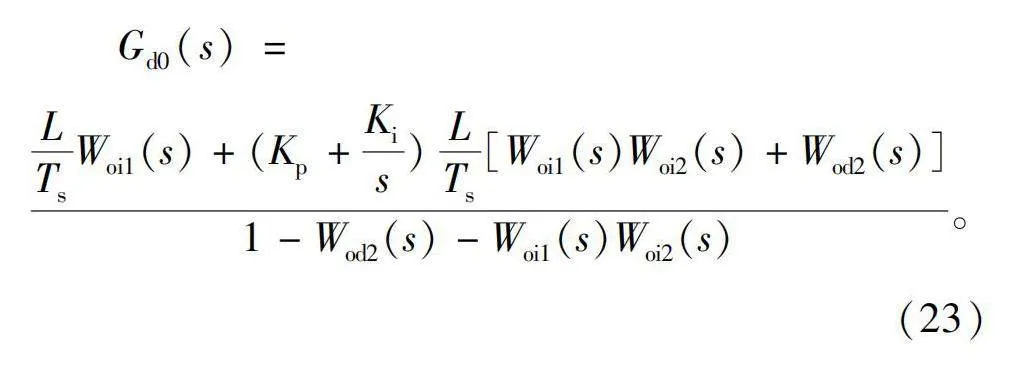
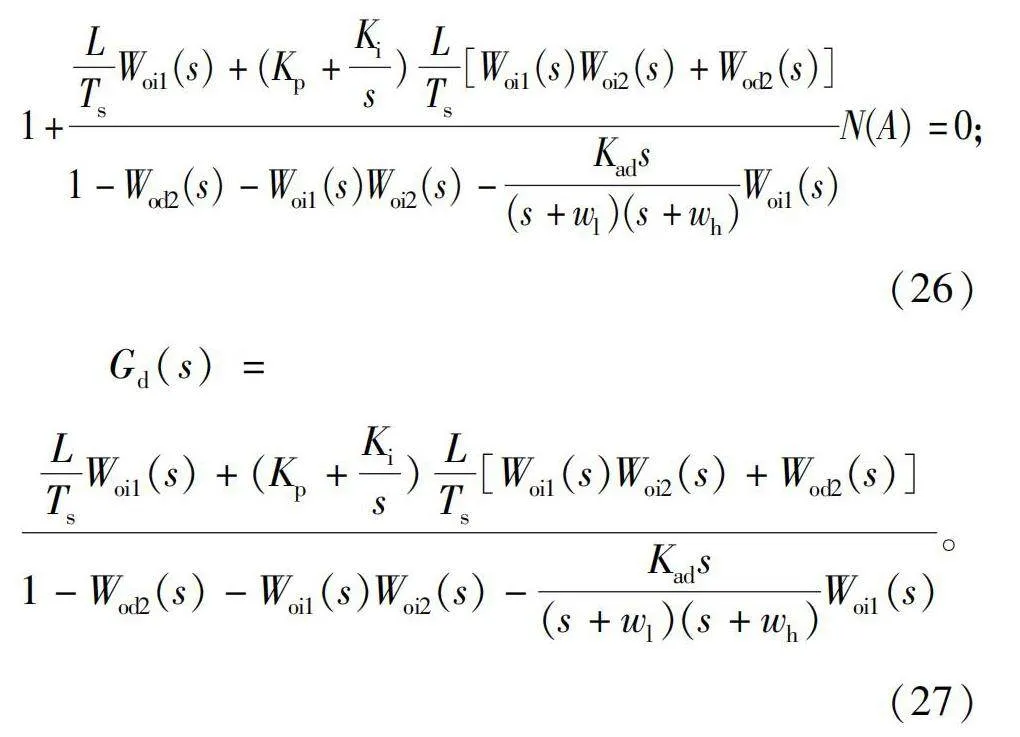


摘 要:在以光伏储能装置为主体的直流微网中,外部扰动容易引起直流母线电压波动,导致系统输出电能质量下降。为提升系统动态响应性能,针对直流微网中常用的Buck型双向DC-DC变换器,提出一种基于残差生成器的改进电流补偿模型预测控制策略。首先,对模型预测控制(MPC)环节进行线性等效,证明采用校正前PI+MPC控制时,系统在0 rad/s时存在失稳风险。然后,由此设计负低-高通滤波器校正环节,并从调节系数变化和模型参数不确定性等角度进行分析,验证改进后系统的稳定性和动态性能得到明显改善。仿真与实验结果表明,基于残差生成器的电流补偿能有效平抑外界扰动引起的母线电压波动,负低-高通校正环节在改善系统性能的同时又进一步抑制电感电流噪声,进而平滑母线电压曲线。最终,证明提出的改进策略可显著提升直流微网的动态响应性能。
关键词:直流微网;DC-DC变换器;残差生成器;改进模型预测;负低-高通滤波器
DOI:10.15938/j.emc.2024.10.009
中图分类号:TM46
文献标志码:A
文章编号:1007-449X(2024)10-0085-14
收稿日期: 2023-11-22
基金项目:电力传输与功率变换控制教育部重点实验室(上海交通大学)开放课题(2023AA02);省部共建电工装备可靠性与智能化国家重点实验室(河北工业大学)开放基金重点项目(EERI_KF2022002);江苏省配电网智能技术与装备协同创新中心开放基金项目(XTCX202305);四川省氢能源与多能互补微电网工程技术研究中心开放基金(2024DWNY005);国家自然科学基金(51807106)
作者简介:
李劲松(1987—),男,博士,副教授,研究方向为新能源储能并网控制与电工装备先进制造;
沈琦丰(1999—),男,硕士研究生,研究方向为光储系统协调控制;
李国锋(1968—2024),男,博士,教授,博士生导师,研究方向为电气设备状态检测与诊断及特种功率变换技术;
吕 敬(1985—),男,博士,副教授,研究方向为新能源发电并网稳定性分析;
华 浩(1988—),男,博士,副教授,研究方向为电力电子系统稳定分析与控制;
杨庆新(1961—),男,博士,教授,博士生导师,研究方向为工程电磁场数值分析;
李永建(1977—),男,博士,教授,博士生导师,研究方向为电力电子磁元件设计与特性分析。
通信作者:李劲松
Improved model predictive control for Buck bi-directional converter based on residual generator
LI Jingsong1,2, SHEN Qifeng1,2, LI Guofeng1,2, LÜ Jing3, HUA Hao3, YANG Qingxin4, LI Yongjian4
(1.School of Electrical Engineering, Dalian University of Technology, Dalian 116024, China; 2.Dalian New Power System Engineering Research Center, Dalian University of Technology, Dalian 116024, China; 3.Key Laboratory of Control of Power Transmission and Conversion, Ministry of Education, Shanghai Jiao Tong University, Shanghai 200240, China; 4.State Key Laboratory of Reliability and Intelligence of Electrical Equipment, Hebei University of Technology, Tianjin 300130, China)
Abstract:In DC microgrids dominated by photovoltaic energy storage devices, external perturbations are prone to cause DC bus voltage fluctuations, leading to degradation of system output power quality. In order to improve the dynamic response performance of the system, an improved current compensation model predictive control strategy based on residual generator was proposed for the Buck bi-directional DC-DC converter commonly used in DC microgrids. Firstly, a linear equivalent of the model predictive control (MPC) link was performed to demonstrate the risk of system instability at 0 rad/s when using pre-correction PI+MPC control. Secondly, the resulting negative low-high-pass filter correction link was designed and analyzed from the perspectives of regulation coefficient variation and model parameter uncertainty to verify that the stability and dynamic performance of the improved system were significantly improved. Through simulation and experiments, the results show that the current compensation based on residual generator can effectively stabilize the bus voltage fluctuation caused by external disturbances, and the negative low-high-pass correction link can improve the system performance and further suppress the inductor current noise, so as to smooth the bus voltage curve. Finally, it is proved that the improved strategy can significantly enhance the dynamic response performance of DC microgrid.
Keywords:DC microgrid; DC-DC converter; residual generator; improved model prediction; negative low-high-pass filter
0 引 言
近年来,随着全球气候变暖、能源短缺等问题的不断加剧,可再生能源受到越来越多的关注。其中,分布式光伏发电因其具有无噪声、无污染、安装方便的优点,已成为我国典型的直流微网发电类型[1-3]。
由于直流微网不存在无功功率的波动,因此直流母线电压是衡量直流微网安全与稳定运行的重要指标[4-6]。如果直流母线电压失稳,会威胁用电负荷的正常工作,甚至导致保护系统误动作,严重情况下将引起区域电压不平衡、电网解列等,危害大电网的经济运行。而当逆变器接入直流微网后,交流侧的三相不平衡也会使直流母线电压出现电压纹波等问题[7-8]。
目前,由分布式光伏组成的直流微网中,广泛使用Buck型双向DC-DC变换器实现光伏和储能之间的能量平衡与电压稳定[9-10]。针对直流微网中的电能质量问题,大量专家学者对变换器控制策略进行改进研究,以期达到主动治理。当直流微网通过双向DC-AC变流器与交流电网之间发生功率交换时,若能够实现直流微网内部的分布式电源或储能单元合理控制,则对双向DC-AC变流器而言,直流侧可等效为恒定直流源,仅需平滑切换双向DC-AC变流器控制模式即可达到整个系统的运行模式无缝切换[11-13]。
目前常用控制方法有PI控制、自抗扰控制、模型预测控制(model predictive control,MPC)等。文献[14]采用传统PI双闭环DC-DC控制器,用于平抑母线电压波动,但在暂态时仍有较大的超调量。文献[15]基于传统PI控制,在电流环中引入fal函数实时调节误差反馈系数,增强系统鲁棒性。文献[16]采用自抗扰控制,增强系统抗干扰性能。但调节参数过多,难度较大。文献[17]提出基于非线性扰动观测器的电压控制方法,以提高直流微网的稳定性。文献[18]基于文献[17],同时考虑外来扰动,设计非线性观测器以抑制母线电压波动。但2种控制方法获得的补偿信号都要再次经过电流内环,存在一定系统延迟。文献[19-20]针对直流微网中因扰动引起的电能质量和环流问题,为每台变换器制定基于观测器的残差补偿控制策略,实现对外部扰动的分散补偿,保证了母线电压稳定。但均仅考虑基于残差生成器的动态补偿器设计,并没有优化变换器控制策略,导致调节参数过多,难以实际应用。
基于观测器控制虽能精准获取扰动信号,进而设计相应的补偿策略,在扰动抑制方面具有良好应用,但观测器的设计难免在原先控制基础上引入额外控制参数和系统延时,可与其他控制方式相结合,在保留观测器精确获取扰动信号优势的同时,以简化系统参数设计。
为简化参数整定复杂度,提高系统动态响应速度,文献[21]提出复合自适应MPC控制器,在有限集模型预测控制基础上加入前馈控制。虽改善了控制器动态响应,但未分析增加的前馈补偿环节对系统稳定性的影响。文献[22]提出完全不使用PI调节器的MPC策略,该方法由模型功率预测控制(model power predictive control,MPPC)和模型预测电压控制(model predictive voltage control,MPVC)组成,再通过MPVC算法和下垂控制保证交流电压输出的稳定和功率的合理分配,但未分析取消PI环节校正后系统的稳定性变化。文献[23]引入开关序列近似实现定频控制,以有效改善蓄电池的电流谐波。但仅涉及直流负载突变和前级输出波动,以致考虑扰动形式过少,难以准确验证变换器在复杂工况下的工作性能。文献[24]采用含虚拟电容器的MPC方法,以避免使用恒定直流电容时系统动态响应差的问题。但仅验证了MPC方法在发生随机负荷变化时的电压波动抑制效果,并未考虑实际应用中其他形式扰动信号影响。为提升MPC精度,文献[25]提出利用扰动观测器补偿外部扰动的控制策略,但未分析引入补偿器后系统动态性能变化。
综上,尽管MPC方法可有效简化变换器控制参数设计,减弱系统延时所带来的不良影响,对扰动信号的抑制能力却较弱,尤其是当扰动形式未知时,仅依靠MPC难以实现母线电压稳定。
鉴于上述现状,本文针对由光伏、储能和交直流负载组成的直流微网,提出一种基于残差生成器的改进电流补偿模型预测控制策略。首先给出Buck型双向DC-DC变换器在离散状态下的电感电流预测方程,定量分析扰动量对模型预测控制的影响;然后对含MPC环节的开关电路进行线性等效,并设计补偿器以消除扰动影响;针对校正前系统缺少稳定裕度的问题,进而设计负低-高通滤波器,并通过仿真计算验证校正环节对系统性能的改善;最终搭建实验电路,结果表明所提控制策略可以有效抑制电感电流噪声和母线电压波动,提高直流微网的动态响应性能。
1 PI+MPC控制下变换器等效建模
1.1 Buck型双向DC-DC变换器建模
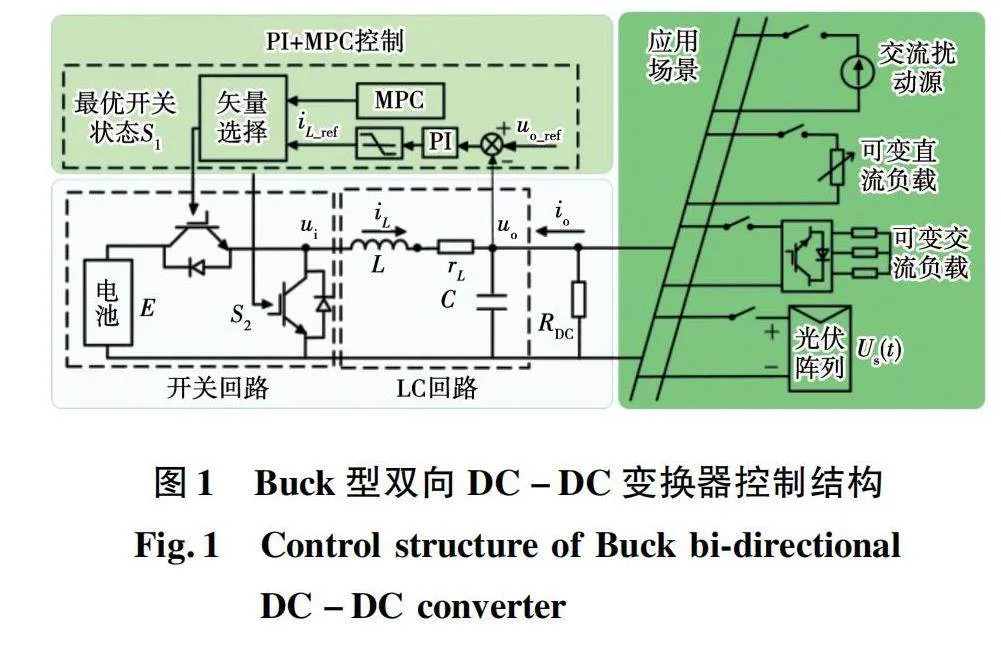
在光伏直流微网中,广泛使用Buck型双向DC-DC变换器控制直流母线电压,其控制结构如图1所示。其中:C为直流母线电容;L为直流侧电感;rL为电感杂散电阻;RDC为直流母线负载;ui为开关回路输出电压,即LC回路输入电压;iL为电感电流;uo为直流母线电压;io为扰动电流。
在图1的控制结构中,iL和uo的离散空间方程为:
x(k+1)=Ax(k)+Bu(k)+Ed(k);
y(k+1)=Cx(k)+Du(k)。(1)
式中:A为系统矩阵;B为输入矩阵;C为输出矩阵;D为直接传递矩阵;E为扰动矩阵;x(k)为k时刻状态量;u(k)为k时刻输入量;y(k)为k时刻输出量;d(k)为k时刻扰动量;Ts为系统采样周期。各参量具体含义如下:
x(k+1)=iL(k+1)uo(k+1);x(k)=iL(k)uo(k);u(k)=[ui(k)];d(k)=[io(k)];A=1-rLLTs-1LTs1CTs1;B=1LTs0;C=1001;D=0;E=0-1CTs。(2)
1.2 基于残差生成器的电流补偿控制
为消除扰动量d对MPC预测的影响,构建基于残差生成器的电流补偿模型预测控制,结构如图2所示。变换器电流内环的参考值iL_ref由补偿器和外环PI控制器共同给出,补偿器Q(z)利用残差生成器得到的残差获得补偿信号,从而消除扰动量对母线电压的影响,抑制母线电压突变。
基于龙伯格观测器的残差生成器方程为:
x^·(s)=(A-LC)x^(s)+(B-LD)u(s)+Ly(s);
r(s)=y(s)-Cx^(s)-Du(s)。(3)
式中:x^·为重构状态量;L为输出误差反馈矩阵。
由图2所示的控制结构可知,扰动输入d会影响被控对象输出y,从而使残差生成器输出残差r,通过补偿器Q(z)得到补偿信号ir,进而抑制扰动d对输出y的影响,提升系统鲁棒性。在考虑电流补偿信号ir后,模型预测控制的代价函数为
J=[iL_ref1(k+1)+ir(k+1)-iL(k+1)]2=
[iL_ref(k+1)-iL(k+1)]2。(4)
1.3 模型预测环节线性等效
MPC是一个非线性离散控制器,为分析系统稳定性,需将控制器线性化。则代价函数可表示为:
J=[iL_ref(k+1)-iL(k+1)]2=GTG;(5)
GT=[iL_ref(k+1)-iL(k+1)]。(6)
联立式(5)和式(6),可得
GT=[iL_ref(k+1)-(1-rLLTs)iL(k)+1LTsuo(k)-TsLui(k)]。(7)
则有:
FT=[iL_ref(k+1)-(1-rLLTs)iL(k)+TsLuo(k)];
GT=FT-TsLui(k)。(8)
因此代价函数J可进一步表示为
J=GTG=FTF-2TsLui(k)F+T2sL2u2i(k)。(9)
为判断代价函数最小时的ui,需对ui求偏导,即
联立式(8)与式(10),可得
ui(k)=LTs[iL_ref(k+1)-(1-rLLTs)iL(k)+TsLuo(k)]。(11)
为确保此时ui是全局最小值,对ui求二次偏导,即
所以ui(k)=LTsF对应代价函数J的最小值。
因Ts很小,即rLLTs≈0,则式(11)又可改写为
ui(k)≈LTs[iL_ref(k+1)-iL(k)+TsLuo(k)]=LTs[iL_ref(k+1)-iL(k)]+uo(k)。(13)
当不考虑MPC的非线性和离散性时,可近似看作一个增益很大的比例控制器,其等效结构如图3所示。
1.4 基于龙伯格观测器的残差补偿器设计
1.4.1 观测器极点配置
根据式(3)的残差生成器方程,定义误差为:
e·(s)=x·-x^·=(A-LC)e(s)+Ed(s);
r(s)=Ce(s)。(14)
则误差传递函数阵为
Wrd(s)=C[sI-(A-LC)]-1E。(15)
系统存在uo、iL 2个输出量(状态量),因此需设计反馈阵L如下:
L=L1L2L3L4。(16)
1.4.2 动态补偿器设计
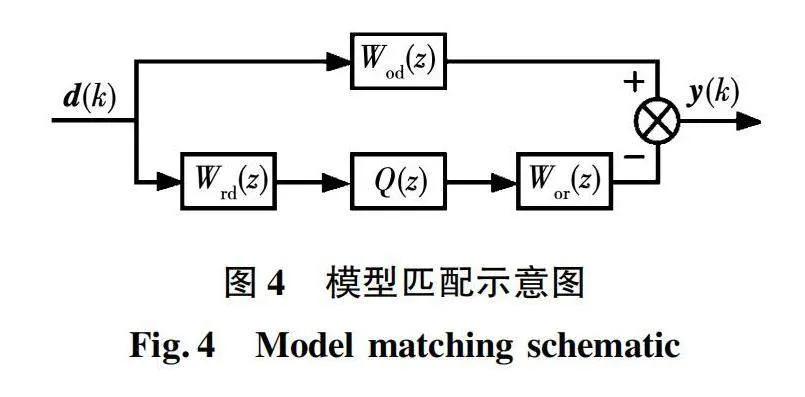
由于MPC是离散控制环节,因此动态补偿器Q(z)的设计应在离散形式下进行。根据模型匹配思想确定动态补偿器Q(z),匹配形式如图4所示。其中:Wod(z)为扰动输入d(k)到y(k)离散传递函数;Wrd(z)为残差生成器离散传递函数;Q(z)为动态补偿器;Wor(z)为补偿量ir(k)到y(k)离散传递函数。
根据鲁棒模型匹配原理,最优控制可描述如下:仅有扰动d(k)输入时,系统输出y(k)为0;系统达到稳态后,母线电压不会因扰动d(k)而出现波动,始终保持稳定。故动态补偿控制器Q(z)可由下式求解:
Q(z):min‖Wod(z)-Wrd(z)Q(z)Wor(z)‖∞。(17)
在实际应用中,首先考虑仅有扰动量d(k)作用的情况,此时补偿器Q(z)输出补偿量ir(k)。在改进MPC达到稳态后,可实现电感电流iL(k)=iL_ref(k)=ir(k)。若实现输出电压稳定不变,即uo(k+1)=uo(k),则由式(2)可知,需iL(k)=io(k),故此时应有ir(k)=io(k)。
再考虑输入量u(k)和扰动量d(k)均不为0的工作场景:假设在k时刻系统实现无差跟踪,有uo_ref(k)=uo(k),若此时iL(k)≠io(k),则uo(k+1)≠uo(k),系统始终无法趋于稳定。
综上,结合图4的模型匹配思想,当且仅当满足下式时,系统可实现最优控制,对扰动信号完全抑制,即
io(k)=ir(k)=Wrd(z)Q(z)d(k)=Wrd(z)Q(z)io(k)。(18)
故当满足下式时,可求得动态补偿器Q(z),即
Wrd(z)Q(z)=1。(19)
1.4.3 基于观测器的残差补偿器系统稳定性分析
经1.4.1节极点配置后,误差传递函数阵所有特征根均具有负实部,观测器系统稳定。此时基于龙伯格观测器的残差生成器补偿系统完整传递函数为
Wpd(z)=Wrd(z)Q(z)=1。(20)
因此,在确保基于观测器系统Wrd(z)稳定后,由于补偿器Q(z)的特征,整个补偿系统自然得到稳定。
1.5 未校正前PI+MPC控制下系统稳定性分析
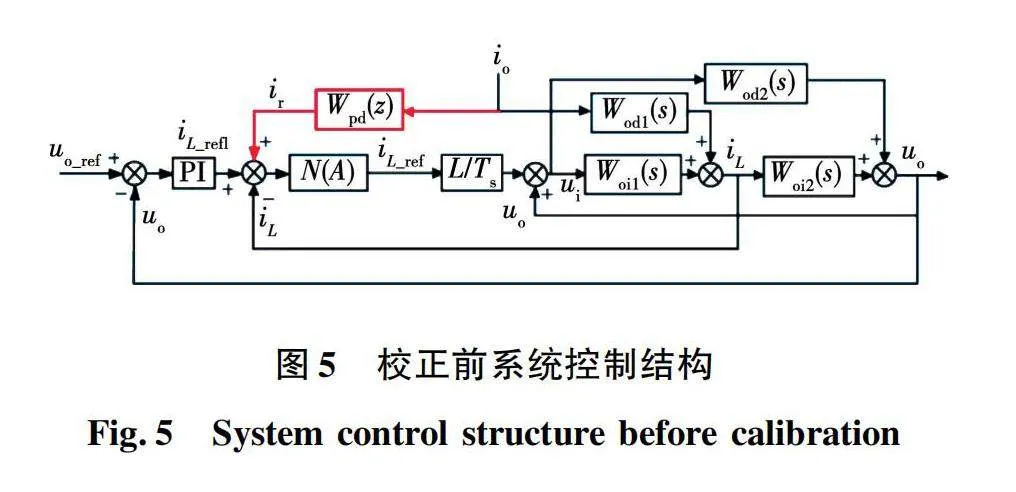
为方便讨论,令反馈阵H(s)=1,经1.4节残差补偿器设计后,图3所示的控制结构可进一步修正为如图5所示的校正前系统控制结构。其中:Woi1(s)为ui到iL传递函数;Woi2(s)为iL到uo传递函数;Wod1(s)为io到iL传递函数;Wod2(s)为ui到uo传递函数;N(A)为非线性饱和特性环节。
在实际应用中,常需使用不同的PI调节系数以满足不同场景下的特定控制需求。但不同的PI调节系数可能会造成系统稳定裕度降低,带来系统失稳风险。因此,需检验不同调节系数下的系统稳定性与动态性能。
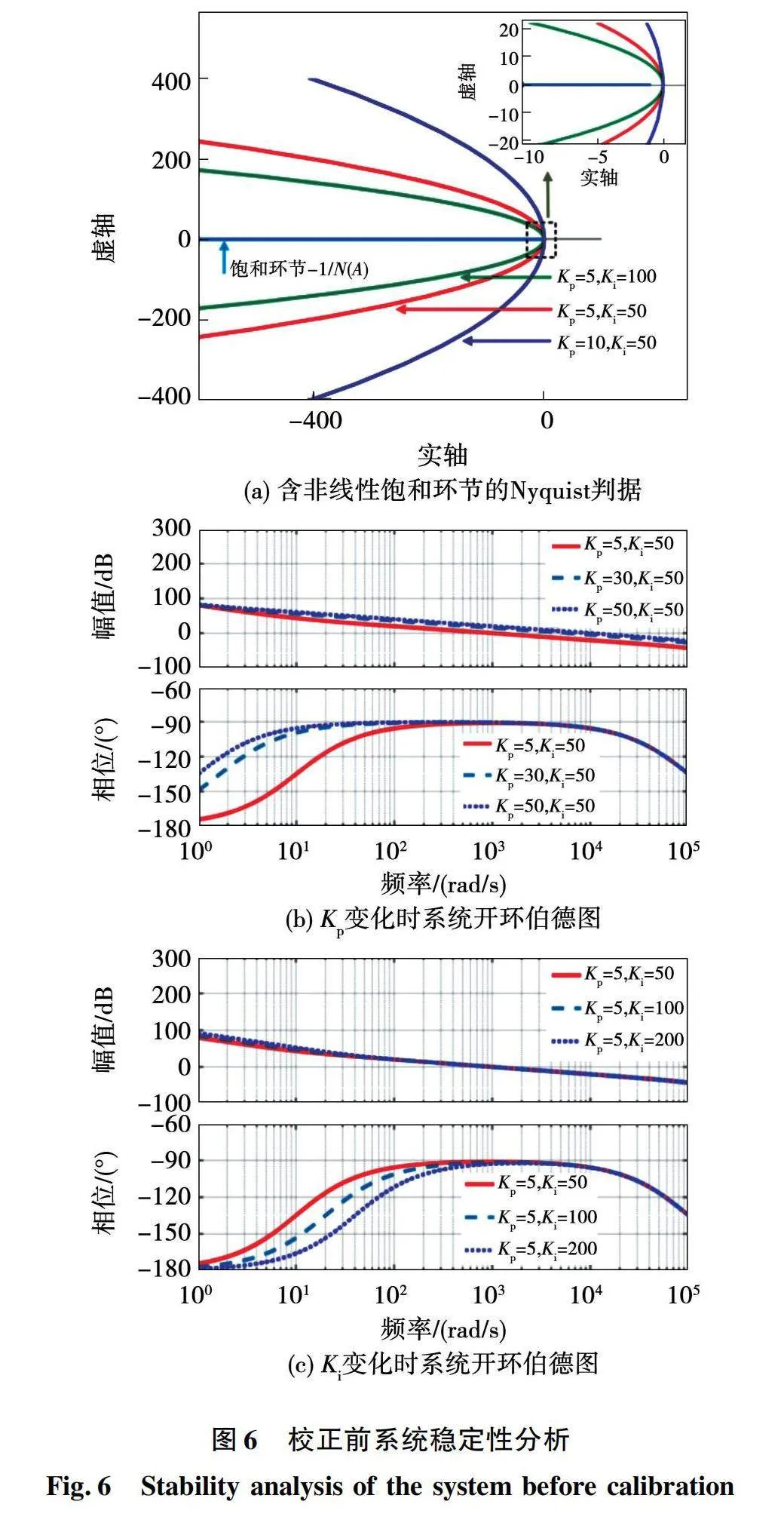
当发生负载投切或电网扰动时,在调节的动态过程中,非线性饱和环节N(A)发挥作用。此时通过非线性环节奈奎斯特(Nyquist)判据判断系统稳定性。
系统闭环特征方程为
因此等效线性环节为
含非线性饱和环节的Nyquist判据如图6(a)所示,由图可知,此时等效线性环节Gd0(s)曲线始终不包括[-1/N(A)]曲线,因此这种情况下系统是稳定的。
当PI+MPC控制达到稳定时,饱和环节N(A)失去限幅作用,可等效为增益为1的比例环节。此时系统开环传递函数为
绘制系统开环伯德图如图6(b)和图6(c)所示。此时PI环节中的比例系数Kp和积分系数Ki均主要影响相频特性曲线中低频段。表现为:随Kp增大,相频曲线低频段上移,由于幅频特性曲线几乎不受Kp变化影响,故Kp的增大使系统在低频段幅值裕度增大;随Ki增大,相频曲线中低频段下移,Ki的增大无助于增大系统低频段,尤其是0 rad/s附近幅值裕度。因此若PI系数选取不当,系统在0 rad/s的幅值裕度非常小,存在失稳风险。校正前控制系统难以满足多数场合的控制需求,应用受限。
1.6 负低-高通滤波器电流反馈校正
根据1.5节分析可知,PI+MPC控制达到稳定后,校正前系统在低频段幅值裕度很小,当系统输入为给定的直流指令uo_ref,系统存在失稳风险,需进行校正以改善系统低频段性能。
观察发现系统在低频段幅值裕度很小的本质原因是系统特征方程缺项,可参考三相LCL型并网逆变器引入电容电流反馈有源阻尼校正的思想,为系统设置“阻尼项”以引入反馈。
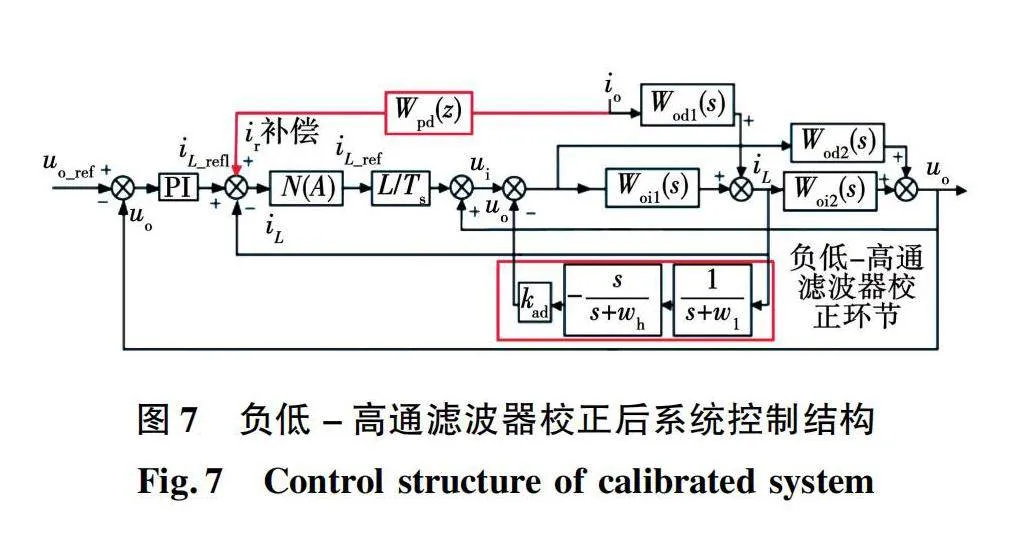
变换器工作过程中,外界干扰会为电感电流iL引入高频噪声,从而引起直流微网电能质量问题。为提高系统低频段幅值裕度并抑制电感电流噪声,本文设计负低-高通滤波器反馈环节对原电流补偿模型预测控制进行校正。校正后系统控制结构如图7所示。同理,可根据开环传递函数和闭环特征方程分析系统性能。
校正后系统开环传递函数为
此时闭环特征方程与等效线性环节为
1.6.1 调节系数对校正后系统性能影响
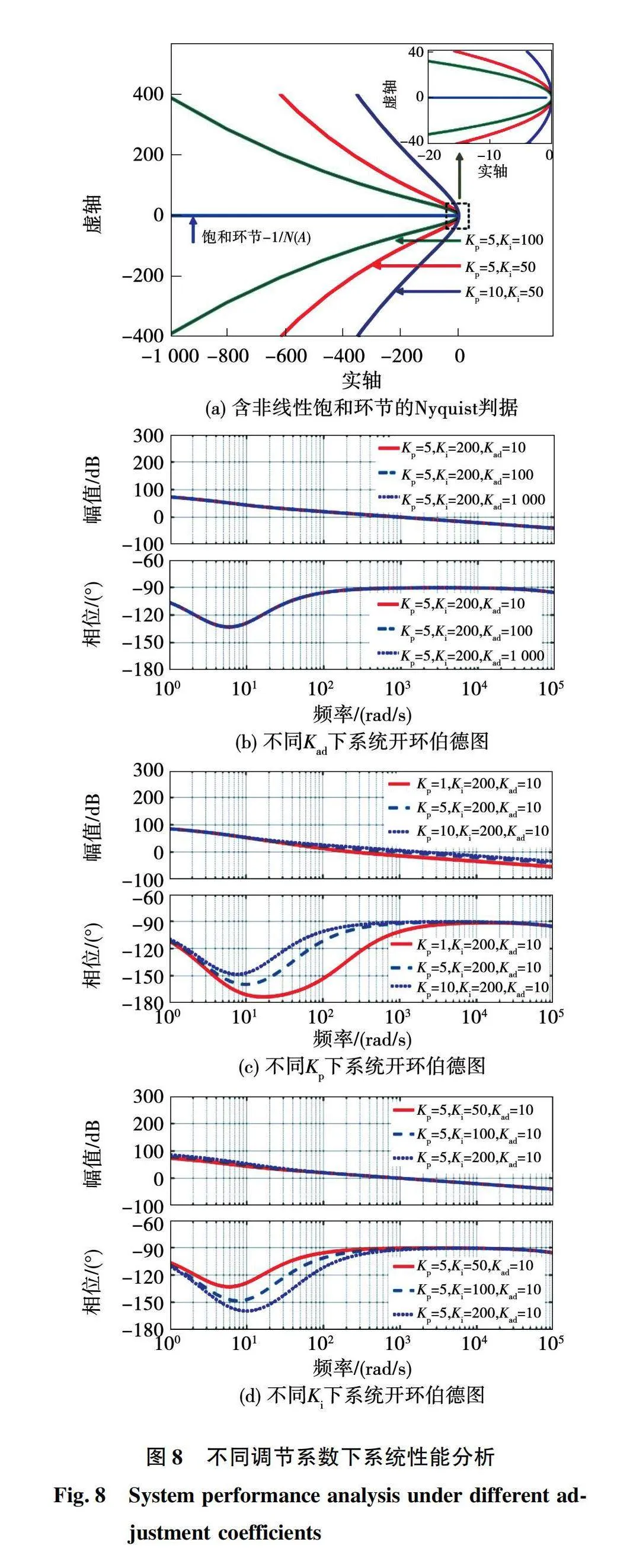
考虑系统工作中不同调节系数下的稳定性和动态性能,根据式(25)~式(27),绘制校正后电流补偿模型预测控制系统Nyquist判据图和开环伯德图,如图8所示。系统参数均设定为L=1 mH、C =5 mF、rL=0.5 Ω、wl=10 rad/s、wh=100 000 rad/s。
由图8(a)所示Nyquist判据可知,此时等效线性环节Gd(s)曲线始终不包括[-1/N(A)]曲线,因此这种情况下系统是稳定的。
当PI+MPC控制达到稳定时,N(A)等效为增益为1的比例环节。根据图8(b)~图8(d),由相频特性曲线进行系统稳定性分析:负低-高通校正环节的校正系数Kad对系统开环伯德图几乎没有影响,即Kad的变化基本不会影响系统性能;比例系数Kp影响中低频段的相位增益,且随Kp的减小相位曲线下降;积分系数Ki影响低频段相位增益,且表现为随Ki的增大,低频段相位曲线下降。这说明随Kp减小,Ki增大,系统稳定裕度会有所下降,但始终具有相当的稳定裕度,明显优于校正前系统。
由幅频特性曲线分析系统动态性能:Kp、Ki、Kad的变化对幅频曲线影响不大,系统在低频段始终具有较大的幅值增益和穿越频率以及较缓的幅频曲线斜率,以确保系统输出uo尽可能跟随输入uo_ref 。在高频段,系统幅值增益小于0 dB,系统具有较好的高频噪声抑制能力和良好的控制性能。
由图8可知,当调节系数变化时,系统带宽始终维持在500 rad/s附近,说明调节系数变化对系统带宽影响较小。同时,这一较大的带宽确保系统在不同工作场景下均具有快速动态响应能力。
综上,在采用负低-高通滤波器校正后,系统稳定裕度得到了明显增大。当调节系数Kp、Ki和Kad根据实际应用情况作出调整时,系统仍能保证全频段内的稳定,且基于改进的PI+MPC系统始终具有较好的直流指令跟踪、高频噪声抑制和快速响应能力。证明改进后的电流补偿模型预测控制在不同工作场景下,始终具有较强的稳定性和良好动态性能,能满足众多工作需求。
1.6.2 参数不确定时系统鲁棒性分析
在Buck型双向DC-DC变换器中,电感L、电感杂散电阻rL和电容C会因为工作时间和环境发生变化,导致模型参数具有不确定性。此时,变换器的离散状态空间表达式为:
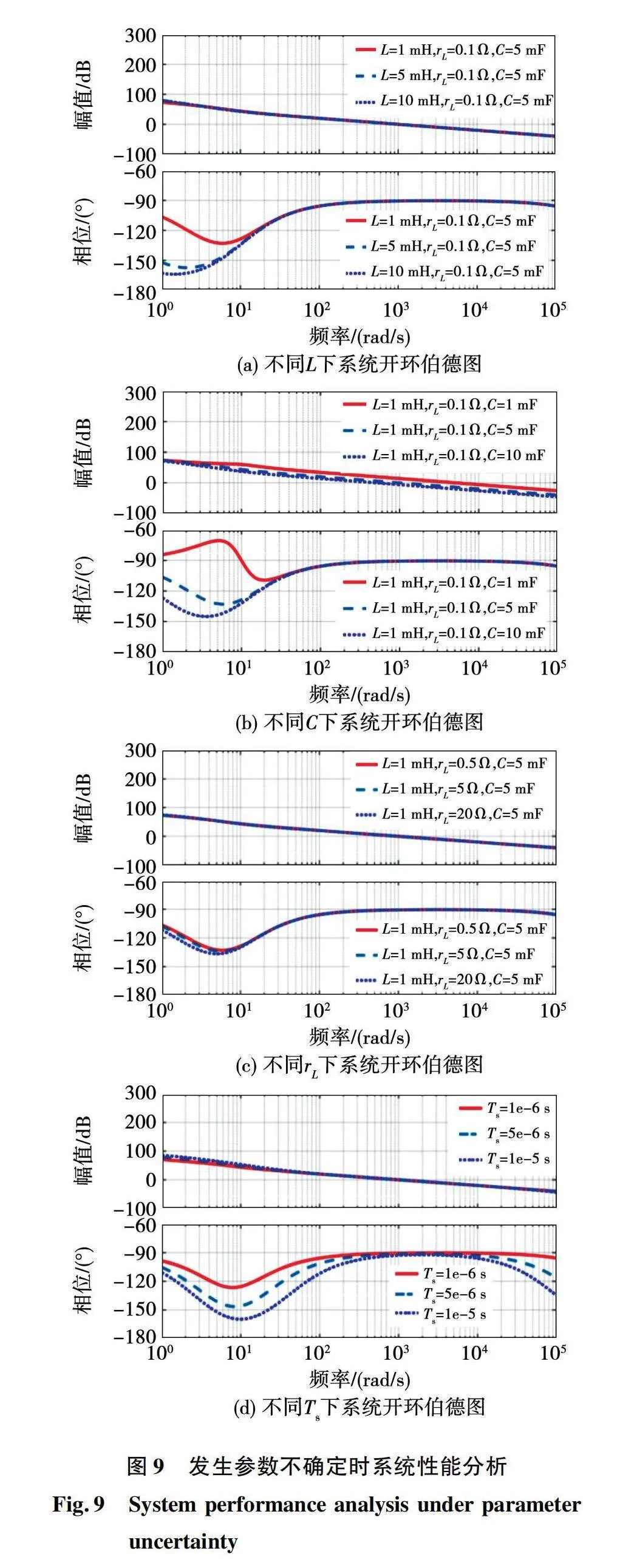
由式(28)可知,当系统存在参数不确定时,MPC预测方程将不再准确,进而影响算法控制效果。目前针对系统参数的不确定性,文献[26-27]提出最优参数辨识方法,可及时完成模型校正,实现最优模型预测控制。但对发生参数不确定时电流补偿模型预测控制的稳定性和动态性能却少有研究。本文为分析模型参数不确定性对系统性能尤其是系统稳定性的影响,绘制了参数发生变化后系统的开环伯德图,如图9所示。系统调节系数均为Kp=5、Ki=50、Kad=1 000。
根据图9,由相频特性曲线进行系统稳定性分析:参数不确定主要影响系统相频特性曲线,从而改变幅值裕度。当L、C增大时,系统相频曲线低频段均发生下移;当电感杂散电阻rL增大时,相频曲线低频段有所下降,高频段则有所上升。这说明当系统发生参数不确定时,系统稳定裕度会相应变化,但始终具有相当的稳定裕度,能在多数工作场景下保持系统稳定。
此外,由于MPC环节控制精度依赖于采样周期Ts,为此还考虑了不同采样周期下的系统性能变化。由图9(d)可以看出,随Ts增大,系统开环相频曲线整体下移,幅值裕度相应缩小。在Ts过大的极端情况下,系统存在失稳风险,这与实际情况相符。
同样,由幅频特性曲线分析系统动态性能:L、C、rL和Ts的变化对幅频曲线影响不大,系统在低频段始终具有较大的幅值增益和穿越频率以及较缓的幅频曲线斜率,以确保系统输出uo尽可能跟随输入uo_ref;在高频段,系统幅值增益小于0 dB,系统具有较好的高频噪声抑制能力。
参数不确定发生时,系统带宽同样始终维持在500 rad/s附近,说明参数不确定亦对系统带宽影响较小。这一较大的带宽也确保系统在不同工作场景下均具有快速动态响应能力。根据图9(b),电容C减小时,可进一步增大系统带宽,以获取更快的动态响应速度。
综上,当变换器因长期使用或外界环境影响发生参数不确定时,基于改进的PI+MPC系统仍旧具有较好的直流指令跟踪、高频噪声抑制和快速响应能力。证明即使模型参数出现不确定时,改进后的电流补偿模型预测控制仍具有良好的控制稳定性,且动态性能较校正前有明显提升。
2 仿真分析
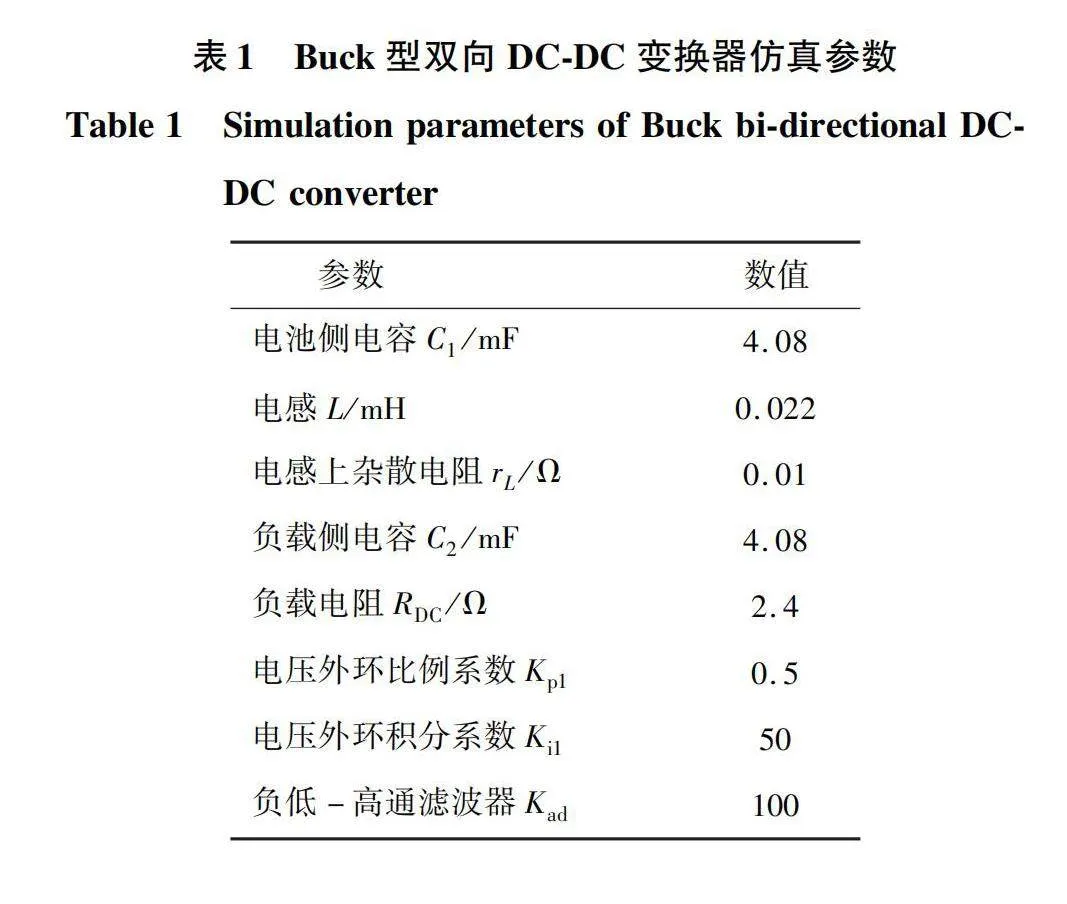
基于MATLAB/Simulink平台搭建双向Buck型DC-DC变换器的直流微网模型,控制拓扑如图10所示,其参数如表1和表2所示。
为验证所提出的改进电流补偿模型预测控制的优越性,比较了不同工作条件下,直流微网在采用传统双PI控制与补偿前后PI+MPC控制下的母线电压曲线变化,结果如图11所示。
由图11(a)可知,当光照强度从0到1 000 lx的标准光强变化时,储能系统能通过双向DC-DC变换器改变实时出力,始终维持母线电压稳定。在相同的电压外环PI参数下,改进后PI+MPC控制的电压毛刺更少,具有更好的控制效果。证明当应用于光伏储能系统时,改进后的电流补偿模型预测控制策略能有效应对光照强度变化下的母线电压波动问题,在光伏储能系统这一典型应用场景中具有良好的控制效果。
在图11(b)中,考虑光伏储能系统中的母线负载突变,使用可变直流负载模拟直流母线上负载投切:0.5 s时令母线负载由8 Ω切换至12 Ω,采用电流补偿双PI控制发生4.16 V电压跌落,电流补偿PI+MPC控制后,仅发生3.12 V电压跌落且可快速平稳地恢复至稳态,几乎没有电压振荡。证明改进后的PI+MPC控制在母线负载投切时具有更优异的控制性能,能有效解决光储系统中母线电压因负载投切而发生的电压跌落和振荡问题。
当直流微网输出经逆变器向三相不平衡负载供电时,负载上会出现三相不平衡电流,引起母线电压的二倍频电压纹波。由图11(c)可知,当交流侧为三相不平衡负载时,补偿前PI+MPC控制下母线电压会在期望值uo_ref上下发生频率100 Hz、幅值2.5 V的周期性振荡。采用补偿后的改进PI+MPC控制,母线电压振荡幅值变为1.08 V。证明所提改进控制策略能有效抑制带三相不平衡负载的逆变器切入后导致的二倍频电压波动,提高系统鲁棒性。
图11(d)为直流微网经逆变器并入电网时交流扰动io引起的母线电压波动。为检验补偿后的改进PI+MPC控制策略对扰动电流的抗干扰能力,考虑扰动为正弦信号的极端情形,因信号采样存在延时,系统无法预知下一时刻的扰动量特征,母线电压仍呈现正弦波动。电流补偿后系统在面对交流侧扰动时,母线电压振荡幅值为3.19 V,明显小于补偿前系统的7.08 V电压振荡。证明系统对因交流侧扰动导致的母线电压波动具有抑制能力,在极端情况下仍能尽可能维持母线电压稳定。
3 实验验证
为验证本文所提出的改进电流补偿模型预测控制有效性,采用STM32F334芯片搭建500 W的Buck型双向DC-DC变换器,实验平台如图12所示。变换器采样主频为200 kHz,采样周期为5×10-6 s,其余仍采纳表1和表2所示实验参数。
3.1 电感电流噪声抑制验证
在1.6节中引入的负低-高通滤波环节,本质是一个带通滤波器。该环节不仅改善改进前PI+MPC控制下稳定裕度欠缺的问题,还可筛选出特定频率的噪声信号,进而在PI+MPC环节内消除噪声信号影响,起到抑制电感电流噪声的作用。
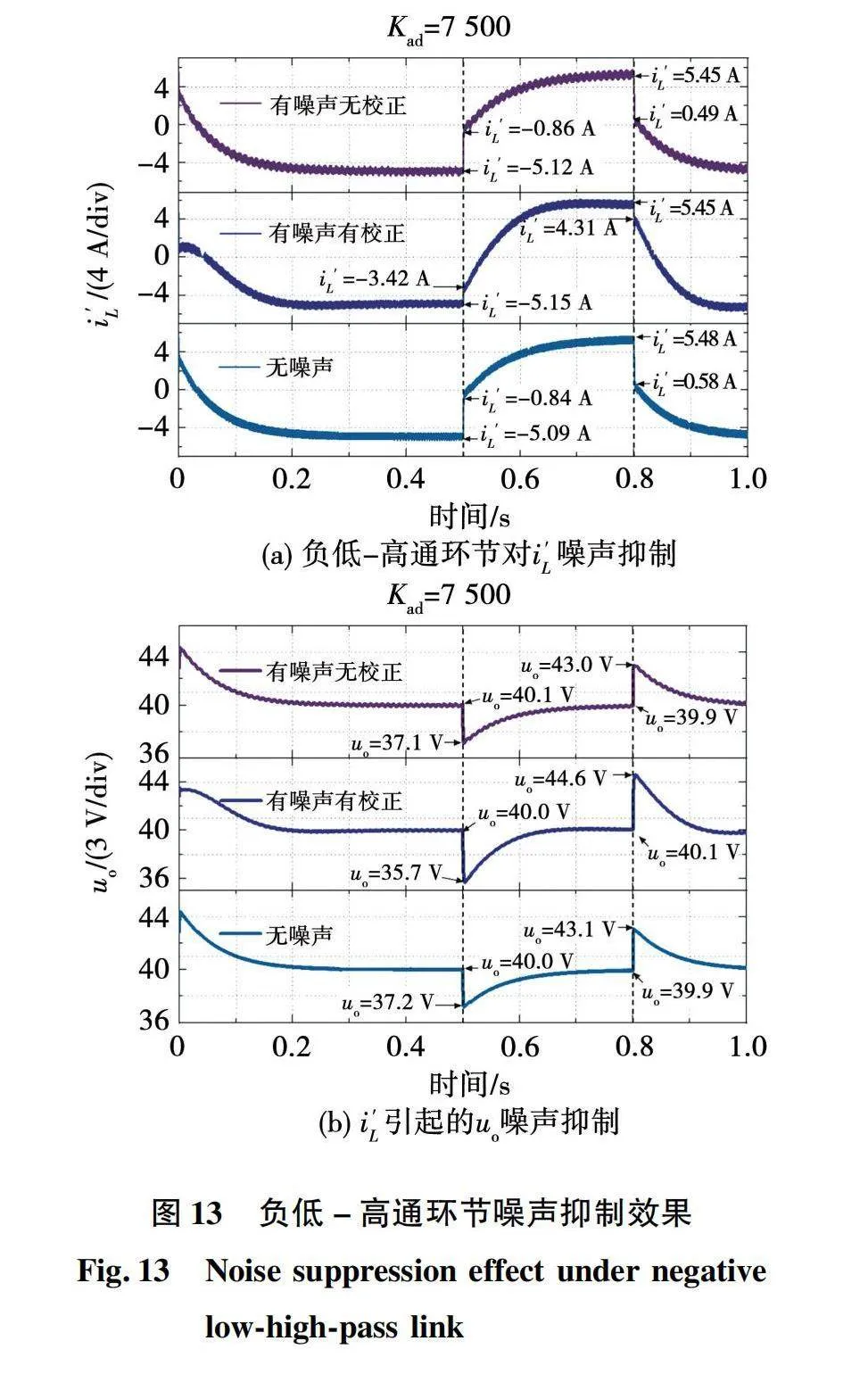
由傅里叶变换可知,任意信号可分解为不同频率正弦信号的叠加。因此,以幅值为0.2 A、频率为50 Hz的正弦信号in作为观测电流噪声,则观测到的电感电流i′L=iL+in。为避免环境噪声对实验结果的影响,根据表1、表2内参数搭建2台相同的DC-DC变换器,以in作为公共噪声同时进行实验,此时电感电流和母线电压如图13所示。
由图13可知,无论噪声与校正的有无,i′L和uo的稳态值均几乎保持一致。但无校正时i′L在0~1 s内始终存在明显的正弦噪声,即改进前PI+MPC控制无法滤除电感电流上出现的噪声信号,反映到图13(b)的母线电压上,使母线电压在0~1 s内也出现噪声,降低电能质量。
在加入校正环节后,i′L和uo上的噪声显著减少。证明所提出的负低-高通滤波环节能有效滤除i′L噪声,进而抑制由噪声信号引起的母线电压uo波动,提高直流微网电能质量。
同时注意到,在0.5 s时,电池充放电状态改变。因负低-高通环节的引入,i′L仅由-5.15 A变化至-3.42 A,小于无校正时由-5.12 A到-0.86 A的跳变。这是由于校正前电流指令iL_ref=iL_ref1+ir,在引入校正环节后改变为
i′L_ref=iL_ref1+ir+TsLkads(s+wl)(s+wh)i′L,(30)
因此实际i′L也会相应变化。
以0.5 s为例,跳变前i′Llt;0,因此瞬间i′L_reflt;iL_ref,导致i′L变化值更小。而随着i′L趋于平稳,噪声信号in更易被分解和滤除,所以i′L稳态值与无噪声时几乎一致。0.8 s时i′L发生跳变同理。
此时,uo由40.0 V变化至35.7 V,大于无校正时由40.1 V到37.1 V的跳变。这是因为i′L_reflt;iL_ref,导致iL(校正后)lt;iL(校正前),由式(1)和式(2)可知,uo(k+1)=TsiL/C+uo(k),则0.5 s跳变发生后,uo(校正后)lt;uo(校正前),导致uo变化值更大。0.8 s时uo发生跳变同理。
综上,负低-高通环节的引入,在改善系统稳定裕度的同时,可有效抑制噪声对iL和uo的影响,并降低电池充放电状态改变时iL的跳变,有助于延长电池寿命。虽然在这一过程中母线电压跳变值有所增大,但波动仍在可接受范围内,可通过后续观测器设计进一步加以抑制。
3.2 母线电压波动抑制有效性验证
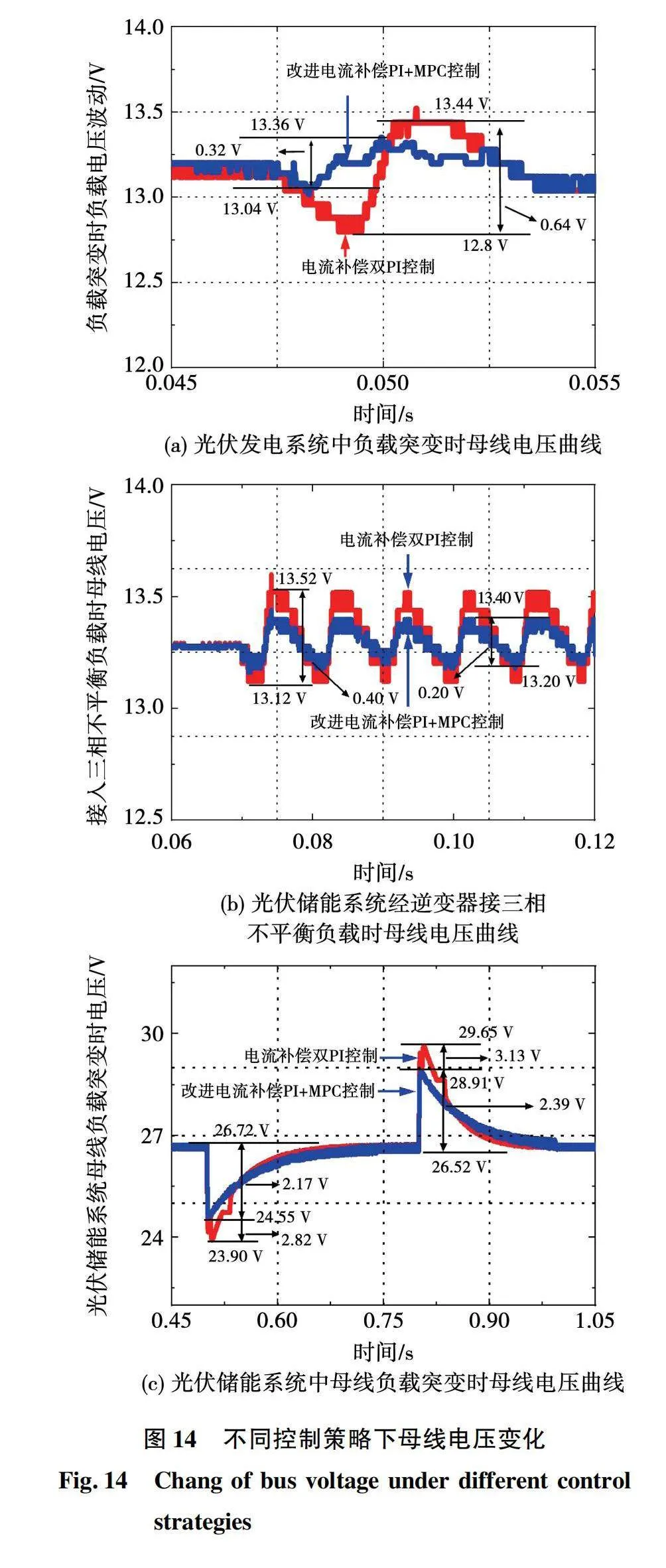
为进一步验证所提出的改进电流补偿模型预测控制的有效性,设计实验比较不同工作条件下,直流微网在采用电流补偿双PI控制与改进电流补偿PI+MPC控制下的母线电压曲线变化,结果如图14所示。
图14(a)为当光伏发电装置通过双向Buck型DC-DC变换器给直流负载供电,直流负载阻值发生突变时的电压波形。最初系统达到稳态,在0.047 5 s时设置直流负载由15 Ω切换至25 Ω,随后始终工作于25 Ω。电流补偿双PI控制在负载切换过程中电压出现波动,最大电压幅值为13.44 V,最小为12.80 V,波动值为0.64 V;采用改进电流补偿PI+MPC控制后虽也发生电压波动,但波动幅值仅为0.32 V,且达到新稳态用时更短。证明使用改进控制策略的系统鲁棒性更强,能更好应对负载突变时的电压波动。
图14(b)为当光伏储能装置组成的直流微网通过逆变器接入三相负载,负载存在三相不平衡时的电压波形。最初系统达到稳态,在0.07 s时设置交流侧三相不平衡负载,此时交流侧会对直流母线施加交流扰动。采用电流补偿双PI控制时,母线电压波形类似正弦波,在稳态13.25 V附近呈现周期性振荡,振荡频率约为100 Hz,振荡幅值为0.40 V,电压波动率为3.0%。采用改进电流补偿PI+MPC控制后,振荡幅值降为0.2 V,电压波动率为1.5%。证明提出的改进电流补偿模型预测方法能有效抑制接入三相不平衡负载后的电压波动,系统具有更强的鲁棒性。
图14(c)为当光储系统通过双向Buck型DC-DC变换器为母线负载供电,母线负载发生突变时的电压波形。最初系统母线负载为6 Ω,达到稳态后母线电压稳定在期望值26.6 V附近。在0.5 s时负载突变为3 Ω,此时电流补偿双PI控制下,母线电压瞬间跌落至23.90 V,跌落幅值为2.82 V,跌落率为10.5%;改进电流补偿PI+MPC控制下,母线电压瞬间跌落至24.55 V,跌落幅值为2.17 V,跌落率为8.1%。在达到新稳态后,设置母线电阻在0.8 s时突变为6 Ω。电流补偿双PI控制下,母线电压瞬间上升至29.65 V,上升幅值为3.13 V,上升率为11.8%;改进电流补偿PI+MPC控制下,母线电压瞬间上升至28.91 V,上升幅值为2.39 V,上升率为9.0%。证明当改进电流补偿模型预测控制策略应用于光储系统时,能有效抑制因母线负载变化引起的母线电压波动。
综上,当改进电流补偿PI+MPC控制应用于光伏储能系统时,能有效抑制因接入三相不平衡负载、母线负载突变等引起的母线电压突变,且较电流补偿双PI控制具有更为平稳的动态恢复过程。
基于电感电流iL噪声与跳变抑制,母线电压uo噪声与波动平抑等实际需求,改进电流补偿模型预测控制在多种工作场景下均表现出良好的控制效果,同时显著改善系统稳定性和动态性能。考虑到上述诸多优势,通过引入负低-高通校正环节的改进电流补偿模型预测控制,将使直流微网具有更强的抗干扰能力和扰动下更平滑的恢复过程,从而提高直流微网电能质量。
4 结 论
针对抑制直流微网母线电压波动,提高直流微网电能质量和动态响应性能的需求,在分析校正前PI+MPC控制稳定性的基础上,提出基于残差生成器的改进电流补偿模型预测控制策略,并从补偿后系统幅值裕度较小的问题出发,设计负低-高通滤波器以提高系统稳定裕度。通过对Buck型双向DC-DC变换器等效建模、仿真分析与实验验证,得出如下结论:
1)根据模型匹配思想,当补偿器满足Q(z)Wrd(z)=1时,电流补偿模型预测控制可以完全消除外部扰动信号对母线电压的影响。通过仿真以及实物实验,可以证明,尽管受限于采样精度和采样延时的影响,改进电流补偿模型预测控制在抑制母线电压波动、提升直流微网动态性能上始终具有良好的控制效果。
2)采用校正前PI+MPC控制时,系统稳定裕度较小,存在失稳风险。由此设计的负低-高通滤波器校正环节能有效提高系统稳定裕度,并且在变换器发生参数不确定时仍具有良好的动态性能,极大提高系统稳定性和鲁棒性。同时,负低-高通校正环节在面对电感电流噪声时,也表现出良好的抑制效果,可进一步改善直流微网电能质量。
3)采用电流补偿模型预测控制策略后,能有效抑制多种工作条件下直流微网母线电压波动。相较于补偿前PI+MPC控制以及同样采用电流补偿双PI控制,所提出的改进电流补偿模型预测控制,在面对交流扰动、三相不平衡负载、母线电阻突变时,均表现出优异的抑制母线电压波动能力。
参 考 文 献:
[1]DRAGIČEVIČ T, LU X N, VASQUEZ J C, et al. DC microgrids—Part I: A review of control strategies and stabilization techniques[J]. IEEE Transactions on Power Electronics, 2016, 31(7): 4876.
[2]ZHENG C, DRAGIČEVIČ T, BLAABJERG F. Model predictive control-based virtual inertia emulator for an islanded alternating current microgrid[J]. IEEE Transactions on Industrial Electronics, 2021, 68(8): 7167.
[3]DRAGIČEVIČ T, LU X N, VASQUEZ J C, et al. DC microgrids—Part II: A review of power architectures, applications, and standardization issues[J]. IEEE Transactions on Power Electronics, 2016, 31(5): 3528.
[4]张国荣, 王新兵, 乔龙洋. 直流微网中母线电压对直流负载影响[J]. 电力系统及其自动化, 2013, 35(2): 65.
ZHANG Guorong, WANG Xinbing, QIAO Longyang. The impact of bus voltage on the DC load for DC microgrid[J]. Power System amp; Automation, 2013, 35(2): 65.
[5]赵书强, 王慧, 田娜, 等. 基于模型预测控制的直流微电网虚拟惯性优化方法[J]. 电工技术学报, 2023, 38(12): 3264.
ZHAO Shuqiang, WANG Hui, TIAN Na, et al. Model predictive control based DC microgrid virtual inertial optimal method[J].Transactions of China Electrotechnical Society,2023,38(12):3264.
[6]李忠文, 吴龙, 程志平, 等. 参与微电网频率调节的光伏发电系统模糊自适应功率控制[J]. 电机与控制学报, 2023,27(9): 126.
LI Zhongwen, WU Long, CHENG Zhiping, et al. Fuzzy adaptive power control for photovoltaic power generation participating in frequency regulation of microgrid[J]. Electric Machines and Control, 2023,27(9): 126.
[7]孙圣欣, 汤晨煜, 解大, 等. 并网型直流微电网的非线性降阶建模及其估计吸引域的优化计算[J]. 中国电机工程学报, 2024,44(2):517.
SUN Shengxin, TANG Chenyu, XIE Da, et al. Nonlinear modeling of grid-connected DC microgrid and optimization of estimated region of attraction[J]. Proceedings of the CSEE, 2024,44(2):517.
[8]栾思平, 苏适, 杨洲, 等. 适应于直流新能源/储能接入的三电平Buck-Boost变换器建模及控制器设计[J]. 太阳能学报, 2022, 43(4): 56.
LUAN Siping, SU Shi, YANG Zhou, et al. Modeling and controller design of three-level Buck-Boost converter adapted to DC new energy and energy storage access[J]. Acta Energiae Solaris Sinica, 2022, 43(4): 56.
[9]李建林, 袁晓冬, 郁正纲, 等. 利用储能系统提升电网电能质量研究综述[J]. 电力系统自动化, 2019, 43(8): 15.
LI Jianlin, YUAN Xiaodong, YU Zhenggang, et al. Comments on power quality enhancement research for power grid by energy storage system[J]. Automation of Electric Power Systems, 2019, 43(8): 15.
[10]林国庆, 何恩义. 一种低输入电流纹波高增益软开关DC-DC变换器[J]. 电机与控制学报, 2023,27(5): 65.
LIN Guoqing, HE Enyi. Low input current ripple high gain soft switching DC-DC converter[J]. Electric Machines and Control, 2023,27(5): 65.
[11]王成山, 李微, 王议锋, 等. 直流微电网母线电压波动分及抑制方法综述[J]. 中国电机工程学报, 2017, 37(1): 84.
WANG Chengshan, LI Wei, WANG Yifeng, et al. DC bus voltage fluctuation classification and restraint methods review for DC microgrid[J]. Proceedings of the CSEE, 2017, 37(1): 84.
[12]李俊波, 闫鹏, 魏业文, 等. 一种新型SEPIC可拓展高增益DC-DC变换器[J]. 电机与控制学报, 2023,27(4): 64.
LI Junbo, YAN Peng, WEI Yewen, et al. Study on SEPIC expandable step-up DC-DC converter[J]. Electric Machines and Control, 2023,27(4): 64.
[13]尚彤, 崔学深, 徐明荣, 等. 蓄电池-超级电容混合储能系统放电控制策略[J]. 电源技术, 2017, 41(4): 595.
SHANG Tong, CUI Xueshen, XU Mingrong, et al. Discharge control strategies of supercapacitor-battery hybrid energy storage system[J]. Chinese Journal of Power Sources, 2017, 41(4): 595.
[14]林国庆, 黄毅敏. 一种非隔离型高增益三端口DC-DC变换器[J]. 电机与控制学报, 2023, 27(2): 98.
LIN Guoqing, HUANG Yimin. Non-isolated high step-up three-port DC-DC converter[J]. Electric Machines and Control, 2023, 27(2): 98.
[15]张勤进, 牛淼, 刘彦呈, 等. 储能双向DC/DC变换器自适应充放电无缝切换策略[J]. 电测与仪表, 2023, 60(2): 186.
ZHANG Qinjin, NIU Miao, LIU Yancheng, et al. Seamless switching strategy of adaptive charge and discharge for bidirectional DC/DC converter with storage energy[J]. Electrical Measurement amp; Instrumentation, 2023, 60(2): 186.
[16]JIA L L, SUN X F, ZHENG Z W, et al. Multimode smooth switching strategy for eliminating the operational dead zone in noninverting Buck-Boost converter[J]. IEEE Transactions on Power Electronics, 2020, 35(3): 3106.
[17]王坦坦, 孙树敏, 王楠,等. 基于混合储能的微电网控制策略研究[J]. 现代电子技术, 2020, 43(21): 119.
WANG Tantan, SUN Shumin, WANG Nan, et al. Research on microgrid control strategy based on hybrid energy storage[J]. Modern Electronics Technique, 2020, 43(21): 119.
[18]孙标广, 李静争, 张迁迁, 等. 基于ZVS的双向全桥DC-DC变换器最小回流功率双重移相分段控制[J]. 太阳能学报, 2023, 44(9): 39.
SUN Biaoguang, LI Jingzheng, ZHANG Qianqian, et al. Dual phase-shift segment control of minimum return power of bidirectional full-bridge DC-DC converter based on ZVS[J]. Acta Energiae Solaris Sinica, 2023, 44(9): 39.
[19]胡长斌, 王慧圣, 罗珊娜, 等. 计及直流微电网扰动抑制的残差动态分散补偿控制策略[J]. 电工技术学报, 2021, 36(21): 4493.
HU Changbin, WANG Huisheng, LUO Shanna, et al. Residual dynamic decentralized compensation control strategy considering disturbance suppression in DC microgrid[J]. Transactions of China Electrotechnical Society, 2021, 36(21): 4493.
[20]胡长斌, 王海鹏, 周京华, 等. 基于鲁棒残差生成器的多DC-DC下垂动态补偿控制策略[J]. 中国电机工程学报, 2021, 41(4): 1410.
HU Changbin, WANG Haipeng, ZHOU Jinghua, et al. Dynamic compensation control strategy for multiple DC-DC droop based on robust residual generator[J]. Proceedings of the CSEE, 2021, 41(4): 1410.
[21]SAJADIAN S, AHMADI R. Model predictive-based maximum power point tracking for grid-tied photovoltaic applications using a Z-source inverter[J]. IEEE Transactions on Power Electronics, 2016, 31(11): 7611.
[22]梅杨, 李晓晴, 齐园园. 光储系统中双向DC/DC变换器预测电流控制[J]. 电力电子技术, 2016, 50(5): 28.
MEI Yang,LI Xiaoqing, QI Yuanyuan. Current predictive control for bi-directional DC/DC converter of photovoltaic energy storage system[J]. Power Electronics, 2016, 50(5): 28.
[23]杨惠, 晁凯悦, 孙向东, 等. 基于开关序列的光伏储能双向DC-DC变换器预测电流控制方法[J]. 电网技术, 2019, 43(1): 300.
YANG Hui, CHAO Kaiyue, SUN Xiangdong, et al. Predictive current control method of photovoltaic energy storage for bidirectional DC-DC converter based on switching sequence[J]. Power System Technology, 2019, 43(1): 300.
[24]朱晓荣, 候顺达, 李铮. 基于模型预测控制的直流微电网电压动态响应优化[J]. 电网技术, 2020, 44(6): 2187.
ZHU Xiaorong, HOU Shunda, LI Zheng. Voltage dynamic response optimization of DC microgrid based on model predictive control[J]. Power System Technology, 2020, 44(6): 2187.
[25]YANG J, ZHENG W X, LI S H, et al.Design of a prediction-accuracy-enhanced continuous-time MPC for disturbed systems via a disturbance observer[J]. IEEE Transactions on Industrial Electronics, 2015, 62(9): 5807.
[26]陆珩, 胡长斌, 罗珊娜, 等. 基于模型预测与残差生成器的Buck变换器并联系统性能提升控制策略[J]. 中国电机工程学报, 2023,43(24):9696.
LU Heng, HU Changbin, LUO Shanna, et al. Performance improvement control strategies for Buck converter parallel systems based on model predictive control and residual generators[J].Proceedings of the CSEE, 2023,43(24):9696.
[27]郭磊磊, 陈墨, 罗魁, 等. 基于滑模观测器的电压源逆变器无模型预测控制[J]. 电机与控制学报, 2023,27(6): 127.
GUO Leilei, CHEN Mo, LUO Kui, et al. Model-free predictive control method for voltage source inverter based on sliding model observer[J].Electric Machines and Control,2023,27(6):127.
(编辑:邱赫男)
