双并列转子永磁电机非对称负载运行特性
2024-12-03戈宝军范阵雨林鹏
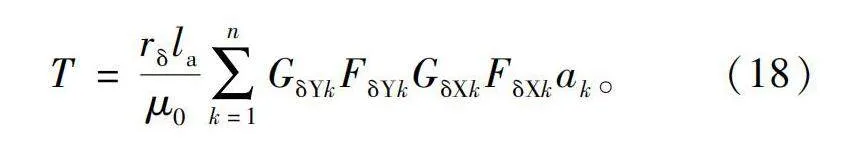
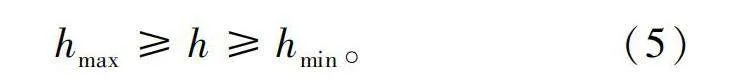
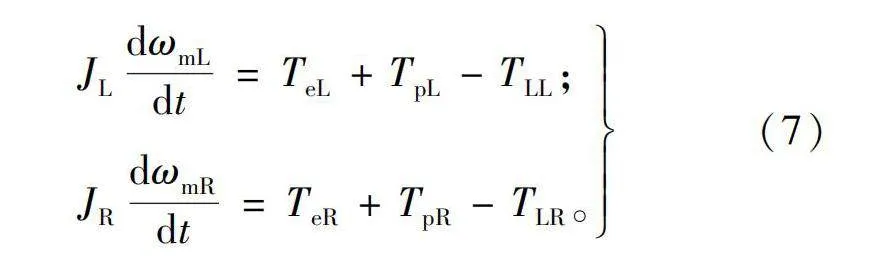


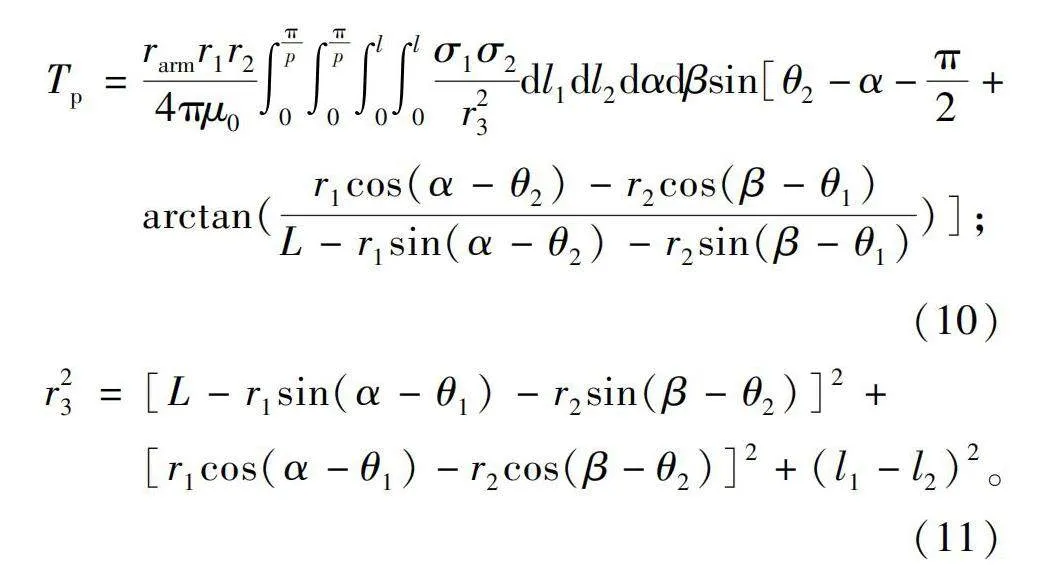
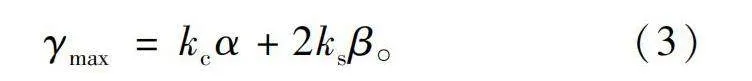
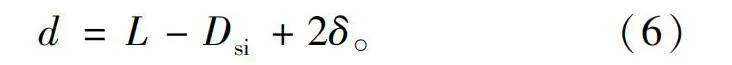
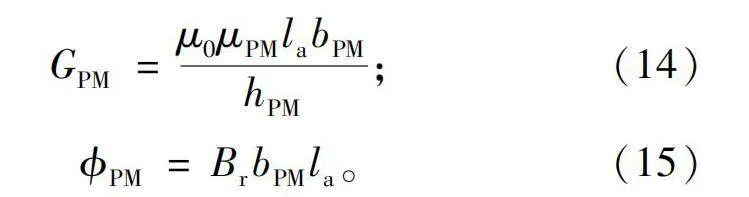
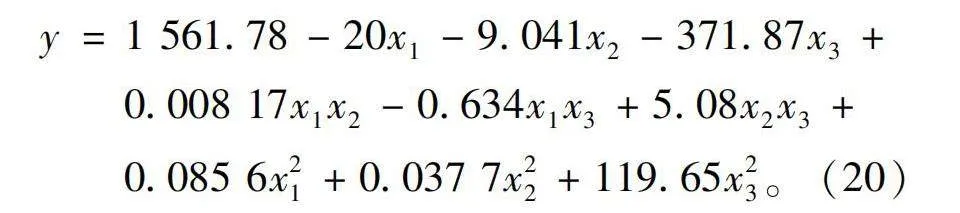

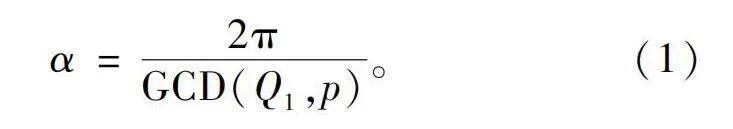
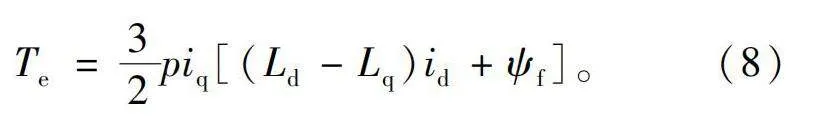
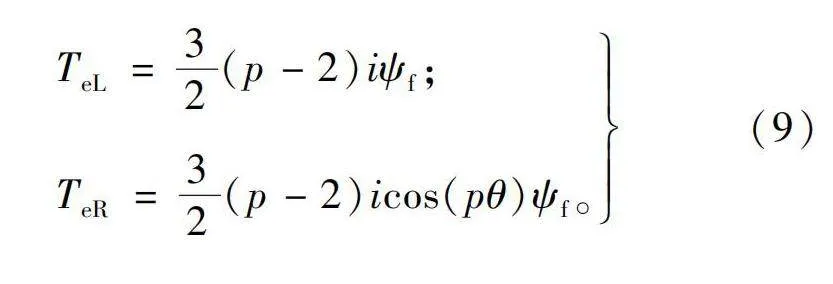

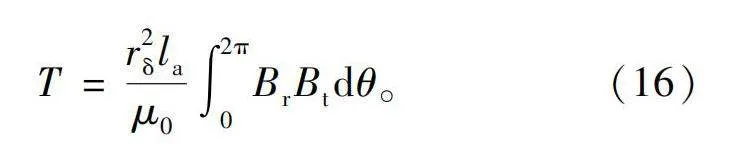
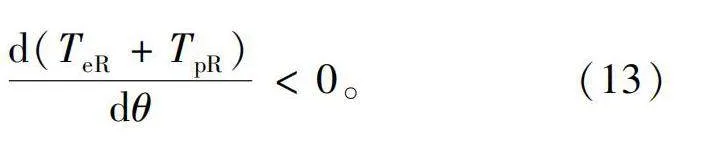
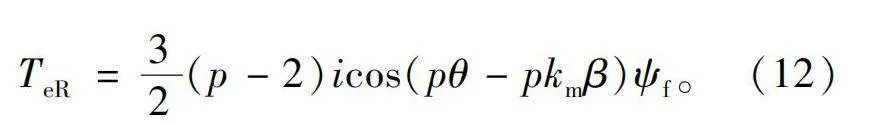
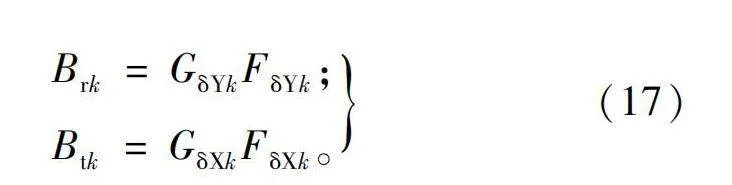
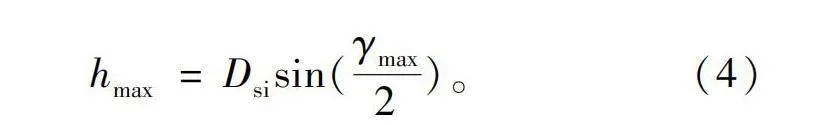
摘 要:双并列转子电机在驱动两侧非对称负载时,轻载侧电机的功角较低,产生了电机材料浪费,效率低等问题。为提升电机整体输出功率,基于双并列转子电机基本理论采用解析法求得电机驱动转矩平均值的表达式,进而提出轻载侧绕组提前的结构设计。而后以一台12极72槽双并列转子电机为例,建立其磁网络模型,通过麦克斯韦应力张量法得出驱动转矩的解析计算式,分析转子偏差角对电机基本转矩脉动的影响,得出最佳绕组提前槽数。最后,针对电机转矩脉动较大的问题,使用响应曲面法,以基本转矩脉动为目标函数,以永磁体偏心距、永磁体极弧系数、并接区高度作为自变量对电机进行优化,有效降低电机转矩脉动,验证了绕组前置的结构改进对提升电机非对称状态下的输出转矩具有显著效果。
关键词:永磁同步电机;双并列转子;转矩脉动;等效磁网络;响应曲面法;耦合区
DOI:10.15938/j.emc.2024.10.006
中图分类号:TM351
文献标志码:A
文章编号:1007-449X(2024)10-0055-11
收稿日期: 2024-05-17
作者简介:戈宝军(1960—),男,博士,教授,博士生导师,研究方向为大型机电能量转换装置的基础理论与应用技术;
范阵雨(2000—),男,硕士研究生,研究方向为永磁电机设计与优化;
林 鹏(1983—),男,博士,讲师,研究方向为永磁电机的电磁场数值分析。
通信作者:戈宝军
Asymmetric load operation characteristics of dual-parallel rotor permanent magnet synchronous motor
GE Baojun, FAN Zhenyu, LIN Peng
(National Engineering Research Center of Large Electric Machines and Heat Transfer Technology, Harbin University of Science and Technology, Harbin 150080, China)
Abstract:When the double-parallel rotor motor drives the asymmetric load on both sides, the power Angle of the light side motor is low, resulting in motor material waste and low efficiency. To improve the overall output power of the motor, based on the basic theory of dual parallel rotor motors, an analytical method was used to obtain the expression for the average driving torque of the motor, and then a structural design for advancing the winding on the light load side was proposed. Then, taking a 12-pole 72-slot double-parallel rotor motor as an example, the magnetic network model was established, and the analytical calculation formula of driving torque is obtained through Maxwell stress tensor method. The influence of rotor deviation angle on the basic torque pulsation of the motor was analyzed, and the optimal number of winding advance slots was obtained. Finally, for the problem of large motor torque pulsation, the response surface method was used to optimize the motor with basic torque pulsation as the objective function, and the eccentricity of permanent magnet, polar arc coefficient of permanent magnet and joint height as the independent variables, which effectively reduced the motor torque pulsation. It was verified that the structural improvement of winding front had a significant effect on improving the output torque of the motor under asymmetric state.
Keywords:permanent magnet synchronous motor; double-parallel rotor; torque ripple; equivalent magnetic circuit; response surface method; coupling area
0 引 言
食品生产、钢铁加工、建材、化工等行业在生产过程中往往要采用一系列平行双轴对驱机械,例如双螺杆液体泵、双轴搅拌机、辊轧机等[1-3]。这种结构在使用时通常要求在两个平行放置的转轴上分别输入方向相反的转矩。传统驱动方式采用单台电机驱动主动轴,被动轴通过同步齿轮结构与主动轴相连以获得驱动力矩,但同步齿轮的使用会带来润滑需求、体积庞大、维护困难等问题。
为解决同步齿轮带来的一系列问题,中外学者提出使用两台电机分别驱动主、被动轴的方案和使用磁力齿轮取代机械齿轮的方案,这两种方案存在机械强度与同步困难等问题[4-5],未能取得理想的效果。在这种局面之下,双并列转子永磁同步电机(dual-parallel rotor permanent magnet synchronous motor,DR-PMSM)应运而生[6],其将上文的两种方案结合,有着结构紧凑、可控性强、维护方便、直接驱动负载等优点。
DR-PMSM问世至今,已得到许多学者的关注。已有的研究包括大型DR-PMSM的设计方法;分析与优化此种电机较大的转矩脉动;推导其运行特性等方向[7-9]。以上研究的目标负载为大小相等、方向相反的对称负载,并未对负载转矩不同时的电机转矩关系进行研究。而在实际工业生产中,存在偏心双轴搅拌机[10]、双转子双级制砂机等两侧负载转矩不同的生产机械,若不加判断就将用于对称负载的DR-PMSM用于非对称负载,会存在电机总输出转矩降低、振动噪声大等问题,严重时还会导致电机失稳、停转。
为提升DR-PMSM在驱动不对称负载时的性能,需要对其结构进行一定改进。本文针对驱动不对称负载时总输出转矩降低问题,通过对电机驱动转矩产生原理进行分析,求得驱动转矩解析方程,提出轻载侧绕组前置改进。将磁网络模型法与响应曲面法结合,对电机关键结构尺寸进行优化。最后通过高精确度有限元验证改进后电机的电磁性能,证明轻载侧绕组前置设计在非对称负载工况下能够输出较大转矩,同时还可以降低电机转矩脉动。
1 双并列转子电机基本原理
1.1 电机结构及工作原理
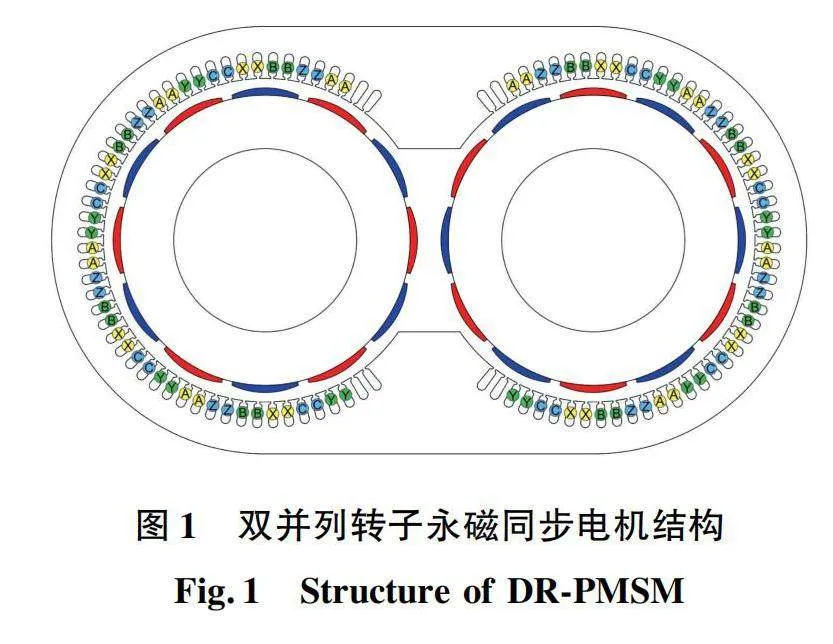
DR-PMSM在结构上可以看作是两台完全相同的永磁同步电机削去一部分铁心与绕组后并行拼接得到的新型电机,整体结构如图1所示。
定子铁心在保留必要绕组槽之外还留有一定的空槽,空槽在槽结构上与绕组槽相同,其内部不放置绕组,不会对电机整体输出转矩产生影响。空槽的存在使电机气隙磁场更加对称,提升电机性能。
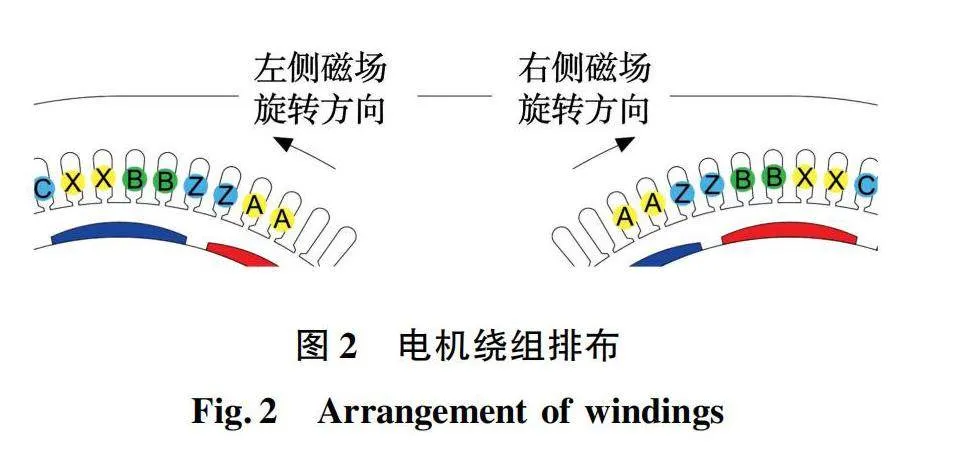
定子绕组采用反向排布,即左侧绕组逆时针排布,右侧绕组采用与之相反的顺时针排布,如图2所示,两侧绕组串联相接,通三相电流后形成两个旋转方向相反的磁场驱动两侧转子,实现DR-PMSM的并行对驱功能。
转子采用表贴式永磁体的结构,其一方面与己侧定子绕组构成永磁电机结构以获得电磁转矩,另一方面与对侧转子构成磁齿轮结构从而传递磁齿轮转矩。在对称运行时,两侧转子上镜像位置的磁极磁性相反,转子整体受到的永磁体切向吸引力为0,可作为常规永磁电机分析;当转子因为某些原因不再镜像对称时,转子会相互吸引,实现更好的同步性。
1.2 并接区设计原则
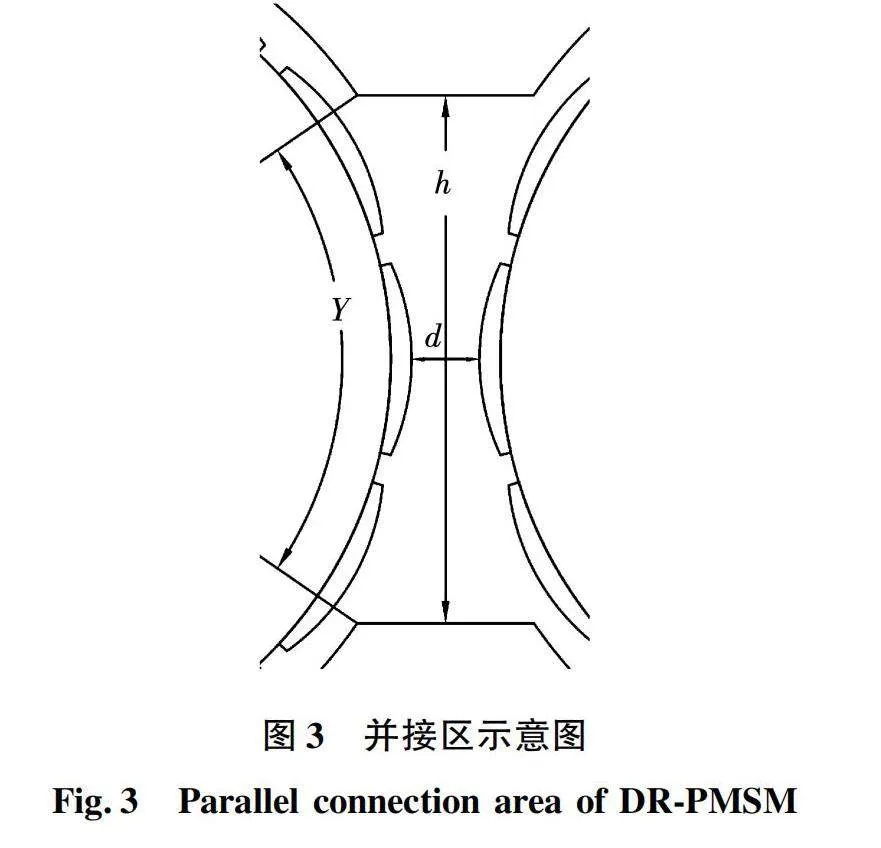
DR-PMSM相较于普通永磁同步电机,最大的不同是其左右两侧之间存在一个磁场交互区即并接区,如图3所示。并接区的存在使得电机的磁场分布发生改变,进而影响电机电磁特性。为进一步研究DR-PMSM,需要明确并接区的尺寸选择原则,选取合适的并接区尺寸。
根据电机定子分块理论[11],一个定子槽数为Q1,极对数为p的永磁同步电机,其定子可以被分解为GCD(Q1,p)个单元模块,在切去整数个单元模块电机后,剩余的部分依然可以产生电磁转矩。每个单元电机所占圆心角为
α=2πGCD(Q1,p)。(1)
式中GCD(Q1,p)为电机定子槽数Q1和极对数p的最大公因数。每个定子槽所占圆心角为
β=2πQ1。(2)
并接区占用最大圆心角为
γmax=kcα+2ksβ。(3)
式中:kc为单元电机切割数,取值范围为小于GCD(Q1,p)的整数,ks为定子空槽对数。确定以上角度后,可以求得并接区最大高度为
hmax=Dsisin(γmax2)。(4)
式中Dsi为定子内径。
并接区最小高度理论上可以取0,但考虑到生产工艺的限制,一般存在一个最小并接区高度hmin对其进行限制,此时并接区高度范围为
hmax≥h≥hmin。(5)
并接区宽度为
d=L-Dsi+2δ。(6)
式中:L为转子轴心距;δ为单边气隙长度。因为转子轴心距由连接的负载决定,无法对其进行修改;而定子内径与气隙长度均为电机重要参数,在修改后会极大影响电机性能,所以在设计后期想要修改并接区宽度较为困难,最好在设计初期确定后就不再更改。
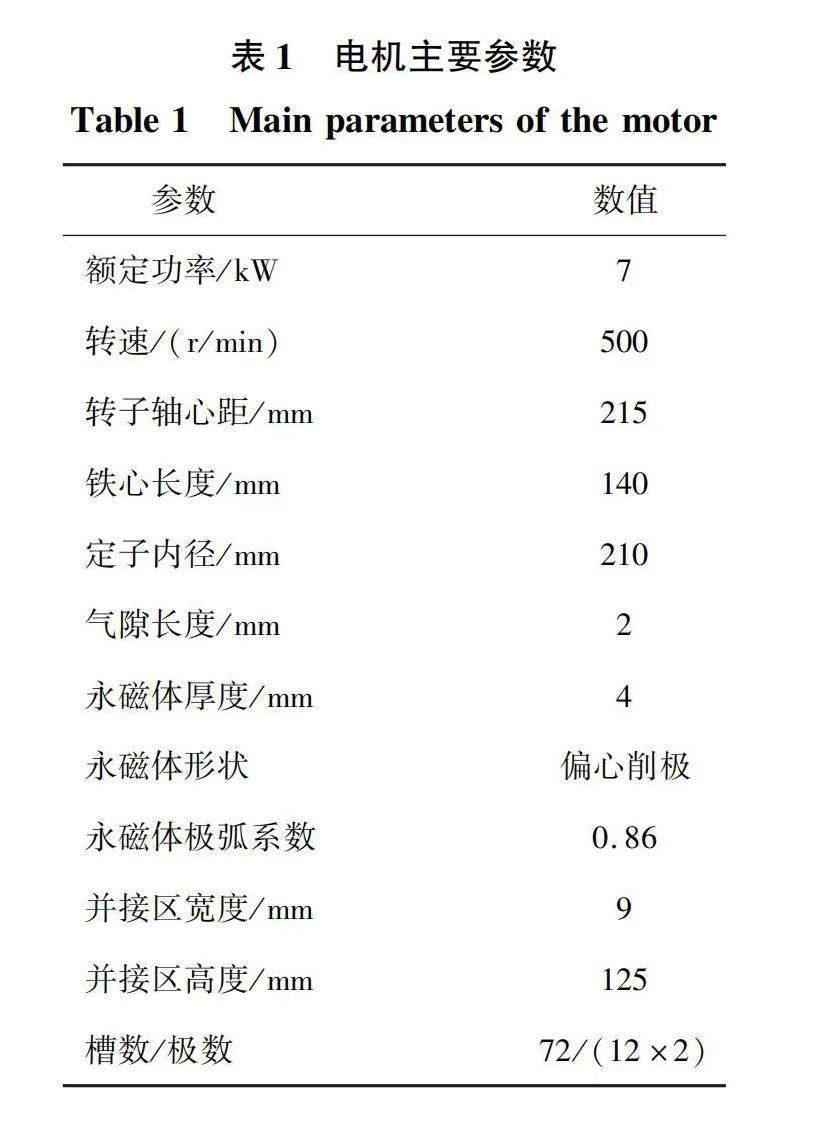
表1为一台DP-PMSM的主要结构参数,此电机用于驱动两侧搅拌叶片不同的双轴搅拌机。
2 电机驱动转矩分析
2.1 电机运动方程
为方便讨论,将轴线左侧定转子及绕组定义为左侧电机,右侧定转子及绕组定义为右侧电机,设左侧电机为重载侧,右侧电机为轻载侧。
根据常规永磁电机理论及平行轴永磁齿轮理论[12]得到DR-PMSM运动方程如下:
JLdωmLdt=TeL+TpL-TLL;
JRdωmRdt=TeR+TpR-TLR。(7)
式中:JL和JR为左侧系统和右侧系统的转动惯量;ωmL和ωmR为左侧和右侧系统的机械角速度;TeL和TeR为左侧和右侧电机的电磁转矩;TpL和TpR为左侧和右侧转子永磁体相互吸引产生的的磁齿轮转矩,其大小相等符号相反;TLL和TLR为左侧和右侧电机的负载转矩。电磁转矩与磁齿轮转矩之和就是电机受到的驱动转矩。
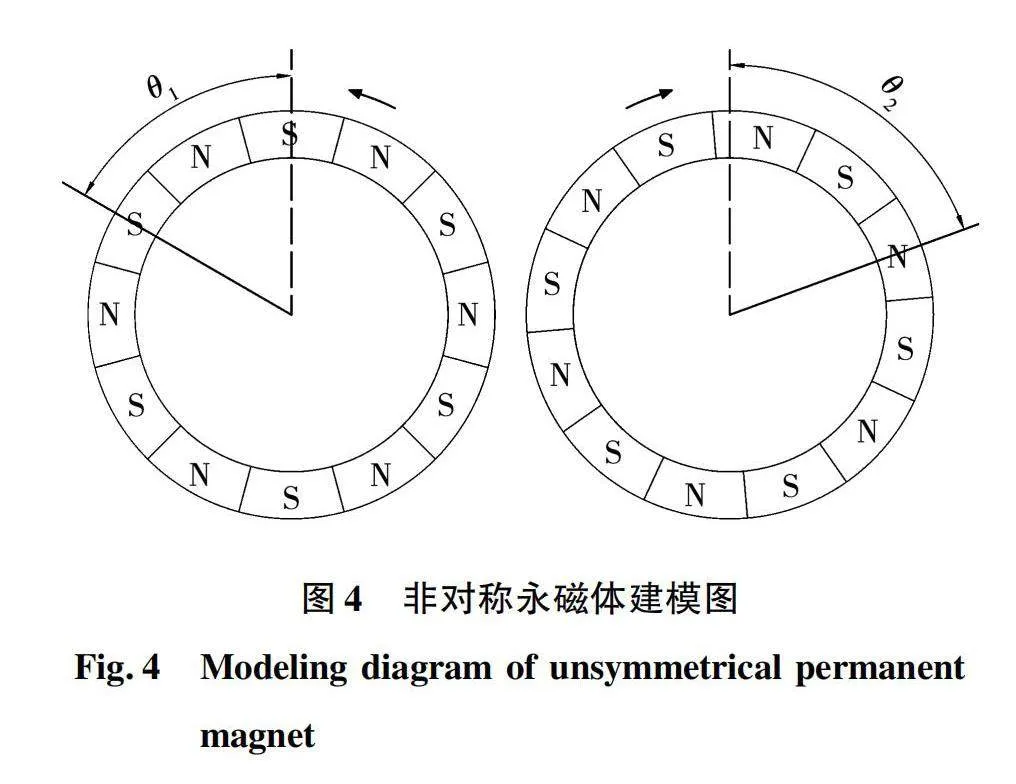
由式(7)可以看出,当一侧负载转矩变小时,转子加速旋转,左右转子将不再镜像对称,如图4所示。
图4虚线为两转子角度起点,θ1和θ2分别为一组对应永磁体轴线与角度起点的机械角度,角度以旋转方向为正方向。定义转子偏差角为θ=θ2-θ1,电机电磁转矩与磁齿轮转矩大小均与转子偏差角相关,一旦转子偏差角变化,电机的转矩关系也会发生变化,进入新的平衡态。
2.2 驱动转矩解析计算
电机控制方式选用在重载侧进行id=0的矢量控制,基本电磁转矩方程为
Te=32piq[(Ld-Lq)id+ψf]。(8)
式中:p为极对数;id,iq分别为电机定子d、q轴电流;Ld,Lq分别为d、q轴电感;ψf为永磁体磁链。
对于目标DR-PMSM,由于其定子切除了两个单元电机以及其具有左右对称、气隙均匀的结构,左右侧电机电磁转矩方程简化为
TeL=32(p-2)iψf;
TeR=32(p-2)icos(pθ)ψf。(9)
式中:i为左侧电机定子q轴电流;角度pθ为右侧电机励磁磁势与电枢磁势的夹角,也是励磁电势与电枢电流的夹角即内功率因数角;icos(pθ)为右侧电机定子q轴电流。
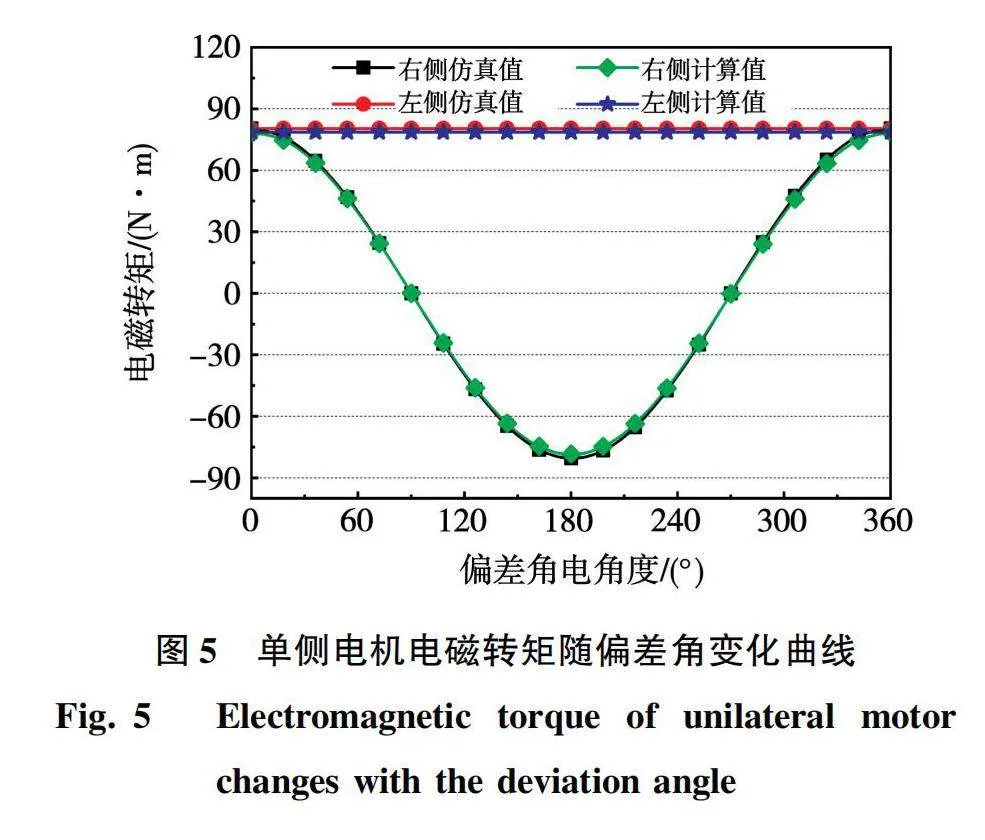
图5为按表1样机尺寸,在电流取额定电流的情况下,按式(9)拟合及有限元仿真得到的两侧电机电磁转矩随偏差角的变化曲线,其中转矩正方向为电机旋转方向。曲线表明左侧电机电磁转矩保持在80.44 N·m,而右侧电机电磁转矩随偏差角电角度在一个周期内余弦变化,其幅值为80.42 N·m,仿真数值变化趋势及数值均与理论推导相符。计算值略低于仿真值的原因是解析计算完全忽略了转子上多余的两对磁极对磁场的影响,但实际上磁极通过并接区等结构闭合后会提供小部分电磁转矩。这部分电磁转矩仅占全部电磁转矩的1.33%,对整体结果影响较小,处于可接受的范围内。
双并列转子电机两侧的磁齿轮转矩采用等效磁荷法[13]对其进行计算,具体计算公式如下:
Tp=rarmr1r24πμ0∫πp0∫πp0∫l0∫l0σ1σ2r23dl1dl2dαdβsin[θ2-α-π2+arctan(r1cos(α-θ2)-r2cos(β-θ1)L-r1sin(α-θ2)-r2sin(β-θ1))];(10)
r23=[L-r1sin(α-θ1)-r2sin(β-θ2)]2+[r1cos(α-θ1)-r2cos(β-θ2)]2+(l1-l2)2。(11)
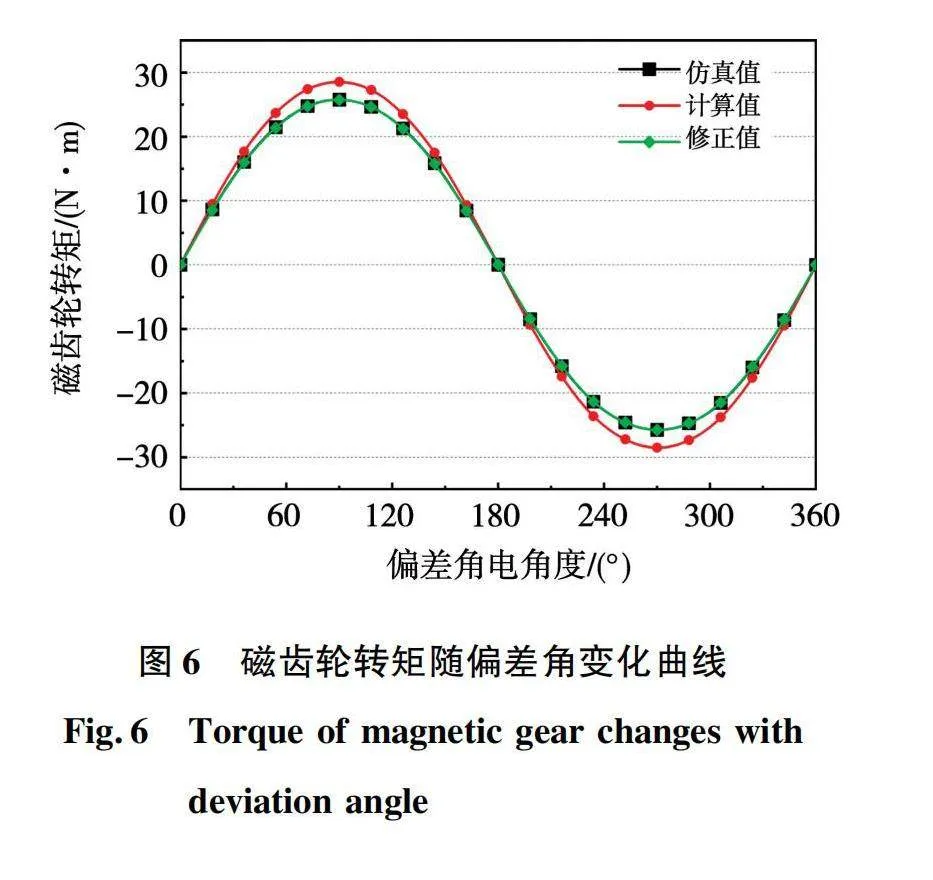
式中:r1和r2为两侧永磁体的外径;rarm为力臂,其大小等于r1或r2;μ0为真空磁导率;σ1和σ2是两侧永磁体端面的磁荷面密度;l1和l2为两侧永磁体长度;r3为两块微元的直线距离。解析计算结果如图6所示。
由图6可知,通过解析计算与有限元仿真得出的磁齿轮转矩均随偏差角正弦变化,解析计算得到的转矩幅值为28.52 N·m,仿真得到的转矩幅值为25.75 N·m,相对偏差为10.68%。出现较大偏差的原因是进行磁荷计算时忽略了定子铁心,而实际上有部分磁力线通过定子铁心垂直穿过气隙不提供切向力矩,使得计算值偏高。为修正这个偏差,可对原计算式乘以一个小于1的修正系数kp,修正后相对误差降低至2.17%,在可接受范围内。
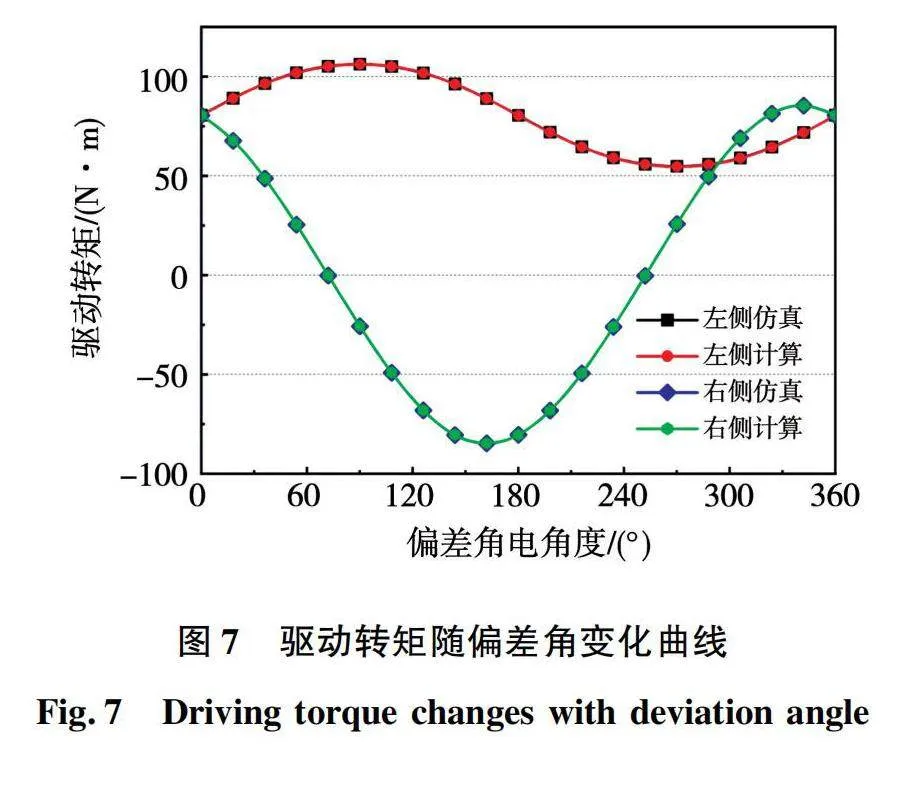
结合式(7)~式(11)对电机总驱动转矩进行计算,计算结果如图7所示。
图7中计算值与仿真值最大偏差仅为2.48%,表明解析计算法能较好地计算电机的总驱动转矩,简化计算。根据曲线变化趋势可以看出,当偏差角变大,右侧电机驱动转矩降低的幅度远大于左侧电机驱动转矩增加的幅度,使电机整体输出转矩降低,性能下降。
2.3 非对称负载下的运行特性优化
由式(7)可得,电机输出总转矩为两侧驱动转矩之和,右侧电机在大偏差角下驱动转矩下降的原因是电磁转矩随内功率因数角变大而降低。解决此问题可采用两套绕组分别控制两侧电机[14]或是重新排布绕组的方式。鉴于分别控制的方式会提升控制成本,故采用改变绕组排布的方式进行改进,具体方式为右侧电机全部绕组顺时针旋转km个槽从而将右侧电机磁场相位提前,因旋转而空缺的首端槽由末端绕组进行逐个填充,旋转后绕组总数不发生改变。图8为顺时针旋转3个槽时的右侧电机绕组。
此时左侧电机电磁转矩不变,而右侧电机因为磁场超前于左侧电机pkmβ个电角度,电磁转矩公式变为
TeR=32(p-2)icos(pθ-pkmβ)ψf。(12)
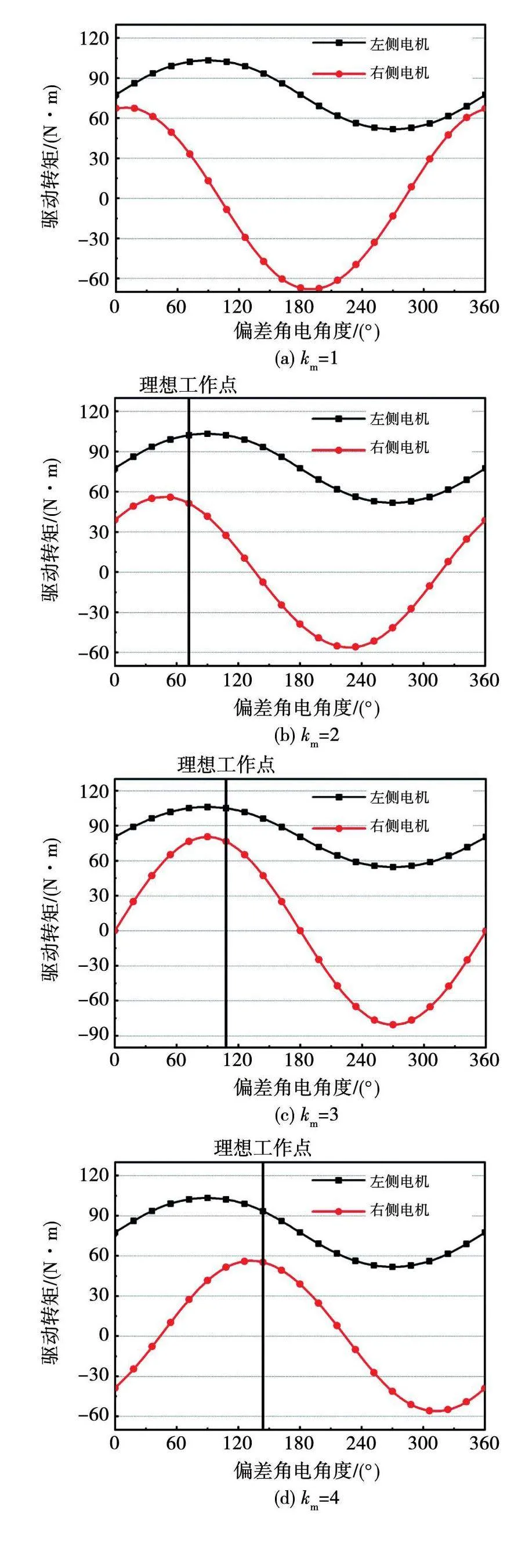
根据式(12)分别计算km取1~6时的右侧电机驱动转矩,绘制其随偏差角变化的曲线如图9所示。
由图9可见,当km = 2,3,4时,电机在理想工作点附近能够实现保证整体输出转矩不降低的同时输出两个大小不等方向相反的驱动转矩,以满足负载要求。而当km=1,5,6时不存在理想工作点。
此处选取km=3对右侧转子进行静态稳定性分析,设负载转矩大小与偏差角无关,当右侧负载转矩增大,右侧电机转速降低,右侧电机转速低于左侧电机转速,偏差角减小,若此时电机驱动转矩随偏差角减小而增大,则电机能够保持同步。根据以上分析,稳定区判据为
d(TeR+TpR)dθlt;0。(13)
结合图9与稳定区判据可以得出,km=2,3,4时的理想工作点位于稳定运行区间,能够同时满足负载要求和稳定性要求。
3 等效磁网络模型的建立及求解
等效磁网络(equivalent magnetic network,EMN)模型有着计算时间短、适用于非线性模型等优点,可以同时兼顾计算效率与计算精确度。为进一步观察DR-PMSM的转矩性能,需要通过建立等效磁网络模型的方法求解电机各部磁密,利用麦克斯韦应力张量法计算每一时刻下的驱动转矩。
3.1 等效磁网络模型的建立
建立磁网络模型时,一般将复杂结构分解为若干典型磁导单元的组合。常用基本磁导单元形状包括弧形单元、矩形单元与梯形单元[15]。
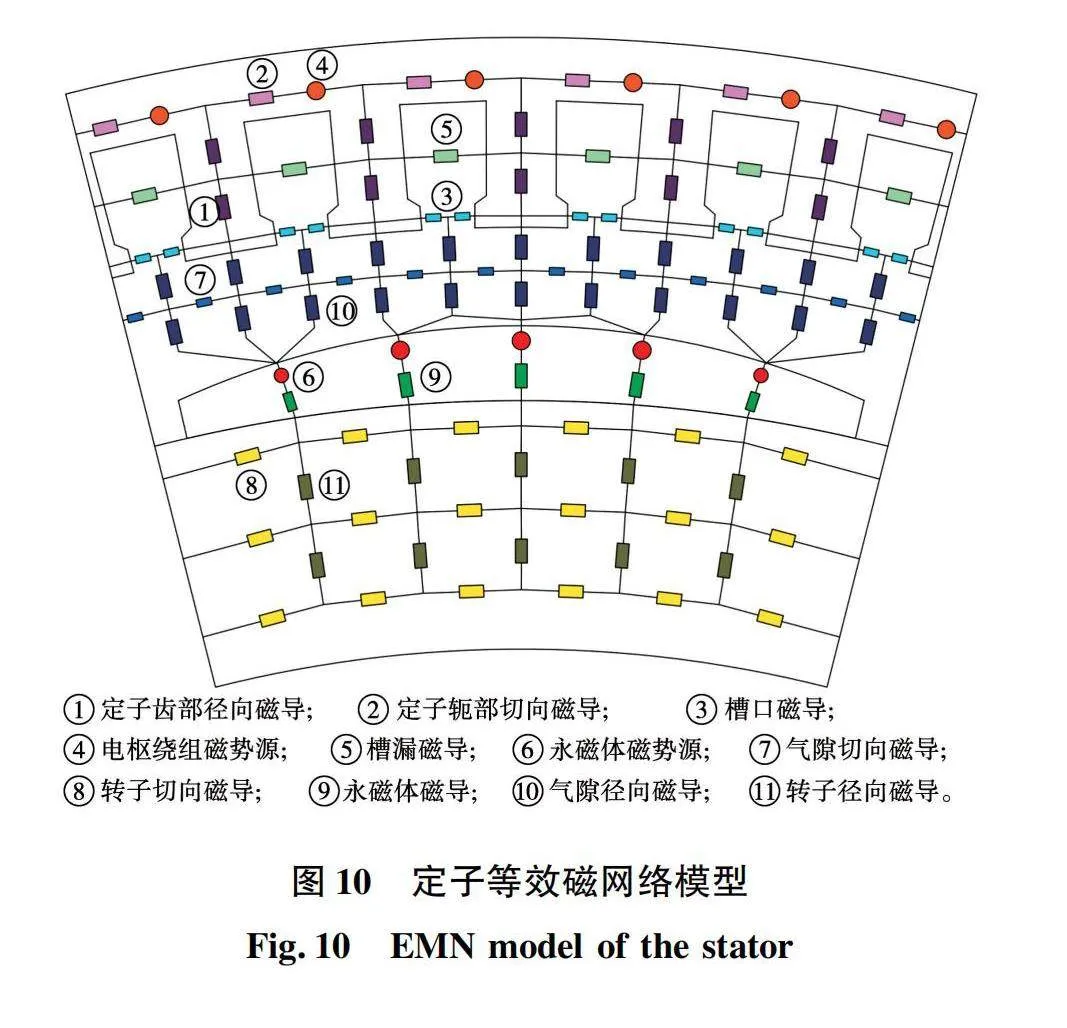
图10为DR-PMSM一个磁极下的等效磁网络模型。其中:定子齿部几何结构可以看作矩形单元与梯形单元的串联;定子轭部、槽漏磁导、气隙磁导、转子磁导的磁导单元均近似于矩形单元;定子槽口处磁导单元形状类似1/4圆弧;定子电枢绕组磁动势与轭部切向磁导串联,其计算式为F=Nci,其中:Nc为槽内每个线圈的匝数;i为绕组当前时刻通过的电流值。
由于永磁体采用偏心削极结构,无法作为一整块永磁体直接进行计算,故对其进行分块处理后近似为矩形永磁体块。具体计算式如下:
GPM=μ0μPMlabPMhPM;(14)
ϕPM=BrbPMla。(15)
式中:μ0为真空磁导率;la为轴向长度;μPM为永磁体相对磁导率;bPM为本段永磁体宽度;hPM为本段永磁体平均厚度;Br为永磁体剩磁。
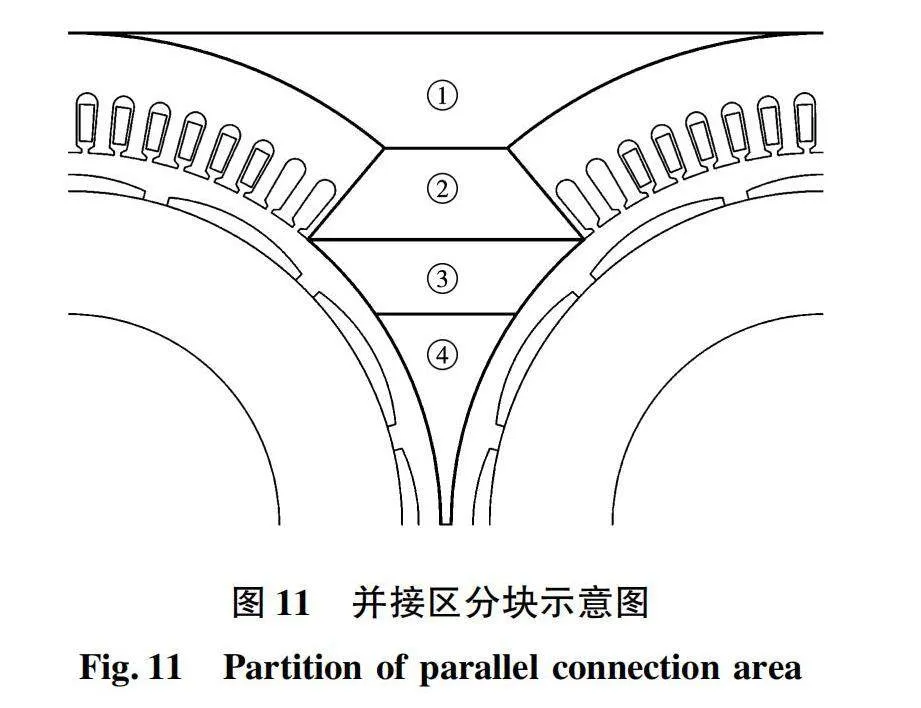
并接区作为DR-PMSM独有的结构,需要单独划分其磁通路径,可依照材料的不同将并接区分为并接区铁心和并接区气隙,如图11所示。
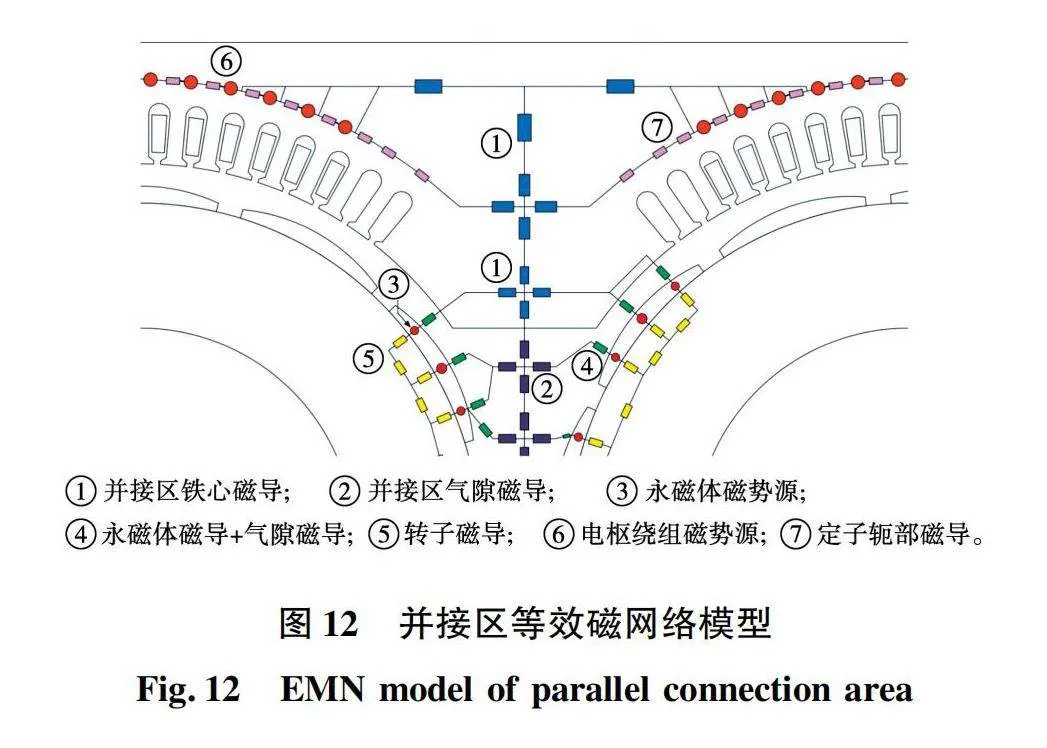
图11表明并接区铁心部分可以分解为标号为①②③的3个梯形单元,并接区气隙④则可以根据计算需要分解为若干个大小不同的梯形单元。根据以上分解方式建立的并接区磁网络模型如图12所示。
至此,电机整体的磁网络模型建立完毕,可进行下一步求解计算。
3.2 驱动转矩的磁网络计算
建立网络模型后,可通过常规矩阵迭代的方式求解得到一个周期内各时刻下的电机磁场状态,进而计算电机在一个周期内的电磁转矩曲线,相较于传统公式计算能够更加细致地分析电机运行时的转矩关系。
麦克斯韦应力张量法利用面电流和体电流替代铁磁材料,利用安培定律得到电机驱动转矩与气隙磁场关系为
T=r2δlaμ0∫2π0BrBtdθ。(16)
式中:rδ为气隙圆周半径;Br和Bt为通过磁网络计算得到的气隙径向和切向磁密。
磁网络气隙单元近似为矩形单元,其气隙磁密可表示为:
Brk=GδYkFδYk;
Btk=GδXkFδXk。(17)
式中:GδYk、GδXk分别为第k个气隙单元的纵向磁导和切向磁导;FδYk、FδXk分别为第k个气隙单元的纵向磁势与切向磁势。将式(17)代入式(16)可得电机驱动转矩表达式为
T=rδlaμ0∑nk=1GδYkFδYkGδXkFδXkak。(18)
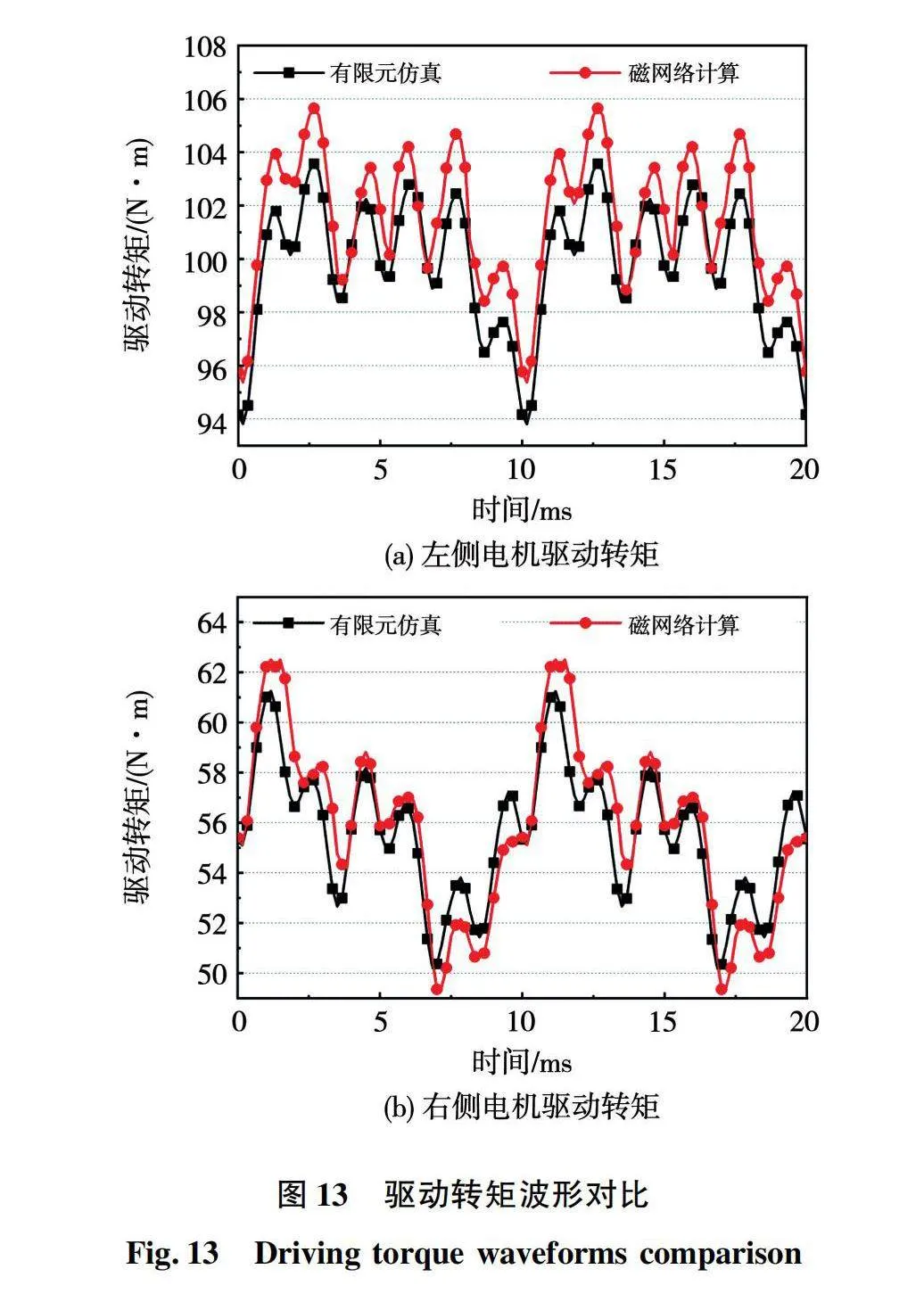
式中:n为转子周围气隙单元总数;ak为第k个气隙单元的切向长度。根据此式计算一个周期内的电机电磁转矩如图13所示。
由图13可见,磁网络计算结果相较有限元仿真计算仅有2.84%的偏差,而后者计算一次所需的时间是前者的数倍。所以使用磁网络模型进行计算既不失精确度又能快速得到结果,可用于电机优化工作。
4 非对称负载状态转矩脉动优化
DR-PMSM转矩脉动分为纹波转矩、齿槽转矩、磁齿轮转矩脉动及端部效应力矩。其中后3种转矩在绕组电流为0时就存在,对其求和后定义为DR-PMSM的基本转矩脉动。
4.1 转子偏差角对基本转矩脉动的影响
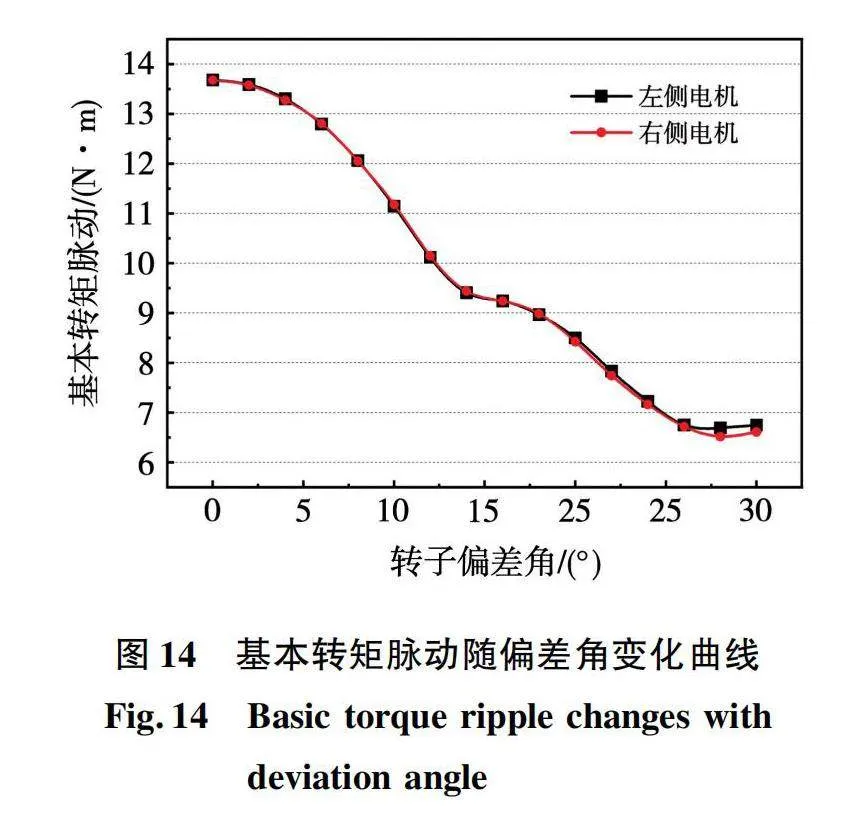
基本转矩脉动中的磁齿轮转矩脉动指磁齿轮在一个周期内传递的转矩存在脉动,其原因是两转子在同步旋转过程中磁化方向夹角总在发生改变,其大小与运行时的转子偏差角有关。图14为不同转子偏差角对电机基本转矩脉动进行仿真计算结果曲线。
由图14可见,两侧电机的基本转矩脉动减小趋势基本一致,均随着转子偏差角的增大而减小,在转子偏差角从0°变化到30°的过程中,基本转矩脉动由13.68 N·m降至6.69 N·m,降幅较大。在设计电机理想转子偏差角时,在满足电机稳定性的同时,让电机工作在较大的转子偏差角下可以减小基本转矩脉动,提升磁齿轮转矩,使转矩性能提升。因此,选取绕组提前系数km=4作为电机最终绕组排布方案。
4.2 响应曲面法优化基本转矩脉动
由式(18)可知,DR-PMSM的基本转矩脉动与并接区结构,永磁体结构、铁心结构等因素非线性相关,而响应面法在优化非线性问题时性能优秀[16]。因此选取表达式中影响较大的并接区高度h、永磁体偏心距hp、永磁体极弧系数αp作为自变量,通过响应曲面法对电机进行优化。
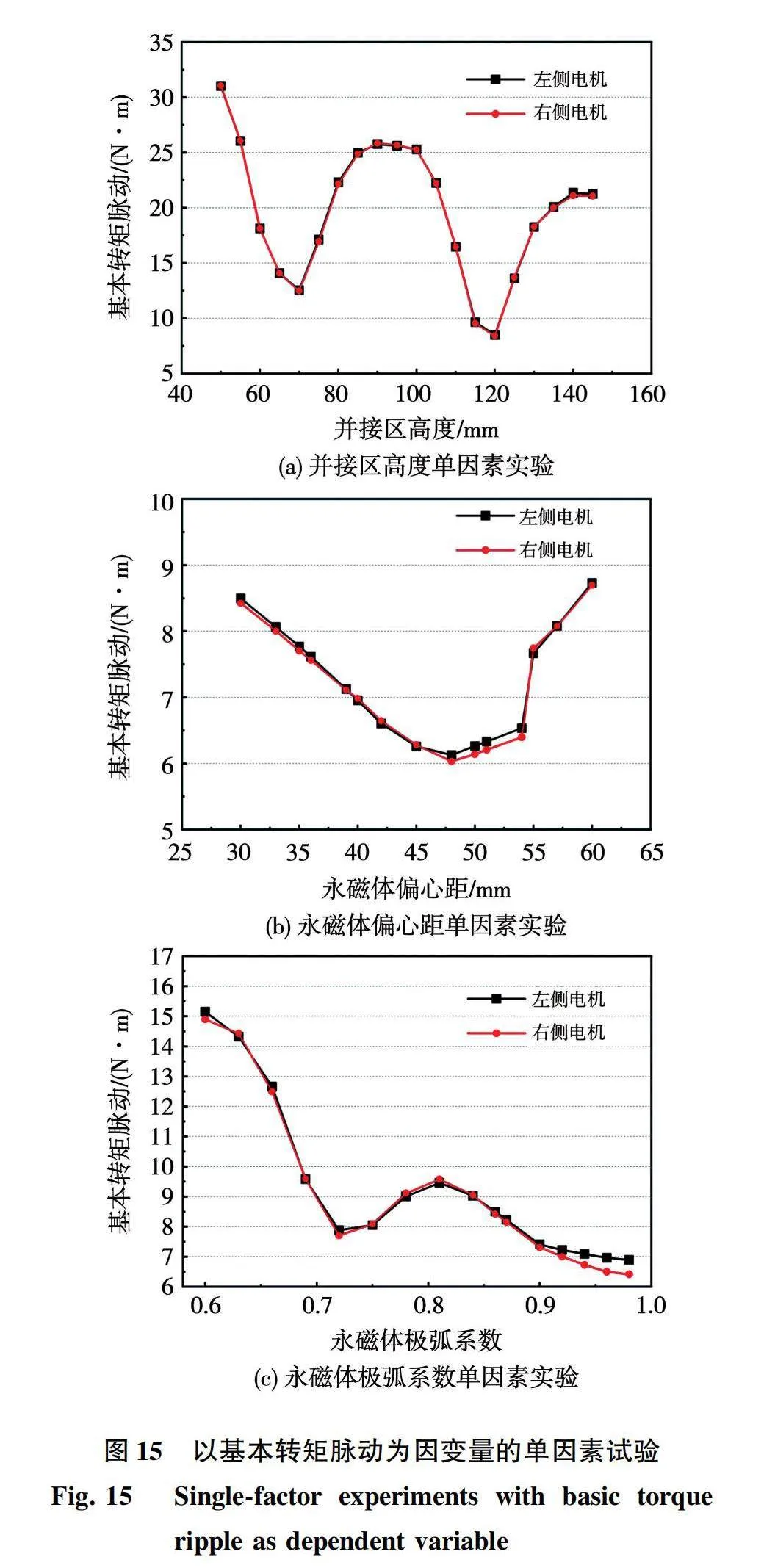
在进行响应曲面法优化前,需要对自变量进行单因素实验以缩小变量取值范围从而得到更好的优化效果,图15为3个自变量对基本转矩脉动的单因素实验曲线。
由图15可见,3个自变量都对基本转矩脉动有较大的影响,与理论推导相符。根据曲线变化趋势,选取的自变量取值范围为:110 mm≤h≤125 mm,42 mm≤hp≤55 mm,0.8≤αp≤1,3个自变量用x1,x2,x3表示。
由于电机模型具有非线性的属性,且存在交互效应与二次效应,所以选用二阶响应模型对响应函数进行逼近,基本模型如下:
y(x)=β0+∑ki=1βixi+∑ki=1βiix2i+∑kilt;jβijxixj+ε。(19)
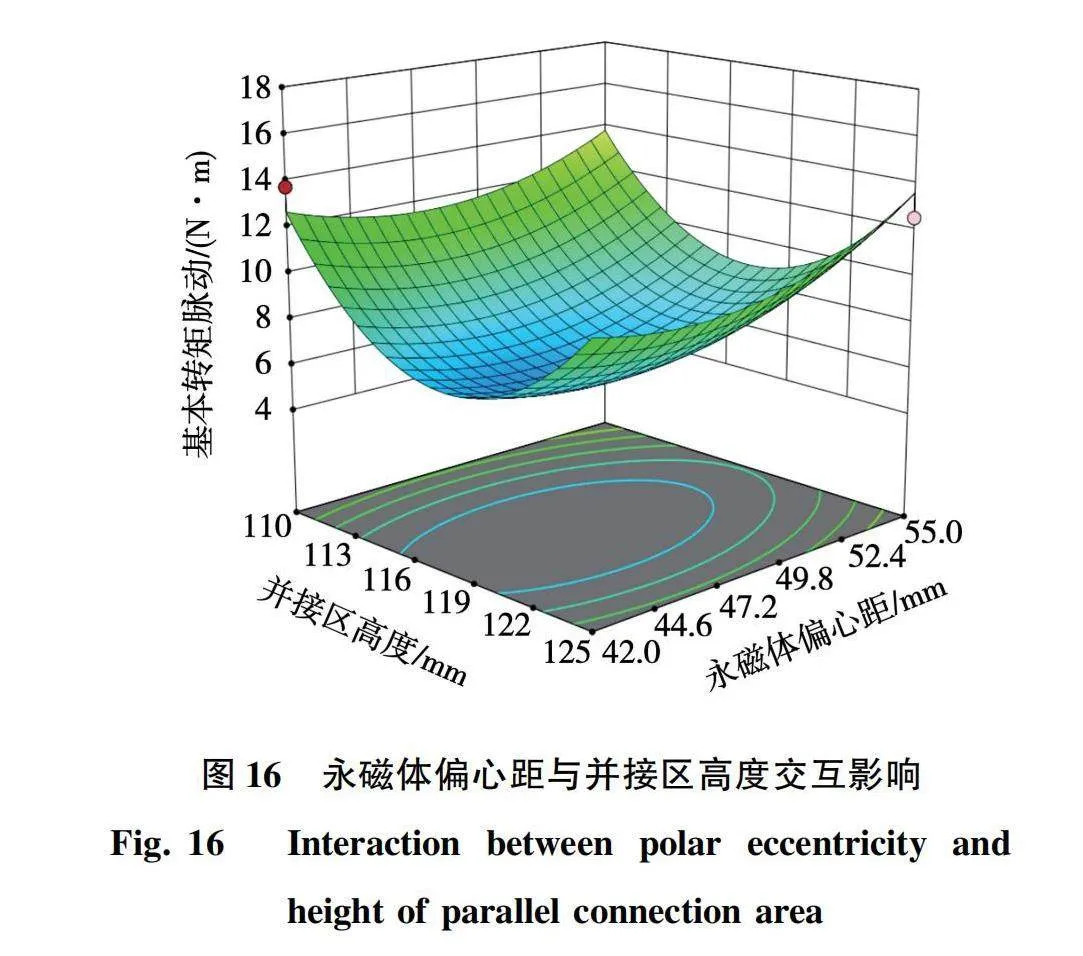
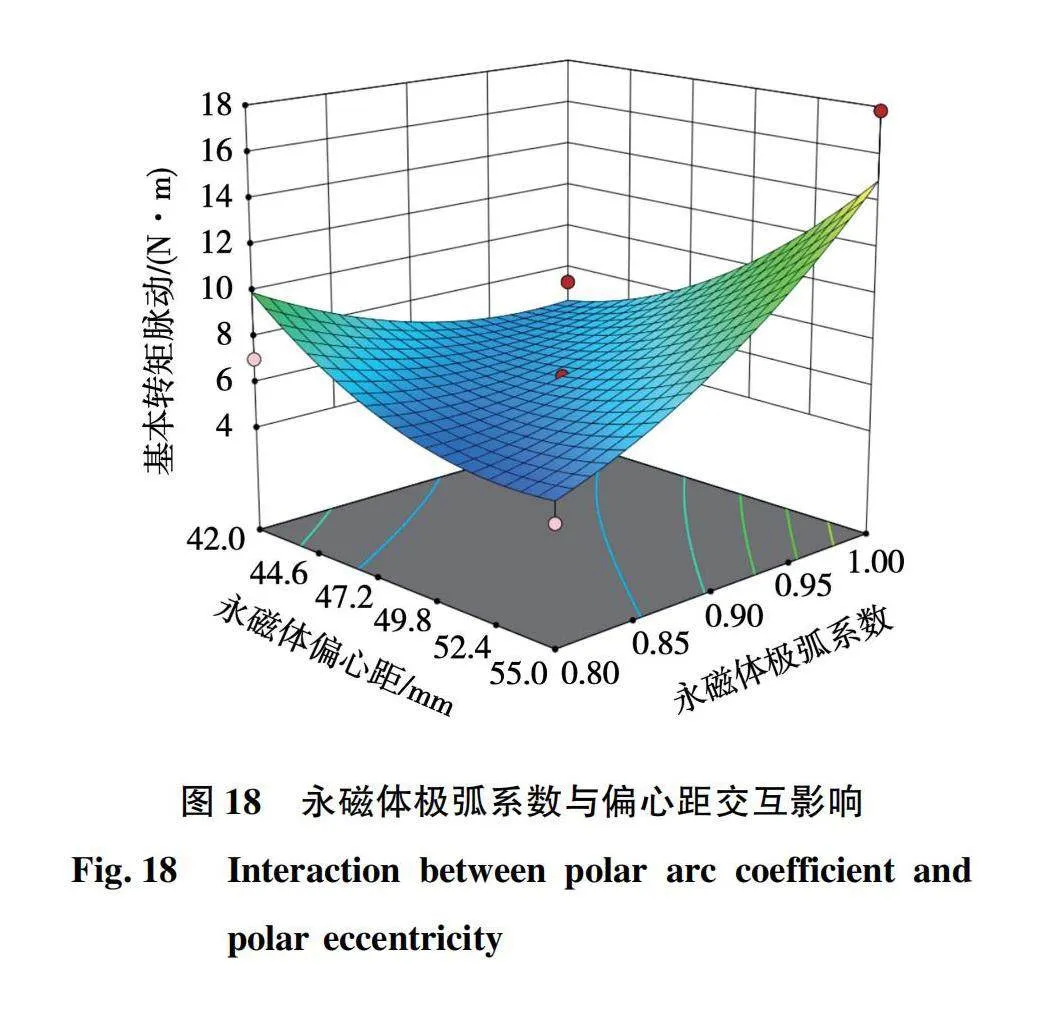
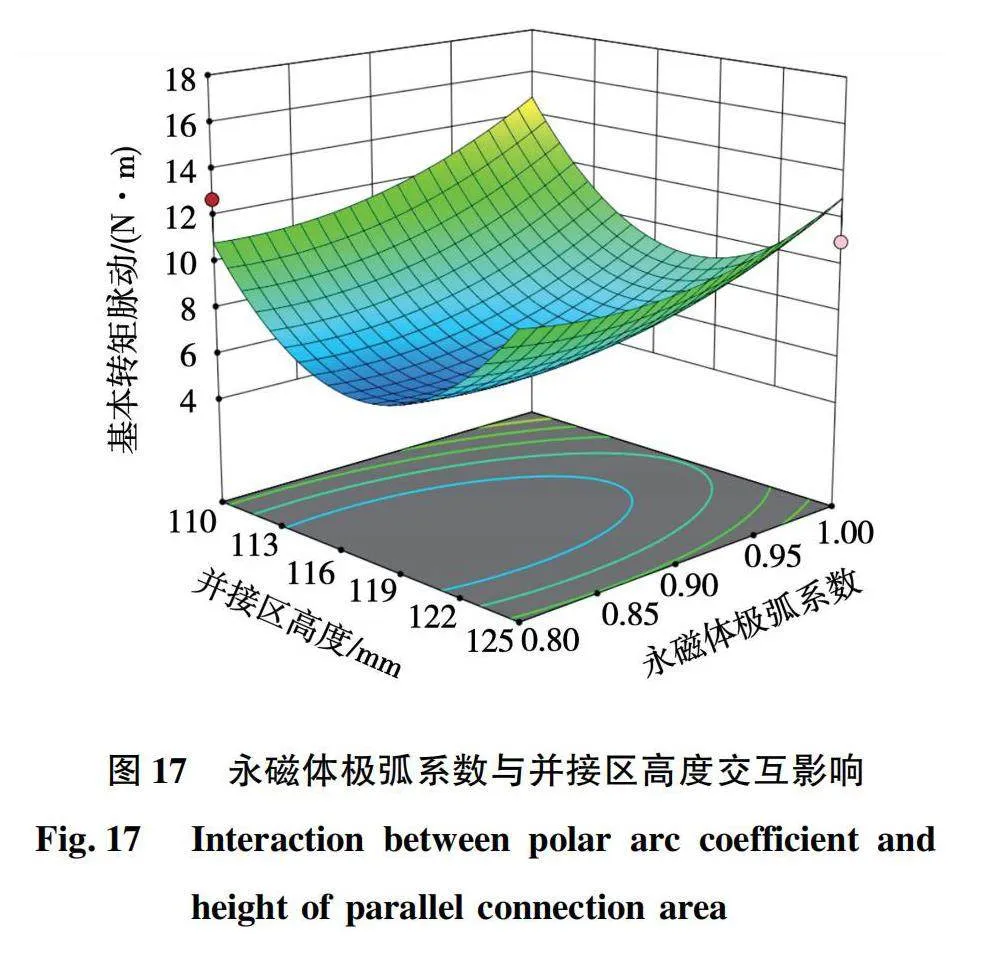
式中:y(x)为目标函数;xi为第i个自变量;βi为xi的线性效应系数;βii为xi的二次效应系数;βij为xi与xj之间的交互效应系数;ε为误差。使用Design-Expert对模型进行交互试验,得到3个变量间两两交互作用对基本转矩脉动影响的三维图如图16~图18所示。
通过软件对试验得到的数据进行分析处理,得到电机模型的二阶回归方程为
y=1 561.78-20x1-9.041x2-371.87x3+
0.008 17x1x2-0.634x1x3+5.08x2x3+0.085 6x21+0.037 7x22+119.65x23。(20)
根据回归方程式(20)对电机进行响应面优化得到的最优尺寸为h=119.5 mm,hp=51 mm,αp=0.96,此时电机基本转矩脉动降低至4.63 N·m,相较于优化前降低了7.65 N·m。
4.3 优化后性能仿真分析
为检验优化效果,对优化前后的电机模型进行有限元仿真分析,对比分析其关键性能。
图19为优化前后的电机空载反电势波形经过傅里叶分解后得到的各次谐波幅值柱状图。由图19(a)可以看出,优化前A相基波幅值略高于另外两相基波幅值,基波电势不对称度较高。同时谐波以3、9、11次谐波为主,总谐波畸变率为4.2%。图19(b)显示优化后三相不对称度降低,谐波以3次谐波与9次谐波为主,总谐波畸变率为2.9%,较优化前降低31%,空载反电势性能得到提升。
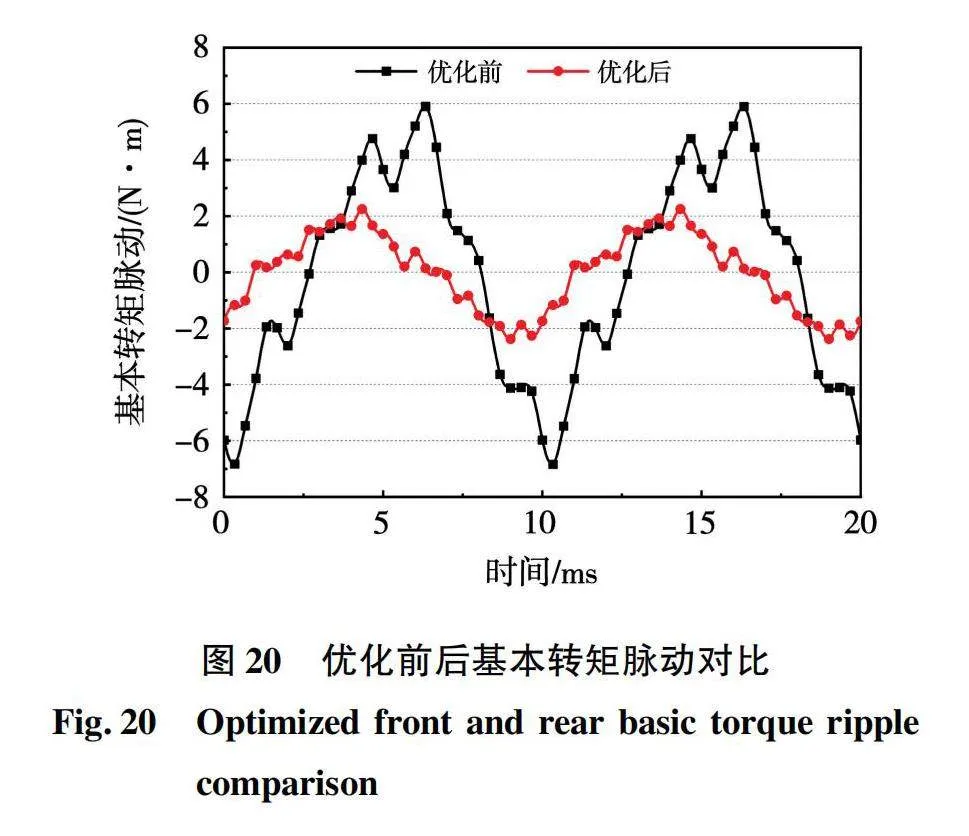
图20为优化前后左侧电机基本转矩脉动。从图中可以看出,经过响应曲面法优化后,电机的基本转矩脉动由最初的12.74 N·m降低至4.63 N·m,降幅为63.66%,优化效果较为理想。
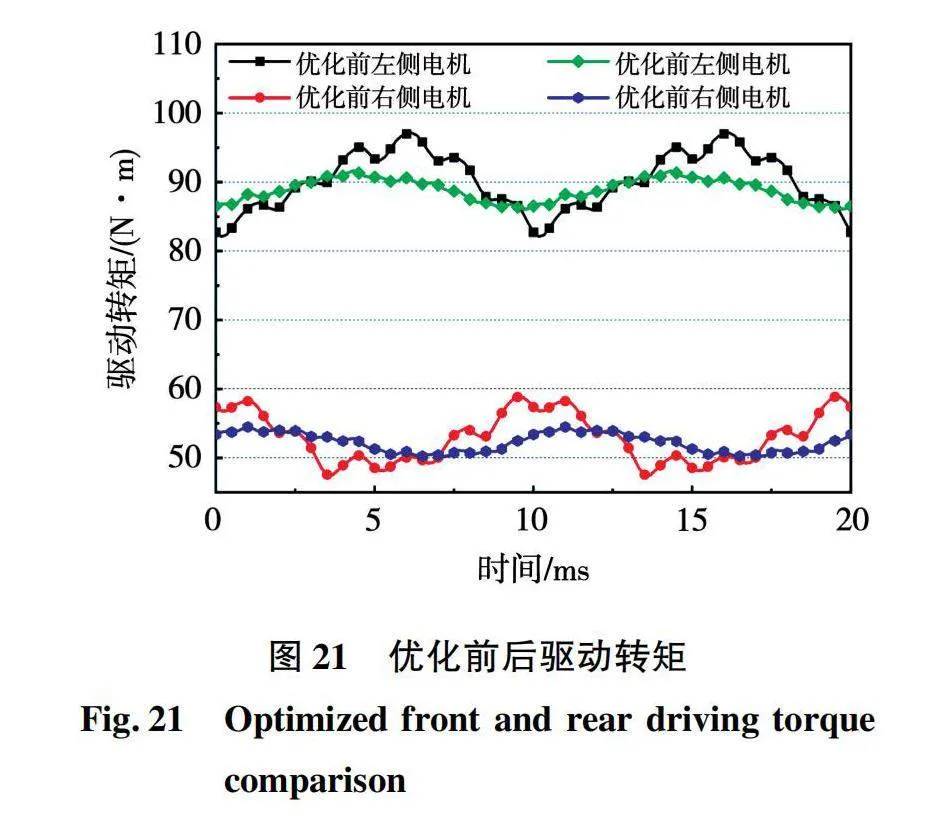
图21为优化前后电机驱动转矩波形图。优化后左侧电机转矩为88.87 N·m,峰-峰值为5.58 N·m,转矩脉动为6.28%,相较优化前的16.68%降低了62.35%;优化后右侧电机转矩为52.21 N·m,峰-峰值为4.24 N·m,转矩脉动为8.12%,相较优化前的21.43%降低了62.11%。可见将响应曲面法用于对电机转矩脉动进行优化能得到较为理想的优化方案,从而大幅降低电机转矩脉动。
此外,经过改良后左侧电机的驱动转矩为右侧电机的1.7倍,而电机总输出转矩相较两侧转矩相等时基本不变,实现了在不牺牲总输出转矩的前提下,两侧转子驱动非对称负载的研究目标。
5 结 论
本文基于双并列转子永磁同步电机基本原理,对非对称运行状态下的电机驱动转矩解析表达式进行推导,改良其在大偏差角下输出转矩降低的缺点。将磁网络模型与响应面法结合,分析影响转矩的关键因素,对电机转矩性能提出优化方案。通过对双并列转子永磁同步电机的建模分析,得出了以下结论:
1)采用轻载侧绕组前置的结构设计,可使电机在转子偏差角较大的状态下能够输出理想的驱动转矩,解决因功角变小引起的转矩下降问题。
2)转子偏差角除影响磁齿轮转矩外,还对电机基本转矩脉动存在影响。在转子偏差角小于180°电角度的区间内,随着转子偏差角的增大,磁齿轮转矩先增大后减小,基本转矩脉动始终降低。在设计中要根据需求选取合适的偏差角对两者进行平衡。
3)对双并列转子电机使用响应曲面法进行优化,优化后基本转矩脉动明显下降,电机性能得到改善,实现两侧电机输出不同大小的驱动转矩的目标,拓宽了双并列转子电机的适用范围。
参 考 文 献:
[1]ALBERTO P R, FRANCESCO T, GJYLIJE H, et al. Sustainable mechanochemical synthesis of β-cyc-lodextrin polymers by twin screw extrusion[J]. Environmental Science and Pollution Research International, 2021, 29(1): 251.
[2]陈作炳, 付云, 艾佳, 等. 立式紊流搅拌机多相流场及混合性能[J]. 排灌机械工程学报, 2024, 42(7): 678.
CHEN Zuobing, FU Yun, AI Jia, et al. Multiphase flow field and mixing performance of vertical turbulent mixer[J].Journal of Drainage and Irrigation Machinery Engineering,2024,42(7):678.
[3]陈长军. 现代铝板带立辊轧机压下方案探讨[J].有色金属加工, 2018, 47(5): 61.
CHEN Changjun. Study on vertical rolling mill of modern aluminum plate and strip[J]. Nonferrous Metals Processing, 2018, 47(5): 61.
[4]张炳义,刘忠奇,冯桂宏.潜油螺杆泵直驱细长永磁电机转轴扭曲对电磁转矩影响分析[J].电机与控制学报,2016,20(2):76.
ZHANG Bingyi, LIU Zhongqi, FENG Guihong. Analysis of shaft torsion deformation on electromagnetic torque of thin permanent magnet motor for direct-driven submersible screw pump[J]. Electric Machines and Control, 2016, 20(2): 76.
[5]UCHIBORI K, ANDO Y, MURAKAMI I. Assignment of limit torque on cylindrical magnetic gear[J].Journal of the Japan Society of Applied Electromagnetics and Mechanics,2015,23(1):68.
[6]戴思锐, 张炳义, 厉伟, 等. 一种定子连体双转子同步并行直驱永磁电机[J]. 电工技术学报,2020,35(10):2107.
DAI Sirui, ZHANG Bingyi, LI Wei, et al. A parallel direct-driven permanent magnet synchronous motor with stator connected dual-rotors synchronous[J]. Transactions of China Electrotechnical Society,2020,35(10):2107.
[7]陶大军, 陈阳, 李凌霄, 等. MW级双并列转子低速永磁直驱电机设计方法与性能分析[J]. 电机与控制学报, 2023, 27(9): 82.
TAO Dajun, CHEN Yang, LI Lingxiao, et al. Design method and performance analysis of MW-level dual-parallel rotor low-speed permanent magnet direct-driven motor[J]. Electric Machines and Control, 2023, 27(9):82.
[8]陈阳, 陶大军, 王立坤, 等. 双并列转子永磁同步电机转矩脉动产生机理及抑制[J/OL]. 电工技术学报, (2023-12-11)[2024-05-07]. https://doi.org/10.19595/j.cnki.1000-6753.tces.231410.
CHEN Yang, TAO Dajun, WANG Likun, et al. Mechanism and suppression of torque ripple of permanent magnet synchronous motor dual-parallel rotor[J/OL]. Transactions of China Electrotechnical Society, (2023-12-11)[2024-05-07].https://doi.org/10.19595/j.cnki.1000-6753.tces.231410.
[9]黄家楠, 章玮. 定子连体双轴永磁电机稳态特性分析[J]. 电机与控制学报, 2023, 27(6): 1.
HUANG Jianan, ZHANG Wei. Analysis of steady state characteristics of connected permanent magnet synchronous motor[J]. Electric Machines and Control, 2023, 27(6): 1.
[10]朱桂华, 张丽欣, 王万斌, 等. 偏心双轴搅拌用于污泥搅拌混合的数值模拟[J]. 环境工程学报, 2017, 11(5): 3128.
ZHU Guihua, ZHANG Lixin, WANG Wanbin,et al.Numerical simulation of mixing on sludge with eccentricity double-impeller[J]. Chinese Journal of Environmental Engineering, 2017, 11(5): 3128.
[11]张炳义, 贾宇琪, 冯桂宏. 新型模块组合式定子永磁电机[J]. 电工技术学报, 2015, 30(12): 243.
ZHANG Bingyi, JIA Yuqi, FENG Guihong. Novel permanent magnet synchronous machines with modules combination stator[J]. Transactions of China Electrotechnical Society, 2015, 30(12): 243.
[12]陈匡非, 杜玉梅. 平行轴永磁齿轮的特性研究[J]. 微特电机, 2004, 32(4): 5.
CHEN Kuangfei, DU Yumei. Study on characteristic of permanent magnetic gear with parallel axis[J]. Small amp; Special Electrical Machines, 2004, 32(4): 5.
[13]LI Jiangang, TAN Qingchang, ZHANG Yongqi, et al. Study on the calculation of magnetic force based on the equivalent magnetic charge method[J]. Physics Procedia, 2012, 129(24): 190.
[14]朱博, 张钰朋, 徐攀腾, 等. 实现位置同步的双电机交叉耦合控制策略[J]. 哈尔滨理工大学学报, 2022, 27(5): 114.
ZHU Bo, ZHANG Yupeng, XU Panteng, et al. Cross coupling control strategy of two motors for position synchronization[J]. Journal of Harbin University of Science and Technology, 2022, 27(5):114.
[15]佟文明, 姚颖聪, 李世奇, 等. 考虑磁桥不均匀饱和的内置式永磁同步电机等效磁网络模型[J]. 电工技术学报,2022,37(12):2961.
TONG Wenming, YAO Yingcong, LI Shiqi, et al. Equivalent magnetic network model for interior permanent magnet machines considering non-uniform saturation of magnetic bridges[J].Transactions of China Electrotechnical Society, 2022, 37(12): 2961.
[16]孔晓光, 刘春浩, 梁文星. 永磁磁阻双转子电机结构参数的优化设计[J]. 大电机技术, 2022(5): 8.
KONG Xiaoguang, LIU Chunhao, LIANG Wenxing. Optimal design of structural parameters of permanent magnet reluctance double-rotor motor[J]. Large Electric Machine and Hydraulic Turbine, 2022(5): 8.
(编辑:刘素菊)
