考虑时滞的涡簧储能用永磁同步电机反推控制
2024-12-03余洋张千慧庞淇余宗哲摘
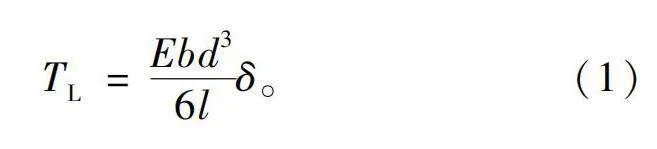
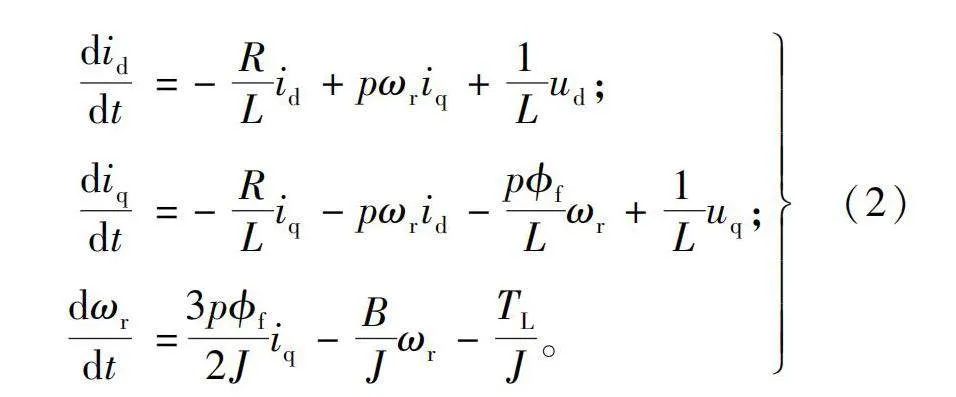







要:针对采样、通信等造成的时滞现象弱化涡簧储能系统运行性能的问题,设计了考虑时滞的涡簧储能用永磁同步电机反推控制方法。首先在dq0坐标系下建立考虑电流延时的永磁同步电机数学模型;在此基础上,采用Lyapunov-Krasovskii理论设计含有时滞的Lyapunov函数,并结合反推控制方法,推导出永磁同步电机时滞反推控制器,以消除时滞对系统的影响,并保证系统闭环稳定性。仿真和实验结果表明,随着时滞的增加,系统控制响应偏差和波动影响也变大,甚至有可能导致系统失去稳定;与常规反推控制器相比,对于常时滞和变时滞情形,考虑时滞的反推控制器下永磁同步电机的速度和电流均能更准确跟踪各自的参考值,同时响应速度更快、且波动更小,极大改善了时滞对于系统运行性能的影响。
关键词:非线性系统;涡簧储能系统;永磁同步电机;时滞;反推控制;李亚普诺夫函数
DOI:10.15938/j.emc.2024.10.001
中图分类号:TM351
文献标志码:A
文章编号:1007-449X(2024)10-0001-12
收稿日期: 2023-12-15
基金项目:国家自然科学基金(52077078)
作者简介:余 洋(1982—),男,博士,教授,博士生导师,研究方向为储能技术、新能源电力系统特性与多源互补;
张千慧(2000—),女,硕士,研究方向为电力储能技术;
庞淇文(1999—),男,硕士,研究方向为电力储能技术;
余宗哲(1999—),男,硕士,研究方向为电力储能技术。
通信作者:余 洋
Backstepping control of permanent magnet synchronous machine for spiral spring energy storage considering time delay
YU Yang1,2, ZHANG Qianhui1,2, PANG Qiwen1,2, YU Zongzhe1,2
(1.State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources, North China Electric Power University, Baoding 071003, China; 2.Key Laboratory of Distributed Energy Storage and Microgrid of Hebei Province, North China Electric Power University, Baoding 071003, China)
Abstract:To mitigate the impact of time delays caused by sampling and communication on the performance of a spring energy storage system, a backstepping control method for spring energy storage using a permanent magnet synchronous motor (PMSM) that accounts for time delays was proposed. Initially, a mathematical model of the PMSM considering current delay was established in the dq0 coordinate system. Subsequently, a Lyapunov-Krasovskii theory-based Lyapunov function with time delay was designed, and a backstepping control method was integrated to derive a time-delay backstepping controller for the PMSM. This controller aims to eliminate the influence of time delays on the system and ensure the closed-loop stability. Simulation and experimental results demonstrate that as the time delay increases, the control response deviation and fluctuation impact also become larger, potentially leading to system instability. Compared to conventional backstepping controllers, the time-delay-considering backstepping controller exhibits more accurate tracking of the PMSM’s speed and current reference values under both constant and variable time delays. Additionally, it offers faster response speeds and reduced fluctuations, significantly improving the impact of time delays on system performance.
Keywords:nonlinear system; spiral spring energy storage system; permanent magnet synchronous motor; time delay; backstepping control; Lyapunov function
0 引 言
新能源发电具有随机性和波动性[1],储能技术是保障间歇式新能源入网的有效手段之一[2]。涡簧储能(spiral spring energy storage,SSES)是近年来提出的绿色、高效的新型物理储能技术[3-4],以机械涡簧作为储能介质,永磁同步电机(permanent magnet synchronous machine,PMSM)为执行机构,利用涡簧的伸缩变形驱动PMSM实现机械能和电能的相互转化。
作为典型的机电耦合系统,由采样、通信、传感器、计算等延迟带来的时滞会直接影响SSES系统运行性能[5-6]。其实,时滞现象广泛存在于控制工程、电力系统、机械传动系统等多个领域[7-8],大量针对时滞动力系统稳定性的研究已表明,时滞是造成系统工作性能恶化、引发系统振荡、混沌乃至崩溃的重要原因[9-10],并且时滞的存在会影响控制器的控制效果[11]。但现有的PMSM建模与控制中大都忽略了时滞,这对于小时滞环境或控制性能要求较低的场合尚可接受,但若时滞较大或控制性能要求较高时,忽略时滞后得到的结果往往是不可靠的。因此,深入研究SSES系统的时滞现象,不仅能够提高其自身运行的稳定性和可控性,也能为减小时滞对于PMSM驱动性能影响提供重要技术支撑。
对于时滞系统的研究方法,主要有频域和时域两大类。频域内分析时滞系统最常用的是Smith预估法[12],其思路是消去特征方程中的时滞项,然后用传统方法设计控制器[13],基本实现了对于常时滞和结构参数已知的系统模型求解,但受数学变换的局限性,难以处理复杂的时滞系统,而且受建模误差和参数变化的影响较大[21]。时域法可以克服频域分析的不足,计算也相对简单,主要有基于Lyapunov-Razuminkhin(L-R)定理的方法和基于Lyapunov-Krasovskii(L-K)定理的方法[14-16],其中后者在PMSM时滞系统中应用最为广泛。如文献[17]对于网络化环境下的PMSM转速控制,在考虑时滞的基础上推导了基于模型的调速鲁棒控制器,并通过构造L-K函数获取了转速稳定性条件;文献[18]针对PMSM矢量控制中逆变器的开关延迟、控制器的计算时间等时滞环节导致系统动态响应过程振荡增大的问题,提出基于自耦PI控制器代替矢量控制中电流环PI控制器,并建立L-K函数讨论了稳定性,但PI控制器仍然存在参数整定复杂的问题。还有一些研究将神经网络引入PMSM时滞控制,如文献[19]考虑PMSM未知参数扰动、混沌和不确定时延,提出了基于径向基函数神经网络的自适应动态表面控制,实现了渐近跟踪稳定性,但神经网络训练难度高,对时滞问题的针对性不强;文献[20]只考虑了PMSM的输入时滞,提出了基于事件触发机制的自适应神经网络控制方法,在具有输入时滞的情况下完成对PMSM系统的跟踪控制,但Lyapunov函数构造复杂,计算量较大;文献[21]进一步针对存在参数不确定和未知时延的分数阶PMSM系统,提出了基于命令滤波反步方法的自适应神经网络控制方法,并采用L-K函数,改善了时滞不确定性的影响,但仍然存在L-K函数构造困难的问题。总之,当前针对PMSM时滞控制的研究相对不多,并且大部分都存在计算复杂、L-K函数构造困难、神经网络训练难度大和不能保证闭环系统稳定性等问题。
此外,对于SSES系统而言,PMSM模型具有多变量、高阶、强耦合的特点[22],同时系统运行中涡簧的扭矩和转动惯量同时变化,针对SSES系统的非线性特征,常规的控制方法往往达不到理想的控制性能,为此,前期研究将非线性反推控制引入系统控制中,取得了不错的控制效果。反推控制是上世纪90年代出现的一种非线性控制方法,通过引入虚拟控制量并结合Lyapunov函数采用倒推方法设计控制器,实现高维非线性系统向低维系统的转化,通过反推控制可在确保闭环系统稳定的条件下达到准确、快速地跟踪效果[23-24]。在数学和控制领域,已有研究将反推控制引入非线性时滞系统的控制器设计中。如文献[25]利用Lyapunov函数和反推方法设计了非线性时滞系统自适应状态反馈控制器;文献[26]研究了具有三角形结构的非线性时滞系统的鲁棒性控制问题,利用反步方法构造了状态反馈控制器,并基于Lyapunov稳定性理论证明了闭环系统的稳定性;文献[27]采用Lyapunov稳定性理论研究了一类具有三角形结构的非线性时滞系统的反推控制鲁棒镇定问题。但上述文献存在Lyapunov函数选取困难、控制器计算量大等问题,并且还未见有将反推控制应用于PMSM系统时滞问题研究的相关报道。
针对时滞影响SSES系统运行性能的问题,考虑采样、控制器计算以及涡簧形变耗时等多种因素造成的电流延时,本文提出SSES用PMSM时滞反推控制方法,采用反推方法设计控制器,并构造合理的Lyapunov函数保证系统控制稳定性,实现时滞情况下PMSM转速和电流的准确快速跟踪控制。仿真和实验结果表明,与传统反推控制相比,本文设计的控制算法使得PMSM状态量能更好、更快地跟踪上参考值,极大改善SSES系统的运行性能。
1 SSES系统及数学模型
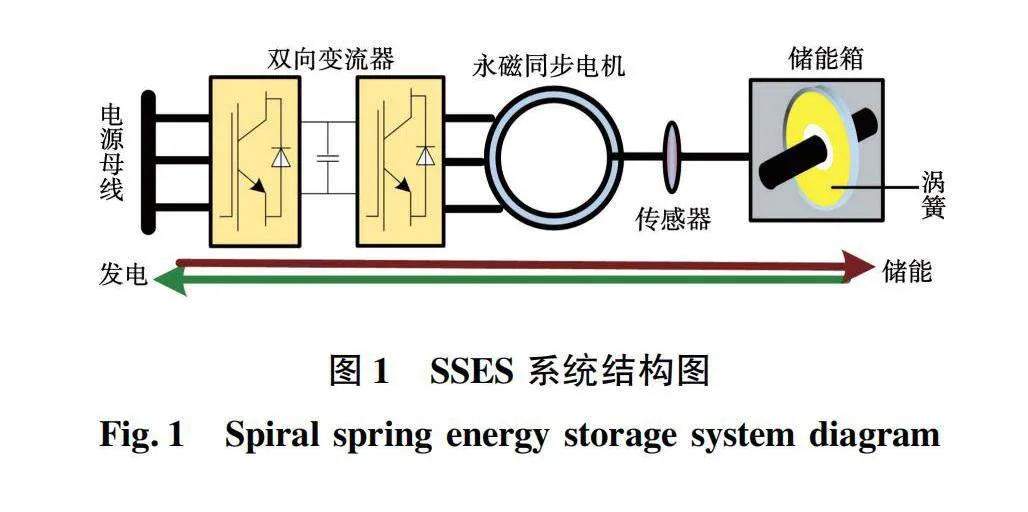
1.1 SSES系统结构及工作原理
SSES系统的基本结构如图1所示,由储能箱、PMSM、双向变流器等部件组成。系统储能时,来自电网的电能通过变流器驱动PMSM旋转以拧紧涡簧,通过涡簧的形变实现电能向机械能的转变,发电过程则相反。
1.2 涡簧数学模型
根据材料力学理论[28],涡簧扭矩可表达为
式中:E、b、d和l分别为涡簧材料的弹性模量、宽度、厚度和长度;δ为涡簧转过的角度。
1.3 PMSM数学模型
选用表贴式PMSM作为SSES系统的驱动电机,其在dq0坐标系下的数学模型[29]可表示为:
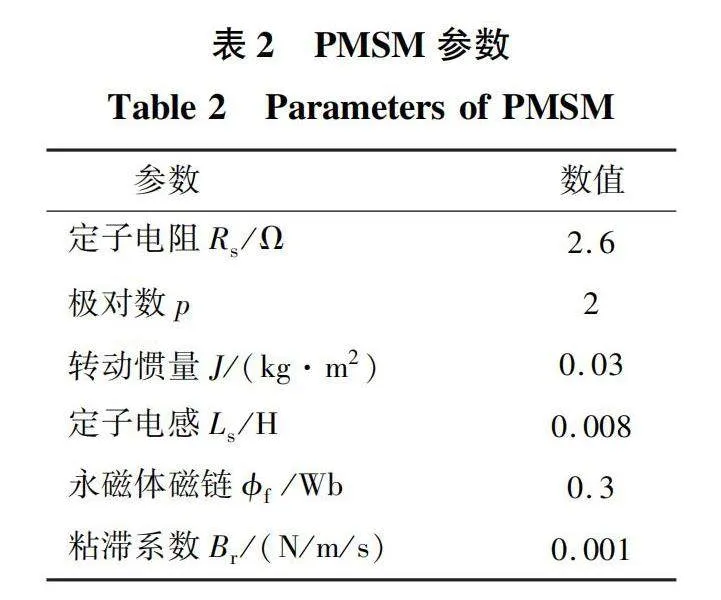
式中:ud、uq分别为d、q轴的定子电压;id、iq为d、q轴的定子电流;L为定子电感;R为定子电阻;B为粘滞摩擦因数;ϕf为永磁磁通;J为转动惯量;TL为涡簧扭矩;p为转子极对数;ωr为转子机械角速度。
令ωr=x1,id=x2,iq=x3,并考虑电流的延时,将式(2)改写为:
式中:t为采样时间;h为由采样、控制器计算以及涡簧形变耗时等因素造成的未知时滞。
2 常规反推控制器设计
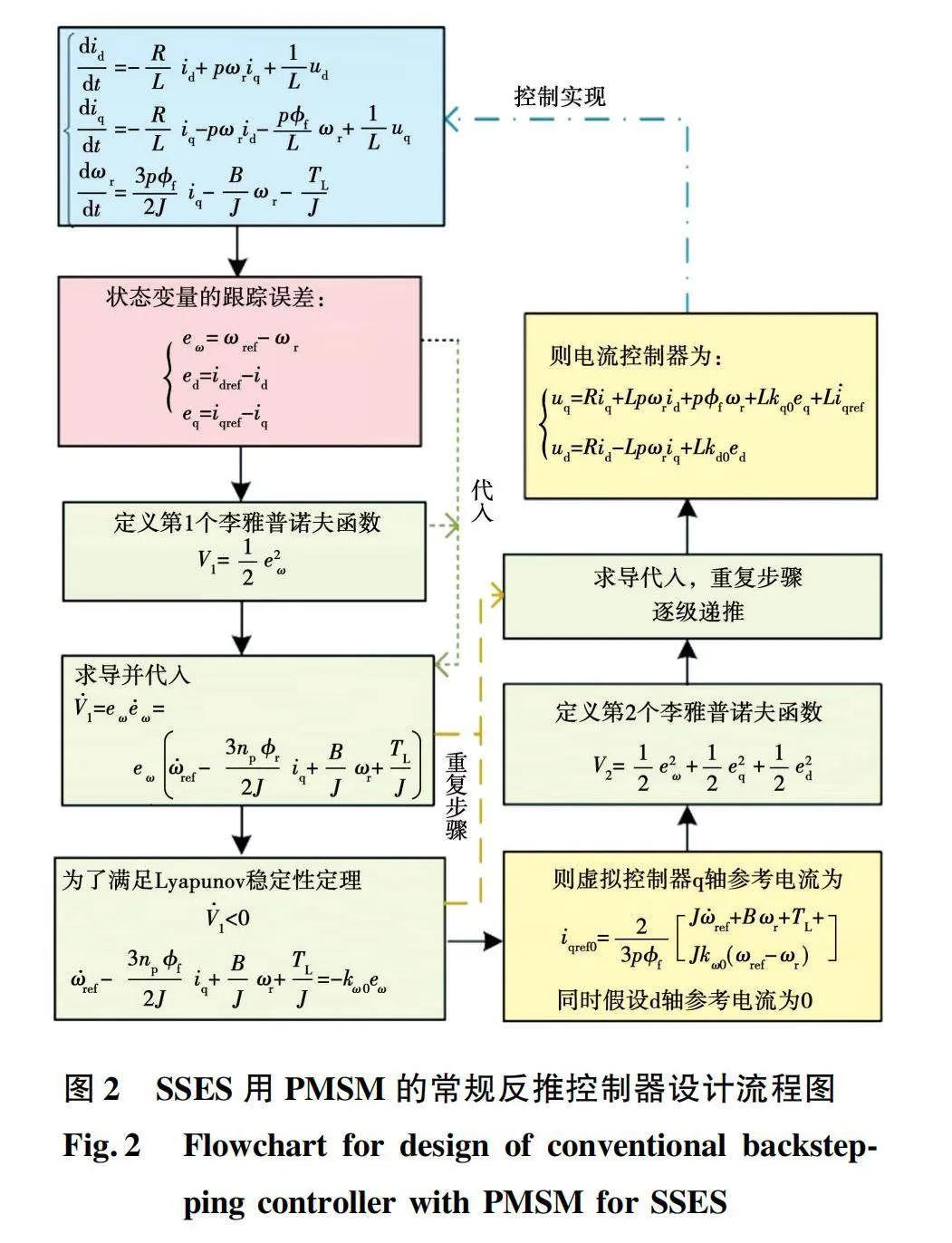
反推控制算法的思想是将复杂的高阶非线性系统分解成若干个不超过系统阶数的子系统,然后为每个子系统分别设计Lyapunov函数和中间虚拟控制变量,一直“后退”到整个系统,直到完成控制器的设计。反推控制算法的出发点是系统输入量,逐级“后退”到系统控制量。在设计控制器时,一般采用各子系统输入量与反馈量的差值作为该级子系统的输入量,并保证控制器参数恒大于0,最终通过Lyapunov稳定性定理得到保证系统稳定且渐近收敛的结论。SSES用PMSM的常规反推控制器设计流程如图2所示。
由文献[28]获取SSES用PMSM的常规反推控制器表达式如下:
式中:iqref0为常规反推控制器下的q轴电流参考值;kω0、kq0、kd0均为大于0的控制参数。
3 考虑时滞的反推控制器设计
3.1 定义误差变量
转速、d轴电流和q轴电流的跟踪误差定义如下:
式中eω、ed和eq分别为转速跟踪误差、d轴电流跟踪误差和q轴电流跟踪误差。
3.2 控制器推导
1)速度控制器设计。
定义第1个Lyapunov函数为
对式(6)求导,得
为了让V·1lt;0,以满足Lyapunov稳定性定理,本文选择:
式中kω为大于0的控制参数。
对式(8)进行整理,得到虚拟控制器q轴电流参考值iqref的表达式为
同时假设d轴参考电流为0。
将式(9)代入式(7)中,可以得到
由式(10)可见,设计的虚拟控制器iqref满足Lyapunov稳定性条件。
2)d轴电流控制器设计。
定义第2个Lyapunov函数[30]为
式中q1(x(τ))为待定的非负函数[25]。
对式(11)求导,得
令H(x(t-h))=|RLx2(t-h)-px1x3(t-h)|,H(x(t-h))为时滞函数,即可得到
接着,取待定的非负函数为:
将式(14)、式(15)代入式(12)中,可得
为了让V·2lt;0,以满足Lyapunov稳定性定理,本文选择:
式中kd为大于0的控制参数。
由于式(17)带有绝对值符号,继续讨论如下:
①当ed≥0时。
对式(18)进行求解,可得到控制器ud的表达式为
②当edlt;0时。
可得到控制器ud的表达式为
将式(18)和式(20)代入到式(16)中,可得
由式(22)可知,设计的d轴电流控制器ud满足Lyapunov稳定性条件。
3)q轴电流控制器设计。
定义第3个Lyapunov函数为
式中q2(x(τ))为待定的非负函数[25]。
对式(23)求导,得
取H1(x(t-h))=|RLx3(t-h)+px1x2(t-h)|,H1(x(t-h))为时滞函数,可得
进一步取待定的非负函数为
将式(26)和式(27)代入式(24)中,可得
由于式(28)带有绝对值符号,继续讨论如下:
①当eq≥0时。
式中kq为大于0的控制参数。
对式(29)进行求解,可得控制器uq的表达式为
②当eqlt;0时。
可得到控制器uq的表达式为
将式(29)、式(31)代入式(28)中,可得
由式(33)可知,设计的q轴电流控制器uq满足Lyapunov稳定性条件。
由此,完成了虚拟控制量iqref和真实控制量ud、uq的推导,并证明它们满足Lyapunov稳定性条件。
4 仿真分析
为验证本文提出的考虑时滞的涡簧储能用永磁同步电机反推控制方法的有效性,在MATLAB平台进行仿真分析。所用涡簧储能系统和PMSM的参数分别如表1和表2所示。为进一步表明算法的优越性,将本文方法与常规反推控制方法进行对比,经过多次仿真对比,2种控制器的参数均选取为:kω=140,kq=180,kd=500,与此同时,d轴电流的参考值设置为0,每组仿真时间均设置为5 s。
为更好地模拟实际环境,本文在常时滞和变时滞2种不同的时滞情况下进行仿真,并设置不同程度的延时,仿真分为3类,共6组,以充分验证控制方法的有效性。前4组在4种时滞下进行仿真:变转速下驱动恒转矩负载,在运行到第2 s时,参考转速由3 rad/s突变为5 rad/s,而负载转矩保持10 N·m不变;后2组仿真为变转速下驱动涡簧负载,即驱动变转矩变惯量负载仿真,同时在运行到第2 s时,参考转速由3 rad/s突变为5 rad/s。
4.1 常时滞仿真
1)第1组仿真:时滞取0.001 s,变转速下驱动恒转矩负载。
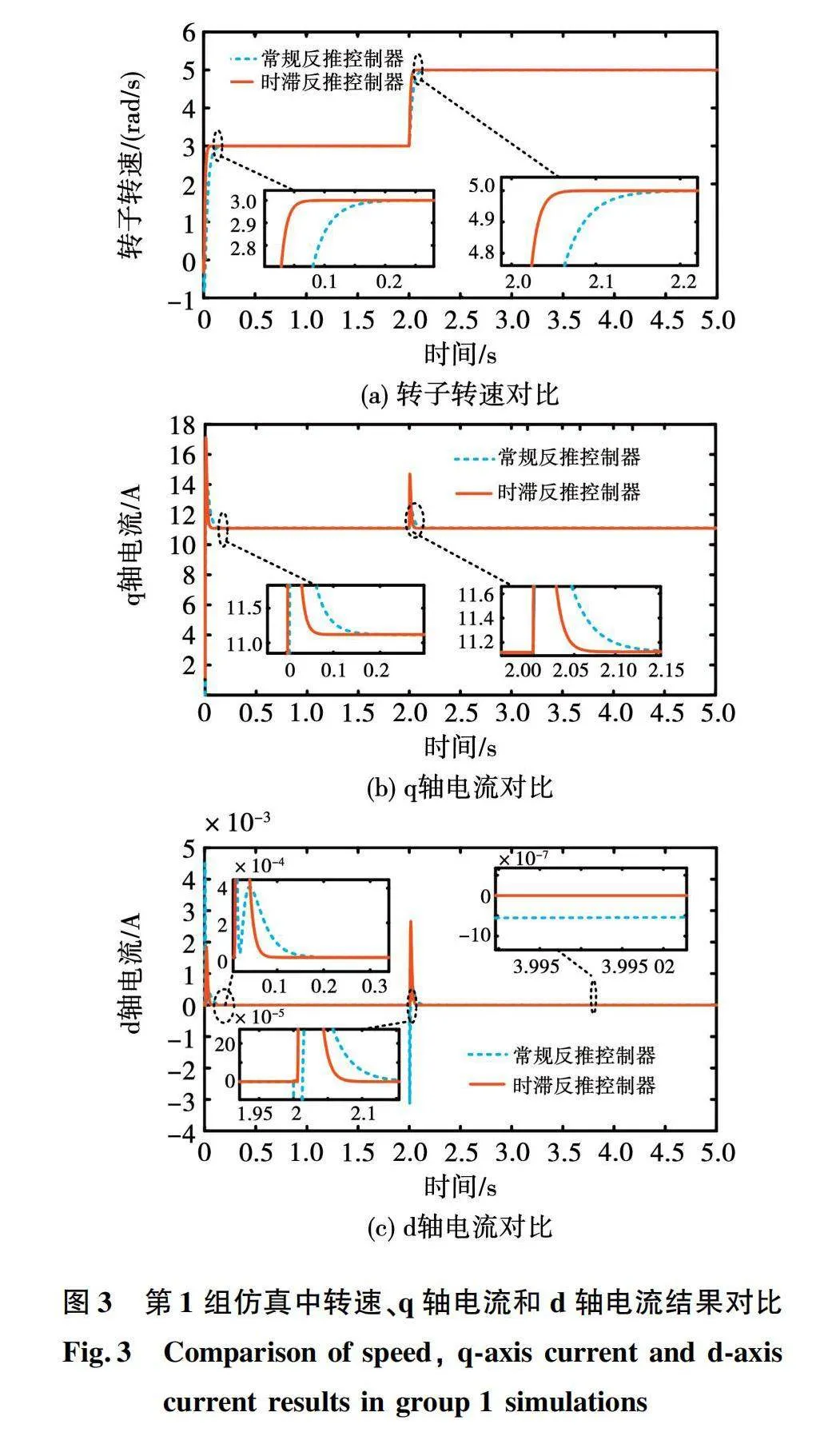
当时滞h取0.001 s,在参考转速第2 s发生突变的情况下,转子转速、q轴电流和d轴电流在常规反推控制器和时滞反推控制器下的对比结果如图3所示。
由图3(a)可知,与常规反推控制器相比,时滞反推控制器下的转速在电机起动和参考转速发生变化时能更快达到参考转速,有更快的响应速度;当系统稳定运行时,常规反推控制器下的转速也能保持平稳,但与参考转速之间存在一个较小的偏差,而时滞反推控制器下的转速则能准确并且平稳地响应参考转速。由图3(b)可看到,在电机起动和参考转速发生变化时,2种控制器下的q轴电流都会发生波动,但时滞反推控制器下的q轴电流恢复至稳定的速度更快。图3(c)表明2种控制器下d轴电流在运行状态变化时均会产生波动,但时滞反推控制器下d轴电流产生的波动更小,具有更快的响应速度,并且在系统进入稳态运行时,常规反推控制器下d轴电流与参考值之间存在偏差,而时滞反推控制器下d轴电流则能保持稳定。
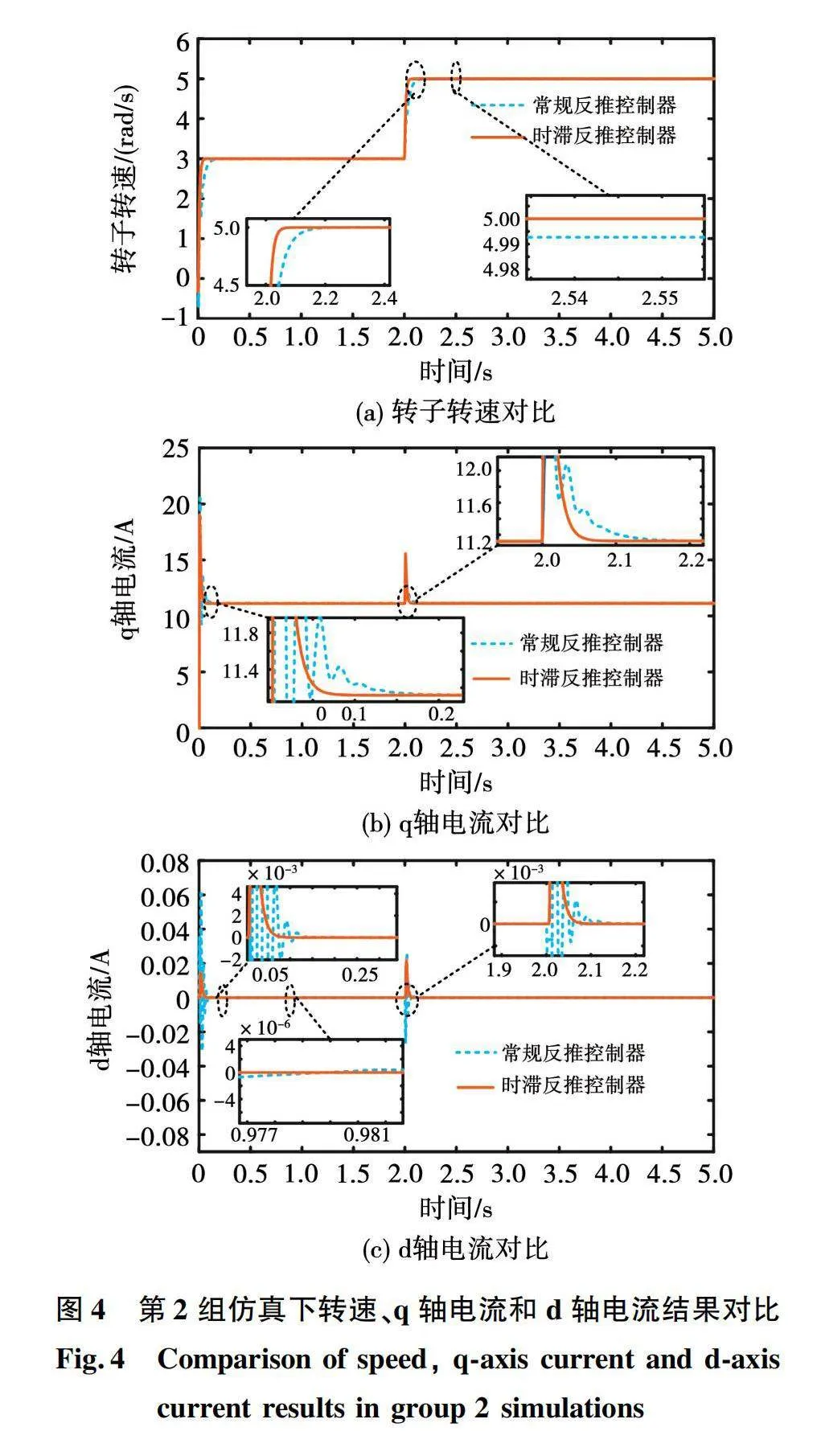
2)第2组仿真:时滞取0.005 s,变转速下驱动恒转矩负载。
接下来加大延迟的程度,取h=0.005,在参考转速发生变化的情况下,转子转速、q轴电流和d轴电流在常规反推和时滞反推控制器下的对比如图4所示。
由图4可看出,与h=0.001时相比,时滞增大,同时转速、q轴电流和d轴电流在电机起动和参考转速发生变化时的波动更加明显,持续时间也更长,可见随着时滞增大,会对系统稳定运行造成更大的影响;与常规反推控制器相比,时滞反推控制器下的3个状态量仍然有更快的响应速度和恢复速度。而且由图4(a)也可看到,在稳态运行时,常规反推控制器下的转速比d=0.001时相比参考转速存在更大的偏差,而时滞反推控制器下的转速则仍能准确并且平稳地响应参考转速。图4(c)表明常规反推控制器下的d轴电流在系统稳态运行时仍然存在波动,而时滞反推控制器下d轴电流则仍能保持稳定。
4.2 变时滞仿真
1)第3组仿真:时滞取0.001sint,变转速下驱动恒转矩负载。
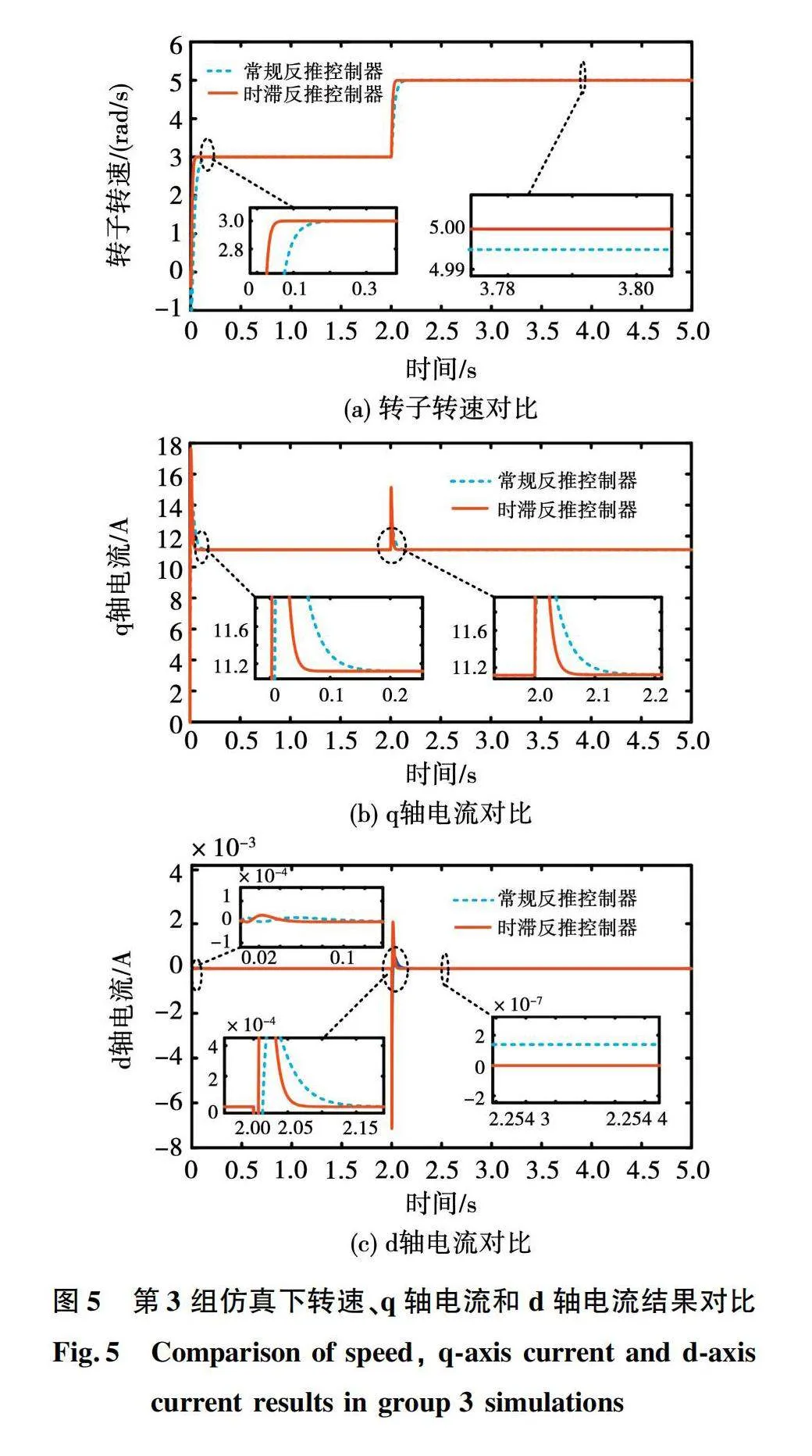
为了尽可能多地模拟系统实际运行时PMSM可能存在的各种延时,考虑延时的多样性,取h=0.001sint,即时滞的大小随着运行时间发生正弦规律的变化。在参考转速发生变化的情况下,转子转速、q轴电流和d轴电流在常规反推和时滞反推控制器下的对比如图5所示。
图5(a)表明,与常规反推控制器相比,时滞反推控制器下的转速有更快的响应速度,在电机起动或者参考转速变化时能更快地达到参考值;在系统稳定运行时,常规反推控制器下的转速仍与参考转速之间存在一个较小的偏差,而时滞反推控制器下的转速则能准确并且平稳地响应参考转速。图5(b)表明,2种控制器下的q轴电流在运行状态变化时均会产生波动,但时滞反推控制器下的q轴电流能更快恢复稳定。由图5(c)可看到,当电机起动和转速突变时,时滞反推控制器下的d轴电流能更快达到参考值0,并且稳态运行时不存在偏差。
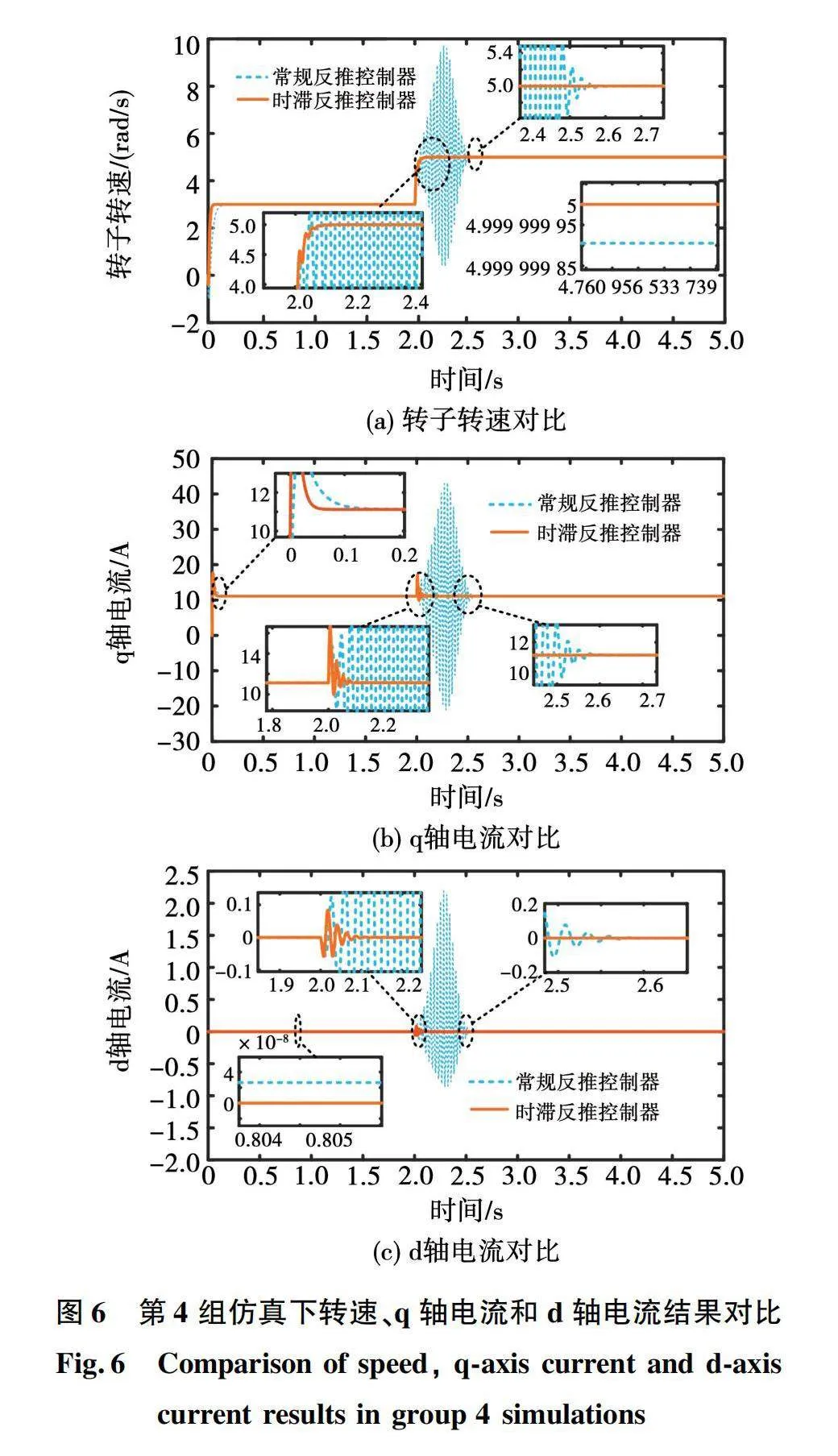
2)第4组仿真:时滞取0.01sint,变转速下驱动恒转矩负载。
当h=0.01sint时,在参考转速发生变化的情况下,转子转速、q轴电流和d轴电流在常规反推控制器和时滞反推控制器下的对比结果如图5所示。
由图6可以明显地看到,相比之前时滞h=0.001sint时,此时的时滞变大,因此在参考转速发生变化时,2种控制器下状态量的波动均更明显,幅度更大,时间更长,这又一次验证了前文得出的结论:时滞越大,对系统产生的影响也就越大。但与常规反推控制器相比,时滞反推控制器下转速和电流的波动更小,仍然保持着较好的稳定性,而且响应参考值的速度更快,能更快恢复稳定状态。
同时图6(a)和图6(c)还表明,在系统运行状态不发生改变时,与时滞h=0.001sint时相比,常规反推控制器下的转速和d轴电流存在的偏差更大,而时滞反推控制器下的转速和d轴电流仍然能准确地跟踪参考值,不存在偏差和波动。
4.3 驱动涡簧负载仿真
为验证本文控制器在PMSM驱动涡簧负载时的控制效果,进行了驱动涡簧负载的仿真,涡簧参数如表1所示,在运行到第2 s时,参考转速由3 rad/s突变为5 rad/s。
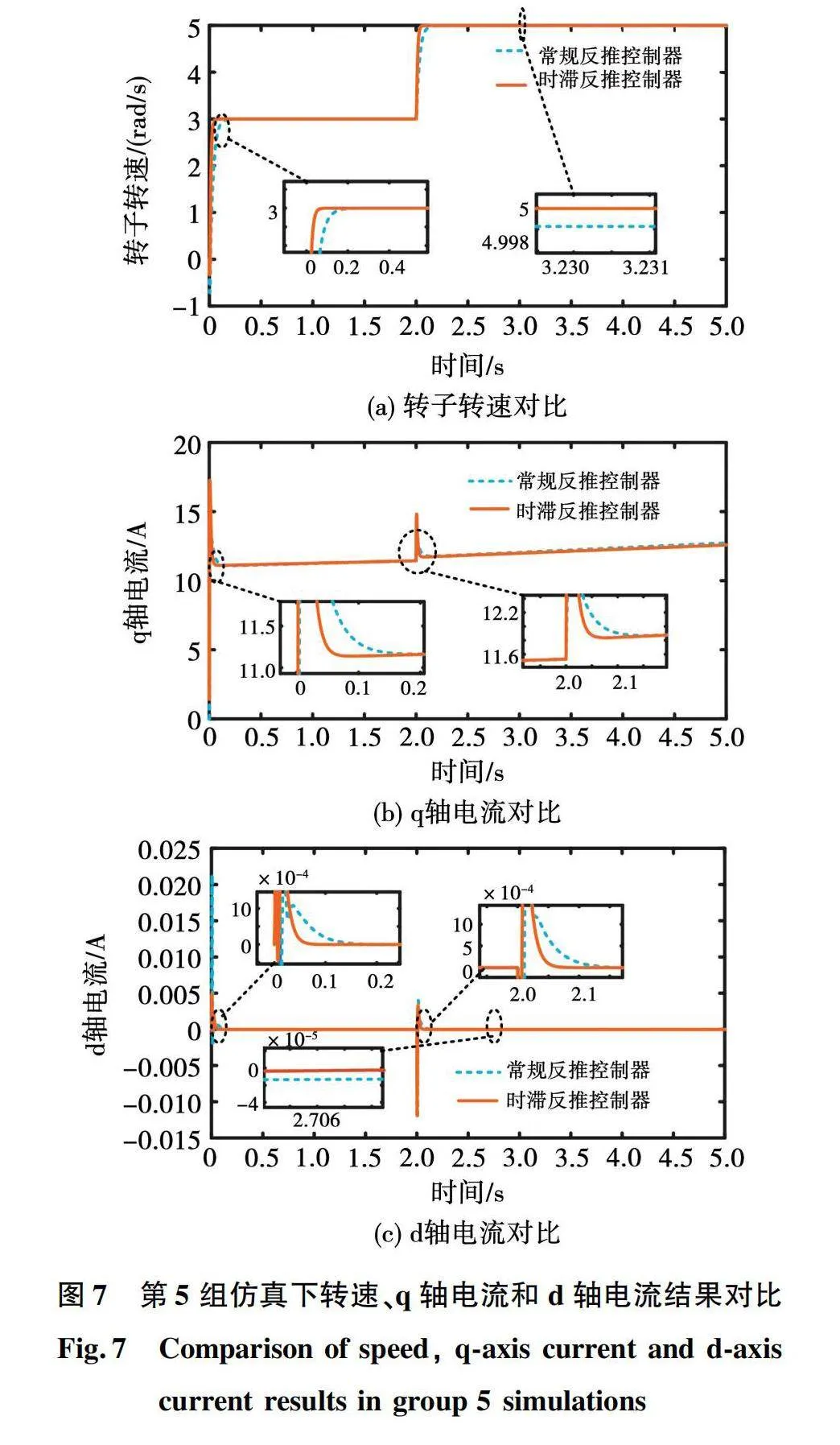
1)第5组仿真:时滞取0.002 s,变转速下驱动涡簧负载。
当h=0.002时,电机驱动涡簧负载,在参考转速发生变化的情况下,转子转速、q轴电流和d轴电流在常规反推和时滞反推控制器下的对比结果如图7所示。
由图7(a)可知,与常规反推控制器相比,时滞反推控制器下的转速能更快达到参考转速,有更快的响应速度;并且当系统稳定运行时,常规反推控制器下的转速仍存在一个较小的偏差,而时滞反推控制器下的转速则能准确并且平稳地响应参考转速。由图7(b)可看到,在参考转速发生变化时,2种控制器下的q轴电流都会发生波动,而且会随着负载转矩的增大而增大,但时滞反推控制器下的q轴电流恢复至稳定的速度更快。图7(c)表明2种控制器下的d轴电流在电机起动和参考转速变化时均会产生波动,但时滞反推控制器下的d轴电流波动更小,且能更快恢复稳态;在系统进入稳态运行时,常规反推控制器下d轴电流与参考值之间存在偏差,而时滞反推控制器下d轴电流则不存在偏差。
2)第6组仿真:时滞取0.002cost,变转速下驱动涡簧负载。
当h=0.002cost时,电机驱动涡簧负载,在参考转速发生变化的情况下,转子转速、q轴电流和d轴电流在常规反推和时滞反推控制器下的对比结果如图8所示。
由图8(a)可知,与常规反推控制器相比,时滞反推控制器下的转速有更快的响应速度并能准确且平稳地维持在参考转速。由图8(b)可看到,时滞反推控制器下的q轴电流恢复至稳定的速度仍然更快;图8(c)表明2种控制器下d轴电流在电机起动时均会产生波动,但时滞反推控制器下d轴电流的波动更小,具有更快的响应速度,并且在系统进入稳态运行时,时滞反推控制器下d轴电流能保持稳定,并且与参考值之间不存在偏差。
5 实验分析
为进一步验证本文提出的时滞反推控制器的有效性,搭建了SSES实验平台及控制平台,平台采用TMS320F28335作为控制芯片,如图9和图10所示,实验参数与仿真部分保持一致。实验分为两组,每组实验均为25 s。
1)第1组:恒转速实验。
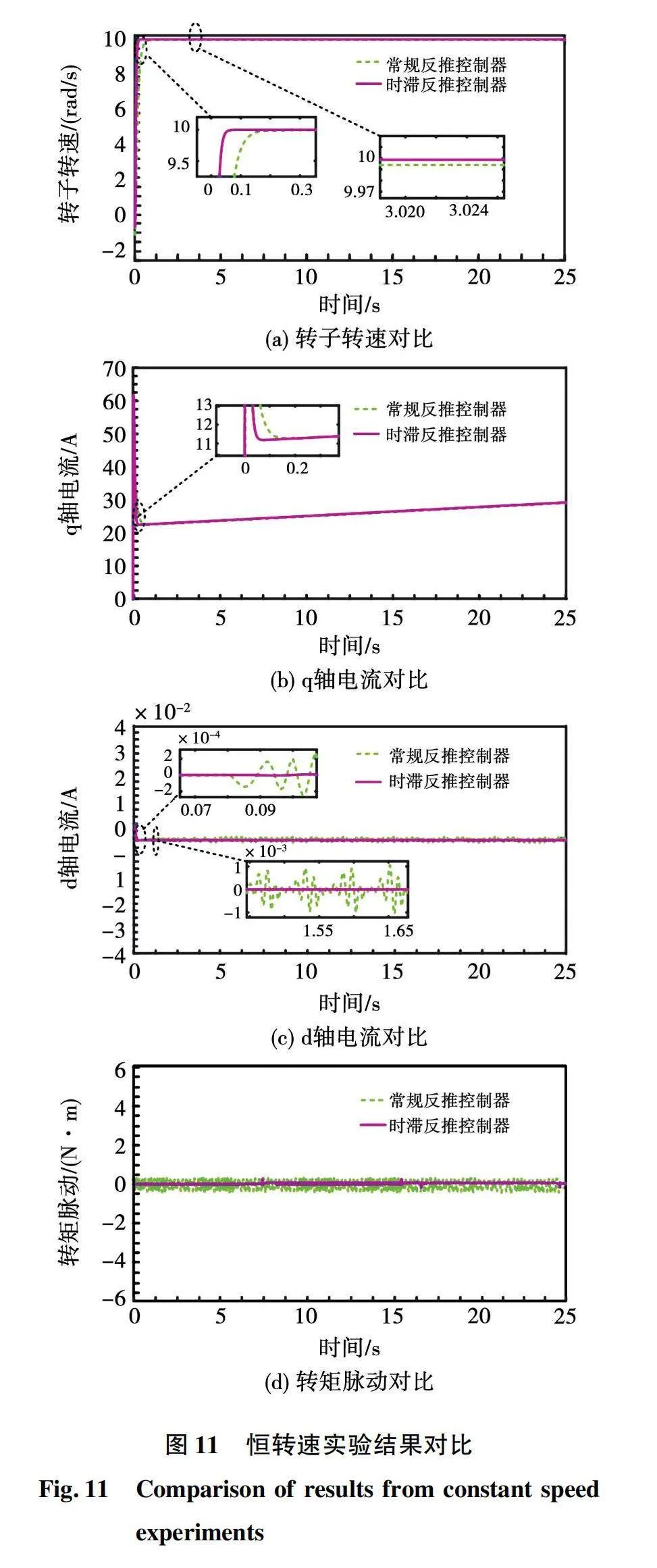
参考转速在实验过程中不发生变化,保持为10 rad/s。实验结果如图11所示。
图11(a)表明,与常规反推控制器相比,时滞反推控制器下的转速在电机起动时能更快达到参考转速,有更快的响应速度;当系统稳定运行时,常规反推控制器下的转速也能保持平稳,但存在一个较小的偏差,而时滞反推控制器下的转速则能准确并且平稳地响应参考转速。图11(b)表明,随着负载转矩的增大,2种控制器下的q轴电流随之增大;在电机起动时,时滞反推控制器下的q轴电流恢复至稳定的速度更快。由图11(c)可看到,在系统进入稳态运行时,常规反推控制器下d轴电流在参考值附近波动,而时滞反推控制器下d轴电流则更加稳定,波动明显减少。由图11(d)可知,与常规反推控制器相比,时滞反推控制器下的转矩脉动明显减少。
2)第2组:变转速实验。
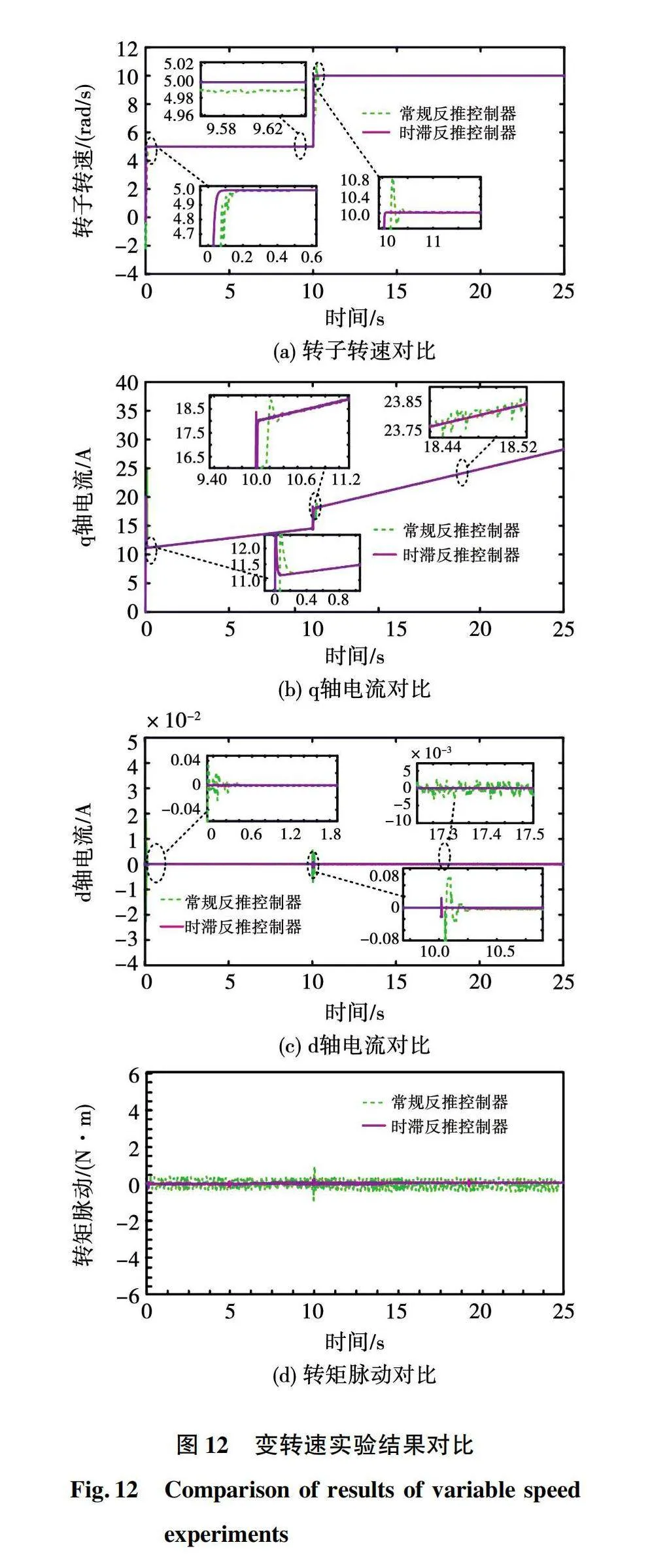
参考转速在第10 s时由5 rad/s变为10 rad/s。实验结果如图12所示。
图12(a)表明,与常规反推控制器相比,时滞反推控制器下转速能更快达到参考转速,且当参考转速发生突变时,常规反推控制器下转速会产生更大突变及波动;当系统稳定运行时,常规反推控制器下转速有小波动且存在控制偏差,而时滞反推控制器下转速则能准确并且平稳地跟踪参考转速。图12(b)表明,在参考转速变化时,2种控制方法下q轴电流均会发生突变,而且常规反推控制器下q轴电流突变更大、波动更明显;还可以看到,q轴电流与负载转矩成比例变化,且当参考转速由5 rad/s变为10 rad/s时,q轴电流斜率变大,其变化速率与转子转速也表现出类似的正比变化关系;在电机起动和参考转速变化时,时滞反推控制器下q轴电流恢复至稳定的速度更快。由图12(c)可知,当参考转速发生变化时,2种控制方法下d轴电流均会产生突变,但时滞反推控制器下的突变更小;在系统稳态运行时,时滞反推控制器下d轴电流更加稳定。由图12(d)可看到,与常规反推控制器相比,在系统运行状态发生变化和稳态运行下时滞反推控制器下转矩脉动均明显减少。
6 结 论
为减小时滞对于SSES系统性能的影响,考虑PMSM电流时滞,本文提出了考虑时滞的SSES用PMSM反推控制方法,通过研究得到以下结论:
1)时滞会对PMSM控制性能产生不利影响,时滞越大,控制性能越弱,甚至会出现控制偏差。
2) 与常规反推控制相比,在本文提出的时滞反推控制器下,PMSM转速和电流在常时滞和变时滞环境下均具有更快的响应速度,并且波动更小,控制效果更优。
3)本文控制方法提升了SSES系统的响应速度,减小了控制偏差,并且抑制了转矩脉动。
参 考 文 献:
[1] 程静, 苏乐, 岳雷. 新能源接入电力系统的宽频振荡风险识别与抑制[J]. 太阳能学报,2023,44(11):565.
CHENG Jing, SU Le, YUE Lei. Power system broadband oscillation risk identify cation and suppression for new energy access acta[J]. Acta Energiae Solaris Sinica, 2023, 44(11): 565.
[2] 张志宇, 庄飞虎, 白海滨, 等. 储能技术在大规模新能源并网中的应用[J].电子技术,2023,52(8):286.
ZHANG Zhiyu, ZHUANG Feihu, BAI Haibin, et al. Application of energy storage technology in large scale new energy grid connection[J]. Electronic Technology, 2023, 52(8): 286.
[3] 余洋, 田夏, 从乐瑶, 等. 基于反推控制和模态估计的永磁同步电机驱动柔性涡簧储能控制方法[J].电工技术学报, 2019, 34(24): 5084.
YU Yang, TIAN Xia, CONG Leyao, et al. Energy storage control method of flexible spiral springs driven by permanent magnet synchronous motor based on backstepping control and modal estimation[J]. Transactions of China Electrotechnical Society, 2019, 34(24): 5084.
[4] 郑晓明, 米增强, 余洋, 等. 机械弹性储能箱结构及并网控制策略优化[J]. 电工技术学报, 2019, 34(22): 4708.
ZHENG Xiaoming, MI Zengqiang, YU Yang, et al. Optimization of energy storage box mechanical structure and grid-connected generation control strategy for mechanical elastic energy storage[J]. Transactions of China Electrotechnical Society, 2019, 34(22): 4708.
[5] 张林闯, 孙永辉, 王建喜, 等. 计及随机传感器时滞的不确定半Markov跳变系统鲁棒滑模控制[J].控制理论与应用, 2023, 40(7): 1172.
ZHANG Linchuang, SUN Yonghui, WANG Jianxi, et al. Robust sliding mode control for uncertain semi-Markov jump systems with random sensor time delay[J]. Control Theory amp; Applications, 2023, 40(7): 1172.
[6] 肖伸平, 张天, 唐军, 等. 基于PI控制的时滞电力系统稳定性分析[J]. 电网技术, 2020, 44(10): 3949.
XIAO Shenping, ZHANG Tian, TANG Jun, et al. Stability analysis for power systems with time-delay based on PI control[J]. Power System Technology, 2020, 44(10): 3949.
[7] SUN F, LIAO X, KURTHS J. Mean-square consensus for heterogeneous multi-agent systems with probabilistic time delay[J]. Information Sciences, 2021, 543: 112.
[8] 崔庆雪, 李霞林, 葛磊蛟, 等. 计及时滞的含风电配电网节点电压安全分析[J].电工技术学报, 2023, 38(5): 1299.
CUI Qingxue, LI Xialin, GE Leijiao, et al. Analysis on node voltage security of distribution network with wind power considering time delay[J]. Transactions of China Electrotechnical Society, 2023, 38(5): 1299.
[9] GU K, CHEN J, KHARITONOV V L. Stability of time-delay systems[M]. Edwardsville:Southern Illinois University at Edwardsville, Springer Science amp; Business Media, 2003.
[10] 陈华, 王梦琪, 陈云. 时滞的非完整动力学系统滑模抗干扰跟踪控制[J].控制理论与应用, 2023, 40(7): 1181.
CHEN Hua, WANG Mengqi, CHEN Yun. Sliding mode anti-interference tracking control for nonholonomic dynamical systems with time delay[J]. Control Theory amp; Applications, 2023, 40(7): 1181.
[11] RICHARD J P. Time-delay systems: an overview of some recent advances and open problems[J]. Automatica, 2003, 39(10): 1667.
[12] NATORI K, OHNISHI K. An approach to design of feedback systems with time delay[C]//31st Annual Conference of IEEE Industrial Electronics Society,December 1,2005,Raleigh,USA. 2005: 6.
[13] SANZ R, GARCA P, ALBERTOS P. A generalized Smith predictor for unstable time-delay SISO systems[J]. ISA Transactions, 2018, 72: 197.
[14] 郭建锋, 钱伟, 王楠, 等. 基于新积分不等式的时滞负荷频率控制系统稳定性分析[J]. 电工技术学报, 2023, 38(15): 4147.
GUO Jianfeng, QIAN Wei, WANG Nan, et al. New integral inequality approach on stability criteria for delayed load frequency control systems[J]. Transactions of China Electrotechnical Society, 2023, 38(15): 4147.
[15] 孙欣, 李俊欣. 具有分布时滞的非线性广义系统一致渐近稳定性准则[J]. 沈阳师范大学学报(自然科学版), 2023, 41(1): 36.
SUN Xin, LI Junxin. Uniformly asymptotic stability criterion for a class of nonlinear descriptor systems with distributed delay[J]. Journal of Shenyang Normal University(Natural Science Edition), 2023, 41(1): 36.
[16] 沈力. 参数扰动时滞电力系统稳定性分析与控制[D].武汉:湖南工业大学,2020.
[17] 汪石川, 祝小元, 李豆豆, 等. 非理想网络环境下永磁同步电机转速鲁棒控制[J]. 排灌机械工程学报, 2020, 38(4): 421.
WANG Shichuan, ZHU Xiaoyuan, LI Doudou, et al. Speed robust control of permanent magnet synchronous motor in non-ideal network environment[J]. Journal of Drainage and Irrigation Machinery Engineering, 2020, 38(4): 421.
[18] 贺勤. 永磁同步电机转速估计与自耦PI电流环控制研究[D].长沙:长沙理工大学,2020.
[19] LUO S, WANG J, SHI Z, et al. Output feedback adaptive dynamic surface control of permanent magnet synchronous motor with uncertain time delays via RBFNN[J]. Discrete Dynamics in Nature and Society, 2014(1):1.
[20] 王宇, 袁家信, 张恒. 基于事件触发机制的自适应神经网络永磁同步电机跟踪控制[J].农业装备与车辆工程,2023,61(8):145.
WANG Yu, YUAN Jiaxin, ZHANG Heng. Adaptive neural network tracking control of permanent magnet synchronous motor based on event trigger mechanism[J]. Agricultural Equipment amp; Vehicle Engineering, 2023,61(8):145.
[21] LU S, WANG X, LI Y. Adaptive neural network control for fractional-order PMSM with time delay based on command filtered backstepping[J]. AIP Advances, 2019, 9(5):055105.
[22] 张云飞, 齐蓉. 永磁同步电机低开关损耗模型预测控制[J].电机与控制学报,2023,27(7):155.
ZHANG Yunfei, QI Rong. Low switching loss drive for PMSM based on model predictive control[J]. Electric Machines and Control, 2023, 27(7): 155.
[23] 赵希梅, 王天鹤. 基于Hermite多项式函数链模糊神经网络的PMLSM分数阶反推控制[J].电机与控制学报,2021,25(9):61.
ZHAO Ximei, WANG Tianhe. Fractional-order backstepping control based on Hermitepolynomial functional link fuzzy neural network for PMLSM[J]. Electric Machines and Control, 2021, 25(9): 61.
[24] 赵希梅, 金洋洋, 王丽梅. PMLSM伺服系统的自适应RBFNN反推控制[J].电机与控制学报, 2020,24(4):149.
ZHAO Ximei, JIN Yangyang, WANG Limei. Adaptive RBFNN backstepping control for PMLSM servo system[J]. Electric Machines and Control, 2020, 24(4):149.
[25] 任勤, 宋林锋. 一类非线性时滞系统通过自适应Backstepping的控制[J].太原理工大学学报, 2006,37(6):721.
REN Qin, SONG Linfeng. Adaptive stabilizability of a class of time-delay nonlinear systems[J]. Journal of Taiyuan University of Technology, 2006, 37(6):721.
[26] HUA C, FENG G, GUAN X. Robust controller design of a class of nonlinear time delay systems via backstepping method[J]. Automatica, 2008, 44(2): 567.
[27] 王刻奇, 杨智, 杨德根. 一类非线性时滞系统的Backstepping控制[J]. 控制工程, 2017, 24(11): 2332.
WANG Keqi, YANG Zhi, YANG Degen. Backstepping control for a class of nonlinear time-delay systems[J]. Control Engineering of China, 2017, 24(11): 2332.
[28] 余洋, 冯路婧, 米增强, 等. 基于增量反推控制的机械弹性储能用永磁同步电机控制方法[J].电机与控制学报, 2021, 25(12): 1.
YU Yang, FENG Lujing, MI Zengqiang, et al. Control method of permanent magnet synchronous motors for mechanical elastic energy storage based on incremental backstepping control[J]. Electric Machines and Control, 2021,25(12): 1.
[29] REN N, FAN L, ZHANG Z. Sensorless PMSM control with sliding mode observer based on sigmoid function[J]. Journal of Electrical Engineering amp; Technology, 2021, 16(2): 933.
[30] 张蕊, 孙丽颖, 张波琦. SVC时滞系统的backstepping控制[J].辽宁工业大学学报(自然科学版), 2012,32(1): 17.
ZHANG Rui, SUN Liying, ZHANG Boqi. Backstepping control for time-delay system of SVC[J]. Journal of Liaoning University of Technology (Natural Science Edition), 2012,32(1): 17.
(编辑:刘琳琳)
