核心任务+五步法：中高年级“画数学”教学的实施路径

［摘 要］“画数学”是一种促进学生深度学习、提升学生数学核心素养的教学手段。文章在分析中高年级“画数学”教学手段时，经历三个研究阶段，提出“核心任务+五步法”的“画数学”教学实施路径，并以“买文具”（简单的一位小数乘整数）为例，介绍具体的实践过程。

［关键词］画数学；小数乘整数；核心素养

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2024）32-0078-03

当前，“画数学”作为一种直观且有效的教学手段，受到教育工作者的关注。那么，中高年级“画数学”有哪些重要价值？有哪些实施路径？笔者与课题组成员对这些问题进行了探究。

一、中高年级“画数学”的价值

“画数学”是指将抽象、复杂的数学概念、数学规律、数量关系和知识结构等，通过直观形象的图示、表格等表示出来，在自主探索和合作交流中，直观地理解抽象的数学知识和原理，有效开展数学探究和数学建构，促进学生深度学习，提升学生的数学能力和数学素养。

“画数学”是中高年级学生理解数学知识和解决数学问题的基础。对人教版教材、北师大版教材和苏教版教材进行深入研究后，笔者发现这三个版本的教材均强调画图的重要性。在第一学段，教材强调通过画图策略帮助学生理解知识、内化知识、寻求最佳的解题策略。从第二学段起，教材注重利用“图”帮助学生分析抽象、复杂的数学问题。随着数学知识的增加和抽象程度的加深，中高年级学生在深入理解数学知识、开展数学探究和进行数学表达的过程中，更需要借助直观的工具。因此，“画数学”是中高年级学生保持数学学习热情、理解复杂数学知识、解决数学问题的基础，是帮助学生克服数学学习难关、提升学习能力的方式，也是提升教学效果的策略。

二、中高年级“画数学”教学实施路径的构建

（一）厘清中高年级“画数学”教学的基本问题

数学教学在以下方面用到图形：几何教学、数的认识与运算、解决问题。此外，“画图”在复习课和总结课中也特别重要。

课题组教师访谈了60多位中高年级数学教师，发现这些教师在“画图”教学中面临的主要问题包括：提供给学生画图练习的机会少；对学生的画图训练不足；画图策略的应用不够深入；画图教学未进一步推进，只关注在当前课程或单元教学中是否运用画图策略，未能从知识的连续性出发，影响了中高年级学生画图意识的提升。

针对以上问题，课题组分三个阶段开展针对性试教，并对各阶段的试教效果进行评价，从而不断探索中高年级“画数学”教学的实施路径。

第一阶段：（1）激励教师加强画图教学研究，提高教师在课堂上采用画图策略的意识；（2）为学生开设主题课，引导学生运用画图策略探索数学知识；（3）指导学生画单元知识思维导图。这一阶段的“画数学”教学与具体课堂教学的结合不足，教学效果有待提高。

第二阶段：（1）按小学数学知识的四大板块对学生进行画图指导；（2）按画图的类型对学生进行针对性画图训练。这一阶段，教师有了“画数学”的整体规划，也尝试将“画数学”落实到课堂教学中，经过一个学期的实践和研究发现，“画数学”教学仍处于零散状态，缺乏重要的抓手。

第三阶段：课题组重点探索如何在每一节课借助“画数学”促进学生深度学习，发展其数学核心素养。这一阶段，课题组整合了前两个阶段的策略，并将其应用于课堂教学实践，取得了显著的教学效果。

（二）中高年级“画数学”教学路径的构建

在三个阶段的探索中，课题组逐步构建了小学中高年级“画数学”教学实施路径，即“核心任务+五步法”，具体流程为画图—说图—理图—用图—构图。对于一节课而言，它对应5个步骤。

1.提出核心任务，画图探究

教师根据课程的核心知识，设计一道画图的题目，让学生通过画图独立探究，并在小组中进行交流。这个核心任务应包含本节课的重点。

2.挑选学生作品，分析解读

教师在课堂上展示并解读学生的画图作品，适时呈现学生没有想到的画图作品，让学生解读图的含义。同时，引导学生对图示进行优化，并请学生说说“喜欢哪一种画图方法，今后遇到这样的问题应该画怎样的图”等。

3.借图揭示规律，明晰原理

画图分析，提炼核心知识点，并对知识点进行解释和辨析。明确画图的目的是探索和理解数学知识、原理，加强学生借助画图解决问题的意识。

4.通过变式练习，拓展应用

根据一节课的核心知识，精心设计与例题相关的基础题、提升题和拓展题，让不同水平的学生在课内和课外选择对应的练习完成，促使学生“学一题，通一类”，发展模型意识和应用意识。

5.构建知识体系，强化关联

小结时，教师让学生画一幅图表示本节课的新知识与旧知识的联系，归纳同类知识的方法，形成集知识结构、数学思想方法和学习感悟于一体的思维导图。

三、中高年级“画数学”教学的实施路径

以北师大版教材四年级下册第三单元“小数乘法”第一课时“买文具”（简单的一位小数乘整数）为例，谈谈应用“画数学”教学的具体做法。

师（出示图1）：买4块橡皮需要多少元？先画图，再列式计算。

（学生独立解题，教师巡视，同时收集学生的画图作品，以便在交流环节中展示）

师（展示学生的画图作品，如图2所示）：请对这些作品进行解读。

生1：每块橡皮0.2元，0.2元=2角，摆2张1角。买4块橡皮，需要4个0.2元，即4个2角，得8个1角，等于0.8元。

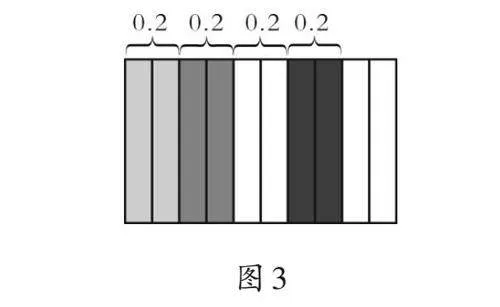
生2（出示图3）：我用涂色表示“0.2×4=0.8”。

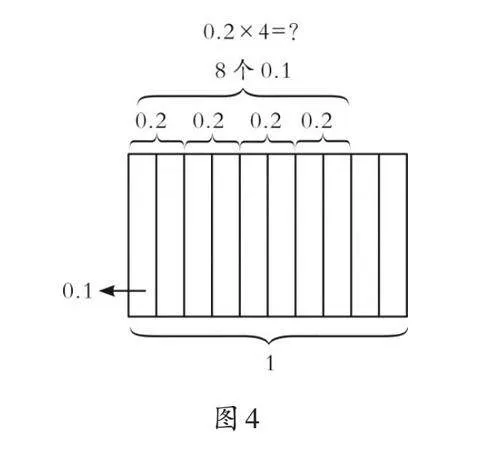
师：请结合你的作品对图4进行分析。

生2：整个图表示“1”，被平均分成10份，每份表示0.1，0.2是2个0.1；0.2×4表示有4个0.2，4个0.2是2×4个0.1，即8个0.1，等于0.8。

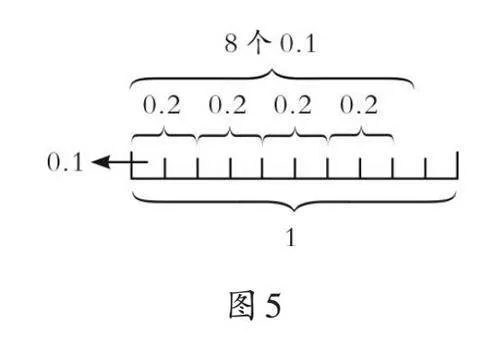
生3（出示图5）：还有不同的表示方法。一条线段表示“1”，被平均分成10份，每份表示0.1，0.2是2个0.1；0.2×4表示有4个0.2，4个0.2是2×4个0.1，即8个0.1，等于0.8。

师：简单的一位小数乘整数就是求有多少个0.1。如果简单的一位小数乘整数中，这个一位小数是[a]个0.1，这个整数是[b]，那么计算结果就是[a×b]个0.1。

师：根据图1，你还能提出哪些数学问题？请解决。

生4：买3支铅笔需要多少元？可列式0.3×3=0.9（元）。

生5：买4个卷笔刀需要多少元？可列式0.7×4=2.8（元）。

师：课后，借助画图，自主计算0.02×4，0.03×7。

师：本节课你有什么收获？

生6：通过画图得到小数乘整数的意义。

生7：小数乘整数的意义是求几个相同加数之和的简便运算，运用小数乘整数的意义可以解决小数乘整数的运算问题和实际问题。

生8：整数的计数单位是1，小数的计数单位是0.1、0.01、0.001……计算整数乘整数，其实是计算一共有多少个1；计算小数乘整数，其实是计算一共有多少个0.1或多少个0.01……因此，小数乘整数与整数乘整数的算理是一致的，都是计算一共有多少个计数单位。

在“买文具”这一课中，教师先提出了一个核心任务“计算0.2×4”，再引导学生通过“画图—说图—理图—用图—构图”五个步骤，探索和理解一位小数乘整数的算理和算法，体会小数乘法与整数乘法的一致性，从而提升学生的运算能力、几何直观、推理意识等核心素养。

［ 参 考 文 献 ］

［1］ 中华人民共和国教育部.义务教育数学课程标准（2022年版）［S］.北京：北京师范大学出版社，2022.

[2] 郑毓信.从“让学生画数学”谈起：“小学数学教学的新热点与关键”系列之一[J].小学教学（数学版），2020（11）：4-8.

【本文系广东省清远市第二十三批（2022年）教育科研立项课题“核心素养导向下小学中高年级‘画数学’教学的实践研究”（23-22）研究的阶段性成果。】

（责编 黄 露）