以谐波为导向的轮辐式磁场调制永磁轮毂电机转速波动抑制研究

摘 要：

结合车辆轮毂直驱应用场合需求，以“低速大转矩”能力出色的轮辐式磁场调制永磁轮毂电机为研究对象，系统性开展以谐波为导向的电机转速波动抑制研究。分析齿槽转矩这一引起电机转矩波动的重要因素，确定与之相关联的主导谐波阶次。并且，将关联谐波作为优化设计目标，有效削弱齿槽转矩，从而有助于在电机设计层面实现电机转速波动的抑制。此外，面临轮毂直驱场合复杂工况及恶劣路况的驱动需求，在电机控制层引入“扰动抑制能力出色”的自抗扰控制技术，在自抗扰控制器误差反馈控制律中针对性引入电机齿槽转矩主导谐波的抑制环节，提出谐波导向型线性状态误差反馈控制律，进一步抑制了电机的转速波动。理论分析与实验结果验证了研究的合理性。

关键词：轮毂电机；磁场调制；低速大转矩；齿槽转矩；速度波动抑制；自抗扰控制

DOI：10.15938/j.emc.2024.09.011

中图分类号：TM351

文献标志码：A

文章编号：1007-449X（2024）09-0125-14

收稿日期： 2023-10-15

基金项目：国家自然科学基金重大项目（51991385）；江苏现代农业重大核心技术创新项目（CX221005）;国家自然科学基金面上项目（52177046）

作者简介：项子旋（1987—），男，博士，副教授，博士生导师，研究方向为高效能永磁电机系统设计与驱动运行研究；

鞠 昊（1998—），男，硕士，研究方向为永磁同步电机系统优化设计及驱动运行研究；

朱孝勇（1975—），男，博士，教授，博士生导师，研究方向为永磁电机设计、分析与驱动控制研究；

周雨婷（1999—），女，博士研究生，研究方向为永磁同步电机设计及优化研究；

樊德阳（1992—），男，博士，讲师，研究方向为高效能永磁电机系统设计与驱动运行研究；

全 力（1963—），男，博士，教授，博士生导师，研究方向为永磁电机设计、分析与驱动控制研究。

通信作者：朱孝勇

Research on speed fluctuation suppression of harmonic-oriented spoke-type flux-modulated permanent magnet in-wheel motor

XIANG Zixuan， JU Hao， ZHU Xiaoyong， ZHOU Yuting， FAN Deyang， QUAN Li

（School of Electrical and Information Engineering， Jiangsu University， Zhenjiang 212013， China）

Abstract：

Based on the requirements of vehicle hub direct drive applications， the spoke type permanent magnet hub motor with excellent “low speed and high torque” was taken as the research object， and systematically the research of harmonic oriented motor speed fluctuation suppression was carried out. By analyzing the cogging torque， which is an important factor causing the motor torque fluctuation， the dominant harmonic order associated with it was determined. Moreover， taking related harmonics as the optimal design goal can effectively weaken the cogging torque， which is helpful to realize the suppression of motor speed fluctuation at the motor design level. In addition， in the face of the drive demand of complex working conditions and bad road conditions in wheel hub direct drive， the active disturbance rejection control technology with “excellent disturbance suppression ability” was introduced into the motor control layer. The harmonic oriented linear state error feedback control law was proposed by introducing the harmonic-dominated harmonic suppression of motor cogging torque into the error feedback control law of the active disturbance rejection controller. The motor speed fluctuation was further inhibited. Theoretical analysis and experimental results verify the rationality of the study.

Keywords：permanent magnet in-wheel motor; flux modulation; low speed and high torque; cogging torque; speed fluctuation suppression; active disturbance rejection control

0 引 言

分布式电动汽车具有系统操控灵活、动力传动形式多样、整车传动效率高等优点，是新能源电动汽车的未来发展方向之一［1］。其中，轮毂电机作为分布式驱动电动汽车的核心运动部件，直接决定着车辆运行的动力性能［2］。磁场调制类电机“低速大转矩”能力出色，在分布式电动汽车轮毂直驱应用场合中拥有着潜在的应用前景［3-5］。然而，“磁场调制效应”的引入可以有效地提升永磁轮毂电机的转矩密度，但与此同时，这也给电机气隙磁场带来了丰富的谐波元素，进而对电机的转矩脉动性能产生负面影响。需要明晰的是，较大的电机转矩脉动会引起较为明显的速度波动问题，这在很大程度上恶化了整个轮毂电机系统的驱动性能［6］。因此，面对磁场调制类电机固有气隙谐波带来的转矩脉动偏大的现象，如何解决由此引起的电机转速波动问题，是将磁场调制技术有效应用于永磁轮毂电机之中需要面临的挑战。

从电机设计层面出发，大多研究工作集中在电机转矩脉动的削弱设计方面，而对于磁场调制类电机而言，齿槽转矩是引起电机转矩脉动的主要因素。一般来讲，定子斜槽与转子斜极是降低电机齿槽转矩最为常见的方法，其抑制效果主要取决于电机的斜槽系数或斜极系数，这将会对电机输出转矩产生一定程度的负面影响，同时还会增加电机的轴长设计要求及加工工艺的复杂度［7-8］。文献［9］针对永磁游标电机，采用一种Halbach永磁转子，改善了气隙磁场，获得了电机齿槽转矩的削弱与转矩脉动的抑制。文献［10］则从磁场调制电机转矩产生机理的角度出发，通过磁导设计针对性抑制非有效工作谐波，最终实现了轮毂电机转矩脉动的降低。在此基础之上，文献［11］尝试从永磁转矩分量与齿槽转矩分量出发，确定及抑制了气隙磁场中与齿槽转矩相关联的谐波阶次，改善了轮毂电机转矩脉动的抑制效果。可见，通过轮毂电机拓扑结构的合理设计，电机的转矩脉动可以获得一定程度上的有效抑制，这将有助于改善轮毂电机的转速波动问题。

此外，相关研究企图通过控制的手段来降低电机的转矩脉动，从而达到抑制电机速度波动的主要目的。比较常见的方法是转矩补偿控制方法，具体通过比例积分（proportional integral，PI）控制器来在线产生额外的电磁转矩，以抵消电机由齿槽转矩引起的脉动转矩，从而抑制电机转速波动［12］。然而，该方法的有效性往往依赖于电机脉动转矩波形的实时获取精度。引入观测器是提升脉动转矩波形获取精度的有效手段之一，然而面对高速运行情况，该方法的使用会面临较大的挑战。文献［13］则采用一种模型预测转矩控制方法，在控制过程中实现了对电机齿槽转矩的在线估计，从而获得了电机转矩脉动的补偿，实现了对电机速度波动的有效抑制。值得一提的是，尽管采用转矩补偿控制方法能够有效抑制电机的转速波动，但电机的转速波动除了由电机本体转矩脉动、磁通谐波等内部因素引起之外，还与实际负载转矩等外部扰动因素有关，尤其是在永磁轮毂电机直驱应用场合中，电机与车轮之间的直接相连更加凸显了外部扰动因素对电机速度波动的影响。因此，如何综合考虑轮毂电机系统的内部扰动因素和外部扰动因素，有效抑制电机的转速波动，是将磁场调制技术有效应用于永磁轮毂电机之中的关键难题。

近年来，国内外学者对永磁同步电机速度平滑控制进行了深入研究，文献［14］为解决现有控制算法中快速收敛速度与减少抖振之间的矛盾，提出一种基于复合趋近律（new compound reaching law，NCRL）的自抗扰速度控制器，提升了扰动的观测精度和系统鲁棒性。文献［15］提出一种基于改进的混合粒子群算法，将其运用于速度与位置控制器的参数优化，有效降低了转速纹波。文献［16］针对永磁同步电机低速状态下的齿槽转矩引起的转速波动问题，提出了一种扩展谐波状态观测器，有效抑制了电机运行过程中的周期性扰动。文献［17］提出了一种虚拟齿槽转矩（virtual cogging torque， VCT）的控制方法来减小直驱永磁同步电机伺服系统的速度波动，显著减小了低速时的速度波动。

本文研究一种以谐波为导向的轮辐式磁场调制永磁轮毂电机转速波动抑制的方法。一方面，深入分析及确定引起电机齿槽转矩的关键谐波，通过对谐波进行有效抑制，降低电机的转矩脉动，从而在电机本体这一内部扰动因素上尽可能降低电机的转速波动。另一方面，通过将具有“扰动抑制能力出色”特点的自抗扰控制（active disturbance rejection control，ADRC）技术引入至轮毂电机的驱动控制运行，针对性将关键谐波作为控制系统的前馈补偿，旨在进一步从内部扰动因素的角度出发，实施电机的转速波动抑制。与此同时，通过自抗扰控制器对外部扰动的估计，使得该研究方法在轮毂电机外部扰动因素层面也能实现对转速波动的抑制。理论分析与实验测试验证研究方法的有效性。

1 轮辐式磁场调制永磁轮毂电机拓扑结构与齿槽转矩关联谐波分析

1.1 轮辐式磁场调制永磁轮毂电机的拓扑结构

12槽14极轮辐式磁场调制永磁轮毂（spoke-type flux-modulated permanent magnet in-wheel，SFM-PMIW）电机的拓扑结构如图1所示。由于在SFM-PMIW电机的定转子两侧同时引入具有调制行为的凸极磁导设计，电机的气隙磁场中形成了丰富的谐波含量。通过合理的设计定子开槽宽度与转子凸极尺寸，增强电机的磁导调制效应，有助于实现气隙磁场谐波特性的改善，从而达到削弱电机齿槽转矩的主要目的。此外，SFM-PMIW电机的主要设计参数如表1所示。

1.2 气隙谐波与电机转矩的理论关系分析

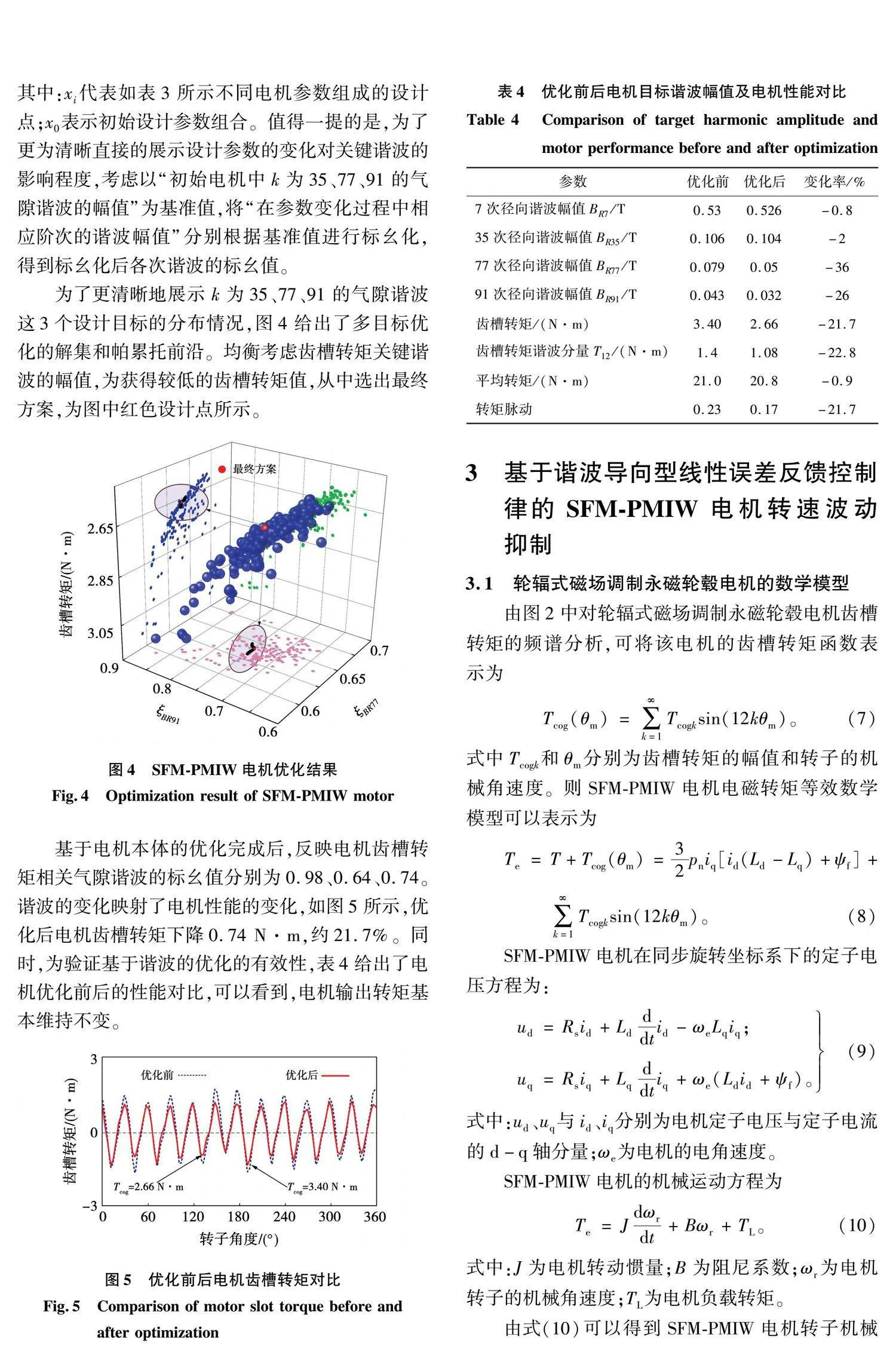
由于轮辐式磁场调制永磁轮毂电机交直轴电感差异很小，因而该电机的齿槽转矩是引起电机转矩脉动的主要因素，图2为SFM-PMIW电机齿槽转矩的波形及谐波频谱分析。如图所示，12次谐波为电机齿槽转矩的主导谐波。为了分析转矩与气隙谐波的关联关系，针对性采用时间阶次n和空间阶次k来分析气隙磁通密度。

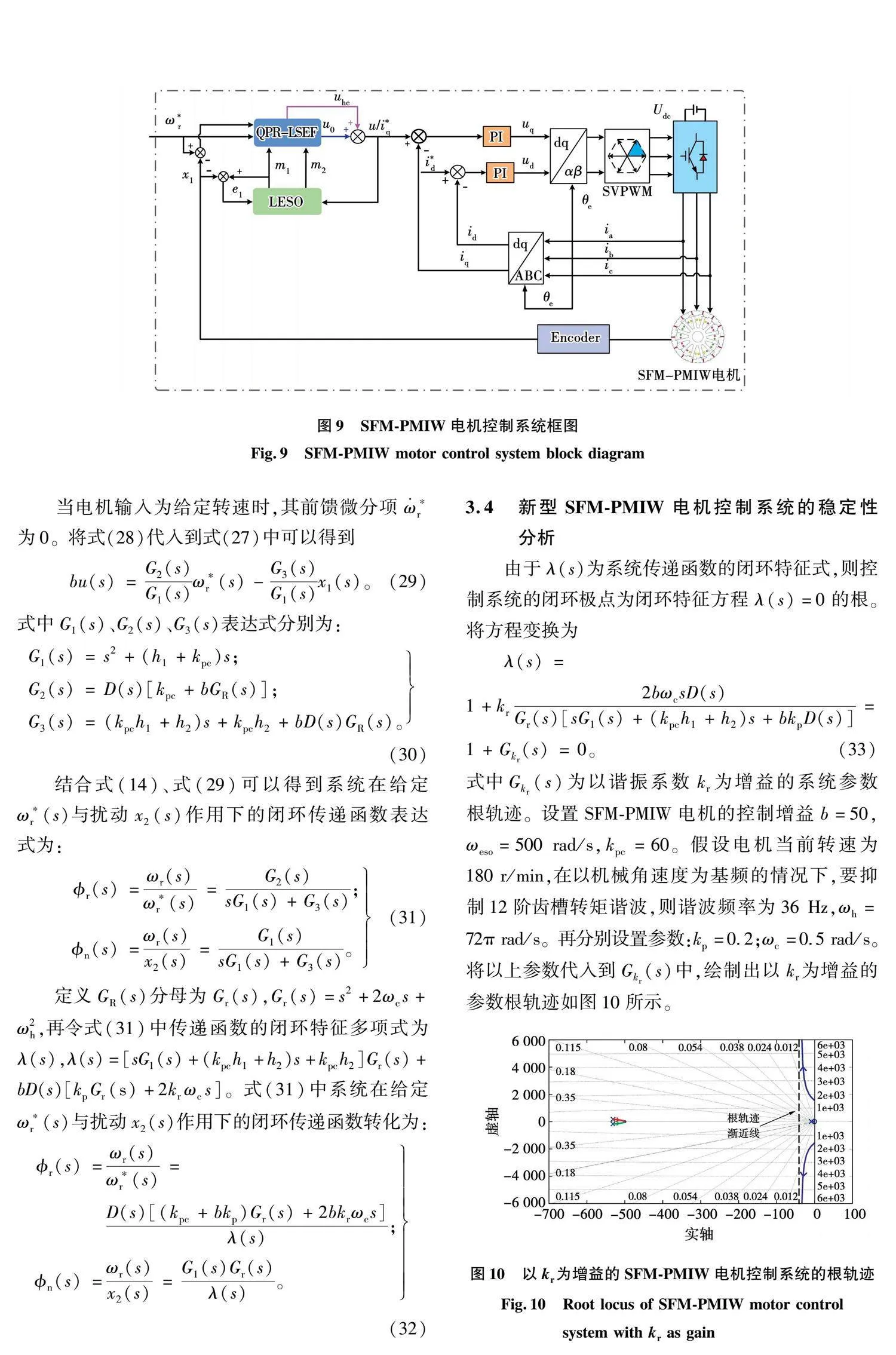
3.4 新型SFM-PMIW电机控制系统的稳定性分析

由于λ（s）为系统传递函数的闭环特征式，则控制系统的闭环极点为闭环特征方程λ（s）=0的根。将方程变换为

λ（s）=

1+kr2bωcsD（s）Gr（s）［sG1（s）+（kpch1+h2）s+bkpD（s）］=1+Gkr（s）=0。（33）

式中Gkr（s）为以谐振系数kr为增益的系统参数根轨迹。设置SFM-PMIW电机的控制增益b=50，ωeso=500 rad/s，kpc=60。假设电机当前转速为180 r/min，在以机械角速度为基频的情况下，要抑制12阶齿槽转矩谐波，则谐波频率为36 Hz，ωh=72π rad/s。再分别设置参数：kp=0.2；ωc=0.5 rad/s。将以上参数代入到Gkr（s）中，绘制出以kr为增益的参数根轨迹如图10所示。

由图10可以看出，以kr为增益的参数根轨迹均位于虚轴左侧，即系统始终能保持稳定。

参照式（33）的变换方法， 再将闭环特征方程λ（s）=0变换为

λ（s）=1+bD（s）［kpGr（s）+2krωcs］Gr（s）［sG1（s）+（kpch1+h2）s+kpch2］=1+Gb（s）=0。（34）

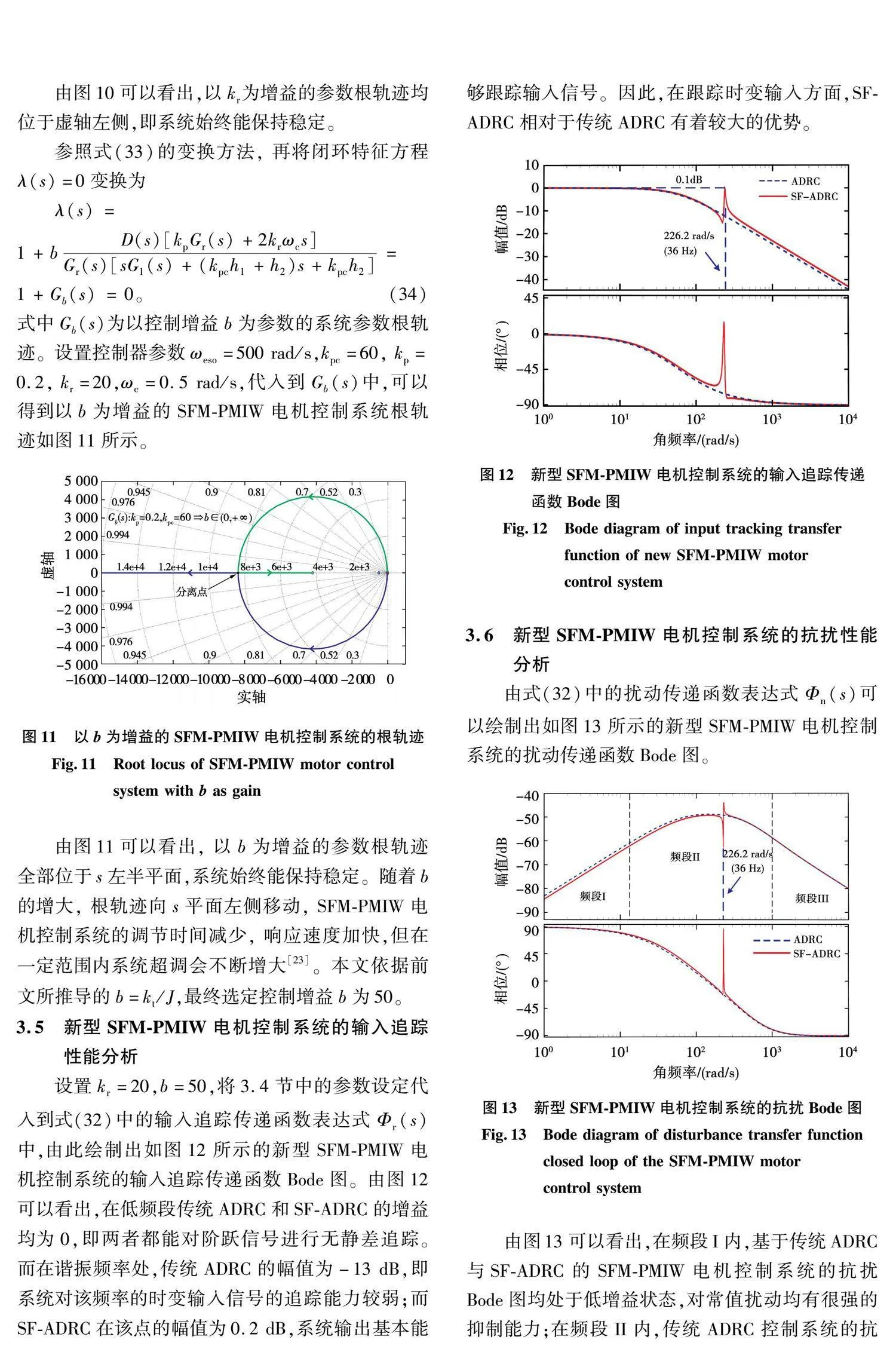
式中Gb（s）为以控制增益b为参数的系统参数根轨迹。设置控制器参数ωeso=500 rad/s，kpc=60， kp=0.2， kr=20，ωc=0.5 rad/s，代入到Gb（s）中，可以得到以b为增益的SFM-PMIW电机控制系统根轨迹如图11所示。

由图11可以看出， 以b为增益的参数根轨迹全部位于s左半平面，系统始终能保持稳定。随着b的增大， 根轨迹向s平面左侧移动， SFM-PMIW电机控制系统的调节时间减少， 响应速度加快，但在一定范围内系统超调会不断增大［23］。本文依据前文所推导的b=kt/J，最终选定控制增益b为50。

3.5 新型SFM-PMIW电机控制系统的输入追踪性能分析

设置kr=20，b=50，将3.4节中的参数设定代入到式（32）中的输入追踪传递函数表达式Φr（s）中，由此绘制出如图12所示的新型SFM-PMIW电机控制系统的输入追踪传递函数Bode图。由图12可以看出，在低频段传统ADRC和SF-ADRC的增益均为0，即两者都能对阶跃信号进行无静差追踪。而在谐振频率处，传统ADRC的幅值为-13 dB，即系统对该频率的时变输入信号的追踪能力较弱；而SF-ADRC在该点的幅值为0.2 dB，系统输出基本能够跟踪输入信号。因此，在跟踪时变输入方面，SF-ADRC相对于传统ADRC有着较大的优势。

3.6 新型SFM-PMIW电机控制系统的抗扰性能分析

由式（32）中的扰动传递函数表达式Φn（s）可以绘制出如图13所示的新型SFM-PMIW电机控制系统的扰动传递函数Bode图。

由图13可以看出，在频段I内，基于传统ADRC与SF-ADRC的SFM-PMIW电机控制系统的抗扰Bode图均处于低增益状态，对常值扰动均有很强的抑制能力；在频段II内，传统ADRC控制系统的抗扰Bode图表现出相对的高增益状态，即系统对该频段内谐波的抑制能力较弱；而基于SF-ADRC的电机控制系统的抗扰Bode图在该频段内的谐振频率附近的增益衰减明显；对该频率范围内的谐波信号有着较强的抑制作用，有利于电机转速谐波的抑制；而在频段III内，两者又都表现出低增益，这表明两者均具有抗高频干扰的能力。

综上所述，在抑制时变扰动方面，SF-ADRC相较于传统ADRC有着明显优势，这也为新型自抗扰控制器结构解决SFM-PMIW电机转速波动问题提供了理论依据。

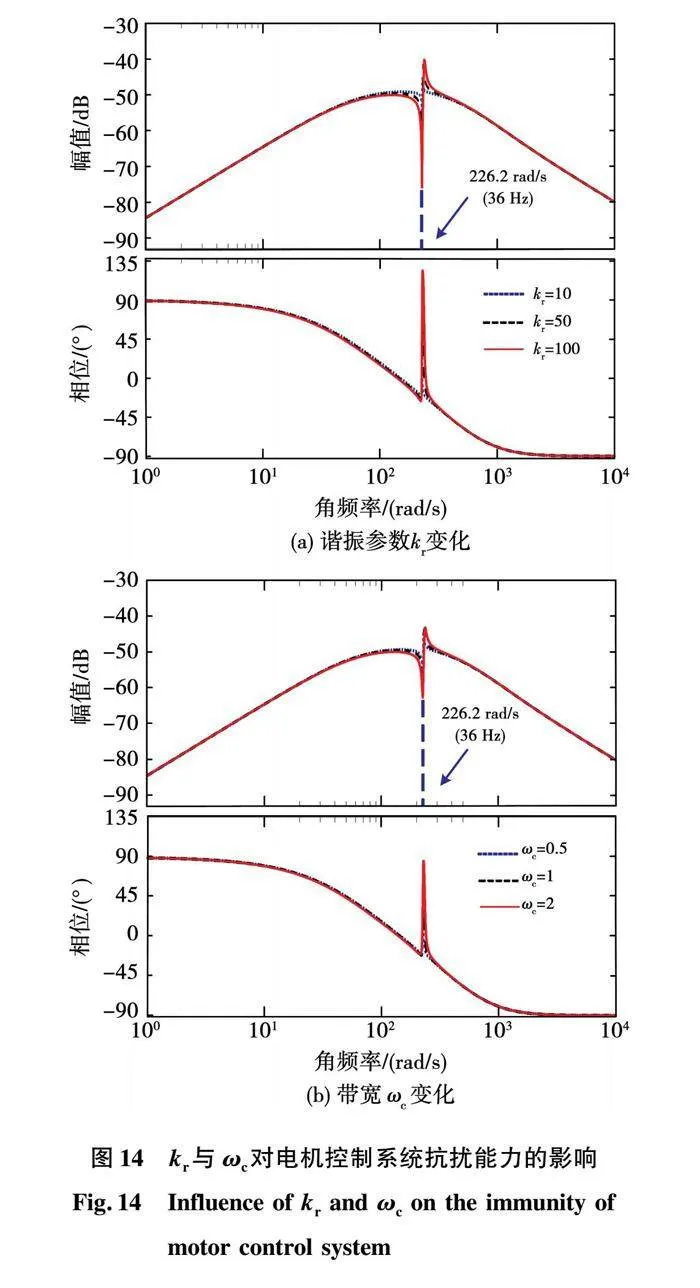
为了减少实验时的参数整定难度，需要对抗扰性能相关的参数进行整定。图14给出了谐振系数kr与带宽ωc变化对基于SF-ADRC的电机控制系统抗扰性能影响的Bode图。

由图14（a）可以看出，增大kr可以增加目标谐波的抑制深度，提升谐波扰动抑制效果，但同时目标谐波频率带右侧的谐波抑制效果会大幅减弱，因此选择kr时要权衡考虑。图14（b）表明增大ωc对目标谐波抑制深度不会造成影响，但谐波抑制的范围得到了拓宽，然而目标谐波频率带右侧的谐波抑制效果也会有一定程度的削弱。需要说明的是，除了理论基础外，参数的选定还要结合仿真与实验效果，本文最终选定kr为20，ωc为0.5 rad/s。

4 仿真分析与实验验证

为了进一步验证所提控制方法的有效性，本节对轮辐式磁场调制永磁轮毂电机控制系统进行了仿真与实验验证，仿真与实验所用的SFM-PMIW电机参数在表1中已经给出。

4.1 仿真分析

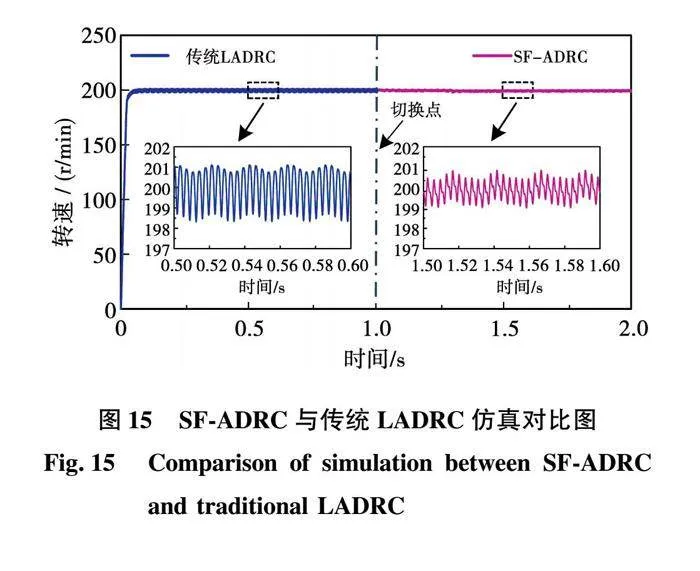
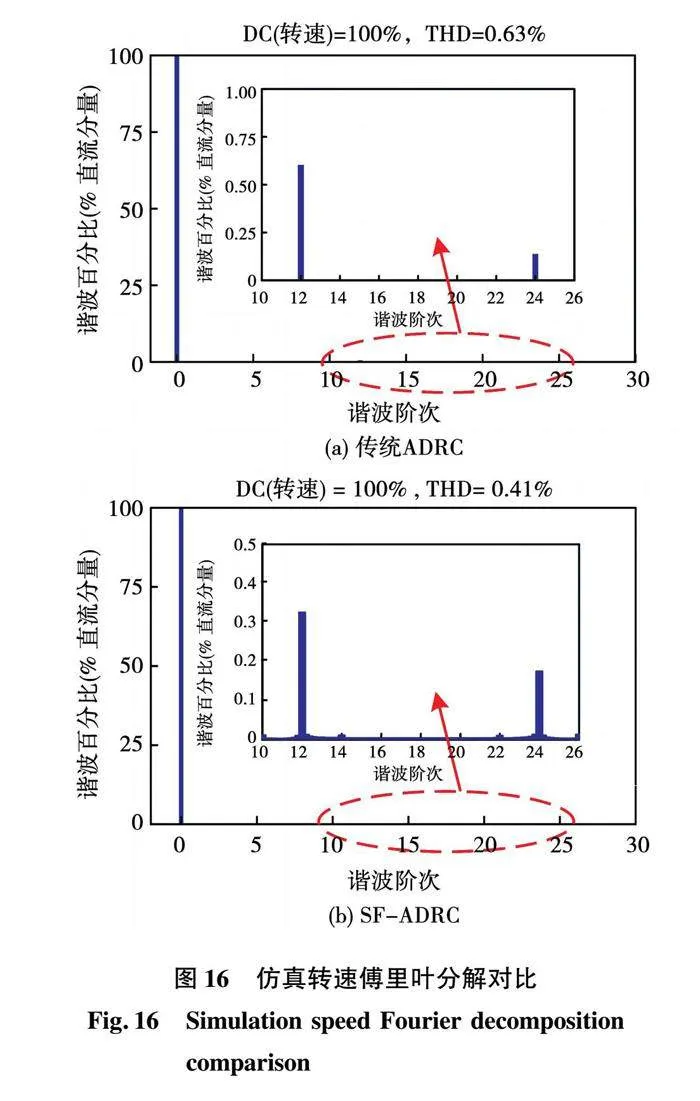
仿真设置母线电压udc=150 V，采用理想的逆变器，采样频率与仿真步长均设置为1e-4 s。SF-ADRC控制器参数设置为：ωeso=500 rad/s；b=50；kpc=60；kp=0.2；ωc=0.5 rad/s；电流环带宽设置为2 000 Hz。给定电机转速为200 r/min，电机初始运行于传统LADRC状态，1 s时切换至SF-ADRC控制算法，仿真波形及其傅里叶分解分别如图15与图16所示。

从图15可以看出，运用传统LADRC控制的SFM-PMIW电机转速波动为2.5 r/min，而采用SF-ADRC算法后，电机转速波动仅为1.6 r/min，转速平滑度提升了36%，这主要是由于引起转速波动的12次谐波获得了有效地抑制。通过对2种控制算法下转速波形进行傅里叶分析，正如所预期，基于SF-ADRC控制的电机转速谐波含量相对于传统ADRC下降了34.9%，进一步反映了所提出算法的有效性，具体如图16所示。

4.2 实验验证

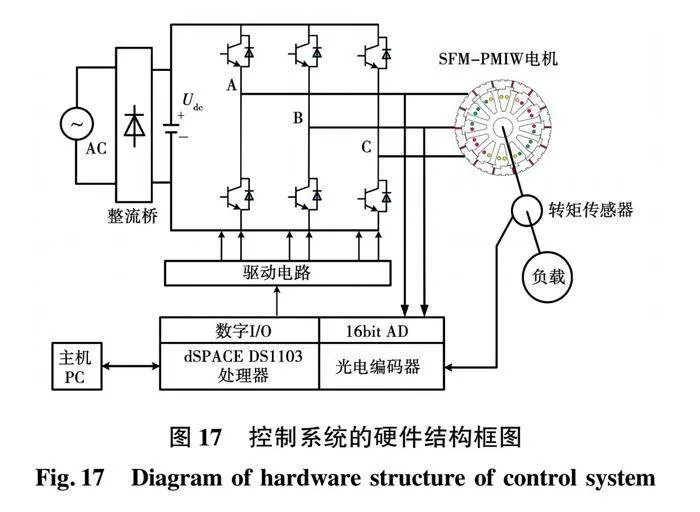
实验采用基于dSPACE-1103的仿真系统，逆变器开关频率与采样频率均为10 kHz。控制参数与仿真保持一致。控制系统的硬件结构框图和实验平台分别如图17和图18所示。

4.2.1 电机基本性能验证

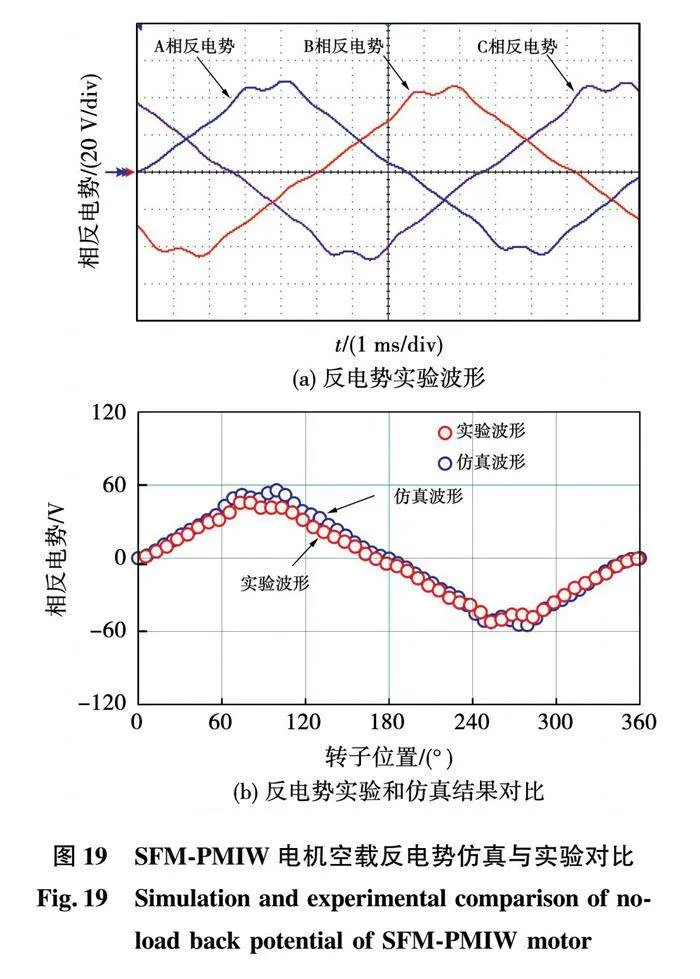
轮辐式磁场调制永磁轮毂电机在600 r/min下的三相空载反电动势波形如图19（a）所示，图19（b）给出了电机三相反电势仿真波形和实验波形的对比，实验表明该电机空载反电势仿真波形与实验结果有较好的吻合度。

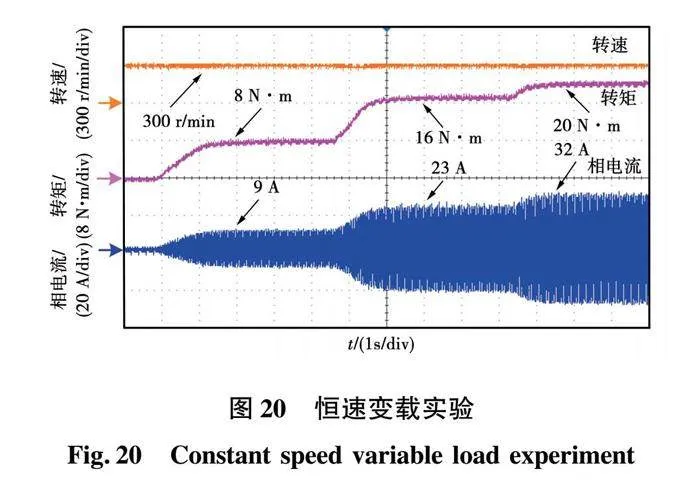
为了进一步评估SFM-PMIW电机的运行特性，对其带载能力进行了测试，如图20所示。实验采用传统自抗扰控制算法，给定转速300 r/min，负载转矩从8 N·m到16 N·m再突变到20 N·m，电机均能够提供可靠稳定的转矩，且稳态转速不受影响，展现了该电机的低速大转矩的优势。可以得出结论，所测试的SFM-PMIW电机在运行过程中可以提供相对稳定的且满足需求的驱动性能。

4.2.2 稳态性能验证

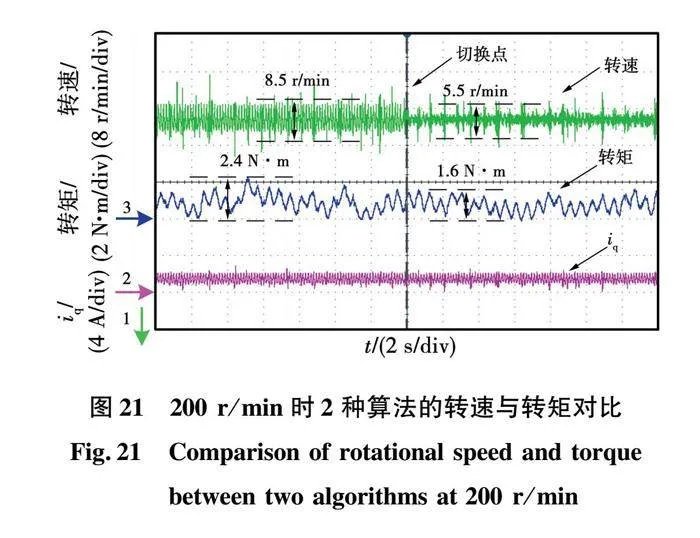
为了验证本文所提的SF-ADRC对电机稳态转速平滑度的提升效果，实验首先让电机运行于传统LADRC， 随后切换至SF-ADRC时，图21给出了SFM-PMIW电机在200 r/min下的转速转矩实验波形。

由图21可以看出，切换至SF-ADRC算法后，电机转矩脉动由2.4 N·m降至1.6 N·m，转矩脉动下降了33.3%，速波动由8.5 r/min将至5.5 r/min，降了35.3%。以上实验结果表明本文所提方法在SFM-PMIW电机速度平滑控制方面具有一定程度的优势。

4.2.3 动态性能验证

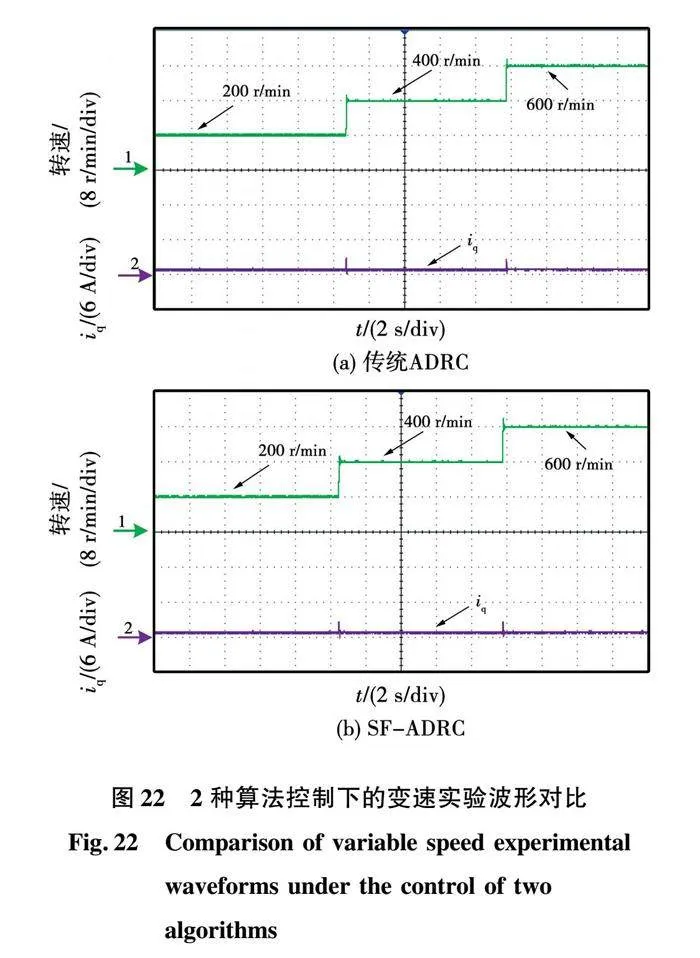
基于轮毂电机复杂的运行工况，在保证稳态转速平滑控制的同时，SF-ADRC的动态性能同样需要评估。为了更全面的验证本文所提方法的实用性，实验对比了基于SF-ADRC与传统ADRC的控制系统的动态响应速度，2种方法的变速实验波形对比如图22所示。由图可以看出，相同的变速工况下，传统ADRC与基于改进SF-ADRC的SFM-PMIW电机控制系统的变速响应时间均低于0.3 s，两者都呈现出较快的动态响应速度。

5 结 论

该文以轮辐式磁场调制永磁轮毂电机为研究对象，系统性开展以谐波为导向的电机转速波动抑制研究，相关研究结论总结如下：

1）深入分析影响电机齿槽转矩的主导气隙谐波，并将其作为优化设计目标，以针对性实施谐波抑制。研究表明经过谐波抑制，电机在维持相对较高输出转矩的情形下获得齿槽转矩及转矩脉动的有效削弱，在电机设计阶段为转速波动抑制提供支撑。

2）充分考虑电机齿槽转矩的主导谐波，建立轮辐式磁场调制永磁轮毂电机的等效数学模型，为后续在电机控制层实施转速波动抑制奠定基础。

3）将电机齿槽转矩主导谐波因素针对性融入自抗扰控制器设计，提出谐波导向型线性状态误差反馈控制律。研究表明，相比传统自抗扰控制算法，所研究的自抗扰控制算法有效抑制了轮毂电机的转速波动，同时还具备了传统自抗扰控制快速响应的优点。

参 考 文 献：

［1］ XIANG Zixuan，LU Zirun，ZHU Xiaoyong，et al. Research on magnetic coupling characteristic of a double rotor flux-switching PM machine from the perspective of air-gap harmonic groups［J］.IEEE Transactions on Industrial Electronics，2022，69（12）：12551.

［2］ 高华敏，张卓然，王晨，等．定子无铁心轴向磁场永磁轮毂电机损耗分析及效率优化［J］．中国电机工程学报，2021，41（6）：2002

GAO Huamin， ZHANG Zhuoran， WANG Chen， et al. Loss analysis and efficiency optimization of ironless stator axial flux permanent magnet in-wheel machine［J］. Proceedings of the CSEE，2021，41（6）：2002.

［3］ CHEN Yiqiang， ZHU Xiaoyong， QUAN Li， et al． A V-shaped PM vernier motor with enhanced flux- modulated effect and low torque ripple［J］． IEEE Transactions on Magnetics， 2018， 54（11）： 8203804．

［4］ XIANG Zixuan， ZHOU Yuting， ZHU Xiaoyong， et al. Research on characteristic airgap harmonics of a double rotor flux-modulated PM motor based on harmonic dimensionality reduction［J］.IEEE Transactions on Transportation Electrification，2024，10（3）：5750.

［5］ LI Xianglin，SHEN Fawen，YU Shiyang，et al．Flux-regulation principle and performance analysis of a novel axial partitioned stator hybrid-excitation flux-switching machine using parallel magnetic circuit［J］．IEEE Transactions on Industrial Electronics，2021，68（8）：6560．

［6］ 戈宝军，姜汉，林鹏，等.并轴式双转子永磁同步电机齿槽转矩分析［J］.电机与控制学报，2023，27（8）：80.

GE Baojun， JIANG Han， LIN Peng， et al．Cogging torque analysis of parallel shaft double rotor permanent magnet synchronous motor［J］. Electric Machines and Control， 2023， 27（8）：80.

［7］ ZHU Xiaofeng，HUA Wei，WU Zhongze，et al. Analytical approach for cogging torque reduction in flux-switching permanent magnet machines based on magnetomotive force-permeance model［J］. IEEE Transactions on Industrial Electronics，2018，65（3）：1965.

［8］ 戈宝军，毛博，林鹏，等.无刷双馈电机转子偏心对气隙磁场的影响［J］. 电工技术学报， 2020， 35（3）： 502.

GE Baojun， MAO Bo， LIN Peng， et al. Effect of rotor eccentricity fault on air gap magnetic field in brushless doubly-fed machine［J］. Transactions of China Electrotechnical Society， 2020， 35（3）： 502.

［9］ 高锋阳，齐晓东. 部分分段Halbach永磁同步电机优化设计［J］.电工技术学报，2021，36（4）：787.

GAO Fengyang， QI Xiaodong. Partial segmented Halbach permanent magnet synchronous motor optimization design［J］. Transactions of China Electrotechnical Society， 2021，36（4）：787.

［10］ FANG Li，LI Dawei，REN Xiang，et al. A novel permanent magnet vernier machine with coding-shaped tooth［J］. IEEE Transactions on Industrial Electronics，2022，69（6）：6058.

［11］ JIANG Min，ZHU Xiaoyong，XIANG Zixuan，et al. Suppression of torque ripple of a flux-switching permanent magnet motor in perspective of flux-modulation principle［J］. IEEE Transactions on Transportation Electrification，2022，8（1）：1116.

［12］ XIA Changliang，JI Bingnan，YAN Yan. Smooth speed control for low-speed high-torque permanent-magnet synchronous motor using proportional-integral-resonant controller［J］. IEEE Transactions on Industrial Electronic，2015，62（4）：2123.

［13］ FEI Qiang，DENG Yongting，LI Hongwen，et al. Speed ripple minimization of permanent magnet synchronous motor based on model predictive and iterative learning controls［J］.IEEE Access，2019，7：31791.

［14］ GUO Xin， HUANG Shoudao， LU Kaiyuan， et al. A fast sliding mode speed controller for PMSM based on new compound reaching law with improved sliding mode observer［J］. IEEE Transactions on Transportation Electrification，2023，9（2）： 2955.

［15］ FANG Shuhua， WANG Yicheng， WANG Wei， et al. Design of permanent magnet synchronous motor servo system based on improved particle swarm optimization［J］. IEEE Transactions on Power Electronics，2022，37（5）： 5833.

［16］ HU Mingjin， HUA Wei， WANG Zuo， et al. Selective periodic disturbance elimination using extended harmonic state observer for smooth speed control in PMSM drives［J］. IEEE Transactions on Power Electronics， 2022，37（11）： 13288.

［17］ DU Feifei. Speed ripple reduction of direct-drive PMSM servo system at low-speed operation using virtual cogging torque control method［J］. IEEE Transactions on Industrial Electronics， 2021，68（1）：160.

［18］ LIU Jinpeng，LI Xianglin，YAN Bo，et al. Electromagnetic performance analysis of a field-modulated permanent magnet motor using improved hybrid subdomain method［J］. IEEE Transactions on Energy Conversion，2023，38（3）：1753.

［19］ ZHU Xiaoyong，JIANG Min，XIANG Zixuan，et al. Design and optimization of a flux-modulated permanent magnet motor based on an airgap-harmonic-orientated design methodology［J］. IEEE Transactions on Industrial Electronics，2020，67（7）：5337.

［20］ XIANG Zixuan，ZHU Xiaoyong，QUAN Li，et al. Multilevel design optimization and operation of a brushless double mechanical port flux-switching permanent-magnet motor［J］. IEEE Transactions on Industrial Electronics，2016，63（10）：6042.

［21］ DU Youwu， CAO Weihua， SHE Jinhua， et al. Analysis and design of active disturbance rejection control with an improved extended state observer for systems with measurement noise［J］. IEEE Transactions on Industrial Electronics，2023，70（1）：855.

［22］ XU Wei， DIAN Renjun， LIU Yi， et al. Robust flux estimation method for linear induction motors based on improved extended state observers［J］. IEEE Transactions on Power Electronics，2019，5（5）：4628.

［23］ 左月飞，李明辉，张捷，等. 控制增益对永磁同步电动机自抗扰控制性能的影响［J］. 电工技术学报，2016，31（3）：58.

ZUO Yuefei， LI Minghui， ZHANG Jie， et al. Influence of control gain on active disturbance rejection controller for PMSM［J］. Transactions of China Electrotechnical Society，2016，31（3）：58.

［24］ ZHOU Zhanqing， XIA Changliang， YAN Yan， et al. Disturbances attenuation of permanent magnet synchronous motor drives using cascaded predictive-integral-resonant controllers［J］. IEEE Transactions on Power Electronics，2018，33（2）： 1514.

［25］ 陈旭，张卓然，于立，等.基于改进型准比例谐振控制的电励磁双凸极电机电流谐波抑制方法［J］.电工技术学报，2023，38（14）：3836.

CHEN Xu， ZHANG Zhuoran， YU Li， et al. Current harmonic suppression method for electromagnetically excited double salient motor based on improved quasi-proportional resonant control［J］. Transactions of China Electrotechnical Society，2023，38（14）：3836.

（编辑：刘琳琳）