兆瓦级高速永磁同步电机偏心状态下电机性能及转子振动特性分析

摘 要：

在电机运行过程中，气隙偏心是一种常见的故障状态，会危害到电机的安全可靠运行，而该问题在大容量高速永磁同步电机中更为严重。因此，本文以一台兆瓦级高速永磁同步电动机为例，研究了气隙偏心对电机电磁性能以及其引发的不平衡磁拉力对转子振动特性的影响。首先，推导了静、动以及混合偏心状态下的不平衡磁拉力表达式。然后，建立了各偏心状态下的电机有限元模型，定量分析了不同偏心程度所引发的不平衡磁拉力变化情况。在此基础上，计算了电机转子系统的动力响应，详细讨论了各种偏心对转子系统轴心轨迹和电磁性能的影响。结果表明，不同偏心状态下不平衡磁拉力存在明显差异，在混合偏心时动偏心会削弱静偏心对转子振动的影响，偏心将增加气隙磁密的偶次谐波且增大转矩脉动。

关键词：高速永磁电机；气隙偏心;不平衡磁拉力；振动特性；电磁性能；轴心轨迹

DOI：10.15938/j.emc.2024.09.008

中图分类号：TM355

文献标志码：A

文章编号：1007-449X（2024）09-0081-14

收稿日期： 2023-08-21

基金项目：国家自然科学基金区域创新发展联合基金重点支持项目（U21A20145）；国家自然科学基金（51977052）；黑龙江省自然科学基金重点项目（ZD2022E006）

作者简介：谢 颖（1974—），女，博士，教授，博士生导师，研究方向为电机内综合物理场计算、新能源汽车用电机设计及多目标优化；

杨艳会（1996—），女，硕士研究生，研究方向为高速永磁同步电机的设计及振动特性分析；

蔡 蔚（1959—），男，博士，教授，博士生导师，研究方向为驱动电机、功率电子控制器及汽车电动化电驱动系统等；

李道璐（1998—），女，博士研究生，研究方向为永磁同步电机设计及振动噪声计算分析；

王泽兵（1999—），男，硕士研究生，研究方向为高速永磁同步电机的设计与优化；

张 燚（1999—），男，硕士研究生，研究方向为磁场调制式复合电机。

通信作者：谢 颖

Analysis of rotor vibration characteristics of megawatt high speed permanent magnet synchronous motor under eccentric state

XIE Ying， YANG Yanhui， CAI Wei， LI Daolu， WANG Zebing， ZHANG Yi

（School of Electrical and Electronic Engineering， Harbin University of Science and Technology， Harbin 150080， China）

Abstract：

During motor operation， air-gap eccentricity is a common fault situation， which will endanger the safe and reliable operation of the motor， and the problem is more serious in the high-power high-speed permanent magnet synchronous motor. Therefore， the effects of air-gap eccentricity on electromagnetic performance of the motor and unbalanced magnetic pull （UMP） due to air-gap eccentricity on vibration characteristics of the rotor were studied. Firstly， the formulas of unbalanced magnetic tension in static， dynamic and mixed eccentricity were deduced. Then the finite element model of the motor under each eccentricity situation were established， and the variations of the UMP caused by different eccentricities were quantitatively analyzed. On this basis， the dynamic response of the motor rotor system was calculated， and the influence of various eccentricities on the axis locus of the rotor system and electromagnetic performance of the motor were discussed in detail. The results show that there are obvious differences in UMP under different eccentricity situations. Dynamic eccentricity will reduce the influence of static eccentricity on rotor vibration during mixed eccentricity. Eccentricity will increase even harmonics of air-gap flux density and torque ripple.

Keywords：high speed permanent magnet motor; air-gap eccentricity; unbalanced magnetic pull; vibration characteristic; electromagnetic performance

0 引 言

永磁同步电机具有功率密度大，响应速度快和效率高等显著优点［1］，在诸多领域得到了广泛的应用。但是由于电机制造和安装误差、轴承磨损等因素的影响，电机定转子间可能会发生偏心，使得气隙磁场发生畸变产生不平衡磁拉力［2］，进一步加剧电机振动，加快轴承磨损，严重情况下还可能引起永磁电机定子铁心与转子接触，危害电机安全可靠运行。此外，偏心会引起磁场分布不均匀、磁阻变化等，进而影响电机的输出转矩等［3］。因此，研究偏心对高速永磁电机转子振动及电磁性能的影响具有重要意义。

转子振动主要受气隙偏心所引发的不平衡磁拉力的影响［4］，因此不平衡磁拉力的研究对转子振动至关重要。最先针对不平衡磁拉力的研究均是基于线性解析法，文献［5］中根据假设，第一次建立了线性的不平衡磁拉力解析式，但是后来通过工程实践发现线性方法误差较大，随后大量学者开始研究不平衡磁拉力的非线性解析式。文献［4-7］对外转子永磁电机的偏心气隙磁场进行直接解析求解，得到气隙中各处的磁密分布，然后对转子表面的Maxwell应力进行积分得到磁拉力解析式，但其推导过程及结果过于复杂，约束了该方法的应用。文献［8］通过将气隙磁导展开为级数形式，从而得到了不同极对数下三相同步电机空载时的不平衡磁拉力，然后分析了不同极数下刚性支承转子系统的振动特性。文献［9］研究了永磁同步电机负载时的不平衡磁拉力表达，代入建立的电机转子系统弯扭耦合方程，讨论了静偏心和质量偏心以及负载类型对转子系统振动特性的影响，但是没有对动静复合偏心进行分析。文献［10］对动偏心和动静复合偏心情形下不考虑重力时和考虑重力时转子系统的轴心轨迹，讨论了静偏心方向对转子系统振动响应的影响，但是所涉及的电机是小型低转速电机。偏心时，气隙长度不再均匀，使得气隙磁场发生畸变进而影响电机性能。文献［11］以一台低速永磁同步电机为例，建立转子偏心的电机模型，分析了偏心对电机电磁力特性的影响。文献［12-15］研究了转子偏心对永磁同步电机气隙磁场的影响，在此基础上分析了气隙谐波磁场的变化对电机转子表面涡流电密的影响。综上所述，目前针对转子偏心对电机振动和电磁性能影响的研究，主要集中在小型电机和中低速电机上，对兆瓦级高速永磁电机的研究较为有限。

本文首先设计一台1.2 MW，20 000 r/min的高速永磁同步电机，利用有限元法验证电磁设计的合理性。然后建立各种偏心状态下的二维电机模型，定量分析不同偏心量以及不同偏心状态对不平衡磁拉力的影响。通过建立转子系统动力模型研究其在不平衡磁拉力作用下的动力响应，详细讨论各种偏心状态下转子系统的轴心轨迹和振动频谱的变化。最后对偏心前后电机性能进行对比分析，得出偏心对电磁性能的影响规律。

1 电机设计与电磁性能分析

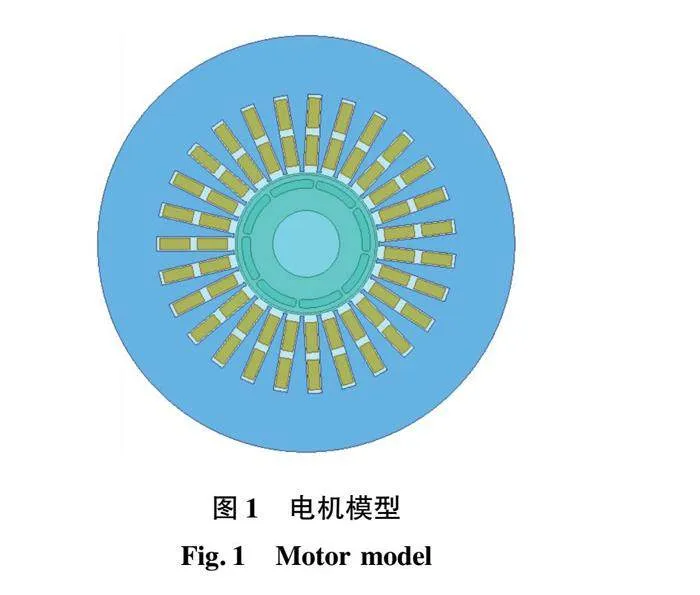
本文设计了一台兆瓦级高速永磁同步电机，电机采用4极转子结构，永磁体径向分为2段。采用碳纤维保护套绑扎转子铁心，来满足转子结构的机械强度要求。定子采用27槽矩形槽结构，电机结构如图1所示，设计参数如表1所示。

高速永磁同步电机按照额定转速20 000 r/min旋转的情况下，其转动频率为

fr=n60。（1）

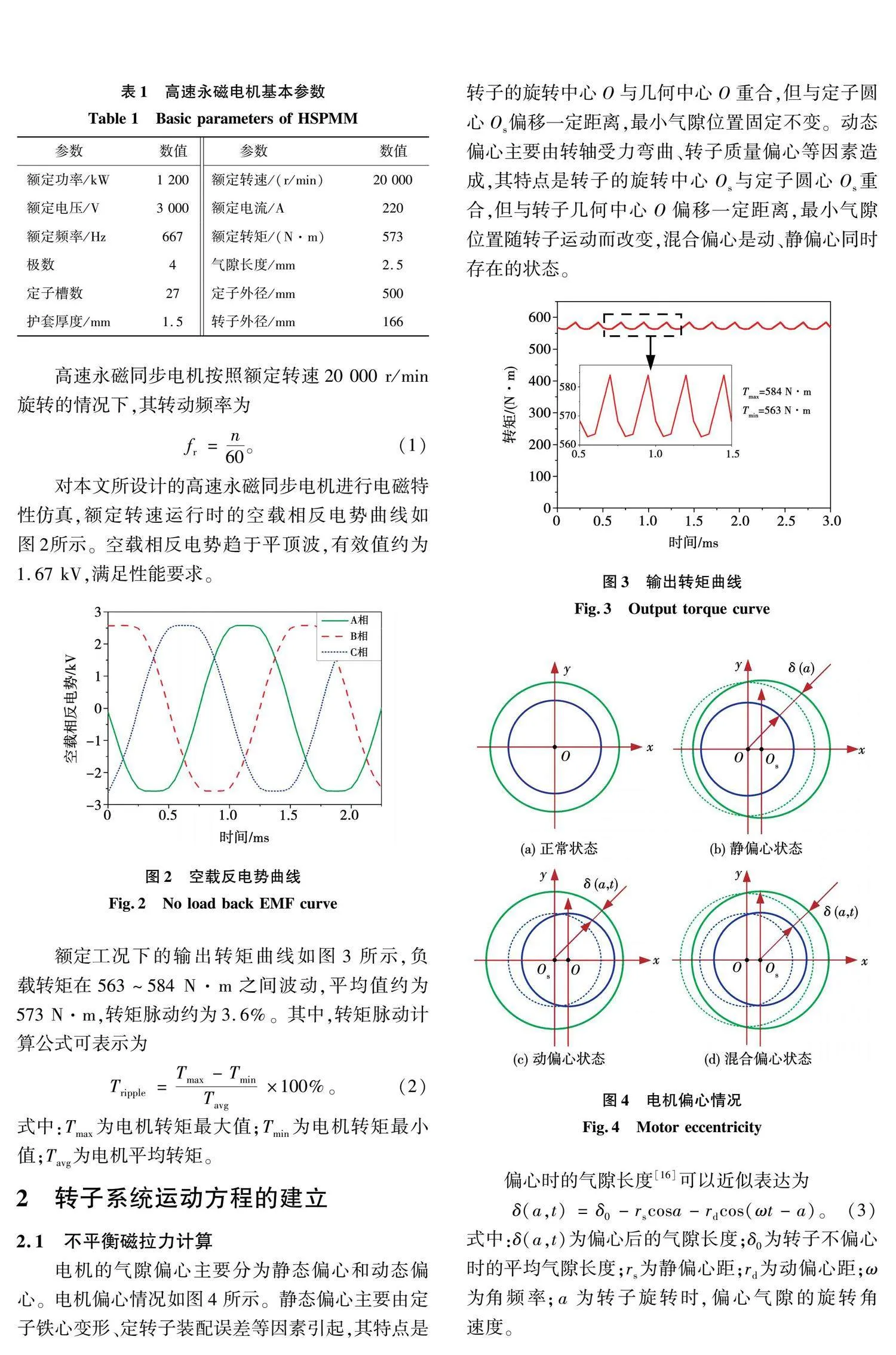
对本文所设计的高速永磁同步电机进行电磁特性仿真，额定转速运行时的空载相反电势曲线如图2所示。空载相反电势趋于平顶波，有效值约为1.67 kV，满足性能要求。

额定工况下的输出转矩曲线如图3所示，负载转矩在563～584 N·m之间波动，平均值约为573 N·m，转矩脉动约为3.6%。其中，转矩脉动计算公式可表示为

Tripple=Tmax－TminTavg×100%。（2）

式中：Tmax为电机转矩最大值；Tmin为电机转矩最小值；Tavg为电机平均转矩。

2 转子系统运动方程的建立

2.1 不平衡磁拉力计算

电机的气隙偏心主要分为静态偏心和动态偏心。电机偏心情况如图4所示。静态偏心主要由定子铁心变形、定转子装配误差等因素引起，其特点是转子的旋转中心O与几何中心O重合，但与定子圆心Os偏移一定距离，最小气隙位置固定不变。动态偏心主要由转轴受力弯曲、转子质量偏心等因素造成，其特点是转子的旋转中心Os与定子圆心Os重合，但与转子几何中心O偏移一定距离，最小气隙位置随转子运动而改变，混合偏心是动、静偏心同时存在的状态。

若式（11）中的ω为0，则为静偏心下的径向电磁力波表达式。根据解析式推导出偏心状态下径向电磁力波的空间阶次和频率特性变化，如表2所示（其中fc为电机额定频率，p为极对数，fr为电机额定转速下的转频频率，n∈0、1、2、3…）。

对偏心下的径向电磁力波沿圆周积分并分解到X轴和Y轴方向上，得到两个方向上的不平衡磁拉力表达式如下：

FX=RL∫2π0prcosθdθ=RL2μ0∫2π0Br（a，t）2cosθdθ；（12）

FY=RL∫2π0prsinθdθ=RL2μ0∫2π0Br（a，t）2sinθdθ。（13）

式中：R为转子半径；L为气隙轴向长度。

2.2 转子系统动力学模型

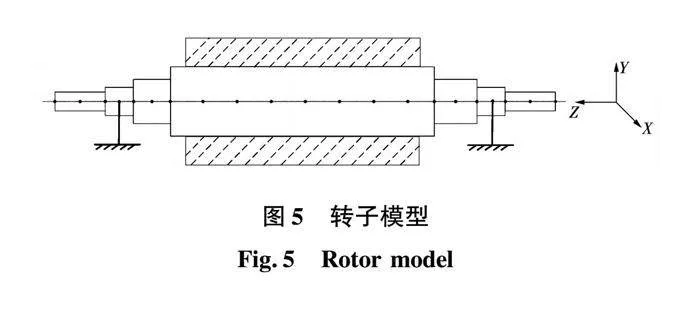
当电机发生气隙偏心时，由此产生的不平衡磁拉力将作用在转子系统上，进而加剧转子振动。为研究偏心下电机转子的振动特性，采用集总参数法建立转子系统模型见图5所示。根据结点总数N应满足N≥1+5.23r的关系［18］（r为要计算的固有频率的最高阶数，因低阶固有频率对系统振动影响较大，故本文只考虑前三阶固有频率，选定r=3，将更高阶舍弃），转子系统整体被划分为21个节点，弹性轴段为20个BEAM188梁单元，2个轴承为COMBI214弹簧单元。

若转子激励频率达到或接近固有频率时，振动将会加剧产生共振，为分析转子系统在固有频率处的振动情况，本文首先对转子系统进行模态分析，得到前三阶固有频率及临界转速如表3所示。

3 偏心对电机电磁性能的影响

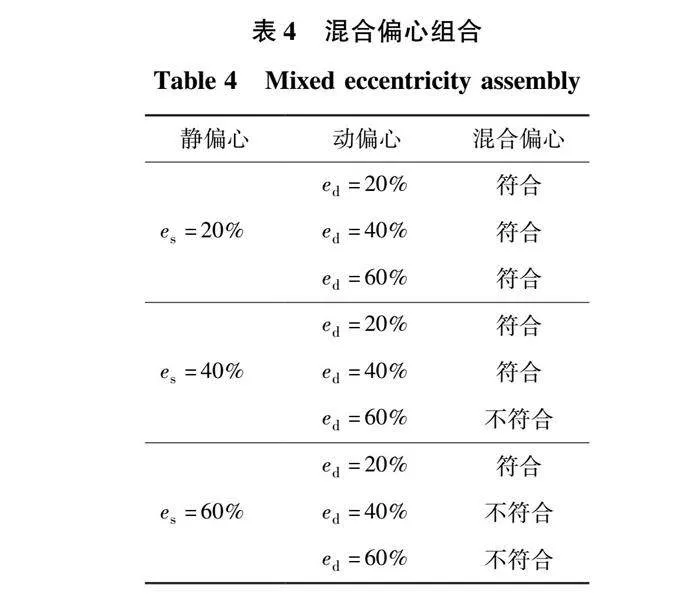
本文中记动偏心为ed，静偏心为es，动、静两种偏心故障下的偏心量均选取0.5、1、1.5 mm分别占气隙长度的20%、40%、60%，偏心方向选取图4所示的X轴正方向。电机实际运行中往往存在动静混合偏心，依据动、静偏心量的设置，混合偏心共有9种组合，但由于电机气隙长度为2.5 mm，因此偏心距离大于或等于气隙长度的组合不符合实际情况，具体混合偏心组合如表4所示。偏心导致电机内气隙长度变化，磁场分布不均匀，进而影响电机输出转矩，因此本节主要对偏心前后的电机气隙磁密和输出转矩进行分析，其中由于气隙磁场是随时间和空间变化的函数，故对气隙磁场从时间和空间两个方面展开分析。

3.1 偏心对气隙磁场时间谐波的影响

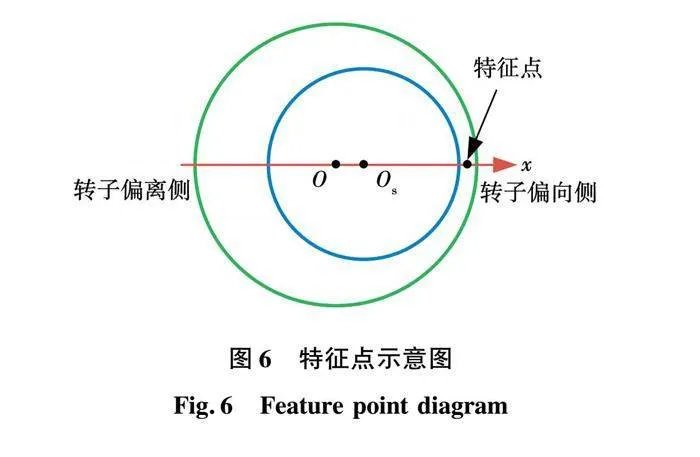
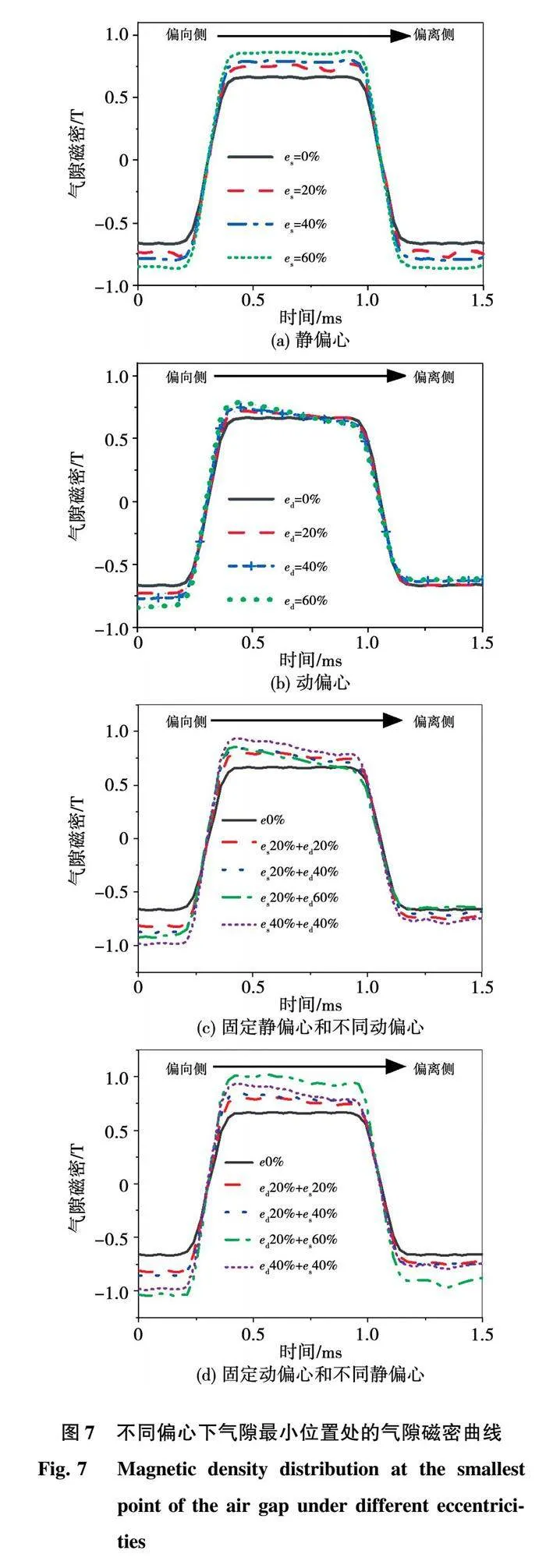
沿偏心方向取电机气隙中的一点记为特征点，偏心方向记为转子偏向侧，与偏心方向相反的一侧记为转子偏离侧，特征点示意图如图6所示。通过有限元法计算得到，一个电周期内该特征点在不同偏心状态下，气隙磁密随时间的变化曲线如图7所示，图中0 ms时刻对应转子偏向侧，电机转动一个电周期即1.5 ms时转至偏离侧。由图6可知，静偏心时，该点的磁密强度随偏心率的增加而增大。动偏心时，电机在转子偏向侧时该点的磁密强度随偏心率的增加而增大，随着电机向偏离侧转动，该点的磁密强度逐渐减小，并会低于正常状态的磁密强度，这是因为动偏心时这一点的气隙长度随电机转动而逐渐增大。混合偏心时由图6（c）和图6（d）可知，当静偏心率大于或等于动偏心率，即静偏心的影响占主要因素时，其磁密强度均大于其他偏心组合的磁密强度。

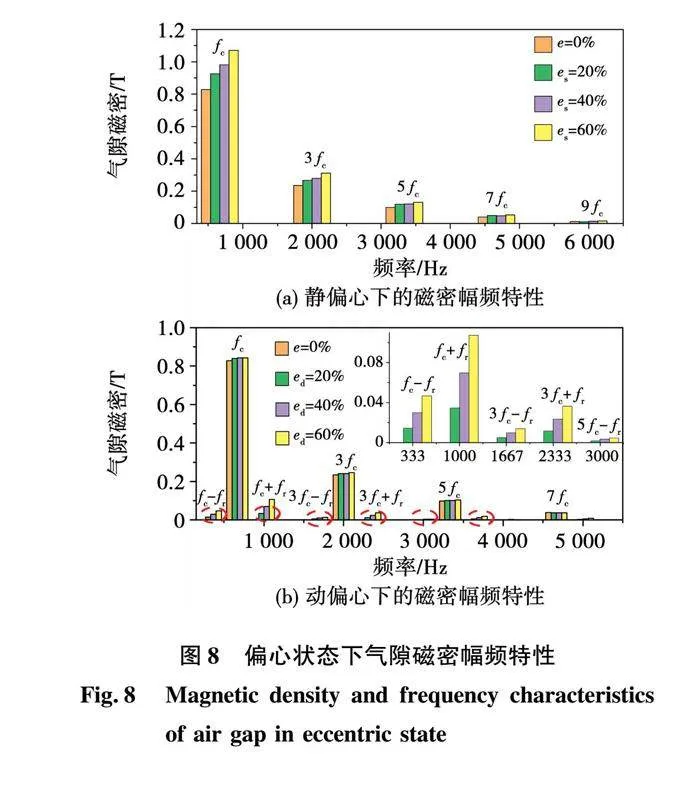
对上述随时间变化的气隙磁密进行傅里叶分解，图8为静、动偏心下的气隙磁密幅频特性，由图可知，静偏心时，气隙磁密各次谐波kfc（k=1、3、5、7，…）的幅值，随静偏心率的增加逐渐增大。动偏心时，主要谐波kfc的幅值变化不大，但引入了kfc±fr的频率成分，如333 Hz、1 000 Hz等，引入的频率成分幅值随动偏心率的增加而增大。

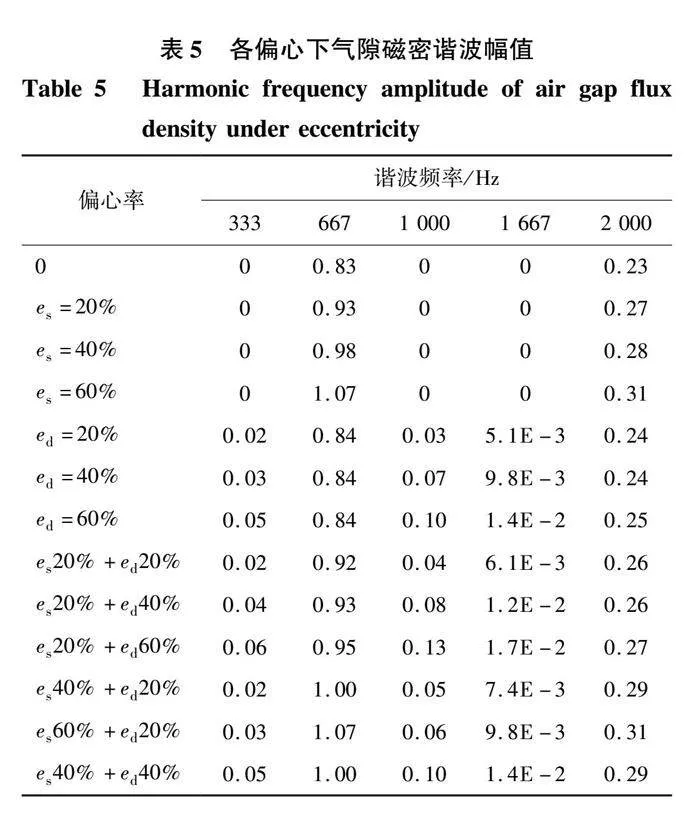
表5为各偏心下气隙磁密的谐波幅值，整体而言，偏心使得谐波幅值发生改变，其中静偏心对主要谐波幅值的影响较大。以基波幅值（fc=667 Hz）为例，静偏心时，基波幅值逐渐增大，动偏心时，基波幅值基本不发生改变。混合偏心时，当静偏心率保持不变，动偏心率由20%增加到60%，基波幅值变化较小；当动偏心率保持不变，静偏心率由20%增加到60%，基波幅值从0.92 T逐渐增大到1.07 T。

3.2 偏心对气隙磁场空间谐波的影响

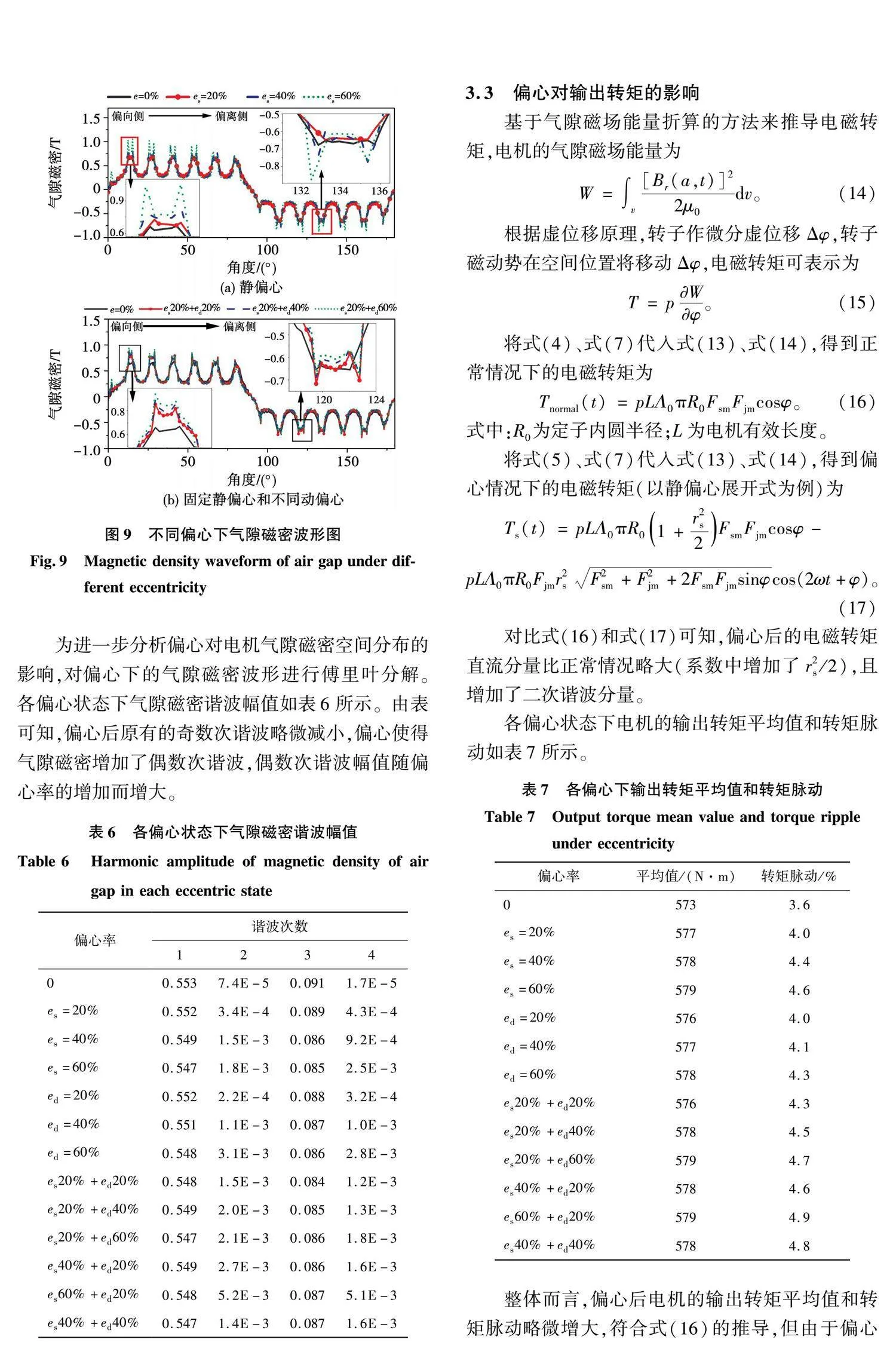
计算得到各偏心下电机气隙磁场的空间分布，对于某一时刻电机磁场的空间分布，可将动偏心看作不同时间的静偏心，所以本文仅绘制了静偏心和保持静偏心率不变，动偏心率从20%增加到60%的气隙磁密空间分布曲线如图9所示。从图可知，随着偏心率的增加，转子偏向侧的磁密强度逐渐增大，偏离侧的磁密强度逐渐减小，并出现不同程度的畸变。

为进一步分析偏心对电机气隙磁密空间分布的影响，对偏心下的气隙磁密波形进行傅里叶分解。各偏心状态下气隙磁密谐波幅值如表6所示。由表可知，偏心后原有的奇数次谐波略微减小，偏心使得气隙磁密增加了偶数次谐波，偶数次谐波幅值随偏心率的增加而增大。

整体而言，偏心后电机的输出转矩平均值和转矩脉动略微增大，符合式（16）的推导，但由于偏心数值较小，所以增幅较小。其中，对比三种偏心状态对输出转矩平均值和转矩脉动的影响发现，存在单一偏心故障时，静偏心引起的转矩脉动比动偏心引起的转矩脉动要大。若为混合偏心故障，当静偏心的影响占主导因素即静偏心率大于动偏心率，此时的转矩脉动略大于动偏心占主导因素时的转矩脉动，这是因为静偏心时，气隙最小位置固定不变，使得磁导和磁密分布具有倾向性，对气隙磁场的影响较大。

4 各偏心故障下转子振动特性分析

4.1 静偏心对转子振动的影响

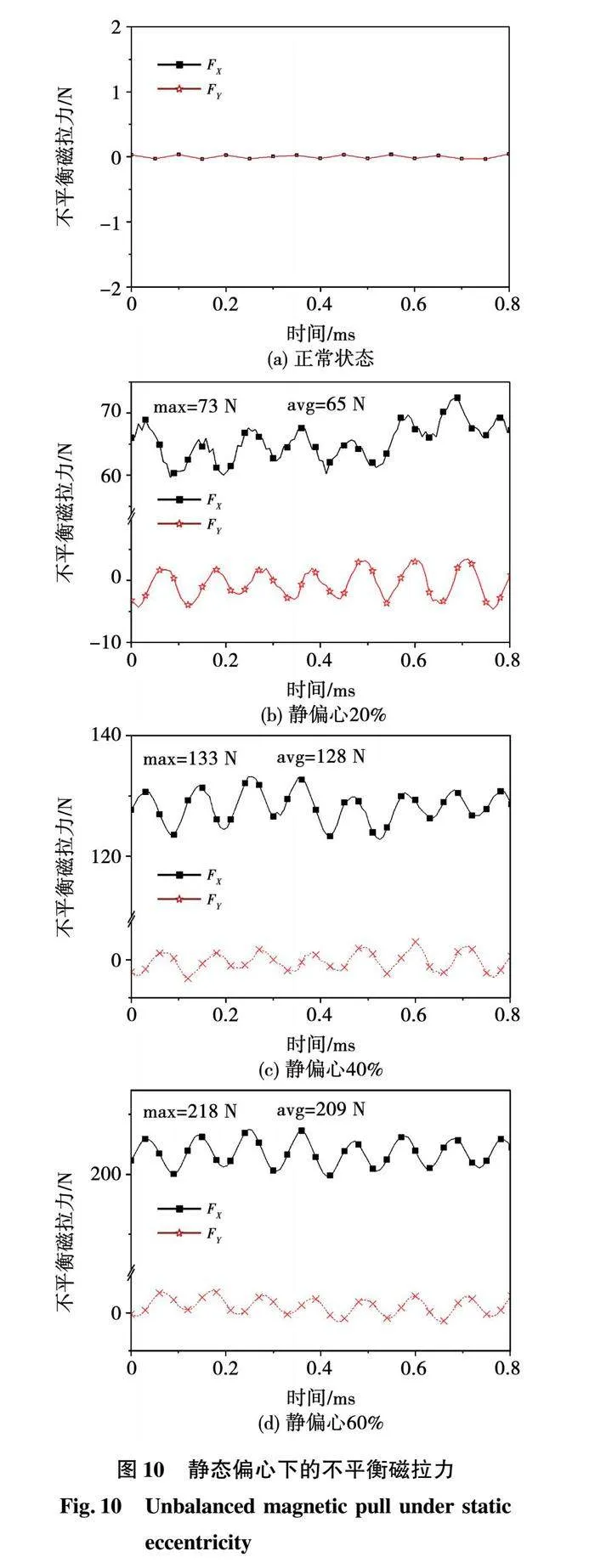
电机偏心导致电磁力分布不均匀，从而产生不平衡磁拉力，静偏心下不平衡磁拉力在X轴和Y轴的分量FX和FY如图10所示。电机未发生偏心时，气隙均匀分布，此时不平衡磁拉力为0。随着偏心率从20%增至60%，FX的最大值从73 N增加到218 N，平均值由65 N增加到209 N，而FY的最大值和平均值变化不大，始终在0上下波动，这是因为偏心方向在X轴，不平衡磁拉力主要集中在X轴方向。

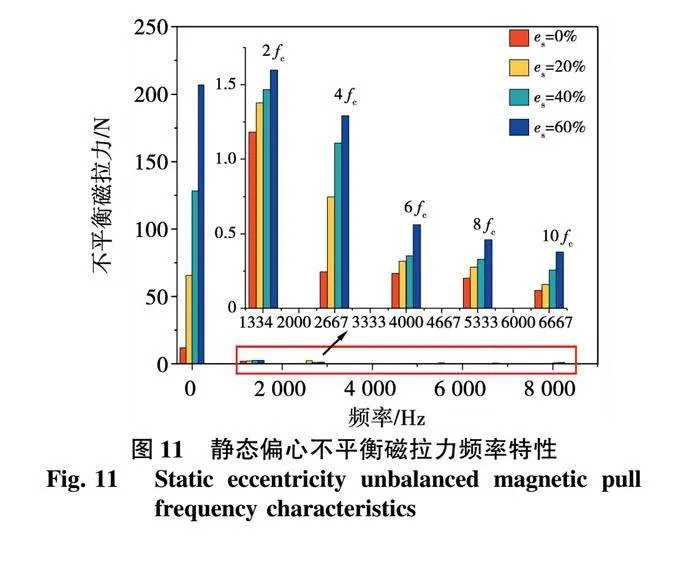
不平衡磁拉力作为转子系统振动的激励源，对转子振动有着重要影响，对求得的不平衡磁拉力进行频率特性分析如图11所示。由于不平衡磁拉力是对径向电磁力波沿圆周积分所得，所以其频率特性与径向电磁力波保持一致（见表2）。静偏心下不平衡磁拉力频率成分为2nfc的关系，各频率对应的幅值随偏心率的增加而增大。

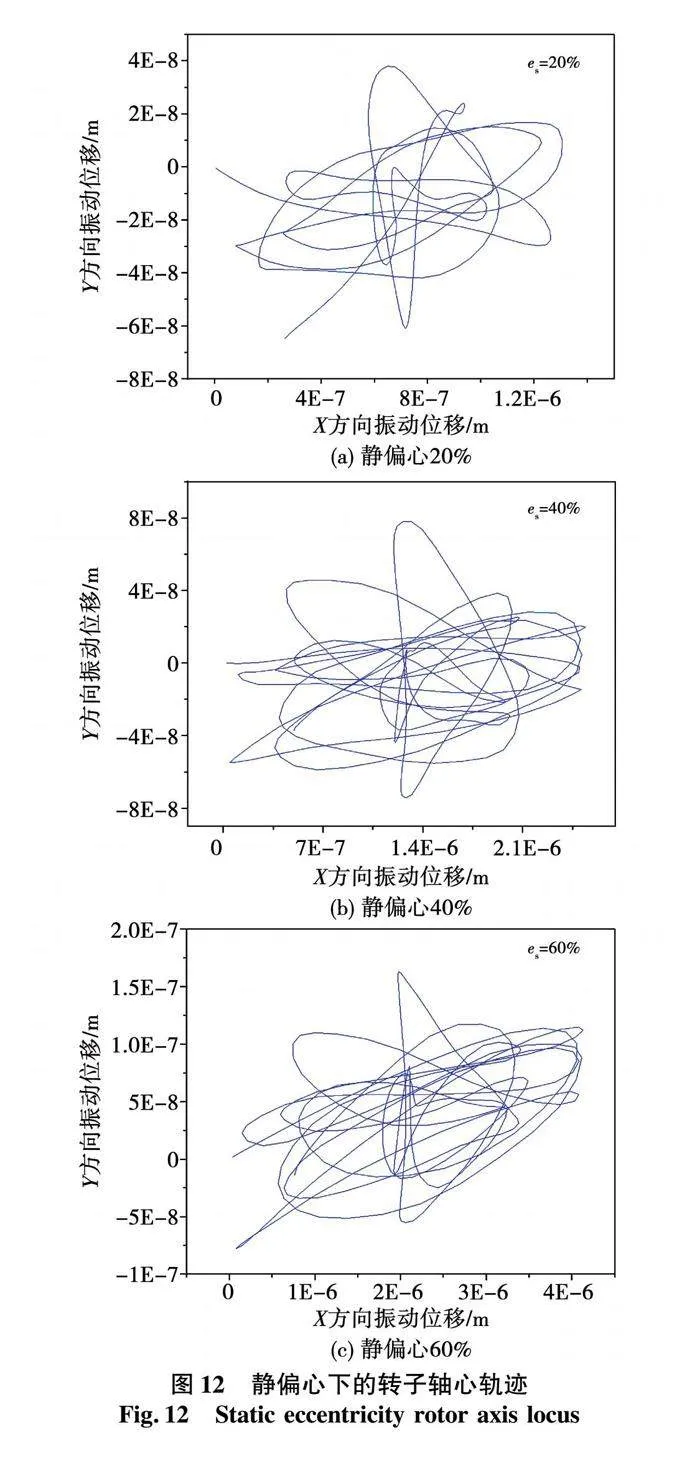
不平衡磁拉力将加剧转子振动，分析转子系统在不平衡磁拉力作用下的动力响应，得到如图12所示的轴心轨迹。由图可知，静偏心时转子轴心轨迹的形态不规则，随着偏心率的增加转子振动位移增大，且轨迹中心偏向X轴正方向，这是由于偏心使得X轴正方向气隙变小，从而不平衡磁拉力增大，故轨迹中心向X轴正方向偏移。

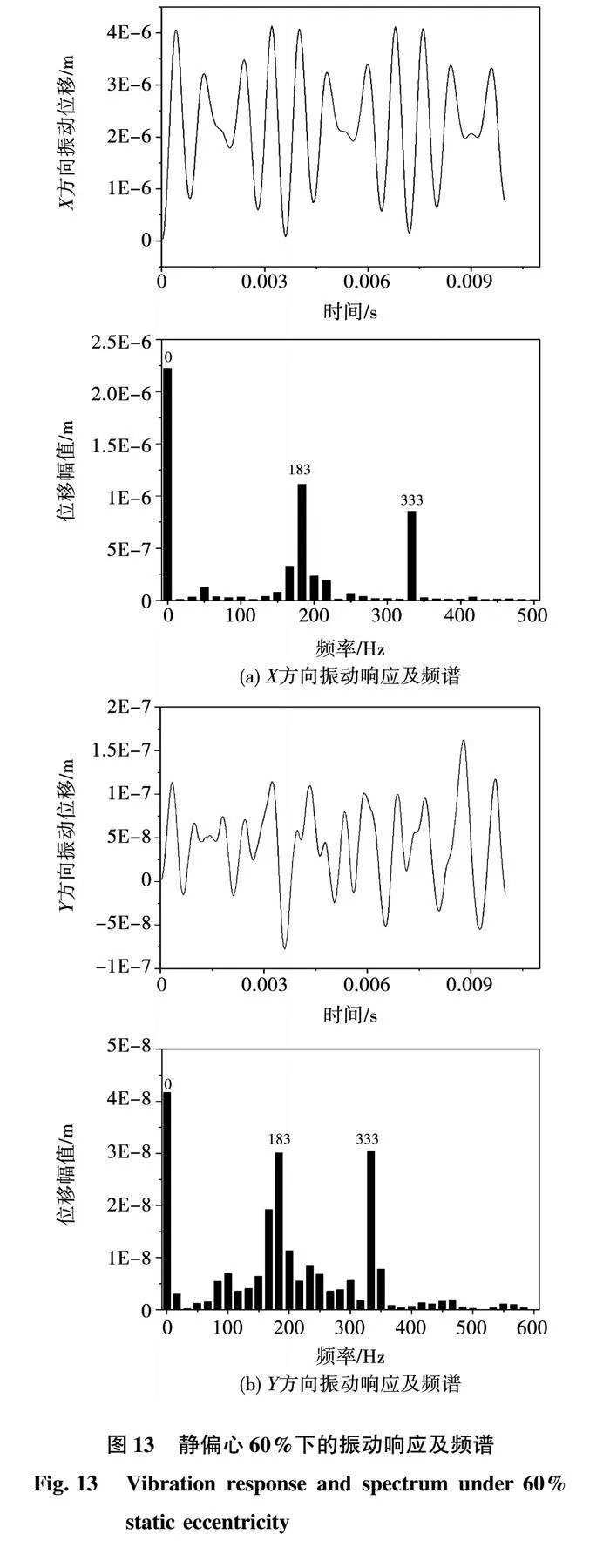
以最大静偏心率60%为例，对X、Y方向的振动响应和频谱进行分析如图13所示。位移频谱中最大振动位移对应零频成分，其次是一阶固有频率和转频成分。因为发生静偏心时，原有0阶力波偏心产生1阶力波（见表2），1阶力波对应频率为0 Hz，又因低阶次力波更易产生振动，故零频下的振动幅值较大。

4.2 动偏心对转子振动的影响

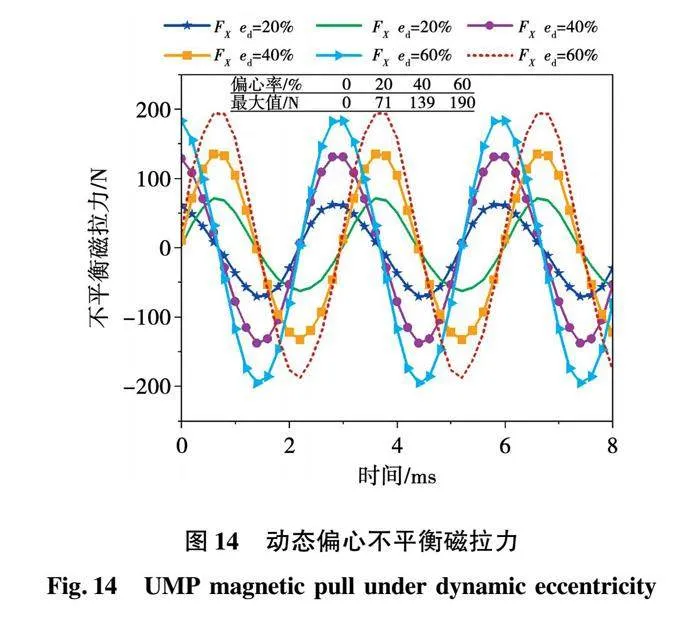
由解析式（11）可知，动态偏心对气隙磁场的影响较为复杂，因此求得动态偏心下电机的不平衡磁拉力如图14所示。

当电机发生动态偏心时，不平衡磁拉力FX和FY都呈现周期性变化，二者周期相等，幅值相等，但在相位上相差90°，不平衡磁拉力最大值随偏心率的增加而增大，动偏心率从0%增大到60%，最大值从0增加到190 N。

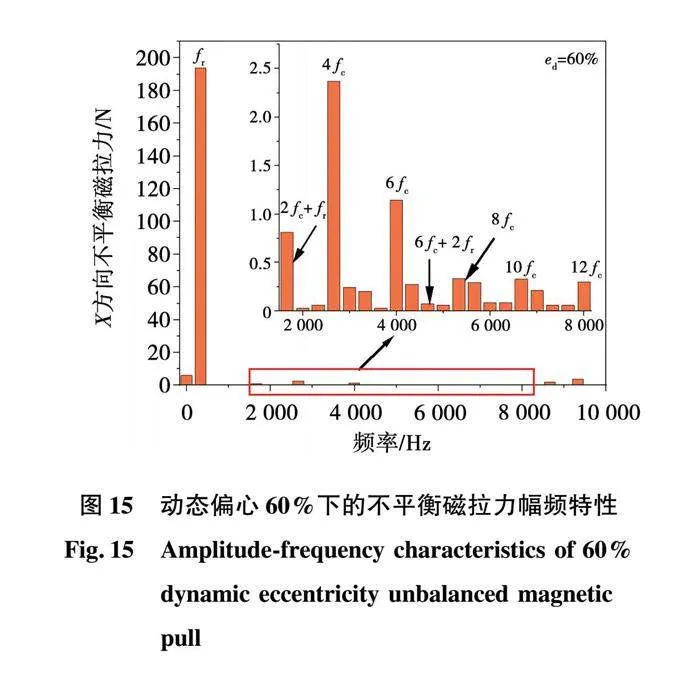
由上文可知，动偏心率仅影响不平衡磁拉力幅值，故以动偏心率60%为例对其频率成分进行分析，如图15所示。动态偏心下不平衡磁拉力的主要频率成分为2nfc，在此基础上产生了±fr和±2fr的频率成分，符合解析式（11）推导的规律。相比静态偏心，零频对应的谐波幅值明显降低，而转动频率fr对应的谐波幅值突出，高阶频率的谐波幅值与静偏心相同且均较小。

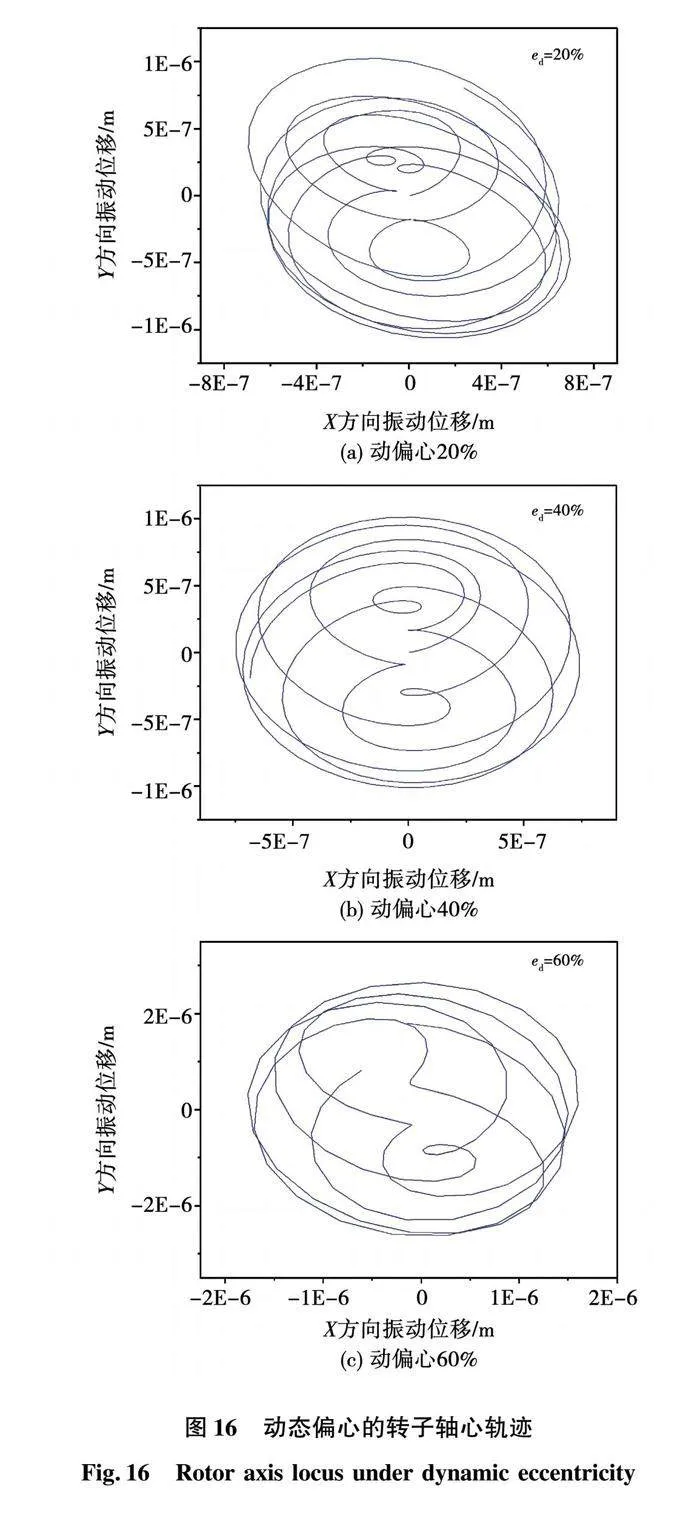
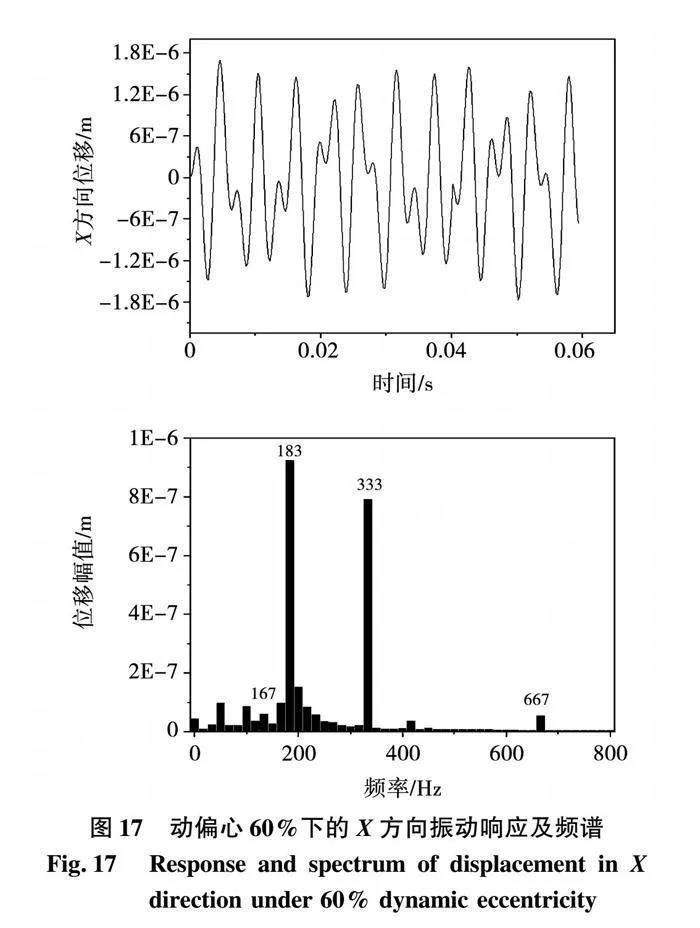
各动态偏心率下的轴心轨迹如图16所示，随着偏心率的增大，转子的振动幅值增加，但转子轴心轨迹的中心不随偏心量改变，保持同心状态，原因是中心位置主要由外加作用力的平均值决定，而动偏心下不平衡磁拉力的平均值不发生变化。图17为动偏心率60%时的X方向的振动响应及频谱图，由图可知，动偏心时转子在一阶固有频率处的振幅最大，其次为转频。

4.3 混合偏心对转子振动的影响

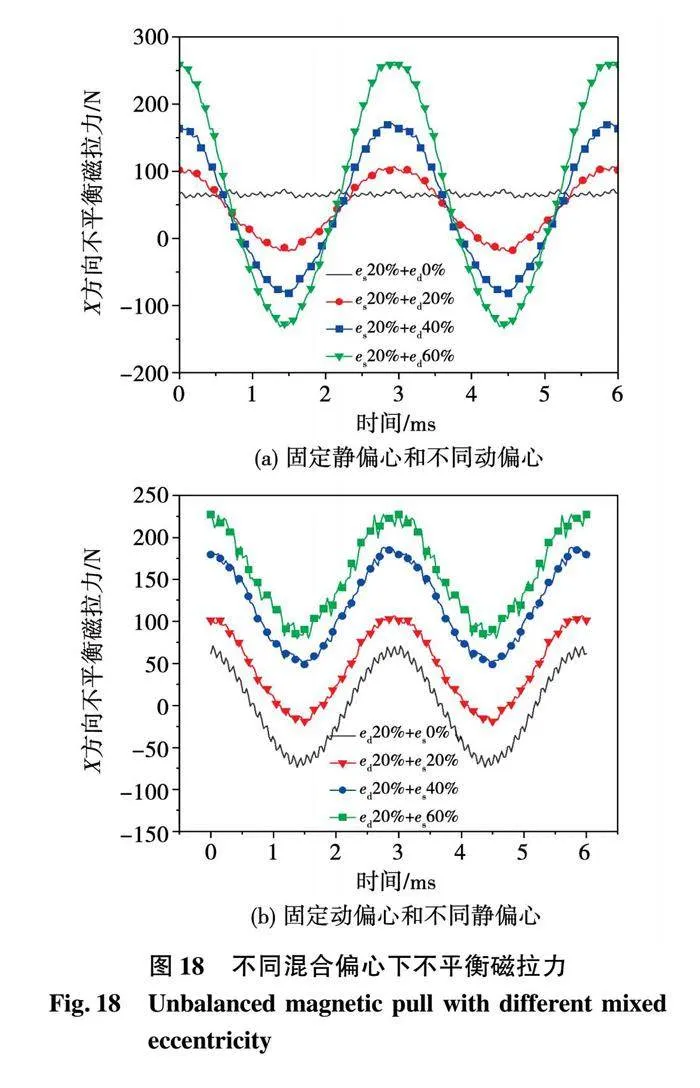
计算混合偏心状态下的不平衡磁拉力如图18所示，当发生混合偏心后，不平衡磁拉力幅值随着偏心程度的增加而增大，且均呈现周期性变化。

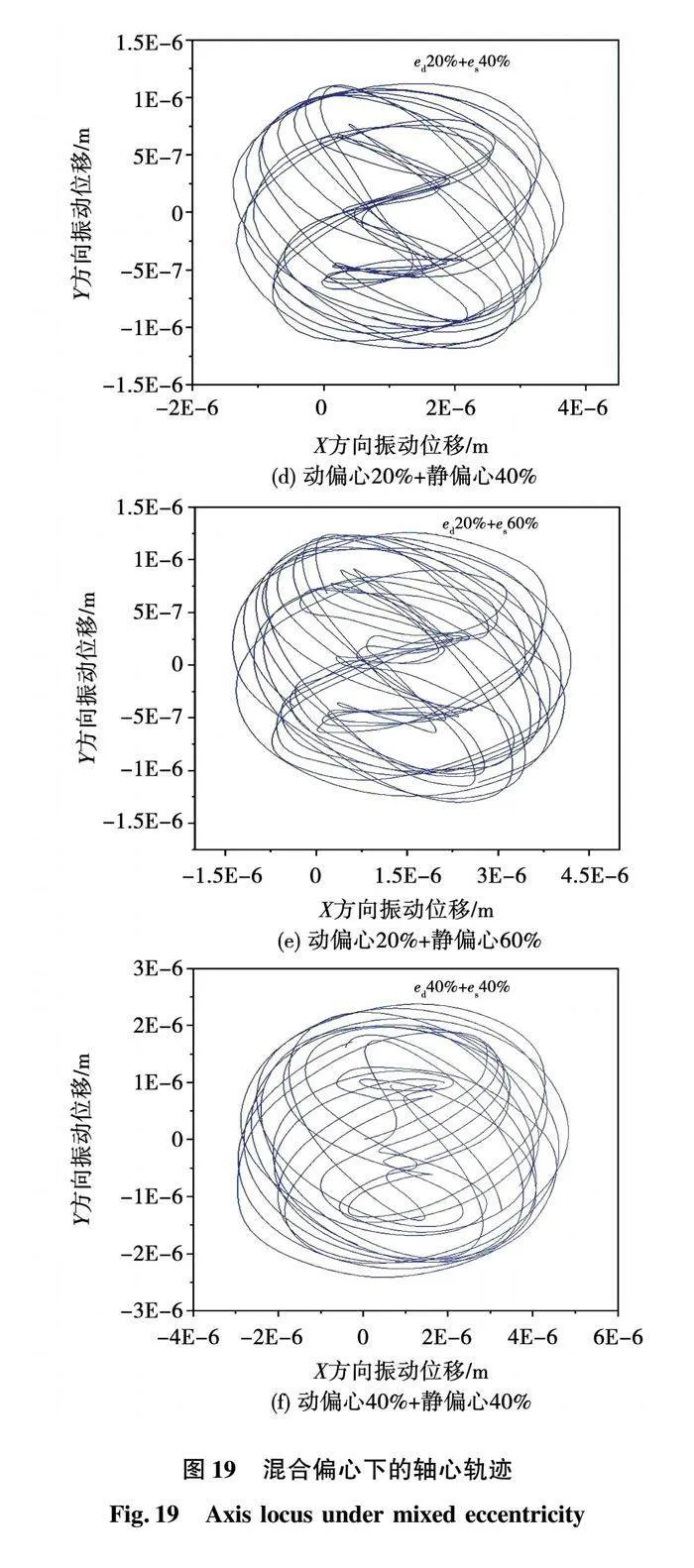
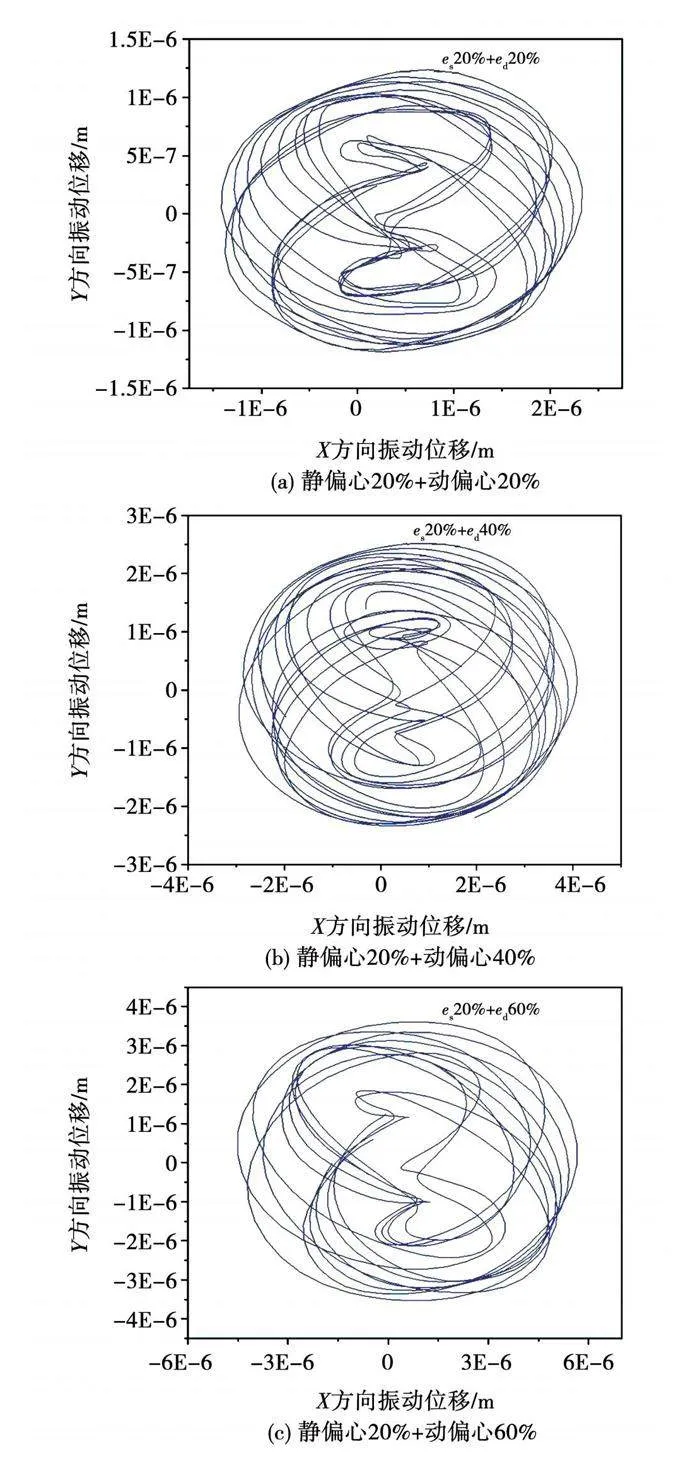
对混合偏心状态下的转子系统进行动力响应分析，得到额定转速下的轴心轨迹如图19所示。图19（a）、图19（b）、图19（c）中为保持静偏心率20%不变，动偏心率从20%增加到60%的轨迹，对比图12（a）静偏心率20%的轨迹可知，动偏心的加入使得轨迹振幅增大，轨迹形态规则化。图19（a）、图19（d）、图19（e）中为保持动偏心率20%不变，静偏心率从20%增加到60%的轨迹，对比图16（a）动偏心率20%的轨迹可知，随着静偏心率的增加，轨迹X方向的振幅逐渐增大，但Y方向的振幅变化不明显，这是因为静偏心时Y方向的不平衡磁拉力始终较小。

图19（f）为动静偏心率均为40%的轨迹，对比图12（b）静偏心率40%、图16（b）动偏心率40%的轨迹，可知偏心程度的加剧，使转子振动位移增大。

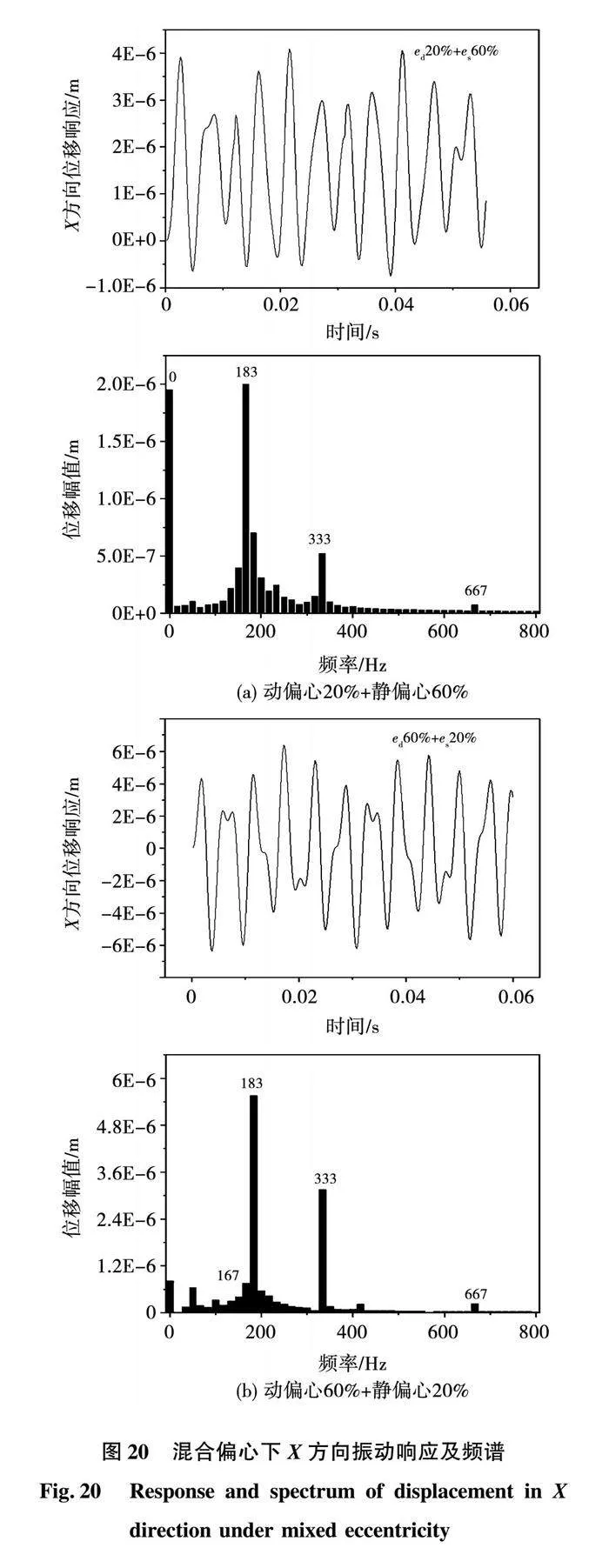
分析混合偏心下转子的振动频谱，以动静偏心率相差较大的混合偏心为例，得到图20所示两种混合偏心下X方向的振动响应及频谱。从图中可以看出，零频对应的谐波幅值随静偏心的增加而增大，转频fr的谐波幅值随动偏心的增加而增大。混合偏心下的主要频率成分是动、静偏心的结合，没有再引入其他的频率成分，同时高阶频率幅值非常小，可忽略不计。

5 结 论

本文首先设计了一台1.2 MW，20 000 r/min的高速永磁同步电机，然后针对电机气隙偏心问题，分别建立了动、静、混合偏心状态下的电机模型，通过有限元法，计算了各偏心下的不平衡磁拉力，研究了不同偏心情况下的电磁性能和转子动力响应，得到以下结论：

1）电机存在偏心故障时，气隙磁密偶次谐波明显增加，其各谐波频率幅值主要受静偏心的影响，动偏心使得气隙磁密引入kfc±fr的频率成分。由于气隙偏心后气隙磁导发生变化，进而影响电机转矩，使得电机转矩脉动增加，转矩平均值略微增大。

2）静偏心对不平衡磁拉力频率成分不产生影响，动偏心的不平衡磁拉力附加了2nfc±fr、±2fr的频率成分，混合偏心时的不平衡磁拉力也附加了2nfc±fr、±2fr的转频成分，且不平衡磁拉力均呈现周期性变化。

3）动、静偏心时转子径向位移振幅随偏心量的增加而增大，但静偏心量影响转子轨迹的中心位置，而动偏心量对转子轨迹的中心不产生影响。混合偏心时，动偏心对轴心轨迹形态的影响占主导作用。

参 考 文 献：

［1］ 唐任远. 现代永磁电机—理论与设计［M］. 北京： 机械工业出版社， 2005.

［2］ 王天煜. 高速永磁电机转子综合设计方法及动力学特性的研究［D］. 沈阳： 沈阳工业大学， 2010.

［3］ 孔汉. 永磁同步电机故障对电机综合物理场的影响机理研究［D］. 西安： 西北工业大学， 2016.

［4］ 于占洋， 李岩， 井永腾. 基于混合磁场解析法的磁极偏心型表贴式永磁同步电机空载特性分析［J］. 电工技术学报， 2020， 35（18）： 3811.

YU Zhanyang， LI Yan， JING Yongteng. No-load characteristics analysis of magnetic pole eccentric surface mount permanent magnet synchronous motor based on hybrid magnetic field analysis method［J］. Transactions of China Electrotechnical Society， 2020， 35（18）： 3811.

［5］ BEHREND B A. On the mechanical forces in dynamos caused by magnetic attraction ［J］. Transactions of the American Institute of Electrical Engineers， 1900， （XVII）： 613.

［6］ KIM U， LIEU D K. Magnetic field calculation in permanent magnet motors with rotor eccentricity： without slotting effect［J］. IEEE Transactions on Magnetics， 1998， 34（4）： 2243.

［7］ KIM T J， HANG S M， PARK N G. Analysis of vibration for permanent magnet motors considering mechanical and magnetic couple effects［J］.IEEE Transactions on Magnetics，2000，36（4）：1346.

［8］ 郭丹， 何永勇， 褚福磊. 不平衡磁拉力及对偏心转子系统振动的影响［J］. 工程力学， 2003， 20（2）： 116.

GUO Dan， HE Yongyong， CHU Fulei. The calculation of unbalanced magnetic pull and its effect on vibration of an eccentric rotor［J］. Engineering Mechanics， 2003， 20（2）： 116.

［9］ 岳二团， 甘春标， 杨世锡. 气隙偏心下永磁电机转子系统的振动分析［J］. 振动与冲击， 2014， 33（8）： 29.

YUE Ertuan， GAN Chunbiao， YANG Shixi. Vibration characteristics analysis of a rotor for a permanent magnet motor with air-gap eccentricity［J］.Journal of Vibration and Shock，2014，33（8）：29.

［10］ 徐学平， 韩勤锴， 褚福磊， 静载荷作用下偏心转子电磁振动特性［J］. 清华大学学报（自然科学版）， 2016， 56（2）： 176.

XU Xueping， HAN Qinkai， CHU Fulei. Electromagnetic vibration characteristics of an eccentric rotor with a static load［J］. Journal of Tsinghua University（Science and Technology）， 2016， 56（2）： 176.

［11］ 冯立帅. 转子偏心对低速永磁同步电机运行特性影响的研究［D］. 沈阳： 沈阳工业大学， 2022.

［12］ 蒋山. 偏心状态下永磁同步电机电磁性能分析［D］. 哈尔滨： 哈尔滨理工大学， 2017.

［13］ 周生通， 郭维年， 肖乾. 偏心故障下动车组牵引电机转子振动特性分析［J］. 工程力学， 2021， 38（7）： 216.

ZHOU Shengtong， GUO Weinian， XIAO Qian. Vibration characteristics analysis of EMU traction motor rotor under eccentric faults［J］. Engineering Mechanics， 2021， 38（7）： 216.

［14］ 党文娟， 不平衡磁拉力作用下偏心转子-轴承系统非线性振动特性分析［D］. 西安： 西安理工大学， 2019.

［15］ 张霄霆， 张炳义， 曹永鹏. 偏心状态下的轴向磁通永磁电机受力分析［J］. 电工技术学报， 2020， 35（1）： 110.

ZHANG Xiaoting， ZHANG Bingyi， CAO Yongpeng， Force analyze of axial magnetic flux permanent magnet motor under eccentricity condition［J］. Transactions of China Electrotechnical Society， 2020， 35（1）： 110.

［16］ 唐贵基， 邓玮琪， 何玉灵. 不同种类气隙偏心故障对汽车发电机转子不平衡磁拉力的影响［J］. 振动与冲击， 2017， 36（15）： 1.

TANG Guiji， DENG Weiqi， HE Yuling. Effect of different kinds of air-gap eccentricity faults on rotor UMP of a turbo-generator［J］. Journal of Vibration and Shock， 2017， 36（15）： 1.

［17］ 孙晶晶. 考虑转子偏心的永磁同步电机电磁力特性分析［D］. 杭州： 浙江大学， 2016.

［18］ 钟一谔， 何衍宗. 转子动力学［M］. 北京： 清华大学出版社， 1987.

［19］ FENG Lishuai， YU Siyang， ZHANG Fengge. Study on performance of low-speed high-torque permanent magnet synchronous motor with dynamic eccentricity rotor ［J］. SCI Energy Reports， 2022， 8（5）： 1421.

［20］ 田拥胜， 孙岩桦， 虞烈. 高速永磁电机电磁轴承转子系统的动力学及实验研究［J］. 中国电机工程学报， 2012， 32（9）： 116.

TIAN Yongsheng， SUN Yanhua， YU Lie. Dynamical and experimental researches of active magnetic bearing rotor systems for high speed PM machines［J］. Proceedings of the CSEE， 2012， 32（9）： 116.

［21］ 乔芳， 盘轴-松动偏心耦合故障转子系统动力学建模与振动特性研究［D］. 南昌： 南昌航空大学， 2021.

［22］ SHEN Quan， ZHOU Jin， MA Yanchao， et al. Dynamic modeling and analysis of magnetic suspension rotor system under foundation excitation［J］.Journal of Vibration and Shock，2022，41（17）：35.

［23］ MA Conggan， CUI Hongwei， ZHENG Ping. Influence of static eccentricity on unbalanced magnetic force of external rotor permanent magnet brushless direct current motor used as in-wheel motor［J］. IET Electric Power Applications， 2019， 13（4）： 538.

［24］ 周晓燕， 李琛， 仇志坚， 等. 基于摄动法的交替级永磁电机偏心磁场解析计算［J］. 电工技术学报， 2013， 28（9）： 321.

ZHOU Xiaoyan， LI Chen， QIU Zhijian， et al. Magnetic field calculation for consequent-pole motor with rotor eccentricity based on perturbation method［J］. Transactions of China Electrotechnical Society， 2013， 28（9）： 321.

［25］ 张岩岩， 耿海鹏， 周健， 等. 永磁同步电机转子偏心磁场解析计算［J］. 西安交通大学学报， 2019， 53（2）： 93.

ZHANG Yanyan， GENG Haipeng， ZHOU Jian， et al. Analytical calculation for magnetic field of permanent magnet synchronous motors with rotor eccentricity［J］. Journal of Xi’an Jiaotong University， 2019， 53（2）：93.

［26］ LI Yanxin， LU Qinfen， ZHU Z Q. Unbalanced magnetic force prediction in permanent magnet machines with rotor eccentricity by improved superposition method ［J］. IET Electric Power Applications， 2017， 11（6）： 1095.

［27］ 戈宝军， 刘海涛， 王立坤. LNG泵用低温高速永磁电机偏心故障动态电磁力［J］. 电机与控制学报， 2022， 26（5）： 55.

GE Baojun， LIU Haitao， WANG Likun. Dynamic electromagnetic force of cryogenic high-speed permanent magnet motors with eccentric fault［J］.Electric Machines and Control，2022，26（5）：55.

［28］ 刘蓉晖， 刘锦坤， 章君达. 基于双曲余切变换的Halbach阵列表贴式永磁电机转子偏心气隙磁场解析模型［J］. 电工技术学报， 2023， 38（6）： 1433.

LIU Ronghui， LIU Jinkun， ZHANG Junda. Analytical model for air-gap magnetic field in Halbach arrays surface-mounted permanent magnet motor with rotor eccentricity based on hyperbolic cotangent transformation［J］. Transactions of China Electrotechnical Society， 2023， 38（6）： 1433.

［29］ 韩雪岩， 王勇， 高俊. 低速永磁同步电机转子偏心的抑制措施［J］. 电机与控制学报， 2023， 27（11）： 58.

HAN Xueyan， WANG Yong， GAO Jun. Suppression of rotor eccentricity of low-speed permanent magnet synchronous motor［J］. Electric Machines and Control， 2023， 27（11）： 58.

（编辑：刘素菊）