永磁同步直线电机位移误差的预设性能反步控制策略

摘 要：

单轴电机的伺服控制主要是对位移跟踪精度的控制，误差较大意味着跟随效果较差。目前对电机位移误差的控制策略大多难以做到定量的约束控制。本文提出一种将位移误差设置在预期范围内的预设性能反步控制策略，来定量调控输出位移误差的响应时间以及超调量等暂态性能，降低直线电机的位移误差。本文设计了预设性能函数作为控制边界，保证位移跟踪误差处于误差范围内并按设定时间快速收敛，利用Lyapunov理论设计反步控制器保证了系统的闭环稳定性和跟踪误差的收敛性。最后，利用直线电机伺服实验平台，通过不同工况高精度点位运动实验，证明了该控制算法能够有效降低点位运动的位置跟随误差。

关键词：永磁同步直线电机；预设性能；反步法；误差转换；有限时间；位移误差

DOI：10.15938/j.emc.2024.09.007

中图分类号：TM921

文献标志码：A

文章编号：1007-449X（2024）09-0070-11

收稿日期： 2023-09-15

基金项目：中央引导地方科技发展资金项目（226Z1805G）;天津市自然科学基金（20JCYBJC00730）

作者简介：滕子铖（1998—），男，硕士研究生，研究方向为电机控制；

陶友瑞（1973—），男，博士，教授，研究方向为先进复合材料制备技术与工程应用；

李珊瑚（1985—），女，博士，教授，研究方向为电机控制、矩阵变换器；

刘 旭（1984—），男，博士，教授，研究方向为电机控制。

通信作者：李珊瑚

Prescribed performance backstepping control strategy for displacement error of permanent magnet linear synchronous motor

TENG Zicheng1，2， TAO Yourui1， LI Shanhu1，2， LIU Xu1，2

（1.State Key Laboratory of Reliability and Intelligence of Electrical Equipment， Hebei University of Technology， Tianjin 300130， China; 2.Key Laboratory of Electromagnetic Field and Electrical Apparatus Reliability of Hebei Province， Hebei University of Technology， Tianjin 300130， China）

Abstract：

The servo control of the single-axis motor is mainly to control the displacement tracking accuracy， and the large error means that the tracking effect is poor. At present， most of the control strategies for motor displacement error are difficult to achieve quantitative constraint control. A prescribed performance backstepping control strategy was proposed to set the displacement error within the expected range， so as to quantitatively control the response time of the output displacement error and the transient performance such as overshoot， so as to reduce the displacement error of the linear motor. A prescribed performance function was designed as the control boundary to ensure that the displacement tracking error is within the error range and converges quickly according to the set time， and the Lyapunov theory was used to design the backstepping controller to ensure the closed-loop stability of the system and the convergence of the tracking error. Finally， the linear motor servo experimental platform was used to prove that the control strategy can effectively reduce the position tracking error of point motion through high-precision point motion experiments under different working conditions.

Keywords：permanent magnet linear synchronous motor; prescribed performance; backstepping control; error conversion; finite time; displacement error

0 引 言

永磁直线同步电机（permanent magnet linear synchronous motor，PMLSM）结构简单、精度高且无传动机构［1］，近年来在高精密制造设备的伺服驱动上得到了广泛应用，如XY平台驱动、数控机床和机器人控制等［2-4］。

在基于永磁直线电机的伺服系统控制方法中，基于PI的二自由度控制虽然拥有结构简单、参数整定快、易于实现等优点［5］，但是在高速高精度定位平台中，其位移跟随误差往往达不到定位精度的要求。同时外界扰动和模型的不确定性更使得基于PI的二自由度控制策略的鲁棒性较差，位置跟随误差无法达到更高的精度要求。

为减小不确定性以及外界干扰对输出位移跟随误差造成的影响，国内外研究者提出了许多滑模控制［6-7］、自适应控制［8-9］等诸多非线性控制方法。滑模控制利用不确定性系统的边界条件设计切变控制律，系统的动态由设计的滑模面决定，与不确定性无关，但是滑模控制中的“抖振”现象给滑模变结构控制在实际系统应用中带来了困难。文献［10］提出一种多周期迭代滑模控制算法用于提高直线电机的控制精度，能够对直线电机受到的多周期干扰进行抑制，但其算法较为复杂。文献［11］提出一种改进多输入多输出无模型自适应控制的二维直线电机迭代学习控制复合控制方案，补偿系统非线性因素，前馈反馈优势互补，但是自适应控制器设计复杂，对系统的实时控制有较长的运行时间，无法保证参数估计值到实际值的渐进收敛。

反步控制［12］（backstepping control，BSC）则是一种静态补偿思想，通过后面子系统中的虚拟控制实现前面子系统的稳定收敛，通过不断递推迭代构造李雅普诺夫能量函数进行控制器设计。反步控制方法有很多优点，如鲁棒性强、需要调试的参数较少，因而被广泛应用于电机控制系统中［13-17］。文献［13］创造性地将反步法应用于电机控制系统；文献［14］则将滑模控制与反步控制相结合，设计的滑模反步控制器，能有效提高伺服系统的鲁棒性；文献［15］考虑了电机负载扰动，提出了基于反步法的PMSM速度环自适应控制；文献［16］利用非线性积分反步法设计了自适应积分反步控制器，不仅可以补偿参数不确定性的影响，抗负载扰动能力也大大提高，但是自适应控制器设计依旧复杂，对系统的实时控制的运行时间依旧较长。文献［17］加入周期性学习算法，设计了一种自适应反步滑模控制器保证直线电机的定位精度，但加入的学习算法也提高了控制器的计算量。这些控制策略都结合了反步控制方法，在电机的稳态性能和鲁棒性方面都有较好效果，但在暂态性能方面难以做到定量控制，有一定的局限性。

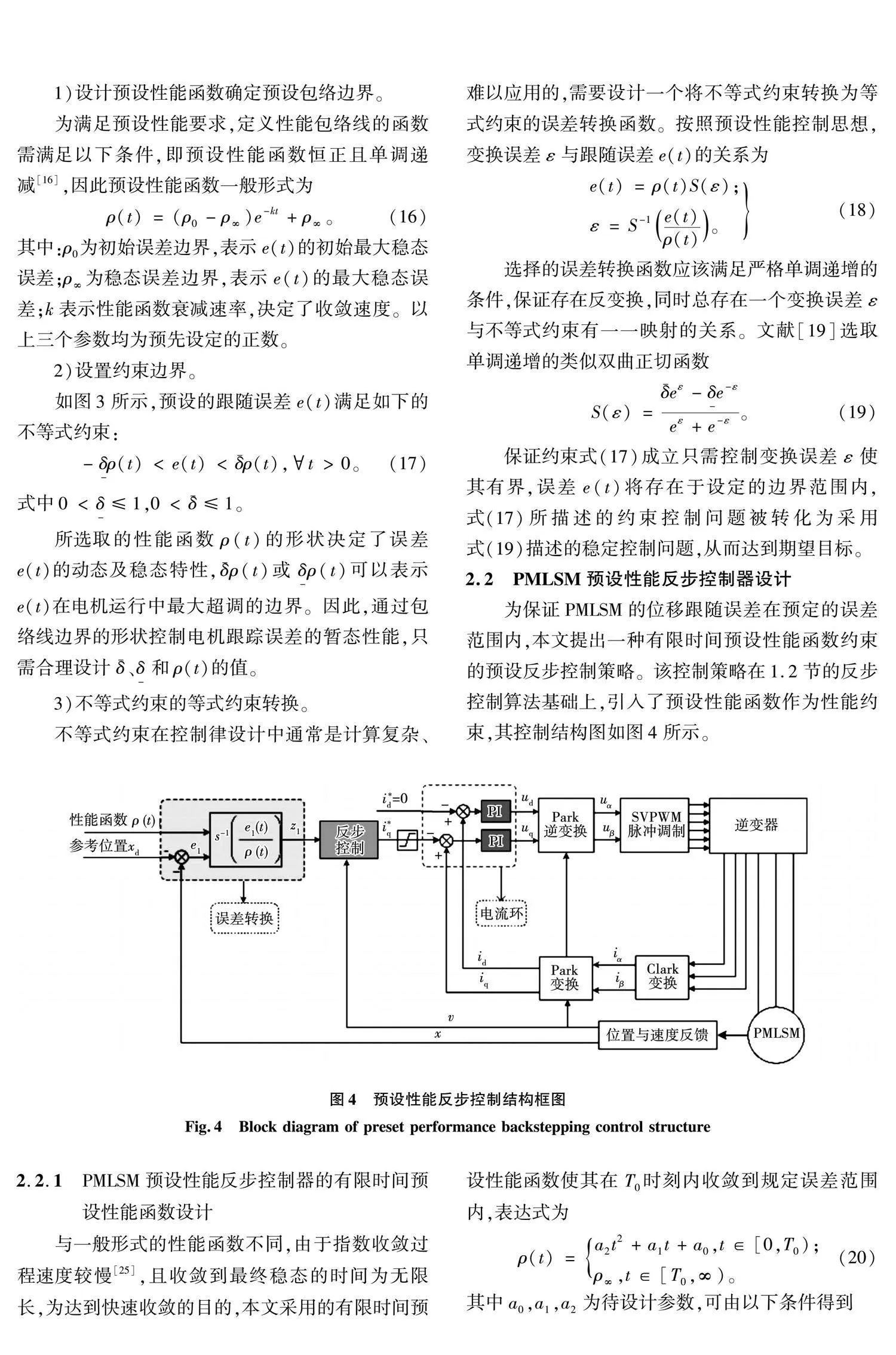
Bechlioulis和Rovithakis于2008年首次提出预设性能函数（prescribed performance control，PPC）［18-19］控制方法，该预设性能控制方法可以预先设定一个边界函数限制收敛速度及超调量，继而使跟踪误差收敛到一个提前设定好的区域内。这种方法不仅可以保证系统稳定，在系统的暂态特性方面还有较好的控制效果。文献［20］提出了一种保预设性能鲁棒自适应控制方案， 利用自适应投影算法对有界时变参数进行辨识，进行了控制器设计。文献［21-23］将预设性能引入到常规反步法中，对解决非线性系统的控制问题有很大帮助，主要应用于编队控制［21］、飞行器飞行控制［22］、汽车悬架控制［23］的位置跟踪问题。此外，文献［24］将预设性能引入到自适应控制中，应用于转台伺服系统中。

对单轴电机而言，实时的伺服控制主要是跟踪精度的控制，位移误差严重影响电机运动过程中的精度，在高速高精高加工场合，误差超限将导致机床振动、零件表面质量恶化、电机失控等严重后果，直接影响零件加工质量以及产品要求。目前对于电机的位移误差难以做到定量的约束控制，同时当前预设性能主要应用在机械控制领域，关于直线电机降低位移误差的应用较少。

针对上述永磁直线电机跟随误差控制方法误差收敛不确定问题，本文通过结合预设性能控制思想，提出一种在有限时间内快速收敛的预设性能反步控制策略（prescribed performance backstepping control，PPBC），可以定量调控输出的响应时间以及超调量等暂态性能，与一般的预设性能函数相比，它的收敛速度更快；此外目前伺服行业考虑到成本以及便于扩展，早已将电流环集成在驱动器中，本文保留采用PI控制器的电流环，更广泛应用于直线电机中，避免反步控制中的微分爆炸，对电机暂态特性有较好控制效果。

1 传统反步控制策略

1.1 反步控制原理

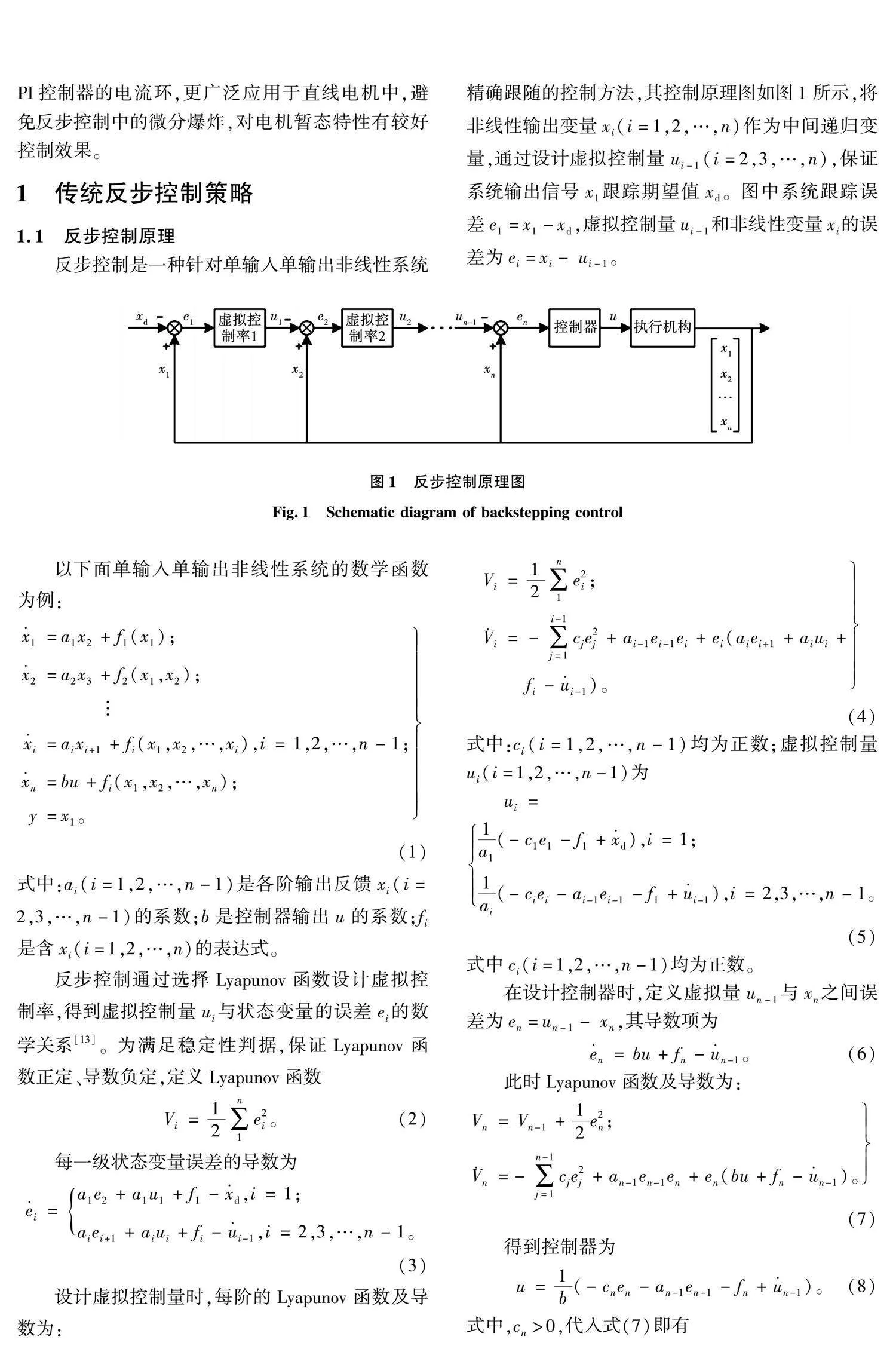
反步控制是一种针对单输入单输出非线性系统精确跟随的控制方法，其控制原理图如图1所示，将非线性输出变量xi（i=1，2，…，n）作为中间递归变量，通过设计虚拟控制量ui-1（i=2，3，…，n），保证系统输出信号x1跟踪期望值xd。图中系统跟踪误差e1=x1-xd ，虚拟控制量ui-1和非线性变量xi的误差为ei=xi- ui-1。

3 仿真与实验

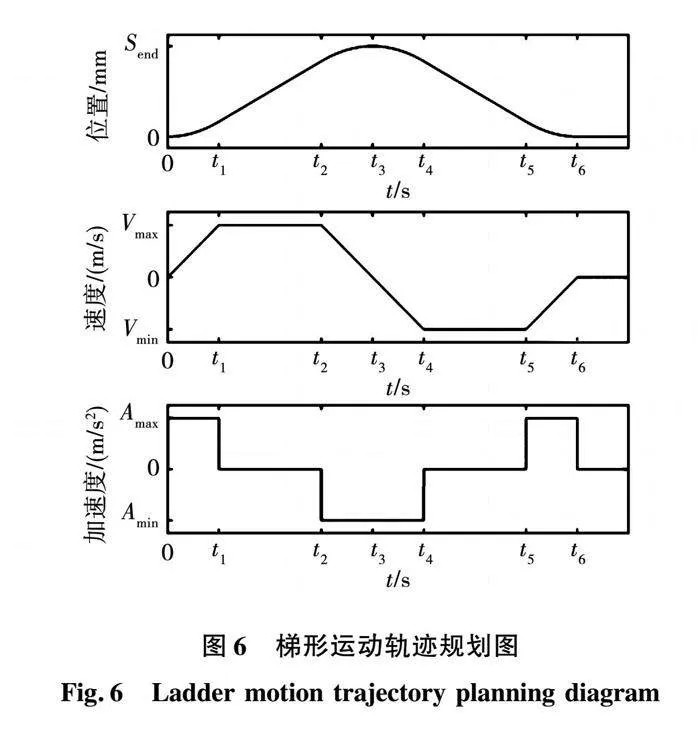
在如芯片封装点胶过程中，点胶工艺主要为点胶（定位运动）和涂胶（轮廓运动），单轴电机跟踪精度的位移误差需要控制在微米级别。在点胶过程中，点胶直线电机通常采用闭环控制的方式，主要用于点到点的高速高精度运动，本文按照时间最短、冲击最小的原则选择梯形运动轨迹为参考位移轨迹。该梯形运动轨迹整个往返运动过程可划分为匀加速阶段［0，t1］ ［t5，t6］、匀速阶段［t1，t2］ ［t4，t5］和匀减速阶段［t2，t4］，如图6所示。

图6中：Send为往返运动最大位移；Vmax、Vmin分别为最大速度和最小速度；Amax、Amin分别为最大加速度、最小加速度。

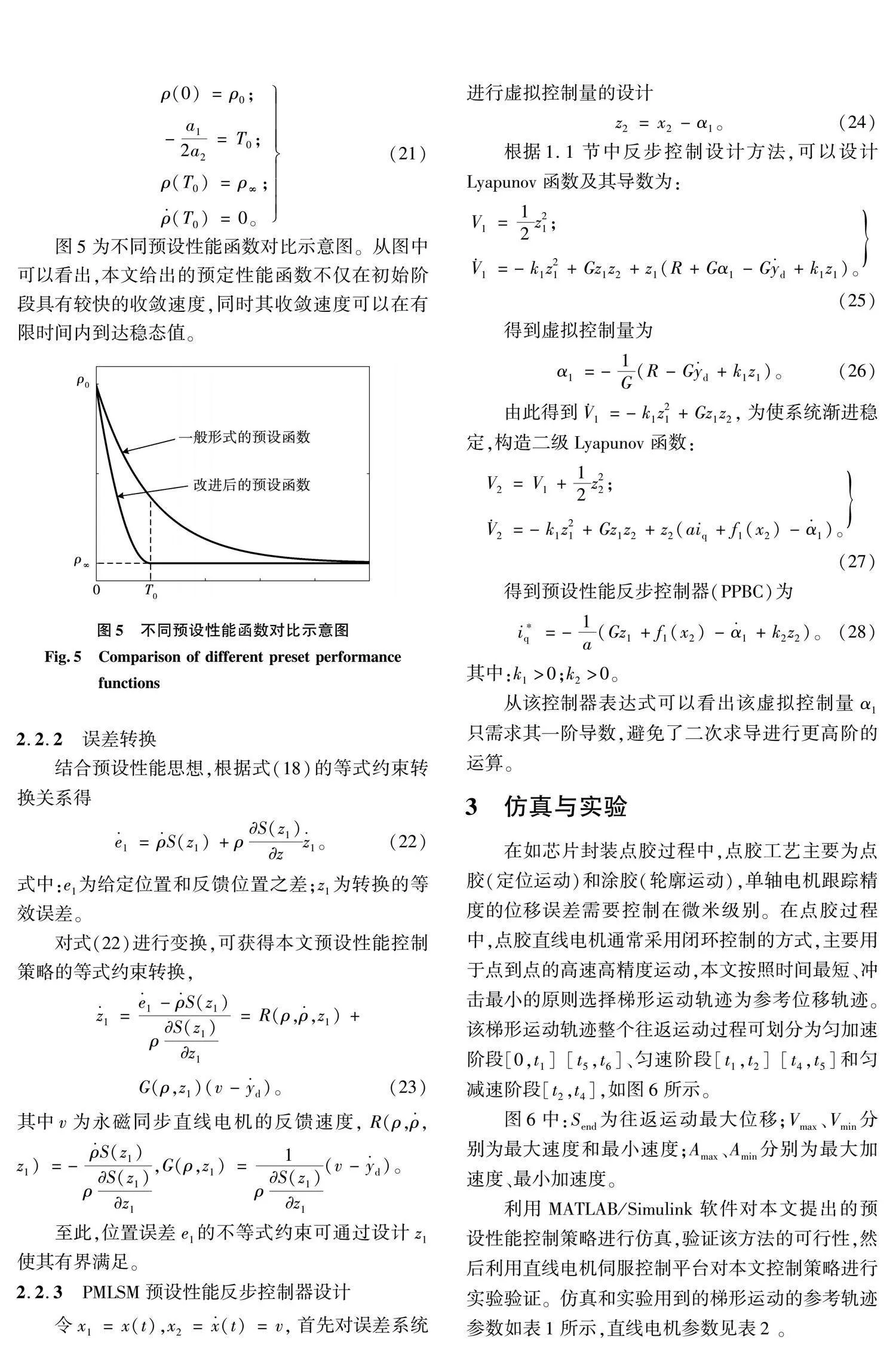
利用MATLAB/Simulink软件对本文提出的预设性能控制策略进行仿真，验证该方法的可行性，然后利用直线电机伺服控制平台对本文控制策略进行实验验证。仿真和实验用到的梯形运动的参考轨迹参数如表1所示，直线电机参数见表2 。

3.1 仿真结果

实际点胶工艺测试中的直线电机伺服系统电流环集成于驱动器中。为验证提出方法的可行性，预设性能反步控制PPBC、传统反步控制BSC策略均保留PI电流环，对图2、图4的控制方法进行仿真验证。

电流环的参数设计考虑环路带宽设计指标，均设计为Kp=330，Ki=1 476，主要优化目标为位移误差均方根值最小和最大误差最小。以优化目标为主导，PI策略中，速度控制器的Kp=255、Ki=800，位置控制器的Kp =250；BSC策略根据式（15）设置的控制参数k1=550，k2=2 500；PPBC策略根据式（26）和式（28）设置的控制参数k1=250，k2=850。预设性能函数PPF参数设计为a0=0.001，a1=-0.099，a2=2.475，最终收敛的误差带设置为10 μm，转换函数中上下限分别设置为10-6和10-7。

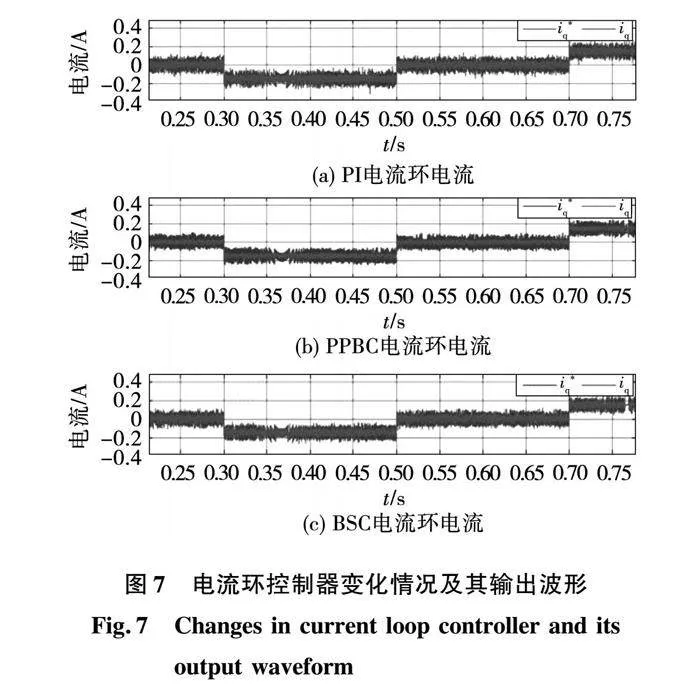
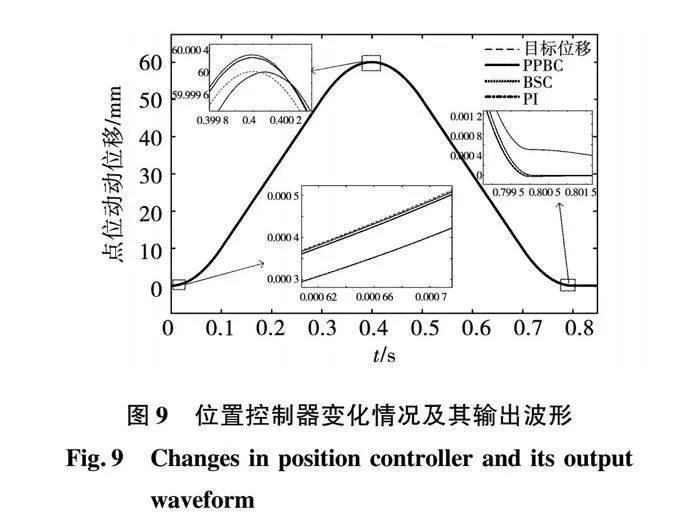
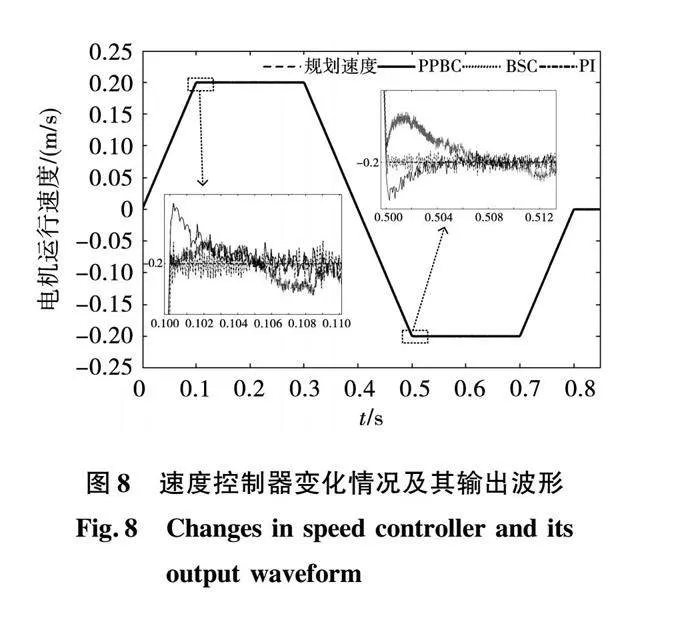
图7、图8、图9分别是三种控制方法在表1轨迹1下电流环控制器的变化情况及其输出波形，位置控制器参数的变化情况及其输出波形、以及速度控制器参数的变化情况及其输出波形。

图7、图8、图9从速度、位移的跟随效果上证明所提策略的可行性。图7中i*q为电流环输入，iq为电流反馈值。图8表明，在加速度变化时，BSC和PPBC的波动较大，尤其是0.1 s和0.5 s前后，但是PPBC在速度突变后，相比于BSC算法可以快速调节稳定，而BSC算法稳定的时间较长；图9给出了跟随效果示意图，启动阶段，相比于PI控制，PPBC和BSC有更快的响应速度和更好的跟随效果，但是在0.8 s运动结束时，BSC有较大的误差，PPBC总体上效果最好，满足定位精度的要求。

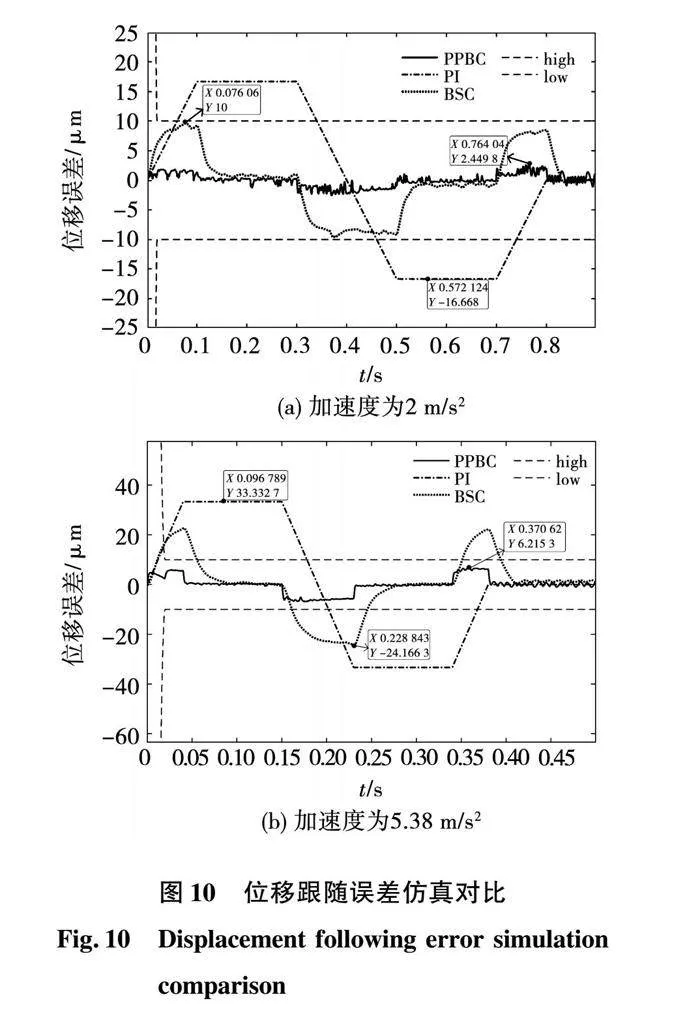
此外，由于电机跟随效果能直观地体现在位移误差上，为验证不同条件下三种策略的可行性，根据表1给出的轨迹规划对三种策略从位移误差的方面进一步进行仿真分析，其仿真结果如图10所示。

图10为不同参考轨迹下三种控制策略的位移误差仿真对比。从图10（a）中可以看出，在a=2 m/s2时，PPBC策略的最大位移误差为2.45 μm；BSC策略的位移误差曲线与加速度曲线呈明显的正相关，最大位移误差为10 μm；传统二自由度PI策略最大位移误差为16.67 μm，高于其余两种策略的位移误差。从图10（b）中可以看出，在a=5.38 m/s2时，PPBC策略的最大位移误差为6.22 μm；BSC策略最大位移误差为24.17 μm；PI策略最大位移误差为33.33 μm；PPBC降低位移误差的效果远优于BSC和PI控制，仿真验证了在不同速度下PPBC策略在降低位移误差方面的可行性。

3.2 实验结果

在3.1仿真的基础上，采用表1给出的轨迹进行不同加速度下的实验，对比预设性能反步控制PPBC、传统反步控制BSC以及传统PI控制策略的位移误差。

实验平台如图11所示，其中主要包括：永磁同步直线电机、驱动器、PowerPMAC控制器以及工控机等。通过工控机对电机进行操作，Power PMAC控制器进行控制程序的编写，同时发出指令信号给驱动器，驱动器驱动电机进行运动，电机运动的同时微米级光栅尺实时准确地把运动电机轴的位置等信号反馈给运动控制系统，继而对与给定位移进行比较后得到的位移误差进行约束控制。

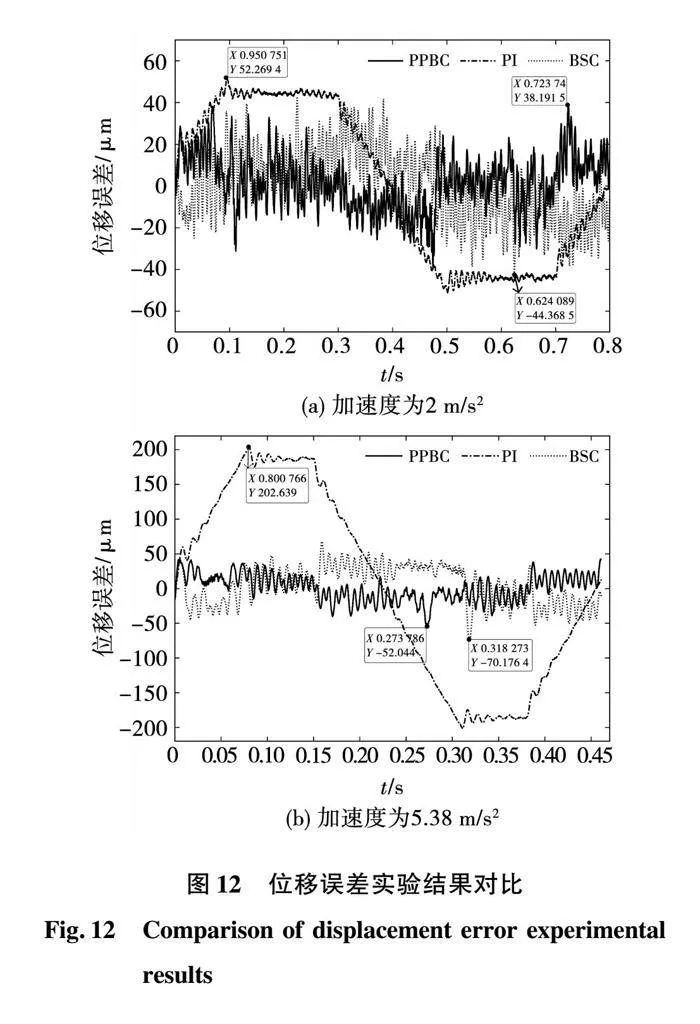
实验参数在仿真参数的基础上，主要以位移误差均方根值最小和最大误差最小为优化目标进行调整，位移误差由实验平台运算后得到其均方根值。最终实验参数为：BSC控制策略的控制参数k1=575，k2=2 850；PPBC控制策略的控制参数k1=250，k2=600。图12给出了不同参考轨迹下3种控制策略的位移误差实验对比。

从图12（a）可以看出，在a=2 m/s2时，PPBC策略的最大位移误差为38.19 μm；BSC策略最大位移误差为44.37 μm；传统二自由度PI策略最大位移误差为52.27 μm，高于其余两种策略的位移误差。从图12（b）可以看出，在a=5.38 m/s2时，PPBC策略的最大位移误差为52.04 μm；BSC策略最大位移误差为70.18 μm；传统二自由度PI策略最大位移误差为202.64 μm。实验证明，PPBC在低速运行条件下由于摩擦力的影响较大，相比于BSC策略，PPBC策略降低位移误差的优化效果不大，但在高加速度条件下，PPBC策略降低误差的能力有明显提升。此外，经测量三种算法在PMAC控制器中的运算时间差异极小，传统反步控制策略的计算时间比传统PI控制多了27%，引入预设性能的反步策略相对于传统反步控制的运算时间仅多了0.681%。

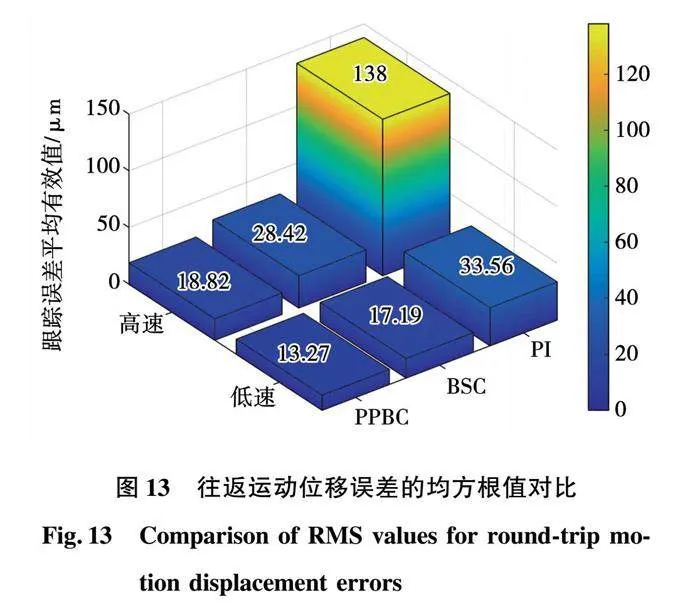
图13是三种控制策略位移误差的均方根值，可以直观看出PPBC高速和低速条件下能有效降低电机的位移误差。

从图13可以看出，在低速条件下，PPBC的误差均方根为13.27 μm，BSC为17.19 μm，PI为33.56 μm， PPBC相比BSC对误差降低的效果不明显，原因是低速条件下摩擦力对误差的影响较大；在高速条件下，PPBC的误差均方根为18.82 μm。BSC为28.42 μm，PI为138 μm，PPBC降低位移误差的能力好于PI控制和BSC控制，更具有鲁棒性。

4 结 论

针对非线性电机驱动控制系统位移误差收敛不确定的问题，提出了一种具有预设性能的反步控制方法。通过引入规定的性能函数和误差变换函数，可以定量地设计系统的暂态和稳态性能。与一般的预设性能函数相比，采用有限时间内收敛到稳态值的预设性能函数来约束直线电机的跟踪误差，不仅具有更快的收敛速度，还可以控制误差收敛的时间，从而快速收敛，有效降低电机的位移误差。

实验结果表明，在低加速条件下，PPBC相对于BSC、PI控制来说，误差分别降低了22.8%、60.46%；在高加速条件下，PPBC相对于BSC、PI控制来说，误差分别降低了33.78%、86.36%；所提出的策略能有效降低永磁同步直线电机电驱系统的位移误差，大大提高了系统的控制性能。

参 考 文 献：

［1］ 严乐阳，叶佩青，张勇，等.圆筒型永磁直线同步电机用线性霍尔位置检测的误差补偿［J］.电工技术学报， 2017， 32（5）：26.

YAN Leyang， YE Peiqing， ZHANG Yong， et al. Error compensation of linear hall based position detection for tubular permanent magnetic linear synchronous motor［J］. Transactions of China Electrotechnical Society， 2017， 32（5）： 26.

［2］ 王丽梅， 李兵. 直线电机驱动XY平台的速度场轨迹规划与控制研究［J］.中国电机工程学报， 2014， 34（3）： 438.

WANG Limei， LI Bing. Research on trajectory planning of contour control for a linear motor drive XY table based on velocity eld［J］. Proceedings of the CSEE， 2014， 34（3）： 438.

［3］ 林献坤， 张薇， 樊振华. 直线电机驱动进给轴热动态伪滞后建模与补偿方法研究［J］.机械工程学报， 2018（19）：7.

LIN Xiankun， ZHANG Wei， FAN Zhenhua. Thermal dynamic hysteresis modeling and compensation for linear motor driven feed mechanism［J］.Journal of Mechanical Engineering，2018（19）：7.

［4］ TING C S， CHANG Y N， SHI B W. Adaptive backstepping control for permanent magnet linear synchronous motor servo drive［J］. IET Electric Power Applications， 2015， 9（3）： 265.

［5］ 肖启明， 杨明， 刘可述， 等. PMSM伺服系统速度环PI控制器参数自整定及优化［J］.电机与控制学报， 2014， 18（2）：102.

XIAO Qiming， YANG Ming， LIU Keshu， et al. Parameter self-tuning and optimization of speed PI controller for PMSM servo system［J］. Electric Machines and Control， 2014， 18（2）： 102.

［6］ 禹聪， 康尔良. 永磁同步电机模糊滑模速度控制器设计［J］.电机与控制学报， 2022， 26（7）： 98.

YU Cong， KANG Erliang. Design of fuzzy sliding mode speed controller for permanent magnet synchronous motor［J］. Electric Machines and Control， 2022，26 （7）： 98.

［7］ 方馨， 王丽梅， 张康. 基于扰动观测器的永磁直线电机高阶非奇异快速终端滑模控制［J］. 电工技术学报， 2023， 38（2）： 409.

FANG Xin， WANG Limei， ZHANG Kang. High order nonsingular fast terminal sliding mode control of permanent magnet linear motor based on disturbance observer［J］. Transactions of China Electrotechnical Society， 2023， 38（2）： 409.

［8［ 曹阳， 郭健. 基于特征模型的永磁同步直线电机自适应控制［J］. 电机与控制学报， 2024， 28（3）： 131.

CAO Yang， GUO Jian.Adaptive control of permanent magnet synchronous linear motor based on characteristic model［J］. Electric Machines and Control， 2024， 28（3）： 131.

［9］ XU L，YAO B.Adaptive robust precision motion control of linear motors with negligible electrical dynamics： theory and experiments［J］.IEEE/ASME Transactions on Mechatronics，2001，6（4）：444.

［10］ 严乐阳， 叶佩青， 张辉， 等. 基于多周期迭代滑模控制的直线电机干扰抑制［J］. 电机与控制学报， 2017， 21（1）： 8．

YAN Yueyang， YE Peiqing， ZHANG Hui， et al. Disturbance rejection for linear motor based on multi-periodic learning variable structure control［J］. Electric Machines and Control， 2017， 21（1）：8.

［11］ 曹荣敏， 郑鑫鑫， 侯忠生. 基于改进多入多出无模型自适应控制的二维直线电机迭代学习控制［J］.电工技术学报， 2021，36（19）：4025.

CAO Rongmin， ZHENG Xinxin， HOU Zhongsheng. An iterative learning control based on improved multiple input and multiple output model free adaptive control for two-dimensional linear motor［J］. Transactions of China Electrotechnical Society， 2021， 36（19）： 4025.

［12］ KANELLAKOPOULOS I， KOKOTOVIC P V， MORSEA S. Systematic design of adaptive controllers for feedback linearizable systems［J］. IEEE Transactions on Automatic Control， 1991， 36（11）： 1241.

［13］ KANELLAKOPOULOS I， KREIN P T， DISILVESTROF. Nonlinear ux-observer-based control of induction motors［C］// 1992 American Control Conference， June 24-26，1992，Chicago，USA. 1992： 1700-1705.

［14］ 张庆超， 马瑞卿. 无刷直流电机转速伺服系统反步高阶滑模控制［J］. 控制与决策， 2016， 31（6）： 961.

ZHANG Qingchao， MA Ruiqing. Backstepping high order sliding mode control for brushless DC motor speed servo control system［J］. Control and Decision， 2016， 31（6）： 961.

［15］ HAMIDA M A， GLUMINEAU A， LEON J D. Robust integral backstepping control for sensorless IPM synchronous motor controller［J］. Journal of the Franklin Institute， 2012， 349（5）： 1734.

［16］ 纪志成， 李三东， 沈艳霞. 自适应积分反步法永磁同步电机伺服控制器的设计［J］. 控制与决策， 2005， 20（3）： 329.

JI Zhicheng， LI Sandong， SHEN Yanxia. Adaptive backstepping design for the servo controller of permanent magnet synchronous motor［J］. Control and Decision， 2005， 20（3）： 329.

［17］ 张康， 王丽梅. 基于周期性扰动学习的永磁直线电机自适应滑模位置控制［J］.电机与控制学报， 2021，25（8）： 132.

ZHANG Kang， WANG Limei. Adaptive sliding mode position control for permanent magnet linear motor based on periodic disturbance learning ［J］. Electric Machines and Control， 2021， 25（8）： 132.

［18］ BECHLIOULIS P C， ROVTHAKIS G A. Robust adaptive control of feedback lineaizable MIMO nonlinear systems with prescribed performance［J］. IEEE Transactions on Automatic Control， 2008， 53 （9）： 2090.

［19］ BECHLIOULIS P C， GEORGE A R. Adaptive control with guaranteed transient and steady state tracking error bounds for strict feedbacksystems［J］. Automatica， 2009， 45（2）： 532.

［20］ 王琦， 陈龙胜. 非仿射纯反馈不确定系统预设性能鲁棒自适应控制［J］. 电机与控制学报， 2017， 21（2）： 109.

WANG Qi， CHEN Longsheng. Prescribed performance adaptive robust control for a class of uncertain non-affine pure feedback system［J］. Electric Machines and Control， 2017， 21（2）： 109．

［21］ CHENG W， ZHANG K， JIANG B， et al. Fixed-time fault-tolerant formation control for heterogeneous multi-agent systems with parameter uncertainties and disturbances［J］. IEEE Transactions on Circuits and Systems I： Regular Papers， 2021： 1.

［22］ 王鹏飞， 王洁， 时建明， 等. 高超声速飞行器预设性能反演鲁棒控制［J］. 电机与控制学报， 2017， 21（2）： 94.

WANG Pengfei， WANG Jie， SHI Jianming， et al. Prescribed performance back-stepping robustness control of a exible hypersonic vehicle［J］. Electric Machines and Control， 2017， 21（2）： 94.

［23］ HUANG Y， NA J， WU X， et al. Adaptive control of nonlinear uncertain active suspension systems with prescribed performance［J］. ISA Transactions， 2015， 54（1）： 145 .

［24］ NA J， CHEN Q， REN X， et al. Adaptive prescribed performance motion control of servo mechanisms with friction compensation［J］. IEEE Transactions on Industrial Electronics， 2014， 61（1）： 486 .

［25］ 陈子印， 林喆， 贾鹤鸣， 等. 永磁同步电机有限时间预设性能控制［J］. 控制理论与应用， 2021， 38（4）： 479.

CHEN Ziyin， LIN Zhe， JIA Heming， et al. Finite-time control for permanent magnet synchronous motor with prescribed performance［J］. Control Theory amp; Applications， 2021， 38（4）： 479.

（编辑：刘素菊）