基于巴特沃斯结构的改进磁链观测器的永磁同步电机无位置传感器控制

摘 要：

由于逆变器非线性因素、电流测量误差等非理想因素，传统的磁链观测器会受到直流分量以及谐波分量的影响，导致转子位置观测准确度降低。将具有通频带最大限度平坦特性的巴特沃斯带通滤波器与纯积分器相结合构建出一种改进的磁链观测器，并对改进的磁链观测器的传递函数进行了详细的理论分析，然后设计出一种离散化结构以便进行实验。结果表明，提出的基于巴特沃斯结构的改进磁链观测器具有出色的消除直流分量以及抑制谐波分量能力，不会造成基波处的幅值衰减以及相位误差，提高了永磁同步电机无位置传感器控制的转子位置观测准确度，同时具有良好的动态性能。

关键词：永磁同步电机；无位置传感器控制；巴特沃斯带通滤波器；磁链观测器

DOI：10.15938/j.emc.2024.09.006

中图分类号：TM351

文献标志码：A

文章编号：1007-449X（2024）09-0060-10

收稿日期： 2023-12-13

基金项目：湖南省自然科学基金（2023JJ30133）

作者简介：骆正红（2000—），女，硕士研究生，研究方向为永磁同步电机控制；

胡亚山（1982—），男，博士，副教授，博士生导师，研究方向为电机驱动及其控制。

通信作者：胡亚山

Improved flux observer based on Butterworth filter for sensorless control of permanent magnet synchronous motor

LUO Zhenghong， HU Yashan

（College of Electrical and Information Engineering， Hunan University， Changsha 410082， China）

Abstract：

The conventional rotor flux observer is affected by the DC offset and harmonics of the back electromotive force caused by non-ideal conditions such as inverter nonlinearity and current measurement errors， which leads to a decrease in the accuracy of rotor position estimation. An improved flux observer was proposed by combining the Butterworth bandpass filter with the maximum flatness of the passband and the pure integrator， the transfer function of the proposed observer was analyzed theoretically， and its discretized structure was designed for experiments. The results show that the proposed observer has an excellent ability to eliminate the DC offset and suppress harmonics， and then extracts the fundamental flux without amplitude attenuation and phase shift， which improves accuracy of rotor position estimation for permanent magnet synchronous motor and has good dynamic performance.

Keywords：permanent magnet synchronous motor; sensorless control; Butterworth bandpass filter; flux observer

0 引 言

永磁同步电机因结构简单、运行效率高、功率密度大等优点被广泛应用于航空航天、数控机床、新能源汽车等领域［1-3］。永磁同步电机驱动系统需要实时获取转子位置信息，传统的转子位置信息获取方案是在电机上安装位置传感器。然而位置传感器的使用不仅增加了系统体积和成本，同时还存在安装维护困难、连接线路复杂、易受干扰等问题，降低了系统的可靠性。为了节省成本，提高系统的可靠性，永磁同步电机无位置传感器控制技术在近年来得到了广泛研究［4］。

永磁同步电机无位置传感器技术主要包括基于电机凸极性的高频注入法［5-6］以及基于电机基波模型的反电势法［7-9］和磁链观测法［11-16］。其中，高频注入法主要应用在零低速域，反电势法和磁链观测法主要应用在中高速域。在传统的磁链观测法［11-16］中，首先通过电压模型计算反电动势，然后对反电动势进行积分得到转子磁链，进而得到转子位置信息。然而计算出的反电动势容易受到逆变器非线性因素、电机磁场空间谐波、电流测量误差等因素影响，导致计算出的反电动势中存在直流分量以及谐波分量［10］。因此，传统的由纯积分器构成的磁链观测器会产生未知积分初值、零漂以及积分器饱和等问题，从而导致无法准确地观测出转子磁链。

在实际应用中，通常采用低通滤波器代替纯积分器来解决零漂和积分器饱和引起的问题，然而引入低通滤波器会导致基波幅值衰减以及相位误差，从而导致转子位置估计误差。大量学者研究了针对低通滤波器的补偿策略，文献［11］提出一种可编程的低通滤波器，避免了幅值衰减以及相位误差，然而该方法需要通过除以电机角频率的方式来修正磁链幅值，导致该方法的精度高度依赖于速度的估计精度，同时可能会造成低速范围内的不稳定。文献［12］提出一种级联高通滤波器、积分器、低通滤波器的磁链观测器，该方法的信号处理过程过于复杂，并且只能在一定程度上减小低通滤波器导致的幅值衰减以及相位误差。

除了改进低通滤波器之外，自适应补偿的方法也得到了大量的研究。文献［13］提出一种具有自适应补偿的磁链观测器，采用PI调节器将观测出的磁链中的直流分量以及谐波分量反馈到磁链观测器的输入端，以达到抑制直流分量以及谐波分量的目的，然而该方法无法有效权衡谐波抑制能力和动态响应。文献［14］提出一种基于PI调节器的相位自整定的磁链观测器，该文章主要考虑了参数失配情况下的相位补偿，没有考虑直流分量和谐波分量的影响。

温度升高以及AD采样校正不准确等问题引起的电流测量误差会导致采样电流中出现直流分量［15］。同时，采样电流中的直流分量经过矢量控制和死区补偿后会导致逆变器的指令电压中出现相应的直流分量［16］。逆变器非线性因素、电机磁场空间谐波等因素会导致电流以及电压中出现高次谐波，尤其是五、七次谐波。电流电压中存在的直流分量以及谐波分量会严重影响到磁链观测器的转子位置观测准确度。针对直流分量和谐波分量的影响，目前的大量研究转向了同时具有抑制直流分量和谐波分量功能的磁链观测器，文献［17］和文献［18］提出了用二阶广义积分器（second-order generalized integrator，SOGI）来估计转子磁链，文献［19］提出一种频率自适应的转子磁链观测器。这些观测器具有较好地抑制谐波分量的效果和一定程度上抑制直流分量的能力，然而，这些方法并不能完全消除直流分量的影响。

为了进一步提高磁链观测器对直流分量以及谐波分量的抗干扰能力，本文采用具有通频带最大限度平坦特性的巴特沃斯带通滤波器与积分器结合构建出改进的磁链观测器，具有频率自适应的效果，可以实现完全消除直流分量，抑制谐波分量的同时提取出基波磁链，不会产生幅值衰减以及相位误差。

本文对提出的基于巴特沃斯结构的改进磁链观测器的传递函数进行详细的理论分析，并且提出改进磁链观测器的离散化结构，最终在实验平台进行验证，实验结果证明提出的基于巴特沃斯结构的磁链观测器具有良好地消除直流分量以及抑制谐波分量的能力，可以提高永磁同步电机无位置传感器控制的转子位置观测准确度，同时具有良好的动态性能。

1 传统的磁链观测器

对于内置式永磁同步电机，采用有效磁链模型［20］，则αβ轴的电压方程可表示为

uαβ=Riαβ+pLqiαβ+pψat。（1）

式中：uαβ=［uα uβ］T表示αβ轴的定子电压矢量；iαβ=［iα iβ］T表示αβ轴的定子电流矢量；p表示微分算子；R表示定子电阻；Lq表示q轴电感；ψat=［ψat_α" ψat_β］T定义为αβ轴的有效磁链矢量，可表示为

ψat=［ψf+（Ld－Lq）id］cosθesinθe。（2）

式中：ψf表示永磁体磁链；Ld表示d轴电感；id表示d轴定子电流；θe表示转子电角度。

根据式（2）可知，只要观测出αβ轴的有效磁链矢量，即可得到转子位置信息。

式（1）可以改写成

ψat=∫（uαβ－Riαβ－pLqiαβ）dt=∫eatdt。（3）

式中eat=［eat_α" eat_β］T，定义为αβ轴的有效反电动势矢量。

根据式（3）可知，对计算出的有效反电动势进行积分即可得到有效磁链。然而，由于各种非理想条件的存在，比如：电流采样误差、逆变器非线性因素、电机磁场空间谐波等，最终会导致计算出的有效反电动势中除了基波分量还存在直流分量以及谐波分量［15-16］。因此，以β轴为例，计算出的有效反电动势可以表示为

eat_β=E0+E1sin（ω1t+φ1）+∑∞n=2Ensin（ωnt+φn）。（4）

式中：n表示谐波分量的阶数；E0、E1、En、φ1、φn分别表示β轴的有效反电动势的直流分量的幅值、基波分量以及谐波分量的幅值和初始相位角；ω1、ωn分别表示基波分量以及谐波分量的电角频率，满足ωn=nω1。

将式（4）进行拉普拉斯变换即可得到s域中β轴的有效反电动势的表达式为

Eat_β（s）=E0s+E1ssinφ1+ω1cosφ1s2+ω21+

∑∞n=2Enssinφn+ωncosφns2+ω2n。（5）

式中s表示拉普拉斯算子。

传统的磁链观测器采用纯积分器的形式，将计算出的有效反电动势通过一个纯积分器得到有效磁链。显然，这种磁链观测器同时对有效反电动势中多余的直流分量以及谐波分量进行了积分，会导致观测出的有效磁链中同样存在直流分量以及谐波分量，进而导致转子位置观测不准的问题。因此，在此基础上存在两种普遍的改进，一种是将纯积分器改为一阶低通滤波器，另一种是将纯积分器改为二阶广义积分器。下面对典型的几种磁链观测器分别进行分析。

1.1 纯积分器

由纯积分器构成的磁链观测器可以描述为

ψat_I（s）=1sEat（s）。（6）

式中：ψat_I（s）=［ψat_Iα（s） ψat_Iβ（s）］T表示纯积分器观测出的有效磁链矢量的拉普拉斯变换形式；Eat（s）表示eat的拉普拉斯变换形式。

以β轴为例，纯积分器观测出的有效磁链可以描述为

ψat_Iβ（s）=1sEat_β（s）。（7）

将式（5）代入式（7）中，然后进行拉普拉斯反变换，可以得到纯积分器构成的磁链观测器在时域中观测出的β轴的有效磁链为

ψat_Iβ=E0t+E1cosφ1ω1+E1ω1sin（ω1t+φ1－π/2）+

∑∞n=2［Encosφnωn+Enωnsin（ωnt+φn－π/2）］。（8）

根据式（8）可知，观测到的有效磁链中存在谐波分量，这会导致转子位置观测误差的出现。除此之外，观测到的有效磁链中存在随着时间持续增大的直流分量E0t，这会导致磁链观测器出现积分饱和的问题，最终导致转子位置观测失败。因此，由纯积分器构成的磁链观测器难以应用，实际应用中通常采用一阶低通滤波器代替纯积分器来解决积分饱和问题。

1.2 一阶低通滤波器

由一阶低通滤波器构成的磁链观测器可以描述为

ψat_LPF（s）=1s+ωcEat（s）。（9）

式中：ψat_LPF（s）=［ψat_LPFα（s） ψat_LPFβ（s）］T表示一阶低通滤波器观测出的有效磁链矢量的拉普拉斯变换形式；ωc表示截止频率。

以β轴为例，一阶低通滤波器观测出的有效磁链可以描述为

ψat_LPFβ（s）=1s+ωcEat_β（s）。（10）

将式（5）代入式（10）中，然后进行拉普拉斯反变换，可以得到时域中观测出的β轴的有效磁链为

ψat_LPFβ=E0ωc－E0ωce－ωct+E1cos（φ1+γ1）ω21+ω2ce－ωct+

∑∞n=2Encos（φn+γn）ω2n+ω2ce－ωct+

E1ω21+ω2csin（ω1t+φ1+γ1－π/2）+

∑∞n=2Enω2n+ω2csin（ωnt+φn+γn－π/2）。（11）

式中：γ1=arctan（ωc/ω1）；γn=arctan（ωc/ωn）。

根据式（11）可知，观测到的有效磁链中的直流分量最终为E0/ωc，直流分量和谐波分量的幅值在一定程度上都存在衰减。积分器饱和的问题得到了解决，然而直流分量和谐波分量的存在仍然会导致转子位置观测误差。除此之外，基波分量产生了幅值衰减以及相位偏差，因此由一阶低通滤波器构成的磁链观测器在实际应用中必须采用相应的补偿策略。

1.3 二阶广义积分器

由二阶广义积分器构成的磁链观测器可以描述为

ψat_SOGI（s）=kω0s2+kω0s+ω20Eat（s）。（12）

式中：ψat_SOGI（s）=［ψat_SOGIα（s） ψat_SOGIβ（s）］T表示二阶广义积分器观测出的有效磁链矢量的拉普拉斯变换形式；ω0表示二阶广义积分器的中心频率；k表示带宽调整系数。

假设二阶广义积分器的中心频率等于电机基波频率，即ω0=ω1，则二阶广义积分器观测出的β轴的有效磁链可以描述为

ψat_SOGIβ（s）=kω1s2+kω1s+ω21Eat_β（s）。（13）

将式（5）代入式（13）中，然后进行拉普拉斯反变换，可以得到时域中观测出的β轴的有效磁链［17］为

ψat_SOGIβ=kE0ω1+E1ω1sin（ω1t+φ1－π/2）+∑∞n=2Enωn（1－n2）2/k2n2+1sin（ωnt+φn+γn1）。（14）

式中γn1=arctan［nk/（n2-1）］。

根据式（14）可知，观测到的有效磁链中的直流分量和谐波分量都存在一定程度上的幅值衰减，同时保证了基波分量无相位误差以及幅值衰减。然而，直流分量的存在仍然会导致转子位置观测误差。

经过以上对3种磁链观测器的分析，发现直流分量的有效消除仍然是有待解决的问题。满足消除直流分量、抑制谐波分量的同时保证基波分量无相位偏差以及幅值衰减是本文磁链观测器的设计目标。

2 基于巴特沃斯结构的改进磁链观测器

经过1.3节中的分析可知，传统的磁链观测器并未有效地解决直流分量的问题，仍有改进的空间。本文采用具有通带最大限度平坦特性的巴特沃斯带通滤波器与纯积分器结合构建出改进磁链观测器。本节中，首先，设计了基于巴特沃斯结构的改进磁链观测器的传递函数，其次，分析了基于巴特沃斯结构的改进磁链观测器对直流分量以及高次谐波的抑制效果，最后，提出了基于巴特沃斯结构的改进磁链观测器的离散化结构。

2.1 基于巴特沃斯结构的改进磁链观测器

巴特沃斯滤波器又称最平幅度特性滤波器［21］，具有在通频带内的幅频特性曲线最大限度平坦，阻频带内逐渐下降为0的特性，被广泛应用于通信系统、图像处理以及生物医学工程等领域。为了满足磁链观测器消除直流分量的设计要求，本文选用四阶巴特沃斯带通滤波器进行磁链观测器的设计。

四阶巴特沃斯带通滤波器的传递函数为

GFBPF（s）=ω2cs2s4+Cωcs3+（2ω20+ω2c）s2+Cωcω20s+ω40。（15）

式中：C=1.414 2；ω0表示中心频率，在应用中为电机的估计角速度；ωc表示带宽，在实验中采用ωc=Kω0，K用来控制带宽。

当中心频率为50 Hz，K取不同值时，巴特沃斯带通滤波器随带宽ωc变化时的伯德图如图1所示。当K为1时，巴特沃斯带通滤波器随中心频率变化时的伯德图如图2所示。

由图1可知，随着带宽的增大，巴特沃斯带通滤波器的通带更加平坦，同时阻带衰减速率减小。由图2可知，巴特沃斯带通滤波器在不同中心频率处表现出相似的频率特性，在实验中可以应用于电机频率连续变化的工况，实现频率自适应的带通滤波效果。

将巴特沃斯带通滤波器与纯积分器结合即可得到本文提出的基于巴特沃斯结构的改进磁链观测器为

ψat_BTWS（s）=GBTWS（s）Eat（s）。（16）

式中：ψat_BTWS（s）=［ψat_BTWSα（s） ψat_BTWSβ（s）］T表示基于巴特沃斯结构的改进磁链观测器观测出的有效磁链矢量的拉普拉斯变换形式；GBTWS（s）表示基于巴特沃斯结构的改进磁链观测器的传递函数，可表示为

GBTWS（s）=GFBPF（s）1s=ω2css4+Cωcs3+（2ω20+ω2c）s2+Cωcω20s+ω40。（17）

当s=jω0时，式（17）可以化简为

GBTWS（s）=1s。（18）

根据式（18）可知，本文提出的基于巴特沃斯结构的改进磁链观测器可以实现纯积分器的功能，因此可以观测出有效磁链，进而得到转子位置信息。

2.2 巴特沃斯磁链观测器性能分析

假设本文提出的基于巴特沃斯结构的改进磁链观测器的中心频率等于电机基波频率，即ω0=ω1，则式（17）可改写为

GBTWS（s）=ω2css4+Cωcs3+（2ω21+ω2c）s2+Cωcω21s+ω41。（19）

以β轴为例，基于巴特沃斯结构的改进磁链观测器观测出的有效磁链可以描述为

ψat_BTWSβ（s）=GBTWS（s）Eat_β（s）。（20）

对于基波分量，将s=jω1代入式（19）中可得

ω2css4+Cωcs3+（2ω21+ω2c）s2+Cωcω21s+ω41=1jω1=1ω1∠－π2。（21）

由式（4）可知，时域中的β轴的有效反电动势基波分量为E1sin（ω1t+φ1），结合式（21）可得，时域中观测出的β轴的有效磁链中的基波分量为

ψat_BTWSβ_f=E1ω1sin（ω1t+φ1－π/2）。（22）

对于直流分量，结合式（5）、式（19）和式（20），采用终值定理，得到时域中观测出的β轴的有效磁链中的直流分量为

lims→0s·ω2css4+Cωcs3+（2ω21+ω2c）s2+Cωcω21s+ω41E0s=0。（23）

对于谐波分量，将s=jωn=njω1和ωc=Kω1代入式（19）中可得

ω2css4+Cωcs3+（2ω20+ω2c）s2+Cωcω21s+ω41=∠γn2ωn［n4－K2n2－2n2+1］2+（CnK－Cn3K）2n4K2。（24）

式中γn2=arctan［（n4-K2n2-2n2+1）/（CnK-Cn3K）］。

由式（4）可知，时域中的β轴的有效反电动势谐波分量为Ensin（ωnt+φn），结合式（24）可得，时域中观测出的β轴的有效磁链中的谐波分量为

ψat_BTWSβ_n=∑∞n=2Ensin（ωnt+φn+γn2）［n4－K2n2－2n2+1］2+（CnK－Cn3K）2n4K2ω2n。（25）

综合以上分析，可得时域中观测出的β轴的有效磁链为

ψat_BTWSβ=E1ω1sin（ω1t+φ1－π/2）+∑∞n=2Ensin（ωnt+φn+γn2）［n4－K2n2－2n2+1］2+（CnK－Cn3K）2n4K2ω2n。（26）

根据式（26）可知，观测出的有效磁链中，直流分量被完全消除，基波分量无幅值衰减以及相位偏差，同时谐波分量也得到了很好地抑制，满足磁链观测器的设计要求。

为了更加直观地比较本文所分析的4种磁链观测器的效果，画出4种磁链观测器的伯德图如图3所示。由于磁链观测器在中心频率处的增益为1/ω0，为了伯德图的效果更加直观，将磁链观测器的传递函数乘以系数ω0后再画出伯德图。图3中，中心频率为50 Hz，一阶低通滤波器的截止频率ωc为10 Hz，二阶广义积分器的带宽调整系数k为2，基于巴特沃斯结构的改进磁链观测器的带宽参数K为2，带宽ωc为100 Hz。

根据图3可以直观地得到4种磁链观测器的对比。纯积分器的直流分量具有很高的增益，进而导致积分饱和的问题。一阶低通滤波器可以在一定程度上衰减直流分量以及谐波分量，但是在基波处存在幅值衰减和相位偏差。二阶广义积分器可以衰减直流分量以及谐波分量，同时在基波处不会产生幅值衰减和相位偏差，然而他不能有效地消除直流分量。最后，本文提出的基于巴特沃斯结构的改进磁链观测器可以在消除直流分量的同时抑制谐波分量，并且实现在中心频率处无幅值衰减和相位偏差。

2.3 离散化结构

本文采用双线性变换法对提出的基于巴特沃斯结构的改进磁链观测器进行离散化处理。将s=2（1-z-1）/Ts（1+z-1）代入式（17）中可以得到离散化公式为

根据式（27）和式（28）可以设计出基于巴特沃斯结构的改进磁链观测器的离散化结构，如图4所示。

3 实验结果

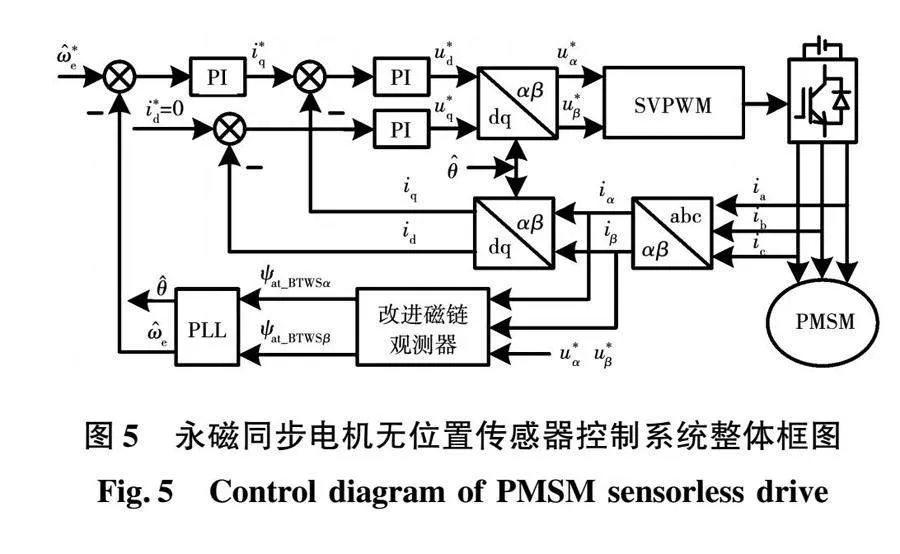
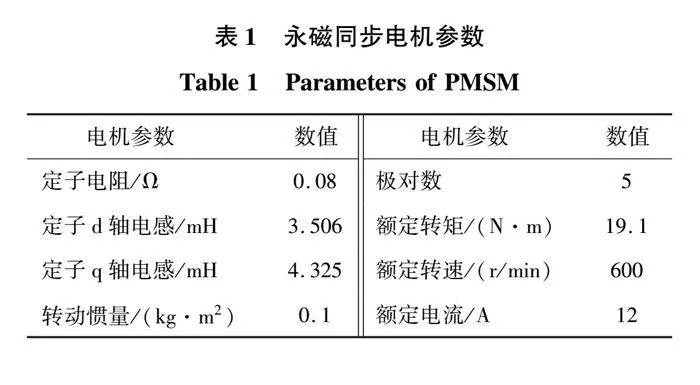
永磁同步电机无位置传感器控制系统整体框图如图5所示。为了验证本文提出的基于巴特沃斯结构的改进磁链观测器的效果，在图6所示的1.2 kW永磁同步电机驱动控制实验平台进行实验验证。实验平台由1.2 kW永磁同步电机、逆变器、直流电源、示波器等组成。永磁同步电机的参数如表1所示。实验平台采用TMS320F28335作为主控芯片，IGBT开关频率设置为5 kHz。采用旋转变压器来获取实际的转子位置和速度信息，用于启动电机，启动后切换到无位置传感器控制运行，此时实际的转子位置和速度信息用于与无位置传感器控制估计出的转子位置和速度信息进行比较。由于纯积分器存在积分饱和的问题，因此本文只对传统的一阶低通滤波器、二阶广义积分器构成的磁链观测器以及基于巴特沃斯结构的改进磁链观测器进行实验比较。磁链观测器的带宽选择要考虑在估计的基波频率波动的情况下，同时能够有效抑制DC和五、七次谐波，实验中磁链观测器的参数选择与图3相同，控制系统中的锁相环PLL按典型的二阶系统来设计［8］。

3.1 稳态实验

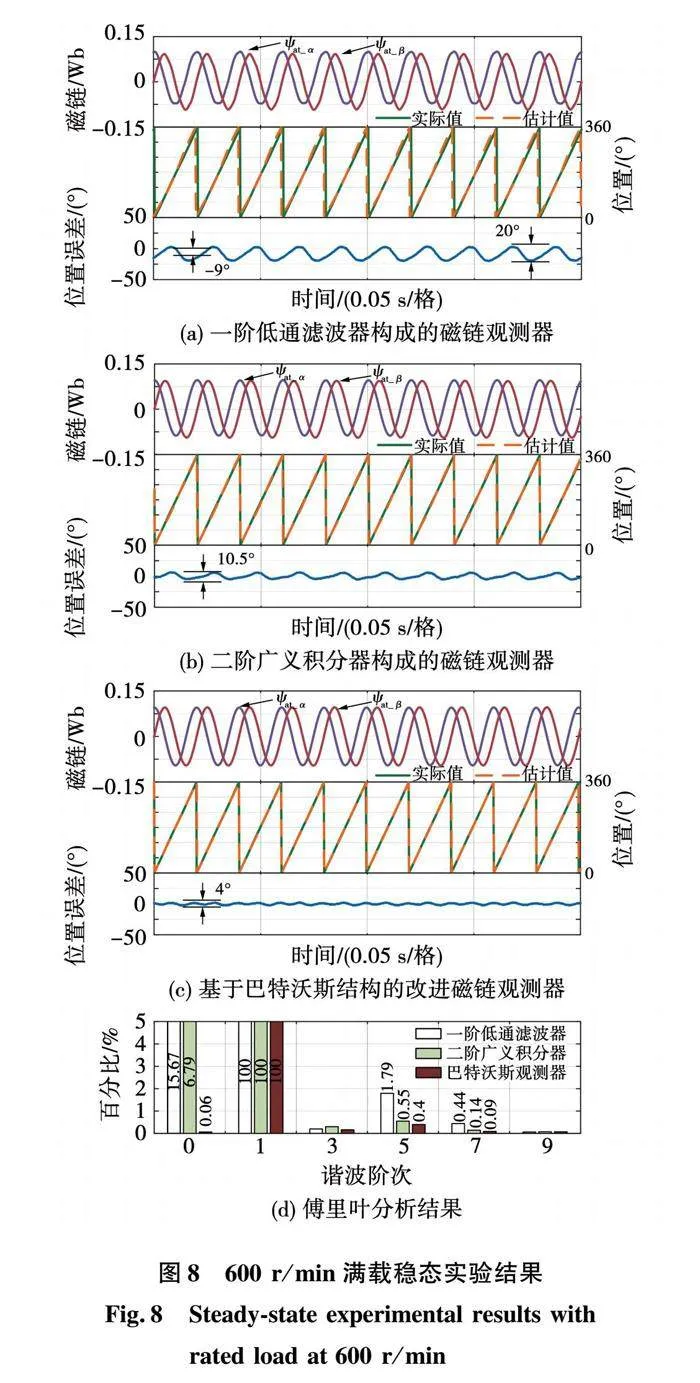
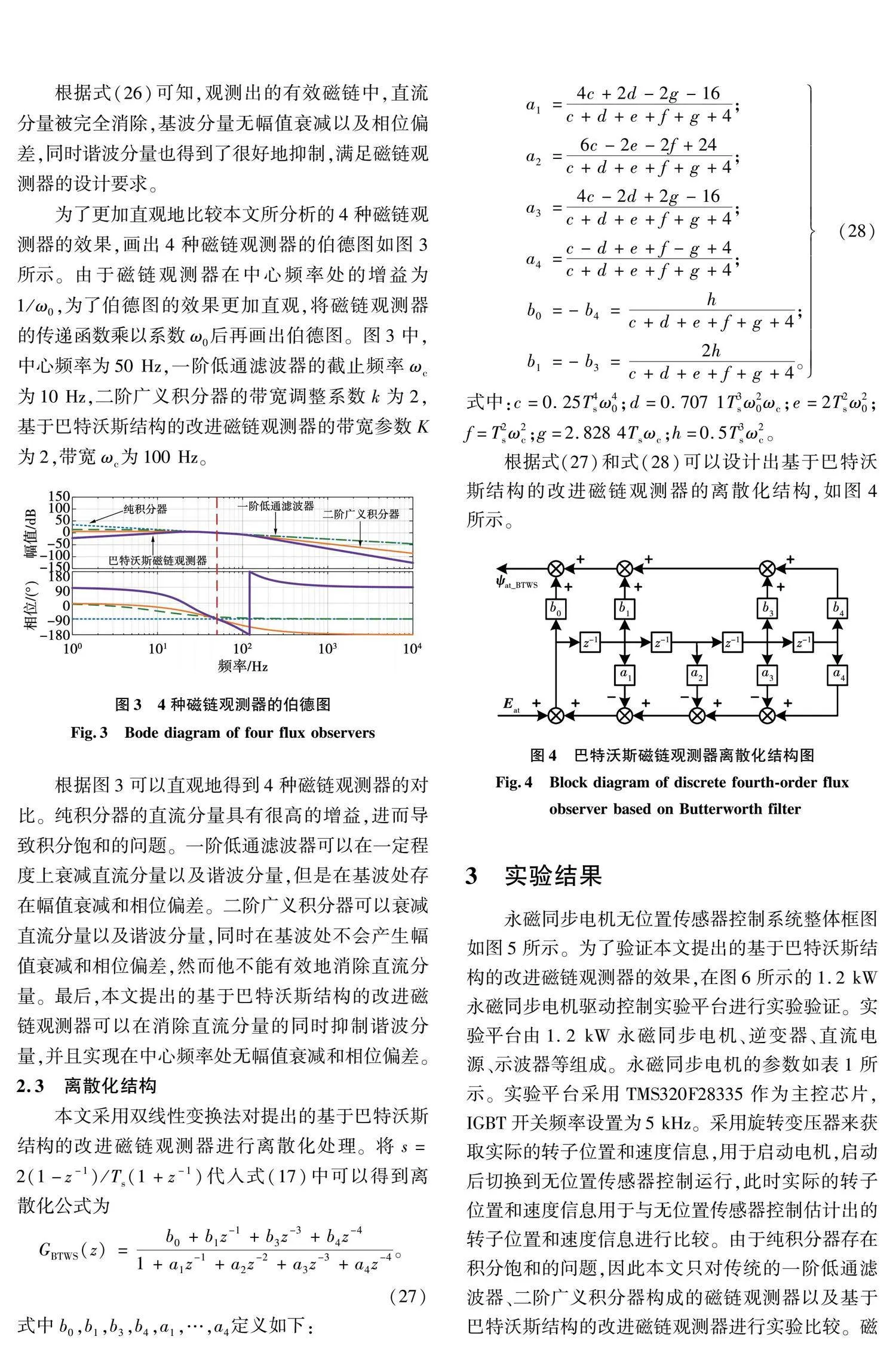
本节中，对传统的一阶低通滤波器、二阶广义积分器构成的磁链观测器以及本文提出的基于巴特沃斯结构的改进磁链观测器的稳态性能进行比较。由于温度升高以及AD采样校正不准确等问题最终会导致逆变器的指令电压中出现相应的直流分量，因此，为了比较3种磁链观测器对直流分量的抑制能力，在计算磁链时人为在α轴添加1 V的直流电压。图7和图8分别给出了3种磁链观测器在150 r/min半载条件下以及600 r/min满载条件下估计出的有效磁链、转子位置、转子位置误差的实验结果以及估计出的α轴有效磁链的傅里叶分析结果。

在受直流分量影响方面，由图7（d）可知，3种磁链观测器在150 r/min半载条件下估计出的α轴有效磁链中直流分量的含量分别为21.1%、22.6%和0.08%。将实验所选参数代入式（11）和式（14）并对比可知，在电机转速为150 r/min时，一阶低通滤波器构成的磁链观测器抑制直流分量的能力比二阶广义积分器构成的磁链观测器稍强，实验结果与公式相符。由直流分量的含量对比可知，在150 r/min半载条件下，一阶低通滤波器以及二阶广义积分器构成的磁链观测器受直流分量影响较大，而本文提出的基于巴特沃斯结构的改进磁链观测器几乎不受直流分量影响。在600 r/min满载条件下，如图8（d）所示的3种磁链观测器估计出的α轴有效磁链中直流分量的含量分别为15.67%、6.79%和0.06%，一阶低通滤波器构成的磁链观测器受直流分量影响最大，本文提出的基于巴特沃斯结构的改进磁链观测器受直流分量影响最小，仅为0.06%，符合图3的理论分析结果。

在受高次谐波影响方面，由图7（d）可知，3种磁链观测器在150 r/min半载条件下估计出的α轴有效磁链中五次谐波的含量分别为0.87%、0.33%和0.09%，七次谐波的含量分别为0.56%、0.15%和0.02%。由图8（d）可知，3种磁链观测器在600 r/min满载条件下估计出的α轴有效磁链中五次谐波的含量分别为1.79%、0.55%和0.4%，七次谐波的含量分别为0.44%、0.14%和0.09%。显然，相比较而言，在负载条件下，一阶低通滤波器构成的磁链观测器受谐波分量影响最大，本文提出的基于巴特沃斯结构的改进磁链观测器受谐波分量影响最小，符合图3的理论分析结果。

在转子位置误差方面，估计出的α轴有效磁链中的直流分量和谐波分量会影响转子位置观测，最终导致转子位置观测误差。由图7（a）、（b）和（c）可知，3种磁链观测器在150 r/min半载条件下的转子位置估计误差峰峰值分别是29°、34°和4.6°，一阶低通滤波器、二阶广义积分器构成的磁链观测器受直流分量以及谐波分量的影响较大，导致转子位置估计误差峰峰值较大，本文提出的基于巴特沃斯结构的改进磁链观测器受直流分量以及谐波分量的影响最小，转子位置估计误差峰峰值最小。在600 r/min满载条件下，如图8（a）、（b）和（c）所示，3种磁链观测器的转子位置估计误差峰峰值分别是20°、10.5°和4°，一阶低通滤波器构成的磁链观测器受直流分量以及谐波分量的影响最大，导致转子位置估计误差峰峰值最大，而本文提出的基于巴特沃斯结构的改进磁链观测器可以有效地抑制直流分量以及谐波分量，几乎不受直流分量以及谐波分量的影响，转子位置估计误差峰峰值最小。

值得注意的是，如图7（a）和图8（a）所示，一阶低通滤波器构成的磁链观测器在150 r/min和600 r/min时估计出的转子位置分别存在40°和9°的稳态误差。由式（11）中γ1的表达式可知，随着电机运行频率的升高，一阶低通滤波器产生的相位误差减小，因此转子位置估计稳态误差减小，实验结果与公式相符。由图7（b）、（c）和图8（b）、（c）可知，二阶广义积分器构成的磁链观测器以及本文提出的基于巴特沃斯结构的改进磁链观测器估计出的转子位置不存在稳态误差，说明观测器对基波信号不产生相位偏移误差，同时也体现了频率自适应的效果。

综上所述，对比3种磁链观测器的效果可知，在稳态时，本文提出的基于巴特沃斯结构的改进磁链观测器消除直流分量和抑制谐波分量的效果最好，转子位置估计误差最小，同时在基波处不产生相位误差，可以实现频率自适应的效果。

3.2 动态实验

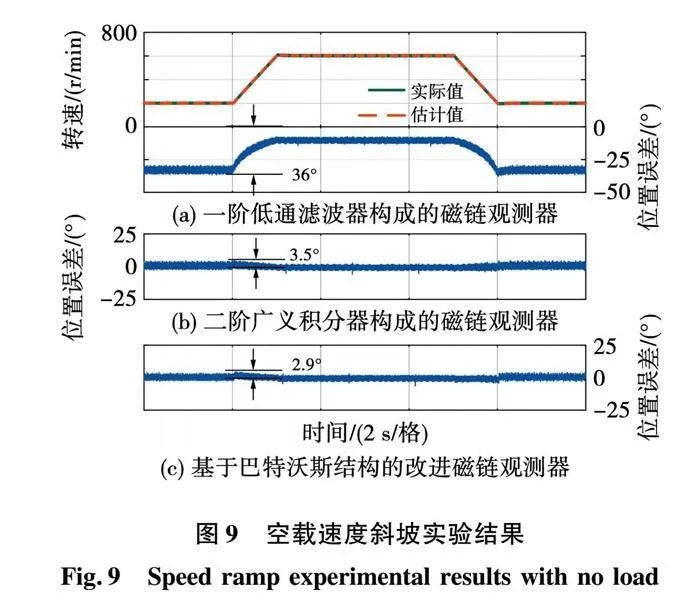
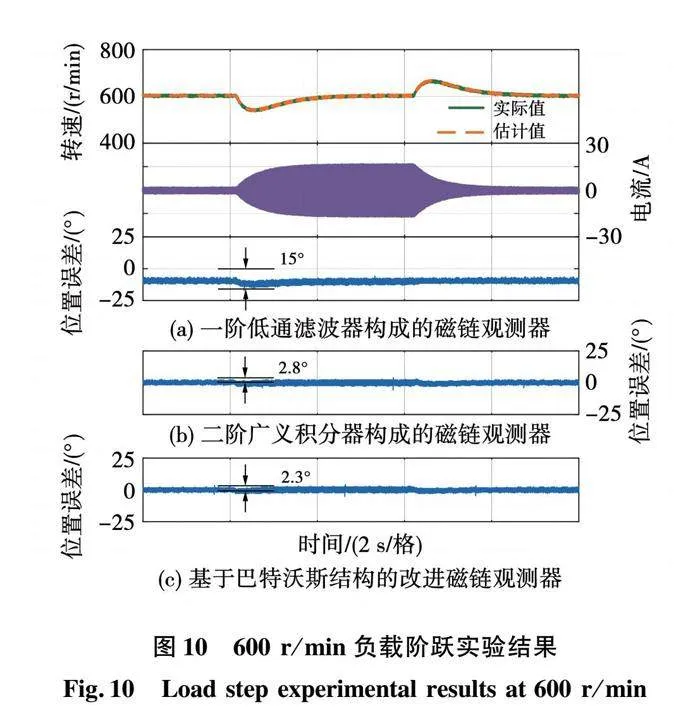
本节中，通过速度斜坡实验以及负载阶跃实验对3种磁链观测器的动态性能进行验证。图9给出了3种磁链观测器在空载条件下速度指令从200→600→200 r/min时的速度波形以及转子位置误差的实验结果。由于3种磁链观测器都能很好地估计出速度，因此速度波形未重复给出。图10给出了3种磁链观测器在600 r/min负载指令从空载到额定负载然后再返回空载时的速度波形、相电流波形以及转子位置误差的实验结果。由于3种磁链观测器都能很好的估计出速度，因此速度波形和相电流波形未重复给出。

由图9可知，3种磁链观测器的最大转子位置估计误差分别是36°、3.5°和2.9°。一阶低通滤波器构成的磁链观测器存在随速度升高而显著减小的稳态误差，二阶广义积分器构成的磁链观测器以及本文提出的基于巴特沃斯结构的改进磁链观测器不存在稳态误差，转子位置误差受速度影响较小。由图10可知，3种磁链观测器的最大转子位置估计误差分别是15°、2.8°和2.3°。一阶低通滤波器构成的磁链观测器存在稳态误差，并且随着负载增大而增大，二阶广义积分器构成的磁链观测器以及本文提出的基于巴特沃斯结构的改进磁链观测器不存在稳态误差，转子位置误差受负载影响较小。

综上所述，速度斜坡实验和负载阶跃实验证明了本文提出的基于巴特沃斯结构的改进磁链观测器具有良好的动态性能。

4 结 论

本文提出了一种基于巴特沃斯带通滤波器与积分器结合的改进磁链观测器以提高对直流分量以及谐波分量的抑制能力。本文提出的基于巴特沃斯结构的改进磁链观测器可以实现纯积分器的功能，具有完全消除直流分量，抑制谐波分量的能力，同时保证了基波分量无幅值衰减和相位误差，能够实现频率自适应的效果。本文通过详细的数学分析以及伯德图证明了巴特沃斯磁链观测器的效果，同时还提出了磁链观测器的离散化结构。最后，本文通过稳态实验证明了提出的基于巴特沃斯结构的改进磁链观测器具有出色的消除直流分量以及抑制谐波分量的能力，转子位置观测准确度高，同时通过速度斜坡实验和负载阶跃实验证明了提出的基于巴特沃斯结构的改进磁链观测器具有良好的动态性能。

参 考 文 献：

［1］ 宋吉来，曲道奎，徐方，等．机器人无力传感器主动柔顺控制研究［J］．电机与控制学报，2020，24（8）：159．

SONG Jilai，QU Daokui，XU Fang，et al．Active compliance control research for robots without force sensor［J］. Electric Machines and Control，2020，24（8）：159．

［2］ 周雅夫，侯克晗，常城，等．零转矩转速燃料电池汽车双绕组电机能量传递［J］．电机与控制学报，2020，24（8）：18．

ZHOU Yafu，HOU Kehan，CHANG Cheng，et al．Energy transfer of dual source motor with zero torque and speed for fuel cell vehicle［J］.Electric Machines and Control，2020，24（8）：18．

［3］ 李建明，蒋孟龙，安林雪，等．机电作动器动力学建模与电流跳变现象分析［J］．电机与控制学报，2020，24（01）：104．

LI Jianming，JIANG Menglong，AN Linxue，et al．Dynamic modeling and current jump analysis of electro-mechanical actuator［J］.Electric Machines and Control，2020，24（1）：104．

［4］ 刘计龙，肖飞，沈洋，等．永磁同步电机无位置传感器控制技术研究综述［J］．电工技术学报，2017，32（16）：76．

LIU Jilong，XIAO Fei，SHEN Yang，et al．Position-sensorless control technology of permanent-magnet synchronous motor-a review［J］．Transactions of China Electrotechnical Society，2017，32（16）：76．

［5］ XU P，ZHU Z Q．Novel square-wave signal injection method using zero-sequence voltage for sensorless control of PMSM drives［J］.IEEE Transactions on Industrial Electronics， 2016， 63（12）：7444．

［6］ JIN X，NI R，CHEN W，et al．High frequency voltage injection methods and observer design for initial position detection of permanent magnet synchronous machines［J］．IEEE Transactions on Power Electronics，2017，33（9）：7971．

［7］ WANG G，LI T，ZHANG G，et al．Position estimation error reduction using recursive-least-square adaptive filter for model-based sensorless interior permanent-magnet synchronous motor drives［J］．IEEE Transactions on Industrial Electronics，2014，61（9）：5115．

［8］ SONG Xinda，FANG Jiancheng，HAN Bangcheng，et al．Adaptive compensation method for high-speed surface PMSM sensorless drives of EMF-based position estimation error［J］．IEEE Transactions on Power Electronics，2016， 31（2）：1438．

［9］ ZHANG Y，YIN Z，BAI C，et al．A rotor position and speed estimation method using an improved linear extended state observer for IPMSM sensorless drives［J］．IEEE Transactions on Power Electronics，2021，36（12）：14062．

［10］ HEJNY R W，LORENZ R D．Evaluating the practical low-speed limits for back-EMF tracking-based sensorless speed control using drive stiffness as a key metric［J］．IEEE Transactions on Industry Applications，2011，47（3）：1337．

［11］ STOJIC D，MILINKOVIC M，VEINOVIC S，et al．Improved stator flux estimator for speed sensorless induction motor drives［J］．IEEE Transactions on Power Electronics，2014，30（4）：2363．

［12］ XU W，LORENZ R D．Reduced parameter sensitivity stator flux linkage observer in deadbeat-direct torque and flux control for IPMSMs［J］．Industry Applications IEEE Transactions on，2014，50（4）：2626.

［13］ WU C，SUN X，WANG J．A rotor flux observer of permanent magnet synchronous motors with adaptive flux compensation［J］．IEEE Transactions on Energy Conversion，2019，34（99）：2106．

［14］ LIN X，HUANG W，JIANG W，et al．A stator flux observer with phase self-tuning for direct torque control of permanent magnet synchronous motor［J］．IEEE Transactions on Power Electronics，2020，35（6）：6140．

［15］ XIAO D，NALAKATH S，SUN Y，et al．Complex-coefficient adaptive disturbance observer for position estimation of IPMSMs with robustness to DC errors［J］．IEEE Transactions on Industrial Electronics，2020，67（7）：5924．

［16］ BOLOGNANI S，CALLIGARO S，PETRELLA R．Design issues and estimation errors analysis of back-EMF-based position and speed observer for SPM synchronous motors［J］．IEEE Journal of Emerging and Selected Topics in Power Electronics，2014，2（2）：159．

［17］ ZHAO R，ZHEN X，LOH P C，et al．A novel flux estimator based on multiple second-order generalized integrators and frequency-locked loop for induction motor drives［J］．IEEE Transactions on Power Electronics，2017，32（8）：6286．

［18］ XIN Z，ZHAO R，BLAABJERG F，et al．An improved flux observer for field-oriented control of induction motors based on dual second-order generalized integrator frequency-locked loop［J］．IEEE Journal of Emerging and Selected Topics in Power Electronics， 2017， 5（1）： 513．

［19］ KIM H S，SUL S K，YOO H，et al. Distortion-minimizing flux observer for IPMSM based on frequency-adaptive observers［J］. IEEE Transactions on Power Electronics，2020，35（2）：2077.

［20］ KOONLABOON S，SANGWONGWANICH S．Sensorless control of interior permanent-magnet synchronous motors based on a fictitious permanent-magnet flux model ［C］// Industry Applications Conference，October 2-6， 2005， Hong Kong， China. 2005： 311-318．

［21］ 李钟慎．基于MATLAB设计巴特沃斯低通滤波器［J］．信息技术，2003，27（3）：1009．

LI Zhongshen．The design of butterworth lowpass filter based on MATLAB［J］．Information Technology，2003，27（3）：1009．

（编辑：刘琳琳）