并联逆变器参数协同自适应VSG控制策略

摘 要：

虚拟同步发电机（VSG）控制的微电网逆变器并联时，因线路阻抗不匹配存在无法实现功率均分的现象，尤其在受到负载功率扰动时系统的频率稳定性变差。针对此问题，提出一种阻抗-惯量-阻尼3个参数协同自适应VSG控制策略。通过建立系统的小信号模型推导出系统闭环的根轨迹方程，进而分析惯量、阻尼等系统主要参数变化对系统稳定性的影响。利用线路首末端电压和输出功率信息准确反算线路阻抗，并通过自适应虚拟阻抗实时修正线路阻抗，使等效输出阻抗与功率容量成比例，实现功率分配。在此基础上，利用自适应惯量和阻尼系数保障系统的频率稳定性。通过上述3个参数协同的VSG控制提升并联系统的功率分配精度和频率响应特性。最后，通过仿真与实验结果验证所提控制方法的可行性和正确性。

关键词：微电网；逆变器并联；虚拟同步发电机；功率分配；虚拟阻抗；自适应控制

DOI：10.15938/j.emc.2024.09.005

中图分类号：TM341;TP273

文献标志码：A

文章编号：1007-449X（2024）09-0047-13

收稿日期： 2023-10-06

基金项目：国家自然科学基金（62173210）；山东省重大科技创新工程（2019JZZY010423）

作者简介：张玉璇（1999—），女，硕士研究生，研究方向为光-储高效变流器及其先进控制技术；

杜春水（1973—），男，博士，教授，博士生导师，研究方向为新能源微电网优化控制与能量管理；

施其国（1997—），男，硕士，研究方向为高性能功率变换与分配技术；

王爱平（1976—），女，学士，工程师，研究方向为计算机智能化信息控制技术；

炊德政（1984—），男，学士，工程师，研究方向为光伏发电系统优化控制技术。

通信作者：杜春水

Parametric cooperative adaptive VSG control strategy for parallel inverters

ZHANG Yuxuan1， DU Chunshui1， SHI Qiguo1， WANG Aiping2， CHUI Dezheng3

（1.School of Control Science and Engineering， Shandong University， Jinan 250061， China; 2.Shandong Jiangxin Intelligent Technology Co.， Ltd.， Jinan 250199， China; 3.Shandong Aotai Electric Co.， Ltd.， Jinan 250104， China）

Abstract：

When virtual synchronous generator （VSG）-controlled microgrid inverters are connected in parallel， power equalization cannot be achieved due to line impedance mismatch， and the frequency stability of the system deteriorates especially when subjected to load power perturbation. To address this problem， a cooperative adaptive VSG control strategy with three parameters of impedance-inertia-damping was proposed. By establishing a small-signal model of the system， the root trajectory equations of the closed-loop system were derived， and then the effects of the changes in the main parameters of the system， such as inertia and damping， on the stability of the system were analyzed. The impedance of the line was accurately calculated by utilizing voltage and output power information at both ends of the line， while real-time correction of line resistance was achieved through adaptive virtual impedance， so that the equivalent output impedance is proportional to the power capacity and the power distribution is realized; based on which the frequency stability of the system is guaranteed by using the adaptive inertia and damping coefficients. The power allocation accuracy and frequency response characteristics of the parallel system are enhanced by the synergistic VSG control of the above three parameters. Finally， feasibility and correctness of the proposed control method are verified by simulation and experimental results.

Keywords：microgrids; parallel inverters; virtual synchronous generator; power distribution; virtual impedance; adaptive control

0 引 言

微电网孤岛模式运行时，由于缺乏大电网支撑，需要分布式微源逆变器并联维持系统电压和频率，逆变器的动态性能对微电网电能质量稳定起着至关重要的作用。然而，由于构成逆变器的电力电子器件本身不具备“惯性”与“阻尼”特性，微电网大容量负荷投切时，易导致系统的频率波动，严重时将影响微电网稳定性［1-2］。虚拟同步发电机（virtual synchronous generator，VSG）控制技术因能够自动调节逆变器的输出电压幅值和频率，为系统提供所需的惯性和阻尼，有利于保障高比例新能源发电微电网系统的稳定性，促进新能源消纳，近年来备受学术界和产业界的青睐［3-5］。

高比例新能源微电网系统目前普遍采用多台逆变器并联连接的方式。然而，分布式微电源与公共连接点（point of common coupling，PCC）的距离不同，微电网逆变器的连线阻抗和等效输出阻抗值不匹配，将会导致无功功率均分困难等一系列问题，必然会对系统的稳定性产生负面影响，甚至导致电力电子器件的损坏［6-7］。针对VSG并联系统要求功率“按需分配”，并满足功频特性技术需求，文献［8-11］建立VSG逆变器并联系统的小信号模型，分析虚拟转动惯量、下垂系数、线路参数、虚拟阻抗等参数变化对小信号稳定性的影响规律，为并联VSG参数设置提供理论指导。

为提升并联VSG系统的功率分配精度，文献［12-13］提出一种基于虚拟电容的VSG控制，通过VSG输出的无功功率自适应地调节虚拟电容，以实现对功率分配的精准控制。然而，这种控制方案在减小稳态无功功率均分误差的同时，会降低系统的稳定性。文献［14-15］采用虚拟负阻抗方法抵消逆变器等效输出阻抗中的阻性成分，确保等效输出阻抗呈现感性特性。这种方法有利于解耦控制有功环和无功环，从而提高下垂控制的精度，但该技术对弱电网情况下的电压和频率支持较弱，而且无法实现孤岛运行。文献［16-17］通过引入积分环节实现无功功率按照指令分配，但未涉及系统稳定性的讨论。文献［18］针对线路阻抗不匹配造成的功率分配不均问题展开分析，实时检测线路阻抗，根据线路阻抗的不同自适应虚拟阻抗值的大小，具有较好的工程应用价值，但其等效输出阻抗与控制方法有关。

为提升并联VSG系统的功频特性，文献［19］采用前馈频率变化率和功率指令的辅助阻尼方式实现有功振荡抑制，但该方法仅在小信号模型下实现，对于负载出现较大扰动时，该方法的有效性有待进一步验证。文献［20-21］利用最优控制的思想对关键参数惯量J和阻尼D进行优化，提升系统在受到扰动时频率和功率的动态响应特性，由于需要对变量进行多次迭代，运算量较大。文献［22］根据VSG的输出功率为二阶系统，利用最优二阶系统推导出J和D参数满足的关系等式，将频率变化率引入2个参数的取值当中，自适应调节惯性阻尼系数。

在实际工程中，线路阻抗Z难以精确测量，上述控制策略既不能实现线路阻抗未知情况下功率准确分配，又不能有效地提升系统的频率稳定性，为此，针对VSG逆变器并联运行线路阻抗不匹配导致的功率分配不均问题，提出一种惯量J、阻尼D和阻抗Z 3个参数协同自适应控制策略。首先分析VSG逆变器并联系统的下垂系数、惯量阻尼系数、线路阻抗参数的匹配方式，为关键参数的选取提供理论依据。其次，采用电力线路电压降落分析方法反算输出线路阻抗，有效避免因线路变化等因素影响系统参数。在逆变器输出功率按照容量配置的前提下，通过实时修正并联VSG逆变器的等效输出阻抗，确保功率的精确分配。此外，为了避免并联系统负荷突变或切换时功率振荡，保障系统频率稳定性，提出基于惯量J、阻尼D和阻抗Z多参数协同自适应的微电网逆变器并联VSG控制策略。MATLAB/Simulink仿真和DSP_HIL实验结果表明，所提出的控制方法可有效提高VSG逆变器并联功率均分精度，提升微电网系统频率稳定性。

1 VSG控制的基本原理

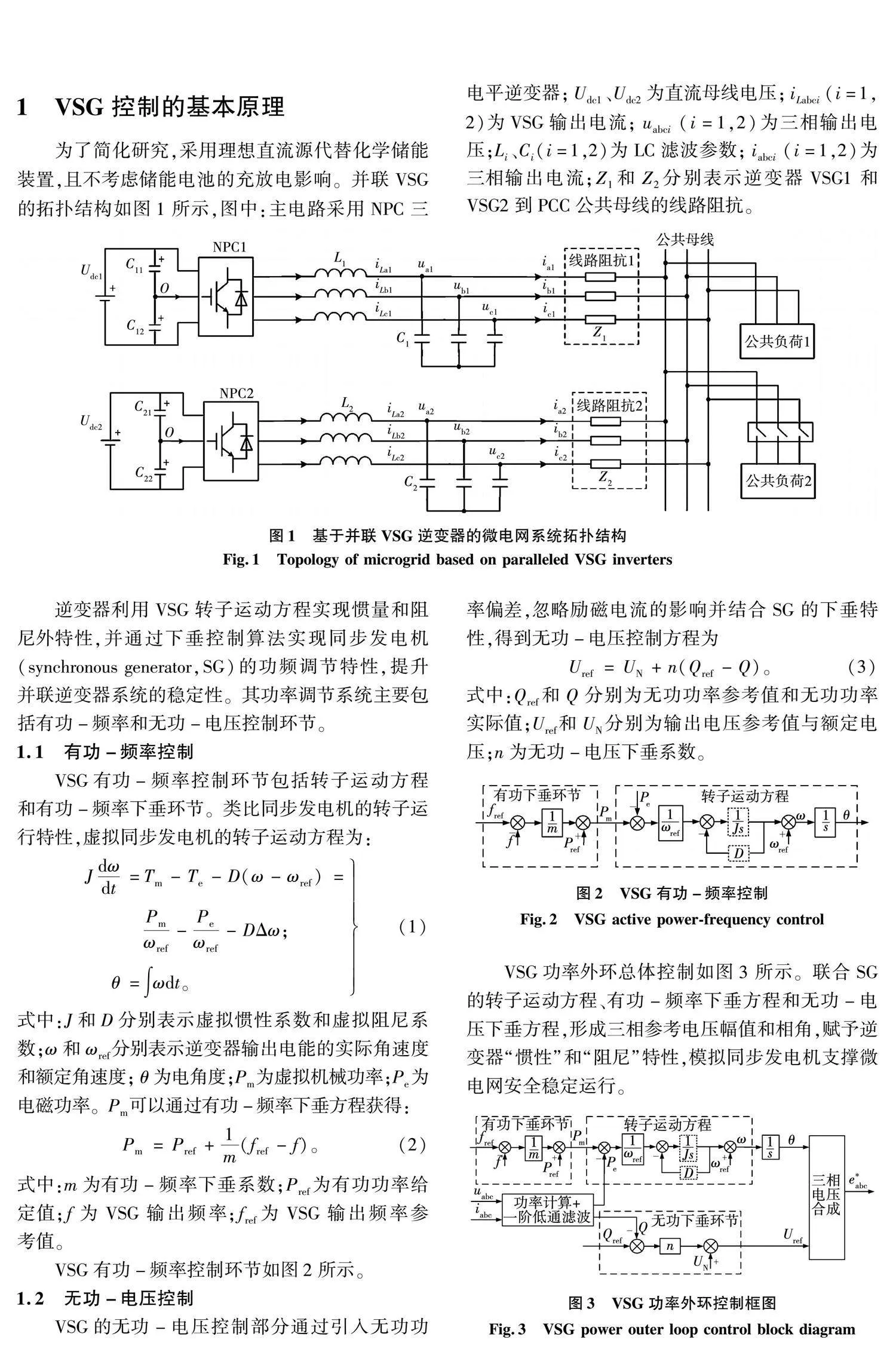
为了简化研究，采用理想直流源代替化学储能装置，且不考虑储能电池的充放电影响。并联VSG的拓扑结构如图1所示，图中：主电路采用NPC三电平逆变器；Udc1、Udc2为直流母线电压；iLabci（i=1，2）为VSG输出电流；uabci（i=1，2）为三相输出电压；Li、Ci（i=1，2）为LC滤波参数；iabci（i=1，2）为三相输出电流；Z1和Z2分别表示逆变器VSG1和VSG2到PCC公共母线的线路阻抗。

逆变器利用VSG转子运动方程实现惯量和阻尼外特性，并通过下垂控制算法实现同步发电机（synchronous generator，SG）的功频调节特性，提升并联逆变器系统的稳定性。其功率调节系统主要包括有功-频率和无功-电压控制环节。

1.1 有功-频率控制

VSG有功-频率控制环节包括转子运动方程和有功-频率下垂环节。类比同步发电机的转子运行特性，虚拟同步发电机的转子运动方程为：

Jdωdt=Tm－Te－D（ω－ωref）=Pmωref－Peωref－DΔω；

θ=∫ωdt。（1）

式中：J和D分别表示虚拟惯性系数和虚拟阻尼系数；ω和ωref分别表示逆变器输出电能的实际角速度和额定角速度；θ为电角度；Pm为虚拟机械功率；Pe为电磁功率。Pm可以通过有功-频率下垂方程获得：

Pm=Pref+1m（fref－f）。（2）

式中：m为有功-频率下垂系数；Pref为有功功率给定值；f为VSG输出频率；fref为VSG输出频率参考值。

VSG有功-频率控制环节如图2所示。

1.2 无功-电压控制

VSG的无功-电压控制部分通过引入无功功率偏差，忽略励磁电流的影响并结合SG的下垂特性，得到无功-电压控制方程为

Uref=UN+n（Qref－Q）。（3）

式中：Qref和Q分别为无功功率参考值和无功功率实际值；Uref和UN分别为输出电压参考值与额定电压；n为无功-电压下垂系数。

VSG功率外环总体控制如图3所示。联合SG的转子运动方程、有功-频率下垂方程和无功-电压下垂方程，形成三相参考电压幅值和相角，赋予逆变器“惯性”和“阻尼”特性，模拟同步发电机支撑微电网安全稳定运行。

2 控制器关键参数对系统的影响

微电网系统负荷扰动具有不确定性，构网逆变控制器参数对系统电能质量影响大。在负荷突增和突减情况下，惯性系数和虚拟阻尼系数对系统频率的影响分析方法相同。不失一般性，以有功负荷减小为例，分析VSG控制器的虚拟惯性系数J和虚拟阻尼系数D对系统频率的影响。

联立式（1）和式（2）可得

ωref－ωPref －Pe=－1（Js+D）ωref+12πm=－mPτs+1。（4）

其中：

τ=JωrefDωref+12πm；

mP=1Dωref+12πm。（5）

式中τ和mP分别表示VSG的惯性时间常数和有功-频率下垂系数。

根据式（4），假设系统负荷发生有功功率单位阶跃，并改变J与D参数，分析 VSG的频率响应特性。Δω（s）与ΔP（s）之间的传递函数为

Gω（s）=1（Js+D）ωref+12πm。（6）

2.1 虚拟惯性系数J对系统的影响

当负荷阶跃减小时，系统频率偏移量Δf正向增加。不同J参数系统频率偏移量的变化情况如图4所示，在J从0增大到1过程中，系统频率偏移速度逐渐减小，而其偏移量随着时间增加最终趋于一致。可见J主要影响系统频率的动态特性，并不会改变频率的稳态偏移量。

2.2 虚拟阻尼系数D对系统的影响

当负荷阶跃减小时，系统频率偏移量Δf正向增加。不同D参数系统频率偏移量的变化情况如图5所示，在D从0不断增大到15过程中，系统频率偏移量逐渐减小而偏移速度相近，可见D主要影响系统频率的稳态特性，对系统频率的动态特性影响较小。

2.3 关键参数对并联VSG系统稳定性的影响

根据电力系统多机静态稳定近似分析方法，分析关键参数对并联VSG系统稳定性的影响［23］。

并联VSG简化模型如图6所示，当VSG并联时，两台VSG逆变器可以等效为2个电压源，Ui∠φi（i=1，2）表示VSGi的输出电压和相位，Upcc表示公共母线电压。Zoi（i=1，2）为逆变器的等效输出阻抗，包含3个部分：VSG输出阻抗、线路阻抗和虚拟阻抗，其表达形式为Zoi=Roi+jXoi。Roi和Xoi分别表示逆变器的等效输出电阻和等效输出电抗。

利用并联VSG简化模型对系统进行稳定性分析。在稳态工作点利用式（1）和式（2）建立系统的小信号模型为：

dΔθidt=Δωi；

dΔωidt=－12πJiωrefmi+DiJiΔωi－ΔPiJiωref。（7）

式中：Δθi、Δωi、ΔPi分别表示功角、角频率和有功功率的小扰动增量；i表示第i（i=1， 2）台VSG逆变器。将式（7）转换到s域，能够得到：

sΔω1=－12πJ1ωrefm1+D1J1Δω1－ΔP1J1ωref；

sΔω2=－12πJ2ωrefm2+D2J2Δω2－ΔP2J2ωref；

sΔθ12=Δω1－Δω2。（8）

将功率增量表示为Δθ12的函数，即：

ΔP1=dP1dθ12Δθ12=Se1Δθ12；

ΔP2=dP2dθ12Δθ12=Se2Δθ12。（9）

式中Se1和Se2分别表示VSG1和VSG2的整步功率系数。联立式（8）和式（9）得到系统的闭环特征方程为

s3+As2+Bs+C=0。（10）

其中A、B、C的表达式为：

A=12πm1J1ωref+12πm2J2ωref+D1J1+D2J2；B=14π2m1m2J1J2ω2ref+D22πm1J1J2ωref+

D12πm2J1J2ωref+D1D2J1J2+Se1J1ωref－Se2J2ωref；

C=12πm2Se1－12πm1Se2+ωref（D2Se1－D1Se2）J1J2ω2ref。（11）

以容量相等的并联VSG为例，设定D1=D2=D，J1=J2=J，m1=m2=m。令Kw=1/（2πm），进一步化简得到：

A′=2（Kw+Dωref）Jωref；

B′=Kw+DωrefJωref2+1Jωref（Se1－Se2）；

C′=（Kw+Dωref）（Se1－Se2）J2ω2ref。（12）

整步功率系数Se1和Se2的表达式为：

Se1=U1U2（－|G12|sinδ12+|B12|cosδ12）；Se2=U1U2（－|G12|sinδ12－|B12|cosδ12）。（13）

Y12=G12+jB12表示VSG1与VSG2之间的导纳。δ12=∠φ1－∠φ2表示两台VSG之间的功角差。为简化分析过程，认为δ12≈0。可以得出

Se1－Se2=2U1U2|B12|。（14）

根据并联VSG等效电路，通过“星形-三角形”阻抗变换，设VSG1与VSG2间的阻抗为Z12，则

Z12=Zo1Zo2+Zo1ZL+Zo2ZLZL=R12+jX12。（15）

为满足P-f、Q-U下垂特性，等效输出阻抗呈现感性，那么Zo1=Zo2≈jωrefLo。假定ZL=1 Ω，可得

Z12=Zo1+Zo2+Zo1Zo2ZL=－ω2refL2o+j2ωrefLo。（16）

因此，B12的表达式为

B12=－X12R212+X212=－2ω3refL3o+4ωrefLo。（17）

将式（16）代入到式（17），可得

Se1－Se2=2U1U2|B12|=4U1U2ω3refL3o+4ωrefLo。（18）

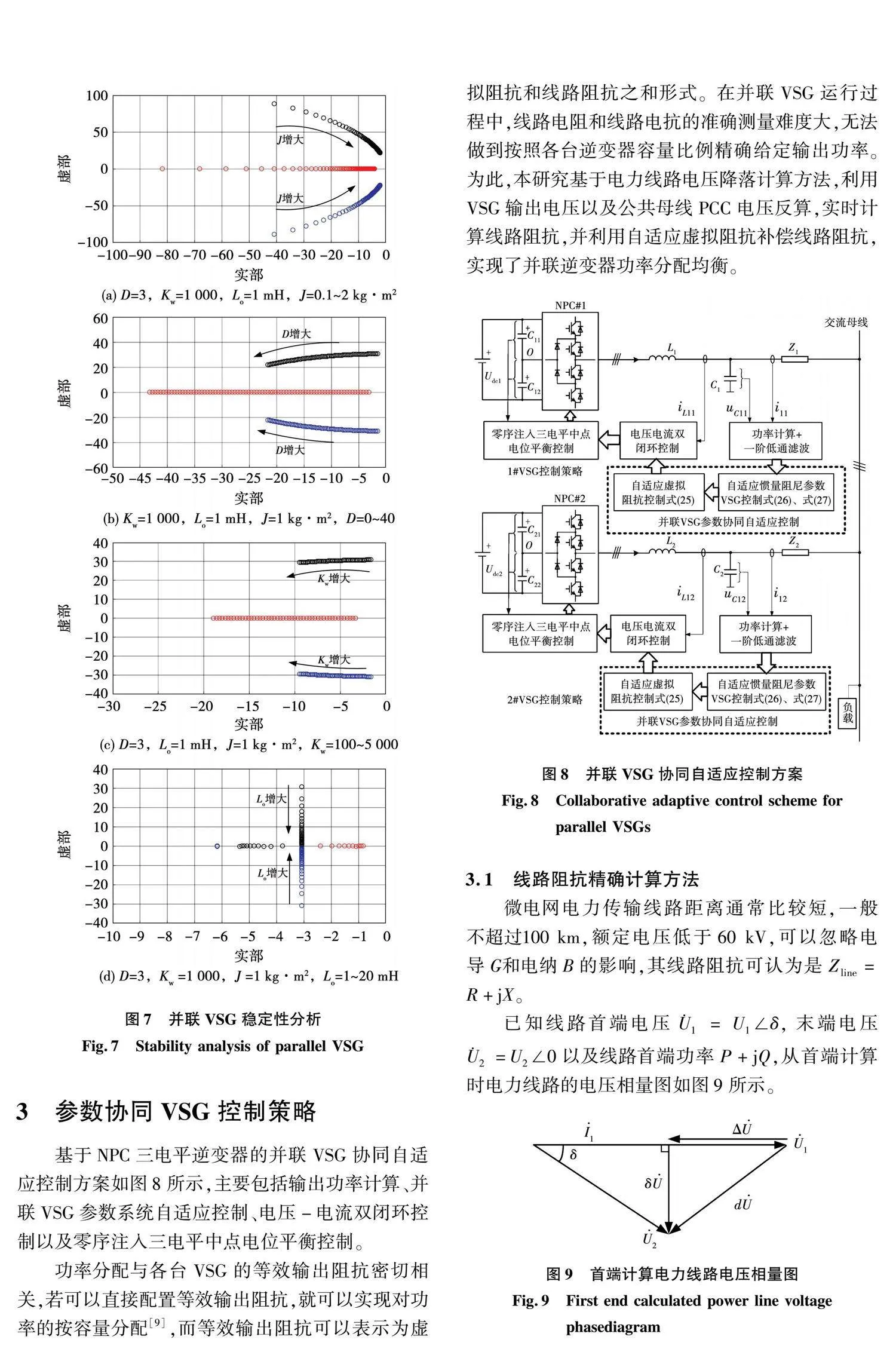
由式（10）、式（12）和式（18）可得闭环的根轨迹如图7所示，进而分析J、D、Kw、Lo参数变化对系统稳定性的影响。

稳态时系统的参数为：J=1 kg·m2，D=3，Kw =1 000，Lo=1 mH。

由图7（a）可以看出，当J从0.1增加到2，其他参数保持不变的情况下，系统闭环根轨迹向虚轴靠近，稳定性变差。由图7（b）可知，在阻尼系数D从0增加到40过程中，其他3个参数值不变的情况下，闭环根轨迹向实轴靠近，系统的稳定性增强。图7（c）和图7（d）分别表示系数Kw和等效电抗Lo增大时系统闭环根轨迹，可以看出随着Kw和Lo的增大，系统的稳定性提高。

可见，阻尼D、下垂系数Kw、等效输出阻抗Lo与系统稳定性成正相关，惯量J与系统稳定性成负相关，为保障稳定性需要合理选择系统参数。

3 参数协同VSG控制策略

基于NPC三电平逆变器的并联VSG协同自适应控制方案如图8所示，主要包括输出功率计算、并联VSG参数系统自适应控制、电压-电流双闭环控制以及零序注入三电平中点电位平衡控制。

功率分配与各台VSG的等效输出阻抗密切相关，若可以直接配置等效输出阻抗，就可以实现对功率的按容量分配［9］，而等效输出阻抗可以表示为虚拟阻抗和线路阻抗之和形式。在并联VSG运行过程中，线路电阻和线路电抗的准确测量难度大，无法做到按照各台逆变器容量比例精确给定输出功率。为此，本研究基于电力线路电压降落计算方法，利用VSG输出电压以及公共母线PCC电压反算，实时计算线路阻抗，并利用自适应虚拟阻抗补偿线路阻抗，实现了并联逆变器功率分配均衡。

3.1 线路阻抗精确计算方法

微电网电力传输线路距离通常比较短，一般不超过100 km，额定电压低于60 kV，可以忽略电导G和电纳B的影响，其线路阻抗可认为是Zline=R+jX。

已知线路首端电压U·1=U1∠δ，末端电压U·2=U2∠0以及线路首端功率P+jQ，从首端计算时电力线路的电压相量图如图9所示。

图9中：dU·为电压降落；ΔU为电压降落横分量；δU为电压降落纵分量。根据图中的电压相量关系，不难看出：

U·2=（U·1－ΔU·）－jδU·；（19）

U·2=U·1－I·1Zline=U·1－（S1U1）*Zline=

U·1－P－jQU1（R+jX）=

U1－PR+QXU1－jPX－QRU1。（20）

因此，电压降落的纵分量和横分量可表示为：

ΔU=PR+QXU1；

δU=PX－QRU1。（21）

由于

U1－U2cosδ=PR+QXU1；

U2sinδ=PX－QRU1。（22）

求解式（10）可得线路电阻R和线路电抗X的计算值为：

R=PQU21－PQU1U2cosδ－Q2U1U2sinδ（P2+Q2）Q；

X=PU1U2sinδ－QU1U2cosδ+QU21P2+Q2。（23）

式中：有功功率P和无功功率Q为三相功率；电压U1和U2为线电压；功角δ的单位为rad。利用式（23）便可实时计算线路阻抗的数值。

3.2 并联参数协同VSG控制算法

利用自适应虚拟阻抗控制，对原有的虚拟阻抗环节进行改进，即对线路阻抗进行补偿，实现VSG等效的输出阻抗与容量成比例。补偿后公共点的输出电压为

U·pcc=U·o－I·oZline－I·oZapd=U·o－I·o［Zline+（Zo－Zline）］=U·o－I·oZo。（24）

式中：Zapd=Rapd+jXapd表示自适应虚拟阻抗的数值；Zo表示等效输出阻抗设定值；Uo为逆变器输出端电压；Io为逆变器输出端电流。将虚拟阻抗上的电压I·oZapd由abc静止坐标系转换到dq旋转坐标系下，可得：

uapd_d=［（Ro－Rline）+s（Lo－Lline）］id－ω（Lo－Lline）iq；

uapd_q=［（Ro－Rline）+s（Lo－Lline）］iq+ω（Lo－Lline）id。（25）

此时对应的自适应虚拟阻抗控制算法框图如图10所示。通过控制逆变器等效输出阻抗不变，实时消除因线路阻抗不匹配导致的功率均分问题。

为了提升并联VSG系统的频率稳定性，在实现功率均分的同时，根据频率变化率和频率偏移量自适应调整J与D参数，以应对功率突变工况。

并联VSG自适应惯量阻尼参数选取方案如下：

J=

J0+kJ1，Δωdωdt≥0∩|dωdt|≥ε1∩|Δω|≥ε2；

J0+kJ2，Δωdωdtlt;0∩|dωdt|≥ε1∩|Δω|≥ε2；

J0，else。（26）

D=D0+kD|Δω|，|Δω|≥ε3；

D0，else。（27）

式中：εi（i=1， 2）表示虚拟惯量参数的阈值；ε3表示虚拟阻尼参数的阈值，具体的参数取值可根据微电网的运行标准和实际运行工况设置。

为了使J可以按照功率突变的状态增大或减小，D随着频率偏移量的增大而增加，设定kJ1gt;0、kJ2lt;0、kDgt;0。具体的参数取值可根据逆变器的实际运行功率来进行设置。

4 仿真验证

基于上述理论分析，将两台VSG逆变器并联后通过LC滤波器输出连接的线路阻抗比设置为Z1∶Z2=9∶4，逆变器功率输出为1∶1。利用MATLAB/Simulink搭建并联VSG三电平逆变器仿真模型，验证所提并联NPC三电平参数协同VSG控制方案的控制效果。并联逆变器的主电路参数和控制参数分别如表1、表2所示。

4.1 功率均分效果验证

基于VSG控制的两台并联逆变器输出功率动态调整过程如图11所示。设定VSG1与VSG2逆变器的负载功率相同，且Pref=15 kW，Qref=2 kVar。系统仿真时长为0.8 s，其中在0～0.2 s阶段采用传统虚拟阻抗控制策略，在0.2 s时刻切入所提参数协同自适应VSG控制策略，在0.4 s时刻系统负载突然增加，在0.6 s时刻恢复额定负载。

由图11（a）和图11（b）可以看出，VSG1与VSG2采用传统虚拟阻抗控制策略时，无功功率分配不均现象明显，差值约350 var；然而其有功功率输出满足f-P下垂特性曲线，仍然能够实现有功功率均分。

在0.2 s切入所提并联参数协同自适应VSG控制策略后，线路虚拟阻抗得到有效修正，两台VSG的等效输出阻抗相同，实现了无功功率的均分。同时，在0.4 s和0.6 s功率扰动时，所提控制策略依然能够实现无功功率的均分。由此可见，并联参数协同自适应VSG控制策略能够在线路阻抗未知情况下，有效实现有功和无功功率精确均分。

4.2 频率稳定性效果验证

下式给出了并联自适应J与D参数的取值方案，VSG1设定参数后，令J1=J2、D1=D2，设置VSG2关键参数为：

J=

J0+0.3，Δωdωdt≥0∩|dωdt|≥5∩|Δω|≥0.2；

J0－0.15，Δωdωdtlt;0∩|dωdt|≥5∩|Δω|≥0.2；

J0，else。（28）

D=D0+5|Δω|，|Δω|≥0.13；

D0，else。（29）

图12为固定参数与参数协同控制VSG控制输出频率响应情况。

对比固定参数VSG控制方案，可以看出系统的频率偏移量进一步减小；在0.4 s加载时，系统的频率响应速度有所减缓；在0.6 s减载时，系统的频率迅速恢复到稳态值。

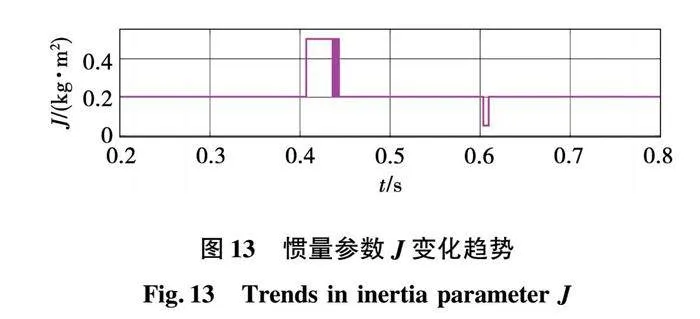
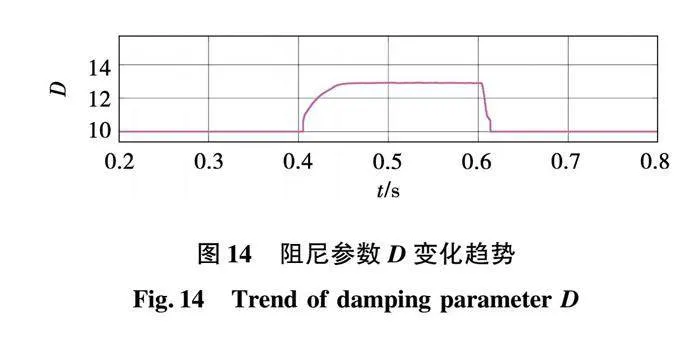
图13和图14给出了加减负载情况下所提控制策略J与D参数的变化情况。在0.4 s加载时，惯量参数J和D都增大，逆变器的输出惯性和阻尼同时增加，频率响应速度降低，有利于减缓系统频率偏移速度和减少频率偏移量；在0.6 s减载时，J和D都减小，逆变器的输出惯性减小，频率响应速度变快，有利于系统频率快速低超调恢复。

自适应J参数与D参数的取值充分考虑小扰动时频率偏移量和频率变化率的波动特性，通过设置频率变化率和频率偏移量阈值，确保系统在受到扰动时不会因为J与D参数的变化而对频率产生影响，进一步提高了并联系统的频率稳定性。

5 实验验证

为了验证上述理论分析以及所提控制策略的有效性，本研究搭建了基于NI-PXI的半实物实时仿真平台如图15所示，该平台主要由上位机、NI-PXI仿真器、I/O接口板和2台VSG控制器组成。上位机搭载MATLAB/Simulink和 StarSim HIL仿真软件进行系统建模、编译调试、模型加载和运行监控；NI-PXI实时仿真器搭载两台NPC三电平逆变器主电路模型；基于TMS320F28335芯片的2台VSG控制器运行所提并联参数协同VSG控制策略；I/O接口板连接VSG控制器与实时仿真器，实现电压、电流和PWM信号的交互。该硬件在环实验平台中并联VSG的系统参数与表1、表2相同。

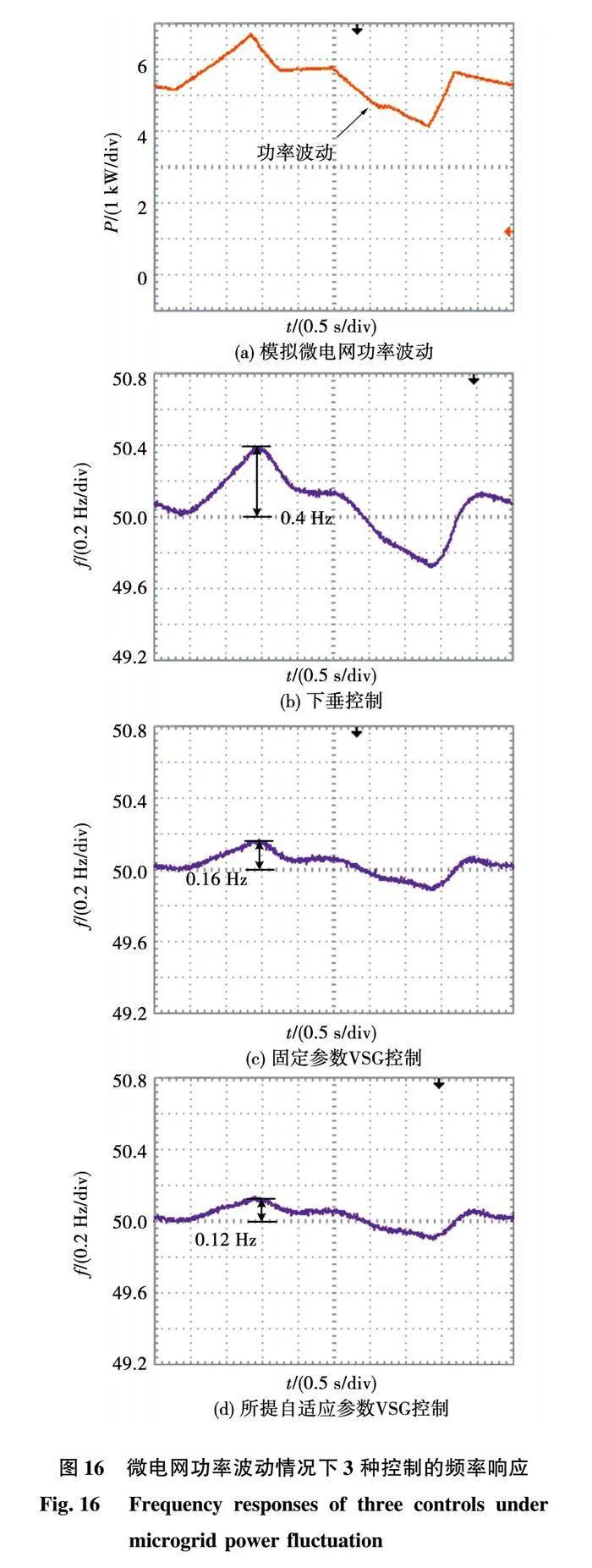
5.1 微电网功率波动实验对比

为验证功率波动下本文所提控制算法的性能，通过PQ控制模拟微电网功率波动如图16（a）所示。设定逆变器的额定功率为10 kW，负荷为15 kW。当逆变器分别采用下垂控制、固定参数VSG控制和本研究所提控制算法时，观察逆变器对微电网运行频率的支撑情况。由图16（b）、图16（c）和图16（d）可以看出，3种控制策略作用下，微电网频率的最大偏移量分别为0.4、0.16和0.12 Hz，所提控制方法的频率偏移量比经典下垂方法减小了70%，比固定参数VSG方法减小了25%；此外所提控制方法的频率偏移速度更慢，显著增加了微电网的惯性和阻尼，提升了系统频率稳定性。

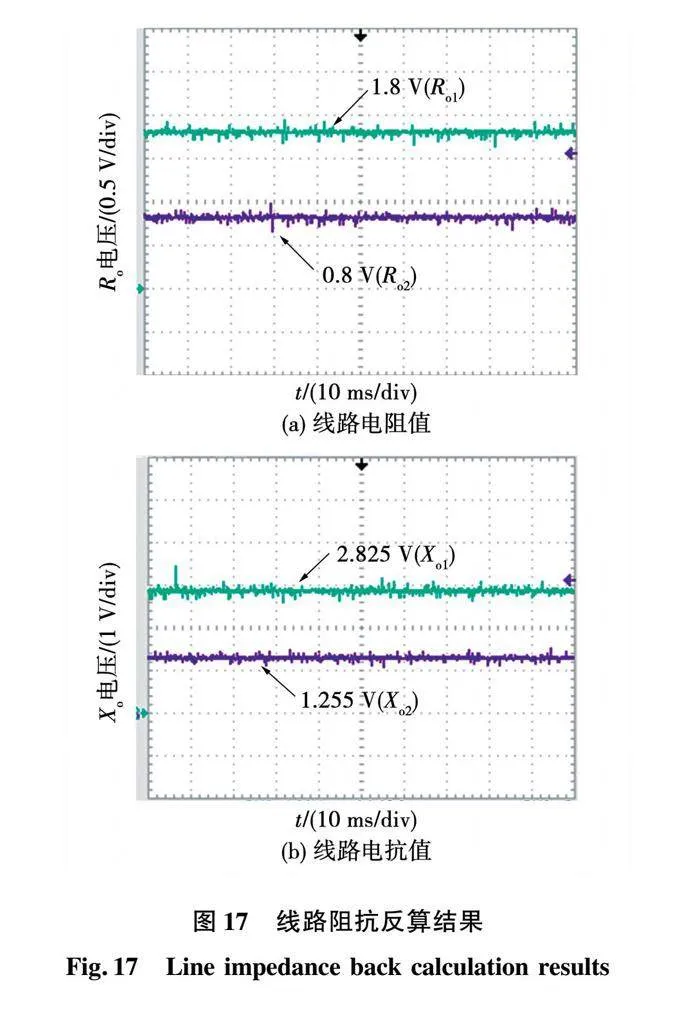
5.2 线路阻抗反算实验验证

R1、L1、R2、L2线路阻抗反算的结果如图17所示。由于示波器的精度有限，对反算出的线路阻抗做了放大处理。线路电阻在控制器中放大10倍输出，线路电抗放大50倍，可以获得反算线路阻抗的结果为：Ro1=0.18 Ω，Ro2=0.08 Ω，Xo1=0.056 5 Ω，Xo2=0.025 0 Ω。计算结果与仿真分析保持一致。

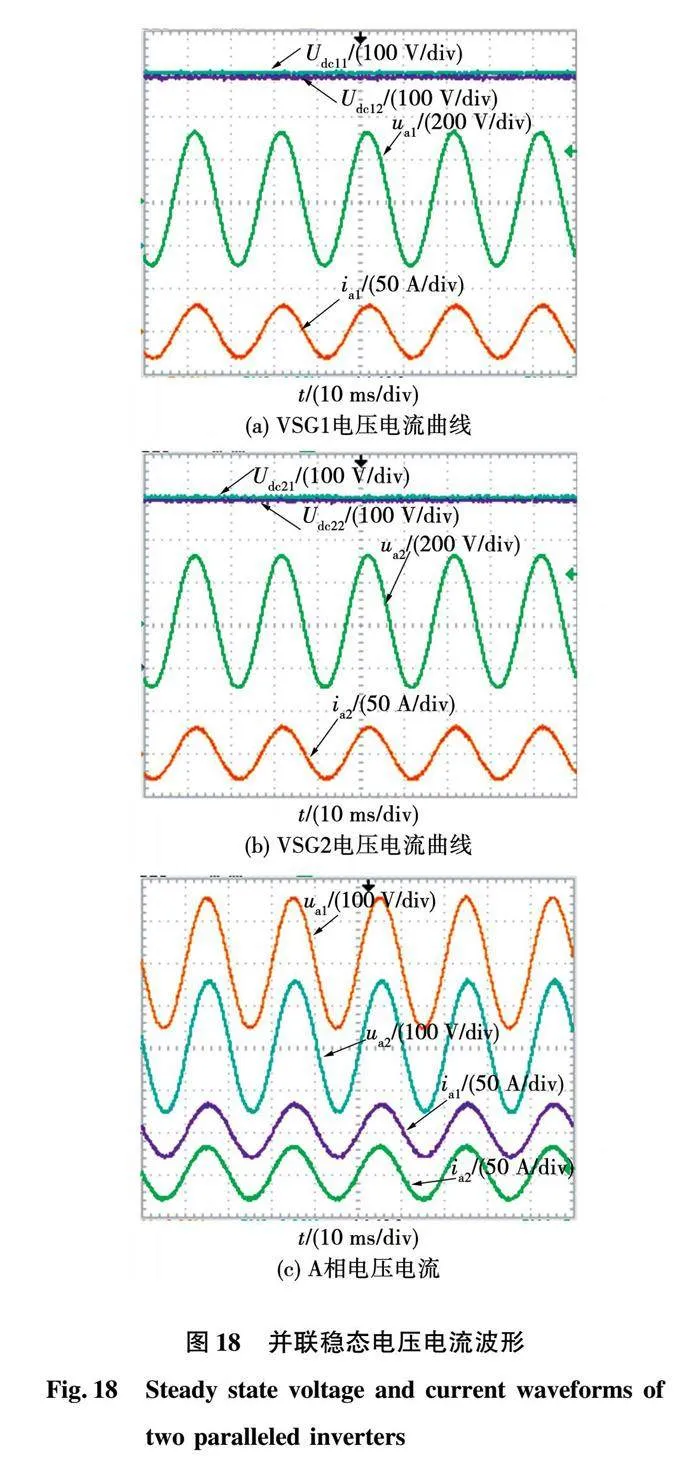
5.3 稳态输出电压电流波形

并联稳态电压电流波形如图18所示。图18（a）、图18（b）分别为VSG1和VSG2逆变器稳态时A相电压电流波形和直流侧电容电压波形，可以看出，在上下电容的中点电位平衡，电压基本重合；其次，A相两台并联逆变器的输出电压和电流幅值分别相同。图18（c）为A相两台逆变器的输出电压电流波形图，可见两台逆变器的电压电流相位保持同步，并联均流效果良好。

5.4 并联参数协同VSG控制策略验证

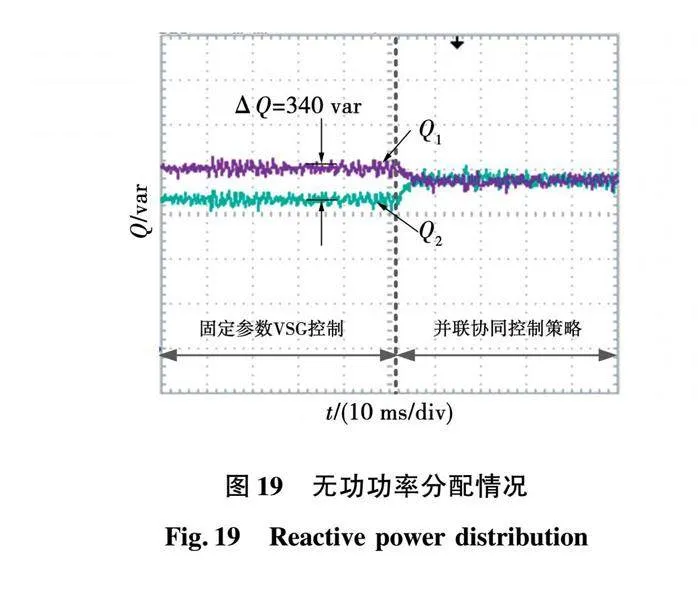
两台VSG并联无功功率的分配情况如图19所示。传统的固定虚拟阻抗方式存在约340 var的无功功率静差，而切入本研究所提的协同控制算法后，两条线基本重合，无功功率均分，可见所提控制算法在线路阻抗不匹配时也能保证功率的均衡分配。

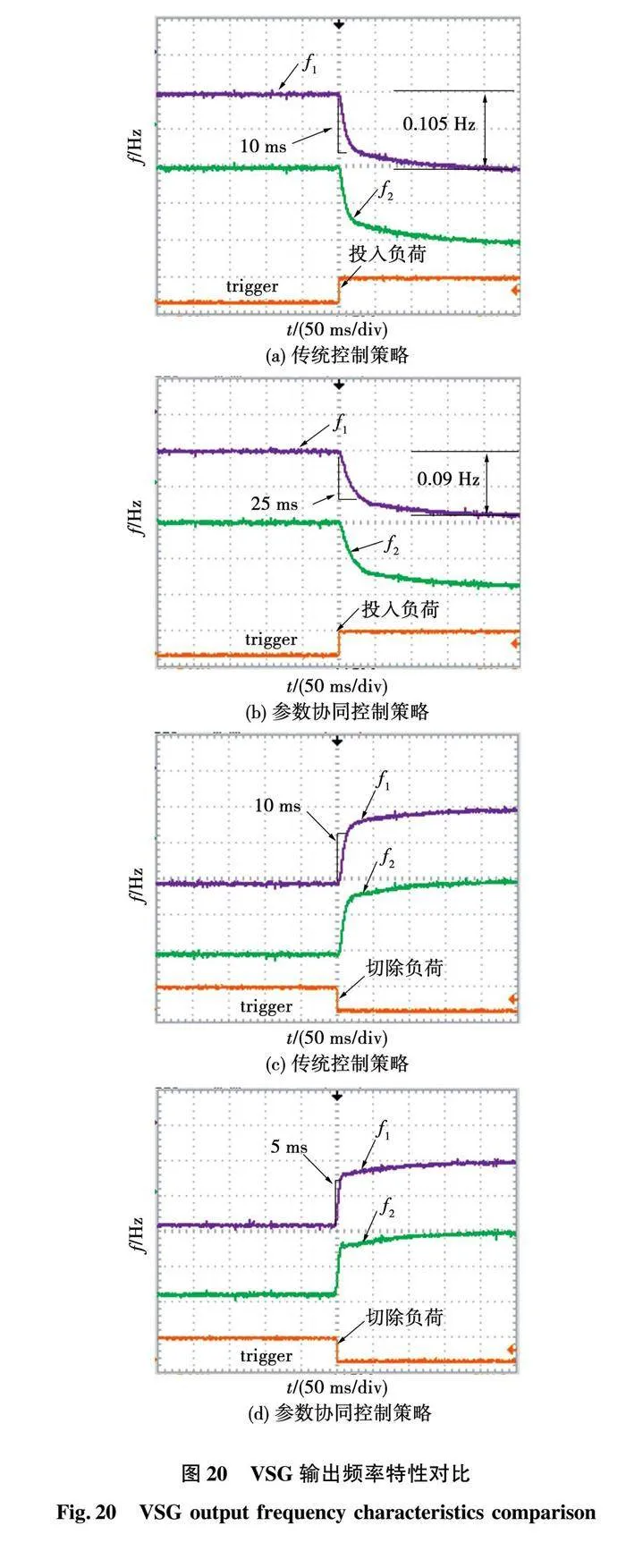
并联VSG采用传统固定参数和协同参数时投入负荷和切除负荷系统的频率输出特性如图20所示。图20（a）和图20（b）分别为加载工况下传统固定参数控制方法和所提控制方法的系统输出频率特性图。可见采用固定参数VSG控制时输出频率降低0.105 Hz，而采用所提参数协同控制方法时频率仅降低0.09 Hz，稳态偏移量减小了14.29%；在频率的动态响应特性方面，以下降相同的频率（0.015 Hz）为例，所提控制方法较传统控制方法所用时间由10 ms增加为25 ms，频率偏移速度减缓了60%。

图20（c）和图20（d）分别为系统减载情况下传统固定参数VSG控制和所提参数协同VSG控制时的输出频率特性。切除负荷时，采用所提VSG控制与传统VSG控制相比较，系统频率上升0.06 Hz所用的时间由10 ms缩短为5 ms，响应时间缩短了50%，恢复到基频工作点的速度更快。

6 结 论

新能源微电网分布式微源逆变器并联时，因受到线路长度、材质以及外界环境等因素的影响，其线路阻抗通常是变化的且不相同，难以按照逆变器容量比例进行精确配置。此外，并联运行逆变器的VSG输出频率特性对整个微电网系统的稳定性有重要影响。针对上述问题，提出一种多参数协同自适应VSG并联控制策略，并通过仿真验证该策略的有效性，主要工作与贡献如下：

1）采用电力系统电压降计算方法精确地反算线路阻抗，并利用自适应虚拟阻抗弥补线路阻抗，通过使两台VSG逆变器的等效输出阻抗按照容量反比配置，实现无功功率的均衡分配。

2）通过自适应惯量阻尼参数，提升负载扰动时系统频率稳定性。

3）所提三参数协同自适应VSG逆变器并联控制策略，通过仿真和实验验证实现负荷功率的精确分配，同时改善系统的频率稳定性。

参 考 文 献：

［1］ WU Heng， RUAN Xinbo， YANG Dongsheng， et al. Small-signal modeling and parameters design for virtual synchronous generators［J］. IEEE Transactions on Industrial Electronics， 2016， 63（7）： 4292.

［2］ 钟庆昌. 虚拟同步机与自主电力系统［J］. 中国电机工程学报， 2017， 37（2）： 336.

ZHONG Qingchang. Virtual synchronous machines and autonomous power systems［J］. Proceedings of the CSEE， 2017， 37（2）： 336.

［3］ ZHONG Qingchang， WEISS G. Synchronverters： inverters that mimic synchronous generators［J］. IEEE Transactions on Industrial Electronics， 2011， 58（4）： 1259.

［4］ 颜湘武， 王俣珂， 贾焦心， 等. 基于非线性最小二乘曲线拟合的虚拟同步发电机惯量与阻尼系数测量方法［J］. 电工技术学报，2019， 34（7）： 1516.

YAN Xiangwu， WANG Yuke， JIA Jiaoxin， et al. Measurement of virtual synchronous generator inertia and damping coefficient based on nonlinear least squares curve fitting［J］. Transactions of China Electrotechnical Society， 2019， 34（7）： 1516.

［5］ 郭建祎，樊友平. 基于改进粒子群算法的VSG参数自适应控制策略［J］.电机与控制学报， 2022， 26（6）： 72.

GUO Jianyi， FAN Youping. Adaptive VSG parameter control strategy based on improved particle swarm optimization［J］. Electric Machines and Control， 2022， 26（6）： 72.

［6］ 王继磊， 张兴， 朱乔华， 等. 虚拟同步发电机暂态稳定性分析与控制策略［J］. 电机与控制学报， 2022， 26（12）： 28.

WANG Jilei， ZHANG Xing， ZHU Qiaohua， et al. Transient stability analysis and control strategy of virtual synchronous generator［J］. Electric Machines and Control， 2022， 26（12）： 28.

［7］ 张赟宁，谢永辉，张磊， 等. 自适应调节有功功率偏差的虚拟同步发电机暂态控制策略［J］. 电机与控制学报：1-12［2023-08-24］.http：//kns.cnki.net/kcms/detail/23.1408.TM.20230823.1802.002.html.

ZHANG Yunning， XIE Yonghui， ZHANG Lei， et al. Transient control strategy of virtual synchronous generator with adaptive regulation of active power deviation ［J］. Electric Machines and Control：1-12［2023-08-24］. http：//kns.cnki.net/kcms/detail/23.1408.TM.20230823.1802.002.html.

［8］ 罗曼. 多虚拟同步发电机并联运行时的环流抑制和功率分配问题研究［D］.成都：电子科技大学， 2016.

［9］ 黄耀智. 基于VSG的逆变器并联运行研究［D］.北京：北方工业大学， 2020.

［10］ 施其国. 微电网三电平逆变器多参数协同自适应VSG控制策略研究［D］. 济南：山东大学， 2022.

［11］ ZHANG Bo， YAN Xiangwu， ALTAHIIR S Y. Control design and small-signal modeling of multi-parallel virtual synchronous generators［C］//2017 11th IEEE International Conference on Compatibility， Power Electronics and Power Engineering， April 4-6，2017， Cadiz， Spain. 2017：471-476.

［12］ XU Haizhen， ZHANG Xing， LIU Fang， et al. A reactive power sharing strategy of VSG based on virtual capacitor algorithm［J］. IEEE Transactions on Industrial Electronics， 2017， 64（9）： 7520.

［13］ XU Haizhen， YU Changzhou， LIU Chun， et al. An improved virtual capacitor algorithm for reactive power sharing in multi-paralleled distributed generators［J］. IEEE Transactions on Power Electronics， 2019， 34（11）： 10786.

［14］ 郭志强. VSG并联运行控制策略的研究［D］.南昌：南昌大学， 2021.

［15］ ZHANG Yabo， WU Songrong， YANG Ping， et al. Research on parallel operation of virtual synchronous generators in microgrid［C］//2019 14th IEEE Conference on Industrial Electronics and Applications， June 19-21， 2019， Xi’an， China. 2019：1659-1664.

［16］ 万晓凤，詹子录，丁小华，等. 基于虚拟同步发电机的多逆变器并联改进控制策略［J］.电机与控制学报， 2020， 24（2）： 118.

WAN Xiaofeng， ZHAN Zilu， DING Xiaohua， et al. Improved control strategy for multi-inverter parallel connection based on virtual synchronous generator［J］. Electric Machines and Control， 2020， 24（2）： 118.

［17］ 王俊凯，牟龙华，刘鑫. 基于动态虚拟阻抗的多并联逆变器间环流抑制控制策略［J］.电力自动化设备， 2021， 41（4）： 94.

WANG Junkai，MOU Longhua， LIU Xin. Dynamic virtual impedance-based control strategy for circulating current suppression among multiple parallel inverters［J］. Electric Power Automation Equipment， 2021， 41（4）： 94.

［18］ 温春雪，黄耀智，胡长斌，等.虚拟同步发电机接口变换器并联运行虚拟阻抗自适应控制［J］.电工技术学报， 2020， 35（S2）：494.

WEN Chunxue，HUANG Yaozhi， HU Changbin， et al. Adaptive control of virtual impedance in parallel operation of virtual synchronous generator interface converter ［J］. Transactions of China Electrotechnical Society， 2020，35（S2）：494.

［19］ CHEN Meng， ZHOU Dao， BLAABJERG F. Active power oscillation damping based on acceleration control in paralleled virtual synchronous generators system［J］. IEEE Transactions on Power Electronics， 2021， 36（8）： 9501.

［20］ MARKOVIC U， FRUH N， ARISTIDOU P， et al. Interval-based adaptive inertia and damping control of a virtual synchronous machine［C］//2019 IEEE Milan PowerTech， June 23-27， 2019， Milan， Italy. 2019：1-6.

［21］ 王淋，巨云涛，吴文传，等. 面向频率稳定提升的虚拟同步化微电网惯量阻尼参数优化设计［J］.中国电机工程学报， 2021， 41（13）： 4479.

WANG Lin， JU Yuntao， WU Wenchuan， et al. Optimal design of inertia damping parameters for virtual synchronized microgrids oriented to frequency stability enhancement［J］. Proceedings of the CSEE， 2021， 41（13）： 4479.

［22］ 温春雪， 陈丹， 胡长斌， 等. 微网逆变器的VSG转动惯量和阻尼系数自适应控制［J］. 电力系统自动化， 2018， 42（17）： 120.

WEN Chunxue， CHEN Dan， HU Changbin， et al. Adaptive control of VSG rotational inertia and damping coefficient for microgrid inverters［J］. Automation of Electric Power Systerms， 2018， 42（17）： 120.

［23］ 宋琼，张辉，孙凯，等. 多微源独立微网中虚拟同步发电机的改进型转动惯量自适应控制［J］. 中国电机工程学报， 2017， 37（2）： 412.

SONG Qiong， ZHANG Hui， SUN Kai， et al. Improved adaptive control of inertia for virtual synchronous generators in islanding micro-grid with multiple distributed generation units［J］. Proceedings of the CSEE， 2017， 37（2）： 412.

（编辑：邱赫男）