PCB绕组盘式电机CFD热分析

摘 要：

印制电路板（PCB）绕组盘式电机具有零齿槽转矩、高功率密度、高效率、高设计灵活性、高加工精度等诸多优点，可广泛应用于航空、工业驱动、风力发电等领域。然而，内定子外转子结构的PCB绕组盘式电机受空间限制，定子散热困难，易产生绝缘老化、永磁体退磁等问题。为实现对PCB绕组盘式电机热特性的精确计算，研究气隙封闭条件下流体域的对流散热问题。探究电机内PCB绕组上热量散出的传热路径，提出一种采用由实验关联式导出空气等效导热系数的计算方法，利用计算流体力学（CFD）方法对内部流体流动和热特性进行仿真分析。结果表明PCB绕组盘上90%的热量进入气隙 ，空气等效导热系数的理论和仿真计算值误差不超过5%。最后设计并制造采用单定子双转子结构的PCB绕组盘式电机实验原理样机，通过实验对理论分析的正确性和仿真计算结果的精确性进行验证。

关键词：盘式电机；印制电路板绕组；计算流体力学；表面传热系数；绕组铜耗；温升

DOI：10.15938/j.emc.2024.09.004

中图分类号：TM351

文献标志码：A

文章编号：1007-449X（2024）09-0036-11

收稿日期： 2023-07-26

基金项目：

作者简介：高 鹏（1985—），男，博士，副教授，研究方向为特种电机的分析与设计；

赵鸿健（1999—），男，硕士，研究方向为PCB绕组盘式电机设计；

王晓远（1962—），男，博士，教授，博士生导师，研究方向为电机电磁场的分析与计算。

通信作者：高 鹏

CFD thermal analysis for disk-type machine with PCB windings

GAO Peng， ZHAO Hongjian， WANG Xiaoyuan

（School of Electrical and Information Engineering， Tianjin University， Tianjin 300072， China）

Abstract：

Printed circuit board （PCB） winding axial-flux machines have many advantages such as zero cogging torque， high power density， high efficiency， high design flexibility， and high processing precision. They can be widely used in fields such as aviation， industrial drives， and wind power generation. PCB winding axial-flux machines with internal stator and external rotor structure are subject to space limitation， which causes the difficulty in dissipating heat from the stator and easily brings about problems such as insulation aging and permanent magnet demagnetization. In order to achieve accurate calculation of the thermal characteristics of PCB-winding axial-flux machines， the convective heat dissipation problem in the fluid domain under closed-end air gap condition was investigated. The heat transfer path of heat dissipation from the PCB winding in the motor was investigated， a calculation method using the equivalent thermal conductivity of air derived from the experimental correlation equation was proposed， and the internal fluid flow and thermal characteristics were simulated and analyzed by using the computational fluid dynamics （CFD） method. The results show that 90% of the heat on the PCB-winding plate enters the air gap， and the error between the theoretical and simulated values of the air equivalent thermal conductivity is under 5%. Finally， the experimental prototype of a PCB-winding disk-type machine with a single stator and double rotor structure was designed and built. Correctness of the theoretical analysis and the accuracy of the simulation calculation results are verified through experiments， and the results correspond well.

Keywords：axial flux machine; printed circuit board winding; computational fluid dynamics; convective heat transfer coefficient; winding loss; temperature rising

0 引 言

基于印制电路板（printed circuit board，PCB）绕组的盘式电机为电枢部分采用PCB板刻画绕组的一类电机的统称，简称PCB绕组盘式电机。PCB绕组盘式电机具有零齿槽转矩、高功率密度、高效率、高设计灵活性、高加工精度［1-4］等诸多优点，可应用于航空、硬盘驱动、风力发电［5-7］等场景，受到学者们的广泛关注。PCB绕组盘式电机可设计为单定子单转子、单定子双转子、多定子多转子结构，其中，单定子双转子结构的PCB绕组盘式电机因无单边磁拉力［8］而被广泛应用。目前，对PCB绕组盘式电机的研究主要集中在电磁性能提升，尤其是对PCB绕组拓扑结构的研究［9-12］，对其热特性研究相对较少。

PCB绕组盘式电机的热分析可分为流体域传热和固体域传热分析。区别于传统电机气隙内的圆柱环流，PCB绕组盘式电机流体域为盘型的绕轴漩涡流，相关的传热规律存在差异。在定、转子系统热交换的研究中，HARMAND S等［13］对已有传统定转子系统基流的流动模式、类型以及不同实验条件下的实验关联式进行了总结。HOWEY D A等［14］从工业应用的角度给出轴向磁通电机定子侧和转子侧的表面传热系数对应的实验关联式，并对无量纲常数间的计算关系进行说明。WROBEL R等［15］设计平滑表面和非平滑表面的转子，通过计算流体力学（computational fluid dynamics，CFD）仿真对气隙内对流传热进行计算。RASEKH A等［16-17］引入与非平滑表面转子相关的无量纲常数，采用CFD仿真计算非平滑表面转子的对流换热情况，通过CFD结果计算取定参考温度，获取转子侧表面传热系数关联式。

现有对电机定、转子系统传热的计算和实验研究中，实验装置及模型均采用开放气隙，即环境空气会影响定、转子系统内空气的温度和流动状态。而实际电机中，定、转子系统位于机壳内，气隙可认为封闭且对流，不受机壳外环境空气的影响，参考温度也与环境空气温度无关。为实现对电机热特性的精确计算，本文着重研究气隙封闭条件下电机流体域内的对流散热问题，探究PCB绕组盘式电机内部绕组产热散出的传热路径。为弥补表面传热系数计算的局限性，提出一种采用由实验关联式导出空气等效导热系数的计算方法。利用CFD仿真分析内部流体流动和热特性。为验证理论分析的正确性和仿真计算结果的精确性，设计并制造采用单定子双转子结构的PCB绕组盘式电机实验原理样机，通过实验对理论分析和仿真计算结果进行验证。

1 PCB绕组盘式电机热理论分析

1.1 传热路径简析

PCB绕组盘式电机中的绕组铜耗为数值占比最大的热源，本文仅考虑绕组热量传递到机壳表面的路径。PCB绕组产生的热量在电机内通过热传导和对流传热两种方式传递，热传导对应PCB绕组盘、轴、转子、轴承、机壳的固体传热，对流传热对应转子与机壳之间空腔区域、气隙的流体传热。

PCB绕组盘包含铜绕组和FR-4基盘。加载电流后，铜绕组产生热量，一部分传导到FR-4基盘上，另一部分直接传递到气隙中。而FR-4基盘上的热量一部分通过对流传递到气隙中，另一部分热量则通过与机壳接触传导到机壳上。PCB绕组盘传递到气隙内的热量绝大部分由转子吸收，转子上的热量一部分进入轴，经过轴承传递到机壳，另一部分进入空腔内的空气，通过对流传递到机壳。机壳的热量在表面以对流传热的方式耗散到空气中。

PCB绕组盘式电机采用无铁心定子结构，与铜绕组直接接触的是FR-4基盘，传统电机为金属铁心。同时，PCB绕组盘式电机采用轴向磁通结构，流体域由盘型的绕轴漩涡流组成，传统电机为圆柱环流。两者传热会有较大差异，4.2节将作具体分析。

1.2 对流传热分析

电机定、转子系统流体域的传热包含辐射传热和对流传热，对流传热又包含自然对流传热和强制对流传热。由于辐射传热和自然对流传热的数值很小，本文仅考虑转子旋转时强制对流传热热量。依照传统实验研究，首先计算2个无量纲常数，即旋转雷诺数Reθ以及气隙比G，计算公式为［13］：

Reθ=ωr2ν；（1）

G=gr。（2）

式中：ω为转子旋转角速度；ν为空气运动黏度；g为定、转子间气隙长度；r为转子半径。

不同旋转雷诺数Reθ和气隙比G对应不同的流动类型，包括Couette流、Batchelor流和Stewarson流。本文主要研究低雷诺数状态下的传热状态，研究设置的转速为0～1 500 r/min低速范围。对应的旋转雷诺数Reθ与文献［15］总结的临界值比较，均使得绕轴漩涡流处于层流状态。在已有对定、转子系统内不同范围Reθ及G下定子与转子表面的平均努塞尔数Nu研究中，通过实验研究得到了层流状态时不同气隙比G下Nu关于Reθ的实验关联式，主要分为0.02lt;Glt;0.06时的层流状态和Glt;0.02时的层流状态。

当0.02lt;Glt;0.06时，转子侧使用Boutarfa和Harmand的实验关联式，实验条件为气隙开放、转子中心开口，测量范围不包括转子盘中心［18］，实验关联式为

Nu=0.05（1+5.47×10-4e112G）Re0.5θ。（3）

定子侧使用Dorfman，通过测量无定子时空盘转动得到实验关联式［19］为

Nu=0.35Re0.5θ。（4）

当Glt;0.02时，转子侧使用由DAILY J W和NECE R E［20］实验研究、OWEN J［21］理论推导验证得到的实验关联式，实验条件为气隙封闭、转子中心无开口，测量范围包括转子整个盘面， 实验关联式为

Nu=1/G。（5）

计算表面传热系数用到的公式为

h=λNur。（6）

式中：h为表面传热系数；λ为空气导热系数。

当定子侧和转子侧表面传热系数研究彼此独立时，传统温度场计算中直接使用定子侧或转子侧单侧的表面传热系数来计算热阻，并未针对不同流动类型的热阻计算方法加以区分，导致传统温度场计算存在参考温度选定标准不一、定转子表面传热系数难以统一的局限性。根据流动类型不同确定等效空气导热系数的计算思路，可避免参考温度的影响，有机统一定、转子侧表面传热系数。本文采用空气等效导热系数代替传统单侧表面传热系数进行研究，并得到单侧表面传热系数和空气等效导热系数之间的关系。

文献［12］中PCB绕组盘式电机气隙比G最小为0.015，接近Couette流。大部分研究文献中气隙比G的数值在0.02～0.06之间（0.024［2］、0.028 5［9］、0.038［22］、0.05［23］），接近Batchelor流。在气隙开放的定转子系统中流动类型为Stewarson流，气隙封闭后会转变成Batchelor流［24］。因此，PCB绕组盘式电机中气隙流体的流动类型通常为Couette流和Bachelor流。

Couette流为粘性流层，局部努塞尔数很小，接近定值，仅在气隙极小的情况下出现。各类研究均以G=0.01为例研究此流型，对Glt;0.01的研究很少涉及。可参照传统温度场计算对气隙热阻的处理思路，直接使用已有研究中的转子侧表面传热系数求取热阻，然后得到等效导热系数。

Batchelor流在气隙较大时出现，定、转子表面的边界层之间为流速、温度基本稳定的区域，定子侧与转子侧表面传热系数对应的参考温度相同，均为定、转子侧边界层之间主体空气的平均温度。由定子侧和转子侧表面传热系数导出的热阻串联可得到定、转子之间的热阻，从而得到等效导热系数。

Couette流和Batchelor流的热阻等效思路如图1所示。

图1中：Tstator表示定子侧表面平均温度；Trotor表示转子侧表面平均温度；Tref为选定的参考温度；RCouette表示Couette流下的等效热阻；Rstator表示Batchelor流下定子侧的热阻；Rrotor表示Batchelor流下转子侧的热阻。利用热阻对等效导热系数进行计算，Couette流下表示为

RCouette=Tstator－TrotorP=1hS=gλCouetteS。（7）

式中：λCouette表示Couette流空气等效导热系数；S为有效面积，取定子、转子、机壳轴向投影交集区域面积［18］。

Batchelor流下表示为：

Rstator=Tstator－TrefP=1hsS；（8）

Rrotor=Tref－TrotorP=1hrS；（9）

Rstator+Rrotor=gλBatchelorS。（10）

式中：λBatchelor表示Batchelor流空气等效导热系数；hr表示转子侧的表面传热系数，由式（1）～式（3）和式（6）联立求得，计算公式为

hr=λ0.05（1+5.47×10-4e112G）（ωr2ν）0.5r；（11）

hs表示定子侧的表面传热系数，由式（1）、式（4）和式（6）联立求得，计算公式为

hs=λ0.35（ωr2ν）0.5r。（12）

Couette流和Batchelor流下的空气等效导热系数计算公式为：

λCouette=kAλgrG；（13）

λBatchelor=kBghshrhs+hr。（14）

式中kA、kB为校正系数。式（2）、式（5）、式（6）和式（7）联立可求得式（13），式（8）、式（9）和式（10）联立可求得式（14）。

式（13）和式（14）中空气等效导热系数在使用时只考虑定子侧和转子侧的温度，无需选取中间空气的某一温度作为参考温度。

2 PCB绕组盘式电机CFD仿真

2.1 计算模型及网络

仿真计算模型如图2所示，轴承的滚珠部分建模通过填充内外滚道间区域形成滚珠圆环，如图3所示。仿真模型的表面网格划分如图4所示。

2.2 数学模型及求解条件

为方便仿真模型计算，本文假设：1）空气流动马赫数小于0.7，为不可压缩流；2）材料热导率不随着温度变化而变化；3）电机内流体处于层流状态；4）假设轴承滚道与滚珠间气隙为定值，轴承径向传热能力恒定。

电机内空气流动为稳态层流时，其控制方程组包括连续性方程、动量方程和能量方程。

加载电流为4、5和6 A，分别计算转速在500、1 000和1 500 r/min下的流体场和温度场。PCB表面铜绕组的热源设置上添加最高温度与平均电阻率之间的线性关系，在转子与空气的接触壁面上添加绕轴的切向旋转速度。

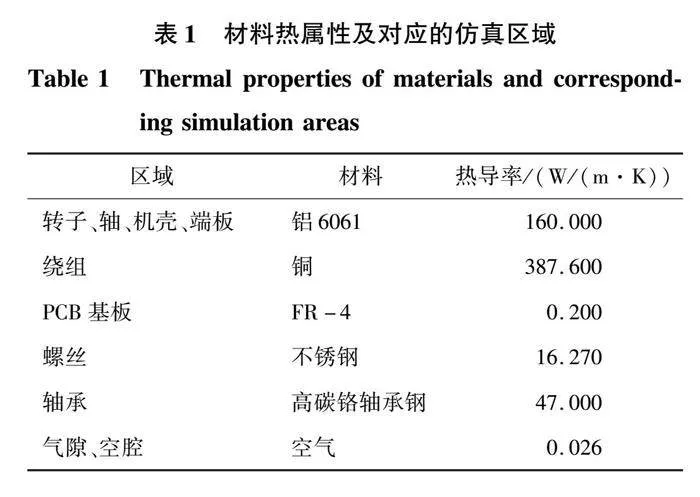
仿真模型中的材料热属性及对应的仿真区域如表1所示。

经仿真与实验反复迭代，在仿真模型中滚珠圆环与内外滚道间分别设置0.001 mm厚度空气对应的接触热阻。机壳和端板表面依照以下经验公式添加表面传热系数［25］：

h=143θ25。（15）

式中θ表示电机所处环境的温度。

3 PCB绕组盘式电机对流实验

3.1 PCB绕组盘静态实验

在进行动态实验和CFD仿真分析之前进行静态实验，以获得最高温度和平均电阻率的对应关系，用于动态实验的绕组温度测定和CFD仿真热源设置。

本文所设计PCB绕组盘如图5所示，采用双层板，正反两面分别均匀排布一层铜绕组，每层全部绕组串联连接，两层铜绕组并联连接。

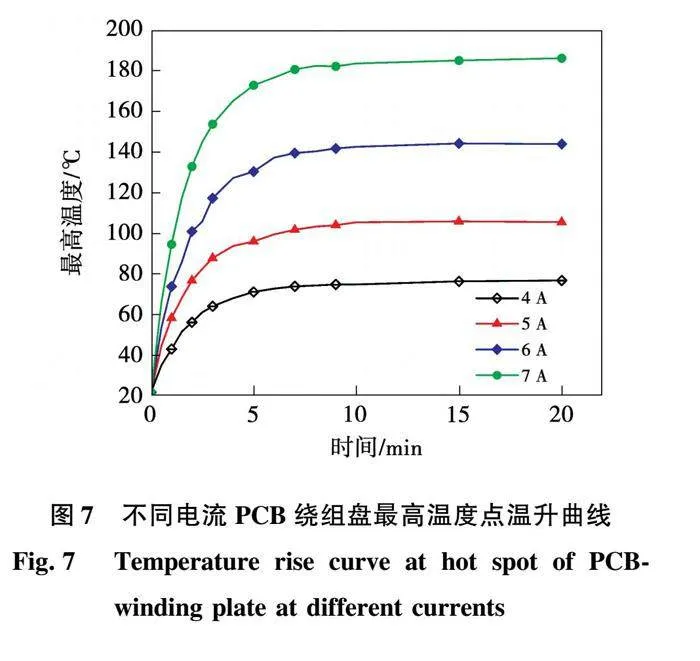
静态实验装置如图6所示，包括热成像仪、示波器、带隔离的电压探头、支撑架、电流源、PCB绕组盘。将PCB绕组盘水平悬空置于桌面上，用支撑架将热成像仪垂直固定于PCB绕组盘正上方，将带隔离的电压探头固定在PCB绕组两端，通过示波器实时读取并记录探头探测到的电压数值。由电流源直接向PCB绕组盘通入不同大小的直流电流，使用热成像仪观测并记录不同时刻PCB绕组盘表面的最高温度，实验中PCB绕组盘最高温度点出现在其最内侧的铜绕组上，温升曲线如图7所示。

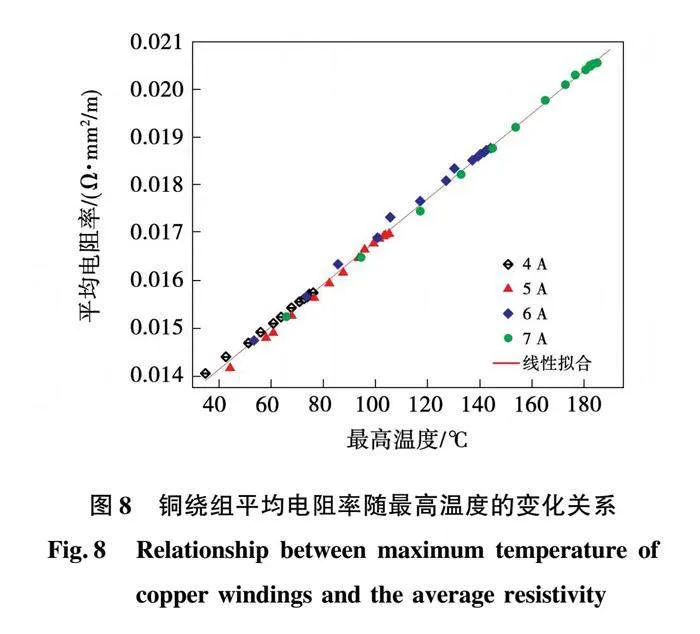
实验过程中每一时刻下的电压与电流相除得到电阻变化，结合铜厚、线长、线宽即可以得到平均电阻率随最高温度的变化关系。加载不同电流时，最高温度与平均电阻率呈线性分布，利用最小二乘法对数据点线性拟合，所得直线将用于动态实验，求得绕组最高温度。铜绕组平均电阻率随最高温度的变化关系如图8所示。

3.2 PCB绕组盘式电机动态实验

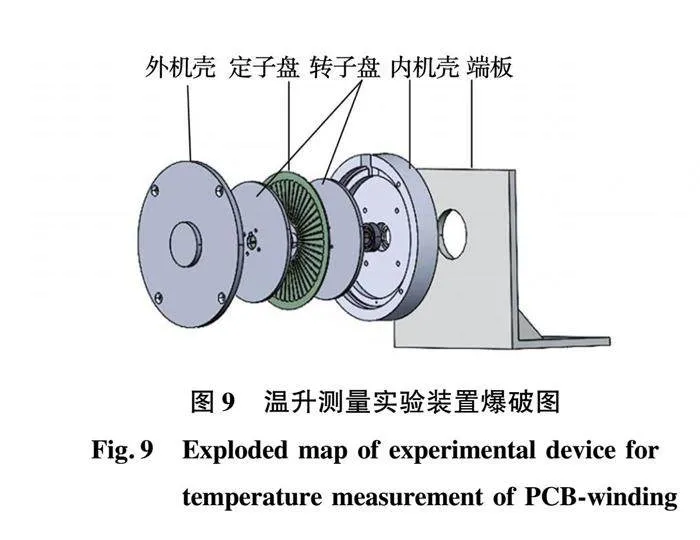
为研究PCB绕组盘式电机的温度场以及流体域对流换热情况及验证实验关联式导出的等效导热系数公式的适用性，本文设计单定子双转子结构的PCB绕组盘式电机的温升测量实验装置，如图9所示。

定子采用静态实验中设计的PCB绕组盘，转子采用不添加磁钢的平滑圆盘。定子与转子之间气隙区域的气隙比G设计为0.006 7，为典型的Couette流。转子与机壳之间空腔区域的气隙比G设计为0.06，为典型的Batchelor流。

动态对流实验的具体实验装置如图10所示。实验装置包括PCB绕组盘式电机实验原理样机、联轴器、无刷直流电机及其控制器、示波器、带隔离的电压探头、电流源。

PCB绕组盘式电机与无刷直流电机通过联轴器相连接，无刷直流电机以恒定转速拖动实验原理样机旋转，带隔离的电压探头固定在PCB绕组两端，通过示波器实时读取并记录探头探测到的电压数值，由电流源向PCB绕组盘加载不同大小的直流电流。

与静态实验的数据处理相似，基于所记录每一时刻的电压与电流值计算出对应的平均电阻率，与静态实验结果中最高温度随平均电阻率变化的拟合直线对照，即可得到不同时刻下PCB绕组盘的最高温度。

4 计算及对比分析

4.1 仿真和动态实验对比

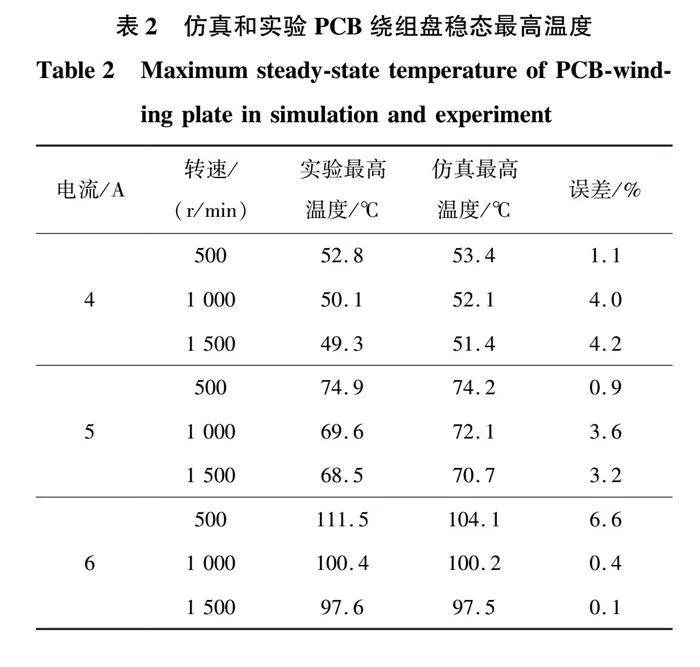
在相同环境温度下，动态实验测量和CFD仿真得到的达到稳态后PCB绕组盘表面铜绕组的最高温度结果如表2所示，结果均取140 min时的稳态温度。

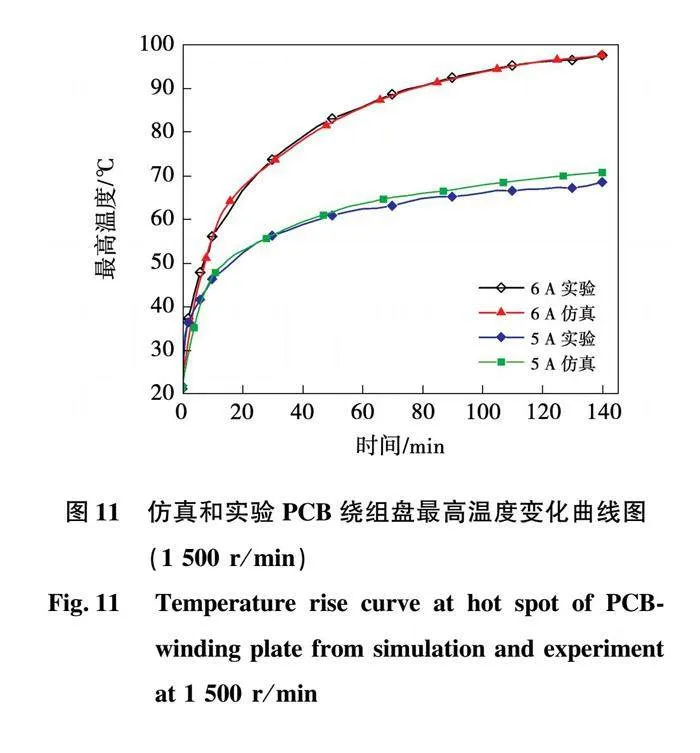
在1 500 r/min转速下，PCB绕组盘加载5 A和6 A电流时，其表面最高温度的变化曲线如图11所示。

仿真结果和实验结果较为吻合，从而验证所建流体场模型和温度场模型的有效性及相应仿真结果的准确性。

4.2 传热路径结果分析

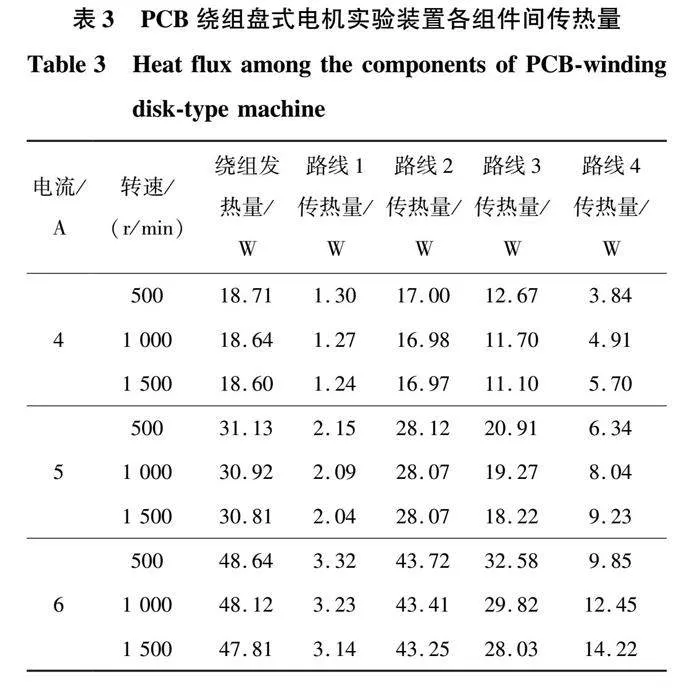
由仿真得出实验装置各主要传热组件之间的传热量如表3所示，主要传热路径由路线1、2、3、4表示，其中：路线1表示气隙内的固体传热，传热路径为FR4-机壳；路线2表示气隙内的流体传热，传热路径为绕组+FR4-气隙-转子；路线3表示空腔内的固体传热，传热路径为转子-轴-轴承-机壳；路线4表示空腔内的流体传热，传热路径为转子-空腔-机壳。PCB绕组盘式电机实验装置各组件间传热百分比如表4所示，由表3计算得到。

路线1与路线2对应气隙内的传热。总体而言，PCB绕组盘约有7%的热量通过固体传热的方式传导至机壳，约有90%的热量进入气隙。PCB绕组盘基盘和空气的导热系数均远低于金属的导热系数，导热性能不佳且与机壳接触的面积很小。因而，与有铁心电机主要通过固体传热的传热路径不同的是：定子上绝大多数的热量通过流体传热传递到转子上，少部分热量通过固体传热直接进入机壳，在Couette流下两部分的传热比率基本保持恒定，受转速和电流的影响较小。

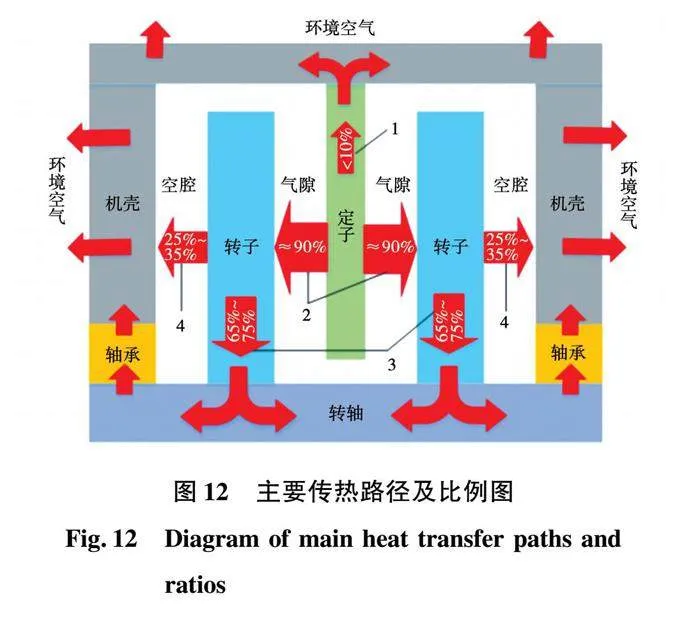
路线3和路线4对应空腔内的传热。空腔内固体传热的比率为60%～75%，流体传热的比率为20%～35%。两部分传热的比率几乎不受电流影响，而随着转速的升高，通过流体传热的比率不断升高，通过轴传导的热量也在不断减少。由于轴向磁通电机结构的特殊性，转子和机壳之间存在空腔且转子旋转同样会在空腔产生漩涡流，转速越高，空腔内空气的对流换热越强，此部分流体传热与轴及轴承的固体传热形成竞争关系。主要传热路径及比例图如图12所示。

其他方向的传热，以转速1 500 r/min、加载电流6 A为例，PCB绕组盘表面有3.3%的热量通过气隙径向传递到轴或直接传递到机壳（（47.81 W-3.14 W-43.25 W）/47.81 W），转子盘上2.3%的热量通过空腔内的空气径向传递到机壳（（43.25 W-28.03 W-14.22 W）/43.25 W）。传热路径中PCB定子盘上的热量约有58%～67%的热量经过轴承，轴承径向传热对PCB绕组盘式电机内部热量散出有较大影响。

4.3 温度、热量和流体分析

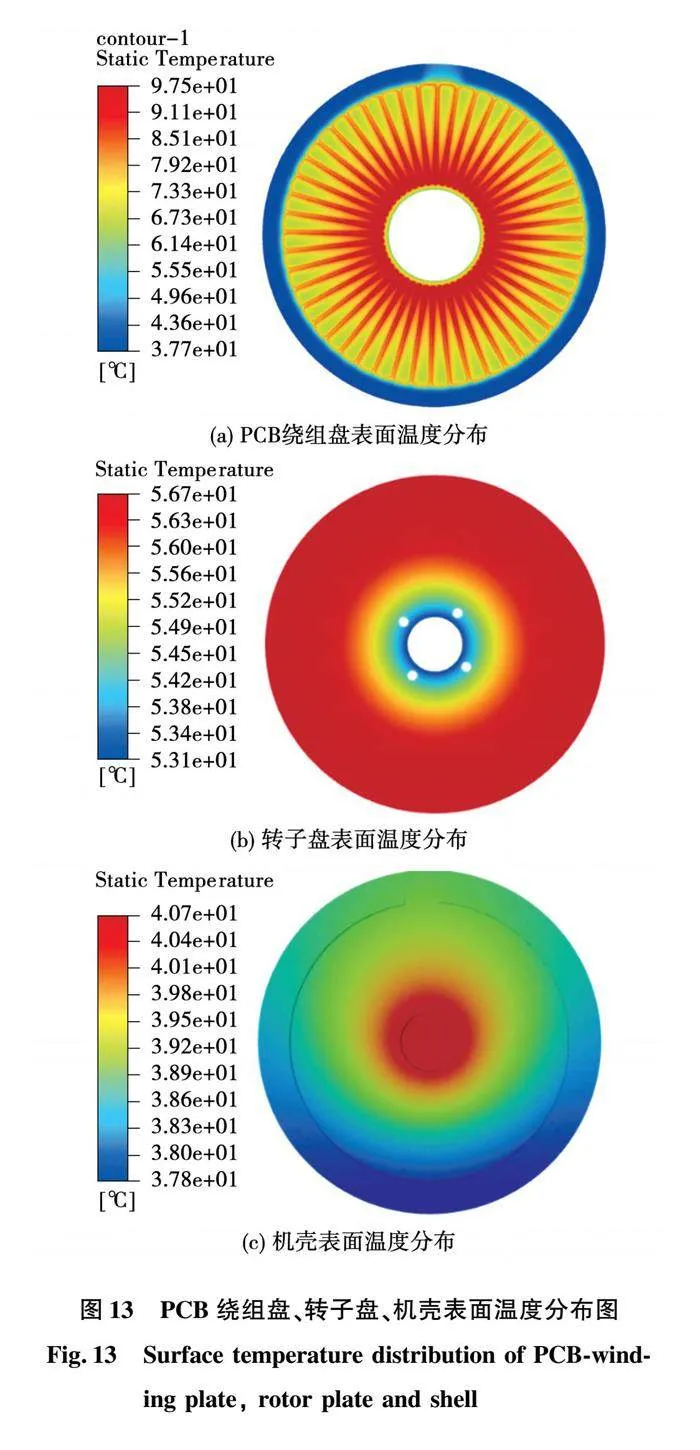
转速为1 500 r/min、加载电流6 A时，PCB绕组盘、转子和机壳内表面的温度分布云图如图13所示。

图13（a）中，由于绕组排布随着径向位置向外变稀疏且铜绕组的热导率要远高于PCB基板材料FR-4，PCB绕组盘表面的温度分布不均匀。沿半径增大方向，铜绕组温度下降明显，铜绕组在最大半径的温度为97.5 ℃，最小半径处温度为86.8 ℃，相差10.7 ℃。相同半径处，基盘上的温度要明显低于铜绕组上的温度。与机壳接触部分的环形基盘区域温度为37.7 ℃，明显低于其他基盘区域，固体传热使得该部分温度与机壳温度接近。图13（b）和图13（c）中，转子和机壳由传热性能较好的Al6061制成，表面最高温度分别为56.7 ℃和40.7 ℃，最低温度分别为52.2 ℃和37.8 ℃，差值分别为4.5 ℃和2.9 ℃，温度分布较为均匀。转子上靠近轴的部分温度较低，机壳上靠近轴的部分温度较高，也可以直观地反映热量从转子流入转轴，再由转轴流入机壳的传热路径。

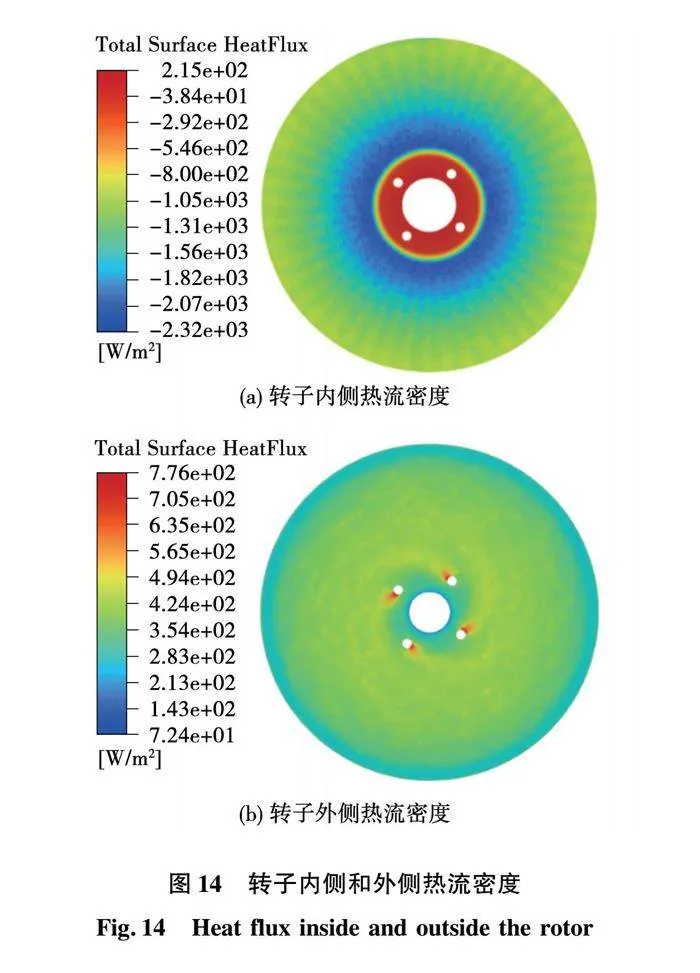
转子气隙侧和空腔侧与空气接触部分的热流密度分布云图如图14所示，正值代表热量从转子表面传入空气，负值则相反。

图14（a）中，气隙空气的热量传入转子内侧， PCB绕组盘在转子盘内侧轴向投影区域的热流密度为负值。转子内侧热流密度分布受PCB绕组盘的温度分布影响十分明显，转子盘上靠近PCB绕组盘上铜绕组的部分热流密度大，最高为-2 320 W/m2，出现在投影后铜绕组最小半径处。图14（b）中，转子外侧的热量传入空腔空气，转子盘外侧的热流密度为正值，分布较为均匀。转子盘边缘的热流密度较小，螺丝孔附近热流密度较大，最高为776 W/m2。转子旋转时，螺丝结构也会影响局部气流，进而影响局部热流。

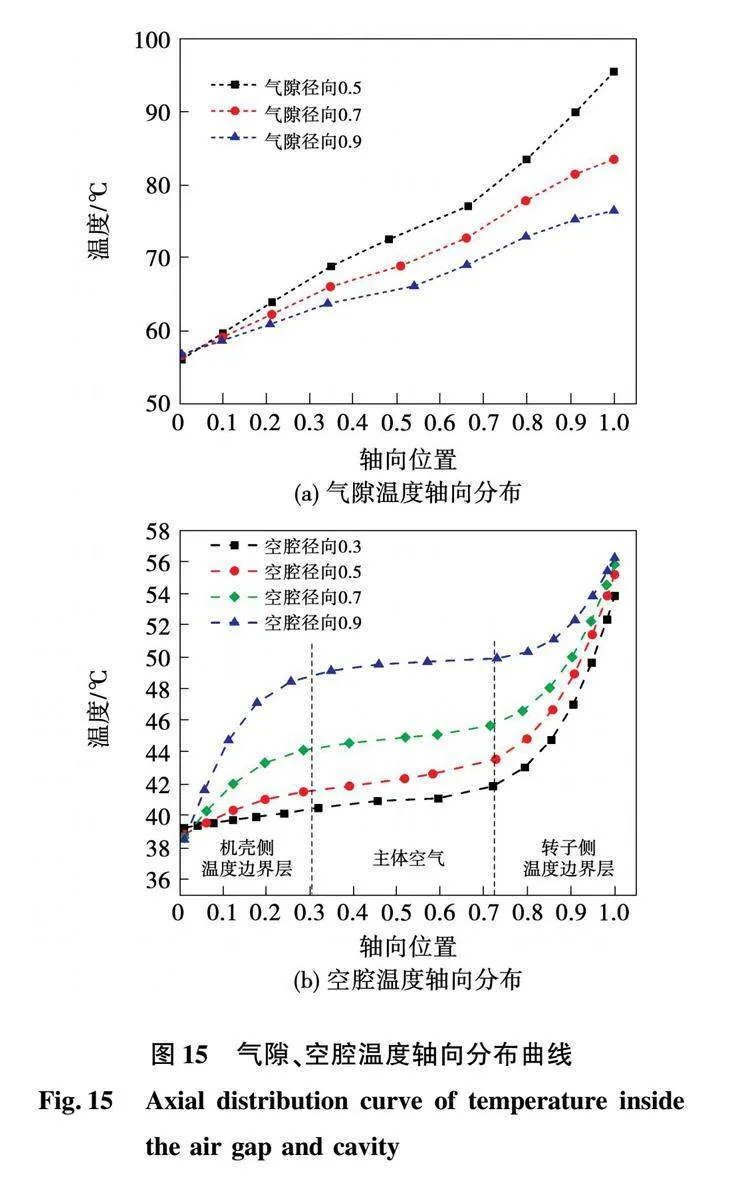
气隙和空腔中不同径向位置下的轴向温度分布如图15所示，取转子到PCB绕组盘方向为气隙轴向位置正方向，取机壳到转子方向为空腔轴向位置正方向，取半径由内向外方向为径向位置正方向，径向位置和轴向位置分别选取转子半径和气隙及空腔轴向间距进行归一化处理。图15（a）中，气隙内的Couette流中的空气黏性作用很强，且层流下流速平缓，不同径向位置下的温度沿着轴向分布呈线性。图15（b）中，空腔内的Batchelor流转子侧和机壳侧温度边界层之间的主体空气区域温度变化明显趋于平缓，此段位置存在大量受黏性效应影响较小的流体。

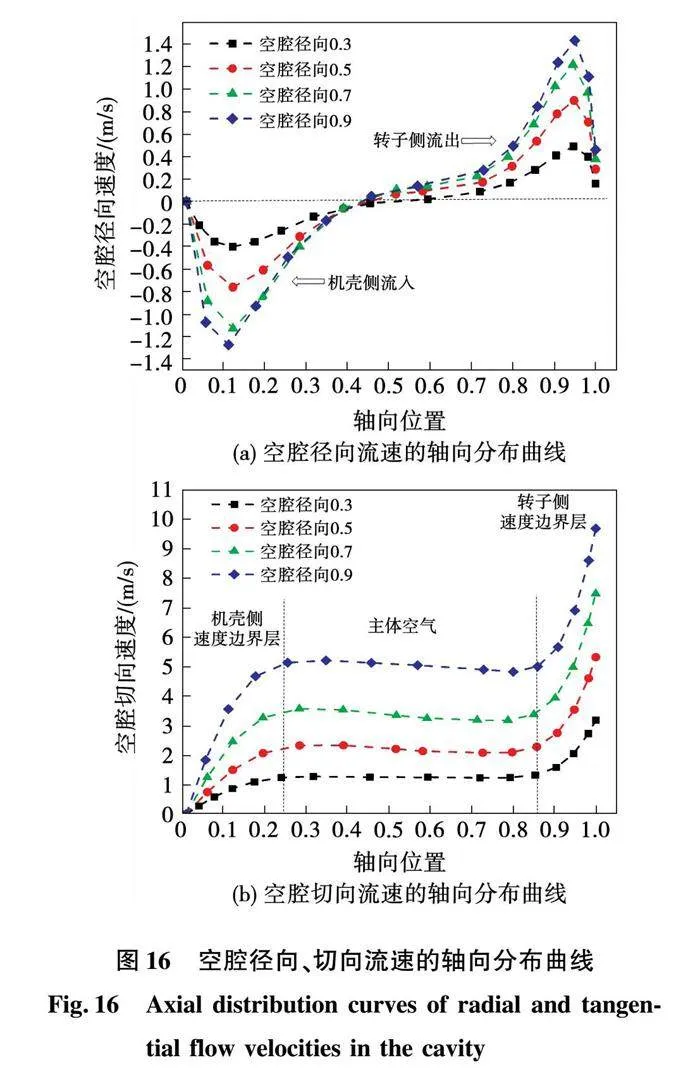
空腔中不同径向位置下流速的切向分量和径向分量的轴向变化图如图16所示。图16（a）中，Batchelor流的径向分量在转子侧流出，在机壳侧流入，且速度大小上流出大于流入，这一结果与RASEKH A等［16］的仿真结果吻合。图16（b）中，Batchelor流的切向分量速度最高，为速度分量的主要成分，且与图15（b）中空腔内轴向温度变化曲线趋势相似。Batchelor流下切向分量是影响对流换热的主要因素，轴向速度分量小于切向分量和径向分量两个数量级，不予考虑。

4.4 空气等效导热系数对比

将空气域视为热传导模型，利用傅里叶定律得到以下公式，由4.3节CFD仿真结果求解平均空气等效导热系数λavg，即

λavg=gPfSΔTavg。（16）

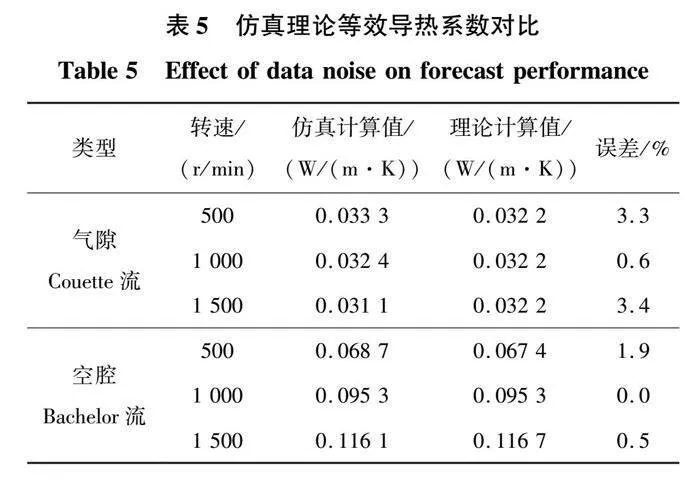
式中ΔTavg表示平均温度之差。气隙Couette流取图13（a）和图13（b）中PCB绕组盘表面和转子表面的面平均温度得到差值。空腔Bachelor流取图13（b）和图13（c）中转子表面和机壳表面的面平均温度，得到差值Pf表示流过流体的热量，气隙Couette流取图14（a）中转子内侧热流密度对面积分得到，空腔Bachelor流取图14（b）中转子外侧热流密度对面积分得到。仿真计算结果与理论计算结果的对比如表5所示，理论计算值由式（13）、式（14）得到，仿真计算结果由式（16）得到。

Batchelor流下等效导热系数计算公式与仿真计算结果的误差在2%以内，Couette流下误差最高为3.4%。PCB绕组盘的热分布不规律、不均匀，会对计算公式的准确性造成一定影响。

5 结 论

本文理论分析PCB绕组盘式电机内的流体传热，得到空气等效导热系数计算公式。设计并制造PCB绕组盘式电机的实验原理装置，通过仿真分析和实验，验证理论分析的正确性和仿真计算模型的精确性。通过本文研究所得结论如下：

1）PCB绕组盘上铜绕组产生的热量主要通过轴向传递，热流传递路径可分为气隙传热和空腔传热，气隙传热中约有90%的热量通过空气传递，极少热量通过PCB绕组盘直接传递到机壳，空腔传热中空腔的流体传热与轴及轴承的固体传热通过竞争共同影响热量传递，随着流速增加，流体传热的比率上升。

2）PCB绕组盘式电机轴承径向传热对PCB绕组盘的散热会产生较大影响，传热路径中PCB定子盘上的热量约有58%～67%的热量经过轴承。

3）所提出空气等效导热系数计算公式弥补了表面传热系数计算参考温度选定以及定转子表面传热系数不统一的缺点，理论计算值和仿真计算值误差不超过5%，为PCB绕组盘式电机的温度场分析提供参考，可应用于PCB绕组盘式电机热网络及有限元模型中，计算气隙或其他相似结构流体域的热阻阻值。

参 考 文 献：

［1］ NEETHU S， NIKAM S P， PAL S， et al. Performance comparison between PCB-stator and laminated-core-stator-based designs of axial flux permanent magnet motors for high-speed low-power applications［J］. IEEE Transactions on Industrial Electronics， 2020， 67（7）： 5269.

［2］ JANG G H， JANG J H. Development of an axial-gap spindle motor for computer hard disk drives using PCB winding and dual air gaps［J］. IEEE Transactions on Magnetics， 2002， 38（5）： 3297.

［3］ KESGIN M G， HAN P， TARAN N， et al. Design optimization of coreless axial-flux PM machines with litz wire and PCB stator windings［C］//12th Annual IEEE Energy Conversion Congress and Exposition （ECCE）， October 11-15，2020， Detroit， USA.2020： 22-26.

［4］ AYDIN M， GULEC M. A new coreless axial flux interior permanent magnet synchronous motor with sinusoidal rotor segments［J］. IEEE Transactions on Magnetics， 2016， 52（7）： 1.

［5］ REED T， BAKHOUM E. Axial flux permanent magnet alternator using printed circuit board stators［C］//IEEE SoutheastCon 2008， April 3-6，2008， Huntsville， USA. 2008： 454-459.

［6］ WU Junfeng. Design of a miniature axial flux flywheel motor with PCB winding for nanosatellites［C］//International Conference on Optoelectronics and Microelectronics （ICOM）， August 23-25， 2012， Changchun， China. 2012： 544-548.

［7］ TOKGOZ F， CAKAL G， KEYSAN O， et al. Design and implementation of an optimized printed circuit board axial flux permanent magnet machine［C］//24th International Conference on Electrical Machines， August 23-26，2020， Gothenburg， Sweden. 2020： 111-116.

［8］ DI STEFANO R， MARIGNETTI F， SCARANO M. Optimal feeding of an etched winding mini-motor［C］//ISIE’97 Proceeding of the IEEE International Symposium on Industrial Electronics， July 7-11， 1997， Guimaraes， Portugal. 1997： 474-479.

［9］ NEETHU S， NIKAM S P， WANKHEDE A K， et al. High speed coreless axial flux permanent magnet motor with printed circuit board winding［C］//4th Annual Meeting of the IEEE Industry Applications Society （IAS）， October 1-5， 2017， Cincinnati， USA. 2017： 1-6.

［10］ NOH M D， KIM J， PARK Y W， et al. Comparisons of concentrated printed-circuit stator windings for axial flux permanent magnet machines［C］//IEEE/ASME International Conference on Advanced Intelligent Mechatronics （AIM）， July 8-12， 2019， Hong Kong， China. 2019： 229-234.

［11］ WANG Xiaoyuan， LU Huaidong， LI Xiang. Winding design and analysis for a disc-type permanent-magnet synchronous motor with a PCB stator［J］. Energies， 2018， 11（12）： 3383.

［12］ MARIGNETTI F， VOLPE G， MIRIMANI S M， et al. Electromagnetic design and modeling of a two-phase axial-flux printed circuit board motor［J］. IEEE Transactions on Industrial Electronics， 2018， 65（1）： 67.

［13］ HARMAND S， PELLE J， PONCET S， et al. Review of fluid flow and convective heat transfer within rotating disk cavities with impinging jet［J］. International Journal of Thermal Sciences， 2013， 67（1）： 1.

［14］ HOWEY D A， CHILDS P R N， HOLMES A S. Air-gap convection in rotating electrical machines［J］. IEEE Transactions on Industrial Electronics， 2012， 59（3）： 1369.

［15］ WROBEL R， VAINEL G， COPELAND C， et al. Investigation of mechanical loss components and heat transfer in an axial-flux PM machine［J］. IEEE Transactions on Industry Applications， 2015， 51（4）： 3000.

［16］ RASEKH A， SERGEANT P， VIERENDEELS J. Convective heat transfer prediction in disk-type electrical machines［J］. Applied Thermal Engineering， 2015， 91： 778.

［17］ RASEKH A， SERGEANT P， VIERENDEELS J. Fully predictive heat transfer coefficient modeling of an axial flux permanent magnet synchronous machine with geometrical parameters of the magnets［J］. Applied Thermal Engineering， 2017， 110（2）： 1343.

［18］ BOUTARFA R， HARMAND S. Local convective heat transfer for laminar and turbulent flow in a rotor-stator system［J］. Experiments in Fluids， 2005， 38（2）： 209.

［19］ DORFMAN L A. Hydrodynamic resistance and the heat loss of rotating solids［M］. Edinburgh： Oliver and Boyd，1963.

［20］ DAILY J W， NECE R E. Chamber dimension effects on induced flow and frictional resistance of enclosed rotating disks［J］. Journal of Basic Engineering， 1960， 82（1）： 217.

［21］ OWEN J， ROGER R. Flow and heat transfer in rotating-disc systems. Volume I-Rotor-stator systems［J］. NASA STI/Recon Technical Report A， 1989， 90： 45759.

［22］ SCHUMANN C， MULLER T， STEIN E， et al. Axial-flux-machine with an ironless fractional slot winding［C］//40th Annual Conference of the IEEE-Industrial-Electronics-Society（IECON），October 29-November 1， 2014， Dallas， USA. 2014：424-430.

［23］ TSAI M C， HSU L Y. Design of a miniature axial-flux spindle motor with rhomboidal PCB winding［J］. IEEE Transactions on Magnetics， 2006， 42（10）： 3488.

［24］ BRADY J F， DURLOFSKY L. On rotating disk flow［J］. Journal of Fluid Mechanics， 1987， 175： 363.

［25］ 魏永田， 孟大伟， 温嘉斌. 电机内热交换［M］. 北京： 机械工业出版社，1998.

（编辑：邱赫男）