数形结合思想在小学数学教学中的实践应用

摘 要：数形结合思想在数学教育领域具有不可替代的核心价值，特别是在小学的数学教学中扮演着极其重要的角色.将数学的抽象概念与形象的图形紧密结合，不仅加深了学生对数学概念的理解，还提升了他们解决具体问题的能力.本文通过分析具体的教学案例，探讨了数形结合思想在小学数学教学中的应用，突出了其在培养学生的数学核心素养中的关键作用．

关键词：数形结合思想；小学数学；实践应用

在数学这一学科领域中，“数字”与“图形”构成基本的研究元素，它们之间存在着一种辩证的对立统一关系.在小学阶段采用数形结合思想的教学方法，可以帮助学生透彻理解数学知识的形成过程，使学生不仅知道各种数学现象的表象，还能洞察其背后的逻辑，从而培养学生深厚的数学认知基础和运用这种思想的技巧.基于对数形结合思想的理解，学生能够积极主动地探索数学，将抽象难懂的数学理论转化为直观的图形表示，实现思考的可视化，从而深刻把握数学概念的真正含义.这种思想会激发学生对数学的兴趣，有效提升他们的数学思维能力及其核心素养的整体发展．

1 数形结合思想在小学数学中的教学实践

数形结合思想强调通过数与形的互相转化和对应关系来解决数学问题.［1］这里的“数”涉及数字、代数式、方程、函数以及数量关系等，它们共同展示了数学的精确性；“形”则指代几何图形和函数的图象，体现了直观性.

作为一种基本的数学思维方式，数形结合思想在小学数学教育中扮演着不可或缺的角色.它通过结合抽象的数学问题和直观的图形帮助学生更深刻地理解和掌握数学概念，从而提升他们的解题技能.［2］本文以“数学广角——数与形”为案例，探讨这一思想在实际教学中的应用．

1.1 课前预习：激发数形结合思想运用意识

在课前准备阶段，教师可以通过设计具体问题来激发学生的数形结合意识.［3］例如，在探究连续奇数求和的问题时，教师可引导学生计算“1+3+5+7”的和，并提示他们注意和与特定几何图形，如正方形的面积之间的联系.当学生完成计算后，他们知道算式总和等于16，这正是4的平方，即一个边长为4的正方形的面积.通过这样的发现，学生不仅体会到数学的趣味性，同时也能观察到数学中数与形之间的相互映射和解释.这种体会能深化学生对数学的兴趣和探索欲望．

1.2 课堂探究：提升数形结合思想的运用能力

在课堂互动环节中，教师利用多媒体工具展现的多种图形不仅可以吸引学生的眼球，也能为他们打开一个直观的数学世界大门.学生被邀请进行独立思考，如分析图中不同颜色的小正方形数量，并探索这些数目与图形序号之间的关系.通过这种方式，学生逐步发现深灰色和浅灰色正方形数量的规律.学生观察到随着图形序号的增加，深灰色正方形的数量等于序号本身，浅灰色正方形数量则表现为递增趋势.这类发现不仅加深了他们对数学规律的理解，也锻炼了他们对数形结合思想的运用能力.进一步地，通过小组讨论，学生之间的互动和合作得到加强.学生在小组内互相启发，探讨分数之和与图形面积的关系.这种探讨帮助他们更全面地理解数形结合的概念.学生可能会发现某个分数序列的和与某种图形的面积直接相关，这种关联使得分数累加与图形面积的相互验证和解释成为可能．

1.3 情境创设：生活中数形结合思想的实际应用

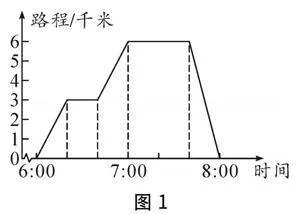
教师可以构建一个紧贴学生日常生活的实例，进一步加强学生在生活中数形结合思想的实际应用能力.例如，小明的爸爸每天清晨跑步前往6千米外的广场进行锻炼，请详细分析小明爸爸的行进路线（如图1）．

接下来，学生将运用数形结合思想来处理以下几个问题.

（1）假设小明的爸爸全程未休息（不考虑速度变化），他跑向广场所需的时间为 分钟.

（2）小明的爸爸在广场逗留了 分钟.

（3）小明的爸爸回家的速度为每小时 千米．

图形展示了时间与路程的关系.直线与时间轴平行时，表明小明的爸爸停止不动.路程从0到6千米说明他前往广场，从6千米回到0则表示他归家.针对问题（1），根据图示，小明的爸爸早上6点出发，7点到达广场，整个过程耗时60分钟.期间有线段平行于时间轴，显示他休息了20分钟.若不停歇，实际到广场的时间为40分钟.关于问题（2），小明的爸爸7点抵达广场，7点40分开始返回，故他在广场的停留时间为40分钟.从图中还可以看出，小明的爸爸8点回到家，回程用时20分钟.通过计算可知，他的返回速度为18千米/时．

1.4 专题训练：巩固数形结合思想的应用

在小学数学的专项练习中，教师精选适合的题目，以加强学生数形结合思想的运用技巧.例如，通过对一个大三角形被切分成数个小三角形的分析，学生可以估算出阴影部分所占的比例.这类习题不仅是对学生数形结合思想观念理解的一种考查，同时也提高了他们使用数学知识来解决实际问题的能力.实际情境与折线图的结合进一步扩大了数形结合思想的使用范围，并且让学生在处理复杂的问题时能更加灵活地运用已学的知识.［4］教师通过这些专项训练，不仅巩固了学生的学习成果，还扩展了数形结合思想的实际应用场景，使他们能够在面对真实世界的问题时，有效地应用数形结合思想．

2 数形结合思想在小学数学教学中的有效应用策略

2.1 “以形助数”在小学数学教学中的应用策略

在小学数学的教学过程中，运用“以形助数”策略显得尤为关键，该策略通过图形的形象表达帮助学生深刻理解数学的各种概念.利用数线和数轴这些工具，学生可以直观地了解数字的顺序及其相对大小.这不仅使他们对整数有了更加深入的了解，同时也为学习分数和小数提供了实用的视觉辅助.在分数的具体教学中，通过使用直观的图形，学生可以更准确地掌握分数的单位和比较分数的大小，进一步加深对数学概念的理解.在探讨算法时，教师利用直观的图形帮助学生具体理解分数加减运算中的通分过程，让学生可以形象地把握复杂的计算步骤.在解决具体问题，如植树问题时，教师运用线段图分析数据关系，构建数学模型，显著增强了学生处理这类问题的技能.在统计学的教学中，统计图的形象展示，不仅简化了数据处理流程，也增强了学生在数据分析和预测方面的技能.“以形助数”的策略不仅加深了学生对数学概念的理解，也有效提高了他们解决实际问题的能力，为他们的数学学习奠定了坚实的基础，使得他们在数学的学习之路上更加得心应手．

2.2 “以数解形”在小学数学教学中的应用策略

教学中应用“以数解形”的策略作为解开“图形与几何”领域之谜的关键，能够帮助学生通过定量分析深入探究几何形状的核心属性.教师通过运用多感官的教学手段，如模型搭建和实际操作，让学生在观察和感觉几何形状的同时，通过测量等活动，将这些感知转换成具体的数据，以此来探讨形状的特征.例如，在学习过程中，学生通过测量线段长度来学习如何用数字描述形状的属性，这种方法基础性地介绍了如何利用数字解释长方形和三角形的边角特征以及圆的基本特性等更高级的几何概念.在进阶学习，如图形的对称性、平移和旋转等概念中，学生通过数学的语言来准确描述和分析，不仅提升了对几何变换的理解，还练习了使用数学工具分析图形运动的技能.在具体解决问题，如计算长方体体积时，教师会引入小正方体模型，引导学生在构建和计算过程中自行发现体积公式.这种教学方式不仅让学生经历数学知识的形成过程，还极大地提高了他们的空间想象力与逻辑推理能力.通过这样的“以数解形”应用，学生对几何知识的理解更加深入，为未来的数学学习奠定了坚实的基础，在数学的世界中更加自如．

2.3 “数形互助”在小学数学教学中的应用策略

“数形互助”的教学方法在小学阶段非常有效，这种方法结合了数学中的数字和几何中的形状，极大地增强了学生对数学概念的理解和应用能力.教师通过此策略引导学生发现数与形之间的密切关系，使用恰当技巧深入挖掘数学的本质.以“角的种类”为例，利用活动角度器及测量工具，学生可以直接操作感受角度的变化.从0°起始，学生主动调整角度器，直到90°.教师解释直角及区分锐角和钝角.当角度增至180°，平角的概念被介绍，360°的完整圆周角则标志着角度分类的结束.这种互动和实践的教学模式不仅帮助学生直观理解角度的大小及其分类，也使他们能够将几何形状与数值紧密结合，建立起完整的数学理念.

2.4 加强指导，培养学生的作图能力

在小学数学的课程中，提高学生的作图能力是实现数学与几何结合教学目的的关键所在.因此，教师需要仔细策划教学活动，确保使用的图形既标准又能精准表示数与形之间的关系，防止学生对图形知识的误解.因而，教师必须有计划地提高学生的作图能力，指导他们如何准确绘制线段图、平面几何图形、三维图形及比例图等，这些能力对于将数学概念具象化非常关键.教师通过有效的示范和指导，可以帮助学生形成正确的作图习惯，并教授他们如何根据具体题目的需求选择合适的图形以辅助思考和解决问题.这样的绘图训练使学生能够将抽象的数学概念直观地转换为具体的图形表达，加深他们对数学原理的理解，从而提高解题效率.总体来说，通过

加强学生的作图能力的培养，教师不仅帮助学生更有效地掌握数学知识，还能激发他们的创造性和想象力，调动学生主动学习数学知识的热情．

3 结语

数形结合思想的教学策略突破了传统教学的界限，成为培养学生综合能力的关键手段.面对数形结合思想的教学需求，教师应不断探索这一策略在新环境下的应用，调整和完善教学方法，以适应教育领域的不断变化.随着教育实践的创新，数形结合思想的教学将在小学数学教育中发挥更加核心的作用，为学生的全面发展和终身学习奠定坚实的基础．

参考文献

［1］于亚群.数形结合思想在小学数学教学中的应用研究［J］.华夏教师，2024（15）：55-57．

［2］付小玲.浅析数形结合思想在小学数学教学中的应用［J］.甘肃教育研究，2024（7）：142-145．

［3］赵晶.“数形结合”思想在小学数学教学中的实践探究［J］.数学大世界（下旬），2024（4）：53-55．

［4］张登妹.数形结合思想在小学数学教学中的应用研究［J］.教师，2024（7）：48-50．