数学文化融入小学数学课堂教学的研究

摘 要：数学文化的传递是数学课堂的重要任务之一.本文以人教版五年级上册数学教材中“多边形的面积”教学为例，对其中的数学文化类型和形式进行研究，分析其中的育人价值，以学生拼剪的数学活动方式对多边形的面积进行探究，通过以文润心的方式育人，又反过来实现以文化人、润心启智的目的．

关键词：数学文化；小学数学；课堂教学

当下应试教育、功利教育等不恰当的教育风气，导致学生以分数为重，认为数学只是一门学习计算和几何图形的枯燥学科，对数学有自己的文化这一认知薄弱甚至缺失.义务教育普及后，小学阶段是接受系统教育的开始，是学生数学观形成和发展的关键时期.学生需要除基本数学知识以外的数学文化的浸润，更需要教师在无形中激发学生学习数学的兴趣，增强数学文化意识.课堂教学是渗透数学文化的重要且关键的实施过程.因此，数学文化在小学数学课堂教学的研究就显得至关重要，从而达到以文化人的目的．

1 小学数学教材中数学文化的内容及形式

为将数学文化更好地融入课堂教学中，需要了解小学数学教材中数学文化的类型、编写方式、呈现方式等，基于这些思考，笔者得出以下分析结果.

小学数学教材中的数学文化大体上分为以下四个类型：①体现科学价值的内容，如学习人教版《义务教育教科书数学五年级上册》在“小数除法”中，对数字黑洞的解释和举例；②体现应用价值的内容，如学习人教版《义务教育教科书数学五年级下册》中“因数和倍数”时，对街道门牌号和身份证号码的知识普及；③体现人文价值的内容，如学习人教版《义务教育教科书数学五年级下册》中“长方体和正方体”时，对几何学和“几何学之父”欧几里得相关知识的了解；④体现美学价值的内容，如学习人教版《义务教育教科书数学六年级上册》中“比”时，对“黄金比”的描述，其中图形的展示给人以优美的视觉感受．

在栏目设置上，教材中多以“你知道吗”“生活中的数学”“数学广角”“数学游戏”等栏目传递相关的数学文化知识.呈现方式上多以情境图形式、纯文字形式或连环画的形式呈现.［1］因为教材纸张的限制，连环画的形式虽然更能激发小学生的阅读兴趣，但在教材中数量是较少的.情境图的形式，如苏教版学习使用计算机计算时，对筹算、算盘、计算器和计算机图片的展示和发展历程介绍，其中，图片的直观展示不仅符合小学生的身心特征，而且更具冲击力，也能给学生留下发挥其想象力的空间.此外，在对文字的阅读中，学生会结合情境尝试去理解文字背后所表述的意义，借此培养学生的数学思维习惯和数学表达的能力，也是数学育人功能的表现之一．

2 数学文化融入教学的案例研究

在数学课程中融入数学文化是基础教育数学课程改革的要求.数学文化不仅承载于数学符号和内容，更多的是通过数学活动得以体现的［2］，所以教师要关注学生在数学活动里的创造性思维和创新意识.因此，笔者以人教版《义务教育教科书数学五年级上册》中“多边形的面积”为例，设计以下教学活动.

2.1 相关数学文化分析

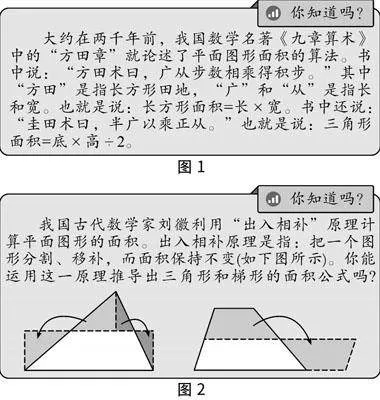
学习“多边形的面积”一章时，涉及的数学文化有体现人文价值、美学价值、应用价值以及科学价值的内容，部分内容融入例题、习题中，最明显的是以“你知道吗”栏目出现的对我国古代数学文化的介绍，一是出现在学习完三角形面积之后的关于《九章算术》中就“方田章”中论述的平面图形面积的算法的介绍（如图1）；二是学习完梯形面f430fcec8b6a02913cce2e3e02b7ad44c5fb3604be3b854dacbb4cedd03cdd39积后对刘徽利用“出入相补”原理计算平面图形的面积的介绍（如图2）．

2.2 相关数学文化的育人价值分析

该单元出现的《九章算术》和“出入相补”原理具有科学和人文的教育价值.“出入相补”原理是中国古代几何中最基本、最基础的原理，其蕴含的思想方法与《九章算术》中的思想方法是一致的.一方面，学生通过数学活动可以深切感悟数学的应用价值，激发其创新意识和创新能力，拓展其数学思维与方法；另一方面，通过数学活动可以引领学生感受数学文化的魅力、数学家的精神和数学思想，厚植家国情怀.此外，数学中的数学思想和方法，不仅可以用来解决数学问题，还可以用该思想和角度看待生活中遇到的挫折与苦难，形成积极向上的生活态度．［3］

2.3 教学活动设计

活动一：探索平行四边形的面积.

活动导入：教师先展示长方形和平行四边形两个图形，然后要求学生比较两个图形的面积大小.学生自行讨论各自的方法.教师对学生自己想出来的好的方法表示赞扬以及适当的补充．

活动过程：教师引导学生在方格纸上通过数格子的方法让学生发现长方形的面积和平行四边形的面积一样且是平行四边形底乘高的计算结果后，通过提供的学具剪一剪、拼一拼，在探究与实践的活动过程中让学生自行探索其中的转化过程．

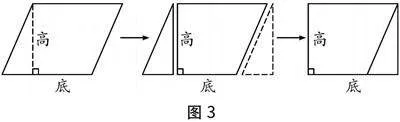
学生通过剪拼发现先将平行四边形沿高剪开，把三角形向右平移，就会发现可以拼成一个长方形（如图3）.教师提问“转化后，长方形的长和宽与平行四边形有什么联系”，学生转化后回答“长方形的长相当于平行四边形的底，长方形的宽相当于平行四边形的高”，通过长方形的面积算法推算出平行四边形的面积＝底×高．

教师提问“如果没有方格纸，我们将如何研究平行四边形的面积”，学生在经过将平行四边形通过剪拼的方式组成长方形的数学活动过程，至少可以很明确地说出通过剪拼的操作，将不熟悉的平面图形转化为我们熟悉的图形进而求面积，其中的本质就是化归思想，因为教学对象是小学生，所以教师可以用通俗的语言将这一思想进行传递，即将一个问题从困难化为复杂，从复杂到简化的过程，是通过问题的转化来解决问题的一种方法.生活中，我们常常没有办法直接解决一个问题，但我们不妨换种思维，另辟蹊径.其中元素的转换等过程涉及数形结合思想，可以借助形的几何直观性来阐明数之间的某种联系，借此推导出图形的面积公式．

活动总结：在学习平行四边形面积时，学生将平行四边形转化为长方形，找出了两者元素之间的转化关系，进而探究出了平行四边形的面积公式，这样的方式是将未知的图形转化为已知图形，有化归思想，也有数形结合的思想，这是我们学习图形面积的一种基础方法.此外，对于这种转化的思想，需要让学生深刻理解，不仅仅是图形的转化，生活中很多看似无解的问题与困难，换一种角度思考后，也常常会迎刃而解，传递积极的生活态度．

活动二：探索三角形的面积.

活动导入：教师指出每一位学生都有佩戴红领巾，红领巾是少先队员的标志，它代表红旗的一角，是用革命先烈的鲜血染成的，戴上红领巾就意味着一份担当、一份荣耀和一份责任.接下来我们看看红领巾的形状，大家想想三角形的红领巾又该如何转换得到它的面积公式？

探索三角形面积时，教师明确学生已经经历了平行四边形的面积探索，因此至关重要的是引导学生类比探索平行四边形面积时的剪拼的方式，化未知为已知，让学生自主进行数学活动探究.学生经过操作发现用两个一样的直角三角形可以拼成一个长方形，两个锐角三角形或是钝角三角形可以拼成平行四边形（如图4），平行四边形的底相当于三角形的底，平行四边形的高相当于三角形的高，发现两个相同的三角形的面积等于拼成的平行四边形的面积，由此推算出三角形的面积＝底×高÷2．

在上述两个数学活动操作并推导出面积公式后，教师提问“过去人们需要计算各种形状的田地的面积时是如何计算的”，由此引出相应的数学文化《九章算术》.小学阶段的学生对具体事物的接受能力比抽象事物强，因此建议以动态的形式介绍《九章算术》“方田章”中的面积计算方法.通过展示“方田章”中平面图形面积求法的展示，学生会发现古人同我们的计算方式是一致的.通过古今对比，教师发出疑问“我们是通过图象之间的剪拼与转化，将未知化为已知，那么古人又是如何发现并得到这些计算的公式”.在此问题下，教师带领学生进行活动三的探究.学生带着问题进行探究，不仅全身心进行数学活动，而且激发了学习与探究兴趣.此外，通过前两个活动探究，学生获得了一定的成就感，特别是发现其探究结果与古人一样时，他们的成就感会更加强烈，学习探究的兴趣则会更加强烈．

活动总结：以上两个数学活动可以看出学生即便之前没有系统接触过化归思想与转化思想，但是在探索过程中会有转化的意识，这是展开后面学习的基础.学生亲历“实验—猜想—证明”的探索过程，以完成更深层次的推理．

文化看点：对于数学文化的引入，可以借助具体的情境导入，如活动二的红领巾，借助红领巾不仅可以进行知识导入，而且红领巾背后的家国情怀与意义需要学生了解，其意义在于促使学生学习先烈的革命情怀，激励其好好学习、艰苦奋斗，激发其勇往直前的精神，传递爱国情怀，以及少先队员的上进与团结力.在学生学习完相应部分的知识后，教师再通过古今对比引出相应的数学文化，如对于《九章算术》的学习，学生感受到古人的智慧，激发自身的自豪感、对中华优秀传统文化的学习热情与对古人的敬佩之情.教师提出古人是如何得到这些面积公式的问题，引领学生回顾历史长河中中国古代数学家的思考过程，感受中华文化的源远流长与博大精深．

活动三：探索梯形的面积.

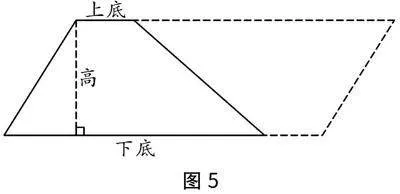
探索梯形的面积的过程依旧类似前两个数学活动，此次操作中，学生发现可以有不同的剪拼方式，可以将一个梯形剪成两个三角形，可以剪出一个平行四边形和一个三角形，还可以将两个一样的梯形拼成一个平行四边形（如图5），观察拼成的平行四边形和原来的梯形，得到梯形的面积＝（上底＋下底）×高÷2．

得到该面积公式后，教师可以回答之前提出的问题.对于这三个数学活动，我们一直贯穿的思想是转化，中国很多数学家也是通过这样的转化得到各图形的面积公式，我们叫作出入相补原理（又称以盈补虚），即把一个图形分割、移补，面积保持不变.［4］［5］教师点明该原理之后，再次引导学生回顾三个数学活动，运用该原理进行推导，感悟其中变中有不变的转化过程.该原理贯穿整个几何理论体系及其发展的始终，适当提及该原理的运用，如赵爽构造“赵爽弦图”证明勾股定理，刘徽首创“割圆术”用以计算圆周率等，表达中国古代数学家孜孜不倦的求学探究精神.在了解整个脉络的过程中，学生感受到数学是可以被创造、被质疑、被超越的，帮助学生形成正确的数学观．

活动总结：在前两个数学活动的基础上，学生对于转化思想的认识较为深刻，因此在探究梯形的面积时可以灵活应用这一化归与数形结合思想.教学中没有先明确讲解出入相补的原理，而是通过三个数学活动让学生自行探究，通过求平行四边形、三角形和梯形的面积的实例，运用分割、移补和倍拼等方式由学生自己推导出结果，再点明出入相补的原理，对于实例的归纳有利于锻炼和培养学生的思考能力、创新意识和创新能力.每一次的转化，在数与形的结合中，学生感悟数形结合的思想，领悟蕴藏其中的数学思维与方法．

文化看点：对于出入相补原理的讲解，学生再次感受到古人的智慧.出入相补原理从无到有过程是中国古代数学家的智慧结晶，这些成就反映了中国古代数学家的聪明才智与刻苦钻研的精神，一代接着一代的学习与探究，不断积累与沉淀造就了今天数不胜数的数学成就.通过追古溯今，继往开来，提升学生的数学文化素养，发扬中国古代数学家的求真务实的创新精神和孜孜不倦的求学精神，自觉树立爱国情怀.此外，对于图形的转化，无论是学生自己拼剪还是通过信息化教学工具的动态展示，都以直观的形式向学生展示了其中的转化过程，学生可以直观感受到变中有不变的奇异之美.感受数学的图形之美和神奇之处．

3 结语

将数学文化融合于教材应是弹性设计的过程，培养出来的也不应只是能背诵数学故事或数学知识的学生.由于数学知识本身内含显性和基本的数学文化知识，小学阶段也正处于接触各种数学知识的初始阶段，学生也并非一开始就对数学没有兴趣，由此在数学文化育人的过程中主要目的不应是数学知识的讲解和刻板记忆，而是在学习数学文化的过程中帮助学生养成阅读的习惯，在了解数学家的过程中激发其数学学习兴趣，学习数学家严谨的态度和治学精神，促进理性精神的形成和发展，养成良好的思维习惯．

以数学活动为形式，将数学文化融于是数学课堂，在活动中以文润心，让文化中的数学家精神进入学生的心里，感悟其中的数学精神与方法，感受数学美以及与生活的联系等，以文育人，通过数学文化的熏陶和积淀，帮助学生更好地理解和把握世界，更全面地认识和发展自身，更好地生活和实现梦想，以文化人，重在学生亲身体验，在各种数学文化的影响下进行个人思想和行为的改变，由内而外得到教化．

参考文献

［1］付天贵，宋乃庆.小学生对数学文化呈现方式的接受度研究［J］.数学教育学报，2017（6）：36-39．

［2］付天贵，宋乃庆.走向小学数学文化自觉的思考［J］.数学教育学报，2019（6）：51-54．

［3］徐海燕.数学文化与小学数学教学深度融合路径探析［J］.河南教育（教师教育），2023（6）：42-43．

［4］黄仙凤，黄红倩，李织兰.出入相补原理的内涵及其在小学数学教学中的价值［J］.桂林师范高等专科学校学报，2022（4）：102-107+112.

［5］王宇.“出入相补原理”进教材、进课堂实证研究——“出入相补原理”融入“多边形的面积”单元的必要性与可行性研究［J］.小学教学（数学版），2022（4）：8-10．