小学数学新增“尺规作图”内容的课程价值

【摘 要】《义务教育数学课程标准（2022年版）》在小学阶段的第二和第三学段新增了“尺规作图”的内容。通过对尺规作图源流的考察，可以发现尺规作图过程中蕴含着严谨的推理和丰富的想象，将其应用于探索性学习活动的设计，对于发展学生数学的眼光、数学的思维以及数学的语言具有特殊的课程价值。同时，小学阶段尺规作图的教育价值还体现在其基础性上，为学生后续的数学学习奠定坚实的基础。

【关键词】尺规作图；推理；想象；课程价值

《义务教育数学课程标准（2022年版）》（以下简称“2022年版课标”）在小学阶段的第二和第三学段新增了“尺规作图”的内容，一线教师在教学中面临的问题有：如何理解这一内容及其课程价值？如何在教学中实现这些课程价值？尺规作图在数学史上具有悠久的历史，其相关内容极为丰富，并贯穿于多个学段的课程内容之中，小学阶段的教学如何凸显其基础性？本文将围绕上述问题展开讨论。

一、背景

“尺规作图”的起源可追溯到古希腊欧几里得（Euclid，约公元前330年—公元前275年）的《几何原本》。在当时，人们认为直线与圆（球）是构成世界万物最基本、最完美的图形，因此，他们期望通过使用制作直线与圆的简单工具，通过推理与想象去建构并描绘无限的世界。以柏拉图（Plato，公元前427年—公元前347年）为代表的唯心主义哲学家，不相信直观所见的真实，他们认为感观所见的、暂时的、不完美的世界必须被抽象的、永恒的、完美的世界所取代［1］。

《几何原本》秉承并沿袭这样的思想，强调所有的命题都应基于已知为真的命题进行推演，因此需要确立最初的逻辑起点。在《几何原本》的第一卷中，开篇阐述了23个定义（Definition）、5条公设（Postulate）和5条公理（Axiom）。定义指的是所用术语的意义，例如，定义15：“圆由一条线包围着的平面图形，其内有一点与这条线上任何一个点所连成的线段都相等。”定义20：“三角形中，三条边相等的称等边三角形，两条边相等的称等腰三角形，各边都不相等的称不等边三角形。”分别描述了圆以及等边三角形、等腰三角形、不等边三角形的概念。

公理与公设则是不证自明、公认为正确的命题，二者的区别在于普适性的差异。公理不仅适用于几何领域，也适用于其他科学领域，因此公理也被称为“共通观念（Common Notions）”。例如，第一条和第二条公理描述了量与量之间的相等关系。

l公理1：等于同量的量彼此相等。

l公理2：等量加等量，其和仍相等。

公设则是几何学内部不证自明的事实，与尺规作图直接相关，它规定了如何从给定的对象构造出确定的对象。例如，《几何原本》第一卷中的前3条公设如表1所示。

综上所述，《几何原本》第一卷中的定义、公设和公理构成了使用直尺和圆规作基本图形的基础。定义指向概念的意义，公设说明了如何作图，而公理则解释了为什么这样作图是正确的1。如果将尺规作图视为一种游戏，那么定义、公设和公理就是游戏过程中必须遵守的规则，正是这些规则确保了尺规作图成为一个严谨的推理过程。下面，以2022年版课标中的例26为例，详细阐释这一推理过程。

二、严谨的推理

2022年版课标中的例26所提及的“作一个给定边长的等边三角形”，实际上是《几何原本》第一卷中的第一个命题。该命题在不同中文译本中的表述存在差异，现将两种表述列举如下：

l表述1：已知一条线段可以作一个等边三角形。［2］

l表述2：在一个已知有限直线上作一个等边三角形。［3］

二者的区别在于，是否将给定线段作为所作等边三角形的一条边。两种中译本都依据同一英文底本，即英国科学史学家希思（Thomas little Heath，1861—1940））的英译评注本《欧几里得原本13卷》，其中命题1的英文表述为：“On a given finite straight line to construct an equilateral triangle.”［4］

《几何原本》第一卷中的命题1可以理解为：若给定一条线段，那么可利用这条线段作为三角形的一条边，进而作出另外两条等长的边，形成等边三角形。构造过程的每一步是否可行及正确，都需依据定义、公设或公理进行验证。为了清晰描述这一过程，采用表格的形式进行展示（如表2）。

推理的最终结论是“三角形ABC为等边三角形”，为此必须阐明三角形的三条边是否存在，以及为什么相等。推理过程包括四个操作步骤和三个作为结论的判断，每一步操作需说明为什么可行的依据，每一个结论都需理由作为依据以阐明为什么正确。因此，可以说尺规作图的过程本质上是推理过程，推理的严谨性体现为“言必有据”，表2右侧列出的依据均源自事先规定的定义、公设和公理，因此可以相信最终结论的正确性。

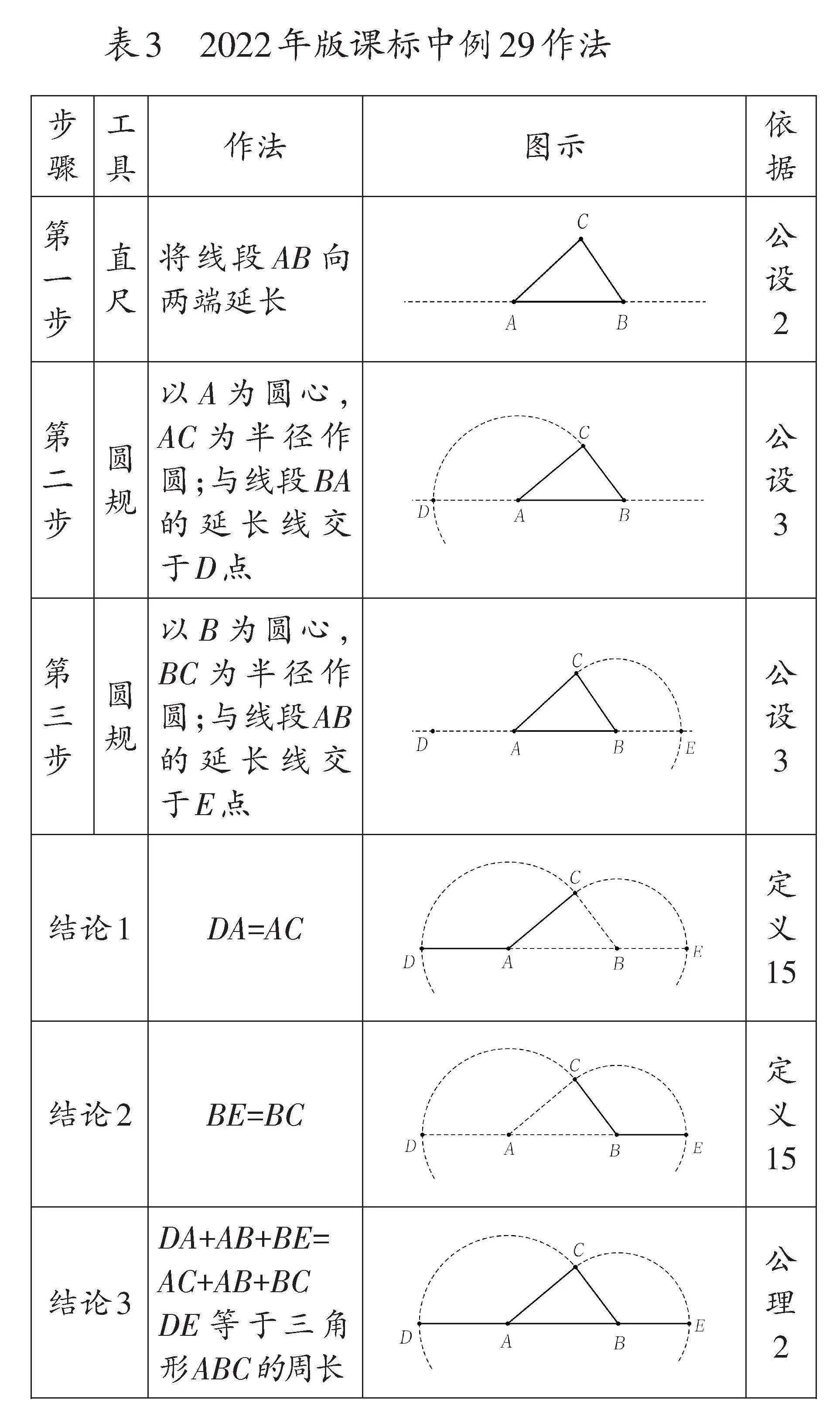
对上述过程稍加变化，能够实现2022年版课标中例32的“给定三条线段作三角形”的作法，其中包括对三角形三边关系的探讨（限于篇幅，读者可自行完成详细的作图和证明过程）。所有这些均属于“给定线段作三角形”的问题范畴。将此过程逆向操作，便成为2022年版课标中例29的作图问题：“把三角形的三条边依次画到一条直线上。”下面用表3详细展示这一作图过程。

表3中的作图过程与表2略有不同，其中第一步“将线段AB向两端延长”的依据是“公设2”；结论3中DE的长度等于三角形的周长，其依据为“公理2”。

综上所述，尺规作图的过程实际上是一个严谨的推理过程。从教育的角度来看，这种推理无疑有助于培养学生逻辑思维和论证习惯。然而，也应注意这种严谨性可能带来的问题。表2与表3中的作图及证明过程具有明显的形式化与程序化特征，只要遵循“模仿记忆、按部就班、依次执行”的原则，便能确保无误。这种严谨性可能会对教学产生消极影响，教师的“教”可能简化为“讲解—示范—留作业”，学生的“学”自然成为“倾听—模仿—做练习”，从而使得尺规作图变成一种无理解的操作过程。因此，在将尺规作图纳入数学课程与教学时，应避免仅注重推理的严谨性，同时应充分彰显其开放性的特征，引导学生发挥丰富的想象进行探索。

三、丰富的想象

2022年版课标中的例26特别强调：“（尺规作图）教学中，可以让学生发挥想象力，用直尺和圆规构建各种可以实现的图形。”这表明尺规作图不仅是严谨的推理过程，也是发挥想象力、进行探索的过程。因此，对尺规作图的作法和结果，教师应持有开放性的认识，即“作法未必唯一，结果可以拓展”。

“作法未必唯一”意味着作图的过程和方法具有多样性。在数学的历史发展中，许多数学家对尺规作图方法的多样性进行了深入探索。比如17世纪丹麦几何学家乔治·摩尔（Georg Mohr，1640—1697）与18世纪意大利数学家洛伦佐·马斯凯罗尼（Lorenzo Mascheroni，1750—1800）分别独立发现并证明了一个结论：每一个能够用直尺和圆规作出的图形都可以摒弃直尺，仅用圆规作出。这一发现后来被称为“摩尔-马斯凯罗尼定理（Mohr-Mascheroni Theorem）”［5］，当然这些内容已经超出了小学数学课程的范畴。下面重点谈谈尺规作图结果的拓展性。

尺规作图结果的拓展性至少体现在两个方面：一是“目标图形未必唯一”；二是“最终结论可以延伸”。以2022年版课标中的例26为例，目标图形等边三角形并非唯一，还可以作出与三角形ABC关于线段AB对称的另外一个等边三角形ABD（如图1）。

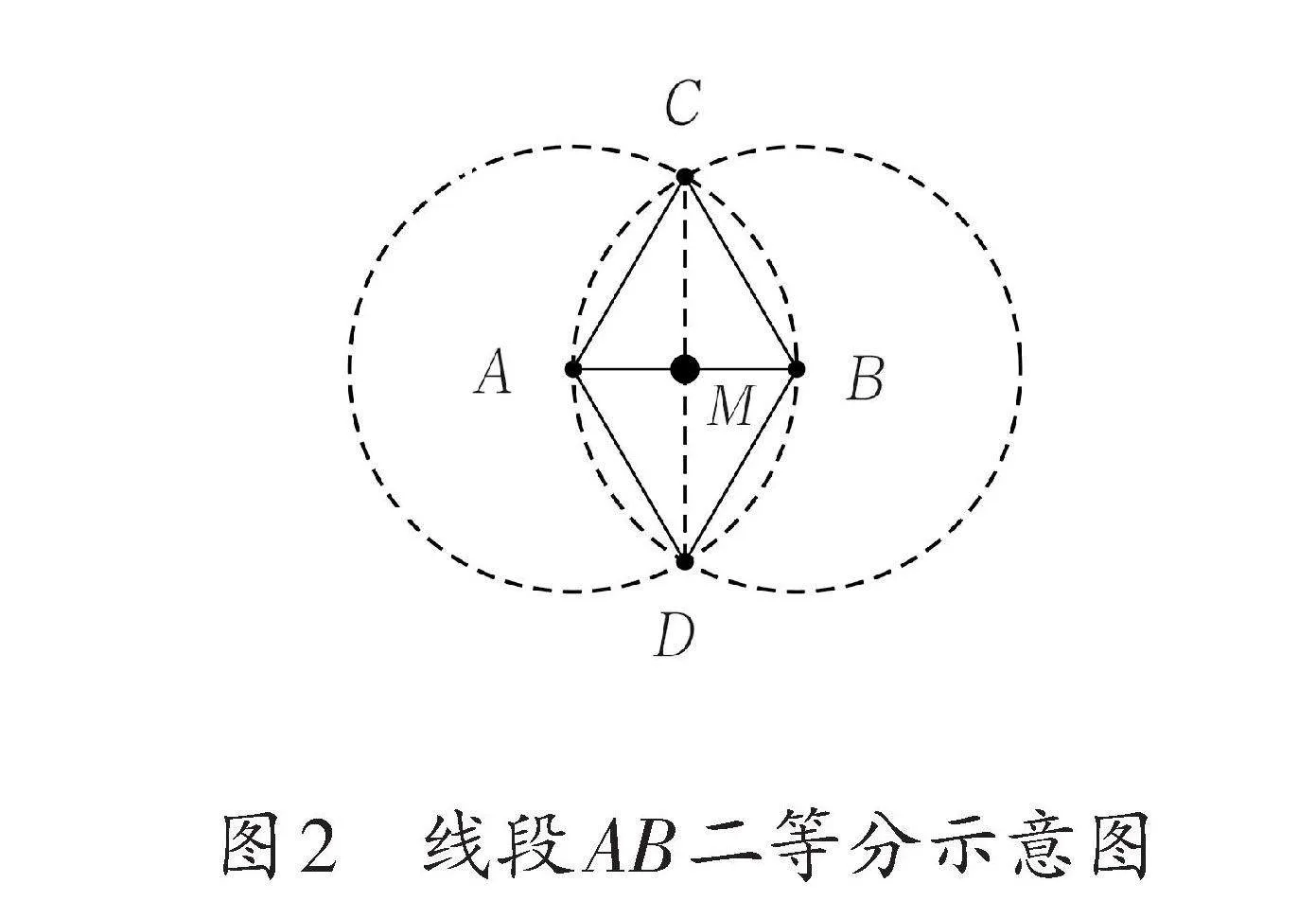
基于这样的作图结果，通过进一步的想象，可以使得最终结论得以延伸。从点C向点D作出线段CD，将会与线段AB形成一个交点M，直观上可以看出这个点是线段AB的中点（小学阶段依靠直观看出即可），实现了将一条线段平均分为两段，即M点将线段AB二等分（如图2）。

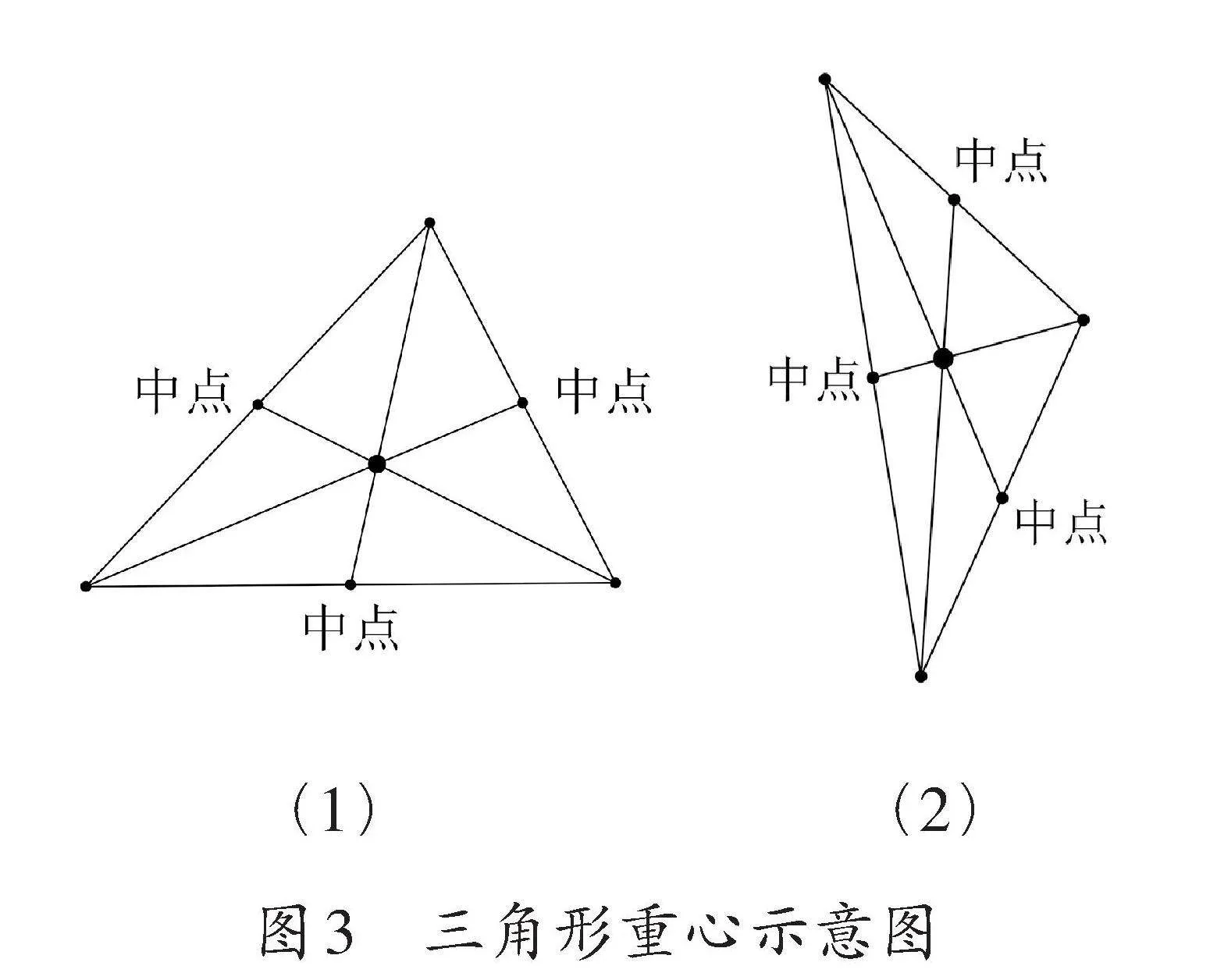
如果将线段二等分或在线段上确定中点视为“基本作图”，则可以以此为逻辑起点，进一步探索几何图形的诸多性质。例如，对于任意大小、形状各异的三角形，在其三边上分别作出中点，并将这些中点与对面顶点相连，可以发现这三条线段相交于同一点（如图3）。

这样三线共点的“点”也叫三角形的重心（又叫质心），是中学数学与物理课程的重要内容。因此，学生在小学阶段经历尺规作图的探索，对于与中学课程内容的衔接具有积极意义。

再以17—18世纪法国数学家、物理学家皮埃尔·伐里农（Pierre Varignon，1654—1722）发现的著名结论为例：在任意四边形四条边上分别作出中点，并用线段连接，构成一个内部的四边形，无论原来四边形是什么形状，该内部的四边形一定是平行四边形［6］（如图4）。

此类现象揭示了“变中的不变”的规律性，通常所说的“探索规律”实质上是在千变万化的现象中发现这种“变中的不变”的规律［7］。因此，在教学中引导学生发挥想象力对目标图形和最终结论进行延伸，实际上是在经历探索规律的过程。

综上所述，简单的“线段二等分”作图可应用于多种几何图形性质的探索，这种应用性可视为作图结果的“延伸”，即拓展性的纵向向度。除此之外，还可从横向向度对作图结果进行“延展”：既然给定一维的线段可以利用尺规作图二等分，那么是否可以三等分、四等分……同样，对于平面图形（如三角形、长方形、平行四边形等）的面积以及平面中的一个角，是否可以通过尺规作图实现类似的等分？

在教学中，引导学生发挥想象力，经历此类纵向的延伸与横向的延展的拓展性思考，不仅有助于学生对于相关课程内容的认识与理解，同时使得数学课程内容超越教材的局限，为学生发挥想象力提供广阔的空间和无限的可能性。

四、小学阶段“尺规作图”的基础性

如前所述，尺规作图历史悠久、源远流长、内容丰富，其中蕴含着严谨的推理和丰富的想象。这无疑可以作为尺规作图的教学目标。同时，教师应当重视小学阶段尺规作图的基础性，主要体现在对作图工具的全面认识与熟练使用上。

在尺规作图中，“直尺（Straightedge）”与如今用于测量长度的“尺子（Ruler）”有所不同，直尺是无刻度的，仅用于构造直线或线段，不具备测量长度的功能，因此尺规作图的过程不涉及数值及其计算，而是纯粹的几何形与量的构造过程。

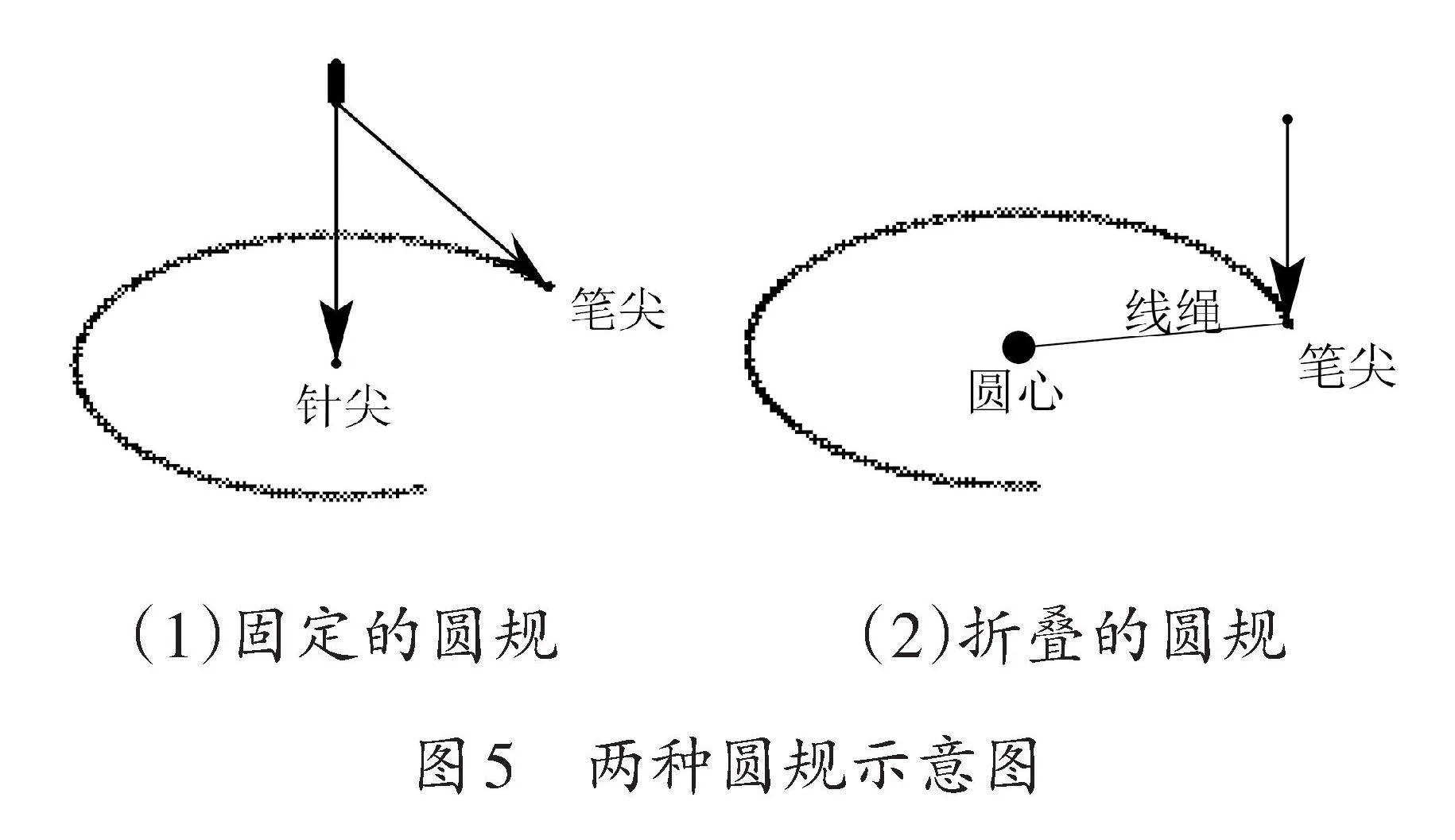
古希腊时期的圆规与现代圆规也有区别，现代圆规由三个部分组成：一是固定圆心的针尖；二是用于描绘轨迹的笔尖；三是可以调整针尖与笔尖距离的装置，即圆的半径。这种圆规具有准确调整与确定半径的特点，其对应的英文名称为“Fixed Compass（中译：固定的圆规）”，如图5（1）所示。古希腊时期的圆规是由线绳捆绑笔尖形成的，作圆时需固定线绳的某一点作为圆心，然后旋转笔尖描绘圆的轨迹，其特点是难以精确确定圆心到笔尖的距离（即半径），这种圆规的英文名称为“Collapsing Compass（中译：折叠的圆规）”［8］，如图5（2）所示。

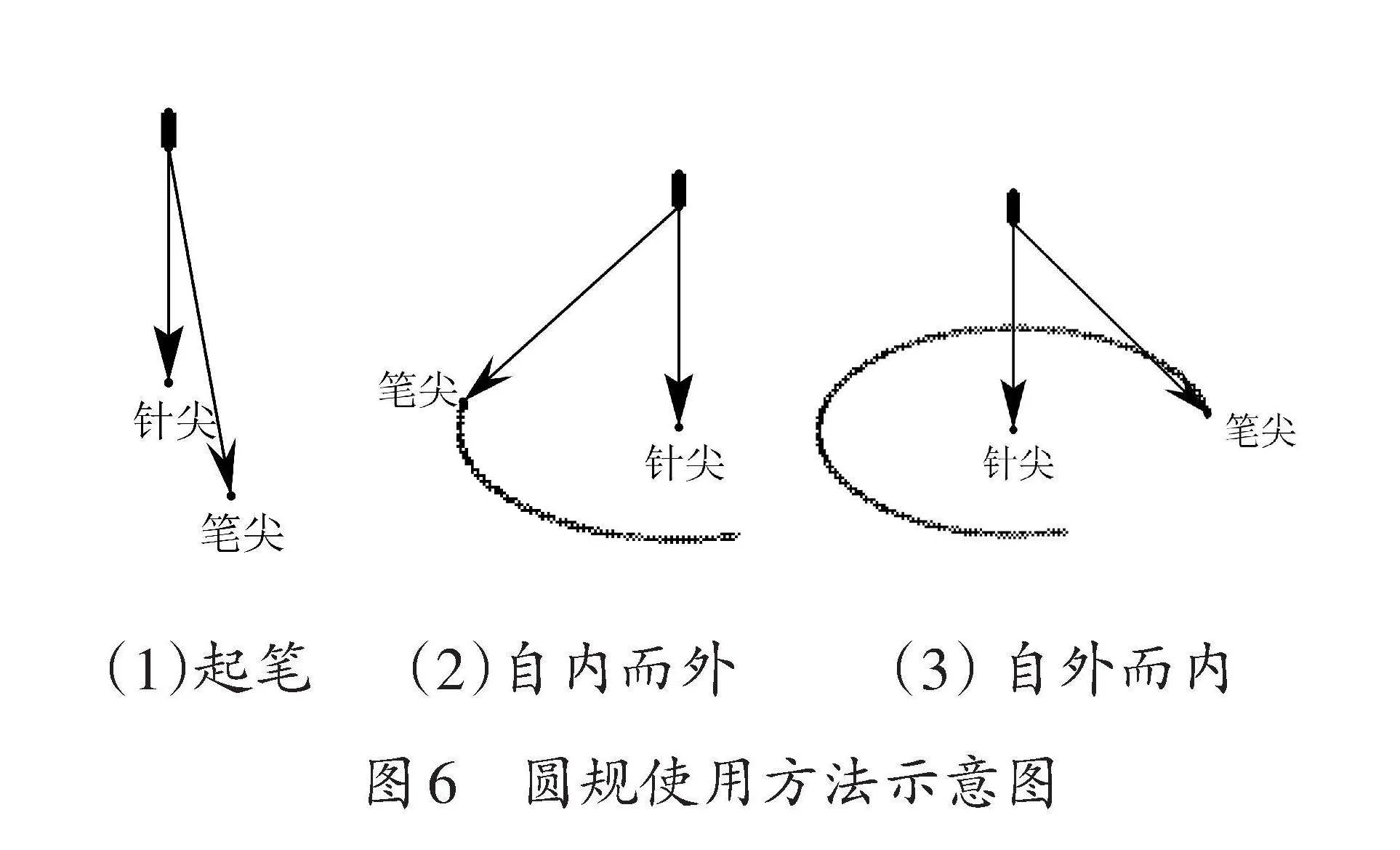
小学尺规作图教学的初始阶段，首先应安排“认识直尺和圆规”的教学环节，让学生通过操作活动对不同直尺和圆规进行比较，从而发现它们的异同。在圆规的使用教学中，应注意引导学生探索“一笔画出”整个圆的方法，这主要JzeKpQBMhhA0uAdTZpj19A==包括起笔位置和笔尖的运行方向。通常的做法是从靠近身体的位置起笔，沿着顺时针方向旋转笔尖，“先自内而外，再自外而内”（如图6）。

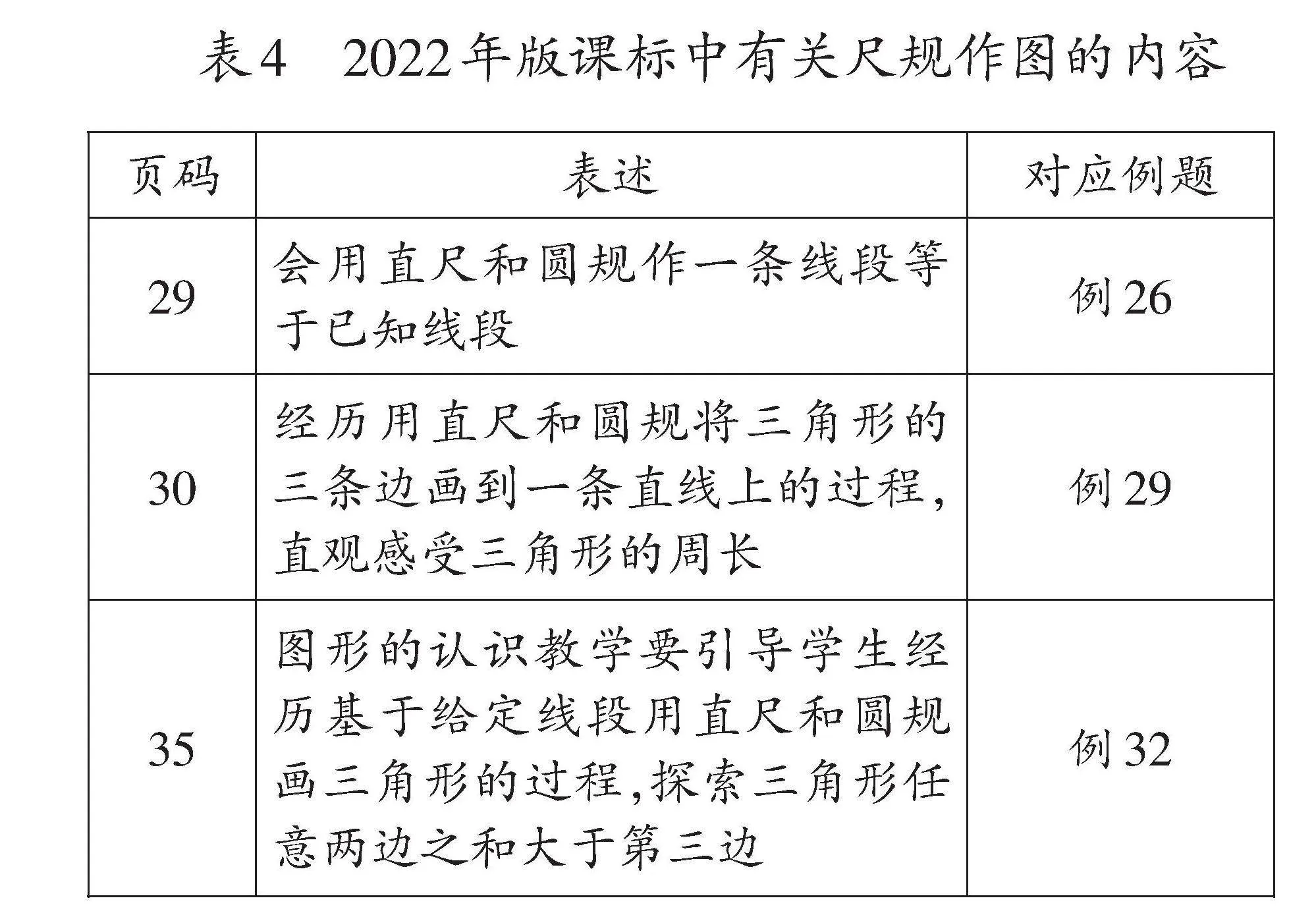
在认识直尺和圆规的基础上，就需要通过经常性的练习逐步达到熟练使用的目的。为了实现经常性的练习，可以将直尺和圆规视为具身学习活动的学具，将其应用于教科书中相关内容的教学。如在2022年版课标的第29页、第30页和第35页分别提及了小学阶段尺规作图的相关内容，并附有相应的例题（如表4）。

实际上，小学数学课程中还有许多其他内容同样适合用尺规作图进行教学。以“平行四边形的认识”为例，如果提供一个不完整的平行四边形，如图7（1）所示，即给定两条边及其夹角，让学生利用尺规作图来“补全”平行四边形。

学生只需“以B为圆心，AC为半径”以及“以C为圆心，AB为半径”分别作圆（只需作出局部圆弧），便能找到两个圆的交点D，如图7（2）所示。接着，使用直尺连接CD和BD，即可实现“补全”平行四边形，如图7（3）所示。在作图过程中，通过圆的半径处处相等的特性，学生能够直观感受到平行四边形对边相等的性质。

总之，尺规作图不仅是画图，其英文表达为“Geometric Construction（中译：几何建构）”，这里的“建构（Construction）”包含双重含义：其一，是基于对现实世界事物的感知和想象，在思维中构建图形；其二，是将思维中的图形通过直尺和圆规的使用转化为可视化的图像，从而实现抽象思维的具体化。因此，尺规作图在沟通现实世界与思维世界之间起到了桥梁的作用，它既是对现实世界具体事物的抽象化，又是将思维中的抽象图形具体化的过程。作图过程中所蕴含的思维活动，既有严谨的推理，也有丰富的想象。将尺规作图应用于探索性学习活动的设计，对于发展学生数学的眼光、数学的思维以及数学的语言具有特殊的课程价值。同时，尺规作图的教育价值还体现在其基础性上，小学阶段全面认识并熟练使用作图工具，为后续的数学学习奠定坚实的基础。

参考文献：

［1］克莱因.西方文化中的数学［M］.张祖贵，译.北京：商务印书馆，2013.

［2］欧几里得.几何原本［M］.燕晓东，编译.北京：人民日报出版社，2005.

［3］欧几里得.几何原本［M］.兰纪正，朱恩宽，译.西安：陕西科学技术出版社，2003.

［4］HEATH T L. The thirteen books of Euclid’s Elements（Vol.1）［M］. New York：Dover Publi cations，1956：276.

［5］MARTIN G E. Geometric constructions［M］. Berlin：Springer，1998：53.

［6］OLIVER P N. Pierre Varignon and the parallelogram theorem［J］. The mathematics teacher，2001，94（4）：316-319.

［7］郜舒竹.“探索规律”释义［J］.课程·教材·教法，2015，35（1）：102-107.

［8］BEN-ARI M. Mathematical surprises［M］. Heidelberg：Springer，2022：2.

（首都师范大学初等教育学院）