高中数学教学中直观想象素养的培养策略探究

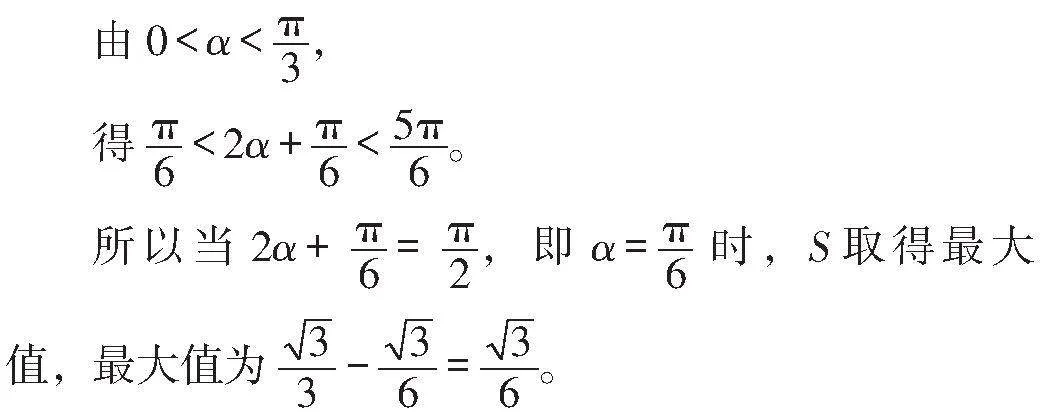
摘 要：直观想象素养是高中数学核心素养的重要组成部分，对培养学生的直观想象素养十分重要。文章旨在探究高中数学教学中直观想象素养的培养路径。具体而言，立足《普通高中数学课程标准（2017年版2020年修订）》的指导意见，将直观想象素养的培养分为建立形与数的联系、利用几何图形描述问题、借助几何直观理解问题、运用空间想象认识事物等方面，以此分别培养学生的数形结合思想、几何直观能力和空间想象能力，逐步促进学生直观想象素养的发展。

关键词：高中数学；直观想象；培养策略

《普通高中数学课程标准（2017年版2020年修订）》指出，直观想象主要表现为：建立形与数的联系，利用几何图形描述问题，借助几何直观理解问题，运用空间想象认识事物。在高中数学教学中，培养学生的直观想象素养，能有效提高学生解决问题的能力和数学学习效果，进一步激发学生的数学探究兴趣。对此，教师需要重视对学生直观想象素养的培养，为学生的全面发展打好基础。

一、引导建立形与数的联系，培养学生的直观想象运用意识

在高中数学知识学习与问题探究过程中，运用数形结合思想建立形与数的联系，是一种有效培养数学思维的方式。形与数之间的转化与联系，对于培养学生的直观想象素养具有关键作用。在立体几何、函数等知识的教学中，教师可以将“建立形与数的联系”作为教学的切入点，通过引导学生感知、理解、建立形与数的联系解决问题，以培养学生的直观想象素养。具体而言，数形结合的运用主要分为化形为数、化数为形、数形兼具三种类型。从化形为数的角度出发，既可以将数学问题中的图形信息转化为数量关系，再加以求解，又可以将图形问题转化为代数问题，以此获得简便的解题思路；从化数为形的角度出发，可以将代数问题转化为图形问题，用几何图形表示代数问题中的数量关系，再通过观察图形求解；从数形兼具的角度出发，教师要为学生提供图形和数量关系，让学生在探究问题的过程中，综合考虑图形特征和数量关系，从而综合运用两者的关系进行求解。运用数形结合思想引导学生建立形与数的联系，能让学生在学习中直观、深入地理解形与数之间的联系，从而培养学生的直观想象意识，为学生后续直观想象素养的深度发展奠定基础。

例如，人教A版《普通高中教科书·数学》（以下统称“教材”）必修第一册“1.3 集合的基本运算”这节课涉及大量数形结合的学习内容。在探究“集合的基本运算”知识点时，教师需要向学生渗透并集、交集、补集的不同表示方式。在学生初步掌握几何的基础运算知识，能自由转化并集、交集、补集的文字、符号语言和图形语言后，教师可以为学生提供练习题，让学生运用数形结合思想解题。

题目1 设全集[U=R，] [A=xx≤1， B=xx+a<0，]且[B⊆A，] 求实数a的取值范围。

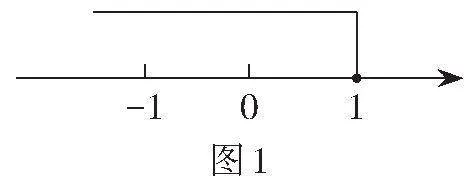
此题正确的解题思路为：先化简并求解集[B=xx<-a。] 随后，借助数轴（如图1），由已知的集合间的关系求出a的取值范围。

学生通过图解，获得答案[a≥-1]。

该题涉及数形结合思想。教师利用“化数为形”的方式引导学生思考问题，使学生掌握用集合图形表示问题中的数量关系的方法，以此来建立题干中形与数之间的联系，培养学生的直观想象运用意识。在数学教学中引导学生建立形与数之间的联系，运用数形结合思想，能促进学生直观想象素养的发展。

二、利用几何图形描述问题，夯实学生的直观想象运用基础

在高中数学教学中，利用几何图形描述问题是培养学生直观想象素养的可行路径。利用几何图形描述问题，能简化学生思考问题的步骤，降低学生解答问题的难度。具体而言，教师可以在讲解立体几何、三角函数等数学知识的过程中，通过绘制图形将抽象的数学表达式形象化，引导学生利用几何图形描述、分析和解决问题。在解题的过程中，教师可以提醒学生注意几何图形的形状、大小，几何图形之间的比例、位置关系等细节，提高学生所画几何图形（数学模型）的准确性；可以鼓励学生在分析几何图形的过程中，深入思考图形背后的数学含义和逻辑，从而理解问题的本质。这一教学过程能使学生更好地掌握利用几何图形描述问题的方法，进而夯实学生的直观想象运用基础。

例如，教材必修第二册“8.3 简单几何体的表面积与体积”这节课的教学重点是让学生掌握棱柱、棱锥、棱台的表面积和体积求解公式，以及圆柱、圆锥、圆台、球的表面积和体积求解公式，并能结合公式解答组合立体图形的相关面积和体积问题。在完成本课新知教学后，教师可以设计以下练习题。

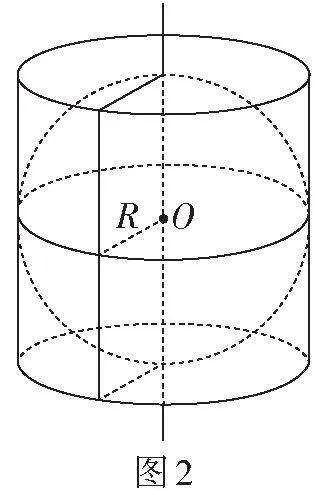
题目2 一个圆柱体滚珠唇油的抽象结构图（如图2）。其中，圆柱体外壳的底面直径和高都与滚珠的直径相等，求外壳和滚珠的体积之比。

此题通过几何图形的展示，将实际问题抽象为数学问题。学生可以尝试利用几何图形描述问题：唇

油外壳的形状是圆柱体，滚珠则是球体，要想获得问题的答案，需要求出圆柱体和球的体积。设球的半径

三、借助几何直观理解问题，提高学生的直观想象分析能力

借助几何直观理解问题，对于培养学生的直观想象分析能力具有重要意义。在立体几何等知识点的教学中，教师可以通过精心设计几何直观教学活动，进一步提高学生的直观想象分析能力。在此过程中，教师可以引导学生从题干中抽象出几何模型，也可以引导学生结合图形直观理解题干信息。学生能在利用几何图形描述问题的基础上，锻炼几何直观能力，逐渐提高直观想象分析能力。

例如，在教学教材必修第一册“5.5.2 简单的三角恒等变换”这节课后，教师可以让学生探究如下问题。

此题需要先结合图形中的信息建立矩形[ABCD]的面积[S]与[α]之间的函数关系[S=fα，] 再求出函数[S=fα]的最大值。在分析几何图形的过程中，需要理解图形中的角度、边长与面积之间的关系，运用三角函数知识，通过适当的代换和变换，将问题转化为求三角函数的最值问题。解题思路如下。

借助几何直观理解问题的方法，不仅能帮助学生深化对知识点的理解，还能帮助学生积累直观想象经验，促使学生能自主运用直观想象来分析数学问题。学生初步掌握此类学习方法后，教师可以为学生布置类似的习题任务，以锻炼学生的直观想象能力、问题分析能力和问题解决能力，促使学生养成运用直观想象的良好思维习惯。

四、运用空间想象认识事物，强化学生的直观想象运用能力

《中国中学教学百科全书·数学卷》指出，空间想象能力是空间知觉、空间观念和想象力的一种独特的结合，是对几何表象进行加工、改造和创新的能力。在高中数学教学中，空间想象能力要求学生能充分联系实际，在脑海中构建三维、立体的空间模型，并能结合此类模型中点、线、面之间的关系加以推理、分析和计算。具体而言，教师在教学实践中可以引导学生根据已知条件画出正确的几何图形，分析空间图形中的数学元素，对图形加以分解、组合或变化，强化对空间图形中几何元素的判断能力，实现图形语言、文字语言和符号语言之间的相互转化，进而更加灵活、深入地理解和运用数学知识，增强直观想象运用能力。

仍以必修第二册“8.3 简单几何体的表面积与体积”这节课为例，教师可以设计如下习题。

题目4 在正方体[ABCD-A1B1C1D1]中，三棱锥[D1-AB1C]的表面积与正方体的表面积之比是多少？

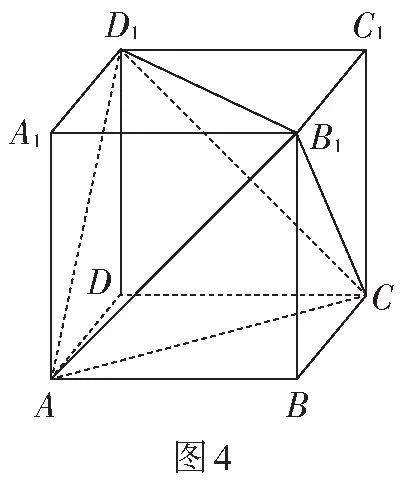
探究问题的过程中，教师可以引导学生运用空间想象能力绘制几何图形。学生先绘制一个正方体，并标注好点[A，B，C，D，A1，B1，C1，D1]的具体位置。随后，学生可以结合题干中给出的“三棱锥[D1-AB1C]”这一信息，在正方体上连接线段[D1A，D1B1，D1C，AB1，] [B1C，AC。] 最终绘制的图形如图4所示。

在解题过程中，学生独自完成了分析题意、空间想象、绘图分析、列式计算等步骤。其中，空间想象素养发挥着重要作用。学生能借助空间想象能力，根据题干信息画出正确的几何图形，进而展开对问题的深层次探究；能结合空间想象分析图形中的几何元素，并加以组合、分解；能正确转化空间图形中的图形语言、文字语言和符号语言，从而提高直观想象运用能力。运用空间想象认识事物的教学方式，有助于学生直观想象素养的发展。

综上所述，在高中数学教学中，学生直观想象素养的培养需要经历层层递进、深化的过程。在这一过程中，不仅需要学生通力配合、积极思考，还需要教师在教学中持续探索与创新。教师可以通过引导学生建立数与形的联系、利用图形描述问题、借助几何直观理解问题、运用空间想象认识事物来培养学生的直观想象素养，并将所学内容引申至生活案例，逐步培养学生运用直观想象素养分析问题、解决问题的能力。

参考文献：

［1］郑雪静，柯跃海，陈清华. 直观想象素养的考查研究［J］. 数学通报，2023，62（12）：46-50，62.

［2］张海峰，杨苍洲. 直观想象素养下的函数导数试题的命题手法［J］. 河北理科教学研究，2023（4）：55-57.

［3］李凯鸿. 试论高中数学教学中直观想象素养的培养策略［J］. 高考，2023（33）：114-116.