从“错误诊断”到“弥补教学”

摘 要：在高三复习课教学中，如何做到有的放矢，让课堂教学高效精准，是一线教师重点关注的话题之一。这需要基于认知心理学，对学生在解题过程中出现的典型错误进行认知诊断，然后通过交流与研讨，精准地确定教学目标，提炼解题方法，并借助“形同”问题设计针对性的弥补教学。

关键词：错误诊断；方法提炼；弥补教学；磁聚焦法

中图分类号：G633.7 文献标识码：A 文章编号：1003-6148（2024）9-0087-6

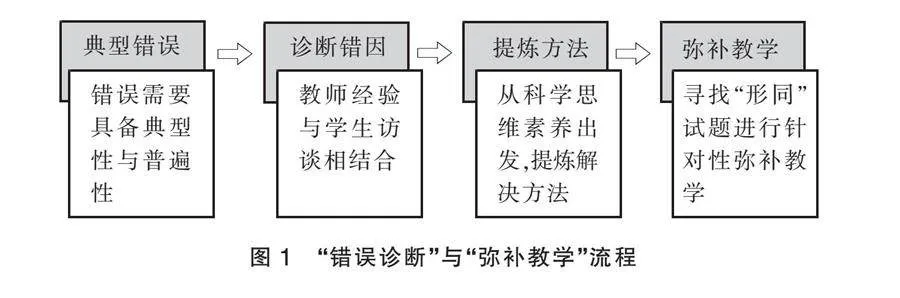
有学者曾经打过一个形象的比方，将试卷讲评过程比喻为医生诊疗过程：高效的诊疗过程往往是先用检测仪器发现病灶，然后对病灶进行病理检测，再参考治疗标准确定治疗方案，最后用科学措施进行有效治疗［１］。而教师试卷讲评过程是通过学生的解题发现错误，然后根据教师个人经验以及通过对学生进行访谈诊断错误原因，再根据诊断结果进行交流与研讨，确定教学目标，进行教学设计，最后寻找或编制“形同”试题对错误进行针对性弥补教学。这一过程可以通过图１体现。

下面以高三选考复习课——带电粒子在圆形边界磁场中运动的问题中，常用到的“等半径磁聚焦（或磁发散）法”为例，介绍由“诊断错因”到“提炼方法”再到“弥补教学”的复习课教学设计。

１ 收集典型错误，进行错因诊断

１．１ 设置典型例题

通过下面例题可以获取学生对“等半径磁聚焦（或磁发散）法”的掌握情况与思维过程。

例题 如图２所示，边长为Ｌ的正方形区域ＳＡＣＤ内的适当区域（图中未画出）中分布有匀强磁场。位于Ｓ处的粒子源，沿纸面向正方形区域内各个方向均匀发射速率为ｖ０的带负电粒子，粒子的质量为ｍ，电荷量为ｑ。所有粒子均从Ｓ点进入磁场，离开磁场时速度方向均与ＳＤ平行，其中沿ＳＡ方向射入磁场的粒子从Ｃ点射出磁场。紧靠ＣＤ放置一收集板，粒子打到收集板后通过接地导线及时导走。不计粒子的重力和相互作用。

（１）求磁场的磁感应强度Ｂ和磁场分布的最小面积Ｓ；

（２）若Ｓ处粒子源每秒射出粒子数为Ｎ，求稳定后每秒打在收集板下半部分的粒子数ｎ。

正确解答：

（１）根据粒子带电性和偏转方向，由左手定则可以判断磁感应强度Ｂ方向为垂直于纸面向里。

由题意，所有粒子离开磁场时速度方向均与ＳＤ平行，根据磁聚焦（或磁发散）结论可知，磁场半径ｒ与粒子轨迹半径Ｒ相等，r=R=L。

１．２ 典型错误表现

（１）对磁场最小面积Ｓ的求解存在的错误：

根据磁聚焦（或磁发散）结论可知，磁场分布为四分之一圆弧，如图４所示，且磁场半径ｒ与粒子轨迹半径Ｒ相等，r=R=L。

１．３ 教师经验诊断

从上面解答可以看出，这些学生对等半径磁聚焦规律，头脑中是有的，而且在解题过程中能及时调用，但从解答情况可以反映出两个问题：

（１）这些学生对每秒打在收集板下半部分的粒子数求解不对，可能存在如下原因：其一，他们知道收集板各位置都有粒子打到，这一点是好的，但他们同时认为打到板上的粒子是均匀分布的，殊不知粒子从Ｓ点射入磁场时各方向是均匀的，但通过磁场偏转后分布已经不均匀，这一点需要清楚；其二，他们知道打到板上的粒子不是均匀分布的，但对粒子出射磁场的位置与入射方向的关系没弄清楚，也就是不知道所谓“径速角相等”，以为打到板的中点对应入射角是４５°。所以，需要对磁聚焦问题的深层次结论进行进一步理解。

（２）磁场分布的最小面积分析有误，只分析出磁场下边界，即构成磁聚焦结论的原磁场的四分之一圆弧，这一点再次说明该同学头脑中是有“等半径磁聚焦”规律的，并能加以应用。但对磁场上边界没有进一步思考，没有对边界粒子轨迹进行分析，或者没有对题中最小面积的“最小”两个字进行深入理解。

１．４ 学生访谈诊断

对学生解答批阅后，笔者找来了几位第1小问“最小面积”和第2小问“收集板下半部分的粒子数ｎ”均求错的学生进行访谈。

师：解题时，你大脑中能涌现“等半径磁聚焦”的结论吗？你清楚它的使用条件吗？

生：以前在磁场习题课中老师讲过，结论依稀记得，但来龙去脉不是很清楚。

师：你认为每秒打在收集板下半部分的粒子数为Ｎ/２，这是基于什么考虑的？

生：所有粒子均打到收集板上，所以收集板上半部分、下半部分各收集到一半粒子。

师：粒子打到收集板上分布均匀吗？

生：解题的时候没想这个问题，看到题设中粒子从Ｓ处向各个方向均匀发射时注意到了。

师：对磁场分布的最小面积求解时，你为什么没考虑到上边界也是圆弧呢？

生：可能只关注了要求粒子出磁场速度方向均与ＳＤ平行，要求构成磁聚焦（或磁发散），磁场边界需要圆形，而没有深究磁场如何分布才使面积最小。

同时，笔者也对求解正确的学生进行访谈。

师：你对“等半径磁聚焦”的结论清楚吗？

生：基本清楚，需要圆形磁场半径与粒子圆轨道半径相等。

师：知道粒子进入磁场时速度的方向与出射时的位置存在什么规律吗？

生：不是很清楚。

通过学生访谈可以知道，对于典型错误的原因，教师根据个人经验进行的判断与学生犯错的实际原因基本吻合。可以断定出现典型错误的原因：一是学生对粒子在圆形边界磁场中运动常要应用到的磁聚焦（或磁发散）的来龙去脉不清楚或一知半解；二是学生对磁聚焦（或磁发散）的深层次结论（如径速角相等）没有挖掘；三是审题不细，对题中关键词句（如最小面积）没有深究。

2 强化核心素养，提炼解题方法

通过学生的错误解答，以及对错解学生的访谈，结合正解学生的访谈，要无障碍解决这类问题需要具备如下学科核心素养。

２．１ 具备准确的物理观念

（１）等半径磁聚焦（或磁发散）规律

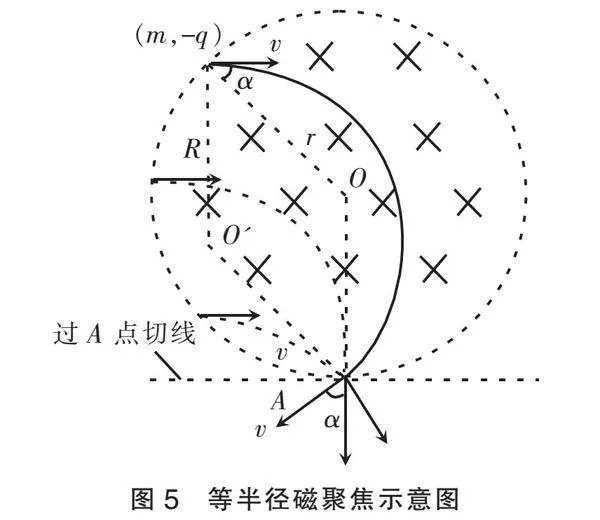
一群相同的带电粒子平行射入有圆形边界的匀强磁场，如果粒子运动的轨迹半径Ｒ与圆磁场半径ｒ相等，则粒子从磁场边界上同一点（如图５中Ａ点）射出，磁场圆边界在该点的切线与粒子入射方向平行。该规律称为等半径磁聚焦。

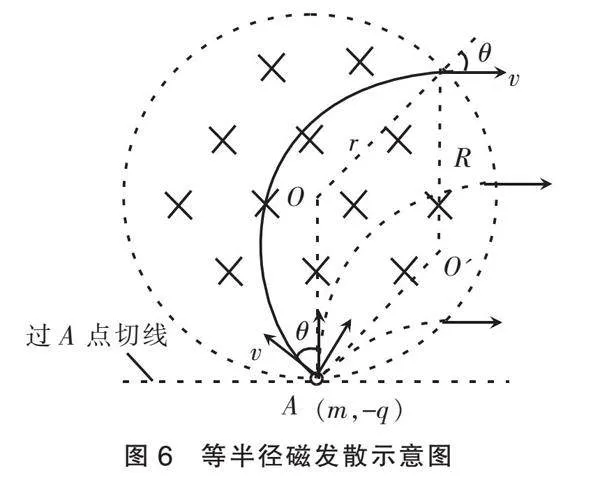
等半径磁发散是磁聚焦的逆过程：一个带电粒子（或一群相同带电粒子）从圆形有界匀强磁场边界上同一点（如图６中Ａ点）射入，如果粒子运动的轨迹半径Ｒ与圆磁场半径ｒ相等，则粒子出射方向与磁场边界在入射点的切线（即过Ａ点的磁场边界圆的切线）方向平行。

（２）磁聚焦（或磁发散）中“径速角相等”规律

在等半径磁聚焦或磁发散问题中，粒子射入磁场时入射速度方向与入射点磁场半径的夹角等于射出磁场时出射速度方向与出射点磁场半径的夹角，即“径速角相等”。比如，图５中两个α角相等，图６中两个θ角相等。

２．２ 需要严密的科学思维

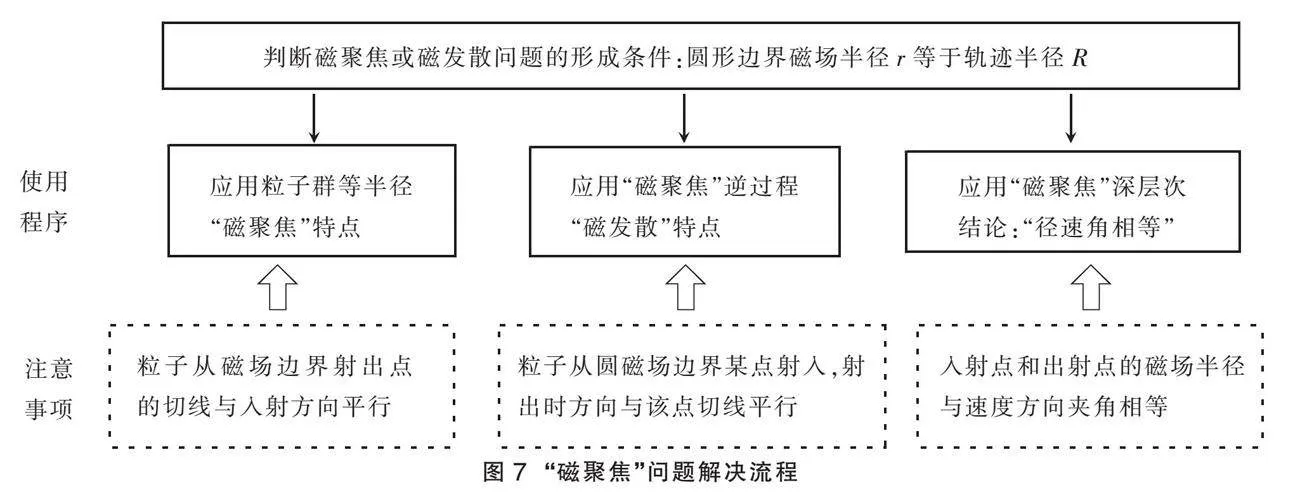
解决“磁聚焦”相关的同类问题可以采用如图7所示的科学思维流程。

75d7b157cdcf5adbecfaf30d0156635f3 设计弥补教学，突破思维难点

诊断错因、并提炼解题方法后，教师应该寻找“形同”试题，采用问题串的形式，由浅入深、循序渐进地进行针对性弥补教学设计［２］。

３．１ 寻找“形同”试题

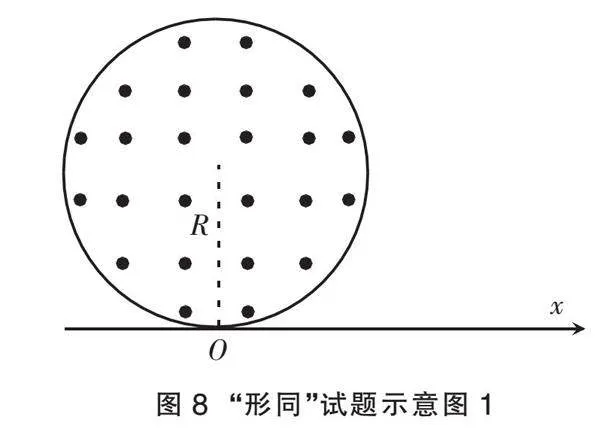
试题 如图8所示，真空中有一半径为Ｒ的圆形匀强磁场区域，磁场方向垂直纸面向外，Ｏｘ为边界上Ｏ点的切线，从Ｏ点在纸面内向各方向均匀发射速率均为ｖ的带正电的α粒子，已知α粒子的电量为ｑ，质量为ｍ，在磁场中偏转半径也为Ｒ，在Ｏｘ上距Ｏ点Ｌ处有一点Ｐ（Ｌ＞２Ｒ）。不计粒子间相互作用和重力，试回答下列问题。

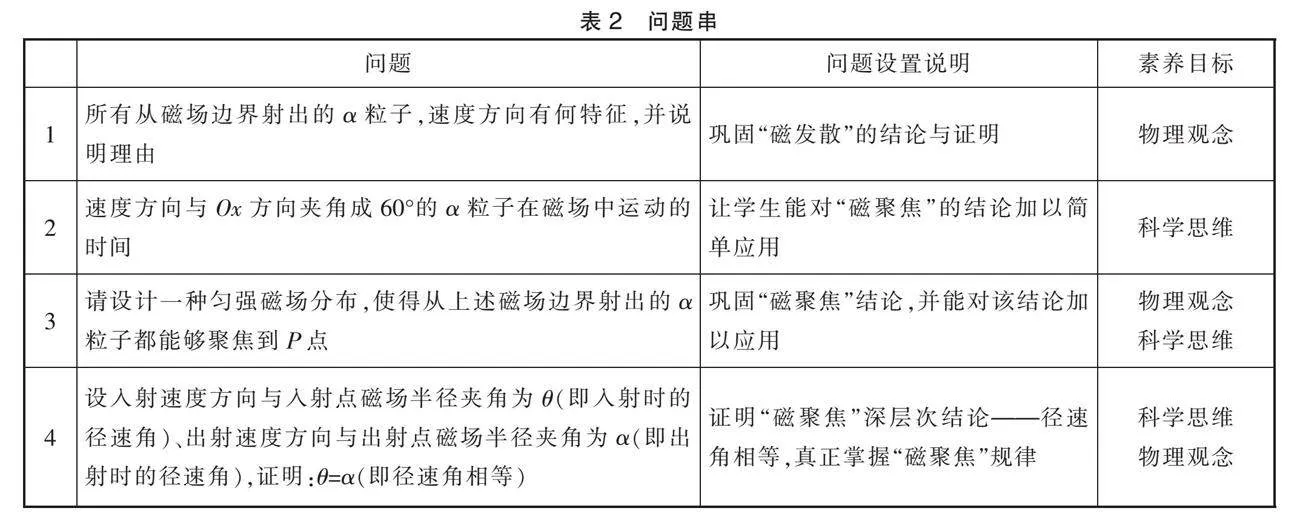
３．２ 由浅入深设置问题串

设置问题串如表２所示。

３．３ 根据思维流程引导解答

问题１解答：所有α粒子从磁场边界射出时，速度方向均与Ｏｘ平行，即水平向右。证明如下：

任取一个α粒子（如图9中，入射方向与入射点磁场半径成θ角），作圆轨迹，连接入射点Ｏ、圆磁场圆心C、出射点Ａ、圆轨迹圆心Ｑ。由题意，圆轨迹半径与圆磁场半径相等，均为Ｒ，四边形ＯCＡＱ为菱形。

所以，OC∥AQ。

又因为圆轨迹半径ＯC与切线Ｏｘ垂直，即OC⊥Ox。

所以，AQ⊥Ox。

又因为粒子在Ａ点出射速度ｖ方向垂直于圆轨迹在出射点的半径ＡＱ。

所以，出射速度ｖ方向与Ｏｘ方向平行。

问题２解答：解题思维流程如图10所示。

由磁发散规律，入射速度方向与Ｏｘ方向夹角成６０°的α粒子，射出时速度与Ｏｘ方向平行，在磁场中偏转６０°，运动的时间为１/６周期，即t=T=。

问题３解答：解题思维流程如图11所示。

如图12所示，由磁聚焦规律，要使所有α粒子都能够聚焦到Ｐ点，可以设计一圆形边界磁场，其半径ｒ＝Ｒ，Ｐ为切点，其圆心Ｄ在Ｐ正上方。

磁场的磁感应强度方向垂直于纸面向外，有

问题４解答：如图12所示，四边形ＣＯＯ１Ａ为菱形，对边平行，对角相等。

因为入射速度垂直于ＯＯ１，又ＯＯ１∥ＣＡ，所以入射速度垂直于ＣＡ，故θ与∠ＯＣＡ互余。

因为出射速度垂直于ＡＯ１，所以α与β互余。

又因为β＝∠ＯＣＡ（同位角），故θ＝α。证毕。

３．４ 检测学习成效

在新情境中，改编练习对弥补教学的成效以及学生的学习成效进行检测，练习设置的问题应该与学生前面出现的典型错误高度相关，且难度要高于诊断题，这样才有利于对学生学习后所达到的核心素养水平进行检测［３］。

检测练习：如图１3所示，在ｘＯｙ坐标系中，第一象限有一对电压为Ｕ１＝３×１０４ Ｖ的平行金属板，板间距离和板长均为Ｌ＝４０ ｃｍ，板的右侧有一粒子接收屏，下极板刚好在ｘ轴上，且带负电。第二象限有一半径Ｒ＝２０ ｃｍ的圆形匀强磁场，与ｘ轴相切于Ｃ点、与ｙ轴相切于Ｄ点。磁感应强度Ｂ＝０．１ Ｔ，方向垂直于纸面向外。第三象限有一个半圆形带正电的电极ＡＯ，圆心在Ｃ点，在其内部存在由电极指向圆心Ｃ点的电场，电极与Ｃ点的电势差Ｕ２＝１×１０４ Ｖ。现有许多质量ｍ＝６．４×１０－２７ ｋｇ、带正电的ｑ＝３．２×１０－１９ Ｃ的粒子在圆形电极附近均匀分布，由静止释放。不考虑粒子之间的相互作用与重力。求：

（１）粒子进入圆形磁场的速度大小；

（２）粒子击中ｙ轴的范围；

（３）粒子接收屏接收到的粒子数和进入平行板总粒子数比值ｋ。

本练习与诊断题“形同”，考查目标也一致，有新的情境，也有更高的难度，但解决的思维方法是一样的，都用到磁聚焦（或磁发散）的规律及深层次结论，可以起到很好地检测学习效果的作用。

参考文献：

［１］梁旭，袁张瑾，顾声和．认知诊断的程序与案例［Ｊ］．物理教学，２０２３，４５（１２）：５１－５４，６４．

［２］张玉峰．为了物理学科核心素养发展的学习诊断：概念、路径与内容框架［Ｊ］．中学物理，２０２０，３８（１）：２－６．

［３］梁旭．基于对学生错误进行认知诊断的教学［Ｊ］．物理教学，２０１３，３５（１１）：５７－６１．

（栏目编辑 李富强）