中考最值问题的几种模型及其解题策略

【摘要】中考数学的最值问题考查的模型较多，其中以将军饮马模型，建桥选址模型和胡不归模型最为常见.这些最值模型主要考查最短路径问题，涉及化归与转化思想、数形结合思想等，是综合性极强的试题.文章先解读上述三种常考的最值模型，然后结合中考真题给出这三种最值模型的解题策略，旨在为一线教学工作者提供最值模型的解题策略与教学参考.

【关键词】中考题；最值问题；将军饮马模型；建桥选址模型；胡不归模型；解题策略

中考的最值问题综合性较强，难度较大，通常以小压轴题的形式出现，有时也会出现在大题中的某一问，主要考查学生的化归与转化思想和数形结合思想，以及应用数学知识解决实际问题的能力.下面结合中考真题谈谈三种常见的最值模型及其解题策略.

一、三种模型的解读

模型1 将军饮马模型

将军饮马模型在考试中主要考查转化与化归等的数学思想，该题型综合考查学生的理解能力和数形结合能力，也是学生感觉有难度的题型.解决几何最值问题主要依据是：①将军饮马作对称点；②两点之间，线段最短；③垂线段最短.涉及的基本知识点还有：利用轴对称变换化归到“三角形两边之和大于第三边”“三角形两边之差小于第三边”等.

模型2 建桥选址模型

建桥选址模型，即沿一个方向平移的定长线段两端到两个定点的距离之和最小.解题时需要理清楚是否含有定长平移线段，且利用平移求出最短路径位置.求解长度时若有特殊角，通常采用构造直角三角形利用勾股定理来求解.该题型主要考查最短路径问题的应用，涉及的主要知识点有矩形的性质、平行四边形的性质、等腰直角三角形的性质、勾股定理等，解题的关键在于如何利用轴对称找到最短路径.

模型3 胡不归模型

对于胡不归“PA+k·PB”型的最值问题，当k等于1时，即为“PA+PB”之和最短问题，可用我们常见的“将军饮马”问题模型来处理，即可以转化为轴对称问题来处理.当k不等于1时，若再以常规的轴对称思想来解决问题，则无法进行，因此必须转换思路.此类问题的处理通常以动点P所在图形的不同来分类，一般分为两类研究，即点P在直线上运动和点P在圆上运动.其中点P在直线上运动的类型通常为“胡不归”问题.

二、三种模型的解题策略

（一）将军饮马模型

将军饮马模型主要以选择、填空形式出现，或者大题的其中一问，难度系数较大，在各类考试中都以中高档题为主.解决这类问题的关键是将所给问题抽象或转化为数学模型，把两条线段的和转化为一条线段.

解题策略：

第一步：观察所求为横向还是纵向的线段长度（定长），将线段按照长度方向平移；

第二步：同侧做对称点变异侧，异侧直接连线；

第三步：结合两点之间线段最短；垂线段最短；三角形两边之和大于第三边等常考知识点；

第四步：利用数学的转化思想，将复杂模型变成基本模型.

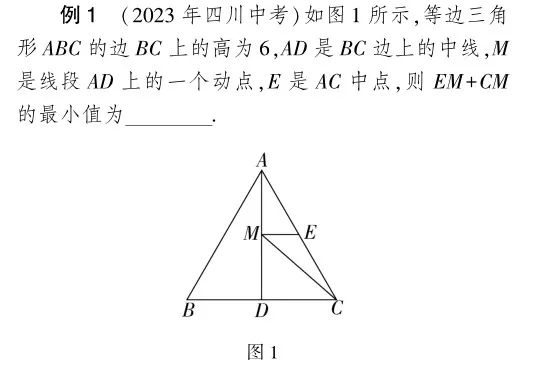
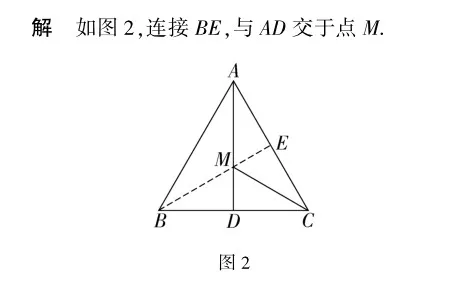
因为AB=AC，AD是BC边上的中线，

所以B，C关于AD对称，则EM+CM=EM+BM，

则BE就是EM+CM的最小值.

因为E是等边△ABC的边AC的中点，AD是中线，

所以BE=AD=6，所以EM+CM的最小值为6.

点评 此题主要考查了等腰三角形的性质“三线合一”、等边三角形的性质和轴对称等知识的综合应用，解题关键是找到M点的位置.连接BE交AD于M，则BE就是EM+CM的最小值，通过等腰三角形的“三线合一”，可得BE=AD即可得出结论.

（二）建桥选址模型

建桥选址模型主要以选择、填空的形式出现，一般较为靠后，有一定难度，主要考查轴对称———最短路径问题、勾股定理等，要利用“两点之间线段最短”等知识求解.很多时候需要将一些线段进行转化，即用与它相等的线段替代，从而转化成两点之间线段最短的问题.

解题策略：

第一步：观察点或图形的变化规律，根据图形的变化规律求出已知关键点的坐标；

第二步：分析变化规律得到一般的规律看是否具有周期性（如点变的循环规律或点运动的循环规律，点的横、纵坐标的变化规律等）；

第三步：周期性的求最小周期看余数，不是周期性的可以罗列求解几组以便发现规律，根据最后的变化次数或者运动时间等，确定要求的点与哪个点重合或在同一象限，或与哪个关键点的横纵坐标相等；

第四步：利用有理数的运算解题.

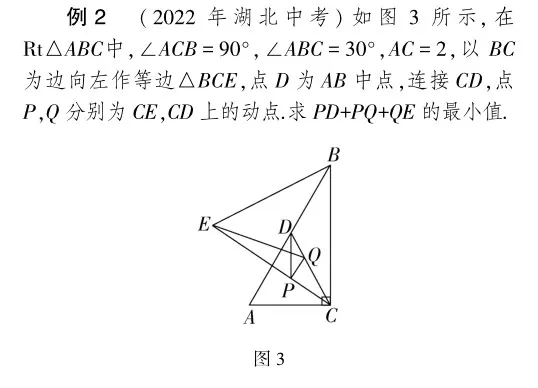
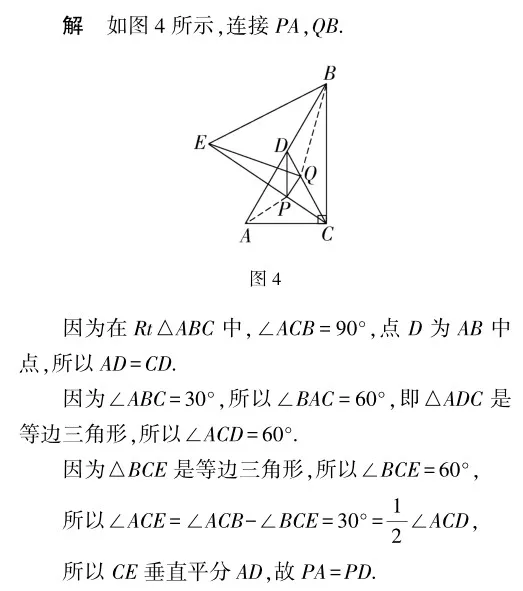
同理可得：CD垂直平分BE，所以QB=QE.

故PD+PQ+QE=PA+PQ+QB.

由两点之间线段最短可知，当点A，P，Q，B共线时，PA+PQ+QB取得最小值AB，

故PD+PQ+QE的最小值为4.

点评本题考查直角三角形斜边上的中线等于斜边的一半，等边三角形的性质，直角三角形的性质和垂直平分线的性质等.根据题意，连接PA，QB，先证PA=PD，QB=QE，故PD+PQ+QE=PA+PQ+QB，由两点之间线段最短可知，当点A，P，Q，B共线时，PA+PQ+QB取得最小值AB.

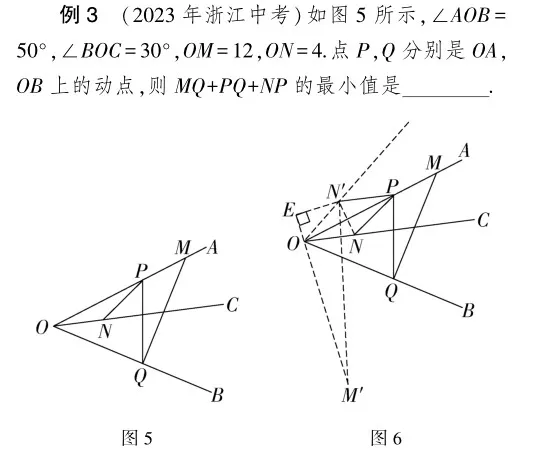
解 如图6所示，作点N关于OA的对称点N′，则NP=N′P，作点M关于OB的对称点M′，则MQ=M′Q，所以MQ+PQ+NP=M′Q+PQ+N′P.

（三）胡不归模型

胡不归模型可看作将军饮马模型的衍生，主要考查转化与化归等的数学思想的应用，近年在中考数学和各地的模拟考中常以压轴题的形式出现，学生不易把握.在解决胡不归问题主要依据是：点到线的距离垂线段最短.

解题策略：

第一步：构造与kPB相等的线段，将“PA+kPB”型问题转化为“PA+PC”型；

第二步：借助三角函数，构造锐角α，将另一个系数也化为1；

第三步：利用“垂线段最短”原理构造最短距离；

第四步：数形结合解题.

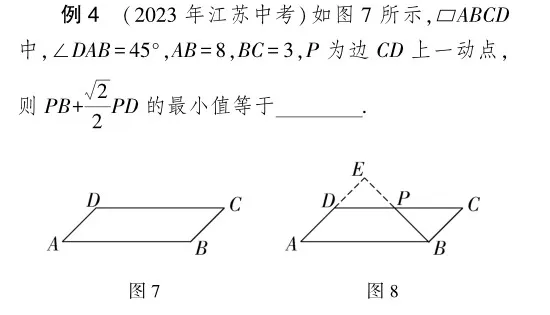
解 如图8所示，过点P作PE⊥AD，交AD的延长线于点E.

因为AB∥CD，所以∠EDP=∠DAB=45°，

结 语

将军饮ux6RAy2S1bmZZQHV5ETNNg==马模型、建桥选址模型和胡不归模型是中考试题中最为常见的三种最值模型.作为一线的教学工作者，在日常教学中要引导学生梳理和总结常见的最值模型及其解题策略，并结合中考真题进行强化训练.学生在总结最值模型和应用最值模型解题的过程中，可提高解题能力，领悟化归与转化思想、数形结合思想，发展数学学科核心素养.

【参考文献】

[1]李传煜.巧用“将军饮马”模型求解最值问题[J].中学数学，2024（2）：74-75.

[2]丁兆全.“胡不归”问题模型及应用[J].中小学数学（初中版），2023（Z1）：45-47.

[3]高峰官.构造模型法在几何最值问题中的运用[J].中学数学教学参考，2021（23）：19-22.

[4]陈礼弦.利用“两点之间线段最短”解决最值问题[J].数理化解题研究，2024（8）：13-15.

[5]胥凤霞.例谈初中数学几何最值问题的两种解题思路[J].数理天地（初中版），2024（5）：24-25.

[6]李鸿昌.“斜椭圆”面积的八种求解方法[J].中学数学杂志，2023（9）：43-46.

[7]李鸿昌，徐章韬.关于对数平均的一个不等式的推广[J].数学通报，2023，62（8）：50-52.

[8]李鸿昌，杨春波.一道课本例题的推广与应用[J].数学通讯，2015（Z4）：99-100.