一道椭圆轨迹问题的多角度探析及其推广

【摘要】轨迹问题是解析几何中的常考问题，有多种解决方法，例如代入法、参数方程法、极坐标方程法.文章结合一道椭圆轨迹问题，依次介绍这些方法的具体应用，以期为教师日常教学提供一些参考.

【关键词】解析几何；轨迹问题；参数方程；极坐标方程；推广

引 言

圆锥曲线中的轨迹问题是一类难度较大、综合性较高的题型.这类问题主要考查圆锥曲线的定义和性质，直线与圆锥曲线的位置关系等知识，需要综合运用数形结合思想、方程思想、转化与化归思想等数学思想方法.求解轨迹问题的常用方法有直接法、定义法、代入法（相关点法）、参数法、极坐标方程法等，其中直接法和定义法是较基础的方法.本文结合一道例题，谈谈代入法、参数法和极坐标方程法在求轨迹问题中的应用.

一、试题呈现

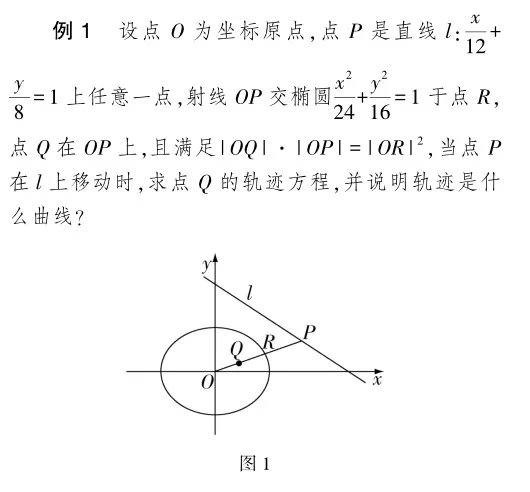
本题主要考查直线的方程、椭圆的方程及性质、直线与圆锥曲线的关系、轨迹的概念和求法等解析几何的核心知识.

二、解法探析

解法一（代入法） 根据条件可知点Q不是坐标原点，设点Q的坐标为（x，y），其中x，y不同时为零.再设点P的坐标为（xP，yP），点R的坐标为（xR，yR）.

当点P不在y轴上时，因为点R在椭圆上且点O，Q，R共线，

以上结论也可以横向类比到双曲线中，不再赘述.

结 语

综上所述，文章探究了一道椭圆轨迹问题的多种解法，通过一道例题呈现了代入法、参数法、极坐标方程法等求轨迹的常用方法.可见原题是一道求解思路开阔，具备一定综合性的优秀试题，有效考查了学生的必备知识、关键能力和数学学科核心素养.此外，原题蕴含丰富的教学价值，可以进行纵向推广和横向类比，在解题过程中，学生的抽象思维能力和发散联想能力可以得到充分的锻炼和提升，为学生未来的学习打下坚实的基础.

【参考文献】

[1]鲁媛媛.关于轨迹方程问题的解法探究[J].数理天地（上），2024（1）：39-40.

[2]南广明.求轨迹方程常用的方法[J].数理化解题研究，2023（28）：57-60.

[3]许莉.求轨迹方程方法研究[J].中学教学参考，2023（17）：13-16+34.

[4]李春林.求曲线轨迹方程的常用方法[J].高中数学教与学，2023（13）：18-20+17.