习题教学功能之助推教学改进和教师成长（上）

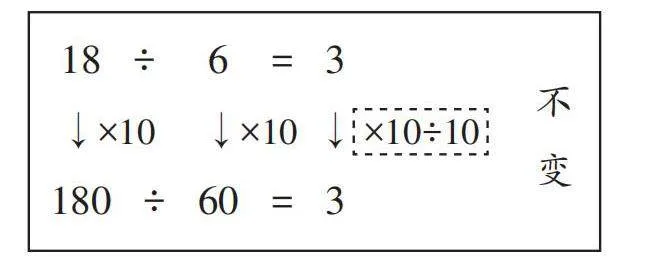
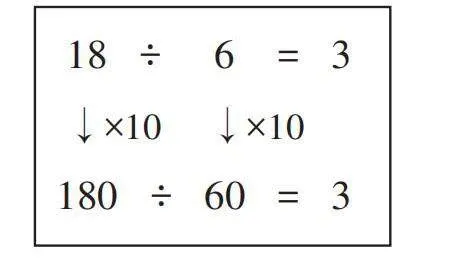
［摘 要］教学改进可以看成是对教学活动中发现的问题的优化，这样的优化过程能于无形中促进教师成长。习题教学在小学数学教学中占有重要地位，同时是小学数学教学的难点。因此，研究并践行习题教学，对助推数学教学改进和教师成长具有重要作用。

［关键词］习题教学；教学改进；教师成长；教学功能

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2024）27-0005-05

教学改进和教师成长是提高教学效率与达成教学目标的重要途径。实践证明，习题教学在助推数学教学改进和教师成长上具有重要的功能。

一、助推数学教学改进

宏观地讲，教学改进是一个永恒的话题，任何一次课程改革都可以视为教学改进的体现。比如，2001年启动的新一轮课程改革提出的“三维目标”便是教学改进的体现，因为要求教学不仅要关注知识与技能维度的目标，还要关注过程与方法、情感态度与价值观维度的目标。2011年修订的《义务教育数学课程标准》提出“四基”“四能”，这又是一次教学改进，因为要求教学不仅要关注学生分析问题和解决问题能力的培养，还要重视学生发现问题和提出问题能力的培养。2022年《义务教育数学课程标准》再次修订，确立核心素养导向的课程目标，这自然也是教学改进的体现。微观地讲，教学改进经常性地发生在教师日常的课堂上。

案例：“商的变化规律”

习题教学记：2020年12月9日，周三

师：这段时间我们在学习除法，现在我写几道题给大家算一算。

[我先板书“16÷8”，在学生回答后再板书“160÷8”。]

师：现在等于多少呢？

[学生马上一起回答“等于20”，我再板书“320÷8”，在学生回答后继续板书“640÷8”。于是，黑板上形成以下一组板书。]

[16÷8=2

160÷8=20

320÷8=40

640÷8=80 ]

师：请大家看看这些算式，有没有特殊的地方？

生（齐）：除数都是8。

师：除了除数都是8，你们还有什么发现吗？

[此处，《教师教学用书》的建议是“提出问题：每组题中的什么数变了？什么数没变？除数（或被除数）和商的变化有什么特点？”。我觉得这样太烦琐了，没有采取这个建议，而是让学生整体观察，自己去发现。]

生1：我发现被除数都是乘2，商也一样。（此话一出，马上有学生表示反对，并围绕算式进行比较，证明这个发现不对）

生2：我发现除数不变，被除数乘几，商也乘几。

[我没想到这个答案会来得这么快，且这么清晰，于是给予该学生“铜钥匙”奖励。一些学生对这奖励有意见了，认为过于简单，不足以奖励“铜钥匙”。]

师：这个发现不简单。不信，谁能再来把这个发现讲一遍？（几个学生的表述都不能达到上述清晰的程度。至此，大家认可了给予“铜钥匙”的奖励）

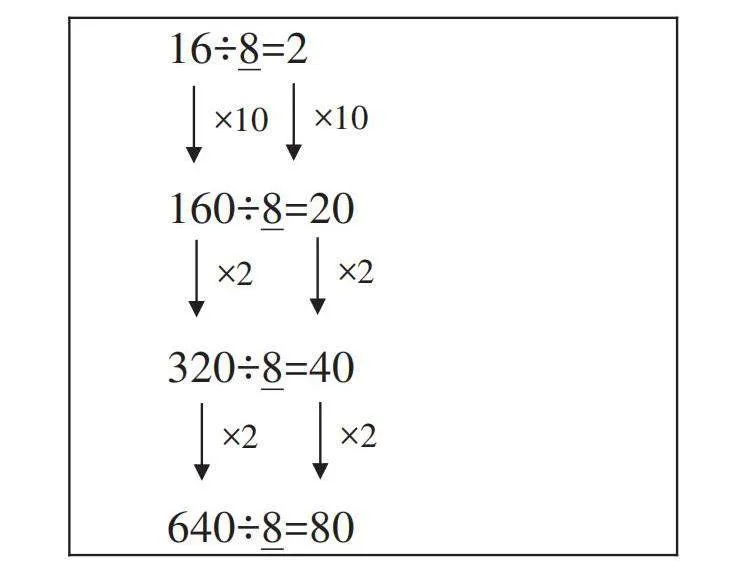
师：现在我们一起来把这个发现讲一遍。（同时配合以下板书）

[16÷8=2

160÷8=20

320÷8=40

640÷8=80 ] [×10] [×10] [×2] [×2] [×2] [×2]

师：谁还能有新的发现？（学生都觉得不可思议）想问题，有时候可以倒过来想。（有了这个提示，反应快的学生马上举手了）

生3：这些算式倒过来看，就是除数不变，被除数除以几，商也除以几。

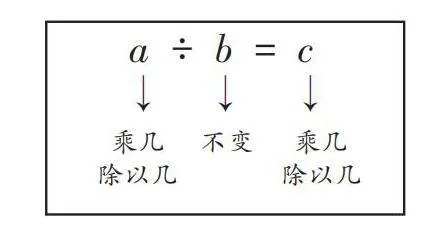
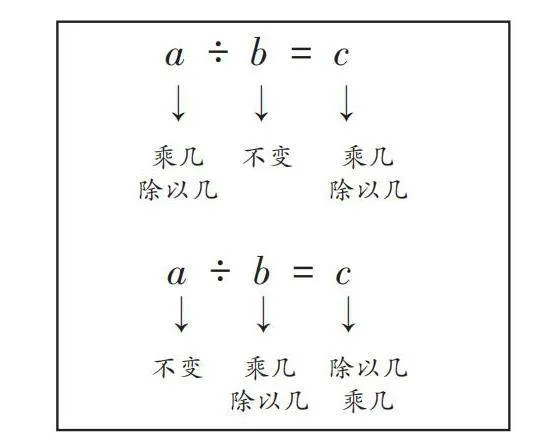
[我同样给予该学生“铜钥匙”奖励，并结合字母式表达形成如下板书。]

[a ÷ b = c][↓][↓][↓][ 乘几

除以几][不变][ 乘几

除以几]

师：现在谁能把这个发现合起来说一说？（学生独立思考后统一说）学到这，你们有问题产生吗？

生4：乘或除以的这个数能是0吗？

[这是意料之外的问题，我与学生一起讨论后板书“0除外”。]

师：谁还有不一样的问题？

生5：如果被除数不变，除数乘几，商会怎么变化呢？

[这是一个好问题，我先给予“铜钥匙”奖励，再通过举例、观察、发现，引导学生理解为什么商的变化与除数的变化相反，最后用如下字母式表达。]

[a ÷ b = c][↓][↓][↓][不变][ 乘几

除以几][除以几

乘几][a ÷ b = c][↓][↓][↓][ 乘几

除以几][ 乘几

除以几][不变]

师：学到现在，不知道你们心里有没有新的问题产生呢？

[我的话音刚落，马上就有学生举手了，这说明问题不是经我提问后产生的，而是他们在前面的学习中就有了。]

生6：刚才都是一个数不变的情况，如果两个数都变，会怎么样？

师：好问题，给予“铜钥匙”奖励！（板书“18÷6=3”后，继续板书“180÷60”）这等于几？

生（齐）：3。

师：有什么发现？

生（齐）：商不变。

师：对的。怎么会商不变呢？

生7：因为被除数乘10，除数也乘10，所以商不变。

[从道理上讲，这样的解释完全正确。但是，现在是要发现道理，且我还想要学生学会解答作业本上的题目，现在自然不能这么简单，毕竟前面那么长的铺垫可不是用来做摆设的。于是，我随着学生的解释，完善如下板书。]

[ 18 ÷ 6 = 3

↓×10 ↓×10

180 ÷ 60 = 3]

师：好奇怪哦！被除数乘10，除数也乘10，怎么商不变呢？（学生陷入沉思，不过还是有勇敢举手的人）

生8：抵消了。

师：抵消！怎么抵消？

生8：被除数乘10，商就乘10；除数乘10，商就除以10，这样乘10和除以10就相互抵消了。

[教室一下子像炸开的锅，学生似乎都明白了。于是，我又让几个学生把这道理复述一遍，并跟进形成如下板书。]

[ 18 ÷ 6 = 3

↓×10 ↓×10 ↓ ×10÷10

180 ÷ 60 = 3][不变]

师：看来，“不变”真的是抵消了的原因。（继续板书“360÷12”，让学生解释不变的原因，并形成以下板书）

[a ÷ b = c][↓][↓][↓][a ÷ b = c][↓][↓][↓][a ÷ b = c][↓][↓][↓][ 乘几

除以几][不变][ 乘几

除以几][不变][ 乘几

除以几][除以几

乘几][ 乘几

除以几][ 乘几

除以几][不变]

[最后，我结合上述板书，总结商不变性质。]

这个案例并不是本系列文章所说的习题教学记，因为这不是在记录一道习题的教学，而是在记录“商的变化规律”的例题教学。之所以还是将其看成习题教学记，是因为案例中的教学源于一道与此相关的习题（见图1）。

还记得在备“商的变化规律”这节课教学时，我的脑海里浮现出以前教学这节课之后学生做相关习题的情景。于是，我在读完《教师教学用书》上的“教材解读”和“教学建议”后，赶紧翻开配套的作业本看看，因为自己已经不止一次在这样的事情上“翻船”了——按照《教师教学用书》的建议进行教学，结果作业本上的习题超出了“教材解读”的要求，这让学生和我都苦不堪言。图1就是我在作业本上看到的与“商的变化规律”一课同步作业的最后一道习题。说实话，这道习题我并不陌生，相信教过这一内容的教师也不陌生，这甚至可以看成是一道与“商的变化规律”相关的经典习题了。令人意外的不是这道习题本身，而是这道习题竟然出现在“商的变化规律”这节课中。试想，如果依据教材编排，通过观察几组除法算式得出商的变化规律，面对这道习题，我和学生岂不又要苦不堪言了？尤其是其中的第（4）小题，因为学生错得多！

“如何在教学之后让学生能较好地解答这道习题呢？”这是我在作业本上看到这道习题之后，脑海中条件反射般出现的问题。为此，我陷入了思考。思之思之，我猛然觉得：“这道习题所要求的解题思路，不正是‘商的变化规律’的原形吗？”于是，新的教学设想在心中逐步形成，我赶紧记录下教学流程，完成备课。我带着新的教学设计走进教室，便有了上述案例所描述的教学。

相信，如果没有作业本上的这道习题，对于“商的变化规律”的教学，我会在学生发现商不变时就止步了。因为这样的“发现”，已经较好地完成教材对这节课的教学要求了，也符合《教师教学用书》上的解读和建议。可是，因为作业本上的一道习题，我的教学又向前走了一步。这一步，不是将“商不变”作为一种特定的发现来对待，而是作为被除数和除数变化过程中的某一种现象来对待，是商随着除数和被除数变化而变化中的一种比较特殊的情况。同时，字母表达式的模型，也为学生解答作业本上的习题提供了支撑。从课后批阅学生的作业情况来看，这样教学取得了比较好的效果。

显然，上述案例的教学，其实就是微观层面上的教学改进。需要指出的是，这次教学改进的起因是作业本上的一道习题，以及我对以往学生解答这道习题出现错误情况的分析。事实上，像上述案例的情况经常性地发生在教师的日常教学中。比如，办公室里，教师之间相互交流学生的解题情况，进而讨论出如何改进教学效果会更好的结论。

换言之，微观层面上的教学改进，常常没有“三维目标”“核心素养”这样高大上的名词来支撑，有的可能只是学生能更好地解答习题的朴素想法。但是，仔细辨析就会发现，学生能更好地解答习题的朴素想法的背后，实际上是教师对学生、对知识、对教学的深度理解。所以，基于习题教学分析学生的解题，可以助推教学改进的发生。为了更好地理解习题教学的这一功能，我们有必要再讨论下面两个问题。

（一）为什么分析学生解题可以助推教学改进

研读教材和研究学生是实现课堂教学改进的两个重要抓手。研读教材，有助于我们更好地把握“教什么”；研究学生，有助于我们更好地把握“怎么教”。一直以来，对教材的研读，我们常常将重心放在例题教学上；对学生的研究，重心则落在学生学习例题上。但是，在实际教学过程中，我们的教学改进常常还有第三个抓手——学生在解答习题中的表现。

如上述案例，对“商的变化规律”一课教学，我研读了教材和《教师教学用书》，也研究过学生，因为这节课之前已教过几次，清楚自己要“教什么”和“怎么教”。但是，当我看到作业本上的习题之后，立刻想起了以往教学这节课之后学生解答此类习题的表现。这让我清楚地意识到：如果仅根据自己现在对这节课“教什么”和“怎么教”的理解，那么学生在解答作业本上的最后一道习题时，就会遇到比较大的困难。这促使我再一次对“教什么”和“怎么教”进行审视，努力寻求解决问题的路径，最终有了上述案例的教学改进。因此，如果把研读教材狭义地理解为研读教材上的例题教学，把研究学生狭义地理解为研究学生的例题学习，那么研读习题、分析学生的解题表现，无疑成为连接教材和学生之间的纽带。也就是说，习题教学具有教学诊断的功能，即可以通过学生解题来检验课堂教学效果。如果习题教学在学生端出现了问题，那么作为教师就该反思自己的教学，从知识端入手并设法改进。

以上是从我个人实践的层面看待习题教学对教学改进的助推作用。从更为广义的层面讲，各地甚至全国范围内开展的教学质量监测，不也是通过学生解答相关习题的形式来分析教师教学中存在的问题，进而提出改进意见的吗？可见，基于习题以及习题教学来分析学生解题，是助推教学改进的一个重要抓手。

（二）如何通过分析学生解题助推教学改进

通过上述分析已经明确，对学生解题的分析可以助推教学改进，进而提高课堂教学效率，那么在具体的教学过程中该如何来实施呢？一般而言，需要把握好以下两个方面。

1.深入分析学生的解题表现

对学生在解题过程中的表现进行分析，是实现教学改进的重要前提。一般在两种情况下，教师能注意到学生在解题过程中的表现：一是学生在课堂上的解题过程；二是学生课后作业的解题结果。下面，重点讨论第二种情况中学生的解题表现。

教师对学生课后作业的批阅，不仅可以了解学生对知识的掌握情况，还可以从中看到自己教学中存在的问题，这便是习题的诊断功能。当然，要实现这个功能，教师在批阅作业时就不能只看“对”“错”，而要对学生的“错”展开深入分析，找到其背后的原因，进而厘清学生在解题中遇到的困难是什么。如在梯形教学之后，学生在解题中经常不认可图2是一个梯形。

深入分析不难发现，这是教师教学不到位造成的，如概念形成太快、变式习题不够丰富等。因此，面对学生的普遍错误或者聚集性的典型错误，教师必须引起重视，因为这时的错误已不是学生的问题，而是教师的问题，是教师对“教什么”和“怎么教”把握不到位造成的，需要对教学进行必要的改进。

2.把握教学改进的两个时机

当发现学生在课后作业中出现的问题后，教师需要反思之前的教学，需要改进的也是之前教学这一内容的策略。由此可见，分析学生解题表现后的教学改进，不是回到从前，而是启示未来。

（1）改进下一课教学——及时补救

通过分析学生的解题表现，发现教学中存在的问题后，教师此时要做的第一件事就是及时补救，想办法改进下一课的教学。这里的“下一课”，可以是紧接着批阅学生作业之后的那节数学课，因为学生解题中出现的问题一般与紧接着的学习内容联系密切，如果不及时解决，会影响后续的学习；也可以不是紧接着的那节数学课，而是在某一阶段教学内容完结之后专门安排的一节课，因为学生课后作业中出现的问题不会影响紧接着的内容学习，所以可以暂时缓一缓。

一般常用以下的改进措施：一是将学生解题中出现的问题在课堂上呈现，组织学生对问题进行讨论，以纠正学生的错误认识，弥补之前教学存在的不足；二是重新设计一道类似的习题，有针对性地展开教学，以此弥补之前教学存在的不足，深化学生的理解。当然，我们还要认识到：如果因为例题教学存在不足而导致学生在解题时出现问题，那么仅凭一次补救教学往往是不够的，需要有一个不断强化的过程。

（2）改进下一轮教学——根源入手

一般情况下，教学是一个循环往复的过程，比较常见的是1～3年级轮回和4～6年级轮回。因此，当我们在学生解题中发现了问题，此时虽不能回到从前，但可以促使我们在下一轮再次教学这个内容时进行改进。这是一种从根源入手的教学改进，在广大教师平时的教学实践中还是比较常见的。比如，平时大家在备课时思考“以前教到这里时学生的问题是什么”，此时的思考对象常常就是学生在解题中出现的问题。因此，这样的思考其本质便是基于上一轮教学中学生解题时出现的问题，而引发的教学改进行为。

不过，从现在发现学生在解题中出现的问题，到下一轮再次教学这个内容，往往要间隔3年或至少1年，甚至3年、6年的时间。这么长的时间，难免会出现一定的遗忘。因此，教师每次备课时先看一看、做一做教材或作业本上的习题，再想一想以前学生在这里出现过什么问题，就可以唤醒自己的记忆，有助于更好地改进教学。

当然，我们更希望从发现问题到教学改进的时间能缩短一些。对此，加强教师间的教学交流便是一种有效的手段。也就是说，教师对学生在解题中出现问题的认识，并不一定要自己亲身经历，还可以从同事那里交流获得。另外，自己发现的问题也可以分享给同事，这样不仅可以为大家提供第一手的教学资料，还可以一起商讨更为有效的教学改进策略。可见，这里的“下一轮”，可以是自己教学的下一轮，也可以是从别人那里学来的下一轮，还可以是自己提供给别人的下一轮。

在习题教学中，教师深入分析学生的解题表现，充分发挥习题的诊断功能，不断改善自己的教学，最终目标是为了促进学生更好地发展。

（未完，待续）

［ 参 考 文 献 ］

[1] 何月丰.分析学生解题助推教学改进[J].小学教学设计，2021（14）：20-23.

[2] 中华人民共和国教育部.义务教育数学课程标准（2022年版）[S].北京：北京师范大学出版社，2022.

（责编 杜 华）