砂岩环状纹理的秘密

天然岩石是传统的建筑材料，最常见的有花岗岩、大理石和砂岩等[1]，在上海外滩及周边的建筑群中，很容易找到这些石料，其中砂岩的使用非常广泛，如上海外滩15号大楼门楣、门柱等部位使用了紫砂岩；延安东路上的高登金融大厦，其大厅所在的外侧墙面也用砂岩装饰，暖色的花纹既显奢华，又不失淳朴。在国际上，一些历史悠久的建筑，如法国巴黎圣母院、罗浮宫，英国白金汉宫，美国国会大厦等，其厚重而典雅的砂岩外墙令人赞叹。

砂岩作为一种沉积岩，是在漫长的地质岁月中逐渐固结形成的。在地质学里，“沙”是沉积物的意思，而“砂”是沉积物的一种类型，它的颗粒直径在0.063～2毫米，大小介于砾石和泥之间。砂岩最初也是松散沉积物，砂粒中有很多孔隙，这些孔隙体积约占总体积的40%。随着时间的推移，这些孔隙逐渐被沉淀的物质所充满，松散的砂转化成了坚固的砂岩，而砂岩的花纹正是由沉淀物形成的。

砂岩环状纹理的色调多种多样，有深色，也有浅色。这种环状图案，其实是分布于三维空间的，因此在不同方位的切面上都能见到，由里向外，环的宽窄和色调有着一致的排列格局。这一现象如何解释？19世纪以前，博物学家和地质学家一直难以回答。

砂岩神奇纹理的近距离观察

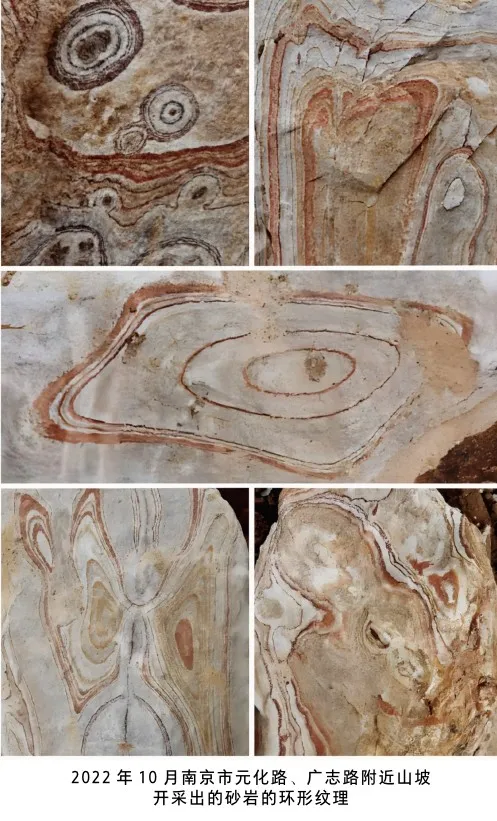
地层里的砂岩有可能在建筑工地、道路工程、采石作业时暴露出来，此时正是近距离观察砂岩神奇环状纹理的机会。比如，2022年6月南京市仙林地区的元化路、广志路交叉路口附近的山坡，由于建筑的需要，变成了开挖的工地，工地南侧的空地则成了一个巨大的堆场，堆放山坡上挖出的砂岩，这些砂岩大多数直径有几十厘米，最大者超过2米。砂岩所在的地层属于两亿年前的三叠纪，当年的松散砂层已固结为岩石。观赏眼前砂岩截面上的各种美丽图案，是一场视觉盛宴。砂岩块体截面上，纹理线条的颜色涵盖从暗红到浅褐色的整个谱系，图形多种多样，有的精致，有的粗犷；有的像是展翅的蝴蝶，有的如同哺乳动物的头像。图形样式之丰富，可以激发出观者无尽的想象。

砂岩里的纹理早就引起了博物学家的关注。现代科学研究的早期，有一个博物学时代。那时候的人们对自然界中的植物、动物、化石、岩石、矿物等很感兴趣，他们采集标本，描述其形态和物性，构建分类系统，并试图作出成因解释，这样的研究者称为博物学家，砂岩中的环形图案自然也引起了他们的关注。

但是，在寻求答案之前，首先要明确砂岩纹理究竟指的是什么。

环形纹理中有几种类似的现象，曾被认为是同一种现象，其实不然。有两种容易混淆的情形。第一，如果把多层不同岩性或颜色的沉积物固结形成的岩石切下一块，再加工成一个球形，在球面上就显示出环状结构，但它与前述的情形不同，真正的砂岩纹理应在任何切面或多个方位的切面上都能看到。第二，砂岩由于风化作用而形成球形块体，称为球状风化[2]，但要注意的是，风化作用是由外向里逐渐推进的，核心部分最后被分化，因此最外层是最薄弱的已经遭受风化的层；虽然三维空间分布的环形纹理有可能影响球状风化，但在时间上是纹理形成在先，风化过程在后，因此球状风化不是环形纹理的成因。

关于砂岩环状纹理成因，德国化学家和摄影学家李泽冈（Raphael Edward Liesegang， 1869–1947）于1896年先于博物学家给出了答案，从此砂岩环状纹理就以这位科学家的名字命名为“李泽冈环”或“李泽冈条带”。

李泽冈的实验和解释

李泽冈理论的诞生要从摄影技术的发展谈起。现在人们都用数码相机拍照（手机也有自带的数码摄影功能），然而就在21世纪初，人们还普遍使用胶卷拍照。照相的原理是，感光物质（通常为盐类）涂抹在胶片上，光线照射后发生化学反应， 经显影、定影，胶片就 成为底片。因此，胶片所用的材料和涂抹方式就成为关键技术。这项似乎已经过时的技术，放在19世纪却是一项重大发明。

当时，李泽冈专攻胶体化学，试图通过化学实验改进摄影技术。1896年，他做了一个有趣的实验：将凝胶与重铬酸钾溶液充分混合后均匀涂抹在圆盘上，然后又在圆盘中心上方滴入含有银离子的溶液。接下来就出现了神奇的现象：围绕着圆盘的中心形成了环状的银离子沉淀物。环的形成有先后次序和宽度差异，随着物质向外扩散，每一圈沉淀物形成的时间不同，内圈先形成，然后逐一向外拓展。每两个圈之间的距离也不同，有向外逐渐扩大的趋势。最终在圆盘上留下的印记犹如一圈圈树木年轮。这个观察结果让李泽冈感到兴奋，因为它正好能够解释砂岩中环状纹理的成因！于是他在第一时间报道了这个实验的全部过程[3]。

李泽冈的实验有什么特别之处呢？首先，实验需要用凝胶（或称为明胶），如用水等常规液体则不行，因为物质在水体中的运动很容易造成紊动，而紊动扩散会破坏任何空间上的有序排列。凝胶则不同，可以有效防止出现紊动现象。在凝胶里面，流体质点相互之间的位置几乎固定。第二，凝胶中混合的基底溶液是重铬酸钾溶液。第三，滴入圆盘的是盐类的溶液，除银盐之外，还有含铁、镁、钙、铜、镍、钴、铅、锡等金属离子的盐类，遇到凝胶中的酸根便可能沉淀析出。这样的情形与砂岩中的物质运动非常相像，砂岩内部有很多空隙，由于砂粒的阻力作用，空隙中的流体运动十分缓慢，就像凝胶中的物质一样，难以形成紊动的状态。此外，砂岩空隙中的流体也含有一定的酸根，如碳酸根。当含有金属离子的物质流体进入，就可能发生化学反应，产生沉淀。经常出现的是铁的沉淀，它可以形成红色的环。李泽冈解释说，这就是流体扩散-沉淀反应所造成的特有图案。

1913年，李泽冈出版了《地质体内的扩散作用》专著[4]，阐述胶体化学理论及其与砂岩环状纹理的关系。同行学者发表书评指出，胶体化学的新进展对地质学具有特殊价值，它详细地描述了可能与地质过程有关的胶体扩散实验，以及周期性沉淀的产生过程，将为地质学开辟一个崭新的研究领域。

李泽冈环形成的经验定律

李泽冈的电解质溶液的扩散-沉淀理论解释了砂岩环状纹理的成因。在此基础上，研究者投入了更多的研究力量，目的是将理论与观测事实之间进行定量联系。科学研究的目标之一是建立定律，以便实现精准预测。就圆盘上的环状纹理而言，需要了解的物理量有三个：①每条纹理的位置，即纹理中轴线到圆盘中心的距离；②每条纹理的宽度；③每条纹理形成的时间。当时的研究者意识到，这三个物理量应该与凝胶的组成、凝胶内部电解质和外部添加电解质的类型和浓度有关，因此首先通过大量的试验，来检验凝胶和内、外电解质不同组合的效果。显而易见的是，各种组合的可能性几乎难以穷尽，幸运的是，实验很快证实，凝胶和内、外电解质的不同组合对前述的三个物理量均有影响[5]。

那么，如何根据凝胶和内、外电解质的性质来确定纹理的位置、宽度和形成时间？可能性之一是根据扩散-沉淀理论建立方程组，然后进行模拟计算，这一方法早在19世纪末就有学者提出[5]，但在20世纪中期之前，由于计算能力的欠缺，这种方法还不太可行。于是，人们转而依据实验记录来建立经验定律，即针对各种凝胶和内、外电解质组合，得到位置、宽度和形成时间的数据，进而寻找数据之间的关联性。高速照相机为此类实验提供了很大帮助。

研究者发现，李泽冈的圆盘实验也可以在试管内进行，所不同的是，圆盘上的物质扩散是平面二维的，而试管内的扩散是一维的，沿着试管长轴方向形成横向的条带状纹理，此时纹理的位置变为其中轴线到纹理生长起始点的距离。显然，试管实验更为简便。在技术上，高速照相机能够精准地获取三个物理量的时间序列。大量数据的获取导致了三个经验定律的建立[6]。

位置定律 随着实验的进行，条带逐一形成，后续条带到起始点的距离并非按照条带数的增加而均匀加大，而是以一种“加速”方式增大，即离起始点越远，相邻条带间的距离也越大，相邻条带到起始点距离之比与凝胶内、外电解质浓度等因素有关。

宽度定律 条带宽度是条带位置的幂函数，而且幂函数中指数的值接近于1，因此离起始点越远，条带宽度越大。

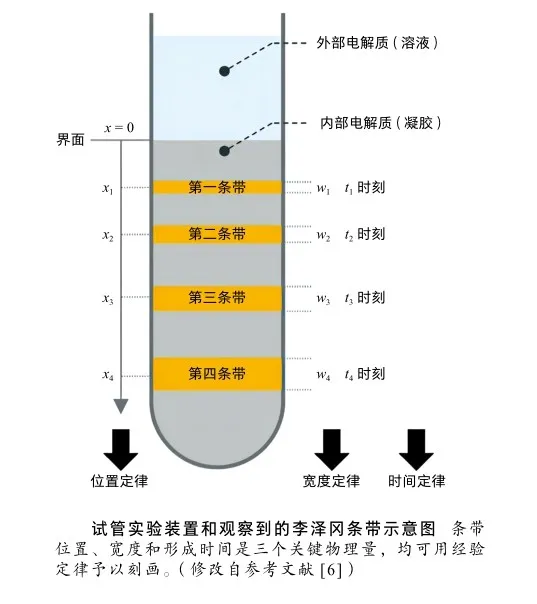
时间定律 任一条带的形成时间与条带所在位置的坐标值的平方成正比，因此，随着条带的不断形成，越到后来所需的时间越长，随着条带位置的变远，其平方的值增大得更快，所需要的时间也就变得更长。

由此，针对任何特定的凝胶-电解质组合，均可根据经验定律来刻画条带特征。假设李泽冈的圆盘是各向同性的，即任何方向的空间尺度、电解质浓度、扩散过程都相同，则试管实验的条带就可以替换为环状纹理，前述三个物理量的经验定律在这里也适用。

上述经验定律表明，条带或纹理的宽度和形成时间均与其位置有关，而位置又与凝胶和电解质浓度等因素有关，这样一来，条带或纹理形成的样式就有诸多可能性，这与多年来众多学者做过的实验结果相符。总之，凝胶和电解质的不同组合有着非常多的可能性，因此可以形成许多形态各异的李泽冈环。

在定性层面上，扩散-沉淀理论能够解释砂岩纹理。但地质环境涉及的因素远多于实验室环境，且砂岩形成演化的时间尺度很大，因此实际看到的砂岩纹理比经验定律所预测的要复杂得多，如前所述的南京仙林地区砂岩就是如此。

首先，砂岩内部是三维空间，与试管和圆盘都不同。流体的流速和方向处于不断变化之中，流体中所含的金属离子也被水流搬运，其运动并非单纯地由于扩散而发生。沿水流方向的运动快于其他方向，因此并不是各向同性的。

其次，砂岩受到层理、断裂等作用而被分离为大小不等的块体，使得砂岩纹理的形成空间受限，在各个块体内部自成体系，这也是造成各向异性的重要原因。

最后，从砂质物质堆积到固结成岩，必然经历漫长的时间，在此期间可能发生多次扩散-沉淀事件，而且每次事件的电解质组分、流体运动方式、金属离子输运强度等均有所不同。更重要的是，后续事件导致的沉淀作用是在既有事件的基础上进行的，因此最终观察到的金属离子沉淀特征是长期重叠、累积的结果。澳大利亚东南部悉尼盆地三叠纪砂岩中壮观的富针铁矿带就是长期演化的产物，多次扩散-沉淀事件的纹理叠加在一起，很难彼此分离[7]。

李泽冈理论的再次激活：复杂系统模型与应用

地质学家的实证研究表明，真实世界里的砂岩纹理可用李泽冈理论来解释，但却不能根据经验定律预测其细节。这个问题可望由于21世纪李泽冈理论研究的再次激活而得到最终解决。

如前所述，为了构建扩散-沉淀体系的控制方程，研究者已经努力了一个多世纪，现在由于复杂系统模型与计算机技术、人工智能的发展出现了重要转机。从数学的视角看，无论一个系统有多复杂，人们感兴趣的变量却是有限的；针对每个变量的时间变率都建立一个方程，就形成一组控制方程，通过解方程的环节，就能获得每个变量的取值（用以表示系统特征）和时间序列（用以表示系统演化）。例如，在扩散-沉淀体系中，内、外电解质的浓度及其时空变化，以及在各个位置的沉淀速率，就是研究者感兴趣的变量，若其值为已知，就应能确定李泽冈环的样式[6，8]。

关键是方程如何表达、如何解答？答案是应用人工智能方法。对于电解质浓度和沉淀速率，其物理定义明确，影响因素也为已知，因此可将其时间变率与金属离子输运和沉淀过程相联系，此类方程称为“基于科学原理的方程”。有时候，影响的因素不够清晰，但关键变量与产物之间存在着显著的相关性，据此可建立经验方程，即“基于相关性的方程”。复杂系统中的控制方程经常是两种方法的结合。

对于方程的解，一方面，从传统数学的角度看，必须要明确扩散-沉淀体系的基本条件，若已知条件不够完整，则方程多解，环境因素的复杂性导致系统行为的多样性。另一方面，在人工智能框架下，可在方程转化为计算模型时加入一些简化的成分，如自组织等算法[8]。描述各种算法的术语有些复杂，但可以打个比方来加以理解：对于函数y=x2，当x的取值在0和1之间时，用y=x来取代，不会造成很大的误差，这就简化了原先的函数。此处的逻辑是，如果并不需要了解系统的一切，而只想了解所感兴趣的部分，那么如此处理将使问题得到简化。简化的算法通常是基于观测数据的，因此被称为“数据驱动”的方法，将其纳入模型，可提高计算的效率和可靠性。

由于人工智能方法的扩展应用，可以预见，砂岩纹理所含的信息将被更多地挖掘出来，成为环境特征及其变化研究的重要数据来源。过去，人们因为砂岩纹理的美丽而挖山取石，而掌握了纹理形成技术，就能大量生产人造砂岩，而把天然砂岩作为自然遗产加以保护。通过控制扩散-沉淀过程，还能制造出具有特殊性质的新材料，它们不仅具备独特的纹理结构，而且沉淀物的各种三维分布方式可以满足人们所需要的观感、质地和功能。

李泽冈环人工智能模型的潜在医学应用也很诱人。人体含有复杂的液体输运体系，水分、血液、尿液在运动中可能受到扩散-沉淀过程的影响，物质沉淀是不少病变的原因[9]。呼吸中进入肺部的气体也属于流体，其中所含的不溶性产物的亚饱和-过饱状态会导致周期性扩散-沉淀的发生，造成病变，损害肺功能[10]。对这些疾病，未来可能发展出新的治疗方法，采用扩散和沉淀控制技术，改变沉淀作用的强度和位置，甚至有一天医生们可能将微型机器人派往病变现场实施清理。

李泽冈本人大概也没有预见到，他的实验最初被用来解释砂岩环状纹理的成因，而一个世纪之后，它的意义早已远远超越环状纹理，研究者追寻的研究方向已经拓展到了地球环境科学、材料科学和医学的纵深之处。这正是科学的魅力所在。

[1]Ries H. Economic geology.7th edition. New York： John Wiley， 1937：720.

[2]Ollier C D. Causes of spheroidal weathering. Earth-Science Reviews， 1971，7： 127-141.

[3]Liesegang R E. Ueber einige Eigenschaften von Gallerten. Naturwissenschaftliche Wochenschrift， 1896， 11：353-362.

[4]Liesegang R E. Geologische diffusionen. Dresden： Theodor Steinkopf， 1913：180.

[5]Henisch H K. Crystals in gels and Liesegang Rings. New York： Cambridge University Press， 1988：197.

[6]Nabika H， Itatani M， Lagzi I. Pattern formation in precipitation reactions： the Liesegang Phenomenon. Langmuir， 2020， 36： 481-497.

[7]Vernon R H. Ferruginous banding in Sydney sandstone. Australian Journal of Earth Sciences， 2021， 68：498-514.

[8]Darbenas Z， Van der Hout R， Oliver M， et al. Conditional uniqueness of solutions to the Keller–Rubinow model for Liesegang rings in the fast reaction limit. Journal of Differential Equations， 2023， 347： 212-245.

[9]Moran M E. Urolithiasis： a comprehensive history. New York： Springer， 2013： 471.

[10]Ahn A R， Sung J J， Shin M G， et al. Liesegang Ring in a patient with allergic bronchopulmonary aspergillosis. International Journal of Surgical Pathology， 2024， 32： 97-99.

关键词：砂岩 扩散-沉淀实验 李泽冈环 经验定律 ■