超对称波导实现光子拓扑态的完美激发

光是人类获取和传递信息的重要载体。近几十年来，在先进微纳加工技术的推动下，光学研究前沿经历了从简单到复杂，从宏观到微观的高速变革。然而，相较发展成熟的集成电路体系，尽管片上光子器件已经有了长足的发展，但大规模、芯片化集成还面临诸多困境。最为突出的是，光信息的传递往往需要通过波导表面的倐逝波耦合来实现，因此对结构极其敏感。现有的片上波导工艺仍然不可避免存在几十纳米量级的加工误差，这将严重影响光子集成器件的性能。为解决这一问题，研究人员做了诸多尝试与努力。其中，拓扑光子学作为一项有趣而富有潜力的课题，逐渐走进人们的视野[1]。

拓扑光子学的概念与发展

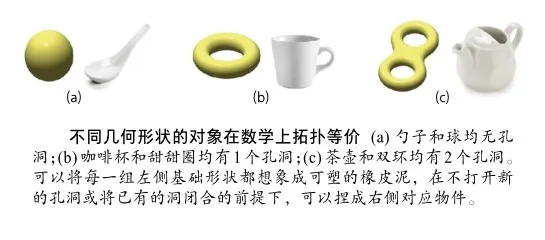
拓扑是一个数学术语，研究几何对象在连续形状变换下的守恒性质。例如水杯和甜甜圈，看似具有两种完全不同的几何形状，但如果对它们进行连续操作（弯曲、拉伸等），水杯的形状可以变成甜甜圈的形状，同样，甜甜圈的形状也可以变成水杯的形状。从拓扑学的角度看二者完全等价——均具有一个孔洞。该孔洞数可由物体表面上高斯曲率的表面积分得到，虽然水杯和甜甜圈的高斯曲率完全不同，但由表面积分得到的孔洞数始终是恒定的，如果不对它们执行拆分或连接这类操作，孔洞数就不会发生突变。这里的孔洞数就是一种拓扑不变量，叫作欧拉示性数。

GhMqBrnG+u7OKehsFbDXs/jjKYByClzEo35w29t1XKs=

此后研究人员发现，在凝聚态物理中物体动量空间的能带也具有类似的物理特性，存在一类拓扑绝缘体，它在整体上绝缘，但表面存在导通的表面态。这种表面态的物理性质非常稳定，环境条件发生一定程度的改变都不会对其有影响——就像揉捏橡皮泥不会改变其孔洞数一样。在描述波的性质中，最重要的参量便是波矢（反映波的传播动量）。波矢在动量空间的变化和演化同样可以产生各种形状，这些形状通过傅里叶变换能反映出波在实空间中的运动。数学上的高斯曲率在动量空间中对应贝里曲率，孔洞数对应陈数等拓扑不变量。正如拓扑学中几何表面的连续变换（即不额外打开或闭合孔洞）不会影响欧拉示性数的取值一样，拓扑绝缘体中的扰动同样不会改变动量空间中的拓扑不变量。因此，拓扑绝缘体所支持的表面态受到了拓扑保护——不会因为微扰而被破坏。

研究人员在光子晶体结构中实验验证了这一现象，通过施加均匀的磁场在光子能带的带隙中得到拓扑边界态。这种拓扑边界态的传播不会被散射体破坏，从而验证了其基于拓扑保护产生的对结构扰动的鲁棒性[2]。

近十几年来，光子拓扑绝缘体在诸如光波导、微环阵列等更加精细的结构中被构造出来。拓扑光子学的理论和实验研究也得以迅速发展。研究人员在绝缘体上硅波导阵列中构造出了支持拓扑非平庸界面态的结构，标志着硅基光子学与拓扑系统的结合[3]。由于对缺陷和扰动具有较好的鲁棒性，光子拓扑态也逐渐应用于构造多种光器件，诸如具有拓扑保护的定向光耦合/分束器和激光阵列等[4，5]。与传统光器件相比，基于光子拓扑态的拓扑光器件具有更好的稳定性，展现出巨大的应用潜力。

光子拓扑态激发的难点

光子拓扑态展现出卓越的光场调控能力。拓扑态通常局域在拓扑相（具有同样拓扑不变量的光子态集合）不等价的界面，具有独特的性质，特别是抵抗结构缺陷与无序的鲁棒性。这一性质对于光子集成和量子计算尤为重要。这是因为，光学芯片中往往需要大规模、高精度的波导和集成元件，稍有扰动就会使光场的振幅和相位出现较大波动，错误叠加累积，最终使系统偏离预期功能。

利用光波导的拓扑态有望缓解这一问题。但是光波导阵列中的拓扑态通常具有复杂的场分布，很难被实际激发并加以利用。比如，仅仅采取常规的单波导输入，将不可避免地激发一些多余的模式。而这些模式是不受拓扑保护的，会降低光传递信息的质量。为了更好地发掘拓扑态的潜能，对拓扑态的完美激发（即精准激发）十分重要，在先前的工作中，研究人员尝试使用分叉波导结构，利用光程差实现相位匹配，通过分光和弯曲损耗实现振幅匹配，尽可能更加准确地激发拓扑态[6]。然而这种设计思路仅在设计波长下起到较好的效果，当波长偏离设计波长时，激发效果明显下降，并且该方案对于结构误差极为敏感。

因此，寻找一种能够简单、普遍地激发光子拓扑态，且激发过程具备宽带性和鲁棒性的方法，对于拓扑光子学的发展与应用十分有必要。

超对称变换准确激发拓扑态

在诸多探索中， 超对称（supersymmetry， SUSY）的概念给予研究人员启发。SUSY变换最早诞生于量子场论中，用于在玻色子和费米子之间建立联系。应用SUSY变换，可以灵活地调控光学势（模式的等效折射率），利用光学势的保护来调节模式的场分布，但其传播常数（即模式的波矢大小）依然保持不变。这为诸多难以实现的光子集成功能提供了新的可能性，例如片上模式转换、单模激光阵列等。2024年，研究人员将SUSY、绝热演化的概念与拓扑态结合，在一维波导结构中产生了精确的拓扑零模，展现了SUSY调控拓扑态的优秀能力。

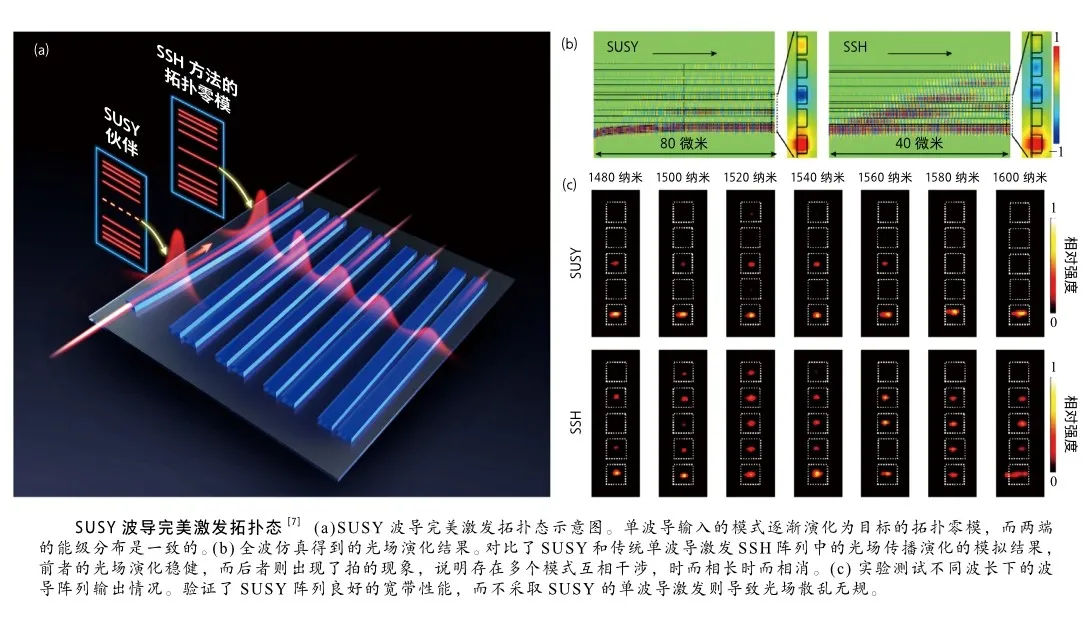
在这一工作中，以一维SSH（Su-SchriefferHeeger）模型为例展示SUSY的设计原理。SSH模型是一维体系中常见的一种拓扑模型，以3位科学家的名字命名，他们在聚乙炔链中发现一种孤子态电子波，具有拓扑保护的特性，这一概念后来被推广到光学领域。在波导系统中，SSH模型描述一种耦合系数交替强弱调制的波导阵列，如果交替耦合出现缺陷（如相邻为“强-强”或“弱-弱”耦合），在弱耦合的边界上会出现拓扑零模（传播常数保持与原单根波导一致，不会被耦合影响）。研究人员以一维的硅波导阵列为体系，基于耦合模理论，调控波导间距实现耦合系数的调制。对SSH模型的哈密顿量矩阵进行SUSY变换，可以得到对应的SUSY伙伴结构。SUSY伙伴结构具有与原结构完全一致的本征能谱（即传播常数），类似孪生兄弟具有相似的基因，但却表示出不同的个性（所支持的模式分布不同）。在得到的SUSY伙伴中，零模被单独隔离开，从而集中在单根波导中。可以看作SUSY变换将光子拓扑态“选择”出来，“投影”到单独隔离的格子里。将SUSY伙伴作为输入端，目标的SSH晶格作为输出端，并将二者绝热连接，从而可以使单波导模式绝热地演化为目标拓扑零模。

通过这样的SUSY设计，可以用“简单”的单波导输入，得到“复杂”的拓扑光子态输出，并且由于在传播过程中，所需模式一直固定在零能级上，因此也不会因为波长的变化或结构的微扰而导致光信号串扰到其他不需要的模式上，使得光波导阵列具有良好的鲁棒性。此外，由于波长的变化不会破坏系统的绝热条件，也可以视为一种对结构的微扰，并不会对光传输过程造成显著破坏。因此，SUSY波导也具有良好的宽带性。

与此同时，研究人员在实验上验证单波导输入的情况，发现由于不可避免地激发出其他模式，光场在传播中会发生空间干涉的现象，并且在一些波长下失去拓扑态的局域性质，预示其不再受到拓扑保护。

此外，如果要求一个系统满足绝热条件，即光模式之间不会串扰，那么它在传播距离上的变化应当极为缓慢，这势必会导致系统尺寸较大。上述设计思路中，在传播方向上，SUSY波导的相邻波导间的耦合系数线性变化，使得各处的变化速率一致，从而能够满足绝热条件。但对于光子拓扑态完美激发这一目标而言，绝热要求显然只是充分条件。如何找到更加紧凑的结构，使得SUSY光波导在打破绝热条件的同时，依然能准确得到目标的拓扑态？由于耦合模方程的含时演化是一个非常复杂的问题，似乎很难找到某种合适的绝热捷径理论来实现这一目标。

受逆向设计的思想启发，研究人员发展出一套目标导向的设计方法——以最终模式的吻合度为评价函数，将问题转化为一个受约束的最优化问题。在波导总长给定的情况下，连接方式单独决定了输入将转化为何种输出。利用Matlab软件的最优化函数得到波导参数，使逆向设计后得到的波导阵列可以在长度减半的情况下依旧准确激发出拓扑态。对其过程分析发现，光场在传播过程中被允许暂时偏离拓扑零模，但最终仍然回归。这一设计使得连接方式更加特殊，尽管体系的宽带性能有所下降，但却极大减少了波导器件的占用面积，这对于大规模光子集成来说也相当重要。

SUSY方法在复杂拓扑体系中的可能应用

SUSY方法不仅能应用在光波导体系中，对于势能能够含时调控的声学波导、冷原子、微波系统等领域也可以适用。当然，有了这一强有力的拓扑态激发手段，不由得让人畅想，对于更加复杂的拓扑光子系统，其中的拓扑态能否得到更好的研究？例如，对于高维的拓扑绝缘体，由于晶格变得更加复杂，拓扑态的模式也随之更加复杂，亦可能出现能级简并的情况，这使得传统的激发方式可能不再有效[8]。把SUSY方法拓展到更高维度，将有助于对高维拓扑效应的进一步观察和研究。

例如，近期研究人员通过亚波长光栅波导实现了Ⅱ型外尔异质结，构造出新颖的拓扑界面态[9]。通过SUSY方法，有望与外尔界面处的光场实现更好的模式匹配，使得其中的拓扑界面态以及界面处光的透反射调控等现象变得更加显著。此外，研究人员以非厄米自由度作为新的人工合成维度，在片上弯曲波导结构中成功构建了新的外尔界面态，发现了合成维度中的外尔环，大大拓宽了拓扑态的存在空间和调控的灵活性[10]。SUSY方法则为研究不同外尔结构之间的界面模式提供了更多可能性。

除了这些新奇有趣的拓扑光子结构，SUSY方法亦有可能与非线性效应、非阿贝尔物理等概念结合。由于克尔效应等非线性效应，在强非线性结构中，光强的增加将使得局部折射率发生变化，这使得输入的初态能够影响后续光场演化，甚至改变整个器件的性质；而在非阿贝尔系统中，物理场作用的效果将不再可交换，输出的结果将与中途的结构顺序直接相关。利用SUSY方法，可以自由地制备初态和中间态，从而可能在这些体系中探索发现新的拓扑效应，开发新的应用。

总结与展望

SUSY方法为拓扑光子学提供了无限的可能，借助这一思想，研究人员可以更加自由地设计结构以调控光子拓扑态，从而发现新的物理效应，有助于拓扑效应的观测，以及提升拓扑光子器件的效率，在大规模光子集成和光量子计算中具有应用潜力。

[1]Lu L， Joannopoulos J D， Solja？i？ M. Topological photonics. Nature Photonics， 2014， 8（11）： 821-829.

[2]Wang Z， Chong Y D， Joannopoulos J D， et al. Observation of unidirectional backscattering-immune topological electromagnetic states. Nature， 2009， 461： 772-775.

[3]Blanco-Redondo A， Andonegui I， Collins M J， et al. Topological optical waveguiding in silicon and the transition between topological and trivial defect states. Physical Review Letters， 2016， 117（16） ：129901.

[4]Song W G， Sun W Z， Chen C， et al. Robust and broadband optical coupling by topological waveguide arrays. Laser & Photonics Reviews， 2020， 14（2）：1900193.

[5]Zhao H， Miao P， Teimourpour M H， et al. Topological hybrid silicon microlasers. Nature Communications， 2018， 9（1）： 981.

[6]Song W G， Sun W Z， Chen C， et al. Breakup and recovery of topological zero modes in finite non-Hermitian optical lattices. Physical Review Letters， 2019， 123（16）： 165701.

[7]Liu X Y， Lin Z Y， Song W G， et al. Perfect excitation of topological states by supersymmetric waveguides. Physical Review Letters， 2024， 132（1）： 016601.

[8]Cerjan A， Jürgensen M， Benalcazar W A， et al. Observation of a higher-order topological bound state in the continuum. Physical Review Letters， 2020， 125： 213901.

[9]Song W G， Lin Z Y， Ji J T， et al. Bound-extended mode transition in type-Ⅱ synthetic photonic Weyl heterostructures. Physical Review Letters， 2024， 132： 143801.

[10]Song W G， Wu S J， Chen C， et al. Observation of Weyl interface states in non-Hermitian synthetic photonic systems. Physical Review Letters， 2023， 130： 043803.

关键词：拓扑光学模式 波导阵列 SUSY变换 完美激发 ■