基于范希尔理论培育几何思维的教学实践研究

摘 要 几何思维培育对几何教学具有重要意义。范希尔理论是以学生思维发展为基础，并结合几何教学实践提出的实践教学理论。以“垂直于弦的直径”为例，经历观察、实践、猜想、证明、应用等数学活动，培养学生的几何推理能力，促进学生几何思维的养成。

关键词 范希尔理论 几何教学 思维水平 垂径定理 教学实践

一、范希尔理论概述

（一）范希尔理论的内涵

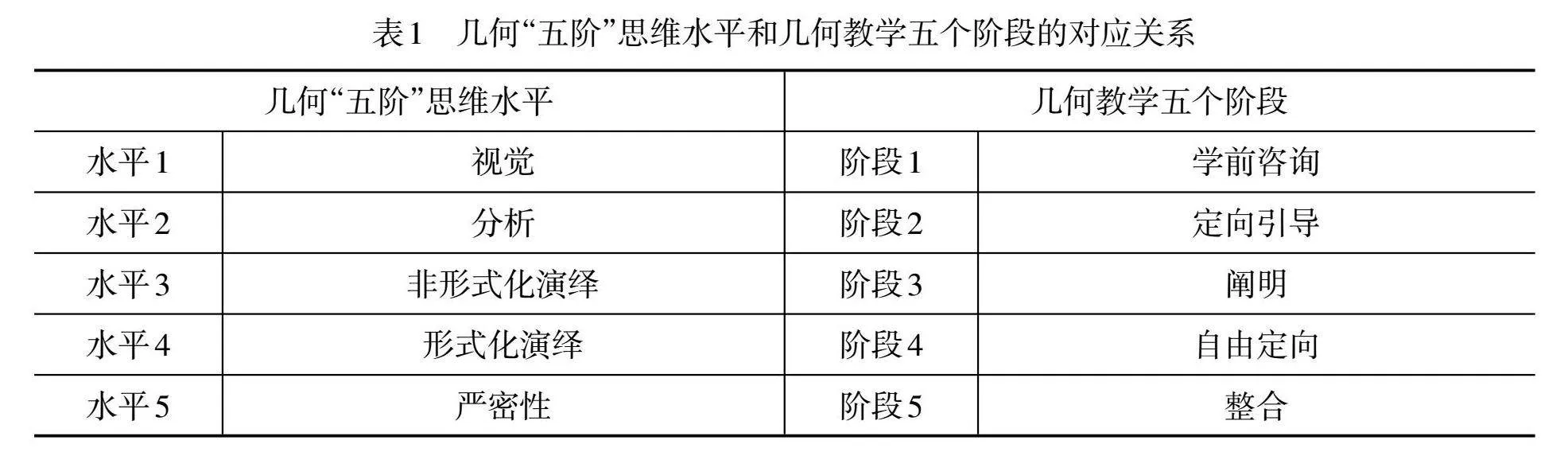
范希尔理论是20世纪50年代，由荷兰人范希尔夫妇提出的。范希尔夫妇基于学生学习几何的现状，以皮亚杰认知发展理论为基础，提出了几何“五阶”思维水平，分别是视觉水平、分析水平、非形式化演绎水平、形式化演绎水平和严密性水平。范希尔夫妇将上述研究成果应用于几何课堂教学中，把几何学习分成五个阶段，分别是学前咨询、定向引导、阐明、自由定向、整合。几何“五阶”思维水平和几何教学五个阶段的对应关系，如表1所示。

表1 几何“五阶”思维水平和几何教学五个阶段的对应关系

[几何“五阶”思维水平 几何教学五个阶段 水平1 视觉 阶段1 学前咨询 水平2 分析 阶段2 定向引导 水平3 非形式化演绎 阶段3 阐明 水平4 形式化演绎 阶段4 自由定向 水平5 严密性 阶段5 整合 ]

学前咨询是指教师与学生间进行互动交流，了解学生的已有知识储备水平或认知结构，并渗透学习目标，学生基于自己的困惑提出问题；定向引导是指教师基于学前咨询所获得的信息，设计有序的学习活动，形成直观感受；阐明是指通过交流讨论和规范化的数学语言表达看法、验证猜想等；自由定向是指通过相对自由的探索空间来获得新的知识经验；整合是指通过分析、解决几何问题，形成新的认知结构，并纳入已有知识结构中。[1]6

（二）范希尔理论在几何教学中的价值

1.基于学生认知发展规律促进学生几何思维发展。几何思维是一种科学的思维过程[2]43，是在进行几何知识学习或解决几何问题时所表现出来的思维加工过程，如观察、分析、归纳、推理等。范希尔夫妇以学生认知发展规律为基础，充分考虑了几何知识学习的特殊性，提出了几何“五阶”思维水平。几何“五阶”思维水平的发展过程需要综合运用观察、分析、综合、归纳、演绎、推理等科学思维方法，从一个水平进阶发展到更高层级水平。

2.基于认知结构发展促进几何知识内化。知识内化是在原认知结构基础上，通过知识学习的不断深入，在头脑中形成新的知识体系，并逐步建构新的认知结构的过程。范希尔理论的“学前咨询”阶段目的是了解学生的已有知识水平或认知结构，通过逐级递进过程，在“整合”阶段形成新的认知结构。因此，范希尔理论为促进几何知识内化提供了重要途径。

（三）基于范希尔理论的课堂教学实践路径

实践需要理论的指导，实践也是检验理论合理性的唯一场所。如何应用范希尔理论指导课堂教学实践呢？将几何教学五个阶段演绎为课堂教学环节，从而发挥其理论指导功能。基于范希尔理论的课堂教学实践路径，如表2所示。

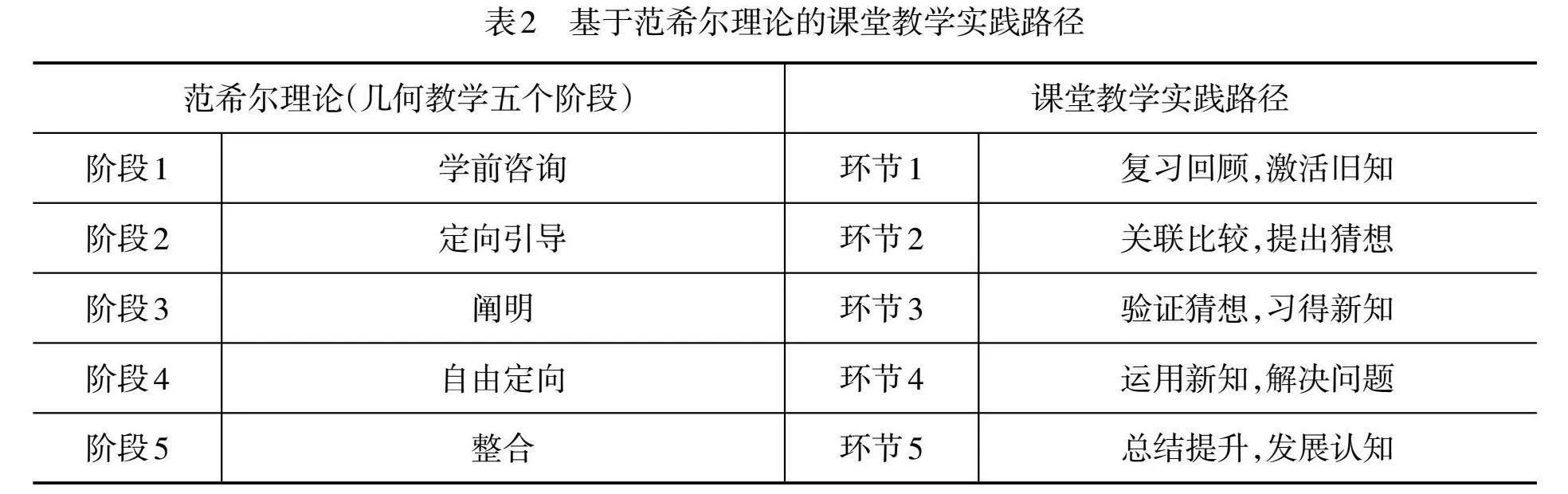
表2 基于范希尔理论的课堂教学实践路径

[范希尔理论（几何教学五个阶段） 课堂教学实践路径 阶段1 学前咨询 环节1 复习回顾，激活旧知 阶段2 定向引导 环节2 关联比较，提出猜想 阶段3 阐明 环节3 验证猜想，习得新知 阶段4 自由定向 环节4 运用新知，解决问题 阶段5 整合 环节5 总结提升，发展认知 ]

从表2可以看出，范希尔理论的阶段性与课堂教学实践环节是一一对应的。基于范希尔理论的课堂教学实践路径体现了建构主义思想，是促进学生的思维发展和认知结构发展的重要途径。

二、基于范希尔理论的教学实践

本研究以人民教育出版社《义务教育教科书·数学》（九年级·上册）中第二十四章的“24.1 圆的有关性质”第2课时“垂直于弦的直径”为例进行教学实践。[3]81-83在学习本节课内容前，学生已经学习过圆的圆心、半径、直径、弦、圆弧、半圆、等圆、等弧等基本概念，这为本节课知识学习奠定了知识基础。

（一）教学目标

（1）通过对折等腰三角形纸片，了解其对称性特征，初步形成轴对称图形的感性认识。

（2）通过对折圆形纸片和理论证明，掌握圆形的对称性特征，实现从感性认识到理性认识的能力提升。

（3）通过计算赵州桥主桥拱的半径，感受数学知识的应用价值，发展科学态度和社会责任意识。

（4）通过课堂教学回顾，初步形成垂径定理的认知结构，发展模型认知素养。

（二）教学环节

【环节1】复习回顾，激活旧知

[师]同学们，手中现在有两张图形纸片，分别是什么？

[生]等腰三角形和圆形。

问题1：等腰三角形是我们已经熟悉的图形，请同学们先拿出等腰三角形纸片，沿底边上的高进行对折，你能得出什么结论呢？

学生活动：沿底边上的高所在直线对折等腰三角形。

[生]等腰三角形沿底边上的高对称。

设计意图：问题1的目的是通过学生亲手实践活动，激活已经学习过的等腰三角形知识，了解其是轴对称图形。为验证圆形的轴对称性特征做铺垫，促进“视觉”思维发展。

【环节2】关联比较，提出猜想

问题2：请同学们拿出圆形纸片，沿不同直径进行对折，重复做几次，你能得出什么结论呢？

学生活动：多次沿不同直径对折圆形纸片。

[生]圆也是轴对称图形。

追问1：对称轴在哪？

[生]圆的直径所在直线。

追问2：通过折纸发现等腰三角形和圆形都是轴对称图形。那么，如何证明圆是轴对称图形呢？

设计意图：问题2的目的是通过折叠圆形纸片活动，基于实践得出圆是轴对称图形的结论；追问1的目的是通过明确对称轴进一步确认圆是轴对称图形。追问2的目的是通过等腰三角形和圆形的关联比较，为理论验证做铺垫，发展“视觉”“分析”“非形式化演绎”等几何思维。

【环节3】验证猜想，习得新知

[师]请同学们结合等腰三角形的特征，证明：圆上任意一点关于直径所在直线（对称轴）的对称点也在圆上。

问题3：根据题中描述，如何证明结论成立？先画出相应的图形，再证明。

学生活动1：分析题意，尝试将文字转换成数学语言和几何图形，并标点。

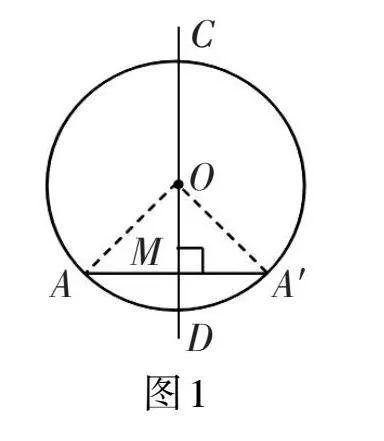
设CD为⊙O的任意一条直径，A为⊙O上除点C、D以外的任意一点，过点A做AA′⊥CD，交⊙O于A′，垂足为M，连接OA、OA′，如图1所示。

[师]根据已学过的等腰三角形相关知识，证明结论是否成立。

学生活动2：根据学习活动1所画的图形进行分析、推理、证明。

在ΔOAA′中，因为OA = OA′，所以ΔOAA′为等腰三角形；

又因为AA′⊥CD，所以AM = MA′。结论得证。

[师]根据证明，圆形是轴对称图形。

设计意图：在环节2折纸实践得出结论基础上，问题3的目的是进行推理证明，初步形成分析、推理能力，感悟“非形式化演绎”“形式化演绎”思维。

【环节4】运用新知，解决问题

[师]通过折纸实践和理论推理，都证明了圆形是轴对称图形。赵州桥是隋代建造的石拱桥，它的跨度（弧所对的弦的长）为37 m，拱高（弧的中点到弦的距离）为7.23 m，如图2所示。

问题4：根据圆的相关知识，赵州桥主桥拱的半径是多少呢？（结果保留小数点后一位）

[师]根据题意和图2所示，画出赵州桥的几何图形并进行求解。

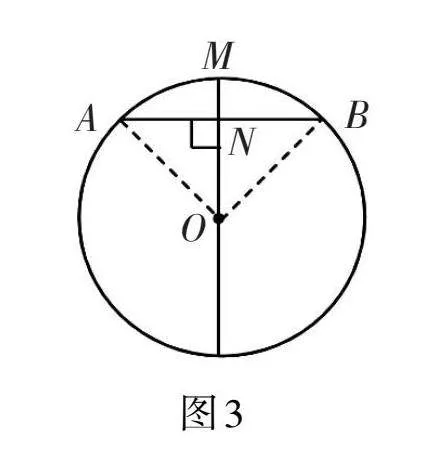
学生活动1：画出赵州桥的几何示意图，如图3所示。

学生活动2：根据图3所示，求解赵州桥主桥拱的半径。

如图3所示，AB = 37 m，MN = 7.23 m，求OB的长度。

根据垂径定理，OM ⊥ AB，OB2 = （OM － MN）2 + NB2

即OB2 = （OB － 7.23）2 + 18.52，所以OB ≈ 27.3 m。

设计意图：通过引导学生运用垂径定理求解赵州桥主桥拱的半径，发展学生基于所学数学知识解决真实问题的能力，感受数学知识的价值，发展“形式化演绎”思维。

【环节5】总结提升，发展认知

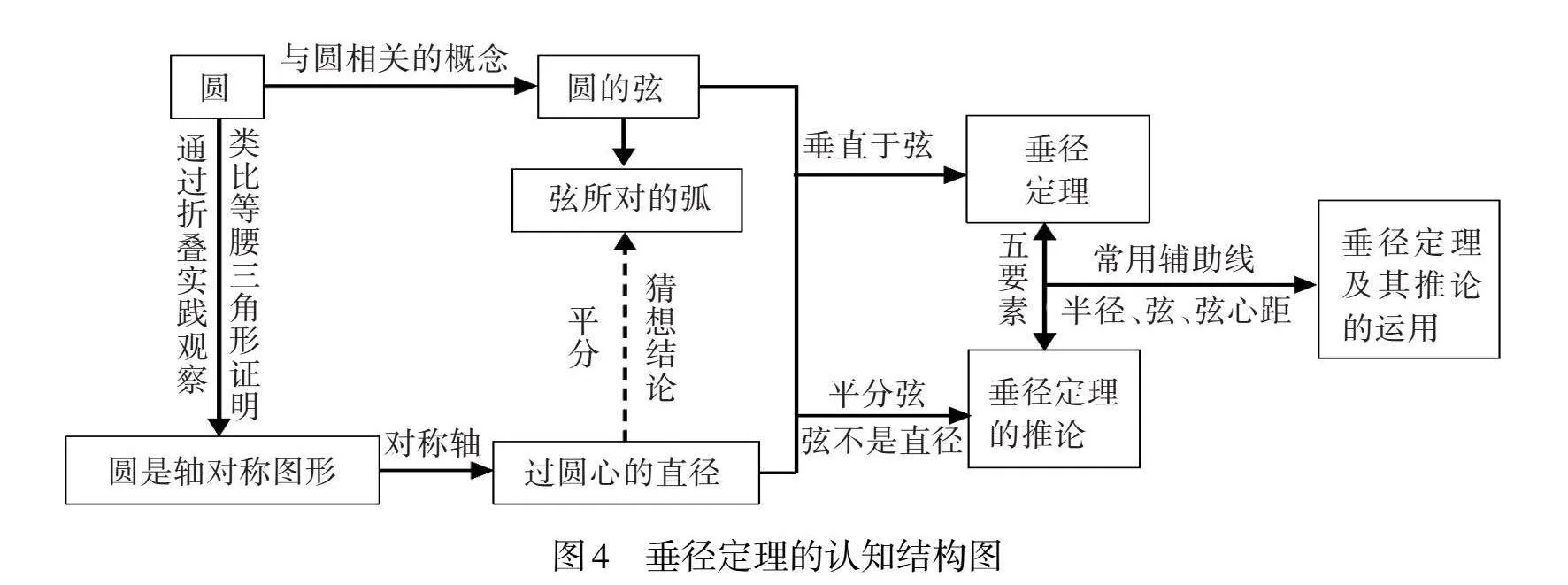
[师]知识学习是一个从感性到理性的过程，也是实践、认识、再实践过程。垂径定理的认知结构图，如图4所示。

设计意图：通过垂径定理的建构思路的重现，引导学生学习知识建构的策略方法，从已知走向未知，最终形成新的认知结构，发展学生“严密性”思维。

三、总结与反思

本研究是以范希尔理论为基础，帮助学生形成促进几何思维发展的分析框架，提高几何知识学习和运用的能力，促进新的认知结构发展。

（一）关注学生已有知识经验降低认知难度

学生已有知识经验是学生进行新知识学习的基础。在本节课中，教师抓住了等腰三角形和圆形都是轴对称图形的特征，通过图形折纸实践，引导学生形成了圆形是轴对称图形的感性认识。激活已有知识，在新旧知识之间寻找相互关联的要素，引导学生经历分析、比较等活动在新旧知识之间建立关联，以降低新知识的认知难度。

（二）解决真实问题感悟知识价值

知识价值是知识存在和发展的先决条件。在理论证明垂径定理的基础上，通过引导学生求解赵州桥主桥拱的半径，不仅渗透了中华民族优秀传统文化，还引导学生感悟了垂径定理的价值，初步形成了分析问题、解决问题的能力。

（三）总结提升形成新的认知结构

认知结构是对客观知识的结构化认知图示。本研究通过课堂总结，把知识的建构和运用过程进行结构化处理，以思维导图的形式呈现出来，这是基于范希尔理论培育几何思维的再现，也为学生未来新知识学习做了准备和铺垫。

范希尔理论是以学生认知发展规律为基础，并结合几何学科特点提出的促进几何知识学习的实践教学理论。该理论对于降低学生认知难度和规范教学过程具有重要价值，在教学过程中，教师可以根据具体学科知识特征，有针对性地加以运用。

[参 考 文 献]

[1]鲍建生，周超.数学学习的心理基础与过程[M].上海：上海教育出版社，2009.

[2]张大均.教育心理学[M].北京：人民教育出版社，2015.

[3]林群 主编.义务教育教科书·数学（九年级·上册）[M].北京：人民教育出版社，2023.

（责任编辑：姜显光）