受限空间下打纬机构力矩平衡分析及其调控策略

摘" " 要： 针对打纬机构惯性打纬力与打纬阻力不平衡造成的不利影响，建立打纬机构的力学模型，以四连杆打纬机构为例，确定打纬机构结构方向的调节方法，考虑空间受限情况进行定量仿真分析，对比分析不同调节方案对驱动力矩和输出力矩的影响，并分析不同杆长设计参数带来的运动特性。仿真结果表明：通过增设平衡构件和改变杆长比例可以有效地调控惯性打纬力；当打纬力不足时，转动惯量与角加速度后打纬力矩分别提升了约14.5%与3%，共同调节提升约17.8%；当打纬力过大时，通过尺度调节后力矩降低了约7.6%；转动惯量和角加速度是惯性打纬力的主要控制变量，通过调节这两个变量可满足不同条件下的织造工艺需求，并为打纬机构尺度及结构设计提供理论参考。

关键词： 惯性打纬力； 转动惯量； 角加速度； 驱动力矩； 四连杆打纬机构

中图分类号： TS103.12" " " " " " " " 文献标志码： A" " " " " " " " 文章编号：" １６７１－０２４Ｘ（２０24）０4－００82－07

Analysis of moment balance in beating-up mechanism and its regulation strategies

under restricted space

YUAN Ruwang1，2，AI" Ming1，2

（1. School of Mechanical Engineering， Tiangong University， Tianjin 300387， China； 2. Tianjin Key Laboratory of Advanced Mechatronics Equipment Technology， Tiangong University， Tianjin 300387， China）

Abstract： In order to deal with the adverse effects caused by the imbalance of inertia beating force and beating resistance of beating-up mechanism， the mechanical model of beating-up mechanism is established， and the adjustment method for the structural direction of beating-up mechanism is determined by taking the four-link beating-up mechanism as an example， and the quantitative simulation analysis is carried out under the consideration of space limitation. Comparative analysis is conducted on the effects of different adjustment schemes on driving torgue and output torque， and the motion characteristics brought about by different rod length design parameters are analyzed. The simulation results show that the inertia beating-up force can be effectively regulated by adding balancing members and changing the rod length ratio. When the beating-up force is insufficient， the beating torque is increased by about 14.5% and 3% after rotational inertia and scale adjustment respectively， and increased by about 17.8% after joint adjustment. When the beating-up force is too large， the torque is reduced by about 7.6% after scale adjustment. The rotational inertia and angular acceleration are the main control variables of the inertia beating force， which can be adjusted to meet the requirements of weaving process under different conditions， and provide theoretical reference for the scale and structure design of the beating-up mechanism.

Key words： inertia beating-up force； rotational of inertia； angular acceleration； driving moment； four-link beating-up mechanism

织机中的打纬机构负责将纬纱打进织口，与经纱交织形成织物[1]，是织机中的重要组成部分。无梭织机打纬机构主要采用四连杆式、六连杆式和共轭凸轮式这3种打纬形式[2-4]，其中四连杆式打纬因具有结构简单、生产成本低等优点而被广泛使用。近年来织造产业高速发展[5-6]，提高织造效率以及增大打纬力通常被作为打纬研究的两大目标[7-8]。

打纬机构的惯性打纬力关系织物的品质及织机的动态特性：如果打纬力小于打纬阻力，织物将无法被打紧，得不到理论纬密；如果打纬力过大，不仅增加断头风险，而且增大主轴及摆轴回转的不均匀性与磨损，限制速度的提升[9]。由于现有打纬机构的结构基本固定，箱体空间受到限制，织造不同织物时，打纬力与打纬阻力间的耦合难以达到理想状态[10]。因此，打纬机构根据工况提供合适的惯性打纬力仍为一个亟需解决的问题。邱海飞等[11]通过改变钢筘材料属性来改变钢筘系统的自重，以此控制惯性打纬力，并进行了动态特性分析。邓威进等[12]分析了打纬机构各构件的转动惯量分布规律以及钢筘系统的最大打纬阻力，得到了最佳打纬区以及可克服打纬阻力范围。毛莹等[13]提出摇轴配重结合冗余伺服电机法，对惯性打纬产生的振动力与振动力矩进行了平衡优化。近年来对于打纬机构减震降噪与提速的应用主要有：海佳等公司[14-15]采用实心打纬轴上安装配重块，改变钢扣系统的整体质心向轴心偏移，达到平衡减振效果；津田驹等公司[16-18]先后使用中空支撑型分段式的摇轴，在分割后的摇轴间加装凹型平衡轴，与通轴配重相比控制了摇轴的质量，而复杂的结构对织造和装配精度有更高的要求[19]。

本文从钢筘系统的力矩平衡出发，考虑到实际应用中箱体空间受限的情况下，基于打纬机构的结构设计，通过调节钢筘系统的转动惯量和运动特性，优化机构的惯性打纬力，以期为打维机构的减振降噪及高速化研究提供理论参考。

1 工作原理

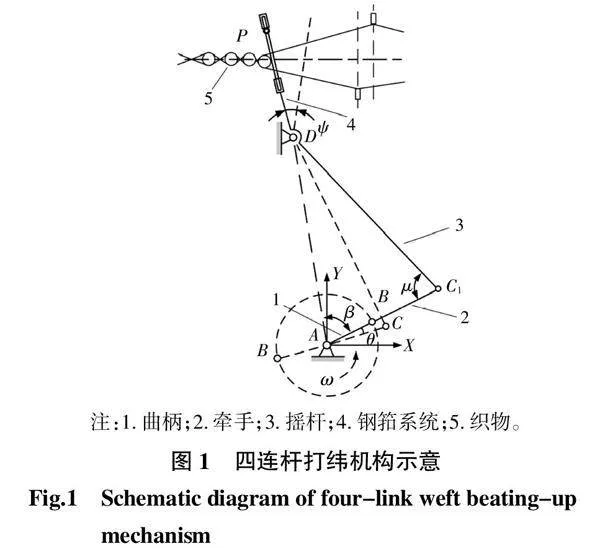
四连杆打纬机构如图1所示。

图1中，通过曲柄1以角速度ω1匀速转动带动摇杆及钢筘系统实现往复摆动。当筘到达P点处，即前死心位置，将纱线打入织口完成惯性打纬。

打纬过程可分为纬纱输送和打纬脉冲2个阶段，如图2所示。图2中，当钢筘从后死心位置E1摆动到E2处时开始输送引入的纬纱，至织口附近E3处时到达织口，纱线间屈曲加剧，打纬阻力开始急剧上升，自此打纬过程进入打纬脉冲阶段，直到钢筘摆动到前心位置E4处，打纬过程结束。

2 打纬机构动力学建模

2.1 钢筘系统力矩平衡分析

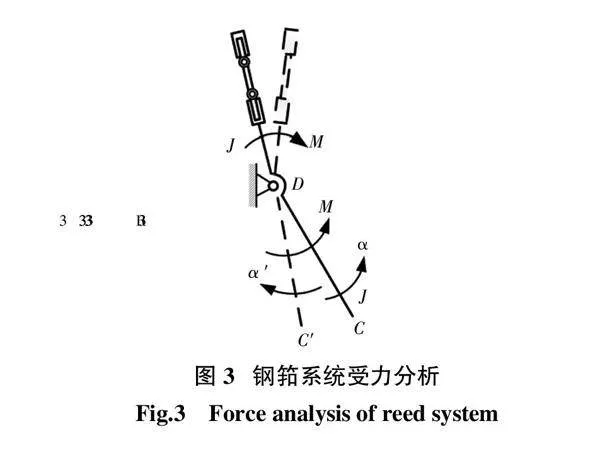
假设在打纬脉冲阶段，忽略钢筘系统重力、摩擦等因素，钢筘系统所受力矩如下：由摇杆驱动的输出力矩M3；由打纬阻力FR产生的阻力矩MR。打纬脉冲阶段中钢筘向前心和后心两位置摆动时的受力分析图，如图3所示。

钢筘系统的力矩平衡方程为：

M3 + （J3 + J4）α3 - MR = 0 （1）

式中：J3为摇杆的转动惯量；J4 为钢筘系统的转动惯量；α3 为摇杆或钢筘系统的角加速度。由此得到输出力矩M3 的表达式为：

M3 = MR - （J3 + J4）α3 （2）

由式（2）可知，打纬阻力矩与惯性力矩的平衡主要与J4、α3的乘积有关，在打纬脉冲阶段，当钢筘由后心摆至前心时：

① 若M3 ＝ 0，此时钢筘刚好完成惯性打纬；

② 若M3 lt; 0，多余的惯性力会加剧打纬机构的负面影响；

③ 若M3 gt; 0，惯性力不足无法打紧纬纱，电机需要提供额外的驱动力来克服打纬阻力矩。

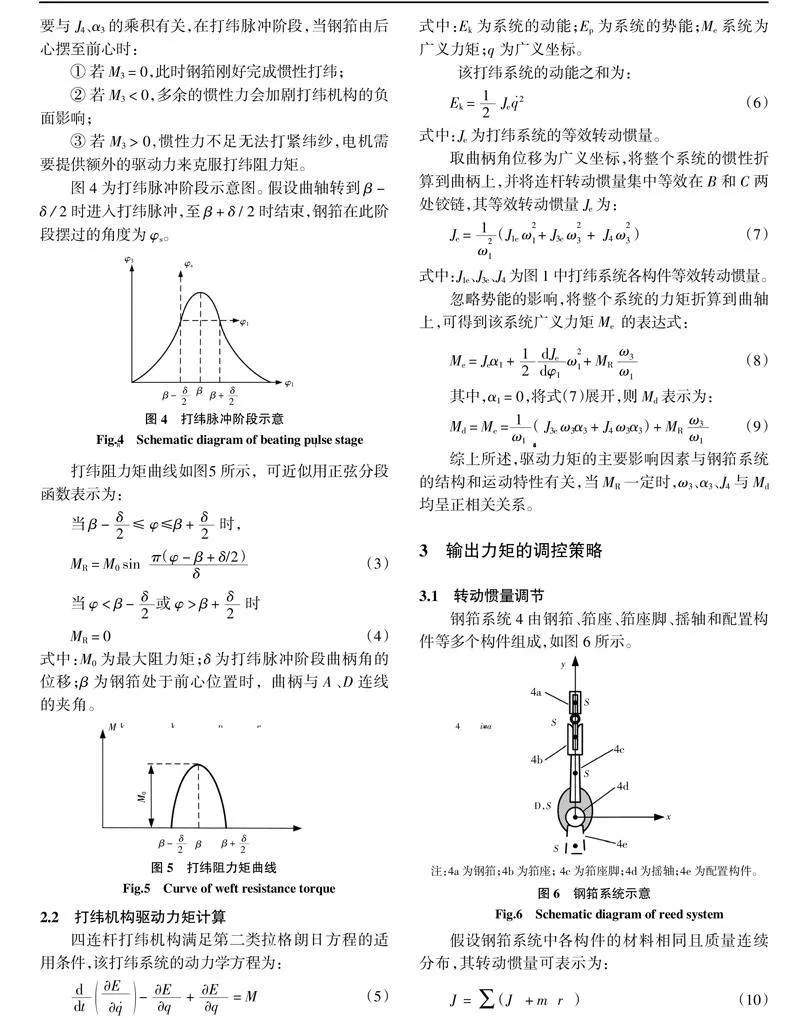
图4为打纬脉冲阶段示意图。假设曲轴转到β - δ / 2时进入打纬脉冲，至β + δ / 2时结束，钢筘在此阶段摆过的角度为φs。

打纬阻力矩曲线如图5所示，可近似用正弦分段函数表示为：

式中：M0为最大阻力矩；δ为打纬脉冲阶段曲柄角的位移；β为钢筘处于前心位置时，曲柄与A、D连线的夹角。

2.2 打纬机构驱动力矩计算

四连杆打纬机构满足第二类拉格朗日方程的适用条件，该打纬系统的动力学方程为：

式中：Ek为系统的动能；Ep为系统的势能；Me系统为广义力矩；q为广义坐标。

该打纬系统的动能之和为：

式中：Je为打纬系统的等效转动惯量。

取曲柄角位移为广义坐标，将整个系统的惯性折算到曲柄上，并将连杆转动惯量集中等效在B和C两处铰链，其等效转动惯量Je为：

式中：J1e、J3e、J4为图1中打纬系统各构件等效转动惯量。

忽略势能的影响，将整个系统的力矩折算到曲轴上，可得到该系统广义力矩Me" 的表达式：

综上所述，驱动力矩的主要影响因素与钢筘系统的结构和运动特性有关，当MR 一定时，ω3、α3、J4与Md 均呈正相关关系。

3 输出力矩的调控策略

3.1 转动惯量调节

钢筘系统4由钢筘、筘座、筘座脚、摇轴和配置构件等多个构件组成，如图6所示。

假设钢筘系统中各构件的材料相同且质量连续分布，其转动惯量可表示为：

式中：i = a、b、c、d、e；JS4i为各构件绕其质心的转动惯量；m4i为各构件质量；r4i为各构件偏心距。

钢筘系统转动惯量的大小与各构件质量和质心位置有关。在实际工况中，其调控方式可通过增设平衡构件以及改变轴的结构来实现，配置构件4e的模型如图7所示。

（1） 采用（a）类配置时，配重块通过与摇轴抱合的方式放置在反筘侧，配置后的J4增大，惯性打纬力上升。

（2） 采用（b）类配置时，将摇轴沿轴向分割为多段摇轴，在反筘侧用凹形轴间隔替代断轴。分段的摇轴降低了m4d，使钢筘系统可以在不增加质量（m4）的情况下降低偏心矩（r4），配置后的J4增大，使惯性打纬力上升。

由式（11）可知，在一定空间下配置构件的质量距m4e r4e越大，对离心力的影响越小，而在实际应用中考虑到箱体空间以及机器负载的影响，r4往往不能降至0。

3.2 角加速度调节

当钢筘摆角与主轴转速一定时，筘的角加速度大小与各杆长比例相关[20]。如图1所示，在曲柄摇杆机构设计过程中，将前心角β作为独立的设计参数，当钢筘运动至前心时，β可表示为：

改变l4的大小不会影响打纬机构的运动规律，只需求得各杆件的相对长度即可。经推导，曲柄的相对长度为：

如图1所示，当曲柄AB运动到与机架AD共线时，μ出现最小值：μmin = [ μ1， μ2]min。其中，μ1指在一个周期内曲柄与机架第一次共线时的μ值；μ2为第二次共线的μ值。

4 仿真分析

4.1 打纬机构的尺度要求

为了验证本文调控方法的有效性，采用了Matlab软件进行了仿真，表1给出喷水织机打纬机构已知设计参数和尺度要求作为仿真参数，为满足打纬工艺需求，打纬机构设计过程要兼顾空间限制、传力性能以及引纬等工艺需求。由于曲轴和连接连杆的连杆销具有一定直径，为设计合理曲柄和牵手的长度应大于等于其许用值：l1≥[l1]min，l2≥ [l2]min；墙板和钢筘系统箱体内的空间限制，牵手长度和图7中钢筘系统配置构件的质心应小于等于其许用值：l1≤[l1]min，r4e≤ [r4e]min。

4.2 偏心距与转动惯量分析

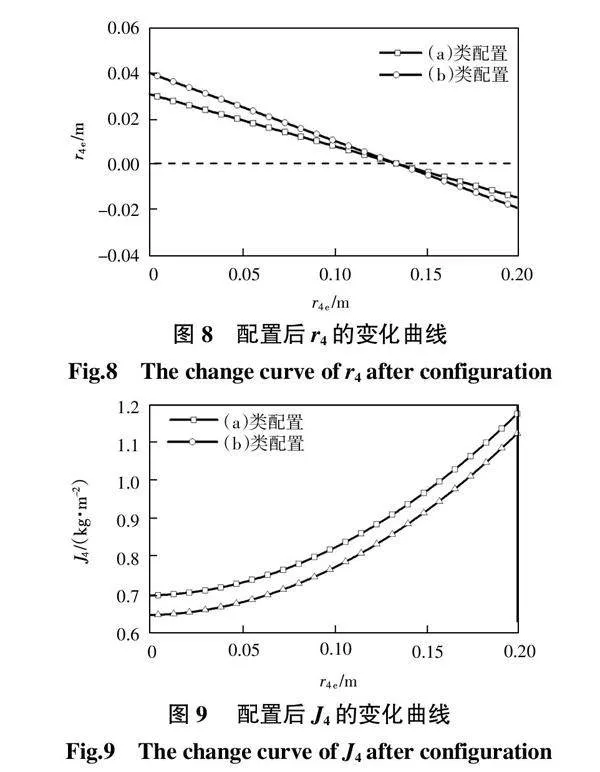
图8、图9为m4e相同条件下，随着r4e增大，r4与J4的变化曲线。

由图8可知，由于（a）类配置中m4较大，则r4的初值较大，变化率更大，当r4e为0.13 m时，两类配置构件皆使钢筘系统达到完全平衡，此时钢筘系统偏心距降至零，离心力为零。由图9可知，随着r4e增大，J4增长率逐渐增大，由于（a）、（b）配置中摇轴转动惯量不同，J4始终具有一定差值， 在一定空间范围内，当配置构件m4e与r4e一定时，（a）类配置后的m4较大，r4较小，对J4和驱动力矩的影响也更大。

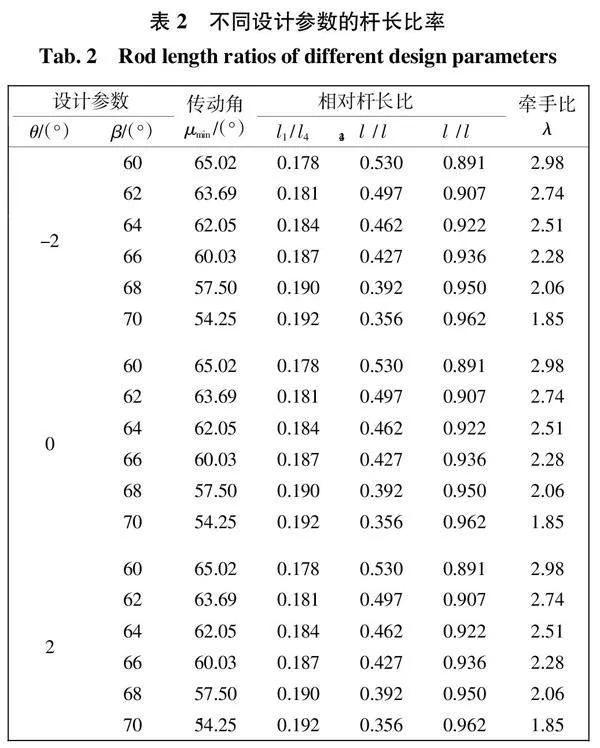
4.3 相对杆长与传动角分析

过大的θ值会导致机构的传动效率变差，以及钢筘角位移的不对称性变大，故极位夹角不应取得过大，即区间为θ = -2°～2°。表2所示为当θ值为-2°、0°、2°时，不同β值的短牵手（λ lt; 3）打纬机构的相对杆长比例和传动角数值情况。由表2可知，当θ值一定时，随着β值的增加，μmin增大，l1/l4和l3/l4增大，而l2/l4和牵手比减小。由此可知，过大的β值会使曲柄与摇杆杆长尺寸过大、连杆空间占有率不足，导致传动效率降低。

4.4 机构的运动特性分析

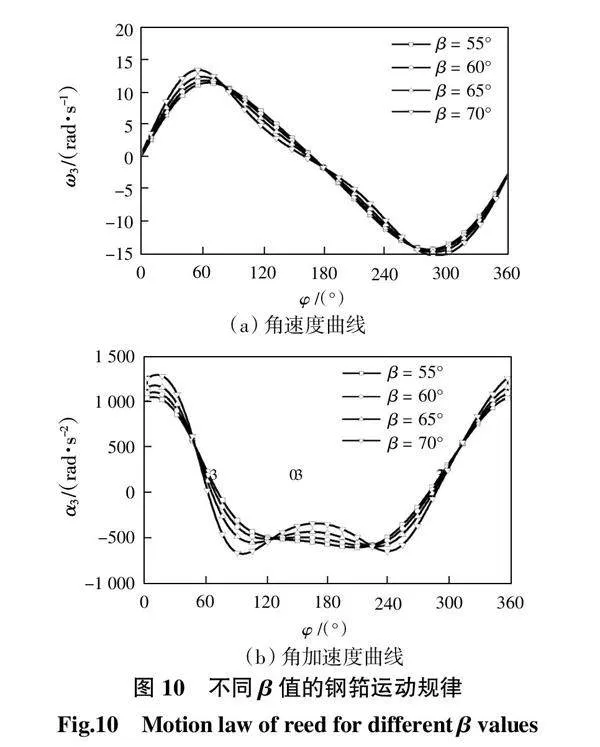
图10所示为无急回特性的打纬机构运动规律曲线。

由图10可见，随着β值增大，钢筘角速度的幅值增大，峰值变大且向前心方向偏移；在前心时刻的角加速度峰值变大，不均匀性增大。

因此，在工况复杂、织造厚重织物时可将极位夹角取为0°，在满足杆长和传动效率条件后，β取较大值，可有效增大前心时刻的角加速度，增大最大打纬阻力，以满足力矩最优；而以织造轻薄织物、高速为目的时可将β与 θ 同取较小值，以此提高织机的稳定性。

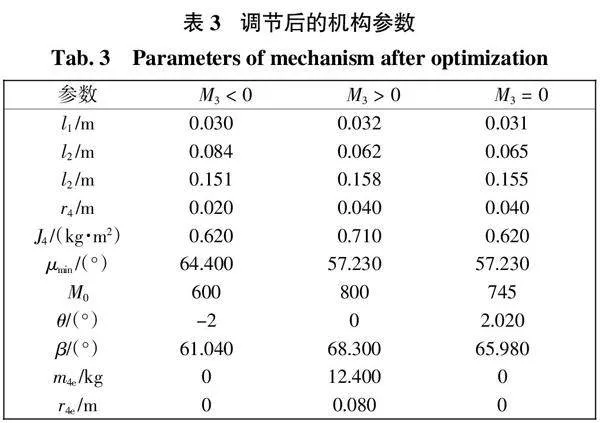
4.5 打纬机构的参数优化设计

针对打纬机构的提速与稳定性要求，考虑传力性能、结构尺寸、运动规律等因素，对机构参数进行优化，得到3组优化结果，如表3所示。

在前心时刻M3 gt; 0、M3 lt; 0以及M3 = 0这 3种情况下，分别调节J与α的设计参数，为效果明显配置构件采用（a）类配重块，当M0 = 745时，M3 = 0，在前心位置惯性力矩与阻力矩达到平衡，此组为对照组，未做任何调节，计算过程中忽略杆长改变时曲轴、牵手和摇杆的质量变化以及质心位置对结果产生的影响。

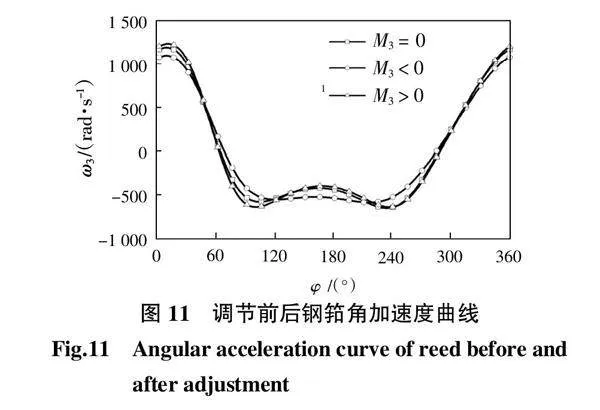
加速度调节曲线如图11所示，当M3 lt; 0时α峰值降低了5%，幅值降低了9%，在后心处较为平缓，且对称性较好；当M3 gt; 0时，其峰值增加了约3%。

调节前后钢筘输出力矩对比曲线和驱动力矩对比曲线如图12、图13所示。在打纬脉冲阶段，钢筘摆向不同时对输出力矩与驱动力矩作用效果不同：在钢筘由前心向后心摆动时打纬阻力矩做正功，钢筘由后心向前心摆动时打维阻力矩做负功。

由图12可知，当筘由后死心向前死心摆动时，当M3 lt; 0，经加速度调节后打纬力矩降低了约7.6%，使前心处的M3从-135 N·m提升至-79 N·m；当M3 gt; 0，转动惯量与加速度调节后打纬力矩分别提升了约14.5%与3%，在仅J调节、仅α调节、二者共同调节下，使前心处惯性力矩M3从调节前的64 N·m分别降低至-41 N·m、-43 N·m、-66 N·m。

由图13可知，当前心时刻M3 lt; 0时，由于调节后的角加速度峰值的降低，驱动力矩峰值降低约13%；当前心时刻M3 gt; 0时，在仅J调节、仅α调节、二者共同调节下，M3峰值上升19%、7%、23%。其数值可见共同调节对结果影响较为明显。

5 结 论

（1） 建立钢筘系统的力矩平衡方程，引出影响输出力矩的2个主要参数，确定了配置附加构件和调节杆长比例的调控方法，在空间限定的实际情况下对两参数进行调节；基于拉格朗日方程求解打纬机构的驱动力矩，分析各调控方法对输出力矩与驱动力矩的影响状况，通过文中仿真验证，调节后的打纬机构对输出力矩和驱动力矩皆有不同程度的影响，验证了本文调控策略的可行性，说明其是提高织机性能行之有效的措施。

（2） 在加速度调控方法中，设计参数β值较大的打纬机构具有更高的前心角加速度，有利于增加惯性打纬力，适合复杂工况织造厚重织物；适当降低β值和θ值有助于减少相对曲轴和相对牵手长度以及后心处加速度的波动。调控过程中可通过对两角度调节获得需要的打纬性能，以满足不同的打纬工艺需求。

（3） 在转动惯量的调控方法中，采用配重块配置转动惯量更大，能够更有效地提升惯性力的同时对驱动力矩的影响也较大；凹形轴配置后的钢筘系统质量较低，偏心距较低，对离心力影响较小。

参考文献：

[1]" " NEJE G， BEHERA B. Geometrical modeling of 3D woven spacer fabrics as reinforcement for lightweight sandwich composites[J]. The Journal of the Textile Institute， 2019， 110（5）： 732-739.

[2]" " EREN R， AYDEMIR A. An approach to kinematic design of four-bar sley drive mechanisms in weaving[J]. The Journal of the Textile Institute， 2004， 95（1/2/3/4/5/6）： 193-205.

[3]" " EREN R， AYDEMIR A. Kinematic design method for" six-bar linkage sley drive mechanisms in weaving[J]. Indian Journal of Fiber amp; Textile Research， 2005， 30（3）： 243-251.

[4]" "TANG X M. Calculation algorithm for kinematics accuracy reliability of conjugate cams beating-up mechanism[J]. Journal of Information and Computational Science， 2014， 11（18）： 6787-6793.

[5]" " MOUNTASIR A， HOFFMANN G， CHERIF C. Development of multilayered woven panels with integrated stiffeners in the transverse and longitudinal directions for thermoplastic lightw-eight applications[J]. Textile Research Journal，2013，83（14）： 1532-1540.

[6]" "ISHMAEL N， FERNANDO A， ANDREW S， et al. Textile technologies for the manufacture of three-dimensional textile preforms[J]. Research Journal of Textile and Apparel， 2017， 21（4）： 342-362.

[7]" " 徐昊月， 孙志宏. 一种立体织机平行打纬机构的设计与优化[J]. 东华大学学报（自然科学版）， 2020， 46（2）： 304-307， 327.

XU H Y， SUN Z H. Design and optimization of the parallel beating-up mechanism for looms[J]. Journal of Donghua University（Natural Science）， 2020， 46（2）： 304-307， 327（in Chinese）.

[8]" " 邱海飞. 高速打纬共轭凸轮理论廓线反求实现[J]. 机械强度， 2021， 43（4）： 1002-1006.

QIU H F. Reverse realization of pitch curve on conjugate cam with high speed beating-up[J]. Journal of Mechanical Strength， 2021， 43（4）： 1002-1006（in Chinese）.

[9]" " 王联晓. 打纬的理论研究[J]. 陕西纺织， 1993（3）：46-50.

WANG X L. Theoretical study of weft beating[J]. Journal of Shanxi Textile， 1993（3）：46-50.

[10]" 吴强， 李佳， 陈革. 立体织造打纬阻力的计算[J]. 东华大学学报（自然科学版）， 2013， 39（5）： 614-617.

WU Q， LI J， CHEN G. Computing on the beating-up force of 3D weaving[J]. Journal of Donghua University（Natural Science）， 2013， 39（5）： 614-617（in Chinese）.

[11]" 邱海飞. 基于ADAMS的四连杆打纬机构动态设计与仿真[J]. 机械传动， 2011， 35（7）： 52-55.

QIU H F. The dynamic design and simulation of 4-bar beating-up mechanism based on ADAMS[J]. Journal of Mechanical Transmission， 2011， 35（7）： 52-55（in Chinese）.

[12]" 邓威进， 周香琴. 基于Pro/E的织机打纬系统载荷特性研究[J]. 机电工程， 2014， 31（3）： 320-324.

DENG W J， ZHOU X Q. Beating-up mechanism in rapier loom based on Pro/E loading characteristic[J]. Journal of Mecha-nical amp; Electrical Engineering， 2014， 31（3）： 320-324（in Chinese）.

[13]" SUN Z H， JIANG C Y， et al. Dynamic balancing optimization of rigid beating-up mechanism on the water-jet loom based on the partial redundant servo motor method[J]. Journal of Dong-hua University（Natural Science）， 2016， 42（6）： 889-893（in Chinese）.

[14]" 李勇，王安俭，吕兴尉. 用于纺织机械上实心打纬轴的配重装置：CN202989444U[P]. 2013-06-12.

LI Y， WANG A J， LYU X W. Counterweight device for solid weft beating shafts on textile machines： CN202989444U[P]. 2013-06-12（in Chinese）.

[15]" 周荣华， 张勤英， 居雪华， 等. 一种喷水织机的打纬结构： CN216404669U[P]. 2022-04-29.

ZHOU R H， ZHANG Q Y， JU X H， et al. A beating-up str-ucture of water jet loom： CN216404669U[P]. 2022-04-29（in Chinese）.

[16]" 名木启一，山岸大吾，田村公一，等. 织机的打纬装置： CN114481417A[P]. 2022-05-13.

KEIICHI N， DAIGO Y， KOICHI T， et al. Weft beating device of loom： CN114481417A[P]. 2022-05-13（in Chinese）.

[17]" 冯文成，张智帆，高玉刚.一种喷水织机平衡打纬装置： CN211897271U[P]. 2020-11-10.

FENG W C， ZHANG Z F， GAO Y G. A kind of balanced weft beating device for water jet loom： CN211897271U[P]. 2020-11-10（in Chinese）.

[18]" 南谷德生， 名木启一." 织机的打纬装置： CN1702212B[P]. 2010-09-22.

NAMIYA D， KEIICHI N. Weft beating device of loom： CN1702212B[P]. 2010-09-22（in Chinese）.

[19]" 董少伟， 张建民， 袁伟， 等. 喷气织机分段式打纬机构与通轴打纬机构对比分析[J]. 纺织器材， 2021， 48（2）： 12-14， 35.

DONG S W， ZHANG J M， YUAN W， et al. Comparison and analysis of sectional beating-up mechanism and shaft beating-up mechanism of air-jet loom[J]. Textile Accessories， 2021， 48（2）： 12-14， 35（in Chinese）.

[20]" 华大年， 唐之伟. 机构分析与设计[M]. 北京： 纺织工业出版社， 1985： 92-100.

HUA D N， TANG Z W. Mechanism Analysis and Design[M]. Beijing： Textile Industry Press， 1985： 92-100（in Chinese）.

本文引文格式：

袁汝旺，艾明. 受限空间下打纬机构力矩平衡分析及其调控策略[J]. 天津工业大学学报， 2024， 43（4）： 82-88.

YUAN R W， AI" M. Analysis of moment balance in beating-up mechanism and its regulation strategies under restricted space[J]. Journal of Tiangong University， 2024， 43（4）： 82-88（in Chi-nese）.

收稿日期： 2022-08-06

基金项目： 天津市自然科学基金资助项目（18JCYBJC20200）；中国纺织工业联合会应用基础研究项目（J202003）

通信作者： 袁汝旺（1979—），男，博士，副教授，主要研究方向为纺织机械设计与机构学。E-mail：yuanruwang@tiangong.edu.cn