含多关节间隙平面柔性六杆机构的动力学分析

摘" " 要： 为提高机构的动力学分析精度，基于平面六杆机构，同时考虑多个关节间隙与构件柔性对多体机构动力学响应的影响。通过实体建模和引用ADAMS软件中“冲击函数”接触力模型，对含有多个间隙关节与柔性连杆的六杆机构进行动力学模拟仿真，研究间隙数量、间隙位置、间隙大小、柔性连杆及其与间隙耦合对系统动力学性能影响。研究结果表明：与单关节间隙相比，多关节间隙会产生更大的接触力，导致构件的加速度波动更加剧烈；间隙关节距离电机位置越近，则对机构的动力学行为影响越明显；考虑连杆柔性时，可以极大地降低间隙对机构动力学波动的影响。

关键词： 多关节间隙； 接触力； 柔性连杆； 动力学； 六杆机构

中图分类号：TH113" " " " " " " " 文献标志码： A" " " " " " " " 文章编号：" １６７１－０２４Ｘ（２０24）０4－００75－07

Dynamic analysis of planar flexible six-bar mechanism with multi-joint clearances

JIN Guoguang1，2， HE Sheng1，2， WEI Zhan1，2， WANG Zhimin1，2， LIU Jun1，2

（1. School of Mechanical Engineering， Tiangong University， Tianjin 30087， China； 2. Tianjin Key Laboratory of Advanced Mechatronics Equipment Technology， Tiangong University， Tianjin 300387， China）

Abstract： In order to improve the accuracy of dynamic analysis， the effects of multi-clearance joints and component flexibility on the dynamic response of multi-body mechanisms is considered， based on the planar six-bar mechanism. The dynamic simulation of the six-bar mechanism with multi-clearance joints and flexible connecting rod is carried out by solid modeling and citing the \"impact function\" contact force model in ADAMS software. The system dynamics under clearance number， clearance position， clearance size， flexible connecting rod and clearance coupling are investigated. The simulation results show that compared with the single clearance joint， the multi-clearance joints will produce greater contact force， resulting in more intense acceleration fluctuation of the component. The closer the clearance joint to the motor position， the more obvious the influence on the dynamic behavior of the mechanism. The influence of clearance on the dynamic fluctuation of the mechanism can be greatly reduced when considering the flexibility of the connecting rod.

Key words： multi-joint clearances； contact force； flexible connecting rod； dynamics； six-bar mechanism

随着现代工业的发展，机构正朝着速度快、质量小、高负载和高精度的方向发展，而机械系统的动态响应受关节间隙和柔性构件变形的影响。由于机构设计、制造和装配等原因，关节间隙问题是不可避免的。关节间隙不仅会改变理想关节的自由度，还会降低系统的精度、可靠性和稳定性，导致机构的运动学和动力学输出失真，甚至破坏机构。因此，在机械系统的设计和分析时，应将关节间隙和构件柔性因素考虑在内，这对提高机构的运动精度和稳定性具有重要意义。

目前，针对关节间隙和构件柔性问题的研究众多。Flores等[1-2]对含间隙平移关节和转动关节的刚性机构进行了理论分析和实验探究。Wu等[3]通过相关维度和分叉效应描述了含多个间隙的曲柄滑块机构的系统动力学，并研究了间隙大小和其他因素对机构的影响。白争锋[4]研究了间隙对空间机构和平面四连杆机构动力学特性的影响。Khemili等 [5]研究了含间隙关节和柔性构件的四杆机构动力学特性，并为此进行了模拟和实验测试。基于碰撞函数的接触模型，开发了用于仿真试验的模型机构。Abdallah等[6]使用NASTRAN创建柔性构件，然后将该构件导入ADAMS，以研究含有多间隙关节与构件柔性的曲柄滑块机构的动力学性能。Dubo-wsky等[7]研究了含有柔性构件机械系统的冲击响应，作为含间隙机械系统动力学研究的一部分。姚廷强等[8]依据多体动力学和有限元方法，提出一种空间机构柔性多体接触动力学方法，计算分析了含三维圆柱铰的空间机构的运动精度和动力学特征。Wang等[9]建立了带有柔性驱动杆和间隙球面接头的4-SPS/PS并联机构的动态模型，讨论了柔性驱动杆的自由模态和固定模态对带间隙球面接头的平行机构动态响应的影响。Gu等[10]利用有限元方法，通过数值模拟软件包ASSET分析了含有关节间隙的柔性曲柄滑块机构的动力学行为，并观察到了混沌行为。刘志元等[11]对含间隙的柔性机械臂展开了动力学建模与求解，并且分析了构件柔性和间隙对该机构动力学特性的影响。Schwab等[12]分析了含有间隙旋转接头的机构和机器的动态响应，对几种连续接触模型和冲击模型进行了比较。Yaqubi等[13]分析了考虑关节间隙与连杆柔性影响的曲柄滑块机构的非线性动力学行为和控制，利用相图和分岔图研究了连杆的运动状态。Tan等[14]利用改进的力模型建立了动力学方程，并分析了曲柄滑块机构单间隙和双间隙的动力学行为。Cheng等[15] 研究了考虑双回转间隙联接的往复式压缩机的动力学响应，分析了其非线性特性，分析了不同间隙数对机构动态特性的影响，发现当间隙数增加时，机构的动态特性和运动性能降低。邱雪松等[16]分析了多间隙和柔性部件对帆板展开机构动力学特性的影响。屈仁英[17]用接触碰撞模型模拟旋转铰间隙处组件之间的作用效果，基于结构的柔性多体系统的动力学响应进行虚拟实验模态分析，分析了转动关节间隙对具有柔性部件的可展机构动力学特性的影响。Chen等[18]提出了一种对具有多个间隙关节的曲柄滑块机构进行动态建模和分析的一般方法， 对柔性的曲柄滑块机构的动态响应进行了测量，揭示了间隙接头如何引起多体系统的振动现象。在考虑部件柔性的情况下，对单间隙关节机构的性能也进行了广泛的研究[19-20]。Li等[21]对面板柔性和接头间隙对机械系统的更复杂耦合效应进行了数值分析。

目前，学者们对四杆机构的动力学研究较为普遍，而对运动构件较多的六杆机构研究较少。本文基于六杆机构，研究含多关节间隙与连杆柔性对其动力学特性的影响。首先，对六杆机构进行实体建模，导入ADAMS软件后对带关节间隙的转动副模型进行建模；其次，结合间隙机构的动力学方程，通过ADAMS软件对多关节间隙和刚性连杆的平面六杆机构进行动力学仿真与分析，具体包括间隙数量、位置和数值对机械系统的影响，并应用有限元软件ABAQUS完成连杆柔性化，从而替代原刚性连杆进行动力学分析。

1 机构三维实体建模

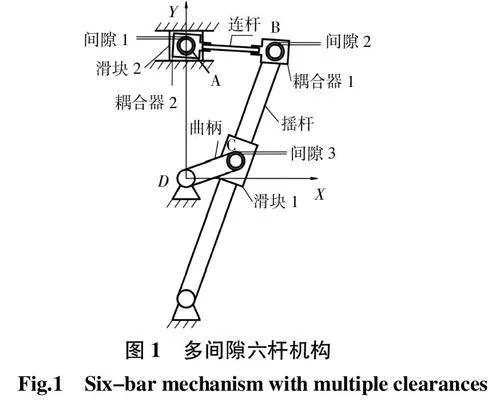
含多间隙的平面六杆机构如图1所示。其中，关节间隙1、2和3分别位于铰接A处、B处和C处。将该机构在SolidWorks中完成实体建模后导入ADAMS中进行仿真研究。

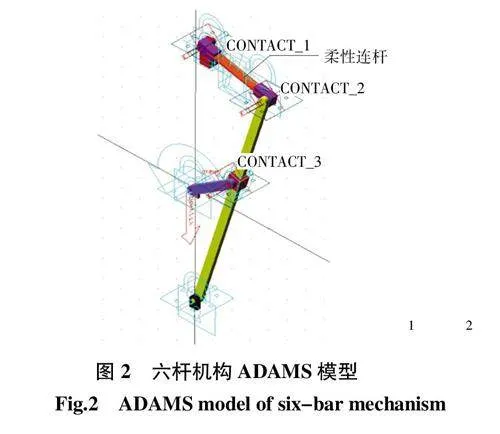
在研究连杆的柔性时，将连杆在有限元软件ABAQUS中进行处理，并计算其固有频率和模态。将柔性连杆生成文件（.mnf）导进ADAMS中，替换原刚性连杆，并重新连接到原六杆机构中。图2所示为ADAMS_VIEW视图中的多关节间隙六杆机构。

2 含间隙转动副模型

2.1 间隙建模

转动副间隙构成如图3所示。图3中：R1和R2分别为轴颈和轴承内圈半径；c为间隙。以轴承中心O为原点建立固定坐标系，以轴颈中心O1为原点建立相对坐标系。轴颈在轴承中的间隙需要通过引入2个附加自由度来表示，即轴颈中心相对于轴承中心的水平位移ex和垂直位移ey。

在含关节间隙的转动副中，轴颈与轴承相对运动时经历3种状态，如图4所示。

（1） 自由状态：轴颈和轴承没有任何接触力，如图4（a）所示。

（2） 接触-分离状态：此状态是在瞬间完成的，是轴颈与轴承冲击-穿透的开始状态或即将分离状态，如图4（b）所示。

（3） 冲击-穿透状态：轴颈和轴承挤压在一起，穿透深度大于0，从而产生接触力，如图4（c）所示。

间隙为：

偏心距：

相对穿透深度为：

根据δ的值去判断轴颈与轴承的相对运动状态。当δ ＜ 0时，轴颈与轴承处于自由运动状态，两者完全分离，接触力为0。因此，在该状态下，在不考虑其他外力时构件速度为恒定，构件加速度降至0；当δ = 0时，为接触-分离状态，这种状态下产生的接触力具有切向分量和法向分量的特征，此状态和理想状态下相似，因此构件速度曲线与机构理想运动曲线重叠；当δ ＞ 0时，为冲击和穿透状态，在轴颈侵入轴承之后，接触力突然增加，构件的动态行为会受到显著影响。

2.2 带间隙机构的动力学方程

当机构为理想状态（理想转动副）时，根据Lagr-ange乘子法，机构的动力学方程为：

3 动态仿真

采用ADAMS软件，基于已建立的含间隙机构的动力学方程式（公式（7）），对含关节间隙的平面六杆机构进行模拟仿真和分析。

3.1 机构模型及参数

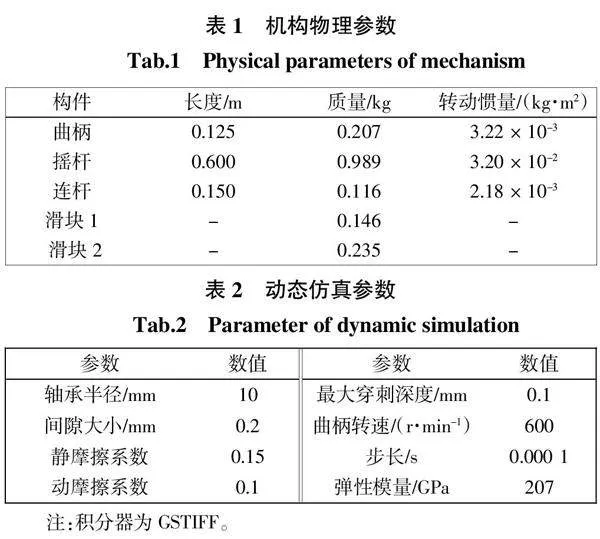
如图1所示的含多关节间隙的平面六杆机构，A、B和C处为间隙关节，设定间隙大小为0.2 mm，曲柄转速为600 r/min。在初始状态下，滑块2在X方向上位于X = 0处。六杆机构的物理参数和动态仿真参数如表1和表2所示。

3.2 刚性六杆机构

在机构运行前，间隙关节中的轴颈中心与轴承中心相重合。系统运行初期，轴颈和轴承发生碰撞，对系统造成冲击，这将导致系统在早期阶段的不稳定运行。为了消除初始状态对系统的影响，现选取稳定后的2个周期作为仿真结果。

3.2.1 间隙数量对机构动力学特性的影响

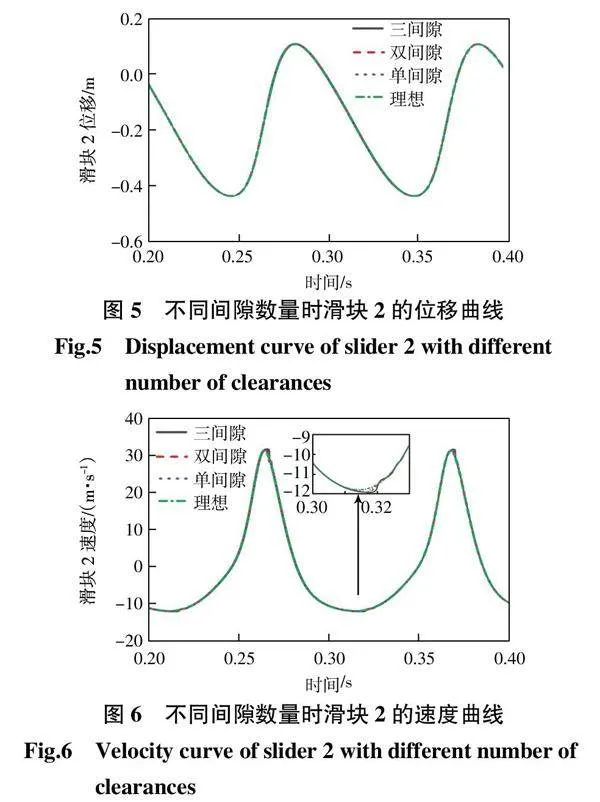
为了研究间隙数量对系统动态性能的影响，假定机构中分别有3个间隙（在A、B、C处）、双间隙（在A和B处）和单个间隙（在A处），对这3种情况分别进行仿真研究。仿真结果如图5—图8所示。

由图5可知，当考虑不同间隙数量时，滑块2的位移曲线基本与理想曲线一致，转动副间隙及其数量对滑块2的位移几乎无影响。

图6所示为含三间隙、双间隙和单间隙时滑块2的速度变化趋势。由图6可知，考虑不同间隙数量时，机构滑块2的速度曲线与理想曲线几乎一致，表明间隙数量对机构的速度影响较小；通过局部放大图可知，虽然速度曲线基本与理想曲线保持一致，但也产生了局部的波动，并且随着间隙数量的增多，滑块2速度波动会更加明显。因此，间隙数量越多，间隙对机构速度造成的影响越明显。

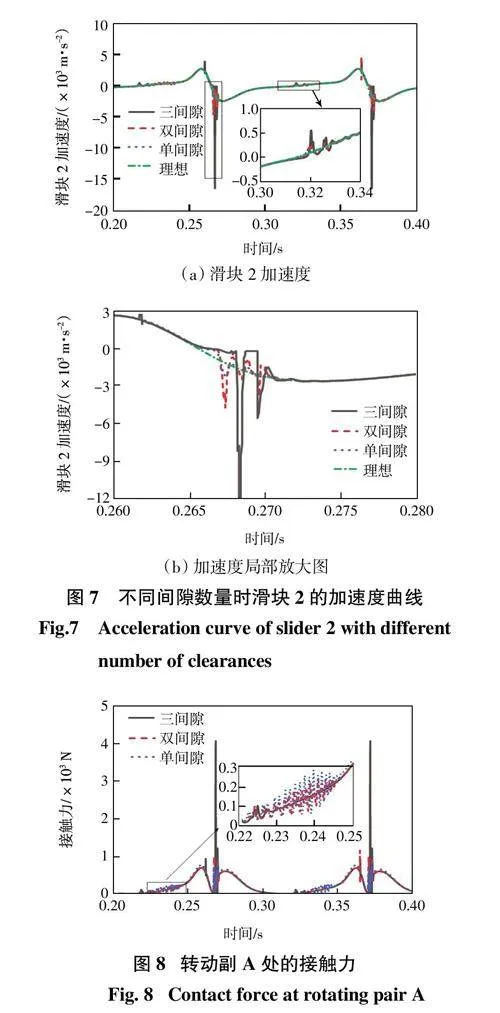
图7所示为含三间隙、双间隙和单间隙滑块2的加速度变化趋势。根据图7可知，间隙数量的增多，滑块2的加速度震荡峰值不断增大，其中三间隙时滑块2的加速度波动峰值是单间隙时的6倍左右。这是由于在多间隙时，各间隙之间相互影响，产生耦合作用，使滑块2的加速度震荡越来越剧烈。对比各项结果可以看出，间隙对加速度影响最大，对位移影响最小。

图8所示为三间隙、双间隙和单间隙时转动副A处的接触力变化趋势。由图8可知，当机构只考虑单间隙时，转动副A处的接触力波动峰值较小；当考虑2个间隙时，转动副A处的接触力波动峰值明显增大；考虑3个间隙时，转动副A处的接触力波动峰值进一步增大。原因在于各间隙之间相互影响，产生耦合作用，使转动副A处轴颈与轴承之间发生剧烈碰撞。

3.2.2 间隙位置对机构动力学特性的影响

考虑不同关节间隙位置对机构动力学特性的影响，其机构动力学响应如图9所示。

由图9（a）和（b）可知，不同的间隙位置对滑块2的位移和速度曲线影响偏小，曲线基本与理想状态曲线重叠。距离电机位置最近的间隙3，对滑块2的加速度波动峰值影响最大，随之是间隙2，再之是间隙1。由图9（c）可以看出，当转动副A、B、C处依次存在间隙时，滑块2的加速度波动幅度依次增加，这说明在传动过程中，最靠近电机位置的关节处间隙对机构的加速度影响最大。

3.2.3 间隙数值对机构动力学特性的影响

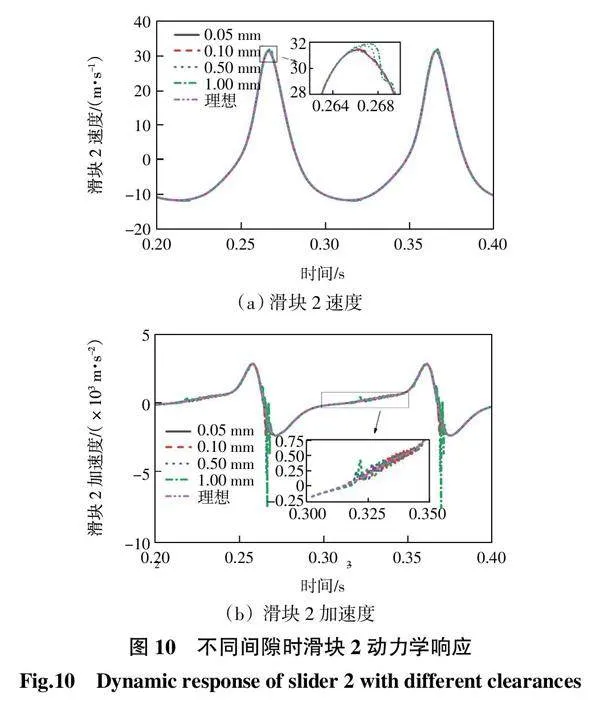
为了研究间隙数值对机构动力学特性的影响，只考虑转动副B处含有间隙，设定间隙c分别为0.05 mm、0.10 mm、0.50 mm和1.00 mm。机构动力学响应仿真结果如图10所示。

由图10（a）可知，当间隙值小于0.50 mm时，速度曲线虽有震荡但幅值特别小，与理想曲线基本吻合，当间隙值增大到1.00 mm时，速度曲线震荡越来越明显。间隙值越大，速度曲线震荡越明显。由图10（b）可知，随着间隙数值的变大，机构动态输出曲线呈现出高幅值震荡特征。

3.3 含柔性构件的六杆机构

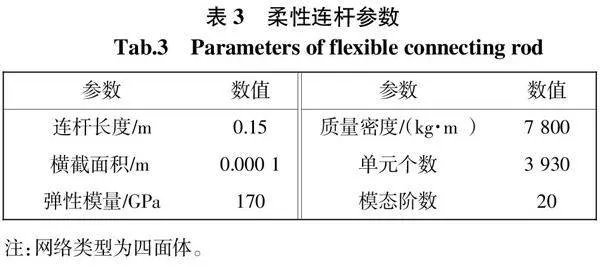
为了研究连杆柔性对含关节间隙机构的动力学影响。通过在有限元软件ABAQUS下对连杆进行网格划分并最后形成图2中柔性连杆，柔性连杆的参数如表3所示。

其中连杆柔性的前三阶模态的固有频率分别为335.29 Hz、864.57 Hz和916.24 Hz，如图11所示。转速为600 r/min时驱动力激励频率相当10 Hz，远未达到构件低阶固有频率，因此不会产生低阶谐振。

最后，将在ABAQUS COMMAND窗口下输出文件（.mnf）后导入ADAMS中，生成含间隙和柔性连杆的六杆机构，如图11所示。

为了研究在柔性连杆工况下间隙数量对机构动力学特性的影响，此次仿真在与刚性连杆同样的条件下进行，机构动力学响应如图12所示。

由图12可知，在含有柔性连杆的机构中，考虑不同间隙数量时，机构滑块2的位移、速度的曲线与理想曲线基本保持一致，表明间隙数量对机构位移、速度影响较小；随着间隙数量的增多，机构滑块2的加速度波动峰值和频率与刚性连杆条件下呈现相同趋势，但滑块2的加速度波动峰值明显减小，表明连杆柔性会对加速度震荡产生一定的抑制作用；考虑连杆柔性之后，加速度不再出现大峰值波动现象，但柔性仍使加速度产生低幅震荡，并且在某些时刻比刚性连杆条件下波动更加强烈。

由图12（d）和图7可知，考虑构件柔性条件下产生的接触力相比刚性机构有明显变化，主要体现在接触力振荡峰值减小。原因是轴颈与轴承发生接触碰撞时，柔性连杆的弹性变形能够缓冲轴颈与轴承之间的接触碰撞，使轴颈与轴承的接触碰撞次数减少，接触力减小。

4 结 论

本文研究了含多关节间隙与连杆柔性的平面六杆机构的动力学特性。所得结果基于ADAMS中使用的接触力模型，突出了关节间隙与连杆柔性耦合对机构动力学性能的影响。

（1） 间隙会使机构加速度和接触力产生震荡，导致机构的实际运动响应偏离了理想状态，加速度对间隙影响的敏感度最强，速度对间隙影响的敏感度次之，位移最弱。

（2） 随着间隙数量的增多，滑块2的加速度和转动副A处的接触力震荡幅度越大，震荡范围越广。

（3） 在考虑单间隙时，间隙关节距离电机位置越近，则对机构的动力学特性影响越明显。

（4） 考虑连杆柔性时，柔性连杆的弹性变形会缓冲间隙处轴颈与轴承的接触碰撞，从而抑制了接触力和加速度的震荡，与刚性连杆比较，震荡范围大幅度下降。

参考文献：

[1]" " FLORES P， AMBR？譫SIO J， CLARO J C P， et al. Translational joints with clearance in rigid multibody systems[J]. Journal of Computational and Nonlinear Dynamics， 2008，3（1）：112-113.

[2]" " FLORES P， AMBR？譫SIO J. Revolute joints with clearance in multibody systems[J]. Computers amp; Structures， 2004， 82（17/18/19）： 1359-1369.

[3]" " WU X Z， SUN Y， WANG Y， et al. Correlation dimension and bifurcation analysis for the planar slider-crank mechanism with multiple clearance joints[J]. Multibody System Dynamics， 2021， 52（1）： 95-116.

[4]" " 白争锋. 考虑铰间间隙的机构动力学特性研究[D]. 哈尔滨： 哈尔滨工业大学， 2011.

BAI Z F. Research on dynamic characterisitcs of mechanism with joint clearance[D]. Harbin： Harbin Institute of Technolo-gy， 2011 （in Chinese）.

[5]" " KHEMILI I， ROMDHANE L. Dynamic analysis of a flexible slider-crank mechanism with clearance[J]. European Journal of Mechanics-A/Solids， 2008， 27（5）： 882-898.

[6]" " ABDALLAH BEN M A， KHEMILI I， AIFAOUI N. Numerical investigation of a flexible slider-crank mechanism with multi-joints with clearance[J]. Multibody System Dynamics， 2016， 38（2）： 173-199.

[7]" " DUBOWSKY S， MOENING M F. An experimental and analyti-cal study of impact forces in elastic mechanical systems with clearances[J]. Mechanism and Machine Theory， 1978， 13（4）： 451-465.

[8]" " 姚廷强， 陈锐搏， 王立华， 等. 考虑三维圆柱铰间隙碰撞的空间机构柔性多体动力学分析方法[J]. 振动与冲击， 2021， 40（1）： 297-307， 316.

YAO T Q， CHEN R B， WANG L H， et al. Flexible multi-body dynamic analysis method of spatial mechanisms considering 3-D cylindrical hinge clearance collision[J]. Journal of Vibration and Shock， 2021， 40（1）： 297-307， 316 （in Chinese）.

[9]" "WANG G X， WANG L. Dynamics investigation of spatial par-allel mechanism considering rod flexibility and spherical joint clearance[J]. Mechanism and Machine Theory， 2019， 137： 83-107.

[10]" GU P Y， DUBOWSKY S， MAVROIDIS C. The design impli-cations of chaotic and near-chaotic vibrations in machines[C]//Proceedings of ASME 1998 Design Engineering Technical Conferences. Atlanta，Georgia，USA： ASME，2021.

[11]" 刘志元， 孙东阳. 含区间铰间隙柔性机械臂控制精度分析[J]. 重庆大学学报， 2021， 44（2）： 53-64.

LIU Z Y， SUN D Y. Tracking accuracy analysis of a flexible manipulator with interval joint clearance[J]. Journal of Chong-qing University， 2021， 44（2）： 53-64 （in Chinese）.

[12]" SCHWAB A L， MEIJAARD J P， MEIJERS P. A comparison of revolute joint clearance models in the dynamic analysis of rigid and elastic mechanical systems[J]. Mechanism and Machine Theory， 2002， 37（9）： 895-913.

[13]" YAQUBI S， DARDEL M， DANIALI H M. Nonlinear dynamics and control of crank-slider mechanism with link flexibility and joint clearance[J]. Proceedings of the Institution of Mechanical Engineers， Part C： Journal of Mechanical Engineering Science， 2016， 230（5）： 737-755.

[14]" TAN H Y， HU Y J， LI L. A continuous analysis method of pla-nar rigid-body mechanical systems with two revolute clearance joints[J]. Multibody System Dynamics， 2017， 40（4）： 347-373.

[15]" CHENG S G， CHEN H W. Dynamic analysis of reciprocating compressor with two revolute joint clearances[J]. IOP Confer-ence Series： Materials Science and Engineering， 2019， 677（3）： 032079.

[16]" 邱雪松， 任志博， 桂朋， 等. 含多间隙柔性可展帆板动力学建模及仿真[J]. 宇航学报， 2018， 39（7）： 724-731.

QIU X S， REN Z B， GUI P， et al. Dynamic modeling and simulation of a flexible deployable solar array with multiple clearances[J]. Journal of Astronautics， 2018， 39（7）： 724-731 （in Chinese）.

[17]" 屈仁英. 含旋转铰间隙的柔性可展机构动态特性分析[D]. 长春： 吉林大学， 2021.

QU R Y. Analysis of dynamic characteristics of flexible and deployable mechanism with rotating hinge clearance[D]. Chang-chun： Jilin University， 2021 （in Chinese）.

[18]" CHEN Y， WU K， WU X Z， et al. Kinematic accuracy and nonlinear dynamics of a flexible slider-crank mechanism with multiple clearance joints[J]. European Journal of Mechanics - A/Solids， 2021， 88： 104277.

[19]" ZHENG E L， WANG T Y， GUO J， et al. Dynamic modeling and error analysis of planar flexible multilink mechanism with clearance and spindle-bearing structure[J]. Mechanism and Ma-chine Theory， 2019， 131： 234-260.

[20]" SALAHSHOOR E， EBRAHIMI S， ZHANG Y Q. Frequency analysis of a typical planar flexible multibody system with joint clearances[J]. Mechanism and Machine Theory， 2018， 126： 429-456.

[21]" LI Y Y， WANG C， HUANG W H. Dynamics analysis of planar rigid-flexible coupling deployable solar array system with multiple revolute clearance joints[J]. Mechanical Systems and Signal Processing， 2019， 117： 188-209.

本文引文格式：

金国光，何升，魏展，等. 含多关节间隙平面柔性六杆机构动力学分析[J]. 天津工业大学学报， 2024， 43（4）： 75-81.

JIN G G， HE S， WEI Z， et al. Dynamic analysis of planar flexible six-bar mechanism with multi-joint clearances[J]. Jo-urnal of Tiangong University， 2024， 43（4）： 75-81（in Chinese）.

收稿日期： 2022-07-26" " " " 基金项目： 国家自然科学基金资助项目（51475330）；天津市高校创新团队项目（TD13-5037）

通信作者： 金国光（1963—），男，教授，博士生导师，主要研究方向为机构学、机械系统动力学及控制。E-mail：jinguoguang@tiangong.edu.cn