任务驱动：推动运算能力发展的重要路径

［摘 要］运算能力的发展能促进学生数学推理能力的提升，有助于学生形成规范化解决问题的品质，养成一丝不苟、严谨求实的科学态度。以苏教版教材三年级下册“两位数乘两位数”为例，通过设置主动性任务、挑战性任务、开放性任务，促进学生不断深入思考，发展运算能力。

［关键词］运算能力；主动性任务；挑战性任务；开放性任务

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2024）20-0028-04

《义务教育数学课程标准（2022年版）》（以下简称《2022年课程标准》）指出，“数与运算”是小学数与代数领域的两大主题之一。在《2022年课程标准》中，“运算能力”是小学阶段唯一以“能力”来描述的核心素养，即学生“能够明晰运算的对象和意义，理解算法与算理之间的关系；能够理解运算的问题，选择合理简洁的运算策略解决问题”。与《义务教育数学课程标准（2011年版）》相比，在《2022年课程标准》补充了数学运算与数学推理能力发展的关系，强调了运算能力对学生形成终身有用的思维品质与科学态度的教育价值。教师可以以“数与运算”内容为载体，落实《2022年课程标准》理念，发展学生运算能力。下面以苏教版教材三年级下册“两位数乘两位数”为例进行研究，尝试通过创设有效的任务情境，推动学生运算能力进一步提升。

一、主动性任务：促进算理和算法的融通

主动性任务是指指向学生自我建构、自我追问和自我反思的任务活动，关注的是“为什么”“有什么联系”“有何用”“好不好”等问题。日常教学算理和算法时，笔者通常会给学生讨论交流的时间，鼓励学生汇报各自的方法，但总会有部分学生参与的积极性不高。那么，如何最大限度地调动学生的积极性，使其沉浸式地进行计算内容的探究学习呢？

（一）深入分析，找准起点

把握教材和了解学情是教师进行有效教学的前提。为了找准学生的学和教师的教的真实起点，笔者进行了全面而深入的分析。

1.研读课标教材，了解学生逻辑起点

苏教版教材中关于“整数乘法”的内容分为4个阶段（见表1）。

其中，“两位数乘两位数”（不进位笔算）在小学整数运算中起着承上启下的作用。在三年级上学期，学生已经学习了两、三位数乘一位数的竖式计算方法，了解了基本的乘法竖式结构，“两位数乘两位数”这一课是在此基础上继续带领学生探究整数乘法。与之前的笔算教学相比，本节课重点在于引导学生了解乘的顺序和第二部分积的书写位置，为后续学习多位数乘两位数以及相关的四则混合运算奠定基础。

2.关注已有经验，了解学生现实起点

课前，笔者借鉴人教版教材例题的情境，将原例题的算式“24×12”修改为“14×12”，并随机抽取了一个班级的30名学生进行学前检测，结果见表2。

通过学前检测发现，许多学生有提前预习的好习惯，并且在借助已有的乘法竖式学习经验的基础上尝试进行14×12的竖式书写。大部分学生虽然能够正确解答，但并不了解每一步的具体含义，这表明他们没有真正理解算理。

3.关注学习感受，了解学生情感起点

课前，笔者就本课内容对部分学生和教师进行了调查，结果见表3。

根据学前检测和调查结果不难发现，教师提供的素材以及学生的生成性素材很丰富，但是学生的学习效果并没有达到预期。如何更加有效调动各个层次学生的积极性，同时给予学习能力较弱的学生充足的思考时间呢？笔者尝试以上述素材为载体，借助任务驱动提高学生的思考质量，推动算理和算法的有效融合。

（二）直观呈现，多元理解

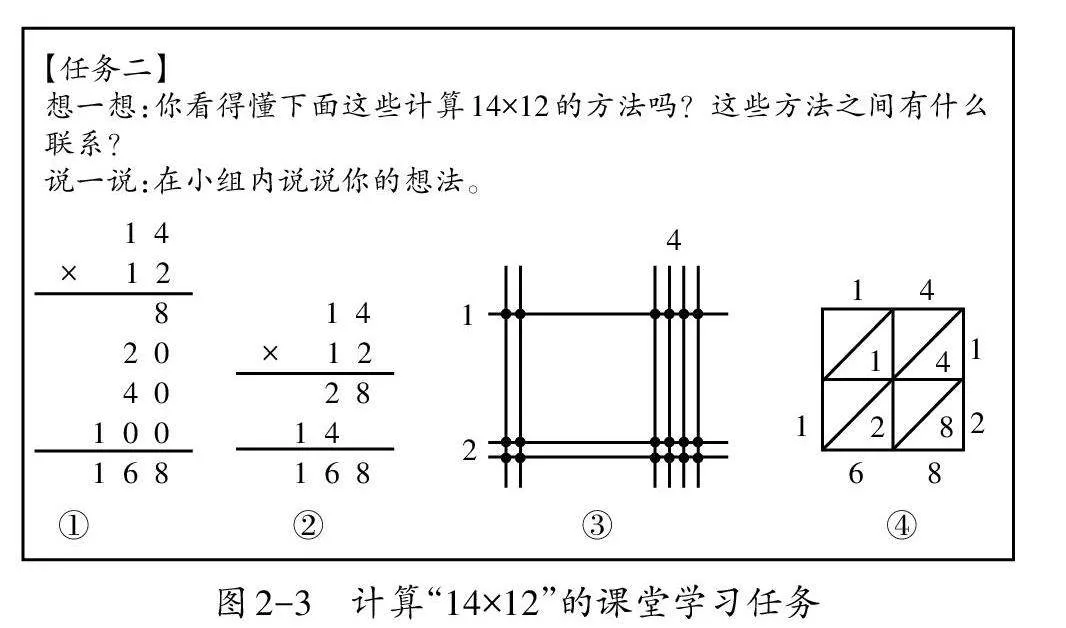
《2022年课程标准》指出，学生要“能够明晰运算的对象和意义，理解算法与算理之间的关系；能够理解运算的问题，选择合理简洁的运算策略解决问题”。课始，笔者根据前测的多样方法设置了课堂学习任务（如图1），旨在让每个层次的学生都能思考方法之间的联系，进一步理解整数乘法的算理。

笔者将全班学生在前测中使用的多种方法整理成素材，直观呈现在学生面前，给学生带来了视觉和思维上的冲击，激发了学生探索的积极性。看到自己未曾想到的方法，学生虚心学习，再次进行思考和分析。

（三）充分探究，理法融通

课堂上，笔者摒弃碎片化的引入，将课堂时间归还给学生，给予他们充分的思考和自主探索时间。笔者鼓励学生思考不同的方法，并比较这些方法之间的异同点，为竖式算理和算法的学习做铺垫。通过交流，学生认识到“无论是拆和、拆积还是列竖式，本质上都是先算出各部分的结果，然后将各部分的结果合起来”。经过充分的探索和有效的小组互助，各个层次的学生对知识的理解都更加深入了。

二、挑战性任务：促进算法抽象走向深入

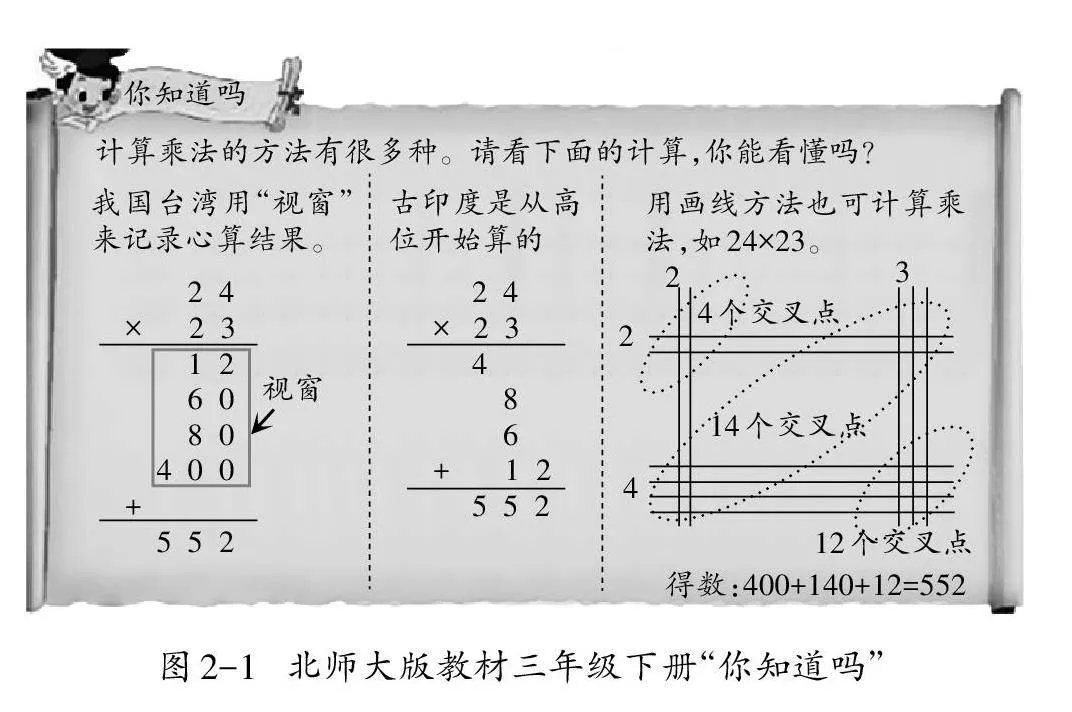
数学挑战性任务是指那些发生在学生最近发展区、能激发其学习动机的素养导向的数学活动。在学生完成两位数乘两位数的基本练习后，笔者借鉴北师大版三年级下册教材中的“你知道吗”（如图2-1）和苏教版教材三年级下册中的“你知道吗”（如图2-2），引导学生了解乘法计算的优化发展过程，并设计了课堂学习任务（如图2-3）。

（一）以史激趣促进推理能力的发展

发展推理能力是运算能力内涵的一个重要表现特征。华东师范大学教授汪晓勤指出，数学史发挥的教育价值体现在知识之谐、方法之美、探究之乐、能力之助、文化之魅、德育之效六个维度。本节课是学生第一次学习两位数乘两位数的竖式结构，在学生理解了算理和算法后，笔者继续组织学生了解计算的发展过程，并借助任务，鼓励学生大胆探索视窗法、画线法以及格子法（铺地锦法），深度了解计算过程。面对前人的智慧，学生的探索积极性高涨。在探索过程中，学生发现自己的一些想法和数学家们不谋而合，体会到了学习的价值和乐趣。该过程极大激发了学生的求知欲，也有效促进了学生核心素养的发展。

学生充分利用小组展示交流的机会，纷纷表达自己对不同方法的理解和感受。课堂上，学生充分感受到数学的学科魅力，对乘法笔算算理和算法的理解也不断加深。面对教师提出的问题，学生不断思考、分析、交流和尝试，顺利解决了问题，使得推理能力得到了发展。

（二）自主尝试，对比中深化算法认知

在学生理解了各种计算方法后，笔者提出问题“这些方法之间有什么联系？”，促使学生借助小组的力量进一步探索。

1. 同中存异

在汇报交流时，学生首先发现了各种方法的不同点——有数有形，有横式有竖式，每种方法都有自己的特点。对于这四种方法，全班学生都认为第二种竖式法更简便。就这样，在激烈的小组讨论中，学生不断加深了对多样化算法的认识。

2. 异中求同

学生通过不断对比、分析、归纳、总结，明确了各种方法的本质都是“先分再合，先算出部分，再将各部分相加”。同时，通过画一画、圈一圈、连一连等操作，学生发现不同算法之间有一些相同点。例如：各种方法都包含乘数12和14，视窗法中2×4+2×10就是本节竖式法的第一步计算，即用第二个乘数个位上的数2去乘第一个乘数14，得28。在完成课堂学习任务的过程中，学生了解了数学方法的本质以及它们之间的联系，不断加深对算理和算法的理解，深刻体会到数学学科的严谨性和简洁性。

三、开放性任务：促进理法有效迁移

《2022年课程标准》指出，要让学生“经历算理和算法的探索过程，理解算理，掌握算法”，同时让学生“感悟数的运算以及运算之间的关系，体会数的运算本质上的一致性”。学习三年级下册“两位数乘两位数”后，学生在四年级下册将进一步学习“三位数乘两位数”的乘法运算。四年级是整数乘法运算学习的最后阶段，侧重算理和算法的迁移。学生是否会迁移知识经验计算三位数乘两位数是检验其核心素养运算能力是否形成的指标。为了促进学生更加系统地建构整数乘法笔算的知识体系，提升数学素养，笔者设计了一项课堂学习任务（如图3）。

（一）初迁移，感悟算理算法的一致性

课末，笔者让学生计算“132×13”，学生跃跃欲试。借助两位数乘两位数的探索经验，学生顺利地算出了答案。接着，笔者引导学生表达计算过程以及其中的道理，并分析两位数乘两位数和三位数乘两位数的异同点。在师生交流的过程中，学生初步感受到成功解决问题的乐趣，同时初步体会到算理和算法的一致性。

（二）再迁移，初步建立整数乘法的数学模型

在学生根据两位数乘两位数的经验顺利完成了132×13的竖式计算后，笔者继续放手，鼓励学生大胆尝试计算多位数乘多位数（如图4）。面对这个比较开放的问题，学生大胆表达自己的想法。有的学生从简单做起，计算的是不进位的两位数乘两位数和三位数乘两位数。部分学生提前预习了相关知识，则计算的是进位的多位数乘多位数，并成功算出了结果。还有学生提出，如果纸张够大，那么还可以计算一百位数乘一百位数。在大家纷纷发言时，几名概括能力较强的学生总结出了多位数乘多位数的计算方法。经过积极的讨论，学生自主完善了整数乘法的知识结构，初步建立了整数乘法竖式计算的数学模型。

本节课通过设置三个不同类型的任务，为学生的自主理解和探索搭建了平台。学生通过不断分析算理、对比算法解决问题，获得了解决问题的幸福感与成就感。笔者给予学生充分自主思考、探究、讨论的时间，让学生能够主动沟通和优化算法，对两位数乘两位数算理和算法的理解层层深入，并逐渐掌握多位数乘多位数的计算方法，初步实现整数乘法知识的整体性建构。学生在深度思考问题的过程中经历了运用数学思维发现和提出问题、分析和解决问题的过程，积累了基本数学活动经验，运算能力得到了进一步的发展。

［ 参 考 文 献 ］

[1] 崔允漷.指向学科核心素养的教学即让学科教育“回家”[J].基础教育课程，2019（Z1）：5-9.

[2] 汪晓勤.HPM视角下的小学数学教学[J].小学数学教师，2017（Z1）：77-83.

（责编 吴美玲）