带恒功率负载多电平Buck变换器逆解耦自适应滑模控制

摘" 要：

针对带恒功率负载（CPL）多电平Buck变换器的强耦合问题及负阻抗特性引起的不稳定问题，提出一种逆解耦自适应滑模控制策略。建立带CPL多电平Buck变换器的非线性数学模型，基于逆系统方法证明系统的可逆性，并推导逆系统表达式，将模型线性化解耦为多个伪线性子系统，抵消负阻抗特性的影响。通过选取线性滑模面和指数趋近律以减弱滑模抖振，并将自适应机制引入到滑模控制中，进而为线性子系统分别设计自适应滑模控制器，进一步提高系统控制性能。基于李雅普诺夫理论对控制系统的稳定性和鲁棒性进行验证。与现有控制方法进行比较，仿真结果表明，所提控制策略具有更强的鲁棒性和优越性。最后，搭建原理样机进行实验对比，实验结果验证了所提控制策略的正确性和有效性。

关键词：多电平Buck变换器；恒功率负载；逆系统；自适应控制；滑模控制；解耦控制

DOI：10.15938/j.emc.2024.06.012

中图分类号：TM46

文献标志码：A

文章编号：1007-449X（2024）06-0120-11

收稿日期： 2022-09-01

基金项目：国家自然科学基金（61561008）；广西高校中青年教师科研基础能力提升项目（2021KY0164）；广西民族大学人才引进科研启动项目（2020KJQD25）

作者简介：吴家荣（1988—），男，博士，副教授，研究方向为电力电子变换器建模与鲁棒控制；

卢振坤（1979—），男，博士，教授，研究方向为电力电子控制系统设计与优化；

文春明（1969—），男，博士，教授，研究方向为新能源汽车及其控制。

通信作者：吴家荣

Inverse decoupling adaptive sliding mode control for multilevel Buck converters with constant power load

WU Jiarong，" LU Zhenkun，" WEN Chunming

（College of Electronic Information， Guangxi Minzu University， Nanning 530006， China）

Abstract：

To solve the problem of strong coupling and the issue of instability caused by negative impedance characteristics of multilevel Buck converters with constant power load （CPL）， an inverse decoupling adaptive sliding mode control strategy was proposed. The nonlinear mathematical model of multilevel Buck converters with CPL was established. The reversibility of the system was proved by the inverse system method， and the expression of the inverse system was deduced. The model is linearly decoupled into multiple pseudo-linear subsystems. The negative impedance characteristics are offset. Linear sliding mode surfaces and exponential convergence laws were selected to reduce sliding mode chattering， and an adaptive mechanism was introduced to the sliding mode control， adaptive sliding mode controllers were designed for the linear subsystems respectively to further improve the control performance of the system. Furthermore， the stability and robustness of the control system were verified based on the Lyapunov theory. Compared with the existing control method， the simulation results show that the proposed control strategy has stronger robustness and better superiority. Finally， a prototype was built for experiments， and the experimental comparison results verify correctness and effectiveness of the proposed control strategy.

Keywords：multilevel Buck converters; constant power load; inverse system; adaptive control; sliding mode control; decoupling control

0" 引" 言

多电平DC-DC（multilevel DC-DC，MD）变换器因较传统两电平DC-DC变换器具有更低的电压应力、更多的电平输出、更小的滤波体积等优点，已逐渐在低压、低功率领域得到了应用与研究［1-2］。为使MD变换器能正常工作且具有良好工作性能，保证飞跨电容（flying capacitor，FC）电压稳定至各自平衡值极其关键［3-4］。然而，MD变换器是一类复杂的非线性系统，具有多输入多输出特性，输出电压与FC电压之间存在强耦合作用，给FC电压的平衡及系统的解耦控制带来挑战［5］。

为了解决上述问题，现有文献的处理方法可大致分为三类，即增加外部电路方法、线性解耦法和精确反馈线性化（exact feedback linearization，EFL）解耦法。对于增加外部电路方法，文献［6］提出增强型FC电压平衡方法，该方法通过在原拓扑上增加外围电路以达到改善FC电压平衡的目标。文献［7］提出一种在MD Buck变换器输出端并联接入RLC谐振电路的控制方案，以加快FC电压的调节速度。然而，增加外部电路法加大了系统的体积和损耗，难以兼顾FC电压和输出电压的耦合性，提高了系统的控制难度。为此，线性解耦法被提出。文献［8］对MD Buck变换器提出一种基于线性解耦矩阵法的平衡控制策略，提升了系统的稳定性。文献［9］基于线性解耦法实现MD Buck变换器系统解耦的基础上，设计了等效滑模控制器以提高系统的控制性能。然而，线性解耦法建立在小信号模型基础上，难以满足现有应用对更高控制性能和更强鲁棒性的要求。为了克服上述缺陷，基于EFL的解耦控制方法被关注。文献［3］采用EFL控制与最优控制相结合的方法实现了MD Buck变换器的解耦控制，提高了系统的动态性能。为实现FC电压和输出电压的解耦，文献［10］对工作于电感电流连续导电模式（continuous conduction mode，CCM）下的四电平Buck变换器提出一种EFL控制方法，降低了控制器设计的复杂度。然而，EFL方法的缺陷在于其强依赖于被控对象的精确数学模型。

滑模控制（sliding mode control，SMC）对系统不确定性、外界干扰和未建模动态具有强鲁棒性，能有效克服EFL方法的上述缺陷［11-12］。然而，SMC的切换增益大小需视不确定扰动的上界值而定，这难以在系统实际运行中进行估量，导致系统的稳定难以维持［13］。此外，随着电力电子应用的推广，大量的电子负载连接到MD变换器上。当电子负载输出功率恒定时，该类负载可视为恒功率负载（constant power load，CPL）［14-15］。CPL的负阻抗特性不仅会增加系统的非线性，还会严重减小系统的阻尼系数，给带CPL MD变换器的稳定控制带来困难［16］。而现有研究对MD变换器的研究仍停留在输出端仅接有纯电阻负载的情形，难以满足同时为纯电阻负载和CPL供电的需求。

鉴于此，本文对带CPL MD Buck变换器提出一种逆解耦自适应滑模控制策略。一方面，采用逆系统方法实现系统的线性化与解耦，抵消CPL负阻抗特性的影响，利于控制器的设计；另一方面，对变换器采用SMC技术，解决EFL方法严重依赖被控对象精确数学模型的问题，提升系统的鲁棒性。此外，引入自适应技术估计SMC的切换增益，提高系统的稳定性能。最后，进行仿真比较和实验对比验证。

1" 数学模型

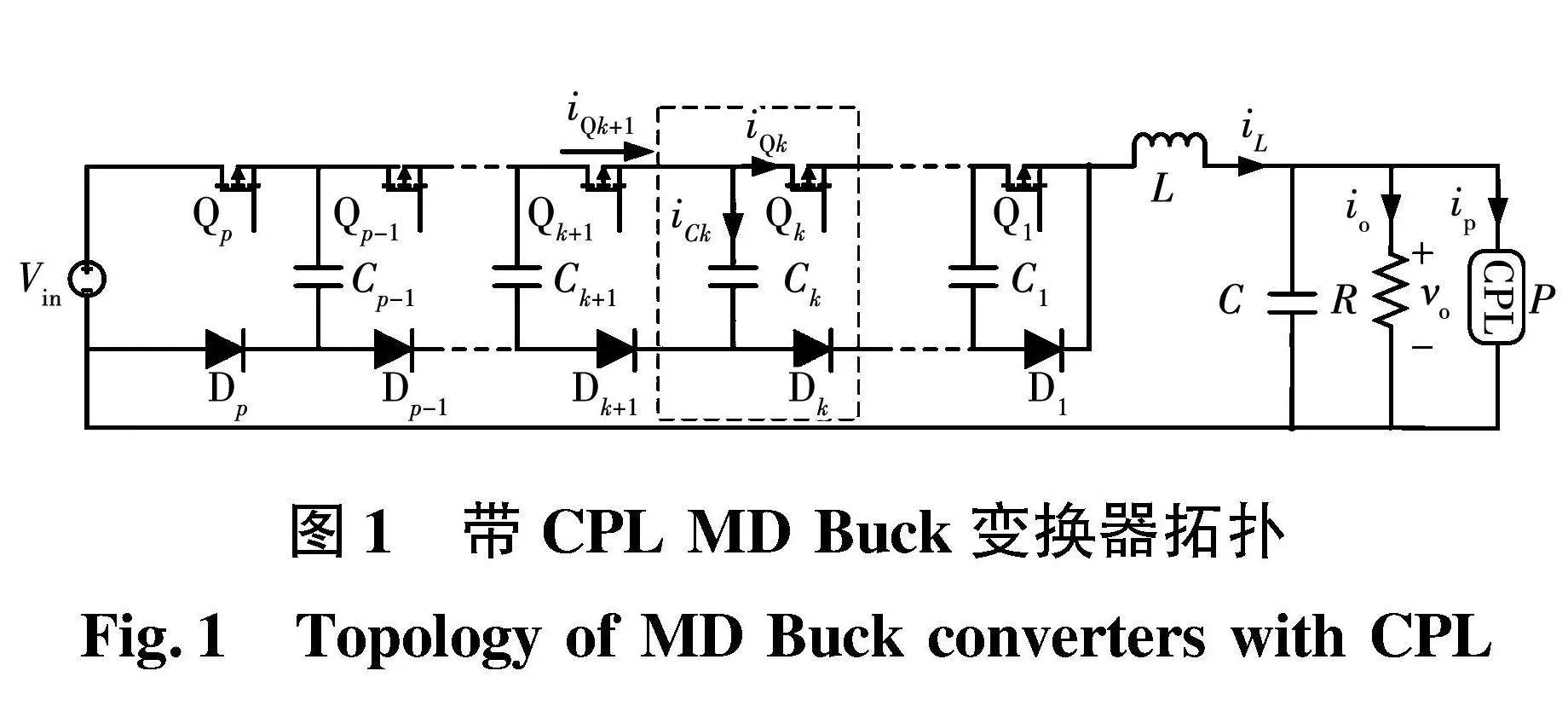
图1给出了带CPL MD Buck变换器的电路拓扑，主要包含输入电压Vin、电感L、电容C、阻性负载电阻R、恒功率负载CPL以及p个串联的基本单元组成。其中，开关管Qk（k=1，2，…，p）、二极管Dk（k=1，2，…，p）及飞跨电容Ck（k=1，2，…，p-1）组成一个基本单元，如虚线框所示。Qk和Dk互不导通，P代表CPL的功率。理想状态下，开关管的占空比均为d，且Qk+1和Qk相位差2π/p，此时FC电压平衡于kVin/p，输出电压vo=dVin。

假设系统工作于CCM，dk为Qk的占空比，取开关管占空比d=（d1，…，dk，…，dp-1，dp）为控制变量，以电感电流iL、Ck两端电压vCk以及vo为状态变量，即（vCk，iL，vo），采用状态空间平均建模法可建立带CPL MD Buck变换器的非线性数学模型为：

C1dvC1dt=iL（d2－d1），…，Cp－1dvCp－1dt=iL（dp－dp－1）；

Cdvodt=iL－voR－Pvo；

LdiLdt=－vo+（Vin－vCp－1）dp+

∑p－1k=2（vCk－vCk－1）dk+d1vC1。（1）

由式（1）可知，FC电压和vo存在强耦合作用。为提升系统性能，有必要对系统进行解耦控制。

2" 逆系统解耦

对于式（1），系统共有p个输入变量和p+1个状态方程，即系统维数n=p+1。为确保系统良好的跟踪性能，分别取vCk和vo作为输出函数，即：

y1=vC1，…，yk=vCk，…，yp－1=vCp－1；

yo=vo。（2）

分别对yk和yo求一阶微分和二阶微分，得：

y·1=iLC1（d2－d1），…，y·p－1=iLCp－1（dp－dp－1）；

y··o=1CL［－yo+（Vin－yCp－1）dp+

∑p－1k=2（yCk－yCk－1）dk+yC1d1］－

iL－yoR－Pyo（PR－y2o）/（RC2y2o）。（3）

由式（3）可知，y·1和y··o均已显含d。定义Y=［y·1，…，y·p－1，y··o］T，则雅可比矩阵YT/dT可得

YTdT=－iLC1iLC10…0

0－iLC2iLC2000

0…0－iLCp－1iLCp－1

vC1CLvC2－vC1CL…vCp－vCp－1CLvCp－vCpCLp×p。（4）

由式（4）可知，行列式det（YT/dT）≠0。根据逆系统理论［17-18］可知，系统式（4）存在向量相对阶α=（α1，α2，…，αp-1，αo）T=（1，1，…，1，2）T，其和为α1+α2+…+αp-1+αo =p+1，系统式（1）可完全解耦。以φ=［φ1，…，φk，…，φp－1，φo］T=［y·1，…，y·k，…，y·p－1，y··o］T作为逆系统的输入，由式（3）可求得逆系统表达式为

d1d2dp－1dp=K+FiLVin×φ1φ2φp－1φo。（5）

式中K、F分别满足：

K=（CR2－L）y4o+LRiLy3o－LPR2iLyo+LP2R2R2CViny3o1111；

F=C1（y1－Vin）C2（y2－Vin）…Cp－1（yp－1－Vin）LCiL

C1y1C2（y2－Vin）…Cp－1（yp－1－Vin）LCiLC1y1C2y2…Cp－1（yp－1－Vin）LCiLC1y1C2y2…Cp－1yp－1LCiL。

将式（5）串接在系统式（1）之前，可构成p个伪线性子系统为：

y1/φ1=1/s，…，yk/φk=1/s，…，yp－1/φp－1=

1/s；（6）

yo/φo=1/s2。（7）

式中s为拉普拉斯算子。

由以上分析可知，带CPL MD Buck变换器经逆系统方法处理后，可得p个单输入单输出线性子系统，包含p-1个一阶线性子系统和1个二阶线性子系统。

3" 自适应滑模控制器设计

为减小系统的抖振，提高系统的鲁棒性，下面对以上线性子系统进行自适应滑模控制器的设计。

3.1" 一阶伪线性子系统的控制器设计

定义p-1个一阶线性子系统的误差为

e1=y1－VC1，…，ek=yk－VCk，…，ep－1=

yp－1－VCp－1。（8）

式中VCk为yk的参考值。对式（8）求一阶导得

e·1=φ1，…，e·k=φk，…，e·p－1=φp－1。（9）

根据滑模控制理论可知，采用指数趋近律能有效减弱滑模抖振［19］。因此，将线性滑模面及指数趋近律分别设计为：

s1=e1，…，sk=ek，…，sp－1=ep－1；（10）

s·1=－c1sgn（s1）－c11s1，…，s·k=

－cksgn（sk）－ckksk，…，s·p－1=

－cp－1sgn（sp－1）－cp－1，p－1sp－1。（11）

式中：ckgt;0为切换增益，决定了控制运动点收敛至滑模面的速率；ckkgt;0为常数。

结合式（9）～式（11），可求得p-1个FC电压的控制律分别为

φ1=－c1sgn（s1）－c11s1，…，φk=

－cksgn（sk）－ckksk，…，φp－1=－cp－1sgn（sp－1）－cp－1，p－1sp－1。（12）

3.2" 二阶伪线性子系统的控制器设计

定义二阶线性子系统的误差为

eo=yo－Voref。（13）

式中Voref为yo的参考值。对式（13）求二阶导，得

e··o=φo。（14）

定义二阶滑模面及滑模控制律分别为：

so=e·o+βeo；（15）

s·o=－cosgn（so）－cooso。（16）

式中：β为大于0的常数；cogt;0为切换增益；coogt;0为常数。结合式（13）～式（16），求得vo的控制律为

φo=－βe·o－cosgn（so）－cooso。（17）

下面对系统的稳定性和鲁棒性进行验证。

由于变换器在运行期间，常受到电路参数变化、外界扰动等不确定干扰的影响，假设系统式（9）和系统式（14）分别存在有界干扰Gk（t）和O（t），则式（9）和式（14）可修改为：

e·1=φ1+G1（t），…，e·k=φk+Gk（t），…，e·p－1=φp－1+Gp－1（t）；

e··o=φo+O（t）。（18）

式中|Gk（t）|gt;0和|O（t）|gt;0均有界， 即|Gk（t）|lt;Nk，|O（t）|lt;M，其中Nk和M分别为|Gk（t）|和|O（t）| 的上界。

取李雅普诺夫函数为

V1=0.5s21+…+0.5s2p－1+0.5s2o。（19）

结合式（11）、式（16）和式（18），对式（19）求一阶导得

V·1=s1s·1+…+sp－1s·p－1+sos·o=

s1［－c1sgn（s1）－c11s1+G1（t）］+…+

sp－1［－cp－1sgn（sp－1）－cp－1，p－1sp－1+Gp－1（t）］+

so［－cosgn（so）－cooso+O（t）］lt;|s1|×

G1（t）－c1|s1|－c11s21+…+|sp－1|×

Gp－1（t）cp－1|sp－1|－cp－1，p－1s2p－1+|so|×

O（t）－co|so|－coos2olt;－（c1－N1）|s1|－

c11s21－…－（cp－1－Np－1）|sp－1|－cp－1，p－1s2p－1－（co－M）|so|－coos2o。（20）

为保证V·1lt;0，则需满足：

N1lt;c1，…，Nklt;ck，…，Np－1lt;cp－1；

Mlt;co。（21）

由式（21）可知，切换增益ck和co的选择分别取决于|Gk（t）| 和|O（t）| 的上界值Nk和M。若ck和co选择过大以确保系统的稳定性，可能会导致运动点趋近滑模面时速率过大，进而引起严重的抖振现象。因此，本文引入自适应律［20-21］来更新ck和co。假设c^k和c^o分别表示Nk和M的估计值，则自适应律可设计为：

c^·1=ρ1|s1|，…，c^·k=ρk|sk|，…，c^·p－1=

ρp－1|sp－1|；

c^·o=γ|so|。（22）

式中：ρkgt;0；γgt;0。

为了验证系统式（6）和式（7），使用式（12）和式（16）中的控制律以及式（22）中的自适应律，闭环系统是渐近稳定的。

取李雅普诺夫函数为

V2=V1+12ρ1（c^1－N1）2+…+

12ρk（c^k－Nk）2+…+12ρp－1（c^p－1－Np－1）2+

12γ（c^o－M）2。（23）

将式（19）和式（22）代入式（23），并对式（23）求一阶导，得

V·2=s1［－c^1sgn（s1）－c11s1+G1（t）］+…+

sp－1［－c^p－1sgn（sp－1）－cp－1，p－1sp－1+Gp－1（t）］+

so［－c^osgn（so）－cooso+O（t）］+

1ρ1（c^1－N1）c^·1+…+1ρp－1（c^p－1－Np－1）c^·p－1+

1γ（c^o－M）c^·o=G1（t）s1－N1|s1|－

c11s21+…+Gp－1（t）sp－1－Np－1|sp－1|－

cp－1，p－1s2p－1+O（t）so－M|so|－coos2olt;

－［N1－G1（t）］|s1|－c11s21－…－

［Np－1－Gp－1（t）］|sp－1|－cp－1，p－1s2p－1－

［M－O（t）］|so|－coos2olt;0。（24）

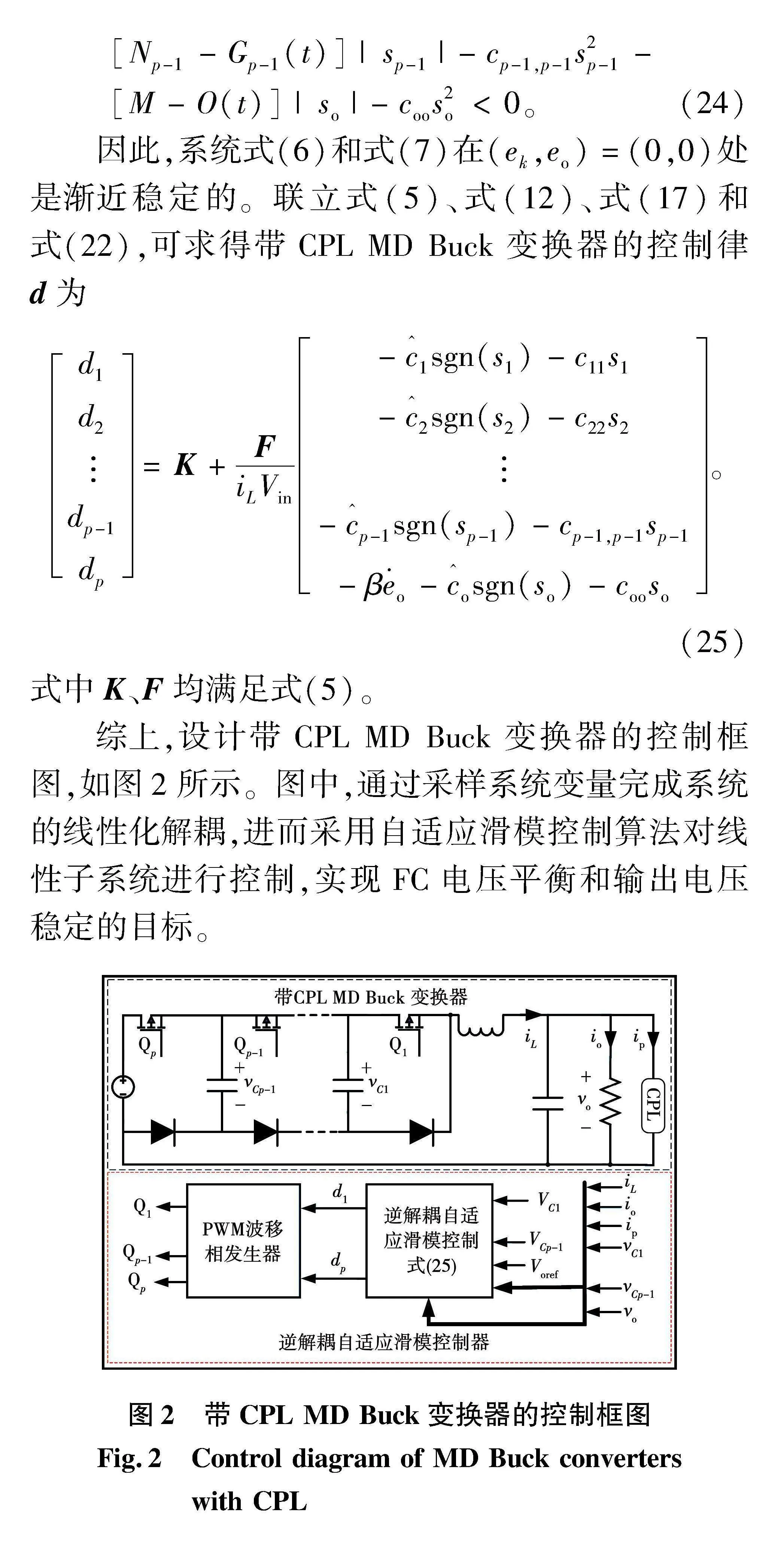
因此，系统式（6）和式（7）在（ek，eo）=（0，0）处是渐近稳定的。联立式（5）、式（12）、式（17）和式（22），可求得带CPL MD Buck变换器的控制律d为

d1d2dp－1dp=K+FiLVin－c^1sgn（s1）－c11s1－c^2sgn（s2）－c22s2－c^p－1sgn（sp－1）－cp－1，p－1sp－1－βe·o－c^osgn（so）－cooso。（25）

式中K、F均满足式（5）。

综上，设计带CPL MD Buck变换器的控制框图，如图2所示。图中，通过采样系统变量完成系统的线性化解耦，进而采用自适应滑模控制算法对线性子系统进行控制，实现FC电压平衡和输出电压稳定的目标。

4" 仿真结果

为了验证所提控制策略的有效性和优越性，在MATLAB/Simulink平台上搭建了带CPL七电平Buck变换器仿真模型进行研究，其中p=6，并采用一个闭环控制Buck变换器来等效CPL。所提逆解耦自适应滑模控制（inverse decoupling adaptive sliding mode control，ID-ASMC）与文献［8］提出的线性解耦比例积分控制（linear decoupling proportional integral control，LD-PIC）进行对比。系统参数取为：Vin=60 V，Voref=30 V，C1=C2=C3=C4=C5=200 μF，L=1 mH，C=330 μF，R=27.5 Ω，fs=50 kHz，P=25 W。为保证系统的稳定性和鲁棒性，所提控制策略的参数选取为：c11=c22=c33=c44=c55=1×105，ρ1=ρ2=ρ3=ρ4=ρ5=200，β=900，γ=800，coo=1×105。

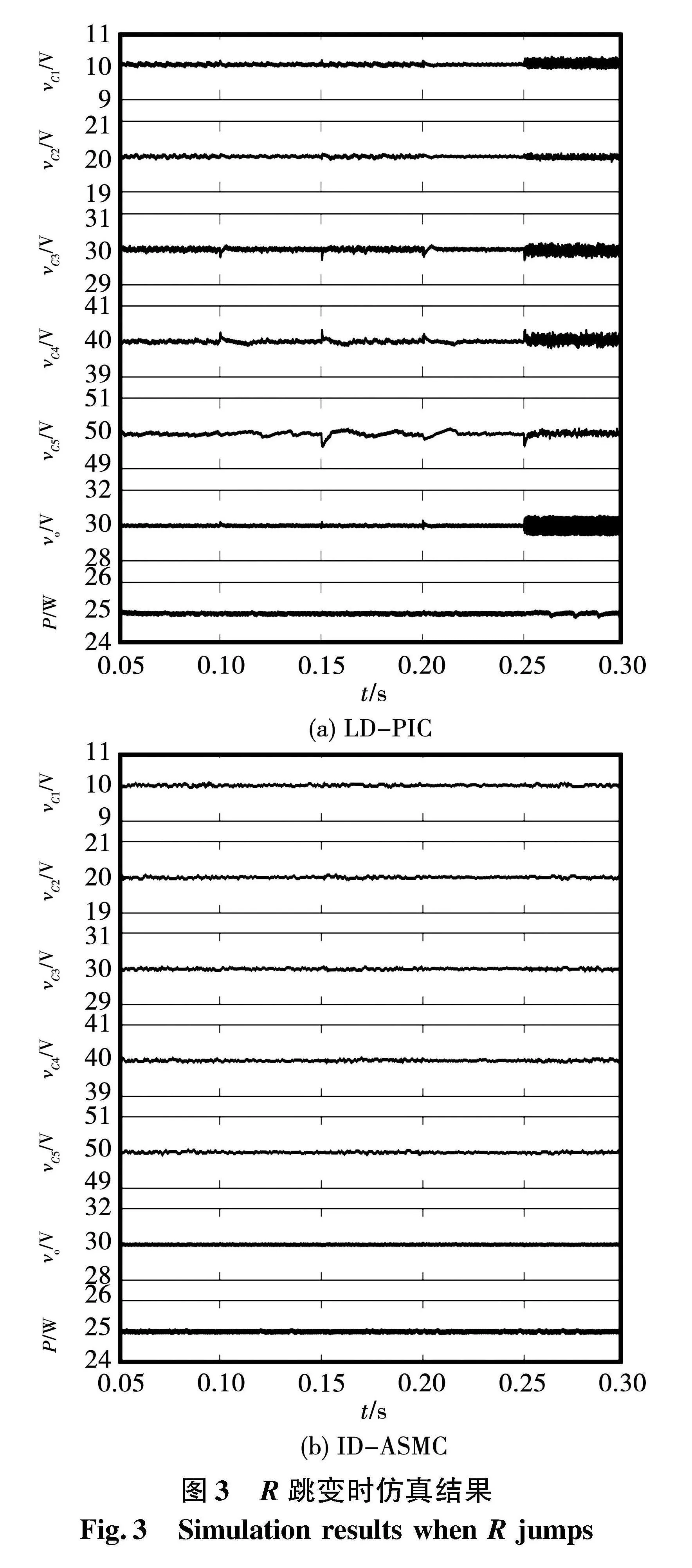
图3给出了R分别在0.1 s（27.5 Ω→70 Ω）、0.15 s（70 Ω→27.5 Ω）、0.2 s（27.5 Ω→10 000 Ω）和0.25 s（10 000 Ω→27.5 Ω）跳变时2种控制方法的仿真结果。可以看出，在2种控制策略下，vC1、vC2、vC3、vC4、vC5分别平衡于10、20、30、40、50 V，即Vin/6、2Vin/6、3Vin/6、4Vin/6、5Vin/6，vo稳定于30 V，并能给CPL提供25 W的功率，保证系统的稳定。当R跳变时，LD-PIC下的FC电压和vo均有一定的波动。如：当R由10 000 Ω下降至27.5 Ω时，在LD-PIC下，vo的电压波动最大值达0.78 V，vC5的电压波动量为0.3 V，其他FC电压有振荡过程。而在ID-ASMC下，阻性负载扰动对vo和FC电压的影响甚微，系统表现出良好的抗干扰性能。

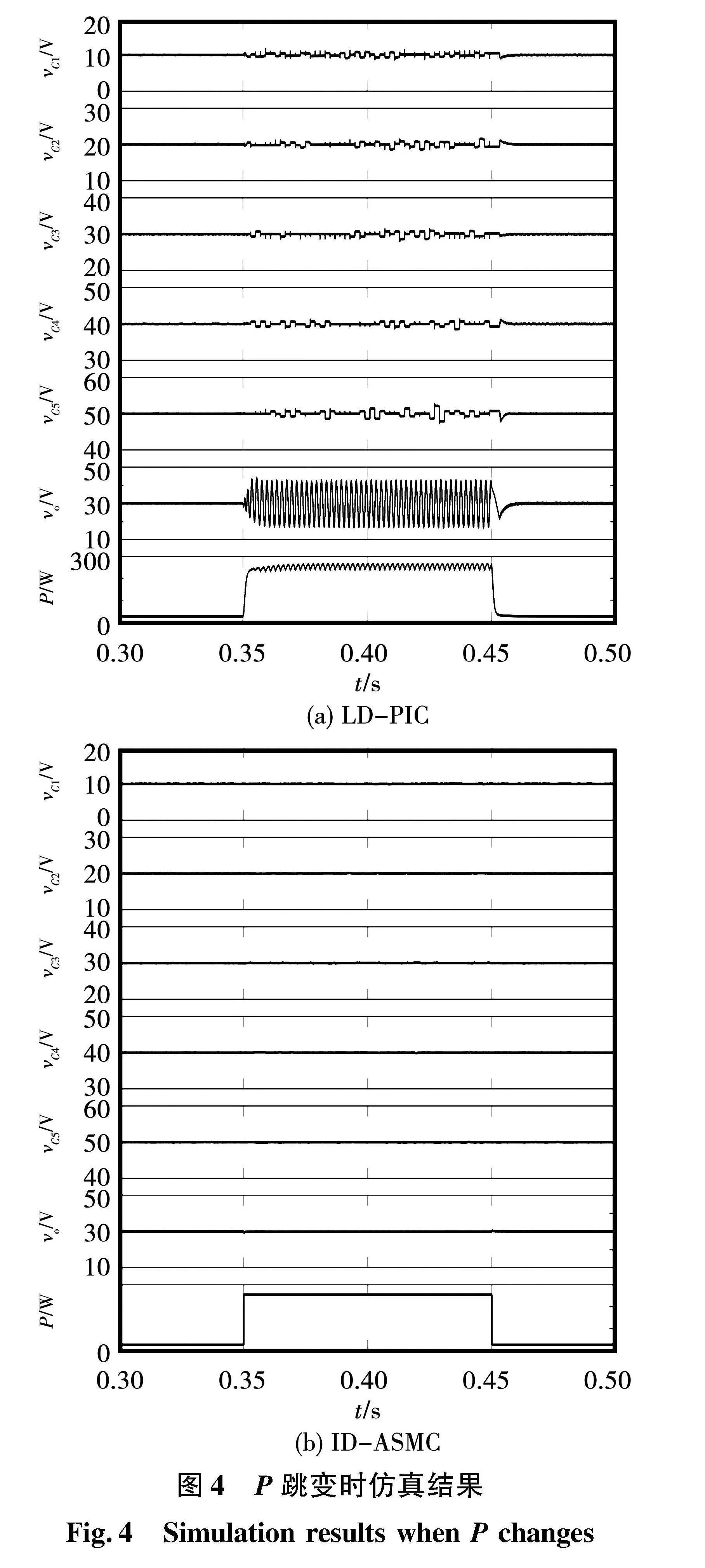
图4给出了P分别在0.35 s（25 W→256 W）和0.45 s（256 W→25 W）变化时2种控制方法的仿真结果。在LD-PIC下，vo出现严重的振荡，难以稳定于30 V，其电压峰峰值为26.8 V。此外，vC1、vC2、vC3、vC4、vC5均存在不同程度的振荡过程，在各自的平衡值附近波动。而在ID-ASMC下，FC电压和vo均无电压波动和振荡过程，稳定于各自参考值，受P变化的影响极小，表现出更强的鲁棒性，有效抑制了负阻抗特性对系统的影响。

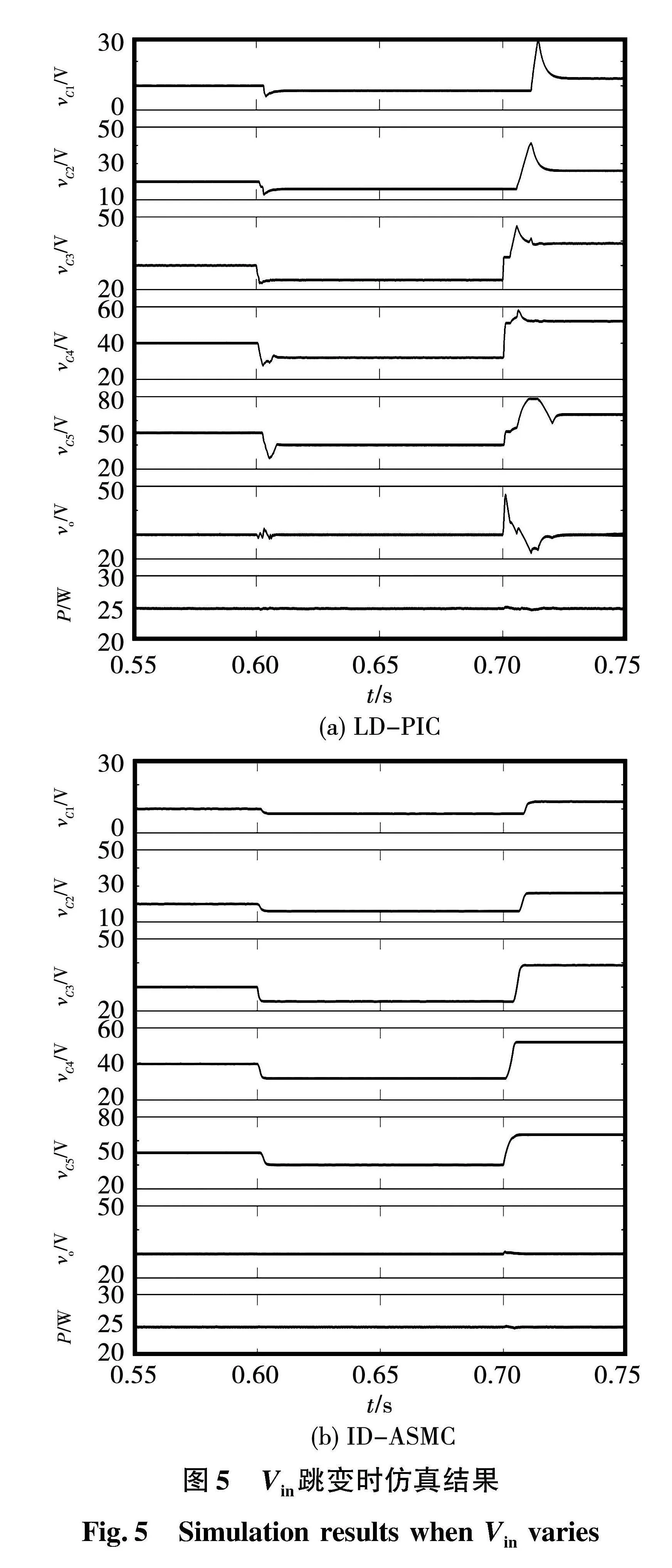
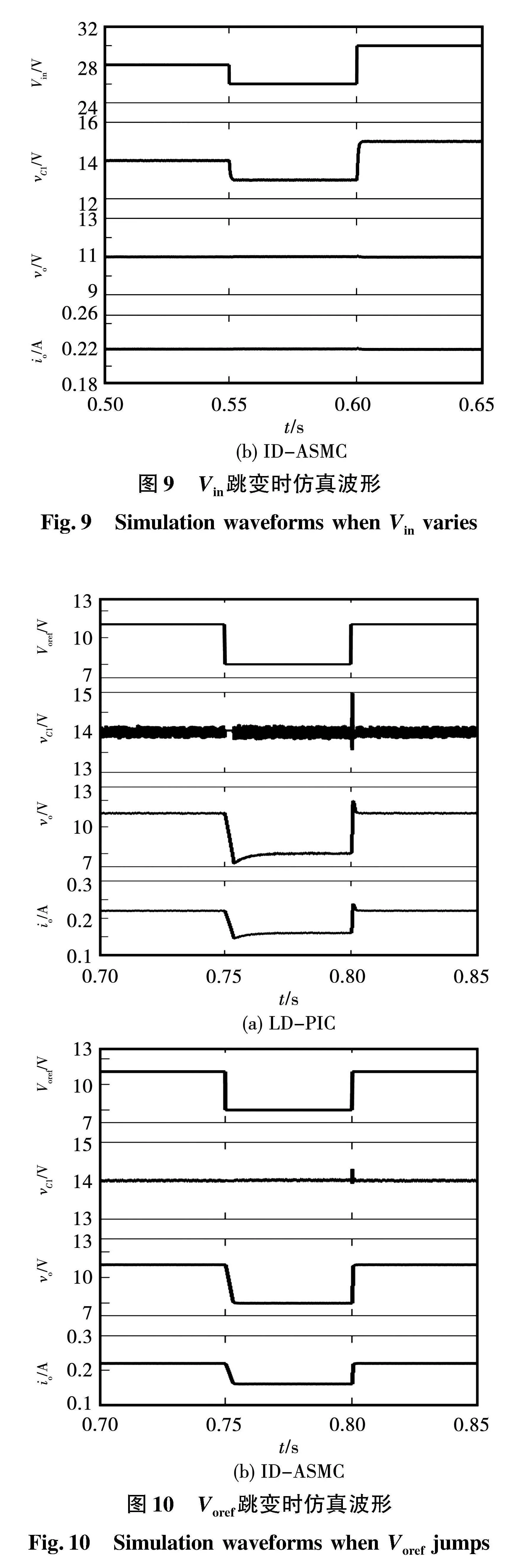
图5给出了Vin分别在0.6 s（60 V→48 V）和0.7 s（48 V→78 V）变化时2种控制方法的仿真结果。由于vCk平衡于kVin / p，所以Vin变化的同时，FC参考电压也随之发生改变。在LD-PIC下，vo波动严重，vCk（k=1，2，3，4，5）均能平衡于kVin / 6，但vCk均存在严重的电压波动。如：当Vin由48 V跳变至78 V时，在LD-PIC下，vCk的电压波动量分别为17、14、8、6、14 V，vo的电压波动量为18.5 V。在ID-ASMC下，vo存在1.2 V的电压波动，而vCk能无超调地稳定于各自参考值，受Vin的影响极小，验证了所提ID-ASMC实现了FC电压和输出电压的解耦。

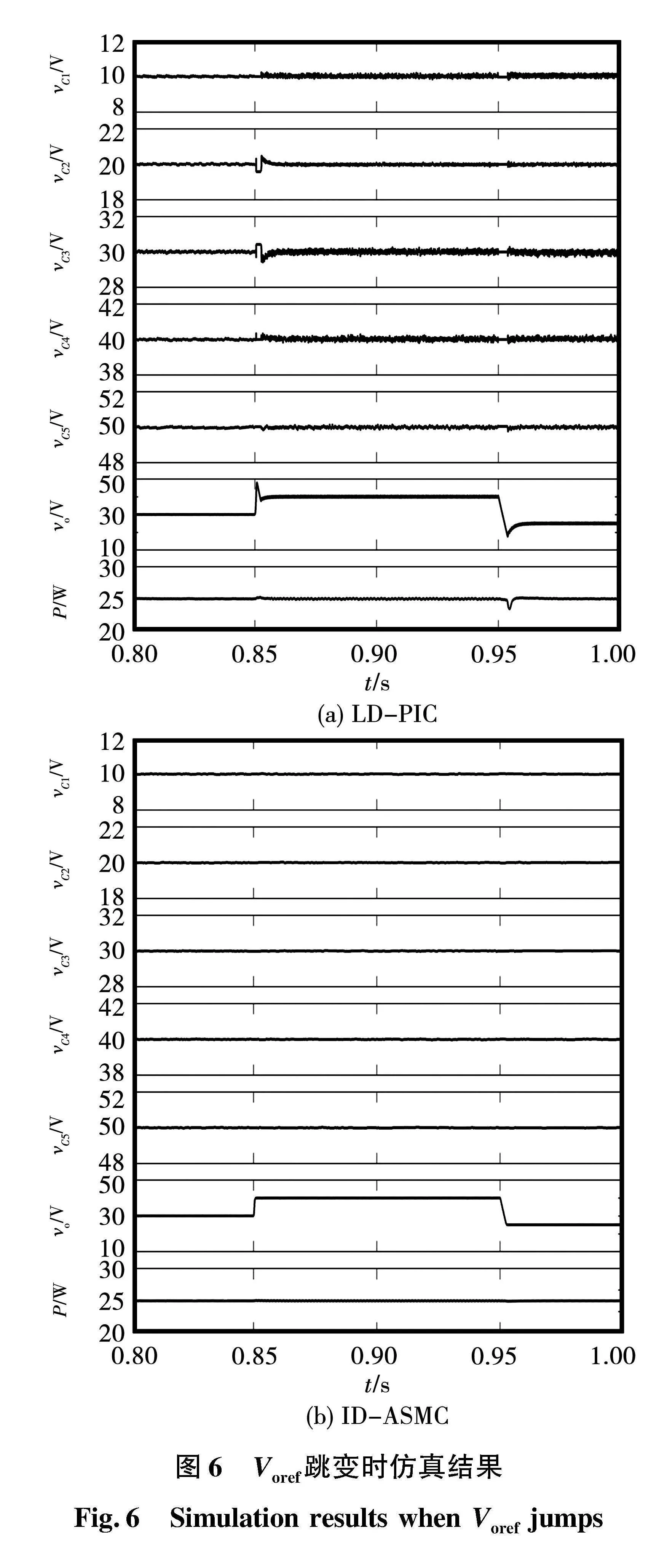
图6给出了Voref分别在0.85s （30 V→40 V）和0.95 s （40 V→25 V）变化时2种控制方法的仿真结果。当Voref由40 V突降至25 V时，在LD-PIC下，vo存在7 V的电压下冲，vCk（k=1，2，3，4，5）均受到Voref突变的影响。在ID-ASMC下，Voref变化对FC电压几乎毫无影响，同时vo能快速平滑跟踪Voref的变化，给CPL提供恒定的25 W功率，进一步验证了所提ID-ASMC能有效实现FC电压和输出电压的解耦。

为了进一步说明所提控制策略在低电平变换器应用的有效性，基于MATLAB平台对带CPL三电平Buck变换器进行仿真研究，并与LD-PIC作比较。变换器参数设计为：Vin=28 V，Voref=11 V，R=50 Ω，C=940 μF，C1=220 μF，L=330 μH，fs=50 kHz，P=7 W。控制参数取为：ρ1=900，c11=1×106，β=6×103，γ= 1×103，coo=1×107。

图7给出了R分别于0.15 s（50 Ω→100 Ω）和0.2 s（100 Ω→50 Ω）跳变时仿真波形。由图7可知，在2种控制策略下，vo均稳定于11 V，vC1均平衡于14 V，即Vin/2。当R由100 Ω变化至50 Ω时，在LD-PIC下，vC1存在0.1 V的电压波动，vo的电压波动量为0.2 V；而在ID-ASMC下，vC1和vo几乎不受R变化的影响，具有更好的抗扰动性能。

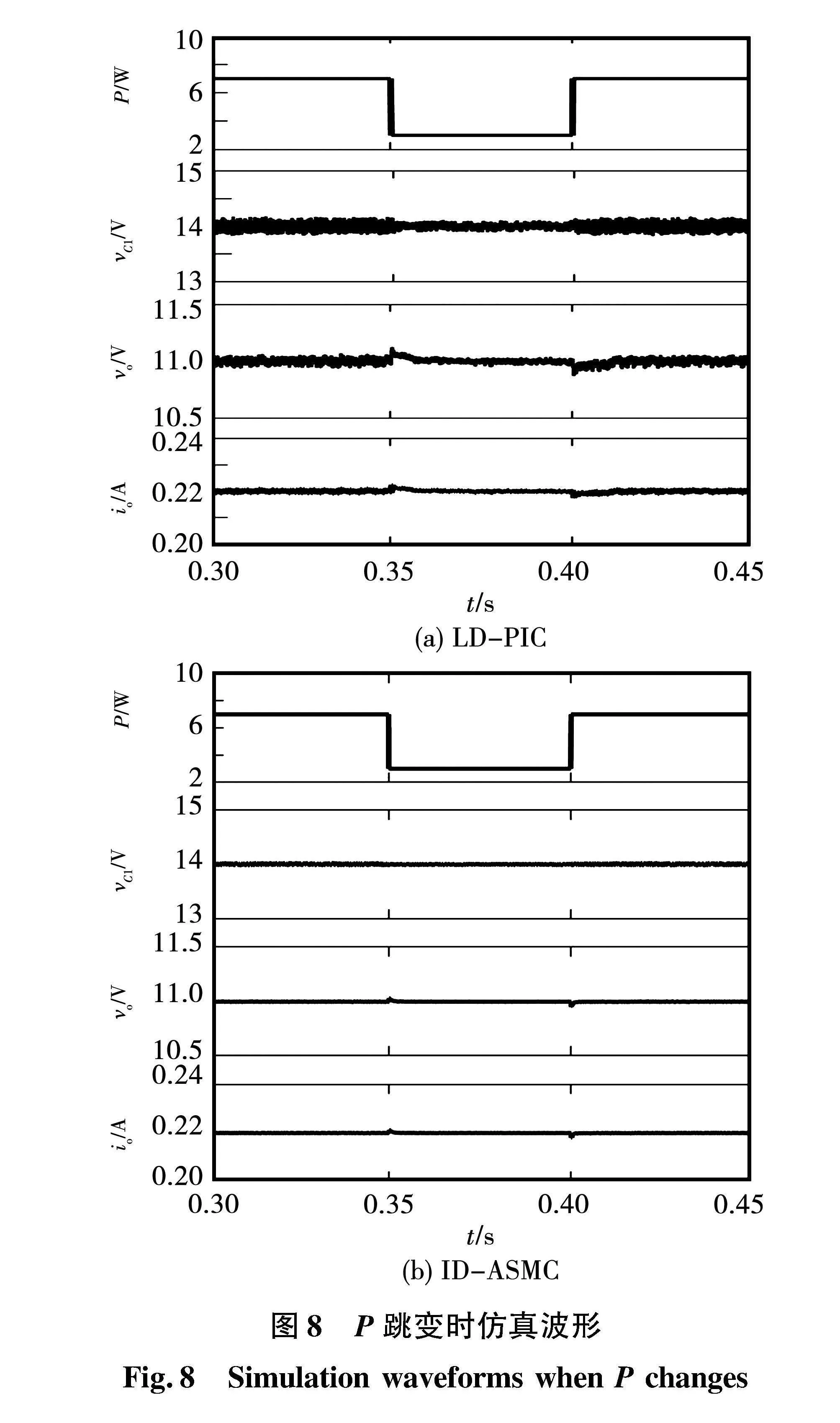
图8给出了P分别于0.35 s（7 W→3 W）和0.4 s（3 W→7 W）改变时的仿真波形。当P由7 W突降至3 W时，在LD-PIC下，vC1电压波动明显，vo电压波动量为0.2 V，而在ID-ASMC下，vC1和vo电压波动不明显，抑制CPL负阻抗特性的效果更佳，具有更强的鲁棒性能。

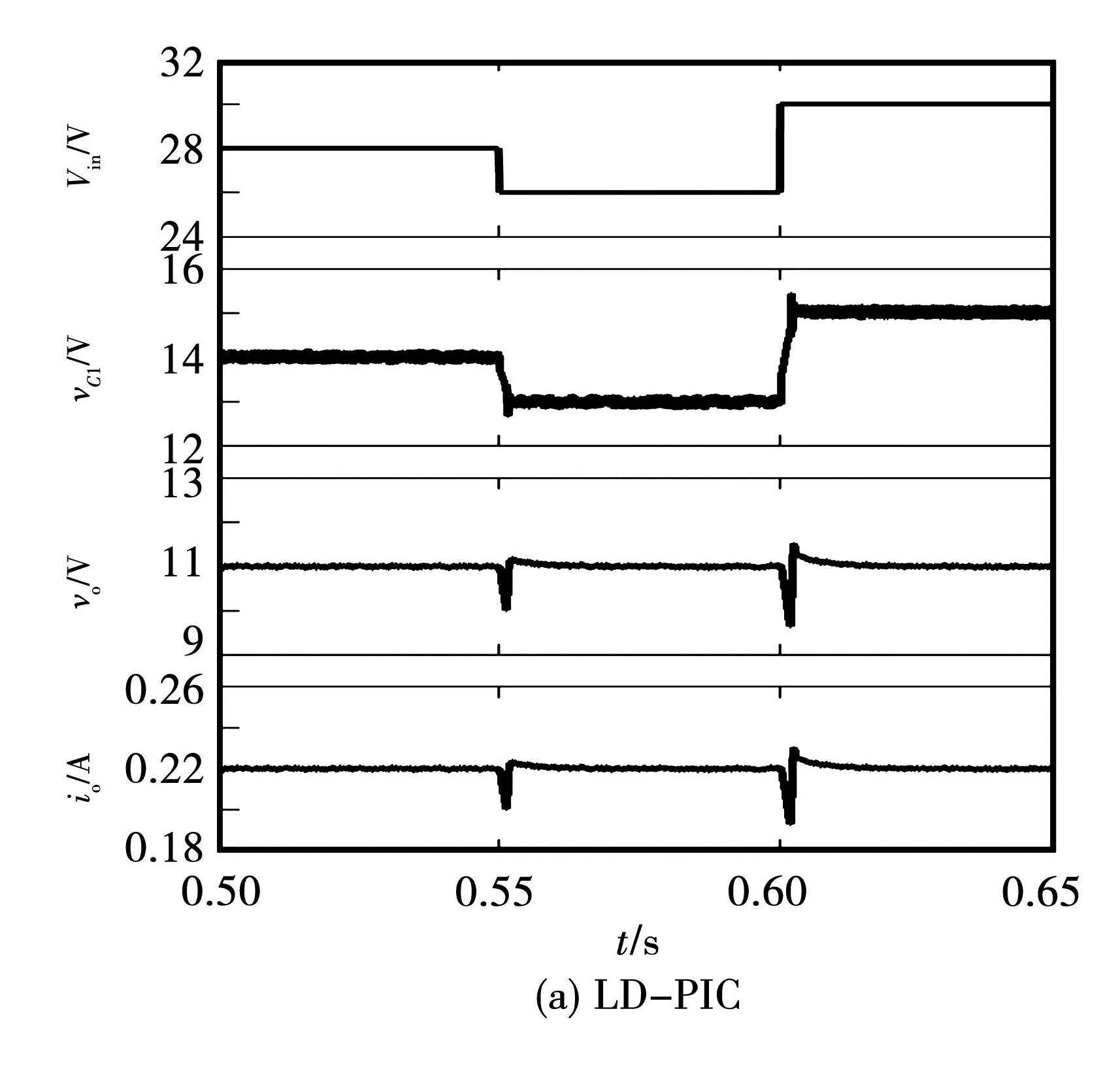
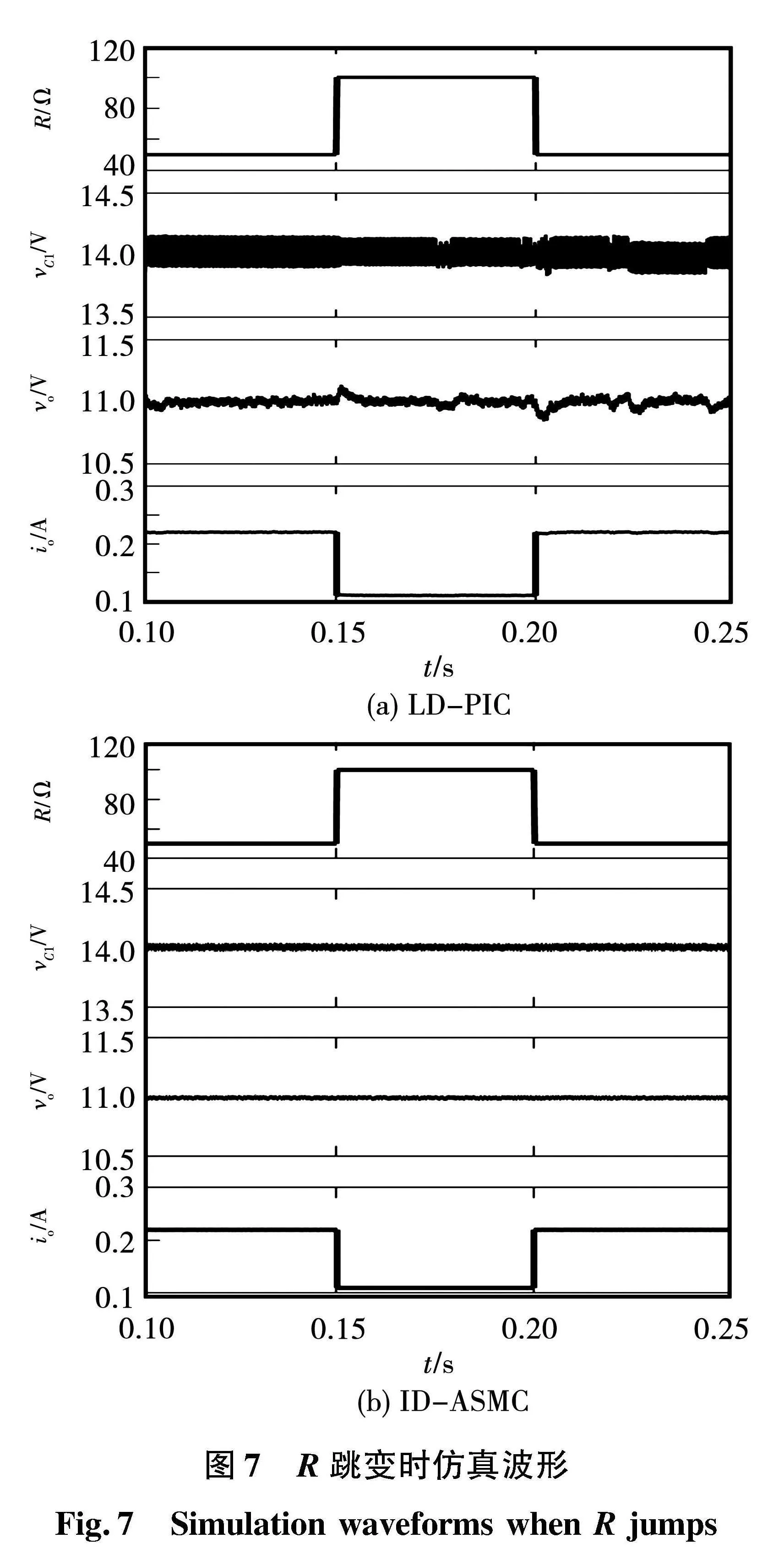
图9给出了Vin分别于0.55 s（28 V→26 V）和0.6 s（26 V→30 V）跳变时的仿真波形。当Vin由26 V突升至30 V时，在LD-PIC下，vC1由13 V上升至15 V，均平衡于Vin/2，但存在0.4 V的电压超调，vo出现1.8V的电压波动；在ID-ASMC下，vC1能无超调地由13 V过渡至15 V，vo无明显电压变化，具有更好的解耦效果。

图10给出了Voref分别于0.75 s （11 V→8 V）和0.8 s（8 V→11 V）变化时的仿真波形。当Voref由8 V突升至11 V时，在LD-PIC下，vC1和vo均存在电压过冲，其值分别为1 V和1.3 V，而在ID-ASMC下，vC1仅存在0.2 V的电压波动，vo能平滑地由8 V跃变至11 V，表现出更好的解耦性能。

5" 实验结果

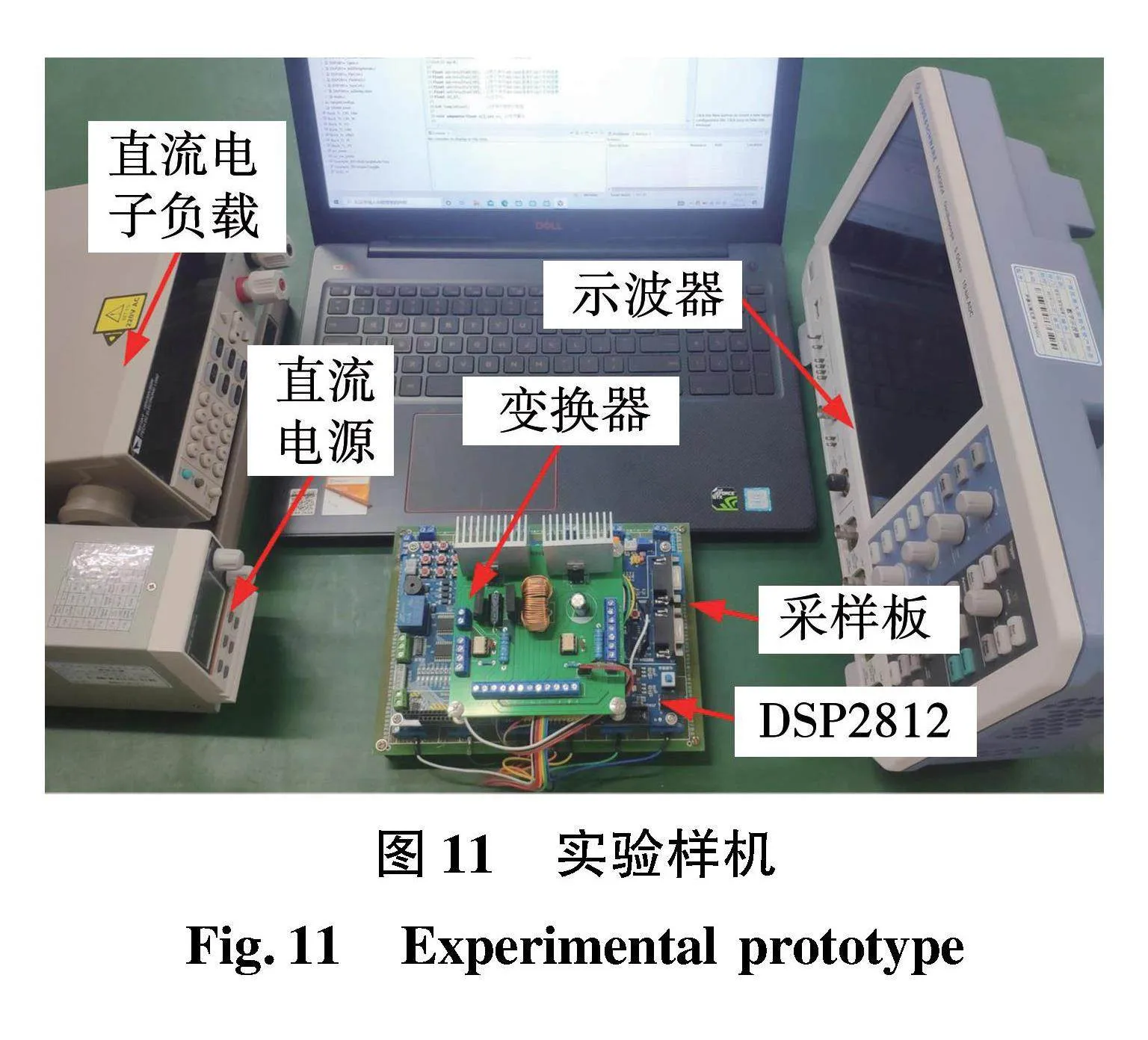
为了验证所提控制策略的正确性，搭建了一台与仿真参数一致的带CPL三电平Buck变换器原理样机，如图11所示。该样机由一个直流电子负载来设定CPL，采用TMS320F2812数字信号处理器（DSP2812）作为主控板，选用IRF840和TLP250分别用作开关管和驱动电路。系统采用CHB-25NP传感器和CHV-25P传感器分别对电流、电压进行采样，并通过DSP2812的12位模/数转换器进行数据转换。同时，所提控制策略的实验结果与LD-PIC方法进行比较。

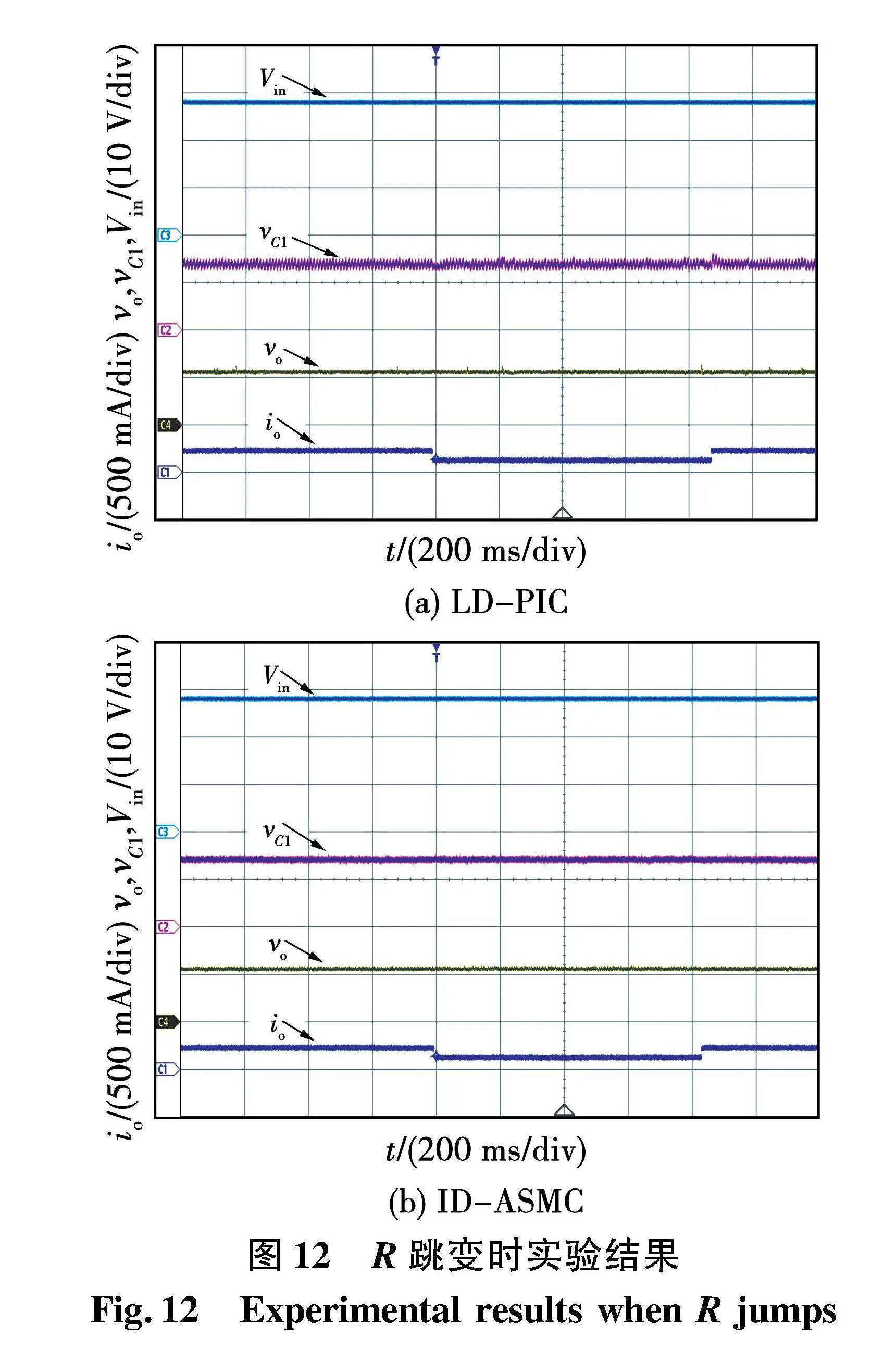
图12给出了与图7跳变过程一致的R跳变实验结果。由图12可知，vo稳定于11 V，vC1平衡于14 V，即Vin/2。当R由100 Ω跳变至50 Ω时，在LD-PIC下，vC1和vo均存在电压波动，其波动量分别为2.3 V和2.1 V，而在ID-ASMC下，vC1和vo几乎不受R变化的影响，表现出更强的抑制阻性负载扰动能力。

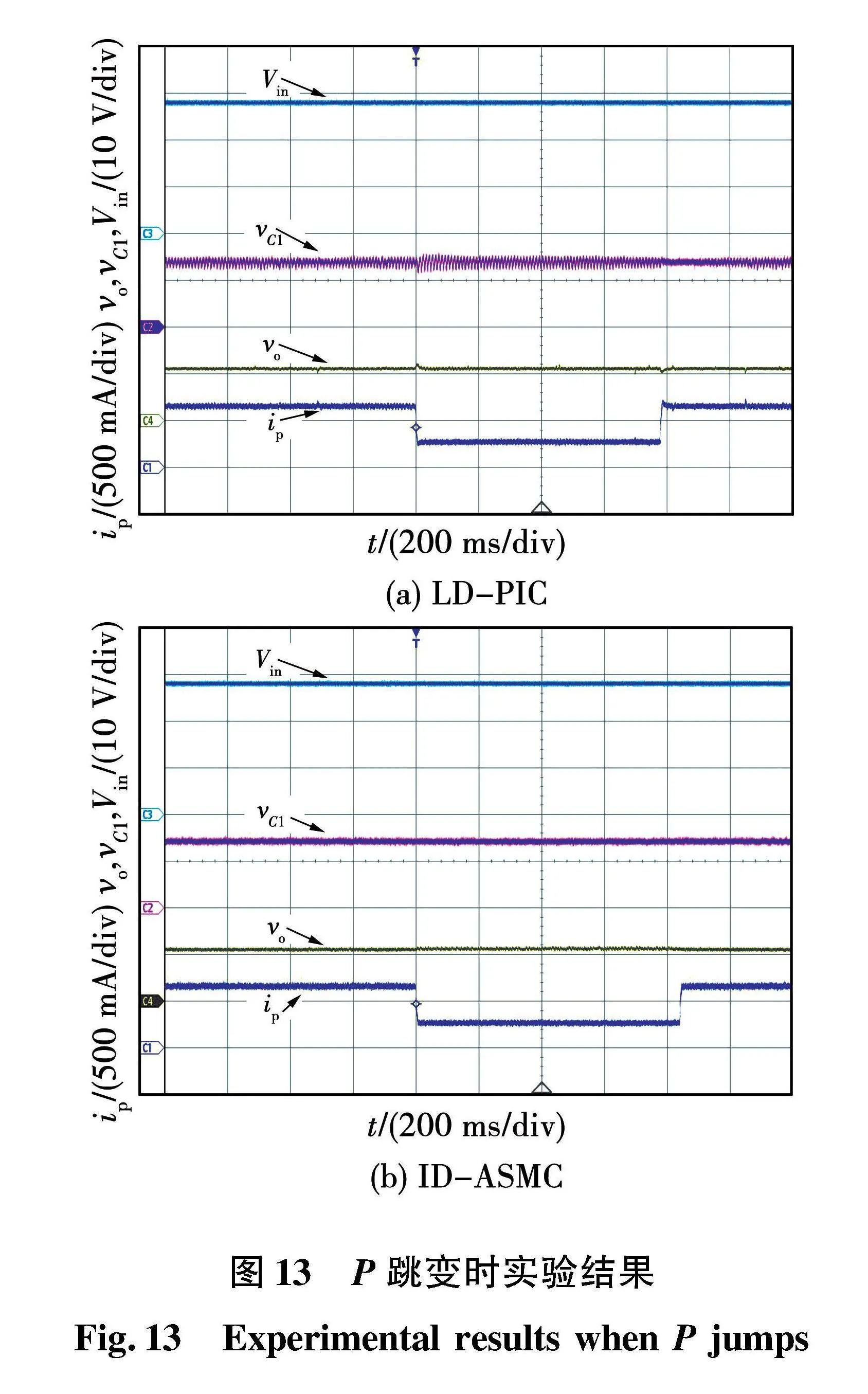
图13给出了与图8跳变过程一致的P改变时实验结果。当P由7 W突降至3 W时，在ID-PIC下，vC1经过严重振荡后平衡于14 V，其电压峰峰值为3 V，vo存在1.5 V的电压波动；而在ID-ASMC下，vC1和vo受P变化影响极小，能有效抑制CPL负阻抗特性对系统的影响，表现出更强的鲁棒性能。

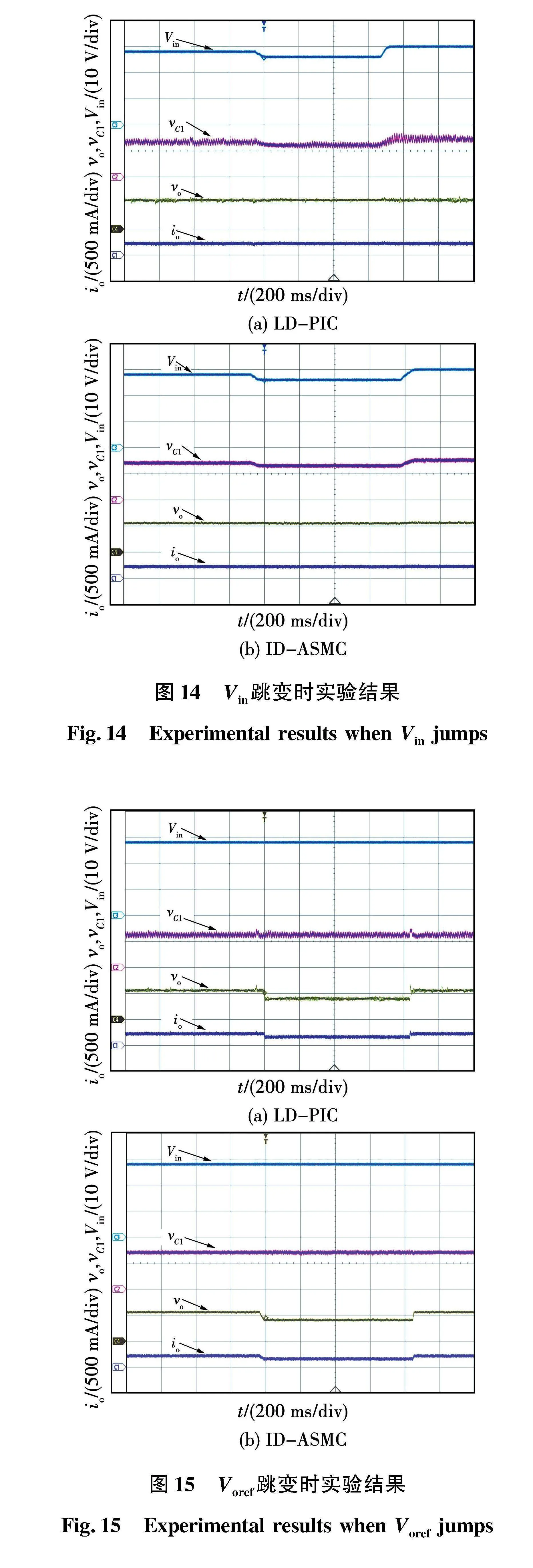
图14给出了与图9跳变过程一致的Vin变化时实验结果。由图可知，vC1平衡于Vin / 2，vo稳定于11 V。当Vin由26 V变化至30 V时，在ID-PIC下，vC1存在3.3 V的电压超调，经振荡衰减后稳定于15 V，vo存在一定的波动，但ID-ASMC较ID-PIC具有更好的控制效果，vC1能无超调变化至15 V，vo受Vin变化的影响甚微，实现了vC1和vo的解耦。

图15给出了与图10跳变过程一致的Voref跳变时实验结果。当Voref由8 V变化至11 V时，在ID-PIC下，vC1和vo分别存在1.8 V和2.9 V的电压波动，之后分别稳定于14 V和11 V，而ID-ASMC比ID-PIC具有更好的动态调节性能，vC1和vo几乎不受Voref变化的影响，进一步验证了vo和vC1的解耦。

然而，通过对相应的实验波形及仿真波形进行分析比较发现，当扰动发生时，实验结果与仿真结果存在一定的误差，如电压波动量不一致等。这是因为电路元器件寄生参数对实际控制系统的动态性能有影响［22］，上述问题可能是由于实验电路不可避免的元器件寄生参数所引起。

6" 结" 论

本文提出了一种逆解耦自适应滑模控制策略，解决了带CPL多电平Buck变换器的飞跨电容电压的平衡问题及飞跨电容电压与输出电压的解耦难题，抵消了CPL负阻抗特性对系统的影响，有效提高了变换器的稳定性能。经过与LD-PIC方法分别带CPL七电平Buck变换器、带CPL三电平Buck变换器的仿真比较，结果表明了本文所提ID-ASMC策略具有更优越的动静态调节性能和更好的解耦效果。最后，与LD-PIC方法带CPL三电平Buck变换器进行实验对比，结果表明本文所提ID-ASMC方法具有更好的控制性能和更强的鲁棒性。然而，由于实验条件的限制，难以及时对带CPL七电平Buck变换器进行实验验证，该验证工作及寄生参数对变换器的性能影响将是下一步的研究内容。同时，本文所提控制策略可推广至其他带CPL多电平DC-DC变换器控制应用中。

参 考 文 献：

［1］" APPARAO D， WU Bin， RICARDO L F， et al. Evolution of topologies， modeling， control schemes， and applications of modular multilevel converters［J］.IEEE Journal of Emerging and Selected Topics in Power Electronics，2017，5（4）：1631.

［2］" LING Rui， SHU Zhihui， HU Qing， et al. Second-order sliding-mode controlled three-level Buck DC-DC converters［J］. IEEE Transactions on Industrial Electronics， 2018， 65（1）： 898.

［3］" WU Jiarong， LU Yimin. Decoupling and optimal control of multilevel Buck DC-DC converters with inverse system theory［J］. IEEE Transactions on Industrial Electronics，2020，67（9）：7861.

［4］" DARGAHI V， SADIGH A K， CORZINE K. New flying-capacitor-based multilevel converter with optimized number of switches and capacitors controlled with a new logic-form-equation based active voltage balancing technique［C］//2016 IEEE Applied Power Electronics Conference and Exposition， March 20-24， 2016， Long Beach， CA， USA. 2016： 1481-1488.

［5］" 冯颖盈， 阮新波．多电平Buck变换器的解耦控制与闭环设计［J］. 中国电机工程学报， 2007， 27（10）： 106.

FENG Yingying， RUAN Xinbo．Decoupling control and closed-loop design of Buck multi-level converter［J］. Proceedings of the CSEE， 2007， 27（10）： 106.

［6］" STALA R. The switch-mode flying-capacitor DC-DC converters with improved natural balancing［J］. IEEE Transactions on Industrial Electronics， 2010， 57（4）： 1369．

［7］" DELMAS L， GATEAU G， MEYNARD T A， et al. Stacked multicell converter： control and natural balancing［C］//2002 IEEE 33rd Annual Power Electronics Specialists Conference， June 23-27， 2002， Cairns， QLD， Australia. 2002： 689-694.

［8］" 张元媛， 阮新波．多电平直流变换器中飞跨电容电压的一种控制策略［J］. 中国电机工程学报， 2004， 24（8）： 38.

ZHANG Yuanyuan， RUAN Xinbo．A novel control strategy for the flying capacitor voltage of the multilevel converter［J］. Proceedings of the CSEE， 2004， 24（8）： 38.

［9］" SUN R Y， WU X H， LI W L， et al．Equivalent sliding mode control for multi-level buck converter［C］//2016 IEEE International Conference on Aircraft Utility Systems， October 10-12， 2016， Beijing， China. 2016： 460-465.

［10］" CAI Pei， WU Xiaohua， SUN Runyu. Exact feedback linearization of general four-level buck DC-DC converters［C］//2017 29th Chinese Control and Decision Conference， May 28-30， 2017， Chongqing， China. 2017： 4638-4643.

［11］" 邵冰冰， 赵书强， 高本锋， 等. 基于反馈线性化滑模控制的直驱风电场经柔直并网系统次同步振荡抑制策略［J］. 中国电机工程学报， 2021， 41（9）： 3093.

SHAO Bingbing， ZHAO Shuqiang， GAO Benfeng， et al．Sub-synchronous oscillation mitigation strategy of direct-drive wind farms via VSC-HVDC system based on feedback linearization sliding mode control［J］. Proceedings of the CSEE， 2021， 41（9）： 3093.

［12］" 刘宇博， 王旭东. 电动汽车车载电源LLC谐振变换器滑模控制［J］. 电机与控制学报， 2020， 24（3）： 133.

LIU Yubo， WANG Xudong. Sliding mode control of LLC resonant converter for electric vehicle power supply［J］. Electric Machines and Control， 2020， 24（3）： 133.

［13］" WU Jiarong， LU Yimin. Adaptive backstepping sliding mode control for Boost converter with constant power load［J］. IEEE Access， 2019，7： 50797.

［14］" 游逍遥， 刘和平， 苗轶如， 等. 带恒功率负载的双极性直流系统稳定性分析及其有源阻尼方法［J］. 电工技术学报， 2022， 37（4）： 925.

YOU Xiaoyao， LIU Heping， MIAO Yiru， et al. Stability analysis and active damping method of the bipolar DC system with constant power loads［J］. Transactions of China Electrotechnical Society， 2022， 37（4）： 925.

［15］" HASSAN M A， SU C L， CHEN F Z， et al．Adaptive passivity-based control of a DC-DC Boost power converter supplying constant power and constant voltage loads［J］. IEEE Transactions on Industrial Electronics， 2022， 69（6）： 6204.

［16］" MARTNEZ-TREVIO B A， AROUDI A E， VALDERRAMA BLAVI H， et al. PWM nonlinear control with load power estimation for output voltage regulation of a Boost converter with constant power load［J］. IEEE Transactions on Power Electronics， 2021， 36（2）： 2143.

［17］" 陈晓芩，周东华，陈茂银.基于逆系统方法的DGMSCMG框架伺服系统解耦控制研究［J］.自动化学报，2013，39（5）：505.

CHEN Xiaocen， ZHOU Donghua， CHEN Maoyin. Decoupling control of gimbal servo system of DGMSCMG based on dynamic inverse system method［J］. Acta Automatica Sininca， 2013， 39（5）： 505.

［18］" 朱熀秋， 顾志伟. 基于模糊神经网络逆系统的五自由度无轴承永磁同步电机自抗扰控制［J］. 电机与控制学报， 2021， 25（2）： 74.

ZHU Huangqiu， GU Zhiwei. Active disturbance rejection control for 5-degree-of-freedom bearingless permanent magnet synchronous motor based on inverse system using the fuzzy neural network［J］. Electric Machines and Control， 2021， 25（2）： 74.

［19］" SINGH S， KUMAR V， FULWANI D. Mitigation of destabilising effect of CPLs in island DC micro-grid using non-linear control［J］. IET Power Electronics， 2017， 10（3）： 387.

［20］" BARABONES O， ALKORTA P， GARRIDO A J. An adaptive sliding mode control scheme for induction motor drives［J］. International Journal of Circuits， Systems and Signal Processing， 2007， 1（1）： 73.

［21］" 赵希梅， 王晨光.永磁直线同步电机的自适应增量滑模控制［J］. 电工技术学报， 2017， 32（11） ： 114.

ZHAO Ximei， WANG Chenguang. Adaptive incremental sliding mode control for permanent magnet linear synchronous motor［J］．Transactions of China Electrotechnical Society，2017，32（11）：114.

［22］" REATTI A， CORTI F， TESI A， et al. Effect of parasitic components on dynamic performance of power stages of DC-DC PWM Buck and Boost converters in CCM ［C］//2019 IEEE International Symposium on Circuits and Systems， May 26-29， 2019， Sapporo， Japan. 2019： 1-5.

（编辑：邱赫男）