考虑逆变器谐波耦合的牵引传动系统机电耦合振动特性研究

摘" 要：

作为牵引传动系统能量转换的关键部件，牵引电机在电气激励作用下会受到各种冲击载荷和周期激振力的作用，从而产生机电耦合振动，威胁牵引传动系统的可靠运行。对此，基于双惯量模型对牵引传动系统机电耦合振动特性开展研究。首先，建立牵引电机的双惯量模型，依据此模型对其固有频率进行计算，并介绍了机械传动系统的同频受迫振动模态。其次，根据逆变器的开关特性，着重分析了脉宽调制（PWM）导致的边带谐波转矩对机电耦合同频共振的影响，探索逆变器的频率耦合产生的间谐波对机电耦合系统的影响。接着，以传递函数的形式对考虑双惯量负载的牵引传动系统进行建模，从频域角度对系统机电耦合共振特性进行理论分析。最后，利用硬件在环测试对所分析结果进行验证。

关键词：牵引传动系统；机电耦合；同频共振；双惯量系统；边带谐波；感应电机

DOI：10.15938/j.emc.2024.06.011

中图分类号：TM343

文献标志码：A

文章编号：1007-449X（2024）06-0109-11

收稿日期： 2023-08-03

基金项目：国家自然科学基金（52177060）

作者简介：葛兴来（1979—），男，博士，教授，博士生导师，研究方向为电力电子与电力传动；

常" 玉（1999—），男，硕士研究生，研究方向为电力电子技术和电机驱动控制；

王帅帅（1995—），男，硕士，研究方向为交流电机驱动；

沐俊文（1995—），男，博士研究生，研究方向为机电耦合共振；

左" 运（1996—），男，博士研究生，研究方向为电力电子技术和电机驱动控制；

王惠民（1994—），男，博士，助理教授，研究方向为高性能交流电机驱动控制和牵引传动系统可靠性分析。

通信作者：葛兴来

Research on electromechanical coupling vibration characteristics of inverter-motor drive system

GE Xinglai1，" CHANG Yu1，" WANG Shuaishuai1，2，" MU Junwen1，" ZUO Yun1，" WANG Huimin1

（1. Key Laboratory of Magnetic Suspension Technology and Maglev Vehicle，Ministry of Education，Southwest Jiaotong University，Chengdu 611756，China; 2.Graduate School of Tangshan，Southwest Jiaotong University，Tangshan 063000，China）

Abstract：

As a key component of electromechanical energy transmission， the traction drive system will be subjected to various impact loads and periodic excitation forces under electrical excitation， resulting in electromechanical coupling vibration. To analyze the electromechanical coupling vibration mechanism of the subway traction drive system， the drive device was simplified， which is equivalent to a two-mass model， and its natural frequency was calculated. Considering different torque excitation forms， the vibration mode of the mechanical drive system was analyzed. Then， according to the switching characteristics of the inverter， the effects of the sideband harmonic torque generated by pulse width modulation （PWM） on the same-frequency resonance of electromechanical coupling was focused on. Then， the traction drive system considering a two-mass load was modeled in the form of a transfer function， and the electromechanical coupling resonance characteristics of the system were theoretically analyzed from the frequency domain perspective. Finally， the analyzed results are verified in a hardware-in-the-loop test system.

Keywords：traction drive system; electromechanical coupling; same frequency resonance; two-mass system; sideband harmonics; induction motor

0" 引" 言

作为牵引传动系统能量转换的重要组成部分［1-2］，牵引电机输出转矩经联轴器、减速齿轮等装置传递给轮对，驱动列车前行。一方面，机械传动部分所引入的联轴器、齿轮箱及其柔性悬挂装置、轴承等柔性环节对电机输出电磁转矩到轮对所受扭矩的力矩传递过程造成延迟，引发电机和负载两端转速失配，进而诱发机械传动系统的扭振［3-5］；另一方面，电气侧逆变器非线性，直流电压二次纹波等非理想因素也会通过电机定转子气隙传递到机械侧，进一步加剧机电耦合振荡。严重的扭转振动会导致轴系的塑性变形，从而导致材料疲劳，在最坏的情况下，可能导致转子部件开裂。根据变形的程度，牵引传动系统的运行性能可能受到永久性的影响［6-8］。牵引传动系统扭振是由机械传动结构的固有属性和电气侧激励下电磁转矩共同作用导致的典型机电耦合共振现象。因此，以机械传动结构为基础，分析电气激励下转矩变化对扭振的影响是探究机电耦合共振机理的关键。

电磁转矩作为机械驱动装置的驱动力矩，是引发机电耦合共振的直接来源［9］。文献［10］针对永磁交流伺服系统，重点分析了弹性传动装置的机械谐振机理，证明了开环系统阶跃响应会加剧机械负载的振荡，闭环系统带宽会影响谐振模式。荷兰代夫特大学Max Wolfgang Winterling等［11-12］将电气驱动系统与机械装置以及轮轨接触特性结合分析，认为二次滤波支路失配等电气环节失效是发生机电耦合振荡主要原因。进一步，文献［11］对万向轴驱动系统进行详细的分析，根据理论与仿真计算了驱动系统的振动模态，并分析了电机的谐波转矩特性，认为转矩脉动是机电耦合振动不可忽略的激励源。此外，针对高速列车机电耦合振动现象，文献［13］建立了传动系统耦合振动模型，并对系统振荡机理和影响因素进行了详细分析。文献［14］采用有限元包对感应电机输出转矩进行瞬态分析，既考虑了电机转子以恒定速度运行引起的谐波转矩，又对电机空载启动到达同步速度的机电耦合振动状态进行了验证。

在列车牵引传动系统中，变流器普遍采用大功率低开关频率供电，而控制闭环系统存在功率开关器件死区效应、采样保持、脉冲重载更新等固有延时，这些延时环节进一步降低系统动态响应性能，增加转矩输出谐波含量。文献［15］结合异步调制下牵引电机输出转矩谐波成分分析，发现死区时间与逆变器5、7、11等次谐波电流成正比，直接影响电机偶数次谐波转矩，导致传动装置振动幅值加剧。文献［16-17］针对电机-负载双惯量模型，讨论了变频驱动系统的各频次谐波转矩与逆变器调制频率的关系，指出了谐波转矩频率与机械固有频率接近时，扭转振动模态可能被放大，但未给出机电耦合振动发生的具体工作频率点或速度点。

综上，多数文献考虑的电气激励形式较为单一，共振谐波转矩来源主要为阶跃转矩指令和基频整数次电磁转矩谐波，分析机电耦合振动模态比较局限，难以厘清包含多种电气激励作用下电磁转矩对振动模态的影响。对此，本文将分析不同的转矩激励形式下牵引传动装置的机电耦合振荡，重点考虑逆变器调制产生的边带谐波转矩，探索传动系统中频域分布极广的间谐波对传动系统的影响，推导其与机械固有频率同频振荡时的关系式，补充机电耦合共振谐波转矩的来源。建立牵引传动系统的机电耦合模型，详细讨论边带谐波转矩对机械传动部件振动的影响。最后，利用硬件在环测试对所提出的理论分析进行有效验证。

1" 机械驱动装置振动分析

1.1" 驱动装置模型构建

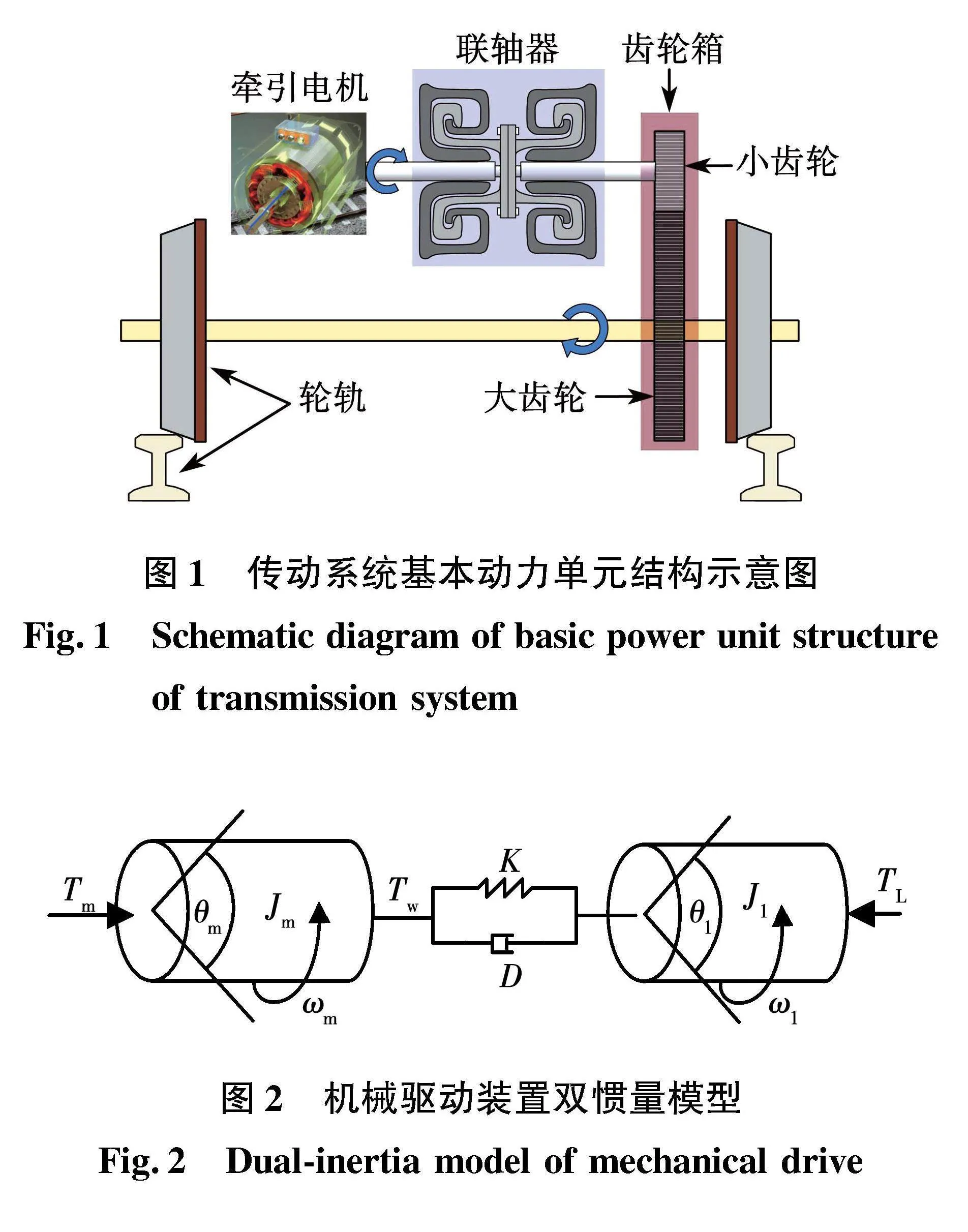
牵引传动系统结构复杂，机械传动装置与电气系统共同构成了一个机电耦合系统，基本动力单元结构如图1所示。

根据国际标准ISO 222666-1，齿轮箱耦合横向、扭转和单斜齿轮轴系的轴向振动导致横向和扭转动力学之间的相互作用。在这种情况下，轴颈轴承可以为扭转振动提供相当大的阻尼。由于齿轮齿的相互作用，齿轮的刚度取决于轴的角度位置和传递的扭矩。考虑到这些影响可能导致需要非常复杂的非线性模型，从而需要花费巨大的精力来评估轴系的动态特性。在许多情况下（例如，如果使用柔性联轴器），扭转-侧向-轴向相互作用可以忽略。在这种情况下，轴系模型应考虑齿轮的传动比、轴系刚度和惯性特性。并且标准指出考虑轴系扭振的机电耦合系统中，电气系统模型一般只包含机械系统的基本信息（具有几个自由度的轴系的总惯性或集总质量模型），将牵引传动系统质量平均等效至传动轴负载侧，并将负载侧转动惯量与电机转动惯量归算至同一转速下。最终，机械驱动装置等效为一个仅有电机-负载的双惯量集中质量模型，中间由具有一定刚度和阻尼的弹性轴连接，并忽略其自身惯量，如图2所示。

当电机电磁转矩Tm驱动电机旋转时，传动轴因存在弹性而发生形变，进而产生传动轴扭矩Tw（以下简称“轴矩”）。轴矩Tw作为内部扭矩，一方面作为电机的负载转矩，另一方面为负载提供驱动转矩。在电机侧，电磁转矩Tm与轴矩Tw共同作用在电机转动惯量Jm，使其产生加速度，在负载侧，轴矩Tw与负载转矩TL共同作用驱动负载加速，最终二者达到同一转速。根据牛顿第二定律建立驱动装置的动力学微分方程：

Jmθ··m+Tw=Tm；

Jlθ··l－Tw=－TL；

Tw=D（θ·m－θ·l）+K（θm－θl）。（1）

式中：Tm、Tw、TL分别为电机电磁转矩、传动轴扭矩、负载转矩；D、K分别为传动轴阻尼系数、传动轴扭转刚度；θm、θl分别为电机转轴转角、负载转轴转角。等效后的相关参数如表1所示。

对动力学微分方程式（1）进行拉普拉斯变换，可以得到机械驱动模型的传递函数模型，进而获得电机转速和负载转速与电磁转矩之间的传递函数分别为：

Gm（s）=ωm（s）Tm（s）=1（Jm+Jl）s×

1+2ξzωzs+1ω2zs21+2ξpωps+1ω2ps2；（2）

Gl（s）=ωl（s）Tm（s）=1（Jm+Jl）s×

Ds+KJmJlJm+Jls2+Ds+K。（3）

式中：

ωp=K（Jm+Jl）JmJl；ωz=KJl；

ξp=D2（Jm+Jl）4KJmJl;ξz=D24KJl。

其中：ωp为自然振荡频率；ωz为抗谐振频率点；ξp、ξz为对应的阻尼系数。

根据式（2）可以看出，传递函数Gm（s）由惯性环节和二阶振荡环节两部分组成。二阶振荡环节给传递函数引入了一对共轭零极点，其中由此得到上述传递函数Bode图如图3所示。可以看出，式（2）所对应传递函数幅值在自然振荡频率ωp处（约为25 Hz）迅速增加，在机械驱动装置中表现为扭振加剧。并且，由于抗谐振频率ωz的存在，在闭环控制中会对系统扭振有一定的抑制作用，但系统增益在谐振频率处很大，因此抑制效果有限；而式（3）负载转速反馈传递函数只存在谐振频率ωp，由于负载转速与电机转速存在相位差，在经过谐振频率ωp时相位穿越-180°，引入负载转速反馈将会使系统发生剧烈振动并引起失稳，因此后续进行机电耦合建模仅考虑电机转速反馈。

1.2" 同频受迫振动

机械传动环节同频受迫振动是指机械环节持续受到与机械系统固有频率相同的外部激励所诱发的振动。考虑到电机谐波转矩频次多，幅值较小，因此外部激振力矩与系统固有频率不同将不会对系统造成较大影响，这里仅考虑二者频次相同的情况。

相对于扭转刚度而言，阻尼系数对传动机构影响很小，因此忽略阻尼系数［13］，假定电磁转矩幅值为Tb，具有和系统固有频率相同的激振力矩，施加在电机转子上，则动力学方程为：

Jmθ··m=Tbcos（ωpt）－K（θm－θl）；

Jlθ··l=K（θm－θl）。（4）

应用拉普拉斯变换和反拉普拉斯变换可以得到电机和负载转子位置的时域表达式为：

θm（t）=λ［1－cos（ωpt）+μtsin（ωpt）］；

θl（t）=λ1－cos（ωpt）－ωp2tsin（ωpt）；

λ=Tb（Jm+Jl）ω2p；

μ=Jlωp2Jm。（5）

该方程式表明，如果电磁转矩以系统固有频率的脉动施加在双惯量系统上，那么转子的位置轨迹可以分离为3个部分。当激励时间超过1 s后，第3个分量将占据主导地位，第3个分量是与系统固有频率相同的脉动，但是它的大小与时间成正比。因此，即使很小的转矩脉动，随着时间的推移，部件也可能产生很大的振幅，导致轴系疲劳加剧。相对应的转速波形如图4所示，当系统运行在125 r/min时电磁转矩中包含与固有频率相等的谐波转矩（电机基频整数次谐波），即使是在转速闭环控制下，仍然会激发同频共振，造成严重的疲劳损伤。由于同频受迫振动的存在严重威胁牵引传动系统安全稳定运行，因此下面将重点分析机电耦合同频振动机理。

2" 电气激励下机电耦合同频共振分析

2.1" 逆变器谐波特性分析

由于逆变器PWM调制的开关特性，逆变器载波频率与调制波频率会交互产生大量的谐波电流，使得电机在变频调速过程中会存在各种谐波转矩，当谐波转矩频率与机械自然振荡频率相同时，将会产生机电耦合同频受迫振动。

2.1.1" 逆变器输出电压谐波特性

牵引传动系统采用空间矢量调制策略，将直流电经三相两电平逆变器转换为电压和频率可变的三相交流电。在现有的文献中，重点关注了低次的谐波电流和谐波电压幅值，而实际机械轴故障主要由驱动器脉动扭矩的频率决定。为了推导出谐波电流与谐波转矩频次的关系，首先对逆变器输出电压谐波特性进行分析，重点讨论异步调制下非整数次边带谐波对牵引系统的影响，得到自然规则采样下逆变器输出线电压的解析式，即

uAB=udc3M2cos（2πfst+π6）－4π∑∞m=1∑∞n=－∞1m×

［Dy（mMπ2）sin（m+n2π）sin（nπ3）×

sin（（mN+n）（2πfct－π3）－nπ2）］。（6）

式中：m、n分别为三角载波频率与调制波频率系数；M、N分别为调制度与载波比；fc、fs分别为载波频率、调制波频率，fc=Nfs；Dy为第一类贝塞尔函数。

式（6）包括两部分，第一部分为逆变器输出电压的基波分量，第二部分为基本谐波分量。其中基本谐波分量可以进行细分，当m=0时，此时谐波为开关频率以下的基带谐波；当m≠0时，此时谐波为载波的边带谐波。不难发现，式中谐波部分包含sin（nπ/3），由于逆变器输出的三相电压对称，因此不包含3的倍数次谐波；同时由于谐波分量中sin［（m+n）π/2］的存在，因此m+n≠0，且m和n应为一奇一偶的整数。根据上述分析，牵引电机的定子谐波电流频次可以表示为

Fmn，Ia=|mfc±nfs|。（7）

式中：m、n为自然数，且满足：

m=2i，i=0，1，2；n=6j±1，j=0，1，2；

m=2i+1，i=0，1，2；n=6j±2，j=0，1，2。

2.1.2" 谐波转矩特性分析

逆变器以高频“斩波”输入直流电压，“斩波”电压（电流）信号包含许多与电机基频相互作用的谐波，由此可能导致同频次的谐波转矩。忽略空间谐波磁动势，认为电机的谐波转矩是由电机磁路中的时间磁动势引起的。这里以m=0为例，考虑6n±1次基带谐波对谐波转矩的影响，然后对其推广。假定空间磁动势只存在基波分量，则可以建立6n-1次谐波电流的时间脉动磁势表达式为

F6n－1=32F6Φ－1sin［（6n－1）ωst+θs］。（8）

式中F6Φ-1、θs分别为6n-1次谐波合成磁动势幅值、ωst=0时的电位移角。

同理可以获得6n+1次谐波电流的脉动磁势表达式为

F6n+1=32F6Φ+1sin［（6n+1）ωst－θs］。（9）

式（8）表明，6n-1次谐波电流产生的脉动磁动势也为圆形旋转磁动势，其速度是基频磁动势的6n-1倍，方向与基波磁动势相反；而从式（9）可知，6n+1次谐波电流磁动势相对于基波磁动势以6n+1倍的速度旋转，方向与其相同。

进一步地，时间磁动势会引起转子电流的变化，从而产生相对应的谐波转矩，按照产生的方式与作用的不同，可以被进一步分为稳定谐波转矩和振动谐波转矩。其中，稳定谐波转矩是由相同频次的脉动磁势与谐波转子电流交互产生，幅值比较下，通常不予考虑。振动谐波转矩是由不同频次的脉动磁势与谐波转子电流交互产生的，且存在的含量较多，对电机转矩脉动影响较大。以6n-1次脉动磁势产生的谐波转子电流为例，可得到异步牵引电机每相转矩的瞬时表达式为：

TA6n－1=np2πfs2Egsin（ωst）×2Ir6n－1sin［（6n－1）ωst－Φn］;（10）

TB6n－1=np2πfs2Egsin（ωst－2π3）×

2Ir6n－1sin（6n－1）ωst－Φn+2π3；（11）

TC6n－1=np2πfs2Egsin（ωst－4π3）×

2Ir6n－1sin（6n－1）ωst－Φn－2π3。（12）

式中：Ir6n-1为6n-1次转子电流归算值；Eg为电动势；Φn为电动势与对应频次电流夹角。

对式（10）～式（12）化简求和，可得到电机谐波转矩的表达式为

T6n－1=3np2πfsIr6n－1Egcos［6nωst+π－Φn］。（13）

由式（13）可知，6n-1次脉动磁势会产生6n次谐波转矩。同理，对6n+1次脉动磁势产生的谐波转矩进行分析，对应的表达式如下：

T6n+1=3np2πfsIr6n+1Egcos［6nωst－Φn］。（14）

综上分析可知，在m=0时，6n±1次的定子电流会产生6n次的谐波转矩，推广至m≠0的时候，可以得到电机谐波转矩频次的表达式为

Fxy，Te=|xfc±yfs|。（15）

经整理后，x、y和m、n分别满足：

x=2i，i=0，1，2；

y=6j，j=0，1，2。

x=2i+1，i=0，1，2;y=3（2j+1），j=0，1，2；

m=x；n=y±1。

2.2" 电气激励下谐波转矩分布及频率转移特性

在仿真平台中搭建基于异步调制的异步电机牵引传动系统仿真模型，设定恒定基波频率50 Hz。电机额定功率为190 kW，直流侧电压为1 500 V，开关频率1 kHz，定转子电阻分别为0.15和0.081 Ω，定转子电感分别为32.24和32.42 mH，定转子互感为31.29 mH。

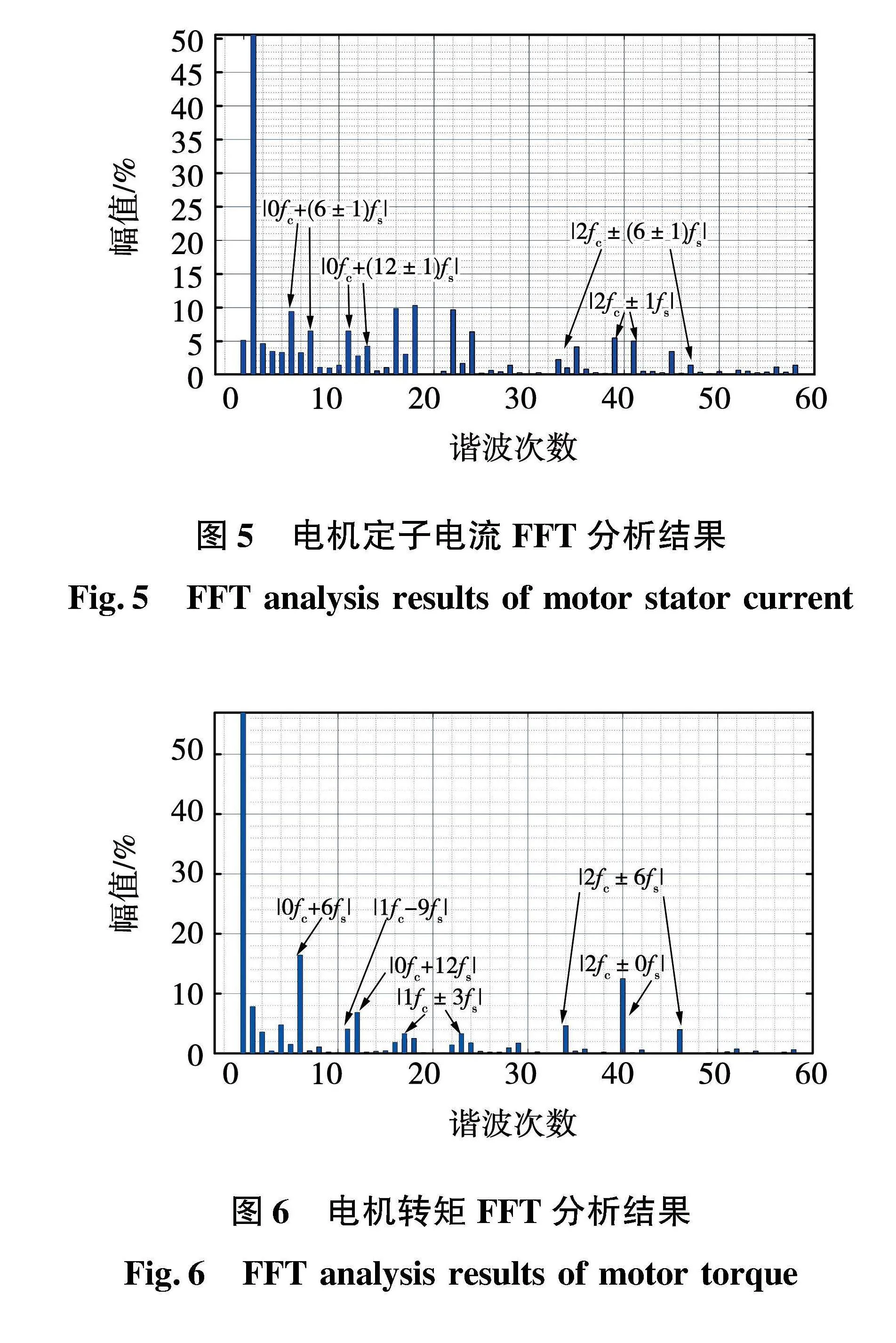
在电机达到稳态之后，分别对电机定子电流与电磁转矩进行快速傅里叶变换（fast Fourier transform，FFT）分析，对应的谐波频谱图分别如图5和图6所示。可以看出，谐波转矩和谐波电流主要分布在低频以及开关频率整数倍的边带处。对于谐波转矩，主要以6、12次基波频率、1倍开关频率加减3倍基波频率、2倍开关频率以及2倍开关频率加减6倍基波频率为主；而电机谐波电流与谐波转矩相对应，分布在谐波转矩两侧，即一个谐波转矩由相邻频次的两个谐波电流产生。同时该频谱的谐波分布基本满足上述公式。

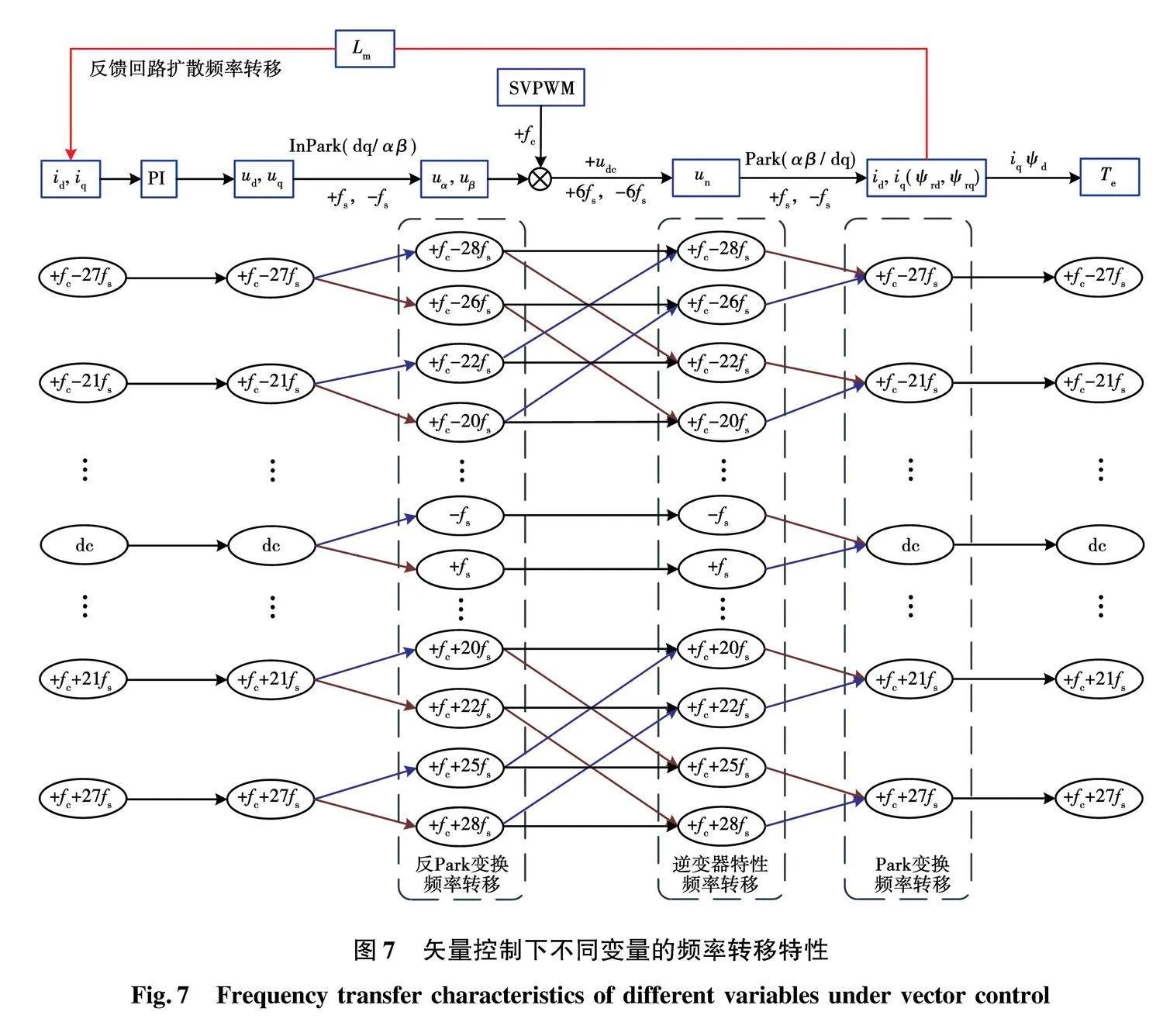
同样地，在闭环矢量控制系统中仍然存在载波频率与调制波频率的耦合特性关系。由于逆变器的开关特性，会引入载波频率整数倍的边带谐波，这里将其视为扰动，以m=1为例，分析特定基波频率fs下电机输出转矩的谐波分布。根据逆变器输出电压的奇次边带谐波可知，开关频率会与6倍的基波频率进行耦合并向外延伸，由此可以得到矢量控制方式下不同变量的频率转移特性，如图7所示。

一般来说，谐波耦合分量均为对称分量，为方便分析，将各频次谐波采用双边傅里叶变换进行展开，以正负频率进行表示，其中，直流分量以上为负频率耦合部分，直流分量以下为正频率耦合部分。在Park变换方式下，电压分量会以基波频率产生的相位角进行旋转，由此可以得到d-q轴坐标系下电流与转子磁链的频率考虑耦合分量，且二者谐波分量频次一致。对于电磁转矩而言，在稳态条件下，其值为q轴电流分量与d轴转子磁链分量乘积，而谐波分量主要考虑q轴电流谐波分量与转子磁链直流分量作用的结果，因此可以得到牵引电机转矩的谐波分布。当谐波转矩频率与机械自然振荡频率相同，即可获得同频振荡点，例如当+fc-27fs=25 Hz时，可以求解得到fs=36.11 Hz，与开环分析结果一致。对于偶数次边带谐波分析方法类似，这里不再赘述。

3" 机电耦合振荡机理分析

牵引电机采用和谐号CRH3牵引电机，参数如表2所示［19］。

牵引电机在恒速运行工况下，电磁转矩仅与q轴电流有关，因此可将整个控制系统简化为等效模型，如图8所示。该模型包含速度外环、电流内环以及机械环节。综合考虑采样延时、计算延时、逆变器死区效应对系统的影响，将数字控制环节等效为一阶惯性传递函数，即

D（s）=1Tds+1。（16）

图8中：kpn、kin为速度环调节参数；kpq和kiq为电流环调节参数；Td为控制延迟参数；F、kt为转矩与电流变换系数、电能变换电路与电机等效增益；Gm（s）为机械传动环节传递函数。

由于高阶的系统不利于清晰分析系统的性能，本节对机械传动环节还是按照双惯量模型进行处理。通过对该理论模型的推导，可以得到整个系统的开环传递函数为

G（s）=（kpn+kins）Giclose（s）Gm（s）。（17）

式中

Giclose（s）=kt（kpqs+kiq）Tds2+（1+kpqktF）s+kiqktF。

其中Giclose（s）为电流闭环传递函数。

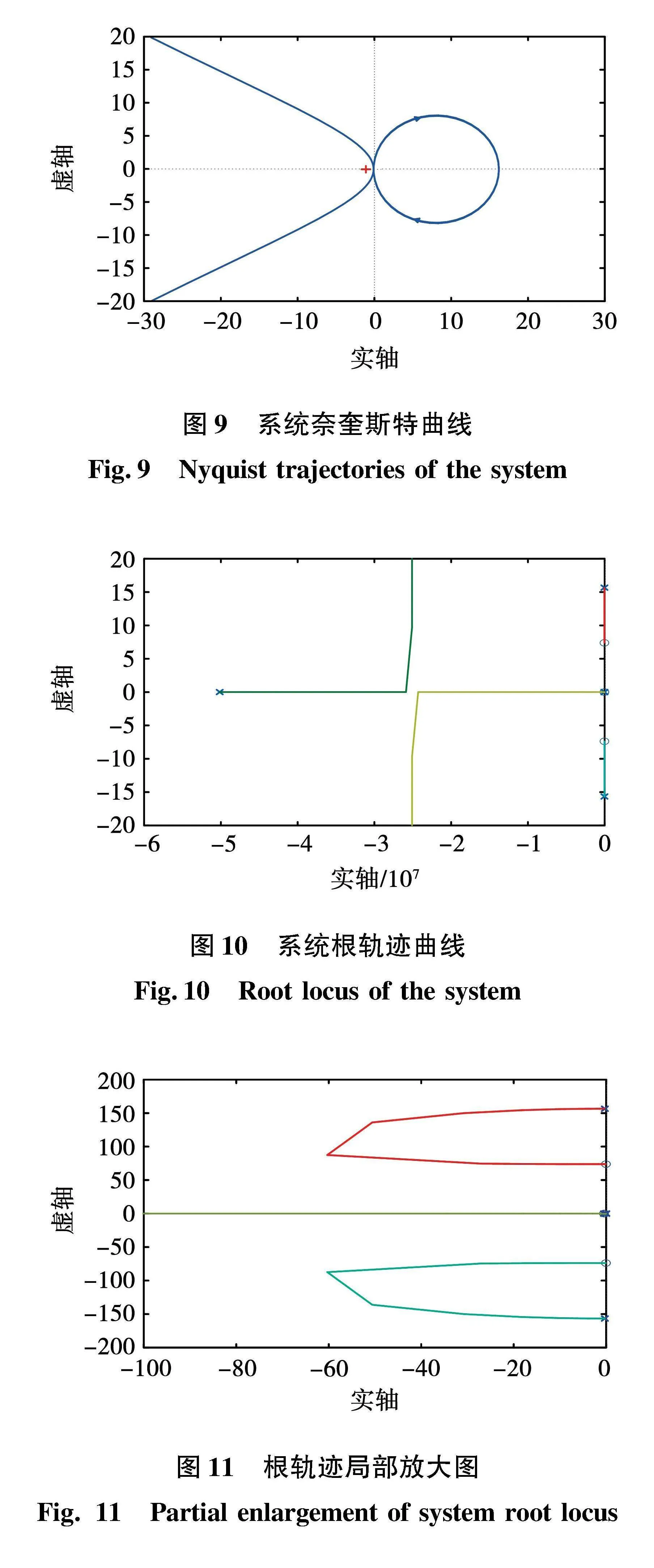
根据开环传递函数，将其化为标准形式，分别绘制出系统的Nyquist图与根轨迹图，如图9～图11所示。由于该开环传递函数为最小相位系统，Nyquist图并未穿越（-1，j0）点，因此该系统是稳定的。而从根轨迹图中可以看出，该系统包含6个极点和4个零点。其中，在负实轴存在1个极点，远离虚轴，该极点是由电流闭环传函Giclose（s）引起的。另外，图中还存在1对共轭复数根形式的零极点，将其放大如图11所示，可知这对零极点是由机械环节引起的，并且接近虚轴，使系统处于欠阻尼状态，当电机谐波转矩频次与共轭极点频率相同时，将会引发机电耦合同频振荡；另外在原点处存在2个极点，靠近虚轴的实轴上存在2个零点和1个极点，且零极点近似重合，这是由电流闭环传函和速度调节器带来的，一般不会对系统稳定性造成影响。

由根轨迹的定义可知，随着开环增益的增大，双惯量环节的共轭极点将移动至共轭零点，系统将由自然振荡频率变为抗谐振频率，与理论分析结果一致。并且，在开环增益较小时，根轨迹与双惯量自然振荡频率接近，靠近虚轴，随着开环增益的增大，根轨迹将向左半平面移动，系统的阻尼系数稍有增加，系统将会处在一个较为稳定的范围。但是，在大多增益范围之内，根轨迹都与机械环节的自然振荡频率接近，转矩或负载扰动均会引起机械传动结构振荡，尤其在激励转矩与自然振荡频率相同时，将会引起机电耦合同频振荡。

4" 硬件在环测试验证

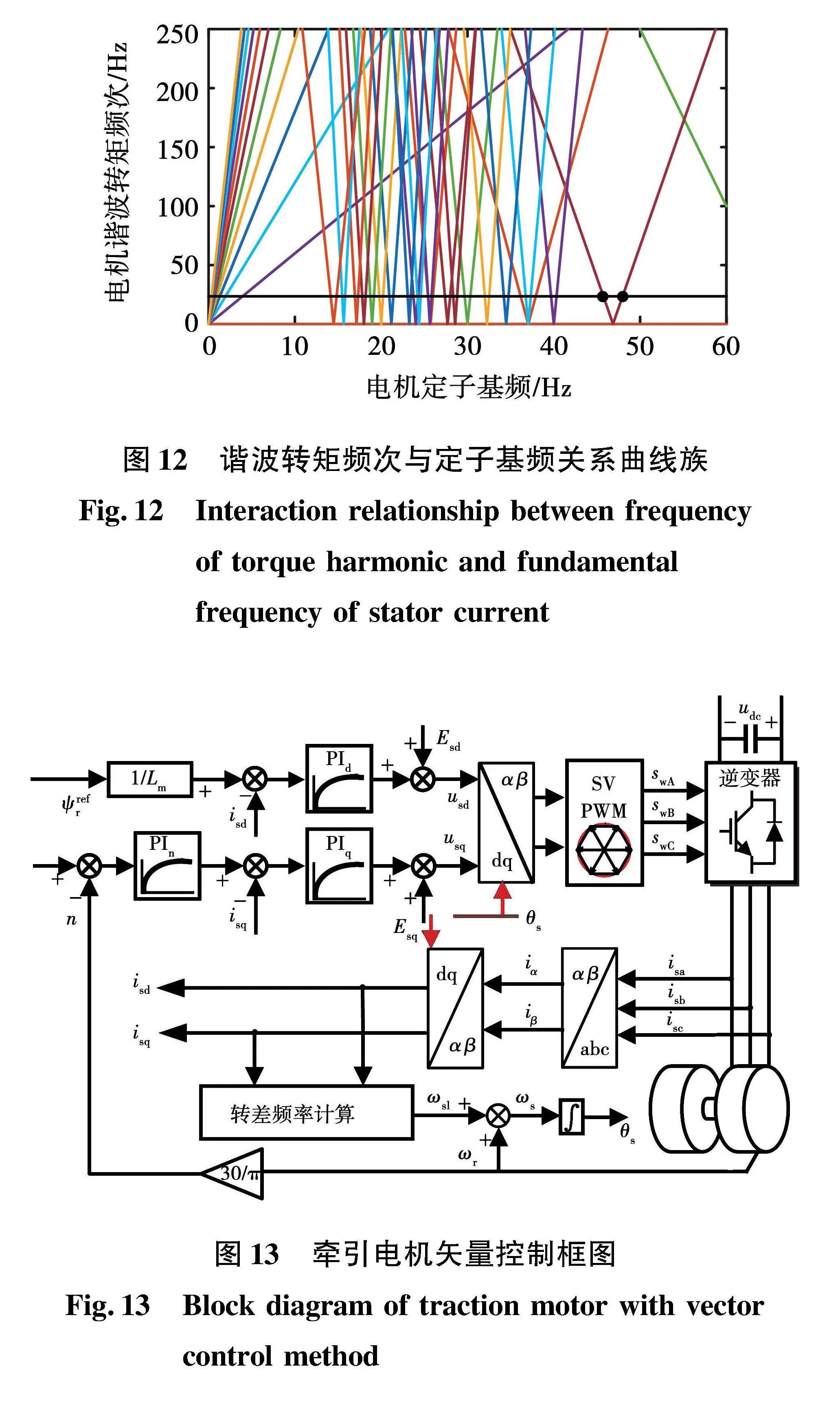
牵引电机采用和谐号CRH3牵引电机，参数如表2所示［19］。谐波转矩的频次由载波频率及调制波频率交互耦合产生，固定开关频率，改变电机定子频率即可获得相应频次的谐波转矩。根据式（15），每一个x、y的取值组合确定一条定子基频和谐波转矩关系曲线，通过对x、y取不同组合可以构建出谐波转矩频率与电机基频的关系曲线族，如图12所示。由表1参数可得机械模型自然振荡频率为25 Hz，同频电磁转矩将引起机电耦合同频振荡，图7中黑线的纵坐标代表机械自然振荡频率，与曲线族存在多个交点表示存在多个定子基频会产生同频谐波转矩。x=2、y=42组合确定的曲线与自然振荡频率存在2个交点，代表存在2个定子频率（47.02和48.21 Hz）会产生25 Hz的边带谐波转矩，而且相比于更低基频下的边带谐波，此时的反电势Eg更大，边带效应更为显著，因此可以选取47.02、48.21 Hz作为同频振荡速度点的验证。采用三相交流异步电机，电机控制策略采用转子磁链定向控制，调制方案采用异步调制策略。电机控制环节包括电流内环与转速外环，分别采用PI控制器进行控制，为了减少PI控制器的运算负担，加快系统的动态响应，在控制器输出前向电压基础上，引入前馈指令电压，其控制框图如图13所示。

根据转子磁场定向的控制方式，在稳态下q轴磁链为0，由此得到转差频率和转子磁链定向角分别为：

ωsl（t）=isq（t）LmTrψrd（t）；（18）

θs（t）=∫ωs（t）dt=∫（ωsl（t）+ωr（t））dt。（19）

式中：isq为电机定子q轴电流；Tr为电机转子时间常数；ψrd为电机转子磁链；ωs、ωsl、ωr分别为电机定子角频率、转差角频率、电机转子角速度。

同时，可以获得稳态下的电磁转矩方程为

Tm=npLmLrisq（t）ψrd（t）。（20）

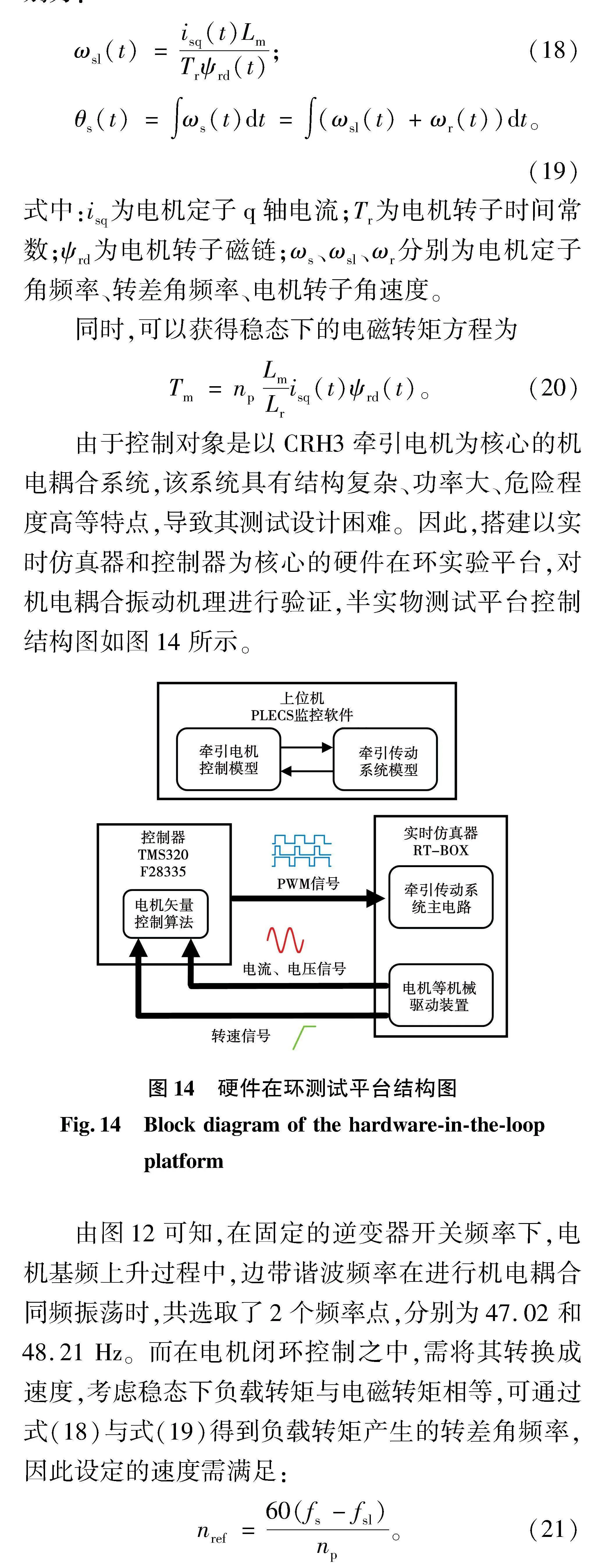
由于控制对象是以CRH3牵引电机为核心的机电耦合系统，该系统具有结构复杂、功率大、危险程度高等特点，导致其测试设计困难。因此，搭建以实时仿真器和控制器为核心的硬件在环实验平台，对机电耦合振动机理进行验证，半实物测试平台控制结构图如图14所示。

由图12可知，在固定的逆变器开关频率下，电机基频上升过程中，边带谐波频率在进行机电耦合同频振荡时，共选取了2个频率点，分别为47.02和48.21 Hz。而在电机闭环控制之中，需将其转换成速度，考虑稳态下负载转矩与电磁转矩相等，可通过式（18）与式（19）得到负载转矩产生的转差角频率，因此设定的速度需满足：

nref=60（fs－fsl）np。（21）

在进行硬件在环测试时，选取负载TL=200 N·m，经计算同频振荡速度分别为1 410、1 446 r/min。以2种工况进行测试：1）升降速工况：设置负载转矩TL=1 000 N·m，给定转速nref=1 410 r/min→1 500 r/min→1 446 r/min。2）加减载工况：设置转速nref=1 410 r/min，负载转矩TL=1 000 N·m→1 500 N·m→1 200 N·m。为了反应机电耦合的严重程度，在2种工况条件下分别测试电机转速与传动轴扭矩。

1）升降速工况。

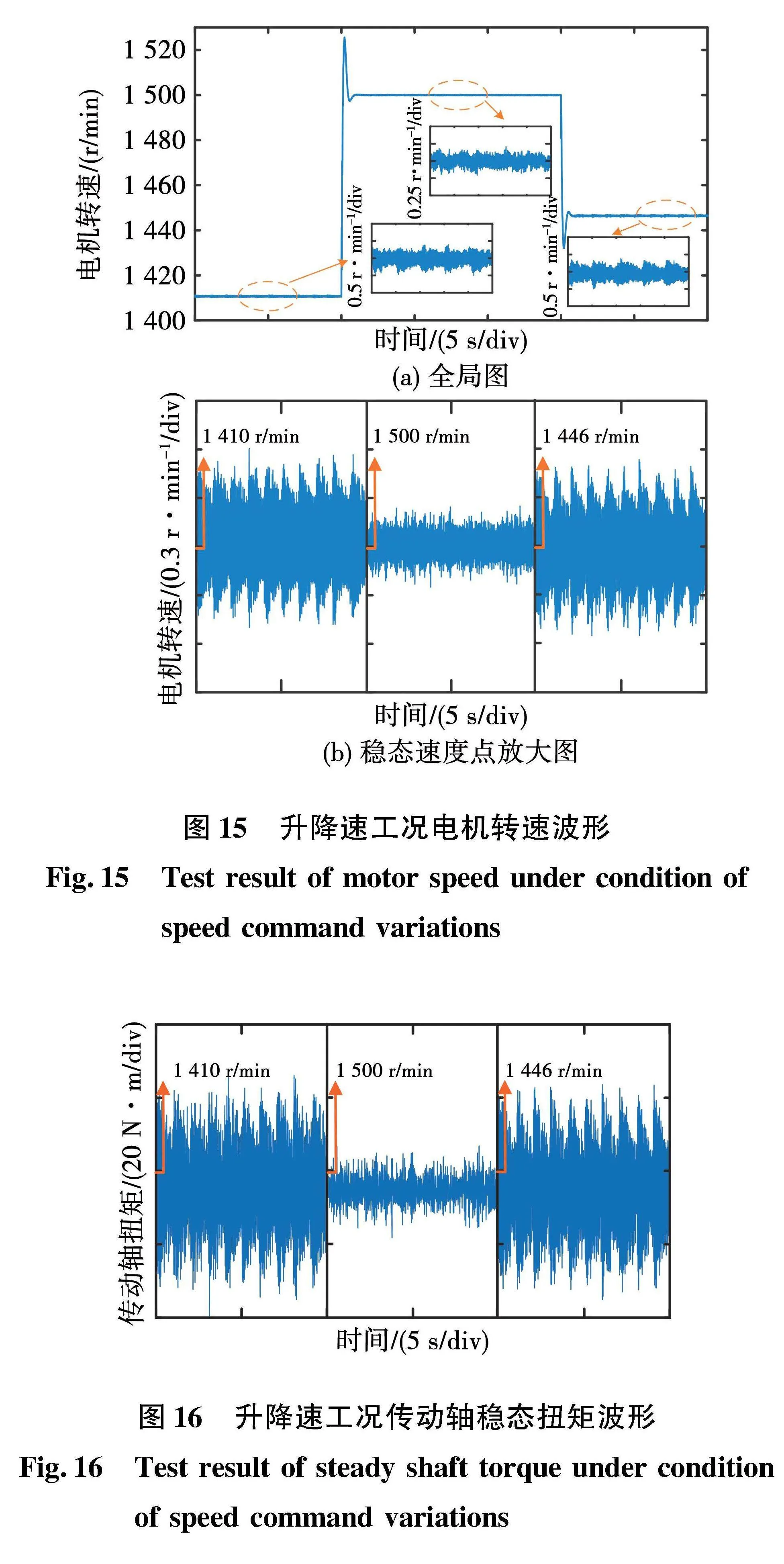
实验结果如图15与图16所示，可知，在给定速度为1 500 r/min下，电机实际转速及轴矩均比较平稳，而在同频振荡频率下，由于谐波转矩的幅值不同，电机实际转速与轴矩均发生了不同程度的振荡。系统如果长期处于扭振状态下，将会导致轴系疲劳损伤，威胁列车的安全稳定运行。

2）加减载工况。

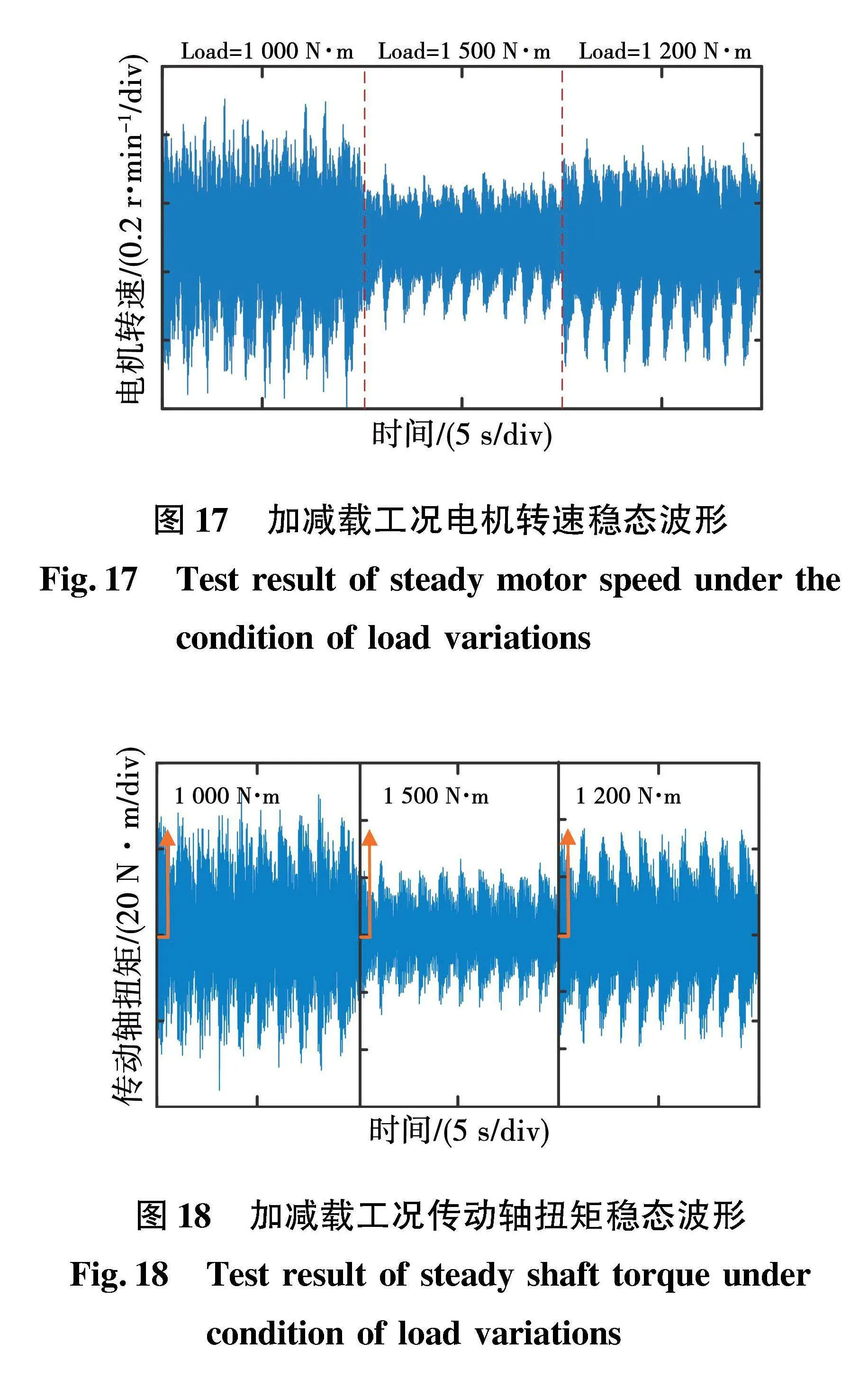
电机加减载阶段，电机在1 410 r/min的同频振荡速度点时，都可以在稳态达到给定转速，而当进行加减载操作时，会使电机的转差频率改变，进而使电机偏离同频振荡点，但由于转差频率很小，系统依旧接近同频振荡点。实验结果如图17和图18所示，可以明显看出，在加减载恢复至稳定转速后，电机转速及传动轴扭矩的振荡幅值均较同频振荡速度点有所减弱，但此时系统依旧有较大的振荡。

5" 结" 论

本文针对牵引传动系统机电耦合振动问题，对其振动机理进行了分析，得到如下结论：

1）分析了牵引传动系统机电耦合扭振的诱因，在双惯量系统模型基础上复现了电机转速闭环控制下不同速度点会发生同频受迫振动。

2）分析了逆变器PWM调制输出的电压谐波特性和牵引电机输出转矩的谐波特性，并依据其伴生间谐波的分布规律，构建了谐波转矩频次与定子基频的关系曲线族。

3）仿真和硬件在环测试表明，在变频调速过程中，由于载波频率和调制波频率的交互耦合关系，边带谐波转矩会在多个速度点产生相同频次谐波转矩，因此逆变器调制引起的间谐波是引发机电耦合同频振动的来源之一。

参 考 文 献：

［1］" 陈再刚， 刘禹清， 周子伟， 等. 轨道交通牵引动力传动系统动力学研究综述［J］. 交通运输工程学报， 2021， 21（6）： 31.

CHEN Zaigang， LIU Yuqing， ZHOU Ziwei， et al. Review on dynamics research of rail transit traction power transmission system［J］. Journal of Traffic and Transportation Engineering， 2021， 21（6）： 31.

［2］" LU B， LIU Z， WANG X， et al. Influence of electric traction drive system harmonics and interharmonicson the vibration of key locomotive components［J］. IEEE Transactions on Vehicular Technology， 2023， 72（10）：12830.

［3］" KIA S H， HENAO H， CAPOLINO G A. Torsional vibration assessment using induction machine electromagnetic torque estimation［J］. IEEE Transactions on Industrial Electronics， 2009， 57（1）： 209.

［4］" WU X， CHI M， GAO H. Damage tolerances of a railway axle in the presence of wheel polygonalizations［J］. Engineering Failure Analysis， 2016，66： 44.

［5］" WU X， RAKHEJA S， QU S， et al. Dynamic responses of a high-speed railway car due to wheel polygonalisation［J］. Vehicle System Dynamics， 2018， 56（12）： 1817.

［6］" SMITH K S， RAN L. Torsional resonance risk management in islanded industrial power systems supplying large VFDs［J］. IEEE Transactions on Industry Applications， 2008， 44（6）：1841.

［7］" SONG-MANGUELLE J， SCHRDER S， GEYER T， et al. Prediction of mechanical shaft failures due to pulsating torques of variable-frequency drives［J］. IEEE Transactions on Industry Applications， 2010， 46（5）： 1979.

［8］" MAURI M， ROSSI M， BRUHA M. Generation of torsional excitation in a variable-speed-drive system［C］//2016 International Symposium on Power Electronics， Electrical Drives， Automation and Motion （SPEEDAM）， June 22-24， 2016， Capri， Italy. 2016： 516-521.

［9］" WANG Q， RAJASHEKARA K， JIA Y， et al. A real-time vibration suppression strategy in electric vehicles［J］. IEEE Transactions on Vehicular Technology， 2017， 66（9）： 7722.

［10］" 杨明， 郝亮， 徐殿国. 双惯量弹性负载系统机械谐振机理分析及谐振特征快速辨识［J］.电机与控制学报，2016，20（4）：112.

YANG Ming， HAO Liang， XU Dianguo. Analysis of mechanical resonance mechanism and fast identification of resonance characteristic for 2-mass system with elastic load［J］. Electric Machines and Control， 2016， 20（4）： 112.

［11］" WINTERLING M W， TUINMAN E， DELEROI W. Attenuation of ripple torques in inverter supplied traction drives［C］//Seventh International Conference on Power Electronics and Variable Speed Drives， September 21-23， 1998， London， UK. 1998： 364-369.

［12］" WINTERLING M W， TUINMAN E， DELEROI W. Simulation of drive line dynamics of light-rail vehicles［C］//International Conference on Simulation 98， September 30-October 2，1998， York， UK. 1998： 79-84.

［13］" 赵心颖， 杨中平， 林飞， 等. 高速列车牵引传动系统机电耦合振动及其影响因素分析［J］.铁道学报，2019，41（10）：38.

ZHAO Xinying， YANG Zhongping， LIN Fei， et al. Study on electromechanical coupling vibration of traction drive system of high-speed train and its influence factor［J］. Journal of the China Railway Society， 2019， 41（10）： 38.

［14］" PHAM T H， WENDLING P F， SALON S J， et al. Transient finite element analysis for an induction motor with external circuit connections and electromechanical coupling［J］. IEEE Transactions on Energy Conversion， 1999， 14（4）： 1407.

［15］" 赵心颖， 林飞， 杨中平， 等. 高速列车牵引传动系统机电耦合振动特性研究［J］. 铁道学报， 2018， 40（9）： 40.

ZHAO Xinying， LIN fei， YANG Zhongping， et al. Study on mechanism and suppression of electromechanical coupling vibration in traction drive system of high-speed train［J］. Journal of the China Railway Society， 2018， 40（9）： 40.

［16］" BROCK S， UCZAK D， NOWOPOLSKI K， et al. Two approaches to speed control for multi-mass system with variable mechanical parameters［J］. IEEE Transactions on Industrial Electronics， 2016， 64（4）： 3338.

［17］" YANG S M， WANG S C. The detection of resonance frequency in motion control systems［J］. IEEE Transactions on Industry Applications， 2014， 50（5）： 3423.

［18］" HOLMES D G， MCGRATH B P. Opportunities for harmonic cancellation with carrier-based PWM for a two-level and multilevel cascaded inverters［J］. IEEE Transactions on Industry Application， 2001， 37（2）： 574.

［19］" 汪斌. 列车牵引传动系统性能分析和仿真技术研究［D］.杭州： 浙江大学， 2013.

（编辑：邱赫男）