基于多特征提取和麻雀搜索算法优化XGBoost的变压器绕组松动诊断方法

摘" 要：

针对使用单一特征量诊断变压器绕组松动，在不同负载条件下存在交叠和抗干扰能力不足的问题，提出一种基于核主成分分析（KPCA）和改进麻雀搜索算法（SSA）优化极端梯度提升（XGBoost）的变压器绕组松动振动诊断方法。首先，从时域、频域和熵值3个维度提取适用于变压器多传感器振动信号的多种特征量；其次，通过网格搜索优化的KPCA对特征量进行降维；最后，构建基于XGBoost的故障诊断模型，并采用改进麻雀搜索算法调参，实现不同电流大小下变压器绕组松动故障准确识别。以某110 kV变压器为对象进行实验验证，诊断结果表明，所提取的特征量能够准确反映故障特征，抗干扰能力更强，诊断模型故障诊断准确率为99.00%，相比于其他诊断算法准确率和稳定性更高，在不同负载情况下均有良好的识别效果。

关键词：变压器振动；绕组松动；核主成分分析；极端梯度提升；麻雀搜索算法；故障诊断

DOI：10.15938/j.emc.2024.06.009

中图分类号：TM41

文献标志码：A

文章编号：1007-449X（2024）06-0087-11

收稿日期： 2023-06-26

基金项目：国家自然科学基金（51577050）；国家电网江苏省电力有限公司重点科技项目（J2022047）

作者简介：马宏忠（1962—），男，博士，教授，博士生导师，研究方向为电力设备状态监测及故障诊断；

肖雨松（1999—），男，硕士研究生，研究方向为电力设备状态监测及故障诊断；

颜" 锦（1995—），男，硕士，研究方向为电力变压器状态监测与故障诊断；

孙永腾（1994—），男，博士研究生，研究方向为电力设备状态监测及故障诊断。

通信作者：肖雨松

Transformer winding looseness diagnosis method based on multiple feature extraction and sparrow search algorithm optimized XGBoost

MA Hongzhong1，" XIAO Yusong1，" YAN Jin2，" SUN Yongteng1

（1.College of Energy and Electrical Engineering， Hohai University， Nanjing 211100， China;

2.Hengyang Power Supply Branch，State Grid Hunan Electric Power Co.， Hengyang 421200， China）

Abstract：

In order to solve the problem of overlap and insufficient anti-interference ability under different load conditions in diagnosing transformer winding looseness using a single feature quantity， a vibration signal diagnosis method for transformer winding looseness based on kernel principal component analysis （KPCA） and extreme gradient boosting（XGBoost） optimized by improved sparrow search algorithm（SSA） was proposed. Firstly， feature quantities in vibration signals were extracted from three dimensions： time domain， frequency domain， and entropy; Then， the feature quantity was dimensionally reduced through grid search optimized KPCA; Finally， a fault diagnosis model based on XGBoost was constructed and sparrow search algorithm was used to optimize the parameters for achieving accurate identification of transformer winding looseness faults under different currents. The experimental verification was conducted on a 110 kV transformer. The diagnosis results show that the extracted feature quantities can accurately reflect the fault characteristics， have stronger anti-interference ability， and the diagnostic accuracy rate of the diagnostic model is 99.00%. Compared with other diagnostic algorithms， the accuracy and stability are higher， and have good recognition effects under different load conditions.

Keywords：transformer vibration; winding looseness; kernel principal component analysis; XGBoost; sparrow search algorithm; fault diagnosis

0" 引" 言

变压器是电力系统的枢纽设备，其运行情况关系着整个电网的安全。变压器事故统计数据显示，约41%的变压器事故涉及绕组故障，主要原因是绕组抗短路能力不足［1］。短路电流冲击、安装不当等因素都会降低变压器绕组的预紧力，造成绕组松动。绕组松动会使得绕组易发生形变，抗短路冲击能力下降，并具有累积效应，严重威胁变压器的安全稳定运行［2-3］。因此，研究变压器绕组松动故障的诊断方法具有重要价值。

针对绕组松动故障，目前常规的检测方法主要有频率响应法、低压脉冲法和短路电抗法［4-5］。频率响应法需要外接激励源，要求变压器退出运行，不能在线检测［6］；低压脉冲法具有首端响应不灵敏的问题，多用于出厂实验［7］；改进后短路电抗法可用于在线检测，但灵敏度难以满足要求［8］。

相比于传统检测方法，振动检测法与被测目标无直接电气联系，不易受电磁干扰，且支持在线监测，已在多领域受到了广泛关注。但振动信号与变压器绕组松动状态缺乏明确的函数关系，为此需要研究提取振动信号中故障特征的方法。文献［9］使用交叉小波对振动信号幅频特征量进行提取，证明幅频特征量用于绕组松动和磁路故障均能有效区分正常和故障状态；文献［10］提出一种基于点对称变换和图像匹配的诊断方法，将振动信号转化为图像再进行聚类从而实现故障分类；文献［11］对振动信号进行相空间重构，再结合奇异值分解和信息熵算法，获取振动信号奇异谱熵，通过支持向量机（support vector machine，SVM）进行诊断。

但仅使用单一特征量对绕组松动进行诊断，反映的故障信息不够全面，精确度和抗干扰能力不足，因负载电流或干扰影响，正常与故障状态的特征量范围可能会出现重叠，使通过单一特征量进行故障诊断失效［12-13］。为此，可以选择提取多种适用于变压器振动信号的特征量进行综合评价。文献［13］提出区分能力的概念，从多方面提取振动信号特征，引入线性判别分析投影法（linear discriminant analysis，LDA）进行筛选及处理，并通过SVM验证识别效果；文献［14］和文献［15］提出频率复杂度、振动能量分布和能量分布比例等特征量，并结合SVM和决策树（decision tree，DT）进行机械状态分类和识别。此外，由于电力变压器体积较大，为了提高故障定位能力，振动信号采集实验往往在变压器不同位置布置有多个振动传感器，因此特征量不仅要能反映单一传感器信号的特征，还要能体现不同传感器信号之间的关系。

变压器振动信号变化规律复杂，传统的诊断模型如SVM等往往存在精确度不足、过拟合、对数据要求高等问题［16］。在使用多种特征量进行故障诊断时，这一问题会更加突出。极限梯度提升（exterme gradient boosting，XGBoost）是一种基于Boosting的集成学习算法，具有不易过拟合、训练速度快、灵活性强等优点，已在故障诊断领域取得了广泛的应用。文献［17］根据油中溶解气体分析，提取9维故障特征，输入遗传算法优化的XGBoost对变压器故障进行诊断；文献［18］提出一种基于孤立森林与过采样技术的数据预处理方法，并结合交叉验证和网格搜索算法优化XGBoost超参数，对换流阀状态进行评估。但XGBoost参数较多，为保证诊断效果，需要结合优化算法进行参数调优。

基于以上分析，本文提出一种基于多特征量提取和改进麻雀搜索算法（sparrow search algorithm，SSA）优化XGBoost的故障诊断方法。首先，搭建实验平台，在不同大小负载电流下进行变压器绕组松动实验，采集振动信号并从时域、频域、熵值3个维度提取多种适用于变压器多传感器振动信号的特征量；然后，使用核主成分分析（kernel principal components analysis，KPCA）降维以减少特征维数，加快分类速度；最后，输入改进麻雀搜索算法优化的XGBoost分类模型进行故障诊断。实验分析结果表明，本文方法在不同大小负载电流下均有良好的识别效果，同时具有较强的抗干扰能力。

1" 变压器振动特性

绕组和铁心是变压器振动的主要来源［19］。将绕组作为主要研究对象，根据毕奥萨伐尔定律和洛伦兹力公式，在磁场中绕组所受电动力F大小正比于电流平方，假设输入电流为i=I0cos（ωt），则

F=12kI20［cos（2ωt）+1］。（1）

式中：ω为电源角频率；I0为输入电流幅值；k为绕组电动力系数；t为时间变量。

由式（1）可知，变压器绕组振动信号基频与输入电流频率为2倍关系，对于50 Hz电力系统振动信号基频为100 Hz。由于电流谐波与机电耦合等因素影响，实际振动信号中还存在大量谐波 ［20-22］。当变压器绕组固有频率与激励频率相近时，就会因参数共振产生谐波，若固有频率接近电源频率，会产生激励的奇次倍频率谐波，若固有频率接近电源频率2倍时，会产生偶次倍频率谐波。

2" 振动信号采集实验

2.1" 实验平台搭建

在实验室中搭建变压器绕组松动实验平台，实验平台主要由变压器、振动传感器、采集仪和调压器等组成。图1所示变压器为南京某变压器公司一台110 kV三相油浸式变压器，型号为SFZ10-31500/110，接线方式为YNd11，低压侧额定电压UN为10.5 kV，额定电流IN为1 732 A。

测量振动信号选用压电式加速度传感器，型号为JF-2020，输出电压和加速度比值为20 mV/g，以磁吸方式固定在变压器油箱顶部。采集仪型号为NICOLET7700，采样频率为10 kHz。

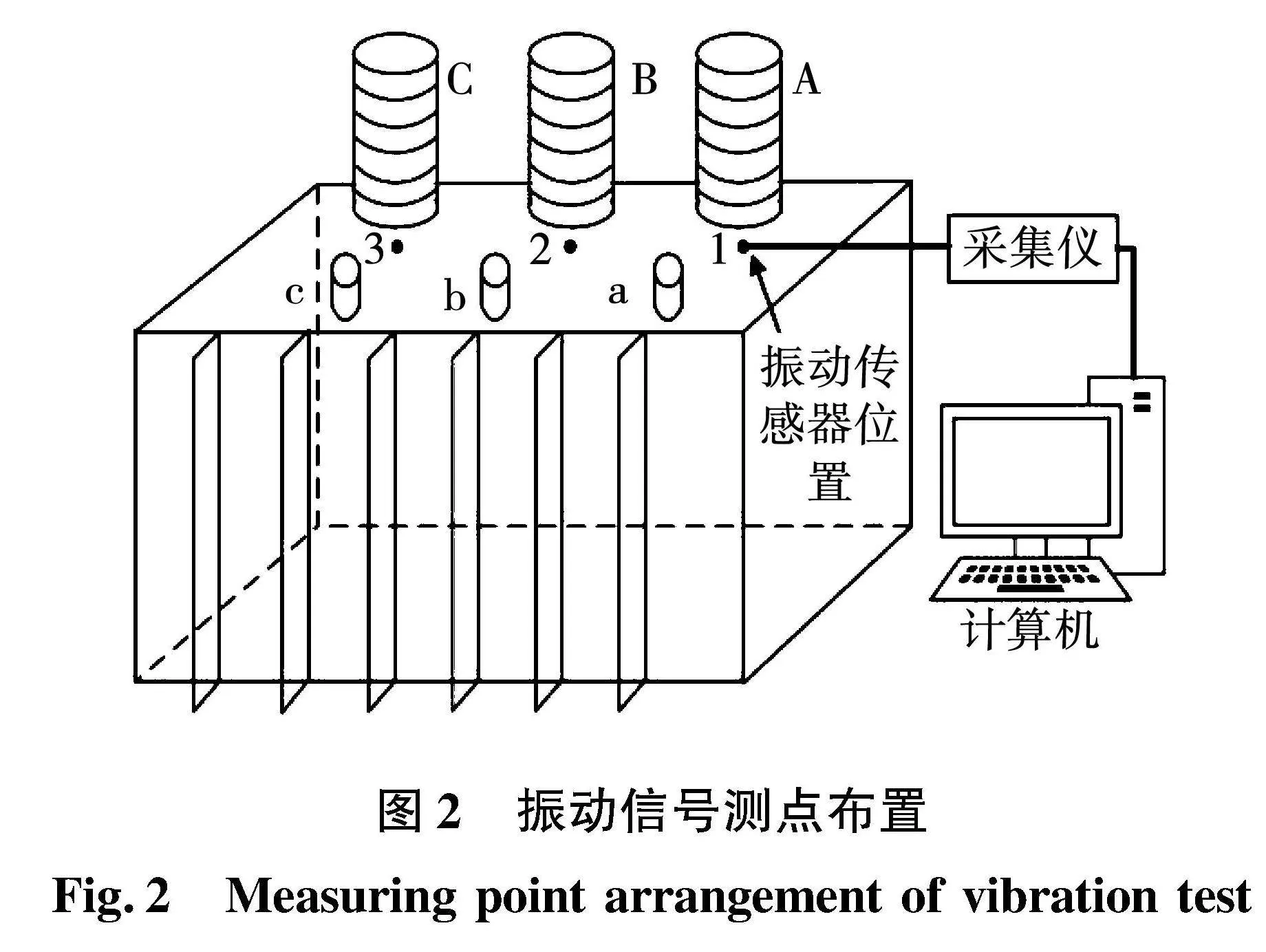
振动传感器布设于变压器油箱顶部，因为大型变压器为钟罩式结构，绕组通过固定构件和油箱顶部紧密相连，油箱顶部所测得振动信号损耗更小，特征更加明显。由于变压器体积较大，为了便于定位绕组松动位置，设置有3个传感器，分别位于顶部1、2、3号位置，对应A、B、C三相绕组，如图2所示。

2.2" 实验过程

实验中使用液压千斤顶来控制绕组松动程度。在设置绕组松动状态时，首先将变压器进行抽油和吊罩，并松开对应相绕组的紧固螺母；然后在绕组和结构件之间加入液压千斤顶压紧绕组，液压表显示千斤顶所施加的压力，以此定量模拟不同程度的绕组松动；最后待液压表示数稳定后，重新拧紧螺母再将千斤顶撤去，将变压器油箱恢复并重新真空注油。

根据实验方案，绕组松动程度分为3种：正常（预紧力28 MPa）、完全松动（预紧力0 MPa）、轻微松动（预紧力14 MPa）；共设置有6种绕组松动类型：三相均正常（正常0）、A相绕组完全松动（故障1）、A相绕组轻微松动（故障2）、B相绕组完全松动（故障3）、AB相完全松动（故障4）和三相完全松动（故障5）。

实验中对变压器进行短路实验，将低压侧短路，在高压侧施加可调电压。当低压侧电流为100%IN时，电压约为额定值的5%～15%，由于铁心振动加速度与电压的平方成正比，故铁心振动远低于额定状态，此时振动信号绝大多数由绕组产生。为了确保在不同的电流大小下均能准确识别故障，共设置有5种实验电流，分别为40%IN、60%IN、80%IN、100%IN、110%IN。为避免偶然性，每种松动-电流组合实验重复3次，每次数据采集时长为10 s。

2.3" 特征量选取

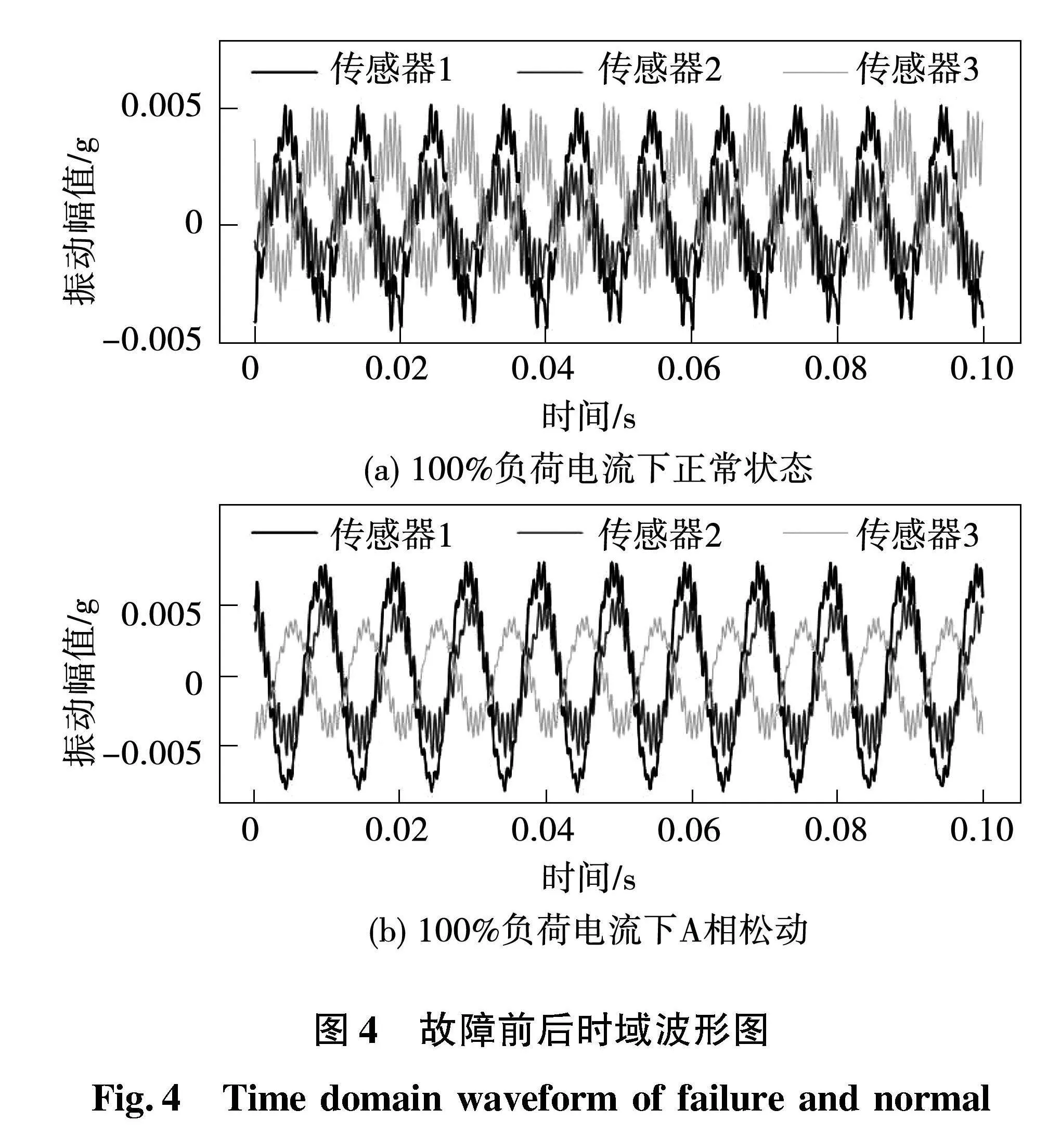
绕组松动后振动波形发生了明显的变化，为了更全面反映其中变化规律，便于故障定位，将从时域、频域和熵值3方面提取适合变压器多传感器振动信号的特征量，如图4所示。

时域特征是最直观的特征，变压器振动信号基频为正弦波，具有明显周期性，对于这类波形常用时域特征包括峰峰值、方差和皮尔森相关系数等。由图4可知，绕组发生松动后，故障相对应传感器峰峰值会增大，但电流大小也会影响振动幅值，因此特征量应为三传感器峰峰值互相之间比值。

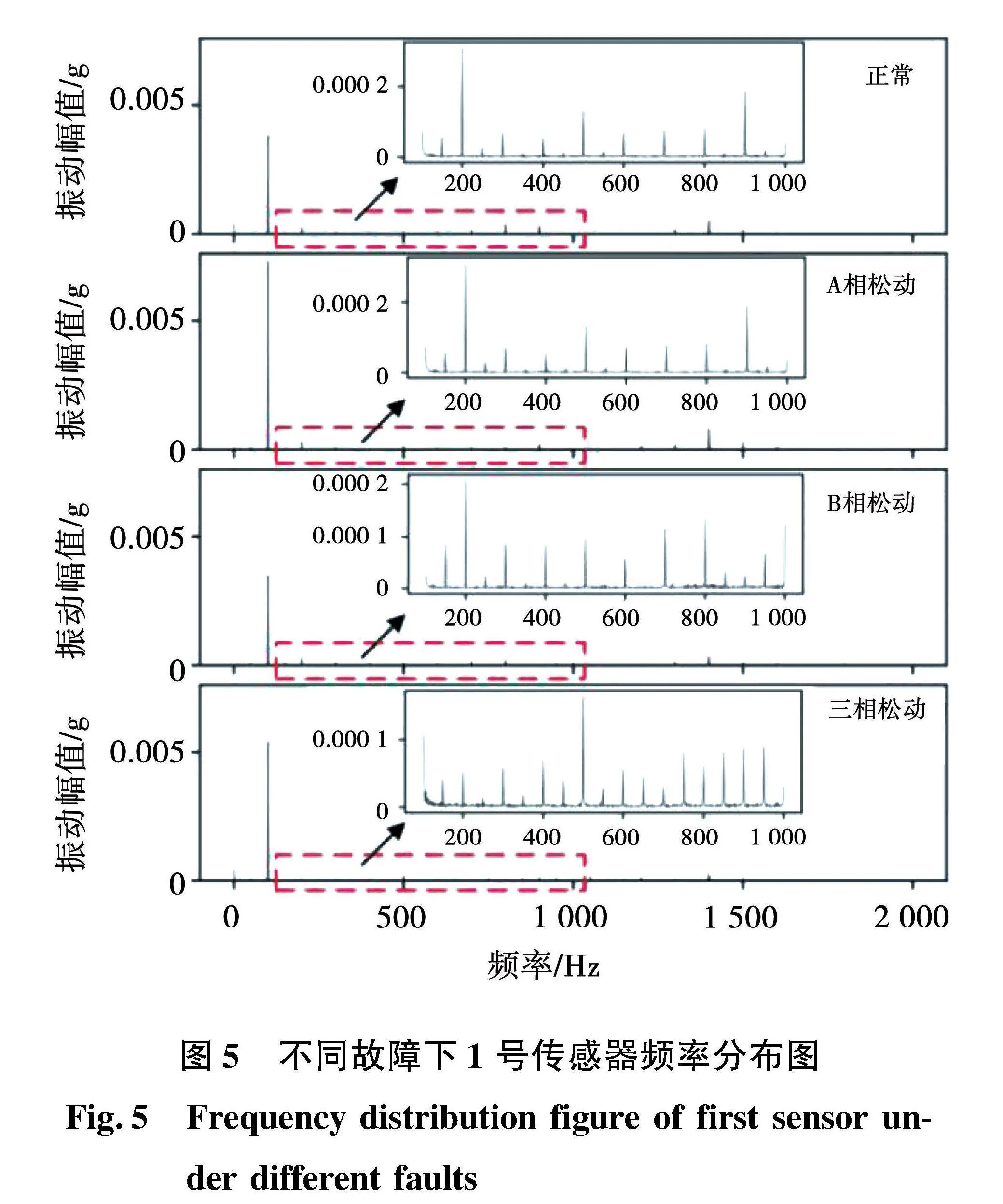
使用频域信息可以滤去无关分量，提取变压器振动产生的特定频率分量。以100%额定电流下，1号传感器为例进行分析，如图5所示。由图5可见，无论是否存在绕组松动，基频100 Hz分量幅值均最高，此外，100 Hz各倍频分量幅值较高，而50 Hz奇数倍频分量幅值较低。绕组松动情况只改变了特征频率的幅值，没有改变频率的分布。绕组松动主要改变100 Hz分量大小［14］，故障相100 Hz分量明显升高，A相松动和三相松动状态下，振动信号中100 Hz分量均超过了0.005 g，正常状态和B相松动时则均不足0.004 g。

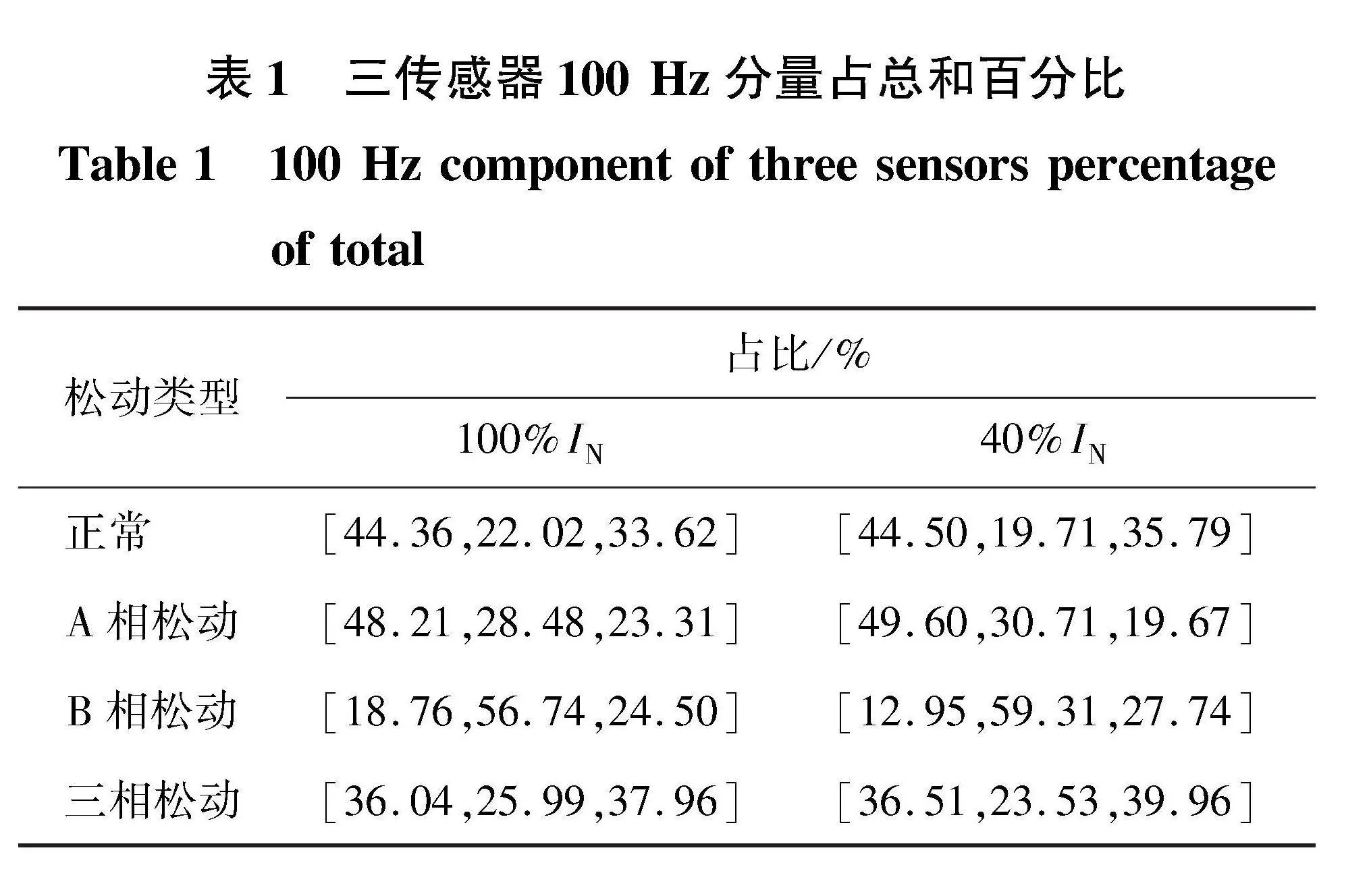
绕组松动也会带来三传感器100 Hz分量幅值关系变化，因此可以将3个传感器100 Hz分量幅值分别占三者总和的百分比作为特征量，如表1所示。从各组实验数据中各取1 s为例，由表1可见，该特征量能很好地反映单相故障，而且因为是相对比值，可以避免负载等造成的整体幅值变化的影响，在100%和40%额定电流下基本不变。但三传感器100 Hz分量幅值在正常状态下就存在明显的偏差，可见该特征量受变压器初始状态影响，此外对于多绕组松动，该特征量与其他状态区分不够明显。

熵值反映了时间信号的复杂程度，与信号绝对幅值无关。因不同电压等级、不同电流情况下的变压器振动幅值不一样，不同测点的振动幅值也不相同，熵与绝对数值无关的特性非常重要。

熵值具有多种类型，其中排列熵计算不依赖数据长度，具有较强的抗噪能力和鲁棒性［23］。排列熵计算前首先对时间序列X按嵌入维数m和时延τ进行相空间重构，得到轨迹矩阵A，再对每个重构分量按升序排列得到V，嵌入维数为m的条件下共有m！种排列方式，每种符号排列出现的概率为Pi。定义排列熵为

H（m）=-∑li=1PilnPi。（2）

在Pg=1/m时，可得Hp（m）最大值ln（m！），归一化处理后得到最终排列熵值

PE=H（m）/ln（m！）。（3）

排列熵虽然能反映时间序列的随机性，但不能反映信号能量在功率谱下的不确定性，因此增加奇异谱熵作为特征量。奇异谱熵计算前同样进行相空间重构，然后对轨迹矩阵A进行奇异值分解，得到奇异谱S（k），k为非零的奇异值总数。第i个奇异值在整个奇异谱中概率为

pi=λi/∑ki=1λi。（4）

定义奇异谱熵值为

SSE=－∑ki=1pilog（pi）。（5）

根据以上分析，最终选取的时域特征量包括三传感器振动信号之间峰峰值之比、方差之比和相关系数；频域特征量包括三传感器0～1 000 Hz范围内所有100 Hz倍频分量共30个、100 Hz基频分量在振动信号中占比、三传感器100 Hz分量幅值占三者总和百分比；熵值上则选取排列熵和奇异谱熵，共有8种51个特征量，这些特征量不仅反映了单一传感器的振动信号特征，而且体现不同传感器之间的差异，有助于提升诊断准确率。

3" 绕组松动诊断模型

3.1" 核主成分分析法

主成分分析（principal components analysis，PCA）是当前最常用的数据降维算法之一，但传统PCA算法在处理非线性数据时存在不足，同时PCA假定数据符合正态分布，用于非正态分布数据效果不够理想［17］。而KPCA通过引入核函数，将输入映射到高维空间，使得低维空间中的非线性特征转化为高维空间中的线性特征，然后在高维空间中进行PCA降维，获得的主成分贡献率更为集中［24-26］。

设输入为m行的矩阵X，xi为其中的数据样本，通过核函数（x）映射为协方差矩阵C，对协方差矩阵进行特征矢量分解，得到特征值λ和特征向量p，满足Cp=λp。等式两边同时做内积得到

〈Cp，（xk）〉=λ〈p，（xk）〉。（6）

特征向量pi可以由（x）线性表示，设线性系数为ai，代入上式可得：

λ〈p，（xk）〉=λ∑mi=1ai〈（xi），（xk）〉；（7）

〈Cp，（xk）〉=〈1m∑mi=1（xi）T（xi）×

∑mi=1ai（xi），（xk）〉。（8）

定义核矩阵K=〈（xi），（xk）〉，a=［a1，a2，…，am］，则在式（6）～式（8）的基础上得到

λKa=1mKKa。（9）

由此将对非线性输入数据X的降维转变为核矩阵K的PCA降维，K由核函数确定。KPCA常用的核函数有高斯核函数和多项式核函数等。

3.2" XGBoost

XGBoost是以梯度提升树（gradient boosting decision tree，GBDT）算法为基础，以分类回归树（classification and regression tree，CART）为基分类器，对boosting进行改进建立的集成模型［27］。训练中每次迭代生成一个子树拟合现有模型的残差，最终输出结果为所有子树输出的累加值。若共有M棵子树，则模型的输出结果为

y^i=∑Mm=1fm（xi）。（10）

式中：y^i为模型输出；fm是第m个树；xi是第i个样本。XGBoost最小化的目标函数为：

L=∑mi=1l（yi，y^i）+Ω（ft）+ε；（11）

Ω（ft）=γT+12λ∑Ti=1ω2j。（12）

式中：l为损失函数；ε为常数；T为叶子节点数；ω为叶子节点的权重；γ、λ为控制模型复杂程度的正则化参数。相比传统GBDT，XGBoost添加了式（12）所示正则项，对模型的复杂程度进行惩罚，正则化参数越大，越不容易发生过拟合［28］。第t次迭代中目标函数可表示为

L（t）=∑ni=1l（yi，y^（t）i）+Ω（ft）=

∑ni=1l（yi，y^（t－1）i+ft（xi））+Ω（ft）。（13）

对L（t）进行二阶泰勒展开，并删除常数项可得

L（t）≈∑ni=1gift（xi）+12hif2t（xi）+Ω（ft）。（14）

式中gi和hi分别为损失函数的一阶和二阶梯度。设第j个叶子节点样本编号集合为Ij={i|q（xi）=j}。其中q（xi）为xi对应的叶子标签值。则将式（11）改写为

L（t）≈∑Tj=1Gjωj+12（Hj+λ）ω2j+γT。（15）

式中Gj和Hj分别为所有g和h之和。令式（15）对ωj的导数为0，求其最小值，得到叶子节点分值为

ω*=－GjHj+λ。（16）

将式（16）代入目标函数式（15），可得其最小值为

L*=－12∑Tj=1G2jHj+λ。（17）

深度学习优点在于能够从大量复杂数据中提取隐藏特征，适合处理图像等非结构化数据；而XGBoost在处理结构化数据时有较好的表现，并且训练速度更快，对样本数量要求更低。

3.3" 麻雀搜索算法

麻雀搜索算法SSA是根据麻雀觅食行为提出的一种群体优化算法［29-31］，其中麻雀可以分为发现者、追随者以及警觉者三类，其中发现者是适应度值较优的麻雀，为种群寻找适应度高的觅食范围；追随者会跟随发现者一起觅食；当存在捕食者威胁时，警觉者会提醒种群做出反捕行为。

发现者位置更新如下：

xt+1ij=xtijexp－iαTmax，R2lt;Rs;

xtij+QL，R2≥Rs。（18）

式中：xij为麻雀的位置；t为当前迭代次数；Tmax为最大迭代次数；R2∈［0，1］，Rs∈［0.5，1］，分别为预警值和安全值；L为全1向量；α为（0，1］内随机数；Q为正态分布随机数。

追随者位置更新如下：

xt+1ij=Qexpxtωj－xtiji2，igt;n/2;

xt+1pj+|xtij－xt+1pj|A+L，其他。（19）

式中：xω为全局最差位置；xp为当前发现者中最优的位置；A+=AT（AAT）-1，其中A为1×d的矩阵，矩阵元素随机取值-1或1。

SSA算法中按一定比例随机选取警觉者，其位置更新公式为：

xt+1ij=xtij+β|xtij－xtbj|，figt;fg;

xtij+K|xtij－xtωj|（fi－fω）+ε，fi=fg。（20）

式中：fi为第i只麻雀的适应度；fg和fω分别为当前最优和最差适应度；xb为当前全局最优位置；β和K为步长控制参数；ε为避免除零的微小常量。

SSA算法迭代过程中，发现者的变化系数会逐渐向0收敛，各维度不断减小，导致搜索效率下降。因此对发现者更新公式进行改进，引入正态分布和权重因子，将其改写为：

xt+1ij=xtij|normrnd（1，bi）|，R2lt;Rs；

xtij+QL，R2≥Rs。（21）

bi=tanπ41－tTmax+θ。（22）

式中：normrnd（1，bi）是均值为1，标准差为bi的正态分布；bi为变异算子，开始迭代时值较大，增强全局搜索能力，随着迭代不断减小，转向局部精细搜索；θ是避免bi为0的小常量。

SSA使用随机初始化方法生成初始种群，提高初始种群质量有助于加快收敛速度，因此采用反向学习策略。设第j维的最大可行范围为［aj，bj］，麻雀对应的反向个体位置为

x*j=aj+bj－xj。（23）

计算随机生成麻雀和反向麻雀个体的适应度值，若反向个体适应度更优， 则使用反向个体取代随机个体。

3.4" 绕组松动诊断流程

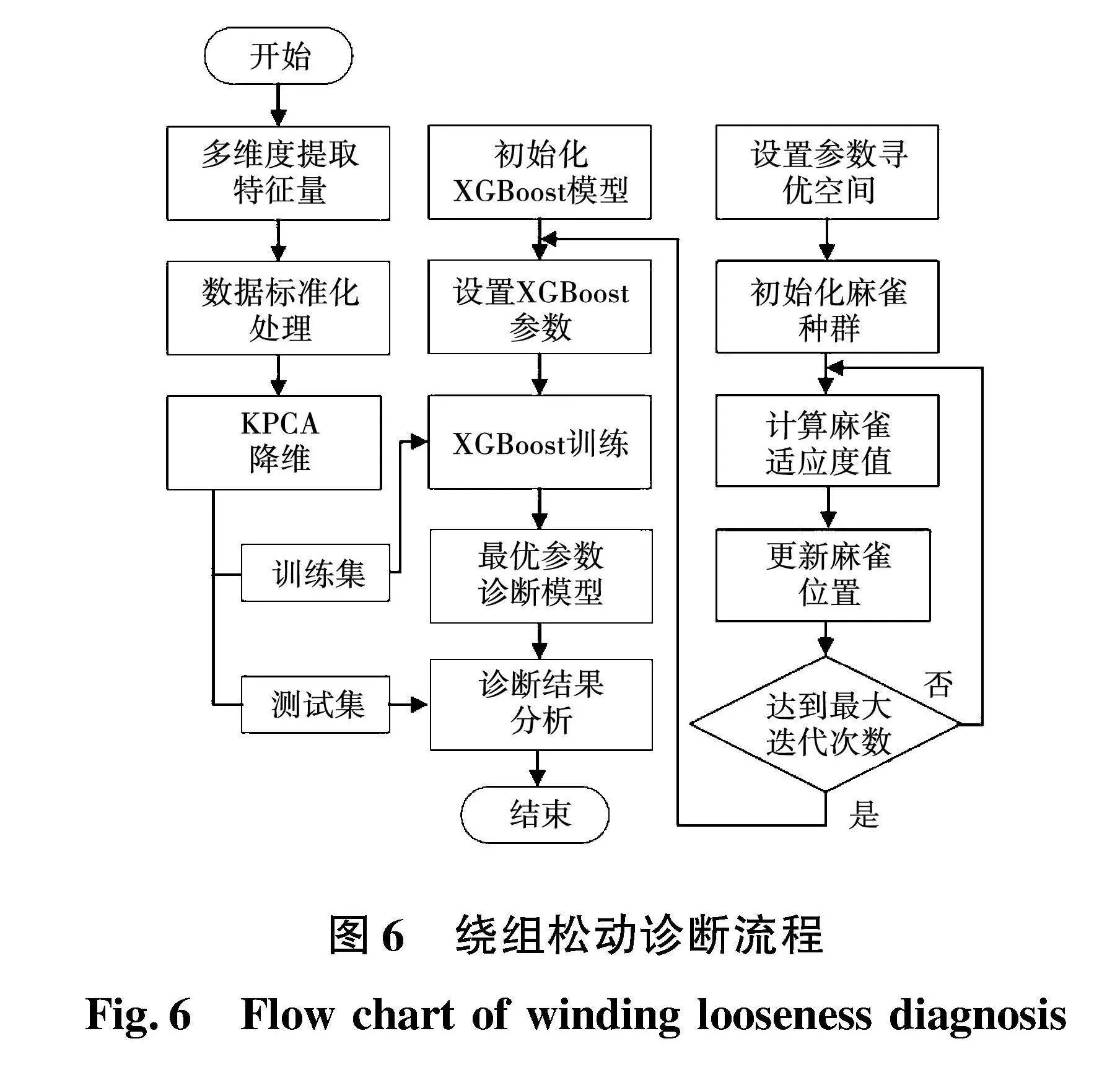
为实现基于多传感器振动信号的变压器绕组松动故障诊断，提出了一种基于多特征量提取和改进麻雀搜索算法优化XGBoost的诊断方法，具体流程如图6所示。

1）振动信号特征量提取，从时域、频域和熵值三方面提取振动信号中特征量；

2）将所提取特征量经过KPCA进行降维，再划分为训练集和验证集；

3）将训练集数据输入XGBoost进行训练，并通过改进麻雀搜索算法调参，得到最优参数，构建绕组松动诊断模型；

4）将测试集数据输入训练好的诊断模型，获得绕组松动故障的诊断结果，并对结果进行分析。

4" 故障诊断及性能分析

4.1" 数据集搭建

为了提取更多的样本进行训练，采用滑动窗口采样，以1 s作为一个窗口，每次向后滑动0.5 s。实验中每组数据采集时长为10 s，每种松动-电流状态组合采集3组数据，故每种组合可得57组样本，其中随机抽取10组用于测试，剩余47组用于训练。因共有30种松动-电流状态组合，共获得训练集样本1 410个，测试集样本300个。为提高分类效果，对故障类型进行独热编码，故障类别划分见2.2节。

因2.3节所提取的不同特征量数值差别较大，量纲也不相同，因此需要对其进行归一化处理。

4.2" KPCA降维

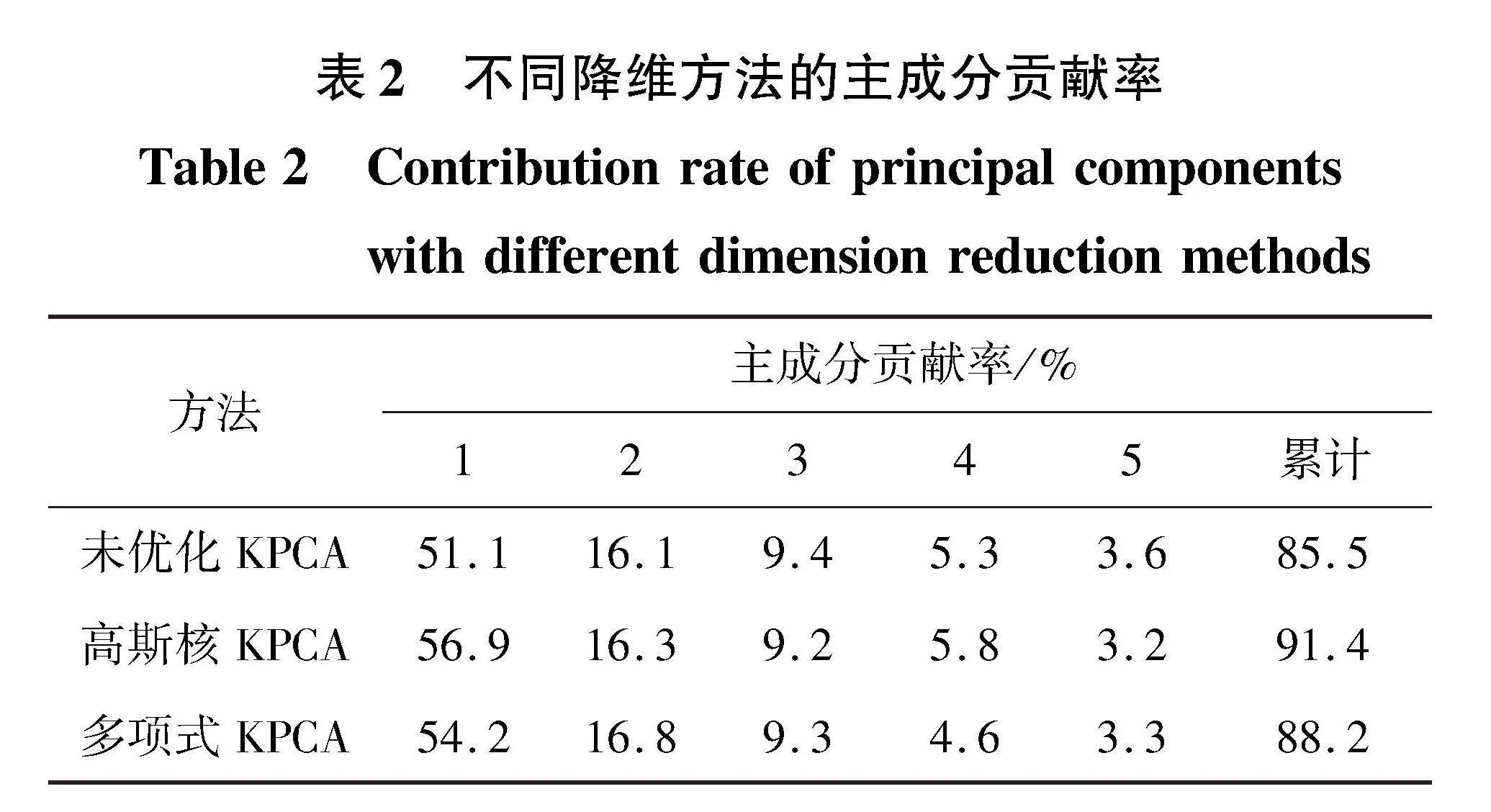
2.3节选取特征量数量较多，为了让特征矩阵在维数较少的情况下包含尽可能多的信息，降低分类模型的计算量和耗时［32］，本文采用KPCA方法进行降维。为提高降维效果，KPCA需要对核函数进行优化，待优化参数包括核函数类型和核函数参数，因待优化参数较为简单，故采用网格搜索算法进行优化，优化目标为第一主成分贡献率，不同降维方法的前5个主成分贡献率如表2所示。

由表2可见，优化后高斯核KPCA取得了最佳降维效果。优化后高斯核KPCA相比于未优化KPCA，第一主成分贡献率提升了5.8%，相比于多项式KPCA算法提升了2.7%。前5个主成分累计贡献率达到了91.4%，已经涵盖了足够的信息特征，因此只需要使用前5个主成分进行下一步的训练和诊断，从而将特征维数由51维压缩到5维。

4.3" 优化XGBoost模型建立

以4.2节提取的前5个主成分作为输入特征向量，对XGBoost进行训练，构建绕组松动诊断模型。因XGBoost参数较多，手动调参非常复杂耗时，因此本文选用改进麻雀搜索算法，以5折交叉验证方式对参数进行优化，从而提升模型的准确率。

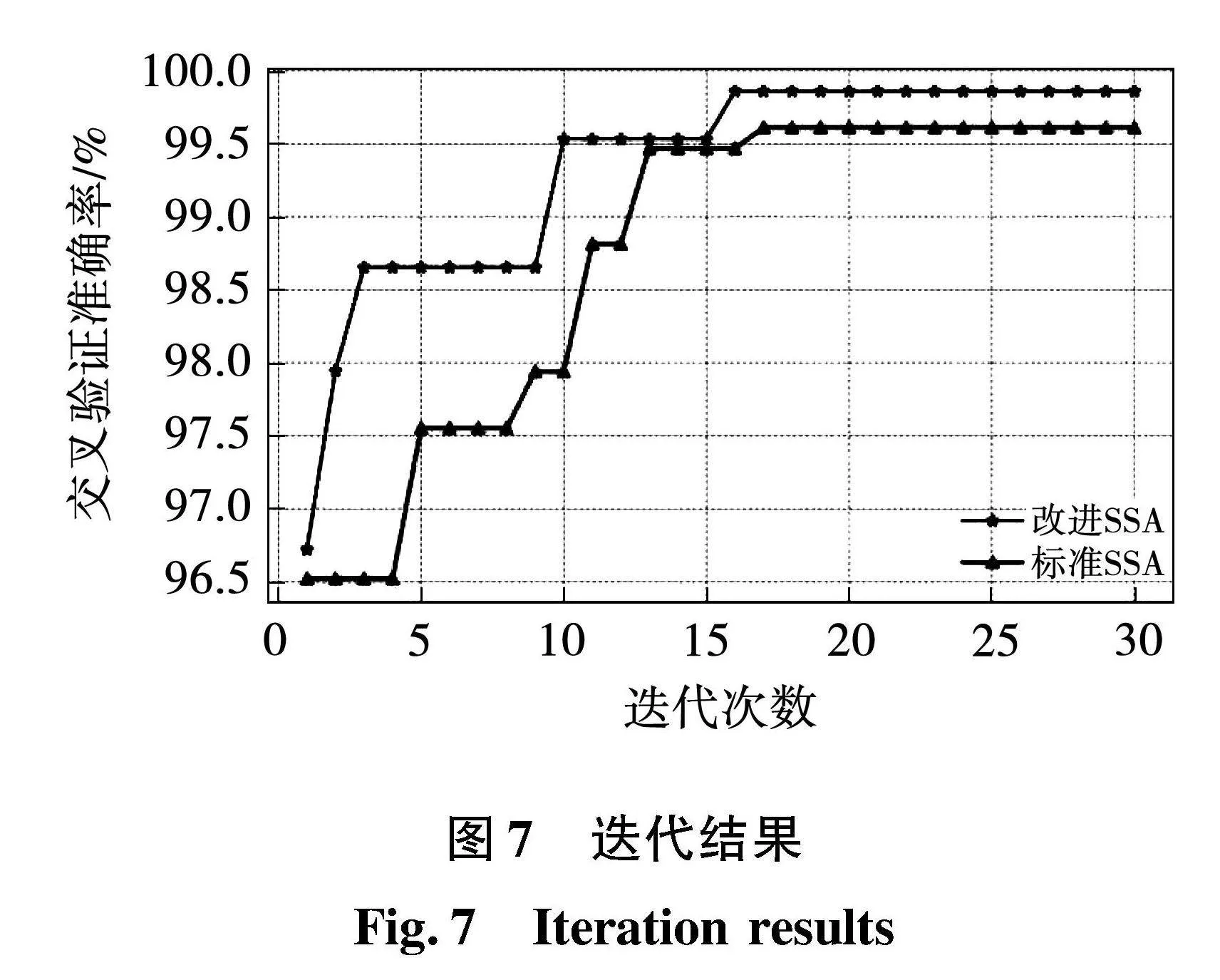
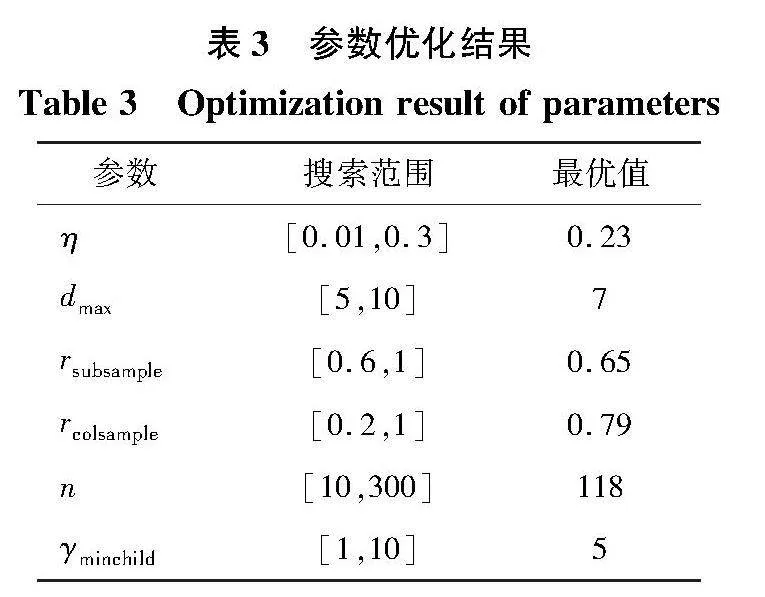
选取对XGBoost训练效果影响最为显著的6个参数作为待优化参数，包括学习率η、最大深度dmax、抽样比例rsubsample、特征采样率rcolsample、基本分类器数量n和最小叶子节点样本权重γminchild，最大迭代次数30次。交叉验证精确度优化曲线如图7所示，参数搜索范围及优化结果见表3。

由图7可见，经过约15次迭代，XGBoost交叉验证精确度达到了99.86%，并保持稳定，最终收敛精确度优于标准麻雀搜索算法。将优化后参数带入XGBoost进行训练，得到故障诊断模型，在测试集上诊断准确率达到了99.00%，而未优化XGBoost的准确率为96.33%，提升了2.67%，证明了优化算法的有效性，能够满足参数优化的需求。

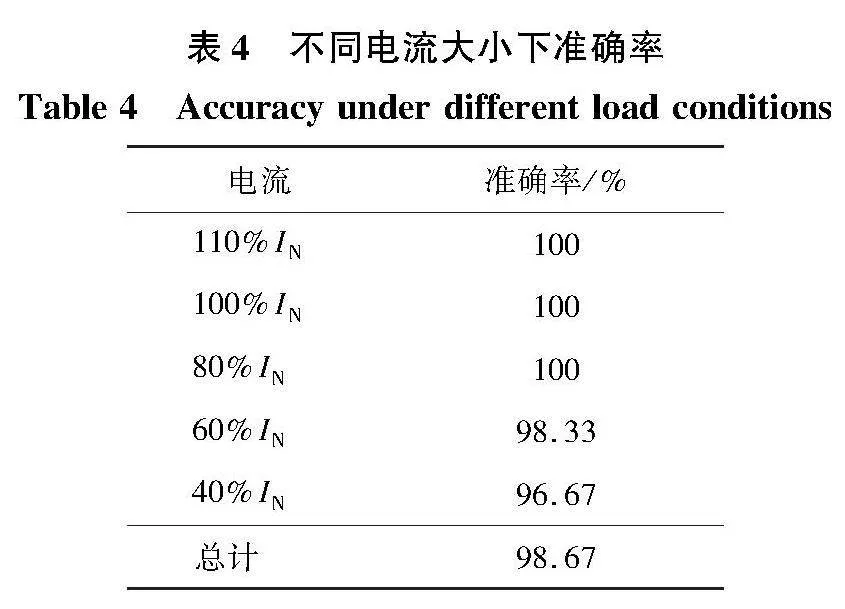
不同电流大小下，绕组松动诊断准确率如表4所示，可见在不同电流大小下本文方法均有较好的诊断效果，能够识别故障类型和故障相，尤其是电流较大情况下，只有在40%额定电流下，由于电流过小导致振动幅值较弱，因此诊断效果较差。

此外，为验证KPCA降维对降低分类难度、缩短训练时间的重要性，使用未降维的原始特征以同样方法进行训练和诊断，耗时和准确率对比如表5所示。由表5可见，由于降维后的特征量数量更少，优化耗时缩短了53.58%，得到最优参数后的训练耗时则缩短了91.67%，证明经过KPCA降维，在保留了区分度的同时大幅减少了训练计算量。随着样本数量扩大，采用未降维特征的耗时会进一步增加，因此采用KPCA降维更具优势。

4.4" 特征量对比

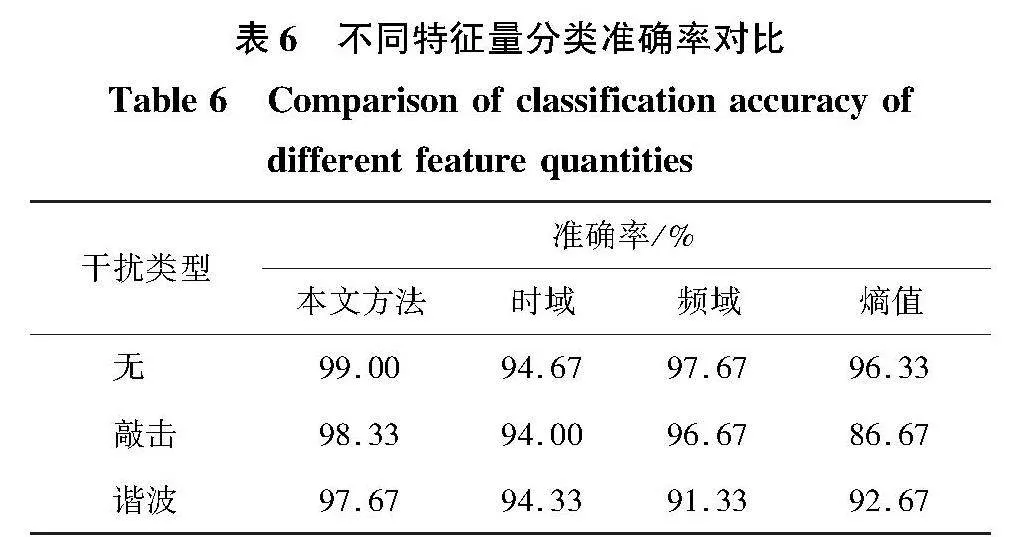
为证明本文所选取的多维度特征量相比单一维度特征量具有更好的诊断效果，对使用不同特征量进行诊断的效果进行对比；并以一定比例将敲击变压器产生的振动信号和谐波分量（300、400、500 Hz）分别作为干扰信号叠加入原始的振动信号中，信噪比约为20 dB，进行不同特征量的抗干扰能力评估。

不同特征量分类准确率对比见表6。可见本文所用的多维度特征量具有较强的抗干扰能力，在添加干扰后依旧有97%以上的准确率，可以有效减少干扰影响，并且无论是否存在干扰，准确率均明显优于仅使用单一维度特征量，相比单一维度特征量具有明显的优势；单独使用某一维度特征量，在存在干扰时，准确率会明显下降；频域特征量对特征频率（50 Hz倍频）含量较低的敲击振动信号有较强的抗干扰能力，但受谐波分量干扰较为明显；敲击振动信号改变了信号的随机性，对熵值特征量的影响较为显著。

4.5" 分类模型优越性验证

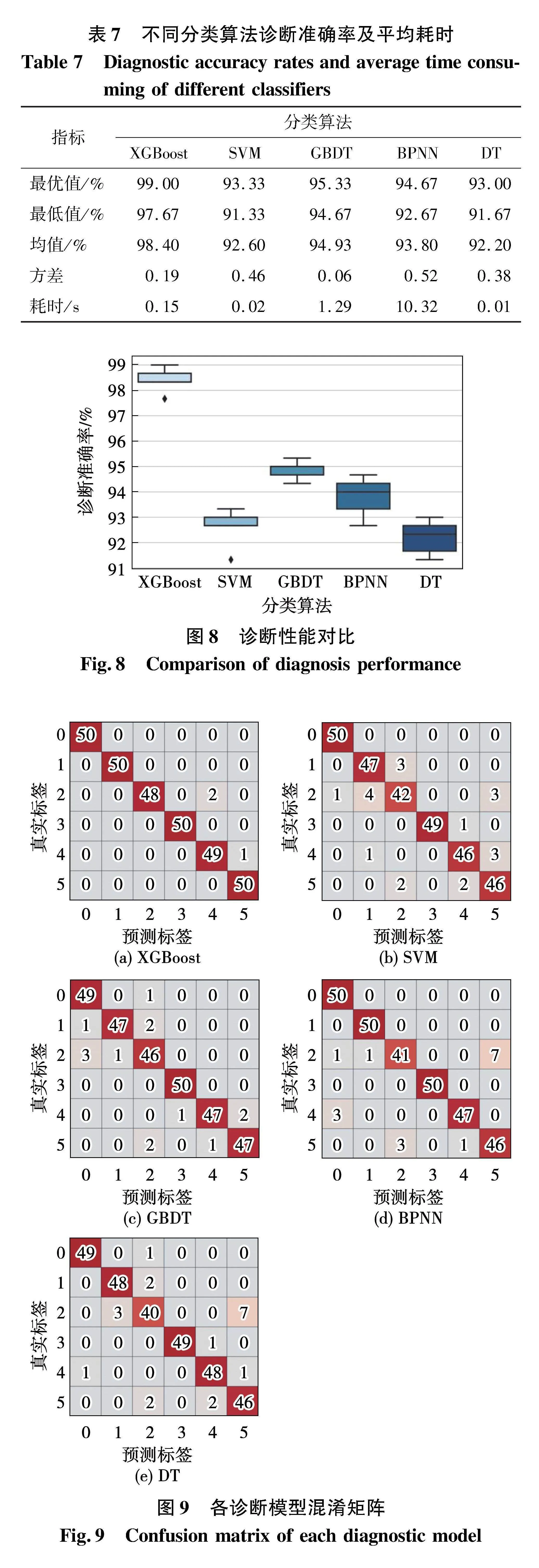
为证明本文分类模型的优越性，使用优化后XGBoost算法与以下4种传统分类算法进行对比，分别为SVM、GBDT、反向传播神经网络（back propagation neural network，BPNN）和DT。同时为证明本文方法具有较强的诊断稳定性并减少偶然性因素，对所有分类模型均进行5次测试，每次随机抽取训练和测试样本，准确率和平均训练耗时对比见表7和图8，最优混淆矩阵如图9所示，根据诊断结果可知：

1）所有分类算法准确率均能达到90%以上，证明本文多种特征量融合的方法能够很好地反映故障特性，避免了因负载电流变化等因素导致的特征量重叠，具有明显的优越性。

2）在精确度方面，本文方法相比于其他分类算法有明显提升。相比SVM、GBDT、BPNN和DT准确率分别提升了5.67%、3.67%、4.33%和6%。由混淆矩阵可见本文方法具有很高的准确率，虽然存在少量故障分类错误的情况，但对是否存在故障的判断准确率达到接近100%，可以准确识别是否存在绕组松动。

3）XGBoost不仅诊断准确率更高，还具有更高的稳定性，准确率方差小于除GBDT外的分类算法，在不同的训练集和测试集上均能有效识别绕组松动。

4）在耗时方面，由于XGBoost加入了正则化方法，限制了模型复杂度，并且支持并行计算，因此训练速度较快，相比于GBDT和BPNN训练耗时明显缩短。

5" 结" 论

1）针对单一特征量易受干扰和负载影响而导致误判、漏判问题，本文提取了多种适用于变压器多传感器振动信号的特征量，反映的故障信息更加全面，有效提高了准确率和抗干扰能力。

2）采用KPCA对特征量进行降维，能够有效减少特征维度而保留主要信息，从而降低后续诊断计算量，在具有较高准确率的同时，大幅减少了优化和训练所需时间。

3）使用改进麻雀搜索算法对XGBoost参数进行优化，经过较少的迭代次数有效提升了诊断精确度，诊断准确率达到99.00%。相比于其他分类算法，优化后的XGBoost具有更高的准确率和稳定性。

4）实验分析结果表明，本文方法可以在40%～110%额定电流下有效判断是否存在绕组松动，并定位松动故障相，大体判断故障程度，对变压器绕组松动在线检测有一定参考价值。

参 考 文 献：

［1］" 汲胜昌，张凡，师愉航，等. 基于振动信号的电力变压器机械状态诊断方法研究综述［J］. 高电压技术， 2020， 46（1）： 257.

JI Shengchang， ZHANG Fan， SHI Yuhang， et al. Review on vibration-based mechanical condition monitoring in power transformers［J］. High Voltage Engineering， 2020， 46（1）： 257.

［2］" 周宇，马宏忠，李凯，等. 基于相空间重构的大型变压器绕组松动的振动特征识别［J］. 电力自动化设备， 2016， 36（12）： 169.

ZHOU Yu， MA Hongzhong， LI Kai， et al.Winding looseness recognition based on phase space reconstruction of large transformer vibration signals［J］. Electric Power Automation Equipment， 2016， 36（12）： 169.

［3］" 侯鹏飞，马宏忠，吴金利，等. 基于混沌理论与蝗虫优化K-means聚类算法的电抗器铁心和绕组松动状态监测［J］. 电力自动化设备， 2020， 40（11）： 181.

HOU Pengfei， MA Hongzhong， WU Jinli， et al. Looseness status monitoring of reactor core and winding based on chaos theory and K-means clustering algorithm optimized by grasshopper algorithm［J］.Electric Power Automation Equipment，2020，40（11）：181.

［4］" 李鹏，毕建刚，于浩，等. 变电设备智能传感与状态感知技术及应用［J］. 高电压技术， 2020， 46（9）： 3097.

LI Peng， BI Jiangang， YU Hao， et al. Technology and application of intelligent sensing and state sensing for transformation equipment ［J］. High Voltage Engineering， 2020， 46（9）： 3097.

［5］" 马宏忠，李楠，杨启帆，等. 基于多特征声纹图谱的变压器绕组松动在线故障诊断方法［J］.电机与控制学报，2023，27（5）：76.

MA Hongzhong， LI Nan， YANG Qifan， et al. On-line fault diagnosis method of transformer winding looseness based on multi-characteristic voiceprint maps［J］. Electric Machines and Control， 2023， 27（5）： 76.

［6］" 赵仲勇，唐超，李成祥，等.基于频率响应二值化图像的变压器绕组变形故障诊断方法［J］.高电压技术， 2019，45（5）：1526.

ZHAO Zhongyong， TANG Chao， LI Chengxiang， et al. Transformer winding deformation fault diagnosis method based on frequency response binarization image ［J］. High Voltage Engineering，2019，45（5）：1526.

［7］" 王琦，付超，王欣盛，等.变压器绕组短路电抗在线测量工程应用研究 ［J］.高电压技术， 2020， 46（11）： 3943.

WANG Qi， FU Chao， WANG Xinsheng， et al. Engineering application research on on-line measurement of transformer winding short-circuit reactance［J］. High Voltage Engineering， 2020， 46（11）： 3943.

［8］" 李宏达，黄鼎琨，张彬，等.改进的低压脉冲法对变压器绕组变形的探测研究［J］.南京理工大学学报， 2020， 44（1）： 15.

LI Hongda， HUANG Dingkun， ZHANG Bin， et al. Research on the detection of transformer winding deformation by improved low voltage pulse method［J］. Journal of Nanjing University of Science and Technology， 2020， 44（1）： 15.

［9］" 赵莉华，丰遥，谢荣斌，等. 基于交叉小波的变压器振动信号幅频特征量提取方法［J］. 高电压技术， 2019， 45（2）： 505.

ZHAO Lihua， FENG Yao， XIE Rongbin， et al. Amplitude and frequency feature extraction for transformer vibration based on cross-wavelet transform［J］. High Voltage Engineering， 2019， 45（2）： 505.

［10］" 赵莉华，徐立，刘艳，等. 基于点对称变换与图像匹配的变压器机械故障诊断方法［J］. 电工技术学报， 2021， 36（17）： 3614.

ZHAO Lihua， XU Li， LIU Yan， et al. Transformer mechanical fault diagnosis method based on symmetrized dot patter and image matching［J］. Transactions of China Electrotechnical Society， 2021， 36（17）： 3614.

［11］" 张琳，马宏忠，姜宁，等. 基于奇异谱熵和支持向量机的变压器绕组松动识别及定位［J］. 电力系统保护与控制，2017，45（18）：69.

ZHANG Lin， MA Hongzhong， JIANG Ning， et al. Recognition and location of transformer winding looseness based on singular value spectrum entropy and SVM［J］. Power System Protection and Control， 2017， 45（18）： 69.

［12］" 杜厚贤，刘昊，雷龙武，等. 基于振动信号多特征值的电力变压器故障检测研究［J］. 电工技术学报， 2023， 38（1）： 83.

DU Houxian， LIU Hao， LEI Longwu， et al. Power transformer fault detection based on multi-eigenvalues of vibration signal［J］.Transaction of China Electrotechnical Society，2023，38（1）：83.

［13］" 赵莉华，张振东，张建功，等.运行工况波动下基于振动信号的变压器故障诊断方法［J］.高电压技术，2020，46（11）：3925.

ZHAO Lihua， ZHANG Zhendong， ZHANG Jiangong， et al. Diagnosis methods for transformer faults based on vibration signal under fluctuating operating conditions［J］. High Voltage Engineering， 2020， 46（11）： 3925.

［14］" HONG K X， HUANG H， FU Y， et al. A vibration measurement system for health monitoring of power transformers［J］. Measurement， 2016， 93： 135.

［15］" HONG K X， HUANG H， ZHOU J. Winding condition assessment of power transformers based on vibration correlation［J］. IEEE Transactions on Power Delivery， 2015， 30（4）： 1735.

［16］" 李楠，马宏忠，张玉良，等. 基于特征筛选和改进深度森林的变压器内部机械状态声纹识别［J］. 电机与控制应用， 2022， 49（9）： 57.

LI Nan， MA Hongzhong， ZHANG Yuliang， et al. Voiceprint recognition of transformer internal mechanical state based on feature screening and improved deep forest［J］. Electric Machines amp; Control Application， 2022， 49（9）： 57.

［17］" 张又文，冯斌，陈页，等. 基于遗传算法优化XGBoost的油浸式变压器故障诊断方法［J］. 电力自动化设备， 2021， 41（2）： 200.

ZHANG Youwen， FENG Bin， CHEN Ye， et al. Fault diagnosis method for oil-immersed transformer based on XGBoost optimized by genetic algorithm［J］.Electric Power Automation Equipment， 2021， 41（2）： 200.

［18］" 李轩，梅飞，沙浩源，等. 基于多状态数据均衡与XGBoost的特高压换流阀运行状态评估［J］. 高电压技术， 2022， 48（2）： 644.

LI Xuan， MEI Fei， SHA Haoyuan， et al.Operation state evaluation of UHV converter valve based on multi-state data equalization and XGBoost［J］.High Voltage Engineering，2022，48（2）：644.

［19］" 颜锦，马宏忠，朱昊，等. 基于LMD边际谱能量熵与FWA-SVM的变压器绕组松动诊断［J］.电测与仪表，2021，58（11）：74.

YAN Jin， MA Hongzhong， ZHU Hao， et al.Diagnosis for transformer winding looseness based on LMD marginal spectrum energy entropy and FWA-SVM［J］.Electrical Measurement amp; Instrumentation，2021，58（11）：74.

［20］" 张仕民，丰遥. 基于振动信号的变压器铁心与绕组故障区分方法［J］. 电测与仪表， 2021， 58（6）： 161.

ZHANG Shimin， FENG Yao. Discrimination method of transformer core and winding fault based on vibration signal［J］. Electrical Measurement amp; Instrumentation， 2021， 58（6）： 161.

［21］" 师愉航，汲胜昌，张凡，等. 变压器绕组多倍频振动机理及特性［J］. 高电压技术， 2021， 47（7）： 2536.

SHI Yuhang， JI Shengchang， ZHANG Fan， et al.Multi-frequency vibration mechanism and characteristics of transformer windings［J］. High Voltage Engineering， 2021， 47（7）： 2536.

［22］" 祝丽花，杨庆新，闫荣格，等.考虑磁致伸缩效应电力变压器振动噪声的研究［J］.电工技术学报， 2013， 28（4）： 1．

ZHU Lihua， YANG Qingxin， YAN Rongge， et al. Research on vibration and noise of power transformer cores including magnetostriction effects［J］. Transaction of China Electrotechnical Society， 2013， 28（4）： 1.

［23］" 常龙康，魏健雄，于飞，等. 基于LMD-WSVD的半球谐振陀螺混合去噪方法［J］.系统工程与电子技术，2023，45（2）：497.

CHANG Longkang， WEI Jianxiong， YU Fei， et al. A hybrid denoising method for hemispherical resonant gyroscope based on LMD-WSVD ［J］.Systems Engineering and Electronics， 2023， 45（2）： 497.

［24］" 李军，常燕芝. 基于KPCA-KMPMR的短期风电功率概率预测［J］.电力自动化设备， 2017， 37（2）： 22.

LI Jun，CHANG Yanzhi. Short-term probabilistic forecasting based on KPCA-KMPMR for wind power［J］. Electric Power Automation Equipment， 2017， 37（2）： 22.

［25］" 王昱皓，武建文，马速良，等. 基于核主成分分析-SoftMax的高压断路器机械故障诊断技术研究［J］. 电工技术学报， 2020， 35（S1）： 267.

WANG Yuhao， WU Jianwen， MA Suliang， et al. Mechanical fault diagnosis research of high voltage circuit breaker based on kernel principal component analysis and SoftMax［J］. Transactions of China Electrotechnical Society， 2020， 35（S1）： 267.

［26］" 乔延辉，韩爽，许彦平，等. 基于天气分型的风光出力互补性分析方法［J］. 电力系统自动化， 2021， 45（2）： 82.

QIAO Yanhui， HAN Shuang， XU Yanping， et al. Analysis method for complementarity between wind and photovoltaic power outputs based on weather classification［J］. Automation of Electric Power Systems， 2021， 45（2）： 82.

［27］" 王愈轩，梁沁雯，章思远，等.基于LSTM-XGboost组合的超短期风电功率预测方法［J］.科学技术与工程，2022，22（14）：5629.

WANG Yuxuan， LIANG Qinwen， ZHANG Siyuan， et al. An ultra-short-term wind power prediction method based on LSTM-XGboost combination［J］.Science Technology and Engineering，2022，22（14）：5629.

［28］" 刘维功，王昊展，时振堂，等.基于改进XGBoost算法的XLPE电缆局部放电模式识别研究［J］.电测与仪表，2022，59（4）：98.

LIU Weigong， WANG Haozhan， SHI Zhentang， et al. Research on partial discharge pattern recognition of XLPE cable based on improved XGBoost algorithm［J］.Electrical Measurement amp; Instrumentation，2022，59（4）：98.

［29］" 宋冬然，晏嘉琪，夏鄂，等．基于改进麻雀搜索算法的大型海上风电场电缆布置优化［J］．电力系统保护与控制，2022，50（12）： 134．

SONG Dongran， YAN Jiaqi， XIA E， et al. Optimization of cable layout for large-scale offshore wind farms based on an improved sparrow search algorithm［J］. Power System Protection and Control， 2022， 50（12）： 134.

［30］" 杜江，郭世炜. 基于多策略改进麻雀搜索算法的铸铜转子感应电动机优化［J］. 电机与控制学报， 2023， 27（2）： 35.

DU Jiang， GUO Shiwei.Optimization of cast copper rotor induction motor based on multi-strategy improved sparrow search algorithm ［J］. Electric Machines and Control， 2023， 27（2）： 35.

［31］" 叶远波， 李端超， 谢民， 等． 基于SSA-SVM的继电保护装置状态评估方法研究［J］． 电力系统保护与控制， 2022， 50（8）：171．

YE Yuanbo， LI Duanchao， XIE Min， et al. A state evaluation method for a relay protection device based on SSA-SVM ［J］.Power System Protection and Control， 2022， 50（8）： 171.

［32］" 崔佳嘉，马宏忠. 基于改进MFCC和3D-CNN的变压器铁心松动故障声纹识别模型［J］. 电机与控制学报， 2022， 26（12）： 150.

CUI Jiajia， MA Hongzhong.Voiceprint recognition model of transformer core looseness fault based on improved MFCC and 3D-CNN［J］. Electric Machines and Control， 2022， 26（12）： 150.

（编辑：邱赫男）