基于d-q变换及WOA-LSTM的异步电机定子匝间短路故障诊断方法

摘" 要：

为了实现对异步电机定子绕组匝间短路故障的可靠在线诊断，提出一种基于d-q变换及鲸鱼优化算法（WOA）优化的长短期记忆网络（LSTM）的故障诊断方法。通过理论推导可知，d-q变换可有效提取定子电流中的特征频谱数据。采用鲸鱼优化算法对长短期记忆网络中的3个关键参数进行优化，建立WOA-LSTM故障分类模型。为了验证基于d-q变换和WOA-LSTM故障诊断方法的有效性，分别以小波变换、快速傅里叶变换及d-q变换提取电流频谱数据作为输入数据集，以一台YE2-100L1-4型异步电机为实验对象进行实验验证。研究结果表明：相比于小波变换及快速傅里叶变换，采用d-q变换能更准确的提取出定子电流中的故障特征，更精确地反映电机故障状态，有助于提高故障分类准确率；相比于传统的LSTM算法，经WOA优化后的LSTM算法分类准确率可达98.3％，能可靠地实现不同程度匝间短路故障的诊断。

关键词：异步电机；故障诊断；定子绕组匝间短路；d-q变换理论；鲸鱼优化算法；长短期记忆神经网络

DOI：10.15938/j.emc.2024.06.006

中图分类号：TM343

文献标志码：A

文章编号：1007-449X（2024）06-0056-10

收稿日期： 2023-07-18

基金项目：

作者简介：王喜莲（1974—），女，博士，教授，博士生导师，研究方向为开关磁阻电机、无轴承电机及其控制、电机故障诊断；

秦嘉翼（1999—），女，硕士研究生，研究方向为电机故障诊断、在线故障诊断；

耿" 民（1980—），男，硕士，高级工程师，研究方向为高速动车组牵引系统、电机故障监测。

通信作者：王喜莲

Asynchronous motor stator turn-to-turn short circuit fault diagnosis based on d-q transform and WOA-LSTM

WANG Xilian1，" QIN Jiayi1，" GENG Min2

（1.School of Electrical Engineering， Beijing Jiaotong University， Beijing 100044，China;

2.Motor Vehicle Maintenance Department， CRRC Tangshan Co.， Ltd.， Tangshan 063035， China）

Abstract：

In order to realize reliable online diagnosis of inter-turn short-circuit faults in asynchronous motor stator windings， a fault diagnosis method based on d-q transform and whale optimization algorithm （WOA） optimized long-short-term memory network （LSTM） was proposed. It is known through theoretical derivation that the d-q transform can effectively extract the characteristic spectral data in the stator current. The whale optimization algorithm was used to optimize the three key parameters in the long short-term memory network and the WOA-LSTM fault classification model was established. In order to verify the effectiveness of the fault diagnosis method based on d-q transform and WOA-LSTM， wavelet transform， fast Fourier transform and d-q transform were used to extract the current spectrum data as the input data set， and a YE2-100L1-4 asynchronous motor was used as the experimental object for experimental verification. The results show that compared with wavelet transform and fast Fourier transform， the d-q transform can more accurately extract the fault features in the stator current， more accurately reflect the fault state of the motor， and help to improve the fault classification accuracy. Compared with the traditional LSTM algorithm， the classification accuracy of LSTM algorithm optimized by WOA can reach 98.3%， which can reliably realize the diagnosis of inter-turn short-circuit faults of different degrees.

Keywords：asynchronous motor; fault diagnosis; stator winding turn-to-turn short circuit; d-q transform theory; whale optimization algorithm; long and short-term memory neural networks

0" 引" 言

随着现代化社会的不断发展，三相异步电机在工农业生产、电力系统及交通运输等领域都占有一席之地，其消耗的电能在电网总负荷中占比过半。然而，由于频繁启动制动、运行工况不稳定以及制造工艺等的影响，电机发生故障的概率较高。研究表明，定子绕组匝间短路故障占异步电机总故障的38%［1］。当电机发生早期匝间短路故障时，若不及时对其进行诊断维修，往往会导致故障扩大，危及电机本身及整个系统的安全，所以进行异步电机定子匝间短路故障诊断的研究对电力系统的安全具有重大意义［2］。

国内外已经有许多学者为准确诊断匝间短路故障做出研究，相继提出了多种各具特色的故障监测与诊断方法，主要可分为三类：基于特征信号的故障诊断、基于解析模型的故障识别、基于人工智能的故障监测。

国内外学者们对于基于特征信号的故障诊断方法一直保持着高度的关注。电机定子发生匝间短路故障后，会产生一系列变化特征量，通过采集信号，利用信号处理方法提取特征量以指示故障的变化。电机定子绕组匝间短路故障会引起电机气隙磁场不平衡，从而在定子电流及转矩中产生一定的谐波分量，因此有学者通过提取定子电流的谐波分量或转矩信号中的二倍频分量［3］来检测匝间短路故障。由于电机运行条件多变，傅里叶分析无法准确提取谐波分量，为了解决该问题，专家们相继提出了多种频谱提取算法，如小波分析［4］、与差分算法结合的Prony算法［5］等，但上述频谱分析算法较为复杂。为了提高故障诊断的高效性，有学者基于多次派克变换提取电流的特征谐波分量，提出了新的故障特征量，避免了复杂的谱分析，但该特征量仍受负载影响，可靠性有待提高［6］。由于定子匝间短路属于不对称故障，会使电机定子电流产生负序分量［7］。有学者对双馈异步发电机在风速恒定时的匝间短路故障状态进行了仿真分析，研究表明定子负序电流有利于轻载状态时的故障诊断［8］。有学者研究了计及转子故障时的异步电动机定子绕组匝间短路故障，并提出了滤除转子故障的负序电流，提高了负序分量法检测的可靠性［9］。此外，不对称故障还会造成定子电流的帕克矢量轨迹发生畸变，因此可通过监测帕克矢量轨迹来诊断故障［10］，但负序电流和帕克矢量轨迹均受电源电压不平衡及负载变化的干扰。为了解决电压不平衡时的故障诊断问题，许多学者提出了与阻抗相关的故障特征量。阻抗主要与电机的固有特性相关，受电机运行工况的影响较小，因此有学者以负序视在阻抗作为故障特征量来诊断异步电机匝间短路故障［11-12］。基于负序视在阻抗理论，有学者提出了拟序阻抗，将其应用至双馈异步电机的故障诊断［13］，但拟序阻抗的表达式涉及转子电流，不适用于普通异步电机的故障诊断。由于电机固有不对称、信号检测及计算误差等的影响，负序视在阻抗法的准确度有待提高。上述特征量及其信号提取方法都具有各自的局限性，特征量在不同工况下的通用性和可靠性，信号提取的准确度和复杂度等问题都亟待解决。

基于解析模型的方法核心在于利用已经建立的电机模型，其中匝间短路故障部分被视为关键辨识参数，通过比较辨识所得的值和实际监测的值判断故障。有学者通过引入不对称矩阵建立故障电机模型，对故障后的电机进行分析［12］；也有学者采用多回路模型对故障瞬变过程进行数字仿真，对不同特征值的灵敏度和可靠性进行研究［14］。通过改变模型参数可以灵活的控制电机状态，为早期故障诊断的研究提供了便捷的工具，但是由于数学模型受电机设计参数的影响较大，且无法模拟实际运行时的多种工况，导致解析模型无法精确建立，容易引起故障误诊断。

随着数据挖掘和智能算法的飞速发展，基于人工智能的诊断方法成为当前的研究热点，不同的信号处理和智能算法可以衍生出多种分类模型，用于故障诊断。有学者利用支持向量机进行故障诊断，在不同负载电流大小时选取不同的特征值作为数据集，效果良好，但支持向量机依赖于参数调节和核函数的选择，当特征数据过大时易出现过拟合［15］。有学者提出小波神经网络对电机故障状态进行识别，该方法采用小波分析处理数据，将特征信息作为BP神经网络输入，输出故障类别，但是BP神经网络容易陷入局部最优，不利于故障识别［16］。卷积神经网络（convolutional neural networks，CNN）作为深度学习的基础模型，在故障诊断领域也备受关注，有学者在传统CNN模型的基础上提出一种多尺度卷积核和多源机电信息融合的故障诊断方法，显著提高了同步发电机的故障诊断准确率［17］。此外， 循环神经网络（recurrent neural network，RNN）在处理长序列数据方面效果良好，但不适于对具有较大的时程数据进行分析。长短期记忆神经网络（long-short term memory，LSTM）是RNN的一种特殊变体，其特殊的细胞状态有效解决了RNN的长期依赖问题，已被应用至故障诊断领域。有学者提出一种基于深度迁移学习与LSTM相结合的微电网故障识别方法，提高了微电网故障诊断模型的精度［18］；也有学者提出了一种基于快速傅里叶变换和LSTM的变速抽蓄机组转子绕组短路故障和转子偏心故障诊断方法，能够克服测量噪声和不同工况的影响，可靠性高［19］。

基于上述考虑，本文首先对电机故障前后的定子电流特征进行理论分析，得到故障后定子电流中的特征频率，并通过理论推导提出以d-q变换提取特征频谱的数据处理方法。在此基础上，引入长短期记忆神经网络，提取电机定子电流的特征频谱数据作为数据集输入至LSTM网络中，并利用鲸鱼优化算法（whale optimization algorithm，WOA）对模型中的3个关键参数（隐藏层神经元个数，初始学习率，学习率下降因子）进行优化，依据最优参数组合对LSTM进行训练，网络输出为故障类型的诊断结果。经过实验对比分析，结果表明，以d-q变换提取电流特征频率作为数据预处理方法，比快速傅里叶变换和小波分析进行预处理的结果准确率高，且WOA-LSTM模型相较于原始LSTM模型，准确率显著提高，能更为可靠的进行异步电机匝间短路故障诊断，为异步电机故障诊断提供新的思路和方法。

1" 定子电流特征频率提取

1.1" 定子电流谐波特征

异步电机正常运行时，定子绕组通电，在转子侧感应出电动势，定、转子磁动势合成了气隙磁动势。当定子某相绕组发生匝间短路，相当于在该相绕组上附加短路环，短路电流产生的磁动势将使合成磁动势发生畸变。

单匝线圈磁动势幅值经过傅里叶分解可展开为

F（α1）=22I1πp∑υ1υkyυcos（υα1）。（1）

式中：I1为流过单匝线圈的电流有效值；p为极对数；kyυ为线圈节距因数；α1为线圈两边相隔的空间电角度；υ为谐波次数，υ=1p，2p，3p…，对于整距线圈υ≠2，4，6…。

设短路后叠加在短路匝上的电流为if=2Ifcos（ωt），短路匝沿气隙圆周的空间电角度为α=pθ，短路电流产生的磁动势傅里叶展开式如下：

F（t，θ）=2Iπp∑υ1υkyυcos（ωt±υpθ）。（2）

式中：I为流过线圈的电流有效值；θ为以定子坐标表示的机械角度；θ=θr+［（1－s）ωt］/p，θr为转子坐标机械角度；s为转差率；p为极对数；ω为角频率。

该磁动势在转子绕组中感应的电流分量可表示为

iR=∑υ2IRυcos［ωt±（1－s）υωt］。（3）

式中IRυ是转子侧电流的有效值。

若电机转子三相绕组对称，则电流iR产生的磁动势可表示为

Fr（t，θr）=

∑υ∑nFυ，ncos（ωt±（1－s）υωt－npθr）。（4）

式中：Fυ，n是n次谐波磁动势的幅值；n是转子谐波次数，n=6k±1，k=0，1，2，…。

其在定子坐标系下可表示为

Fr（t，θ）=

∑υ∑nFυ，ncos{［1+（n±υ）（1－s）］ωt－npθ}。（5）

根据上述分析可知，电机定子某相发生匝间短路故障后，将在定子侧感应出频率为［1+（n±υ）（1－s）］f1的电流谐波分量，f1为定子频率。因此，当电机发生匝间短路故障后，定子电流的频谱数据可以作为诊断故障的特征数据。

1.2" d-q变换提取电流频谱特征

d-q变换是一种常用的分析交流电机模型的坐标变换方法，三相静止坐标系下电流的基波正序分量通过d-q变换可以变为直流分量。坐标变换的原理图如图1所示。

设电流信号中含有角频率为ω的基波分量及角频率分别为ω1，ω2，…的谐波分量，则该电流可以表示为

is1=Imcos（ωt+θ）+I1cos（ω1t+θ1）+

∑∞n=2Incos（ωnt+θn）。（6）

式中：n为正整数；Im，I1，I2，…分别为基波、各谐波分量的幅值；ω，ω1，ω2，…分别为基波、各谐波分量的角频率；θ，θ1，θ2，…分别为基波、各谐波分量的初始相位角。

设频率为ω1的分量周期为T1，将电流信号is1在时间轴上向左移动2T1/3生成信号is2，向左移动4T1/3生成信号is3，则is1，is2及is3中角频率为ω1的分量相位互差120°。其表达式如下：

is2=Imcos（ωt+θ+θ′）+I1cosω1t+θ1－2π3+

∑∞n=2Incos（ωnt+θn+θ′n）；

is3=Imcos（ωt+θ+θ″）+I1cosω1t+θ1－4π3+

∑∞n=2Incos（ωnt+θn+θ″n）。（7）

式中：θ′，θ′n是is2中基波分量及各谐波分量相较于is1中各分量的相位差；θ″，θ″n是is3中基波分量及各谐波分量相较于is1中各分量的相位差。

is1，is2，is3组成了一组用于d-q变换的电流，记为转子电流矩阵Is=is1is2is3T，对Is进行d-q变换，有

idiq=

23cos（ω′t）cos（ω′t－2π3）cos（ω′t+2π3）－sin（ω′t）－sin（ω′t－2π3）－sin（ω′t+2π3）Is。（8）

令ω′=ω1，d-q变换矩阵记为P3/2，将式（6）、式（7）代入上式整理可得

idiq=P3/2Imcos（ωt+θ）Imcos（ωt+θ+θ′）Imcos（ωt+θ+θ″）+23I1cos（－θ1）sin（－θ1）+

P3/2∑∞n=2Incos（ωnt+θn）∑∞n=2Incos（ωnt+θn+θ′n）∑∞n=2Incos（ωnt+θn+θ″n）。（9）

由上式可知，id、iq中除第二项之外，其余项均为周期分量。令idz、iqz分别为id、iq中的直流分量，即：

idz=23I1cos（－θ1）；

iqz=23I1sin（－θ1）。（10）

其模值的平方和为

i2dz+i2qz=23I21。（11）

令Iz=i2dz+i2qz，则Iz表征了is1中角频率为ω1的分量大小。

上述理论表明，is1中任意频率的分量经过d-q变换可以变为id、iq中的直流分量，通过傅里叶频谱提取出id、iq中的直流分量idz、iqz后，再经式（11）便可计算出该频率分量的幅值。

综上所述，通过d-q变换可以提取出电机定子电流故障后的谐波分量幅值，从而获得电流的特征频谱数据。

2" WOA-LSTM的分类算法

2.1" LSTM的基本原理

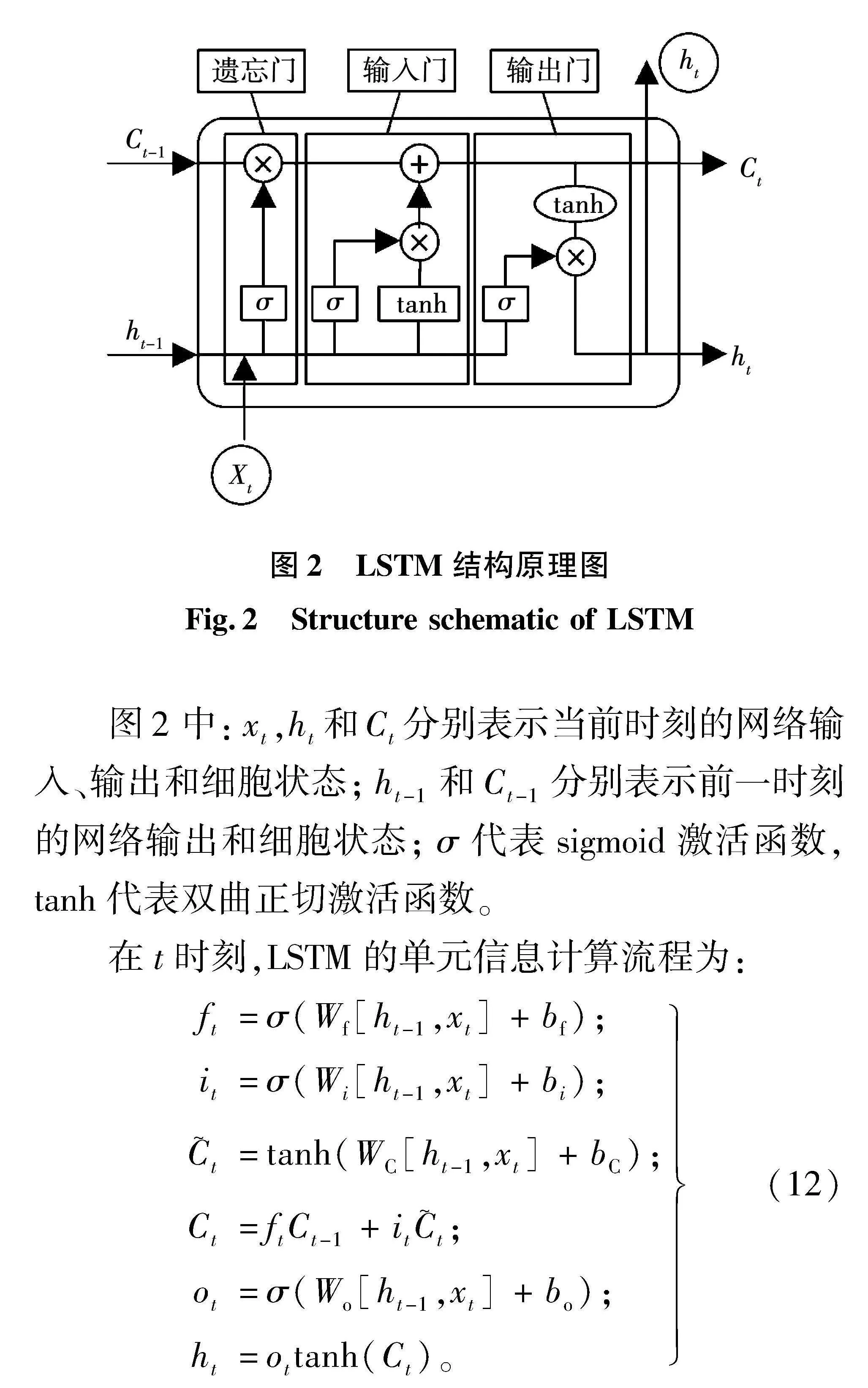
LSTM是一种特殊的循环神经网络，它通过独有的记忆网络记录历史数据，并对当前时刻数据对历史数据的影响程度进行控制。与经典的循环神经网络相比，LSTM能够快速捕捉到时序数据间的关联信息，有效改善了经典循环神经网络中梯度消失或梯度爆炸的问题。同时，LSTM的结构也更加复杂，主要包括遗忘门、输入门、输出门3个控制门，如图2所示。

图2中：xt，ht和Ct分别表示当前时刻的网络输入、输出和细胞状态；ht－1和Ct－1分别表示前一时刻的网络输出和细胞状态；σ代表sigmoid激活函数，tanh代表双曲正切激活函数。

在t时刻，LSTM的单元信息计算流程为：

ft=σ（Wf［ht－1，xt］+bf）；

it=σ（Wi［ht－1，xt］+bi）；

C～t=tanh（WC［ht－1，xt］+bC）；

Ct=ftCt－1+itC～t；

ot=σ（Wo［ht－1，xt］+bo）；

ht=ottanh（Ct）。（12）

式中：ft为遗忘系数；it为输入系数；C～t为输入数据；ot为输出系数；Wf、Wi、WC和Wo分别为遗忘门权重、输入门权重、输入数据权重和输出门权重；bf、bi、bC和bo分别为遗忘门偏置、输入门偏置、输入数据偏置和输出门偏置。

在LSTM的计算过程中，遗忘门读取前一时刻的输出和当前时刻的输入并进行非线性映射，其作用是丢弃无关信息，保留关键信息。输入门的主要作用是将当前时刻的关键信息提取出来输入到网络中，最终由输出门决定最终的分类结果。而细胞状态可以视为存储关键信息的库，细胞状态的更新过程是解决长期依赖问题的关键环节。

2.2" 鲸鱼优化算法的基本原理

鲸鱼优化算法主要通过模拟座头鲸捕猎，采取随机或最佳搜索代理的方式来模拟鲸鱼捕猎行为，并采用螺旋攻击模拟气泡网攻击机制，属于元启发式算法。与其他优化算法相比，WOA的优化机制简单，寻优能力强且收敛速度快。WOA优化求解的过程主要包括3个阶段：猎物搜索、包围捕食和气泡攻击。

座头鲸进行猎物搜索的过程，即WOA更新寻优的过程可表示为：

D=|CX*（t）－X（t）|；

X（t+1）=X*（t）－AD。（13）

式中：D为搜索空间维数；X*为最优解；X为当前解；A、C为系数向量。

当鲸鱼锁定新的猎物后，将对其进行攻击围捕。座头鲸捕食的机制主要包括2种：包围捕食和气泡网捕食。当鲸鱼采用螺旋攻击方式（气泡网捕食）时，运动方程为

X（t+1）=Deblcos（2πl）+X*（t）。（14）

式中：b为常数，表示螺线的形状；l为随机数，介于［－1，1］之间。

鲸鱼在螺旋包围猎物时，需要不断收缩包围圈，通过概率p选择包围机制和螺旋模型，即

X（t+1）=X*（t）－AD，p＜0.5;

Deblcos（2πl）+X*（t），p≥0.5。（15）

式中p为随机数，介于［0，1］之间。

随着概率p的变化，鲸鱼会不断选择不同的方式对自己的位置进行更新，直至达到最大迭代次数或适应度满足要求。

2.3" 基于WOA-LSTM的故障分类算法

LSTM的训练效果受网络模型中参数的影响非常大，主要参数为隐藏层神经元个数，初始学习率及学习率下降因子，它们对神经网络的分类精度有着不可忽视的影响。传统LSTM分类模型中的参数主要依靠经验进行调节，人为寻找其参数的最优组合费时费力，故引入鲸鱼优化算法对LSTM模型中的参数进行自寻优，提高故障分类的准确率。利用WOA对网络参数进行自寻优时，不同的优化方案可视作不同的鲸鱼个体，神经网络中需要优化的参数个数即为鲸鱼所处空间的维数，所有的参数构成了鲸鱼的位置，故对参数进行更新寻优的过程即为鲸鱼位置的变化过程。

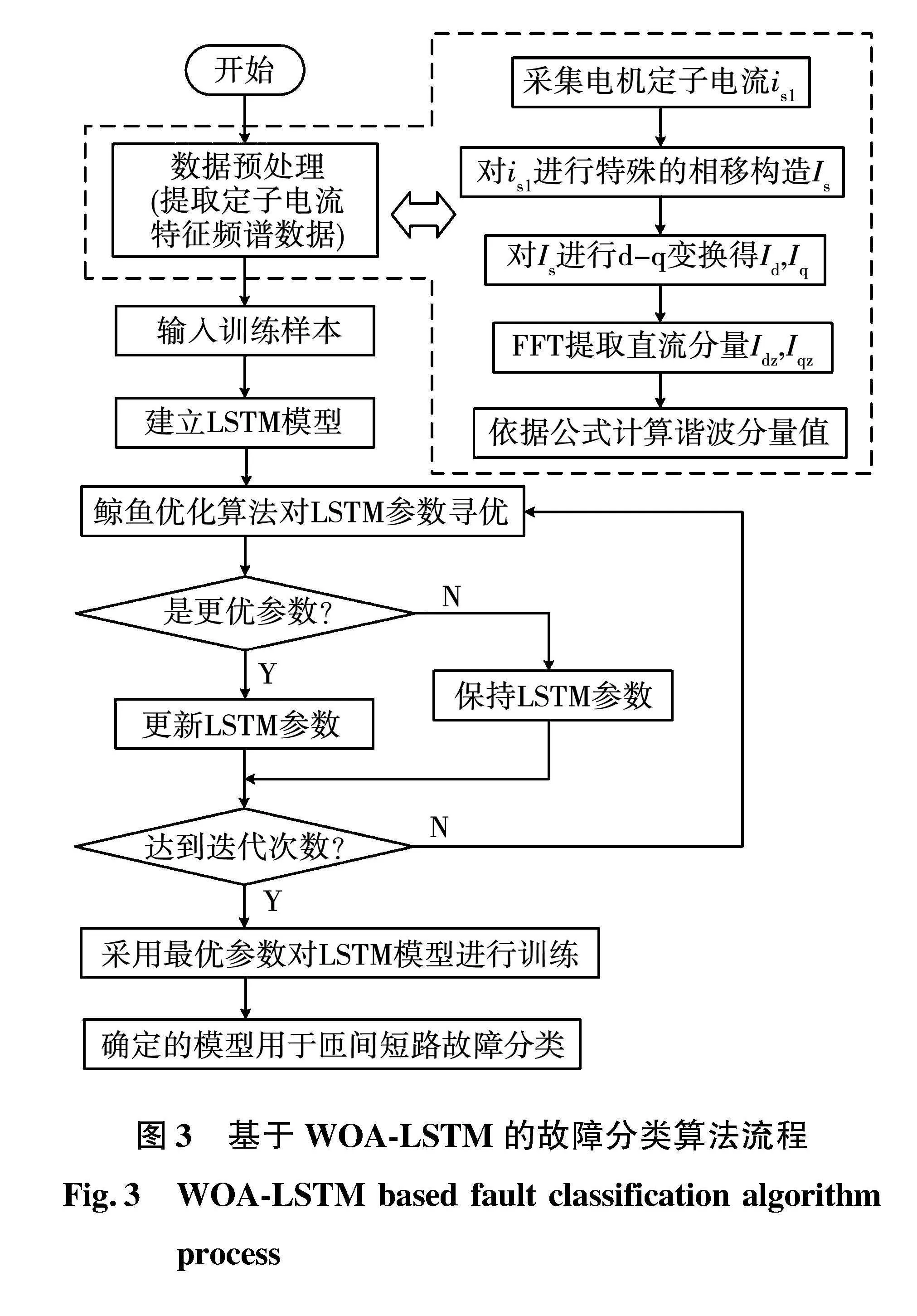
基于WOA-LSTM的故障分类算法流程如图3所示。首先输入采集到的定子电流数据，对原始数据进行数据预处理获得定子电流的特征数据，将处理后的特征数据作为数据集输入LSTM网络中进行训练。在训练过程中通过WOA对LSTM参数进行优化，获得适应度值最优的一组LSTM参数。最后采取最优参数组合进行LSTM模型训练，获得用于故障分类的LSTM神经网络模型。

3" 实验研究与结果分析

3.1nbsp; 数据采集及数据预处理

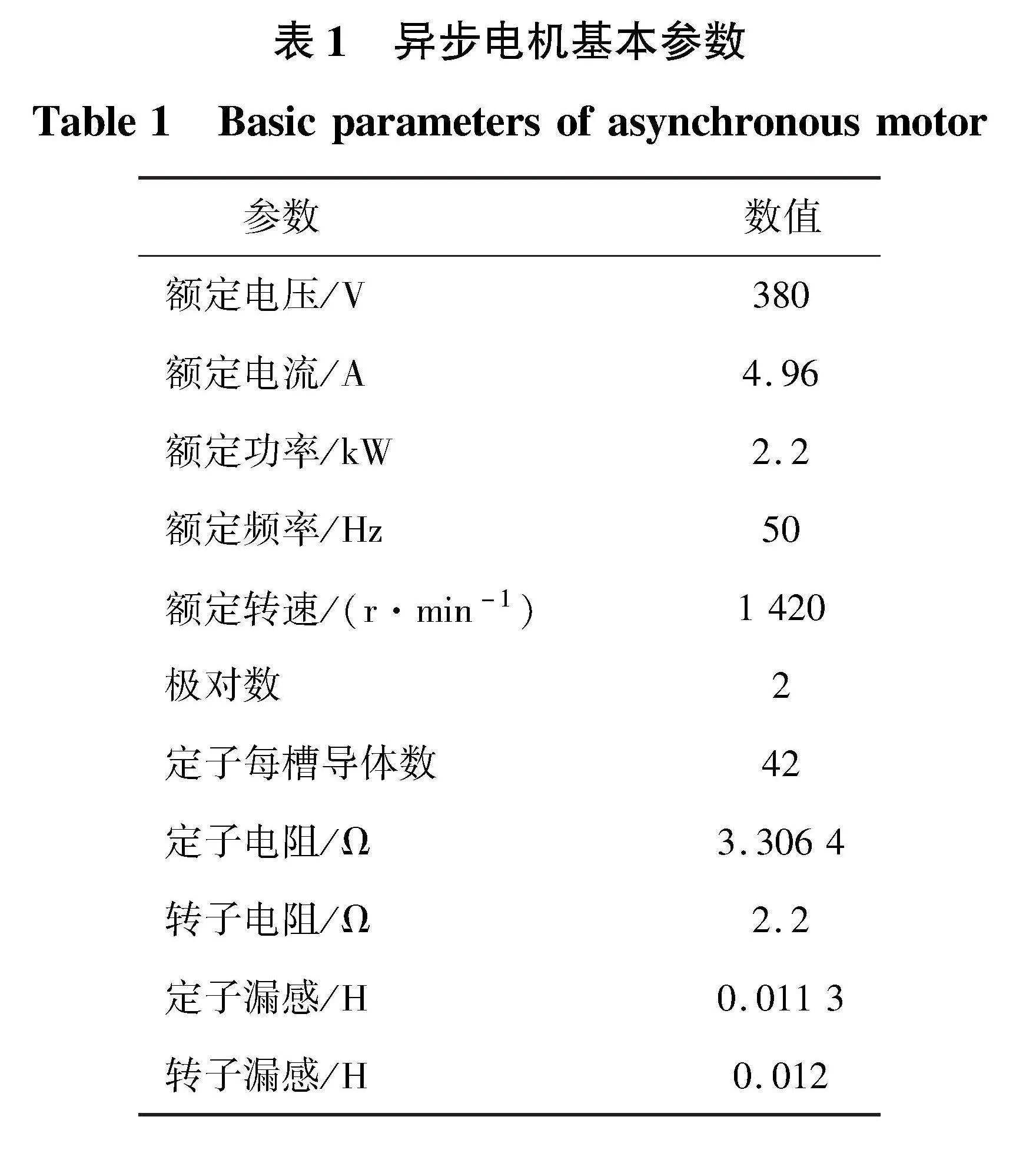
实验所用电机型号为YE2-100L1-4型三相异步电动机，基本参数如表1所示。

实验平台如图4所示。为了模拟异步电机定子绕组匝间短路这一故障，所用的实验电机为经过特殊处理后的故障电机。在电机定子A相某线圈的2、3、5、7、12匝绕组选取一点破坏其绝缘。在每个点处接入导线，并延长至机壳外部以便对其进行操作，正常运行时用绝缘胶带将6个引出线端子分别包裹，实现物理隔离。实验中仅需将其中2个抽头连接在一起，便能实现不同短路匝数的匝间短路，例如将第2匝和第7匝的引出线相连，可以实现5匝的短路故障。

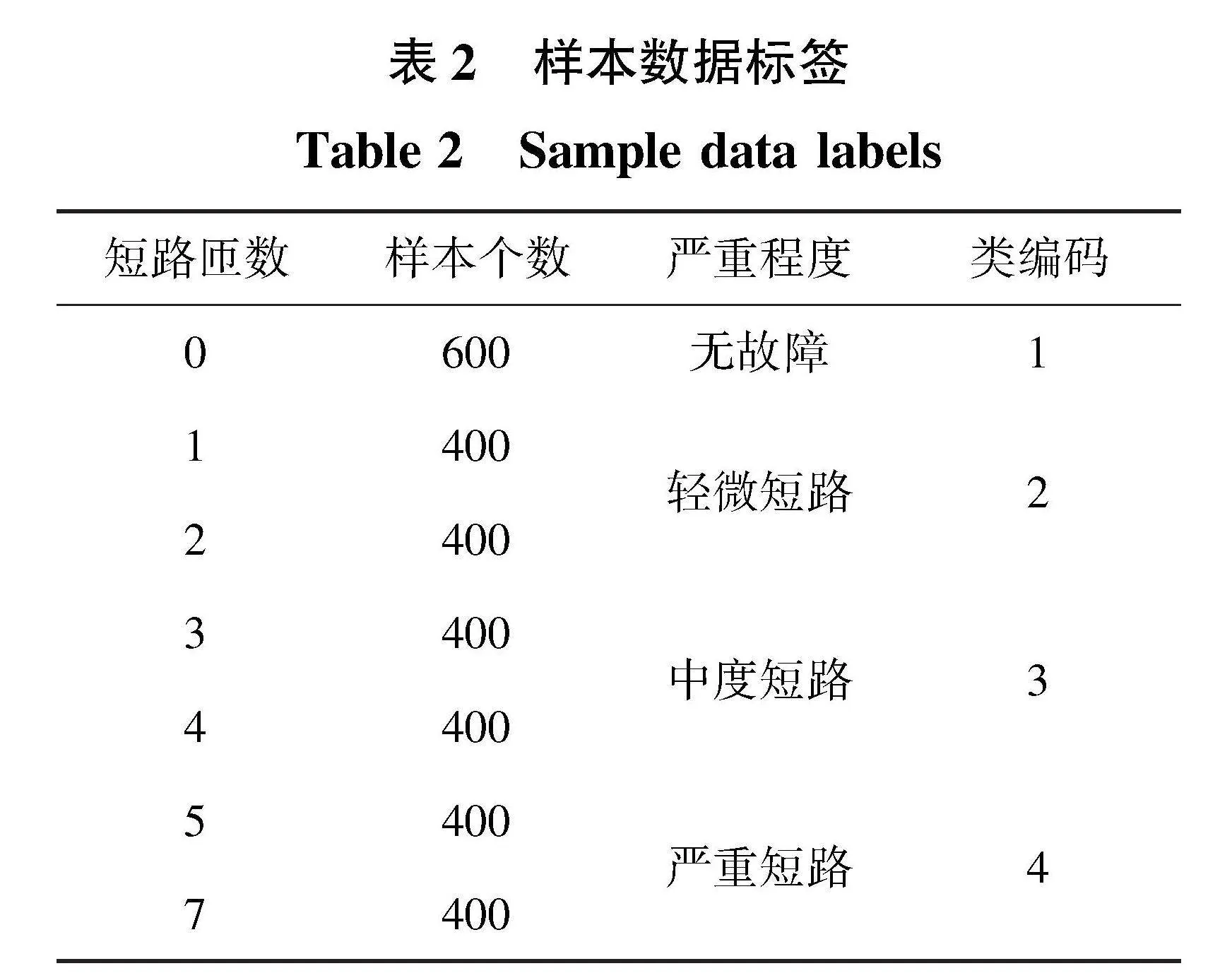
由于实验电机匝间短路故障模拟均为A相故障，故采集定子A相电流作为原始数据。采集异步电机在不同短路匝数下的定子A相电流，采样频率为10 kHz，采样时间为100 s。将每次采样数据切片以50个周期为单位长度的数据组，每个原始数据被切分为100个数据。在不同短路匝数下多次采样并切片，共获得3 000个样本数据，并对不同的短路匝数划分严重等级，对其进行类编码，具体样本分布及等级编码如表2所示。

获得电机定子电流数据后，还需对其进行数据预处理以降维。经过分析可知故障前后电机的定子电流频谱会发生明显变化，故对定子电流数据进行频谱分析，选取前0～200 Hz的特征频率幅值作为特征数据集，并随机抽取2 100个数据样本作为训练集，900个数据样本作为测试集。

3.2" 不同数据集下的LSTM训练结果分析

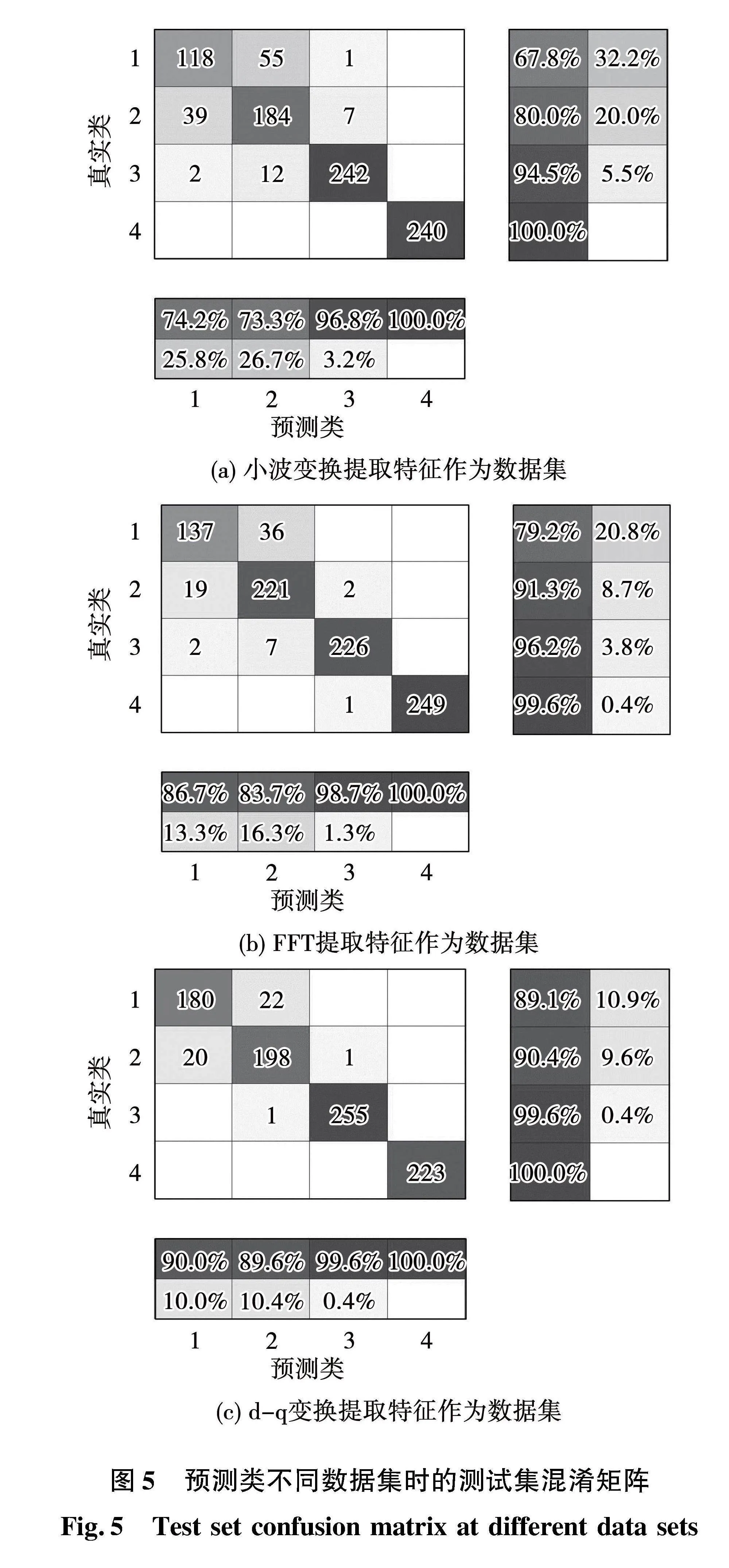
为了评估所选数据预处理方法的性能，选取小波变换、快速傅里叶变换和d-q变换提取电流特征频谱数据生成3类数据集，将其分别输入至LSTM网络中进行训练。LSTM网络模型的参数设为：初始学习率0.005；经700次训练后学习率衰减，学习率下降因子0.01；最大迭代次数2 000次；求解器为Adam。将测试集样本输入已训练完成的LSTM网络中，引入混淆矩阵对训练结果进行分析，3种数据集下的测试集混淆矩阵如图5所示。

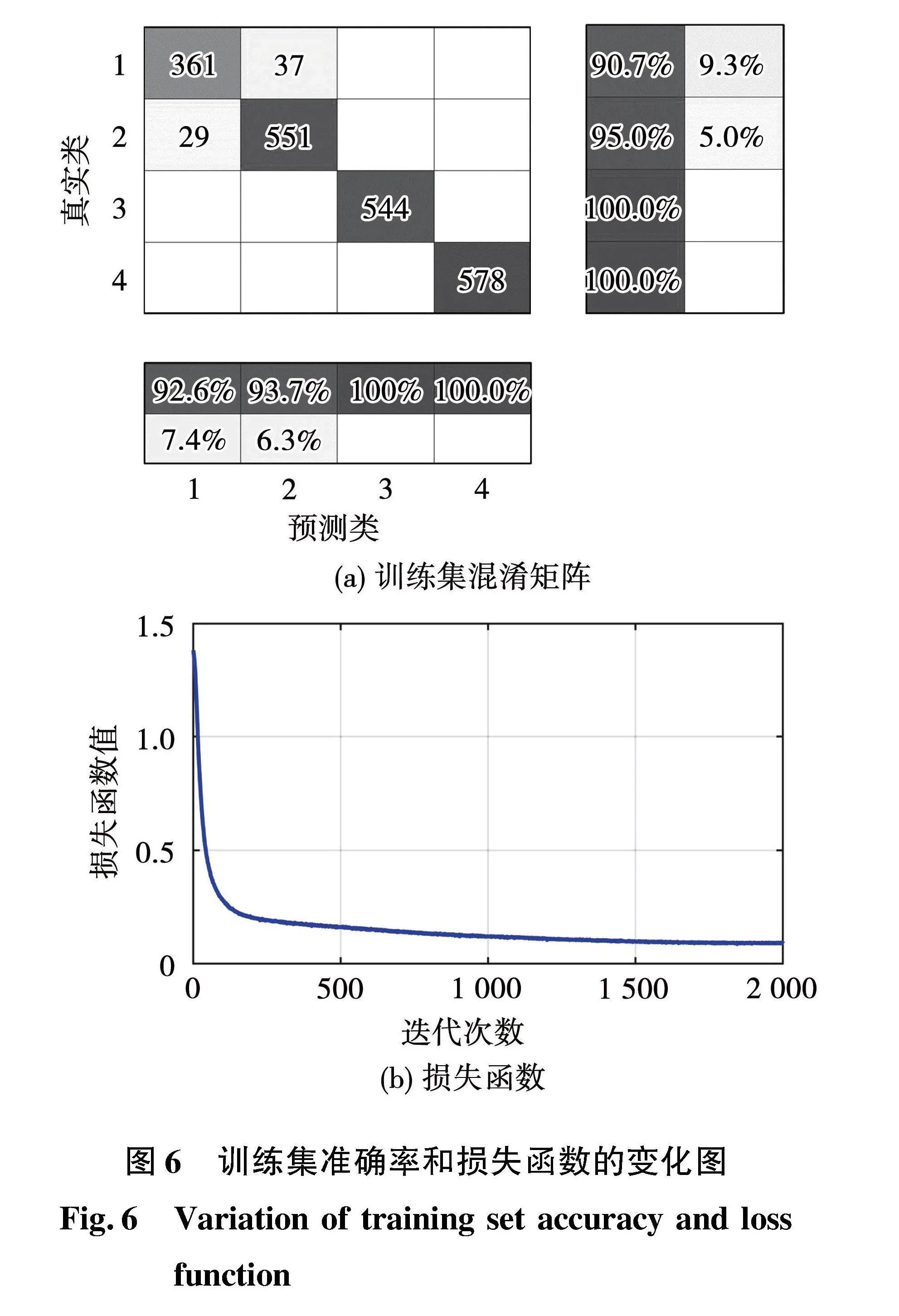
从图5可知，以小波变换、快速傅里叶变换和d-q变换提取电流特征频谱作为数据集时的测试集准确率分别为87.11%、92.56%、95.11%。以d-q变换提取电流特征频谱数据作为数据集进行训练时的训练集混淆矩阵和损失函数如图6所示，最终训练集准确率达到96.86%，所有数据集的综合准确率为96.33%。其中误判类别最多的为轻微匝间短路和无故障电机，3匝及以上的短路严重程度仅有2组数据诊断错误。实验结果表明，与小波变换，快速傅里叶变换相比，采用d-q变换提取电流频谱数据能更好的表征故障特征变化，获得更高的分类准确率。

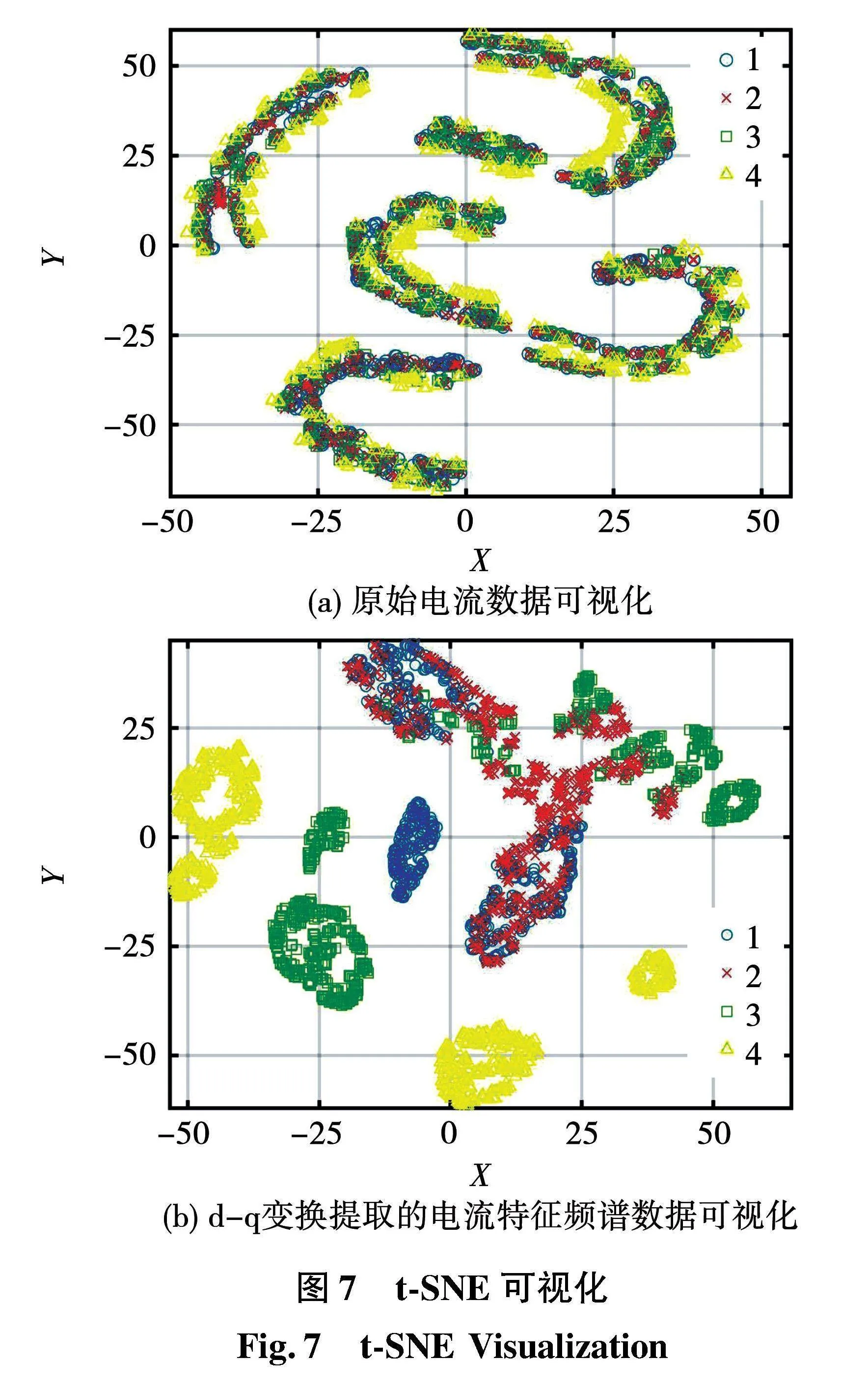
为进一步验证所选数据集的分类有效性，采用t分布随机邻域嵌入算法（t-distributed stochastic neighbor embedding，t-SNE）对原始电流数据和d-q变换处理后的电流特征频谱数据进行可视化处理，结果如图7所示。

将每组样本可视化为二维平面中的一个数据点，不同形状代表不同的故障严重程度，可以明显看出，不同故障程度下的原始电流数据出现严重重叠，而经预处理后的数据类别划分明显，更好地体现了不同故障严重程度下的特征，从而有效提高故障分类的准确率。

3.3" WOA-LSTM网络训练结果分析

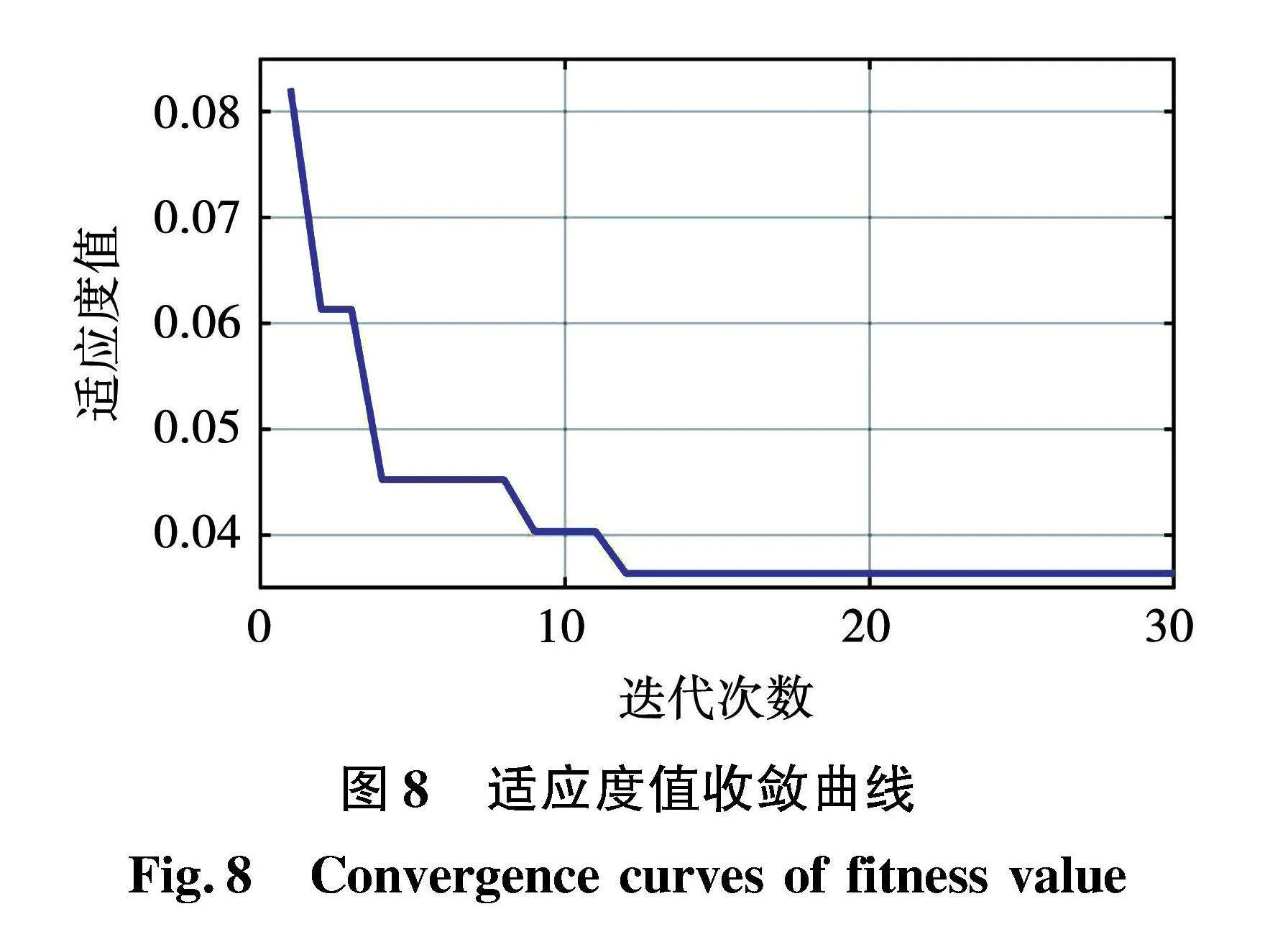
设置WOA算法参数：种群数量5、最大迭代次数30、维度3，以d-q变换进行数据预处理，选取LSTM训练集均方误差与测试集均方误差之和作为适应度值，优化过程如图8所示。

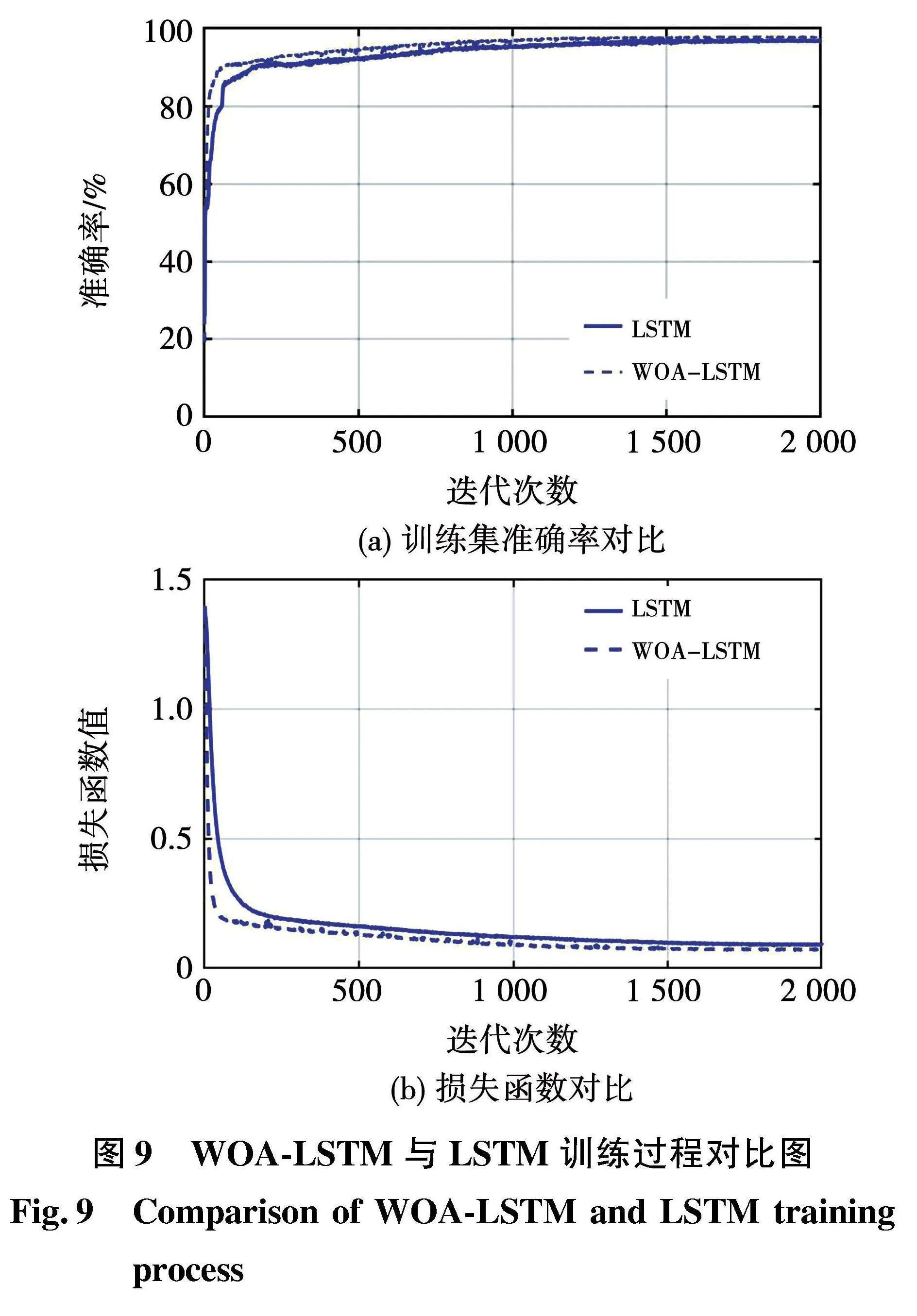
由图8可知，迭代12次时适应度值收敛至最优值，所对应的均方误差之和为0.036，经WOA优化后LSTM网络故障分类的准确率显著提升。优化前后网络训练过程中训练集准确率和损失函数的变化如图9所示。由图可看出，WOA-LSTM模型的准确率较原始LSTM模型有所提升，损失函数值降低了0.03。

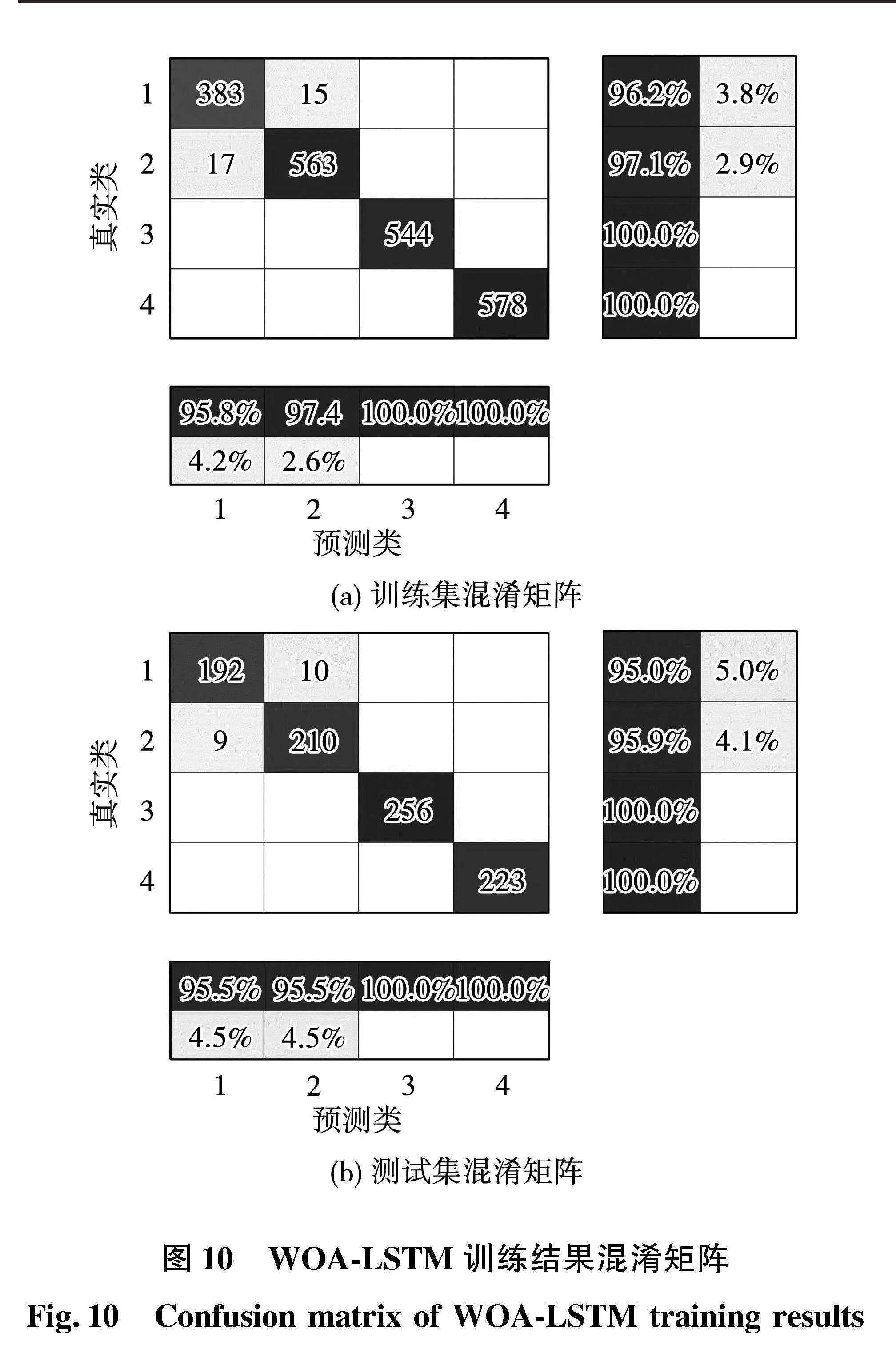
将训练集和测试集输入训练好的WOA-LSTM模型进行分类预测，所得混淆矩阵如图10所示。3 000个样本中，2 949个样本分类正确，仅有51个样本分类错误，短路3匝及以上的故障分类准确率为100%，综合准确率为98.3%，相较于原始LSTM模型提高了1.97%。

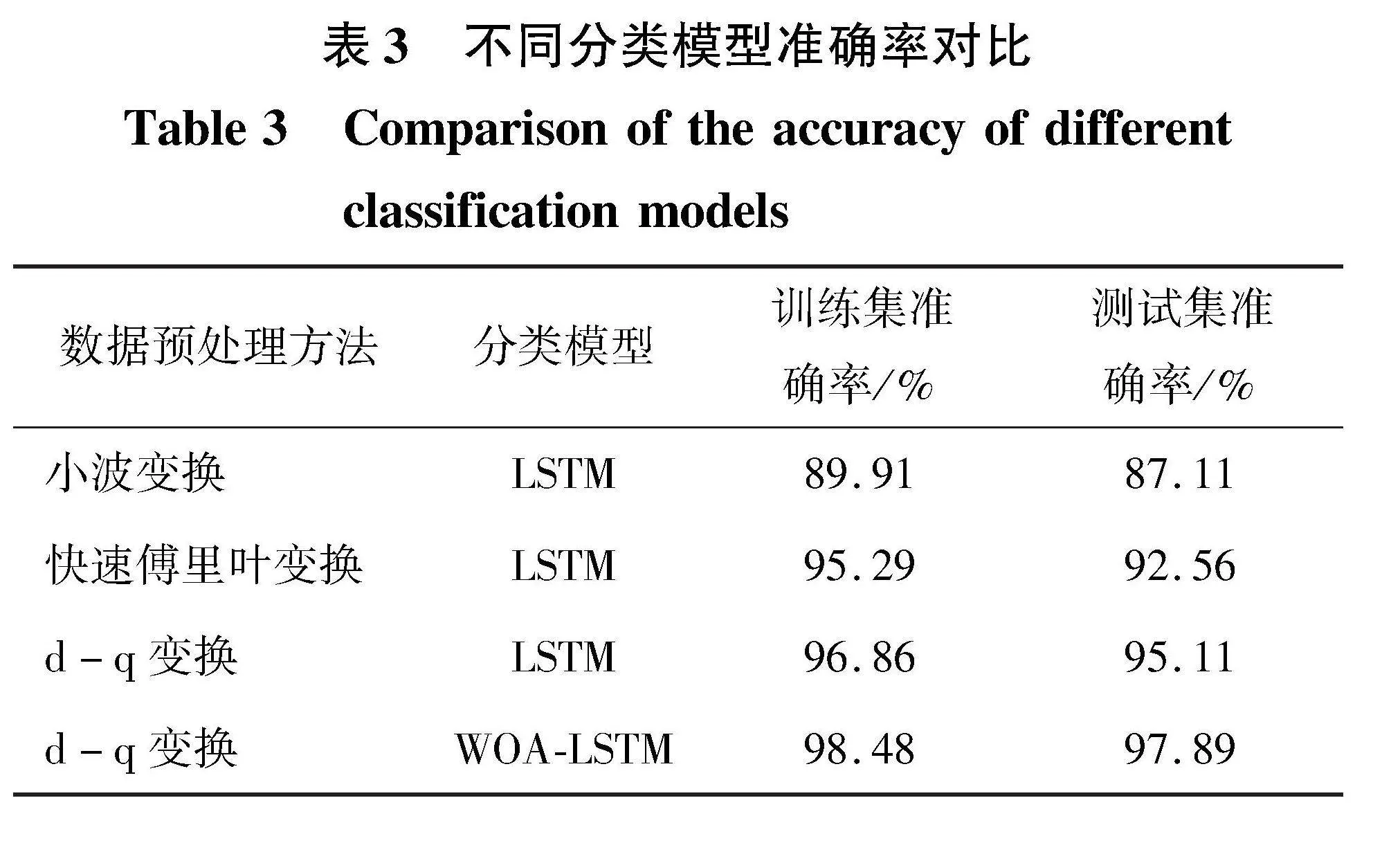
综合上述分析，可得不同数据预处理方法及网络模型时的训练集和测试集准确率，列于表3中。由表3可知，采用d-q变换提取电流频谱数据作为数据集，并用WOA优化LSTM网络参数，可使模型的训练集准确率达98.48%，测试集准确率达97.89%，较其他传统方法出现了显著提升，可以更为可靠地用于匝间短路故障分类领域。

4" 结" 论

针对三相异步电机定子匝间短路故障，本文提出了一种基于d-q变换理论和WOA-LSTM神经网络的故障分类方法，经过实验分析，得到如下结论：

1）采用d-q变换可以精确提取出定子电流中与故障相关的频谱，与小波变换、快速傅里叶变换相比，将d-q变换作为数据预处理方法，能获得更精确的特征信息，可以更好地表征故障，极大地提高了故障分类的准确率。

2）采用WOA对LSTM模型中的关键参数进行优化，在最优参数组合的基础上训练网络，可以有效提高故障分类的精度。

3）实验结果表明，以d-q变换作为数据预处理方法，输入WOA-LSTM网络训练，综合准确率可达98.3％，与其他数据预处理方法和传统LSTM模型相比，故障分类准确率显著提高。

参 考 文 献：

［1］" 马宏忠.电机状态监测与故障诊断［M］.北京：机械工业出版社，2008.

［2］" GANDHI A， CORRIGAN T， PARSA L. Recent advances in modeling and online detection of stator interturn faults in electrical motors［J］. IEEE Transactions on Industrial Electronics，2011，58（5）：1564.

［3］" JOHN S H. Monitoring of defects in induction motors through air-gap torque observation［J］. IEEE Transactions on Industry Application，1995，31（5）：1016.

［4］" WATSON S J， XIANG B J， YANG W， et al. Condition monitoring of the power output of wind turbine generators using wavelets［J］. IEEE Transactions on Energy Conversion， 2010， 25（3）：715.

［5］" 李俊卿，朱锦山.基于Prony算法的双馈异步发电机定子匝间短路特征分析［J］.电机与控制应用，2016，43（7）：86.

LI Junqing， ZHU Jinshan. Characteristic analysis of stator inter-turn short circuit fault in doubly-fed induction generator based on Prony［J］. Electric Machines amp; Control Application， 2016， 43（7）：86.

［6］" 陈众，伍雅娜，冷鹏，等.异步电机定子绕组匝间短路故障诊断研究［J］.电机与控制应用，2019，46（5）：120.

CHEN Zhong， WU Yana， LENG Peng， et al. Diagnosis of inter-turn faults in stator windings of asynchronous motor［J］. Electric Machines amp; Control Application，2019，46（5）：120.

［7］" 张世聪.大功率电力机车异步牵引电机的典型故障研究［J］.北京交通大学学报，2018，42（2）：122.

ZHANG Shicong. Research on typical of asynchronous traction motor for high power electric locomotive［J］. Journal of Beijing Jiaotong University，2018，42（2）：122.

［8］" 马宏忠，张志艳，张志新，等.双馈异步发电机定子匝间短路故障诊断研究［J］.电机与控制学报，2011，15（11）：50.

MA Hongzhong， ZHANG Zhiyan， ZHANG Zhixin， et al. Research on DFIG stator winding inter-turn short circuit fault［J］. Electric Machines and Control，2011，15（11）：50.

［9］" 李和明，孙丽玲，许伯强，等.异步电动机定子绕组匝间短路故障检测新方法［J］.中国电机工程学报，2008，28（21）：73.

LI Heming， SUN Liling， XU Boqiang， et al. A novel detection method of stator winding inter-turn short circuit fault in induction motors［J］. Proceedings of the CSEE，2008，28（21）：73.

［10］" 魏书荣，张路，符杨，等.基于派克矢量轨迹椭圆度的海上双馈电机定子绕组匝间短路早期故障辨识［J］.中国电机工程学报，2017，37（10）：3001.

WEI Shurong， ZHANG Lu， FU Yang， et al. Early fault detection based on the Park’s vector locus ovality for inter-turn faults in stator windings of the offshore wind DFIG［J］. Proceedings of the CSEE，2017，37（10）：3001.

［11］" CHENG S W， ZHANG P J， HABETLER T G. An impedance identification approach to sensitive detection and location of stator turn-to-turn faults in a closed-loop multiple motor drive［J］. IEEE Transactions on Industrial Electronics，2011，58（5）：1545.

［12］" LEE S B， TALLAM R M， HABETLER T G. A robust，on-line turn-fault detection technique for induction machines based on monitoring the sequence component impedance matrix［J］. IEEE Transactions on Power Electronics，2003，18（3）：865.

［13］" 魏书荣，张路，符杨，等.基于拟序阻抗的海上双馈电机定子绕组匝间短路早期故障辨识［J］.中国电机工程学报，2017，37（1）：273.

WEI Shurong， ZHANG Lu， FU Yang， et al. Early fault detection based on the quasi-sequence impedance for inter-turn faults in stator windings of offshore wind DFIG［J］. Proceedings of the CSEE，2017，37（1）：273.

［14］" 李俊卿，康文强，沈亮印.基于多回路理论的双馈异步发电机定子绕组匝间短路故障分析［J］.电机与控制应用，2016，43（9）：99.

LI Junqing， KANG Wenqiang， SHEN Liangyin. Analysis of stator winding inter turn short circuit fault in doubly fed induction generator based on multi loop theory［J］. Electric Machines amp; Control Application，2016，43（9）：99.

［15］" YAGAMI Y， ARAKI C， MIZUNO Y， et al. Turn-to-turn insulation failure diagnosis of stator winding of low voltage induction motor with the aid of support vector machine［J］. IEEE Transactions on Dielectrics and Electrical Insulation，2015，22（6）：3099.

［16］" HUA Su， KIL T C. Induction machine condition monitoring using neural network modeling［J］. IEEE Transactions on Industrial Electronics， 2007， 54（1）：241.

［17］" 马明晗，侯岳佳，李永刚，等.基于MSK-CNN和多源机电信息融合的同步发电机故障诊断方法［J］.电机与控制学报，2023，27（1）：1.

MA Minghan， HOU Yuejia， LI Yonggang， et al. Synchronous generator fault diagnosis nethod based on MSK-CNN and multi-source electromechanical information fusion［J］. Electric Machines and Control，2023，27（1）：1.

［18］" 吴忠强，卢雪琴.基于深度迁移学习和LSTM网络的微电网故障诊断［J］.计量学报，2023，44（4）：582.

WU Zhongqiang， LU Xueqin. Microgrid fault diagnosis based on deep transfer learning and LSTM network［J］. Acta Metrologica Sinica，2023，44（4）：582.

［19］" 尹项根，乔健，贺儒飞，等.基于FFT-LSTM的变速抽蓄机组转子绕组短路故障和偏心故障诊断方法［J］.电力系统保护与控制，2023，51（6）：73.

YIN Xianggen， QIAO Jian， HE Rufei， et al. FFT-LSTM-based fault diagnosis method for a rotor winding short circuit fault and rotor eccentricity fault of a variable-speed pumped storage unit［J］. Power System Protection and Control，2023，51（6）：73.

（编辑：刘琳琳）