无刷同步发电机稳态短路电流控制

摘" 要：

过载运行能力和突然短路时稳定的短路电流输出能力是无刷同步发电机的重要性能要求。在发电机发生突然短路时，发电机控制器需要配合无刷同步发电机进行短路电流控制，在保证足够的短路电流输出能力的同时也要避免短路电流过大损坏电机。针对无刷同步发电机可能发生的5种短路类型进行了分析，提出梯形电压电流的控制目标曲线，利用无模型自适应控制算法进行短路电流控制，使发电机能在发生各种类型的突然短路故障时输出符合要求的短路电流。建立了发电机和控制器的仿真模型，进行无模型自适应控制方案的仿真验证，同时搭建了实验平台进行实验验证。经过验证无模型自适应算法可以将无刷同步发电机的短路电流很好地控制在目标值，验证了该控制算法在发电机短路电流控制方面的有效性。

关键词：无模型自适应控制；无刷同步发电机；突然短路；短路电流控制；故障保护；过载运行

DOI：10.15938/j.emc.2024.06.005

中图分类号：TM31

文献标志码：A

文章编号：1007-449X（2024）06-0045-11

收稿日期： 2023-06-16

基金项目：

作者简介：茆林仪（1998—），男，硕士，研究方向为三级式无刷同步发电机控制器；

陈志辉（1972—），男，博士，教授，研究方向为航空电源系统、电机及电控技术。

通信作者：陈志辉

Control of steady short-circuit current in brushless synchronous generator

MAO Linyi，" CHEN Zhihui

（College of Automation， Nanjing University of Aeronautics and Astronautics， Nanjing 210000， China）

Abstract：

Overload operation capability and stable short-circuit current output capability in case of sudden short-circuit are important requirements for brushless synchronous generators. When a sudden short-circuit occurs in the generator， the generator controller needs to cooperate with the brushless synchronous generator to control the short-circuit current， ensuring sufficient short-circuit current output capacity while also avoiding excessive short-circuit current damage the generator. Five types of short circuits was analyzed that may occur in brushless synchronous generators， a trapezoidal objective curve was proposed to control the voltage and current， and model free adaptive control algorithm was used to control short-circuit current， enabling the generator to output the required short-circuit current when various types of sudden short circuit faults occur. A simulation model was established for the generator and controller， and the model was used to simulate and verify the model free adaptive control algorithm. At the same time， an experimental platform was established for experimental verification. After verification， the model free adaptive algorithm can effectively control the short-circuit current of brushless synchronous generators at the target value， verifying effectiveness of this control algorithm in generator short-circuit current control.

Keywords：model free adaptive control; brushless synchronous generator; sudden short-circuit; short-circuit current control; fault protection; overload operation

0" 引" 言

随着航空工业的发展，飞机的功能日益完善，多电或全电飞机也开始逐渐发展。飞机上先后采用过低压直流电源系统、高压直流电源系统、变频交流电源系统、恒速恒频电源系统以及变速恒频电源系统，而无刷同步发电机作为一种变频交流发电机，由于其结构成熟、可靠性高，因此广泛应用于航空交流电源系统中［1-2］。同时，无刷同步发电机控制器（generator control unit，GCU）的研究已经比较成熟［3-4］，众多学者对GCU的调压功能、控制功能、保护功能、自检功能、通讯功能等都有了较为充分的研究，但是对于无刷同步发电机发生突然短路故障后的短路电流控制方面的研究比较少。针对这一情况，本文进行了无刷同步发电机在发生突然短路后短路电流控制方面的研究。

在航空电源系统中，出现短路故障时，为了给断路器、熔断器等充足的反应时间，从而保护用电电器的安全，对发电系统有着相应的短路能力的要求，需要发电系统单台或并联运行时，在二相、三相的相间短路状态和单相、二相、三相的对地短路状态下，至少应能提供300%的额定负载电流（IN），并维持5 s。

当三相同步发电机发生突然短路时，由于此时的瞬间磁链守恒，磁链不会发生突变，因此感应出非常大的瞬变电流阻止短路产生的磁通穿过磁极铁心，同时产生的瞬变电流也会在很短的时间内快速衰减下来。突然短路时瞬变电流的大小主要与电机的瞬变电抗、超瞬变电抗、阻尼绕组等参数设计有关［5-7］，本文主要研究瞬变电流衰减后的稳态短路电流控制过程［9-11］，不涉及瞬变电流峰值的抑制。

目前，大部分GCU对短路电流的控制策略是根据工程经验，将控制MOS管通断的PWM占空比维持在一个固定值从而控制励磁电流，而突然短路的短路类型不同，所以维持3倍额定短路电流所需的励磁电流也不同。通常情况下，三相对地突然短路时，维持3倍额定短路电流所需的励磁电流最大。因此，为了满足5种短路类型，将占空比维持在三相对地短路时所需励磁电流的占空比，这就导致当发生单相对地短路或者其他短路类型时，控制的短路电流将远大于3倍额定短路电流，给发电机带来额外的负担，导致降低电机的寿命。

当发电机发生各种类型的突然短路时，为了将稳态短路电流控制在3倍额定短路电流状态，需要自适应控制算法进行短路电流控制。综上，本文利用数字方法实现GCU对发电机的控制，针对发电机相应的短路电流输出要求，设计理想的电压电流控制目标曲线，将短路电流作为反馈的一部分，将无模型自适应控制（model free adaptive control，MFAC）算法运用在短路电流控制上，利用该算法的自适应能力将5种突然短路类型下的稳态短路电流控制在3倍额定短路电流，降低发电机短路运行的负担。同时，建立无刷同步发电机的仿真模型，通过仿真以及实验验证该控制算法的有效性。

1" 无刷同步发电机短路电流控制策略

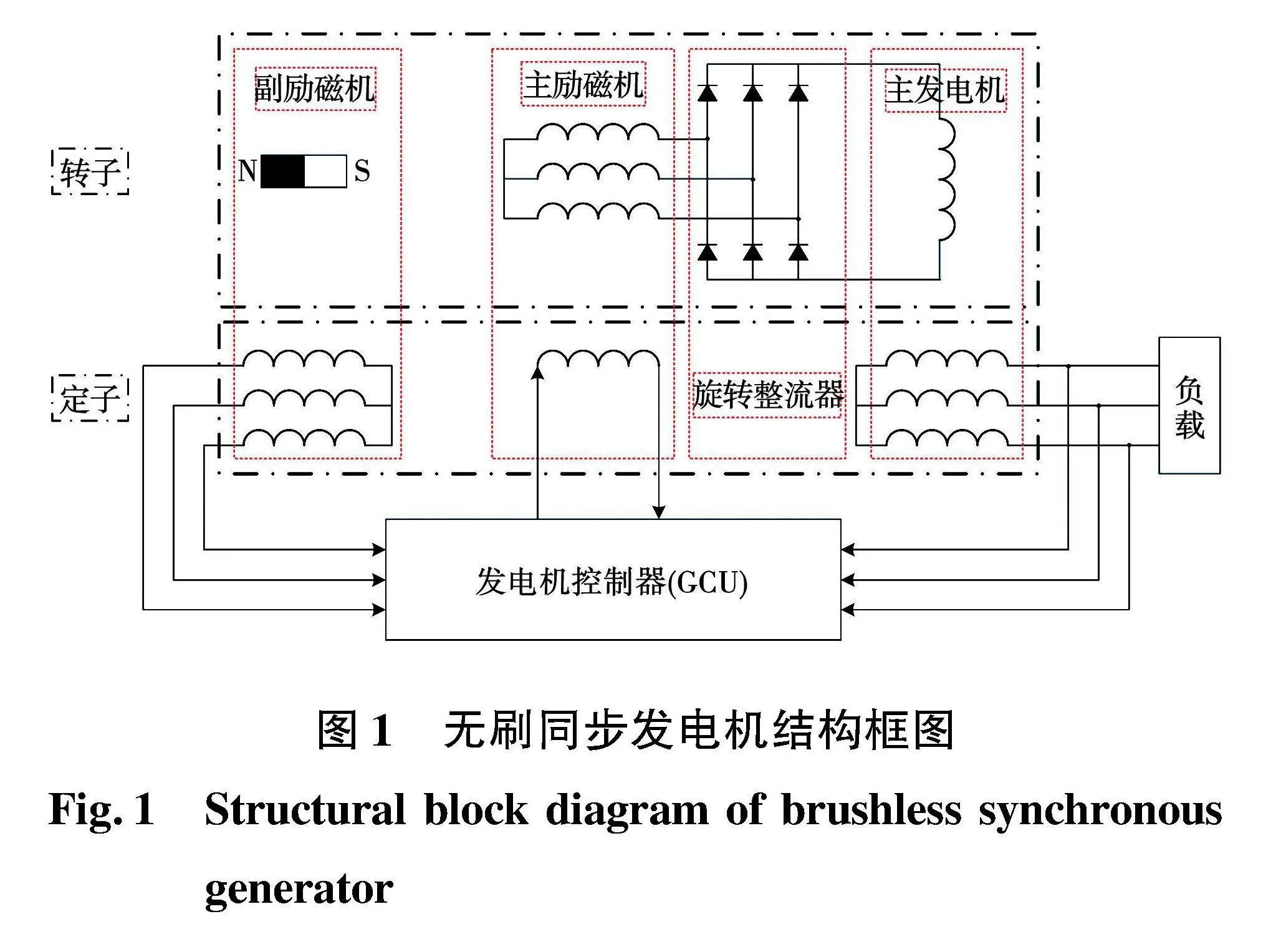
1.1" 无刷同步发电机系统结构

无刷同步发电机主要由3部分构成，分别是副励磁机、主励磁机和主发电机，因此也叫做三级式无刷同步发电机，具体的结构框图如图1所示。

副励磁机一般使用永磁同步发电机，它的主要作用是输出交流电，经过二极管整流后给控制器供电，控制器根据主发电机的发电情况，输出一定的励磁电流给主励磁机。主励磁机一般是交流同步发电机，主励磁机输出的交流电经过旋转整流器整流后给主发电机的励磁绕组，最终主发电机输出飞机需要的交流电［12-13］。

1.2" 短路电流控制思路

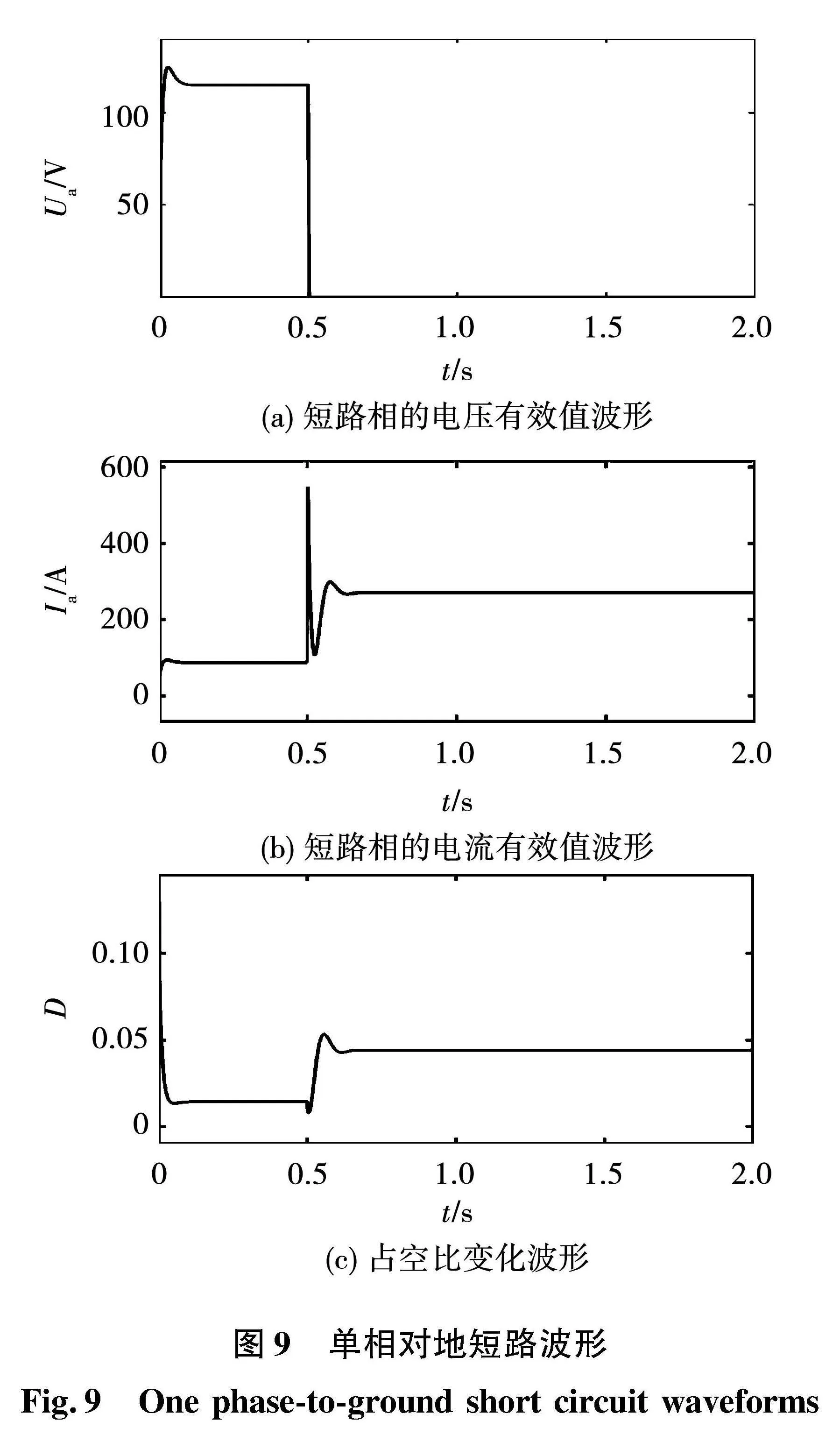
正常发电时，仅需要三相电压的测量值进行闭环控制，如图2（a）所示；当发生突然短路时，则需要加入短路电流进行闭环控制，如图2（b）所示。

当发生突然短路时，根据图2（b）的闭环控制方案，需要将短路电流折算到电压反馈上，从而实现对短路电流的控制，具体做法如下。

首先需要对短路状态进行判断，当发电机三相中电流最大相的电流有效值超过2倍额定电流时判断为短路状态。此时的负载阻抗有可能处于0到2倍额定负载阻抗之间，这样的负载状态称为短路过渡状态，此时的阻抗称为过渡阻抗。

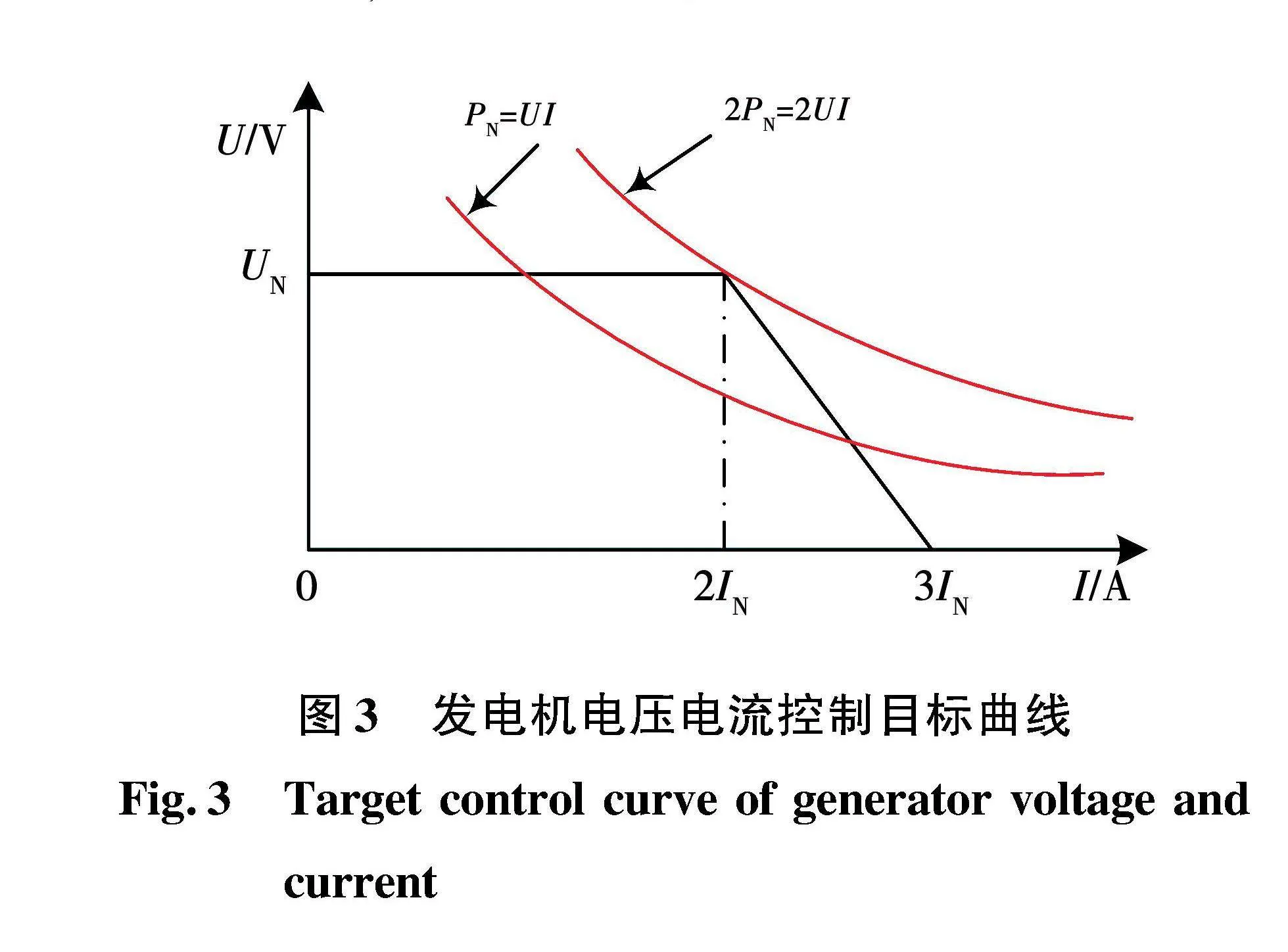
当发电机发生金属性短路时，短路点的阻抗接近0，短路点的相电压接近0，此时控制GCU输出励磁电流，使得短路后的稳态短路电流能够达到3倍额定负载电流，因此可以得到电压电流对应的控制目标曲线［14］，如图3所示。

该电压电流控制目标曲线的特点是，在空载到两倍过载的范围内发电机可以保持输出电压在额定电压（UN），当负载电流超过2IN时，通过降低输出电压的方式减小发电机的输出功率，当负载电流达到3IN时输出电压值降至0，即发电机输出端发生金属性短路时将其短路电流控制在3IN。如图3所示，其中两条曲线分别为额定功率曲线和两倍额定功率曲线，PN为发电机一相的额定功率，可以看出电压电流控制曲线可以将发电机在短路状态下的输出功率维持在两倍额定功率以下。

在利用该方案进行无刷同步发电机的短路电流控制时发现，当发电机发生突然两相相间短路时，短路点与中线间有一定的相电压，导致该方案无法将此种短路类型的短路电流控制在3IN。为了可以兼容两相相间短路，同时为了保证短路电流可以一直维持在3IN，改进的电压电流控制目标曲线如图4所示。

在图4中，当发生突然短路时，检测短路相的电压，短路相的相电压小于UK时，判断为金属性短路，直接利用电流作为反馈进行控制，可以将短路电流控制的目标值设置为3IN。为了将发电机的输出功率维持在两倍额定功率以下，负载电流在2IN～3IN之间的电压电流曲线的斜率必须小于2倍额定功率曲线在点（2IN，UN）处的斜率，因此UK必须小于等于UN/2，计算方法如下：

UK－UNIN≤－2PN（2IN）2；

PN=UNIN。（1）

同时当发生两相相间短路时，短路相的相电压为非短路相的一半，而非短路相的相电压由于发电机短路去磁作用，电压远小于额定相电压，因此UK可以取小于UN/2的值。所以如图4所示，发电机短路状态下的输出功率可以维持在两倍额定功率以下，根据控制目标曲线，可以得到具体的电流折算公式。

在负载电流I∈［0，2IN）时，闭环控制的反馈量为

Ufd=Urms。（2）

在负载电流I∈［2IN，3IN）时，闭环控制的反馈量为

Ufd=Urms+Irms－2IN3IN－2IN（UN－UK）。（3）

在负载电流I≥3IN时，闭环控制的反馈量为

Ufd=Irms3INUN。（4）

式中：Ufd为在闭环控制中与给定值进行比较的反馈值；Urms为发电机三相输出电压中最小相的电压；Irms为发电机三相负载电流中最大相的电流。

2" 基于无模型自适应控制的短路电流控制

无刷同步发电机是一个强耦合高阶非线性系统，建立准确的数学模型较为困难，可以采用基于数据驱动（data driven control，DDC）的控制方式来对无刷同步发电机进行控制。现有的GCU在电压控制环节多采用PID这样基于数据驱动的控制方式，而在短路电流控制时采用开环控制，导致短路电流远大于3IN。

为了将短路电流控制在略超过3IN，同时解决五种短路类型下，电流反馈闭环控制的自适应问题，采用MFAC控制算法来进行短路电流控制。MFAC也是一种基于在线数据的数据驱动控制方法，它直接应用受控系统的I/O数据解决非线性系统控制问题。MFAC具有自适应的特点，它是基于动态线性化在线地估计系统输出关于输入的梯度值，从而实现自适应控制［15-17］。

MFAC根据动态线性化方法的不同，分为基于紧格式动态线性化的无模型自适应控制（compact form dynamic linearization based MFAC，CFDL-MFAC）、基于偏格式动态线性化的无模型自适应控制（partial form dynamic linearization based MFAC，PFDL-MFAC）和基于全格式的无模型自适应控制（full form dynamic linearization based MFAC，FFDL-MFAC）。根据控制系统的特点，选择CFDL-MFAC的控制方式进行控制。

无刷同步发电机的控制输入为励磁电流，闭环控制时反馈量只有一个，因此，可以将其看作单输入单输出（SISO）的离散非线性系统，即有

y（k+1）=f（y（k），…，y（k－ny），u（k），…，u（k－nu））。（5）

式中：y（k）∈R，u（k）∈R分别表示系统在k时刻的电压输出和控制励磁大小的占空比输入；ny，nu是两个未知的正整数；f（…）：Rnu+ny+2MT ExtraaA@R为未知的非线性函数。

对无刷同步发电机系统进行如下合理化假设。

假设1：除有限时刻点外，f（…）关于第（ny+2）个变量的偏导数是连续的；

假设2：除有限时刻点外，系统公式（5）满足广义Lipschitz条件，即对任意k1≠k2，k1、k2≥0和u（k1）≠u（k2）有

|y（k1+1）－y（k2+1）|≤b|u（k1）－u（k2）|。（6）

当系统满足假设1和假设2，并且对所有的时刻k有Δu（k+1）≠0成立时，其CFDL数据模型可表示为

y（k+1）=y（k）+c（k）Δu（k）。（7）

式中c（k）∈R为系统式（5）的伪偏导数（pseudo partial derivative，PPD）。

对于离散系统，由最小化一步向前预报误差准则函数得到的控制算法有可能产生过大的控制输入，使控制系统本身遭到破坏，而由最小化加权一步向前预报误差准则函数得到的控制算法又有可能产生稳态的跟踪误差，因此考虑如下控制输入准则函数

J（u（k））=|y*（k+1）－y（k+1）|2+λ|u（k）－u（k－1）|2。（8）

式中：λ是一个权重因子，用来限制控制输入量的变化，λgt;0；y*（k+1）为期望的输出信号。

将式（7）代入准则函数（8）中，对u（k）求导，并令其等于0，可得到如下控制算法：

u（k）=u（k－1）+

ρc（k）λ+|c（k）|2（y*（k+1）－y（k））。（9）

式中ρ∈（0，1］是步长因子，它的加入目的是使控制算法更具一般性。

同样对于伪偏导数c（k）也设计了相应的估计准则函数，如下：

J（c（k））=|y（k）－y（k－1）－c（k）Δu（k－1）|2+

μ|c（k）－^c（k－1）|2。（10）

式中μ是权重因子，μgt;0。

对式（10）的c（k）求极值，可得PPD的估计算法为

^c（k）=^c（k－1）+ηΔu（k－1）μ+Δu（k－1）2（Δy（k）－

^c（k－1）Δu（k－1））。（11）

其中：η∈（0，1］是加入步长因子，目的是使该算法具有更强的灵活性和一般性；^c（k）为PPDc（k）的估计值。

综合无刷同步发电机PPD估计算法和控制算法，可以得到该电机的CFDL-MFAC方案如下：

^c（k）=^c（k－1）+ηΔu（k－1）μ+Δu（k－1）2（Δy（k）－

^c（k－1）Δu（k－1））；

u（k）=u（k－1）+ρ^c（k）λ+|^c（k）|2（y*（k+1）－y（k））；

^c（k）=^c（1）。（12）

其中：λgt;0，μgt;0，ρ∈（0，1］，η∈（0，1］；^c（1）是^c（k）的初值。

3" 无刷同步发电机发电系统模型的搭建

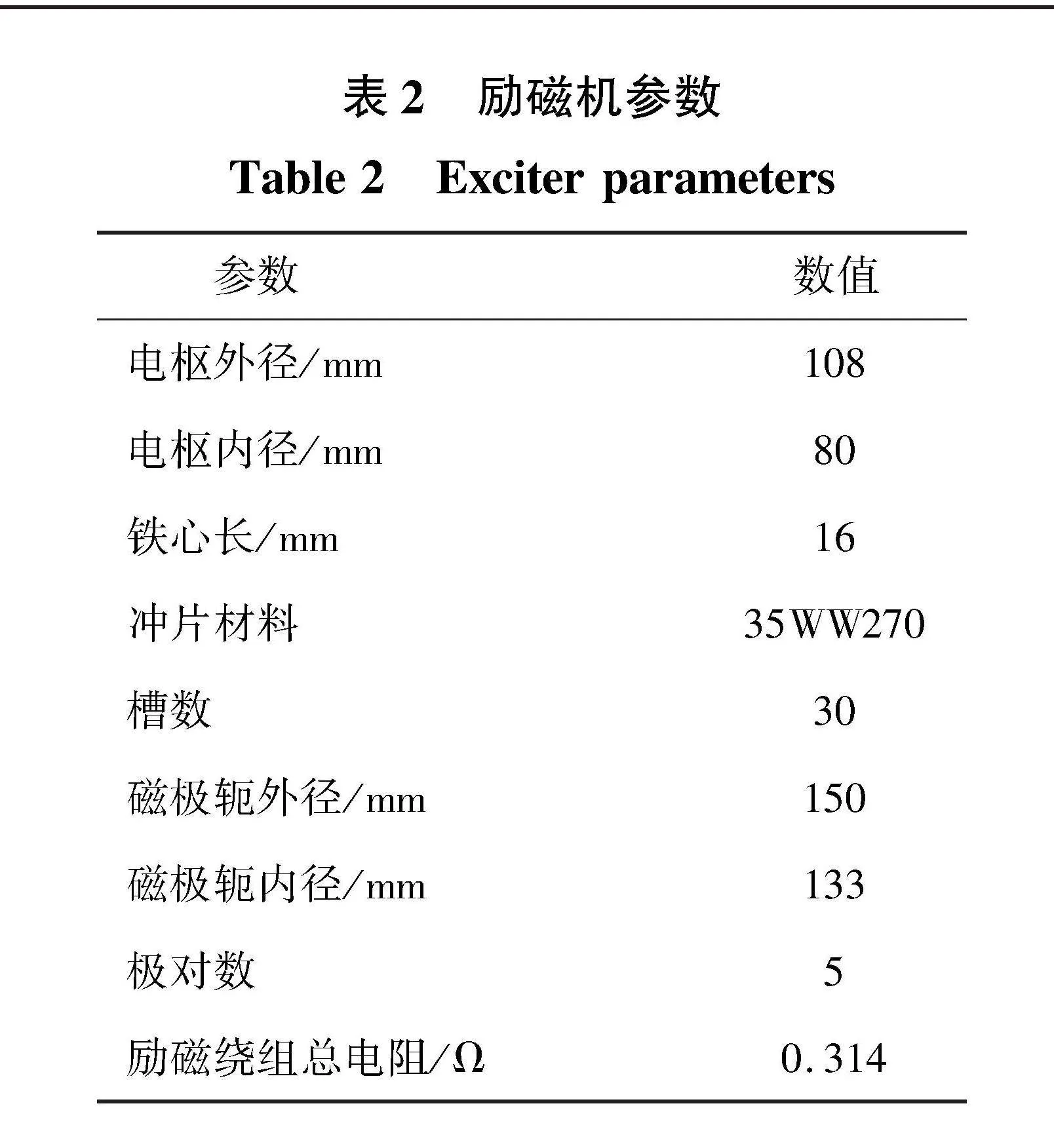
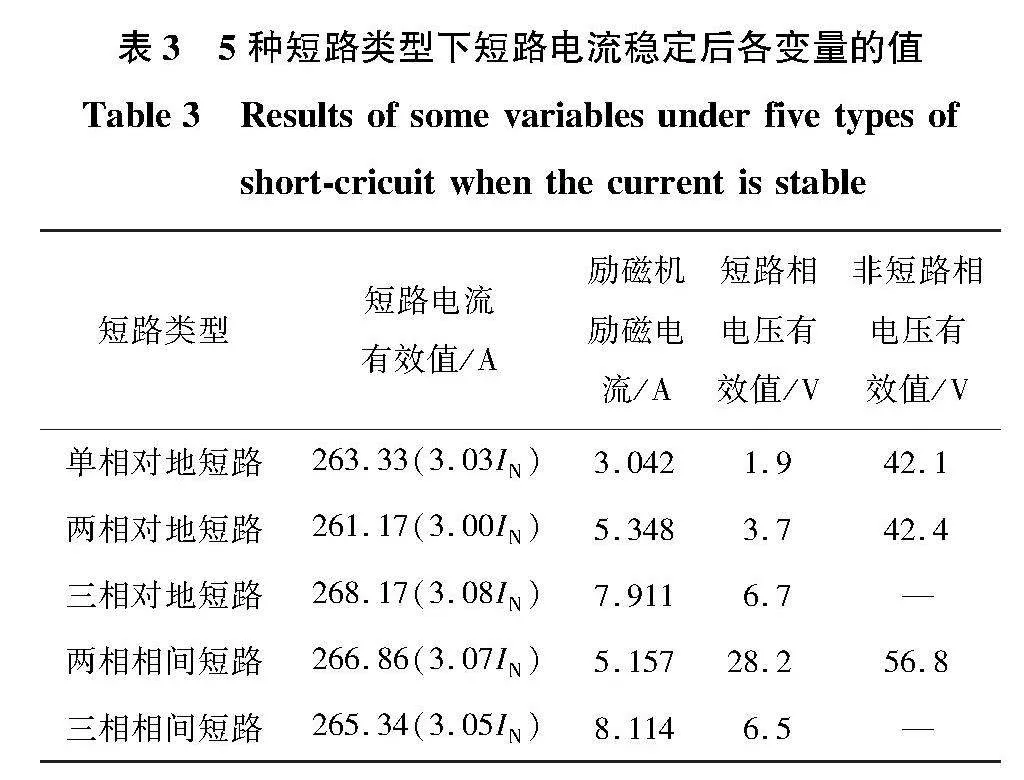
在得到具体的短路电流控制方案后，需要建立相应的无刷同步发电机模型进行仿真验证，仿真验证可行后再做相应的突然短路电流控制实验，因此，首先需要建立一个较为准确的无刷同步发电机和控制器的模型进行算法验证。依据实验室现有条件，建立一台额定容量30 kVA的三级式无刷同步发电机，电机的具体参数如表1、表2所示。

3.1" 无刷同步发电机模型的建立

设计的无刷同步发电机是由永磁同步发电机和2个交流同步发电机构成的无刷同步发电机，如图5所示。在具体仿真时可以将永磁同步发电机视作一个稳定的电压源，给励磁机提供稳定的励磁电压。励磁机输出的交流电桥式二极管整流器整流后输出到主发电机的励磁绕组上。

主励磁机是一个五对极的隐极同步发电机，主发电机是一个两对极的凸极同步发电机，利用仿真软件自带的电机模型进行建模，根据实际的30 kVA无刷同步发电机的特性曲线以及电机参数，调整模型参数，得到与实际电机特性相近的仿真模型。

3.2" 发电机控制器电压电流控制建模

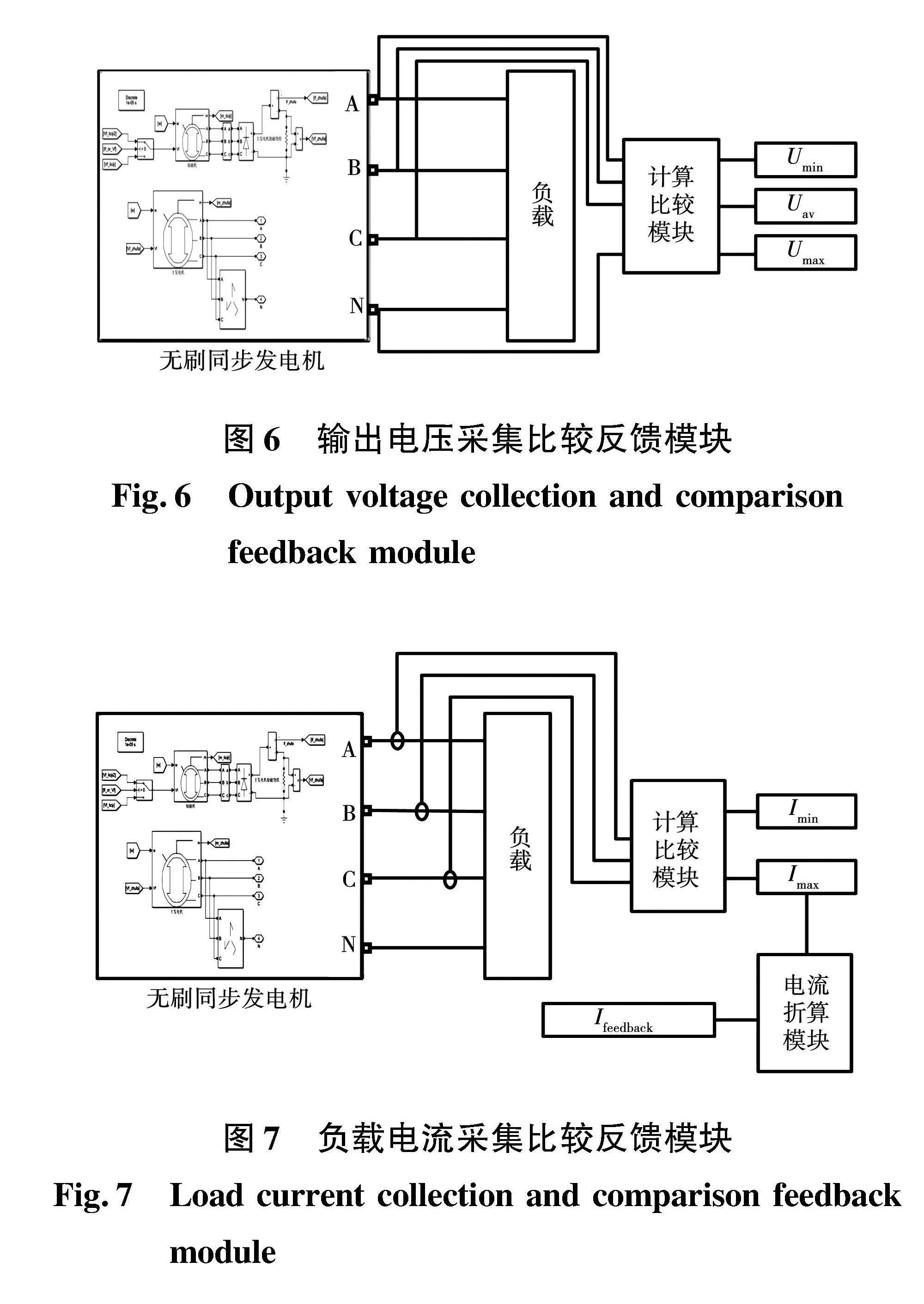
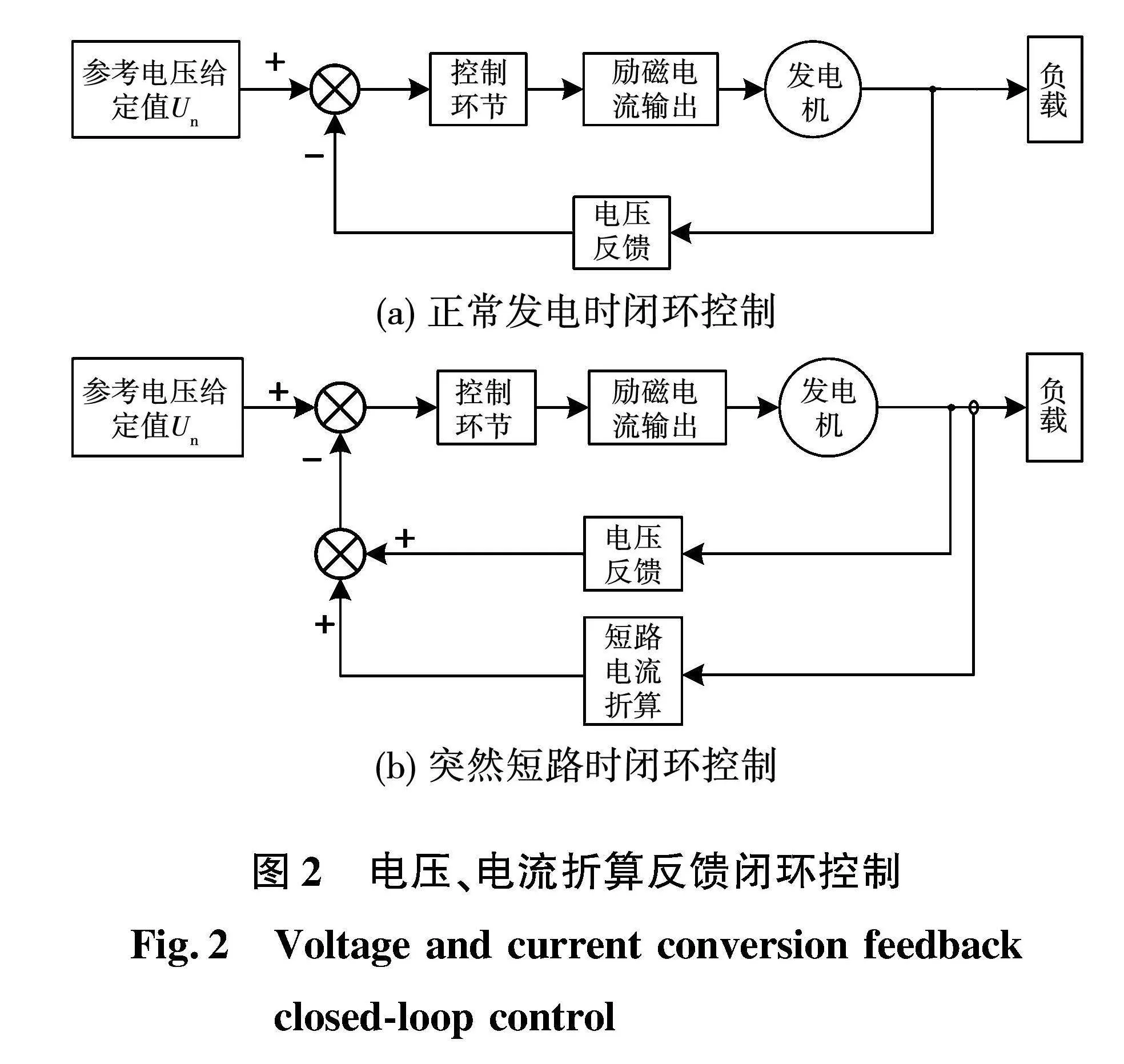
将检测到的无刷同步发电机输出端的三相电压进行有效值计算，然后进行比较，得到最大相和最小相的输出电压。当电压有效值最大相电压大于过压保护值时，采用最大相电压作为电压反馈，当电压有效值最大相过压保护值时，采用三相电压的平均值作为电压反馈。

将检测到的三相负载电流进行有效值计算，然后进行比较，得到负载电流最大相和最小相的负载电流，将负载电流最大相的电流有效值折算后加入反馈。

通过电压、电流的采集比较，如图6和图7所示，将输出电压最小相的电压Umin与UK比较，也就是判断是否为金属性短路。根据实验使用电机的参数以及实验短路去磁情况，UK的值选为35 V。当发生金属性短路时，即Uminlt;UK时，按照式（4）直接将电流有效值的最大相的电流折算到反馈中。如果不是金属性短路，即Umingt;UK时，则按照式（3）将折算后的电流加上最小相的电压有效值作为反馈。

当无刷同步发电机发生突然短路时，将折算后的电压反馈信号输入到MFAC控制模块，采用CFDL-MFAC控制。经过控制算法计算后的到相应的占空比，从而输出相应的励磁电流。

其中CFDL-MFAC控制模块涉及到5个具体的参数，分别为λ、μ、ρ、η和^c（1），对于这5个参数的整定已经有学者进行了比较充分的研究［18］，可以通过Z-N经验公式、Z-N临界比例度等整定方法，同时通过仿真调试，最终得到适用于搭建的电机模型的一组参数：λ=30，ρ=0.003，μ=1，η=0.05，^c（1）=0.003 8。

4" 基于CFDL-MFAC短路电流控制的仿真

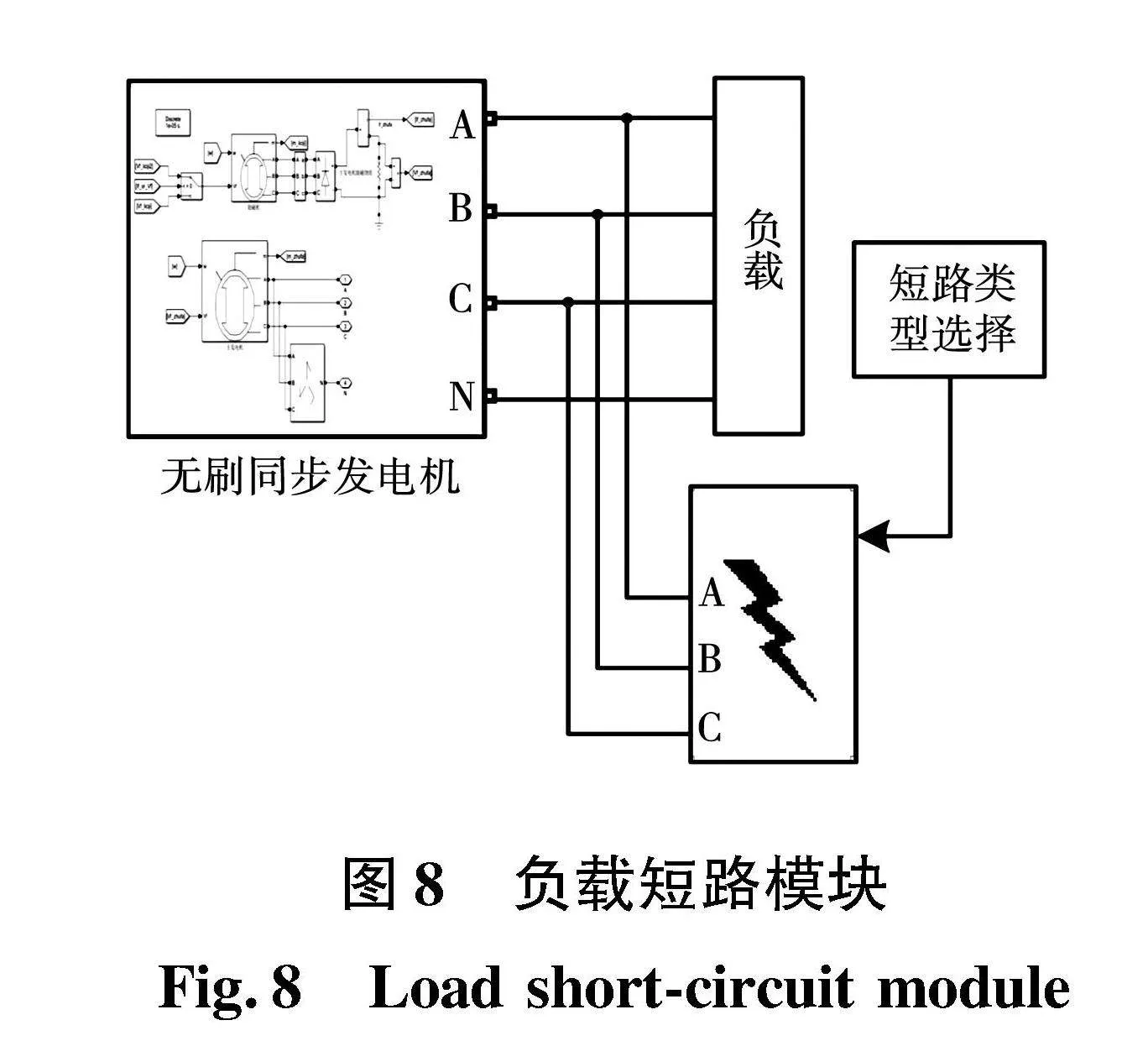
当无刷同步发电机进入短路状态后，使用CFDL-MFAC算法进行短路电流控制。利用仿真软件自带的三相故障模块模拟发电机负载的各种短路状况，进行短路实验仿真。图8为负载短路模块。

4.1" 对地短路的短路电流控制仿真分析

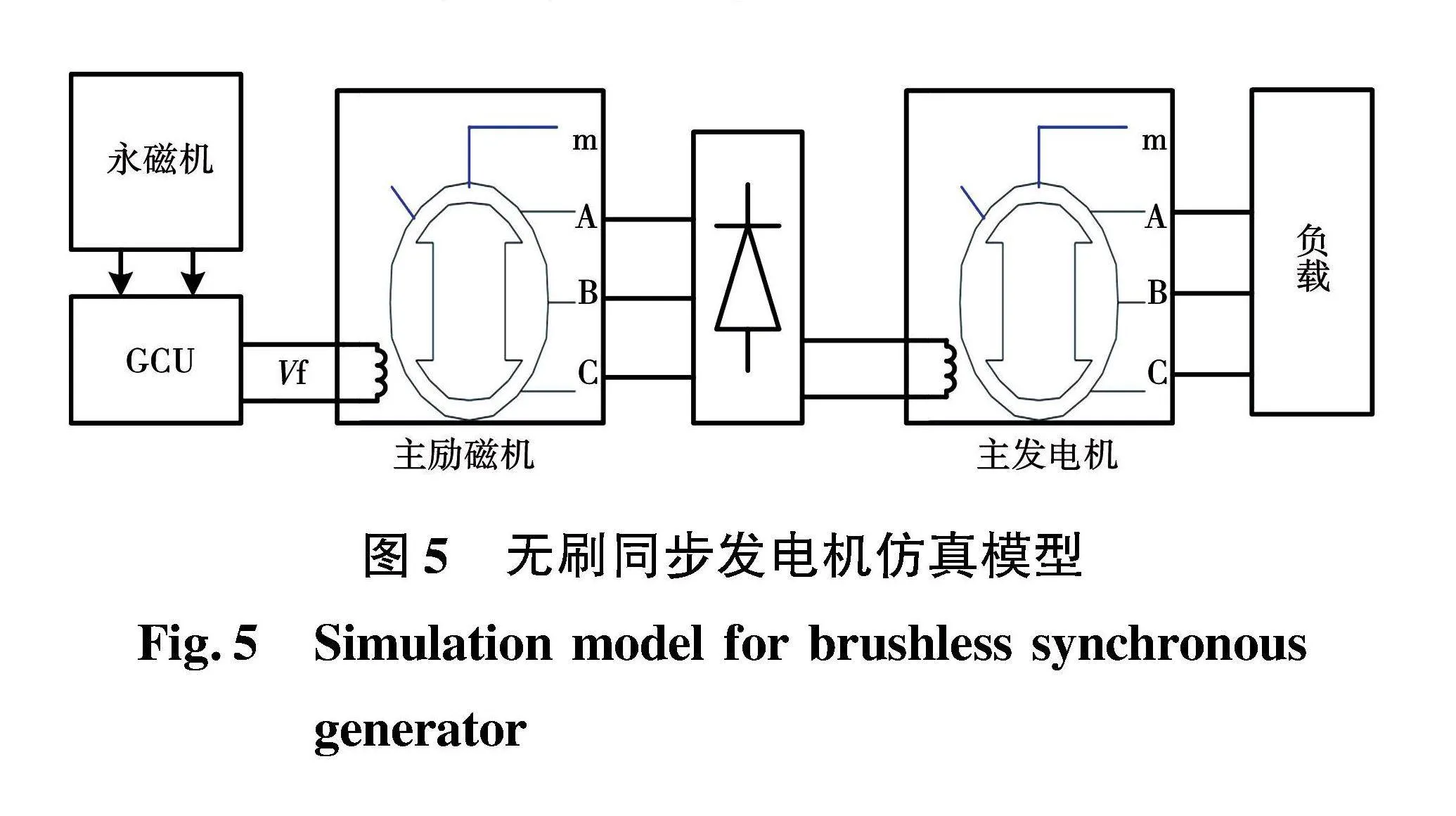
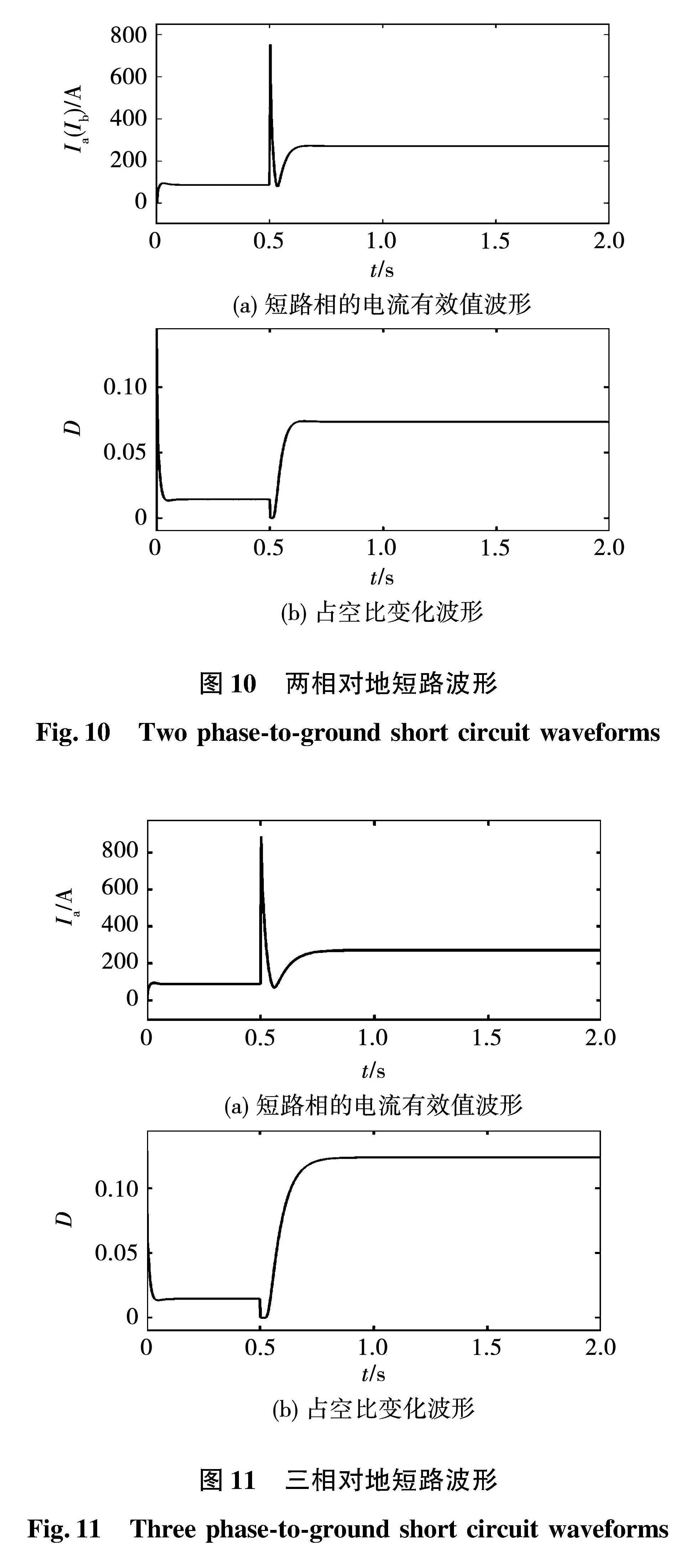
当无刷同步发电机发生对地短路时，会出现一定的突然短路尖峰，然后迅速衰减，同时突然短路相的输出电压由额定电压115 V降到0左右，此时利用CFDL-MFAC控制算法控制励磁电流，从而将短路电流有效值控制在3IN，即261 A。最终得到的单相对地短路仿真波形图9、两相对地短路仿真波形图10和三相对地短路仿真波形图11。

单相对地的短路相电压有效值波形与两相对地、三相对地和三相相间短路一致，根据A相对地短路的仿真结果的有效值波形图9（a）可以看出，在0.5 s发生突然短路后，短路相的电压迅速降到0。

短路电流经过突然短路的电流尖峰衰减后，逐渐上升到目标值后稳定下来，短路电流上升存在一定的超调，超调量在允许范围内。同时GCU主要通过控制MOS管开关的占空比来控制励磁机的励磁电流，从而控制发电机的发电。从波形的变化来看，在0.65 s左右，短路电流可以稳定控制在3IN。

两相对地短路和三相对地短路相比于单相对地短路，短路瞬间的电流峰值更大，并且短路电流稳定下来需要的时间更长，分别为0.67 s和0.81 s。通过仿真结果图10（a）和图11（a）可以看出，MFAC控制算法仍可以将短路电流稳定在目标值3IN，即261 A。

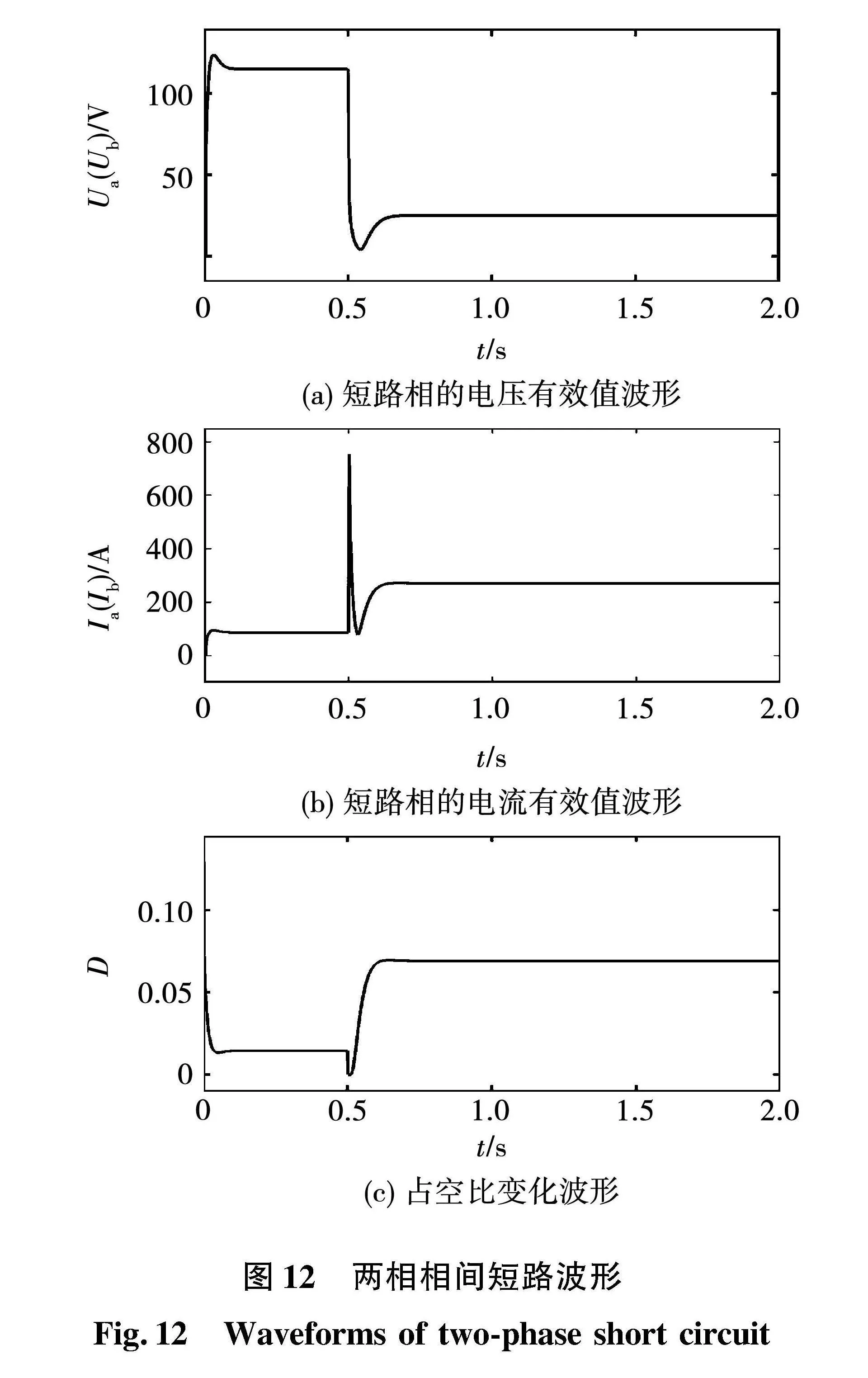
4.2" 相间短路的短路电流控制仿真分析

无刷同步发电机是三相四线的，因此相间短路与对地短路在相电压方面存在一些差异，两相相间短路时，短路相的电压并不是降到0，而是仍存在一定的幅值。

根据两相相间短路的波形图12可知，两相相间短路电流稳定需要的时间较两相对地短路更长。

根据理论分析与仿真结果来看，三相相间短路与三相接地短路时的电压电流变化是相同的，不再重复放电压电流波形图。

4.3" 仿真结果分析及与PID控制对比

通过对无刷同步交流发电机的5种短路状况进行仿真，验证了在发电机发生突然短路时，利用CFDL-MFAC控制算法对短路电流的控制的效果。根据仿真结果显示，CFDL-MFAC有较好的自适应能力，可以利用一组MFAC的相关参数控制5种不同短路状况下的短路电流，将短路电流稳定的控制在目标值3IN，即261 A。

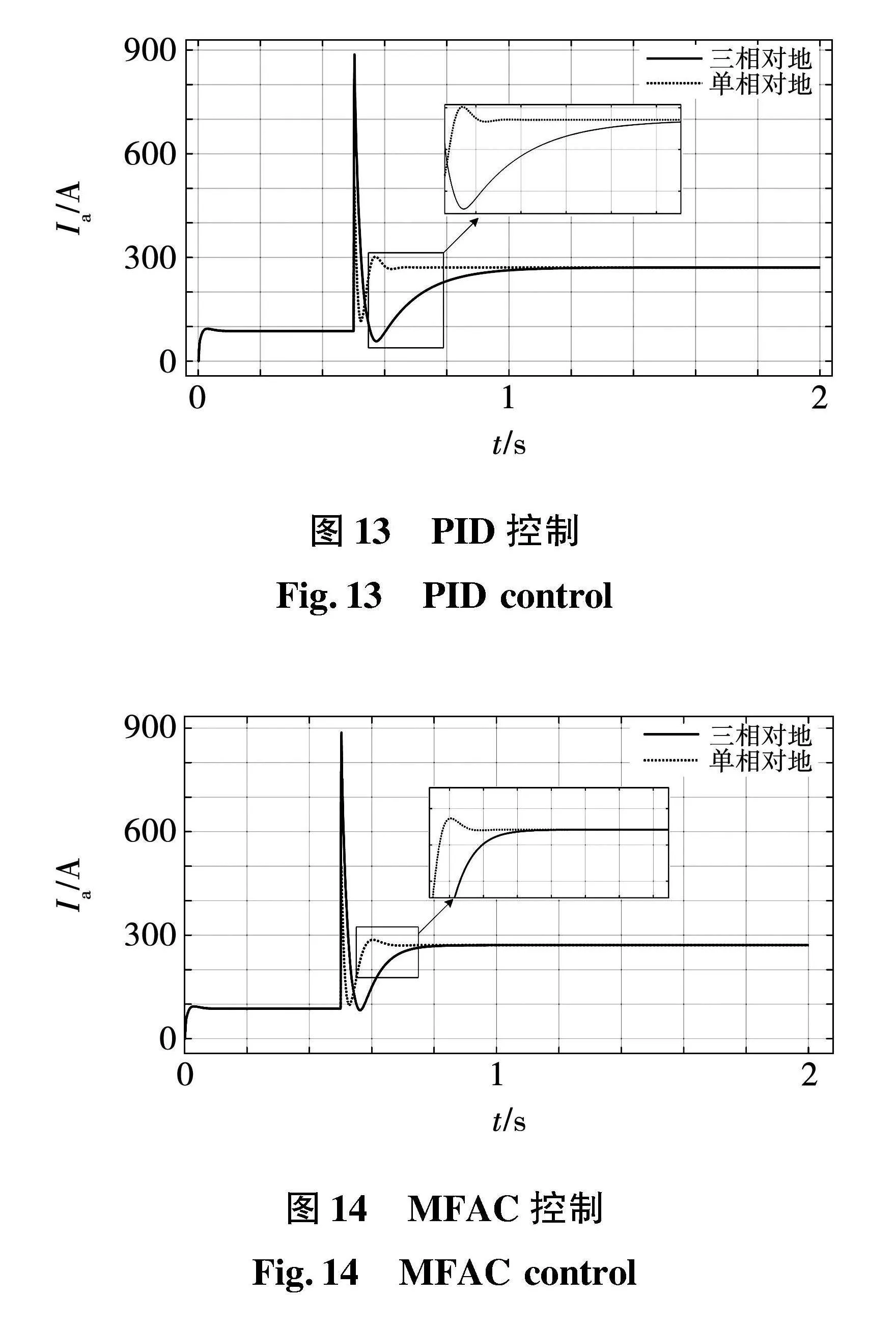
同时将采用的MFAC控制方式与工业上最常见的PID控制方式进行仿真对比，如图13、图14所示。

仿真比较PID控制和MFAC控制在短路运行情况差别最大的单相对地短路与三相对地短路下的控制效果。根据仿真结果来看，当PID控制将三相对地短路时短路电流的波形的超调量控制在规定范围内时，单相对地短路所控制的短路电流超调量就会较大，这就会导致在实际应用中一组PID参数难以同时兼顾各种类型的短路情况。相比较而言，MFAC控制的自适应能力可以更好的控制两种短路类型下的短路电流，并且控制的短路电流更平滑。

5" 实验验证

5.1" 实验平台

为了验证基于CFDL-MFAC的短路电流控制的实际效果，利用已有的30 kVA三级式无刷同步发电机、拖动台和设计的GCU作为具体实验平台进行实验验证，如图15所示。

5.2" 5种短路类型的实验波形

为了模拟5种短路类型的实验，将发电机的输出三相接到塑料外壳式断路器上，当空载发电正常后，人工合闸模拟短路。

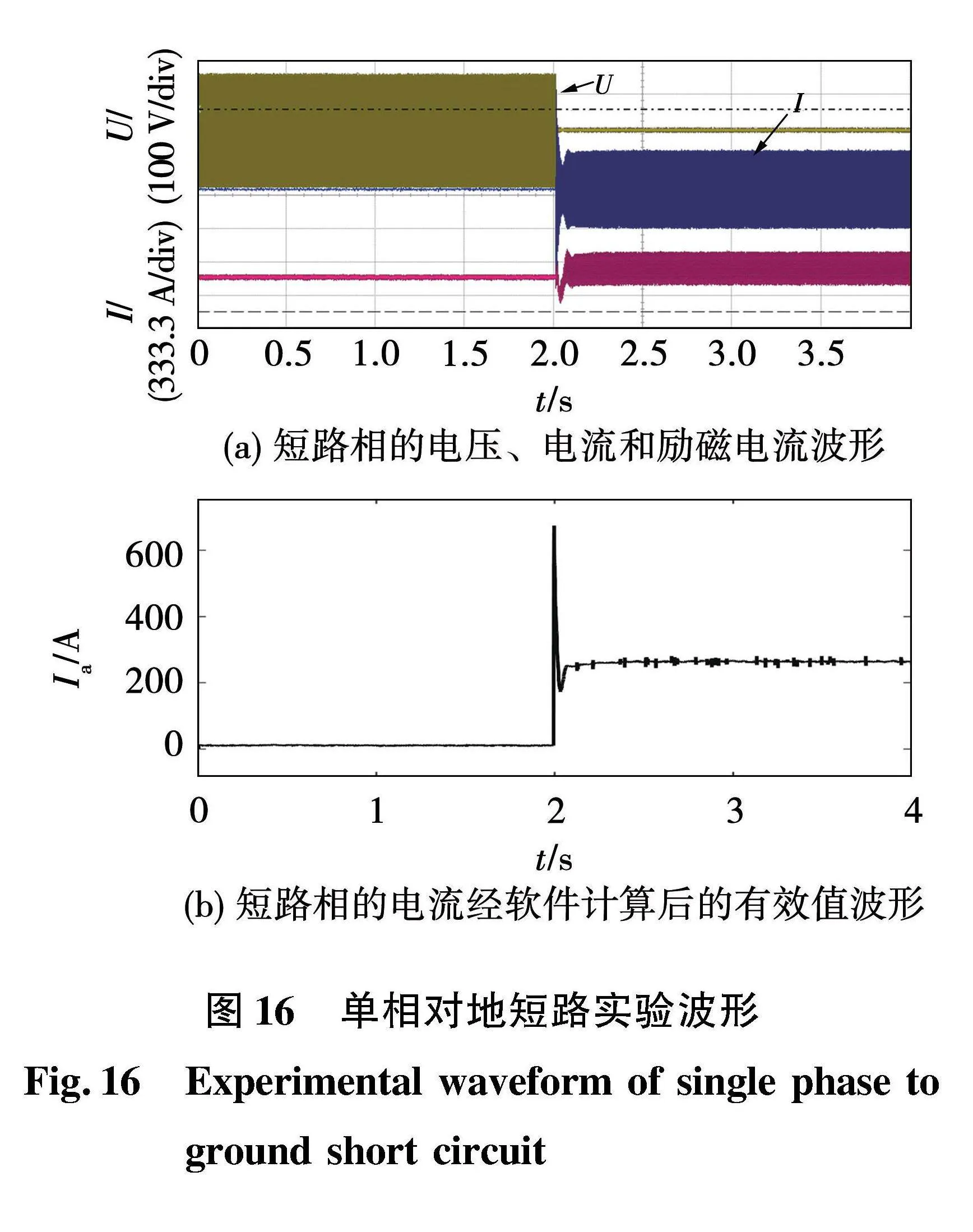
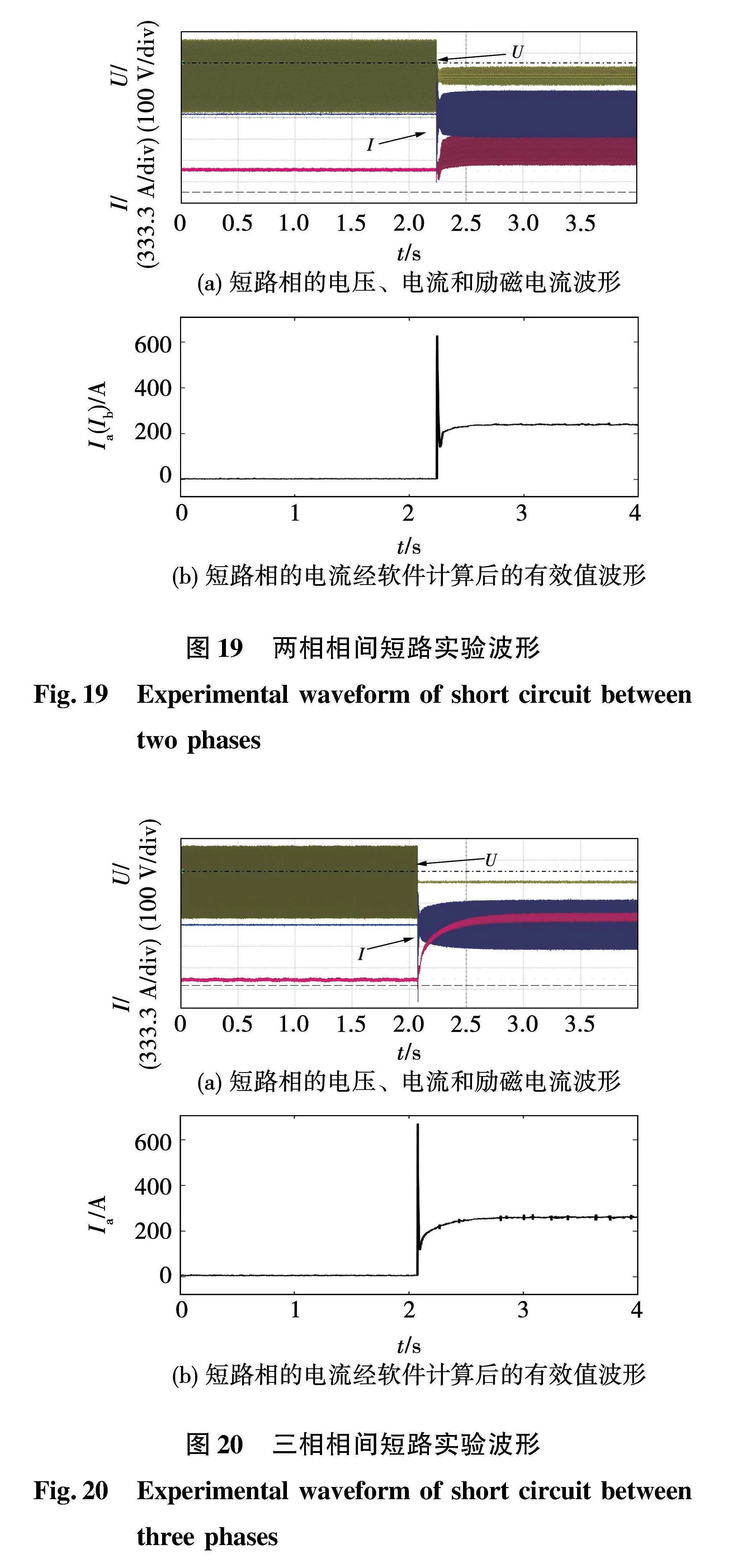
利用示波器检测短路发生时的短路电压、短路电流波形和励磁机励磁电流波形，如图16（a）～图20（a），其中C1通道测量的是短路相的电压， C3通道测量的是短路相的短路电流， C2通道测量的是励磁机的励磁电流。图16（b）～图20（b）是实验波形短路电流的有效值计算波形。

从实验波形图16可以看出，当无刷同步发电机发生A相单相对地短路时的瞬变短路电流快速衰减后由MFAC控制算法控制短路电流，短路电流在经过较短的时间后快速稳定在3倍额定电流以上，存在一点超调。

与无刷同步发电机模型的仿真结果图9相比，短路后的电压、短路电流的变化与仿真结果基本一致，只是仿真时突然短路瞬间的瞬变电流比实际仿真时的瞬变电流小。

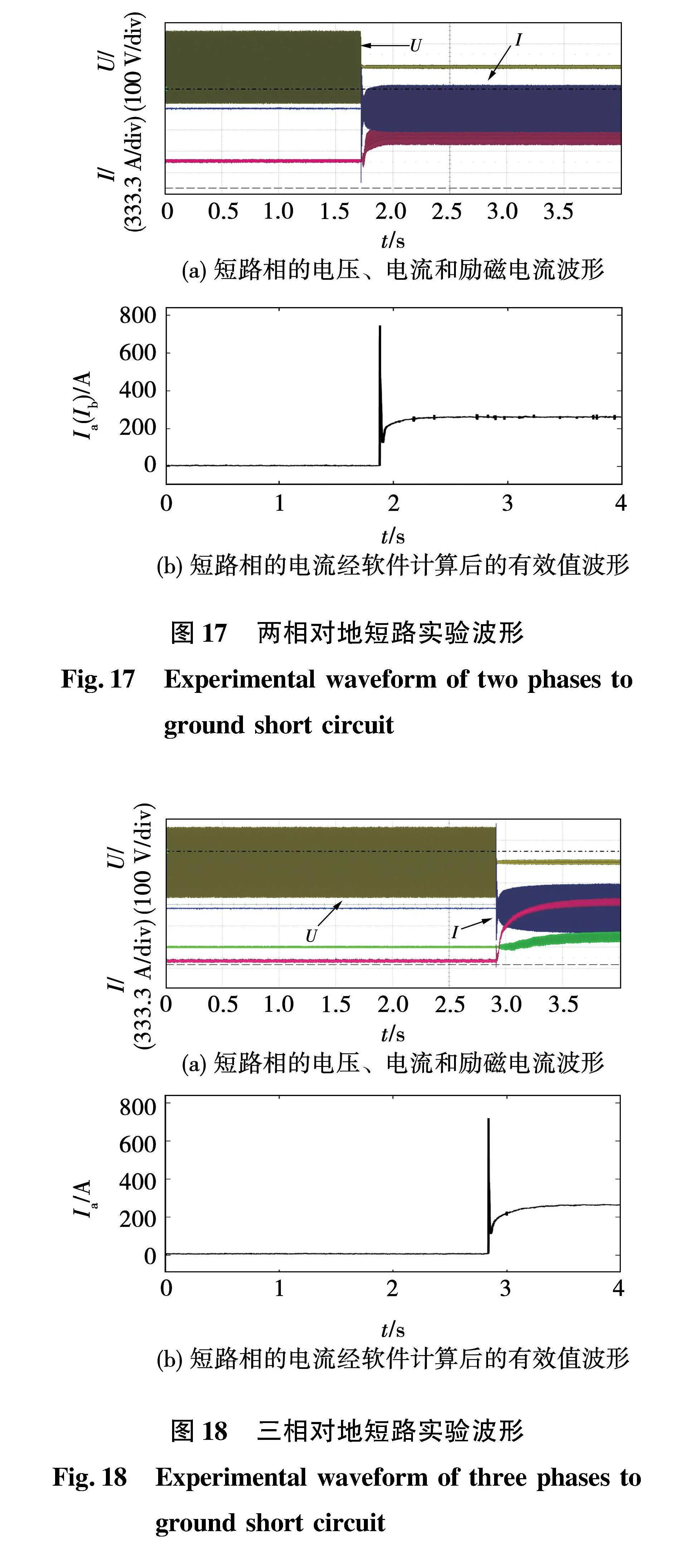
A、B两相对地短路时，如图17所示，也可以快速的将短路电流稳定在3倍额定电流以上，相较于单相对地短路，短路电流上升时间更长。同时，两相相间短路时，短路电流上升到稳定值的过程更加平滑，没有超调。

短路电压电流有效值波形与仿真结果相比较，短路瞬间的瞬变电流相似，并且短路电流上升的时间和短路电流稳定的时间与仿真结果基本一致，既反映了模型的准确性，又体现了MFAC控制算法的自适应能力。

三相对地短路同样可以将短路电流快速稳定在3倍额定短路电流以上，相较于两相对地短路，稳定时间又更长一点。

短路电压电流有效值波形与仿真结果相比较，瞬变电流比仿真结果小，但是短路电流稳定时间基本与仿真结果一致。

从实验波形图19可以看出，当发生A、B两相相间短路时，由于短路点与中线并不相连，因此短路处与中线之间存在一定的电压值在28 V左右，与仿真得到25 V相近。同时不对称短路时，励磁电流受短路电流影响，存在一定的周期性分量。

三相相间短路与三相对地短路的情况基本相似。短路电压电流有效值波形与仿真结果相比较，同样是瞬时电流峰值较小。

5.3" 实验结果分析

根据5种短路类型的实验波形，与仿真波形进行比较可以看出，在短路瞬间的峰值电流并不完全一致，这是因为突然短路的瞬变电流与电机的参数、材质等有很大的关系，这些在建立模型时很难量化成数学公式，同时实际实验时电流采样采用的是电流互感器，当电流过大时会导致互感器饱和。

在稳态短路电流波形方面，实验波形与仿真波形基本一致， CFDL-MFAC控制算法可以将短路电流很好的控制在3倍额定短路电流以上，如表3所示，从表中可以看出，MFAC控制算法可以将短路电流控制在3IN以上，最大不超过3IN的2.75%，控制效果较好，具有良好的自适应能力与鲁棒性。

6" 结" 论

本文利用MFAC控制算法，将其运用在30 kVA的无刷同步发电机短路电流控制上。根据仿真与实验验证，MFAC控制算法具有较好的自适应能力，在无刷同步发电机上利用该算法可以适应5种不同类型的短路状况，并且可以将短路电流的稳态值控制在3倍额定电流以上。只是MFAC算法较复杂，需要控制芯片有足够的资源和算力。此外，该控制方案也可以应用于其他类型电机的短路电流控制，有较好的实用价值。

参 考 文 献：

［1］" 朱新宇，龚凯越，彭旭，等. 400 Hz航空地面电源研究综述［J］. 民航学报， 2022， 6（2）：86.

ZHU Xinyu， GONG Kaiyue， PENG Xu， et al. Review of 400 Hz aviation ground power unit research［J］. Journal of Civil Aviation， 2022， 6（2）：86.

［2］" 戴卫力，王慧贞，严仰光，等.航空起动/发电系统的发展趋势与研究现状［J］. 航空科学技术， 2010， 126（5）：28.

DAI Weili， WANG Huizhen， YAN Yangguang， et al. Development trend and current situation of starter-generator for aircraft engine［J］.Aeronautical Science amp; Technology，2010，126（5）：28.

［3］" 赵君，花璐，韩佳玮，等. 一种高性能航空直流起动发电机控制器设计［J］. 航空计算技术，2020，50（1）：88.

ZHAO Jun， HUA Lu， HAN Jiawei， et al. Design of a high performance aviation DC staring engine controller［J］. Aeronautical Computing Technique， 2020， 50（1）：88.

［4］" 文力. 三级式同步电机发电控制的研究［D］. 南京：南京航空航天大学， 2020.

［5］" CHIVER L， NEAMT， MATEI O. Compara-tive study on sudden short-circuit currents of a synchronous generator［C］//2015 IEEE 15th International Conference on Environment and Electrical Engineering （EEEIC），June 10-13， 2015， Rome， Italy. 2015：1688-1693.

［6］" 庄圣伦，黄文新，卜飞飞，等. 变频交流发电系统双定子绕组异步发电机短路瞬态分析［J］. 航空学报， 2017， 38（8）：155.

ZHUANG Shenglun， HUANG Wenxin， BU Feifei， et al. Short circuit transient analysis of dual stator-winding induction generator based on aircraft variable frequency AC generating system ［J］. Acta Aeronautica et Astronautica Sinica， 2017， 38（8）：155.

［7］" ESNIC＇ S， SOLDO A， POLJAK D. Transient impedance of the synchronous generator grounding electrode due to short circuit current［C］//2020 International Symposium on Electromagnetic Compatibility-EMC EUROPE，September 23-25， 2020， Rome， Italy. 2020：1-4.

［8］" 欧阳金鑫，熊小伏.计及转子励磁控制的双馈感应发电机短路电流研究［J］.中国电机工程学报，2014，34（34）：6083.

OUYANG Jinxin， XIONG Xiaofu. Research on short-circuit current of doubly-fed induction generators under rotor excitation control［J］. Proceedings of the CSEE， 2014，34（34）：6083.

［9］" DENG Z， WANG H， QIN Y， et al. An optimal short-circuit current control method for self-synchronization controlled wind turbines［C］//2022 IEEE Transportation Electrification Conference and Expo， Asia-Pacific， October 28-31， 2022， Haining， China. 2022：1-6.

［10］" 戴卫力，严仰光.电励磁双凸极发电机的短路运行分析［J］. 微电机， 2010， 43（10）：1.

DAI Weili，YAN Yangguang.Short circuit analysis of doubly salient electromagnetic generator［J］.Micromotors，2010，43（10）：1.

［11］" ZHANTLESOVA B， LSSABEKOVA B B， NOSOVSKII D A. The control system of a steady short-circuit current measurement using the expert estimation method［C］//2015 International Siberian Conference on Control and Communications （SIBCON）， May 21-23， 2015， Omsk， Russia. 2015：1-5.

［12］" 宋勇刚.基于Simscape航空三级式起动/发电机建模仿真研究［J］. 西安航空学院学报， 2023， 41（1）：49.

SONG Yonggang. Modeling and simulation of aviation three-stage starter/generator based on simscape［J］. Journal of Xi’an Aeronautical Institute， 2023， 41（1）：49.

［13］" 马鹏，刘卫国，骆光照，等.一种三级式航空无刷同步电机起动控制策略［J］. 电机与控制学报， 2012， 16（11）：29.

MA Peng， LIU Weiguo， LUO Guangzhao， et al. Starting control strategy for three-stage aviation brushless synchronous motor［J］. Electric Machines and Control， 2012， 16（11）：29.

［14］" 张卓然， 杨善水， 陈志辉. 交流发电机电压调节器负载电流限制电路的研究［J］. 南京航空航天大学学报， 2003， 35（2）： 143.

ZHANG Zhuoran， YANG Shanshui，CHEN Zhihui. Research on load-current-limiting circuit in voltage regulator of AC generator［J］. Journal of Nanjing University of Aeronautics amp; Astronautics， 2003， 35（2）：143.

［15］" 侯忠生，金尚泰． 无模型自适应控制：理论与应用［M］． 北京：科学出版社，2013．

［16］" 侯忠生.无模型自适应控制的现状与展望［J］. 控制理论与应用， 2006， 23（4）： 586.

HOU Zhongsheng. On model-free adaptive control： the state of the art and perspective［J］. Control Theory amp; Applications， 2006， 23（4）： 586.

［17］" 姚文龙，裴春博，池荣虎，等. 基于无模型自适应控制的船舶微电网二次调频控制策略［J］.电机与控制学报，2023，27（3）：135.

YAO Wenlong， PEI Chunbo， CHI Ronghu， et al. Secondary frequency modulation control strategy of ship microgrid withmodel-free adaptive control［J］. Electric Machines and Control， 2023， 27（3）：135.

［18］" 郭代银. 无模型自适应控制参数整定方法研究［D］.北京：北京交通大学，2014.

（编辑：刘琳琳）