转子激励对永磁同步电机电磁振动影响分析

摘" 要：

对于电动汽车用永磁同步电机，气隙内的电磁激励会产生高频振动和噪音。通常将气隙电磁激振力施加到定子齿部，并通过理论计算或仿真得到定子或壳体外表面的振动噪音响应，而由转子激励引起的振动噪音被忽略。为研究转子激励对整体电磁振动噪音的贡献度，首先依据麦克斯韦应力张量法对气隙电磁力谐波进行理论分析，同时建立单电机的电磁振动仿真模型。然后以一台8极定子48槽内置式永磁同步电机为样机，通过试验模态分析和仿真分别对定子和转子的材料参数进行修正。再分别进行转子动力学和电磁激励下的整机动力学仿真，结果表明由转子偏心引起的不平衡电磁激励能够引起转子系统共振，并且在单位电磁力波的激励下，转子激励引起的响应与定子激励引起的响应在低频段具有同等的重要性。最后通过样机振动试验对上述结论进行了验证。

关键词：永磁同步电机；转子偏心；电磁力波；模态分析；临界转速；电磁振动

DOI：10.15938/j.emc.2024.06.004

中图分类号：TM351

文献标志码：A

文章编号：1007-449X（2024）06-0036-09

收稿日期： 2023-10-25

基金项目：国家自然科学基金区域创新发展联合基金重点支持项目（U21A20145）；国家自然科学基金（51977052）

作者简介：郭冠宁（1986—），男，博士研究生，研究方向为永磁同步电机的设计及振动噪声优化；

蔡" 蔚（1959—），男，博士，教授，博士生导师，研究方向为驱动电机、功率电子控制器及汽车电动化电驱动系统、低振动噪声电机等；

邵佰成（1994—），男，博士研究生，研究方向为永磁同步电机的设计与优化。

通信作者：郭冠宁

Analysis of rotor excitation influence on electromagnetic vibration of permanent magnet synchronous motor

GUO Guanning，" CAI Wei，" SHAO Baicheng

（School of Electrical and Electronic Engineering， Harbin University of Science and Technology， Harbin 150080， China）

Abstract：

For permanent magnet synchronous motors of electric vehicle application， high-frequency vibration and noise could be induced by the electromagnetic excitation within air-gap. In current research， electromagnetic forces of air-gap are usually applied to the stator teeth， and then the vibration and noise response of the stator or outer surface of housing is obtained through theoretical calculation or simulation， while the vibration and noise induced by rotor excitation is ignored. In order to study the contribution of rotor excitation to the overall electromagnetic vibration and noise， first， the electromagnetic force harmonics were analyzed theoretically with the Maxwell stress tensor method， and then the vibration simulation model of single motor was established. Secondly， taking an 8-pole 48 stator slots interior permanent magnet synchronous motor （IPMSM） as the prototype， the stator and rotor material parameters were corrected through experimental modal test， and then the rotor dynamic and whole motor dynamic response under the electromagnetic excitation was simulated. The results show rotor resonance could be excited by the unbalanced electromagnetic force induced by the eccentricity; the responses induced by rotor and stator respectively are of equal importance in the low frequency range. Finally， the conclusions above are verified through vibration test on prototype.

Keywords：permanent magnet synchronous motor; rotor eccentricity; electromagnetic wave-force; modal analysis; critical speed; electromagnetic vibration

0" 引" 言

磁钢内置式永磁同步电机具有高功率密度，高效率和较宽的调速范围等优点，因而在国内外被广泛应用于混合动力汽车或纯电动汽车的主驱动系统中。电驱动总成的声品质与传统的内燃机动力总成有明显区别，易产生高频电磁啸叫［1-4］。近年来许多学者和工程师对不同类型的永磁同步电机电磁振动噪声机理进行了研究。文献［5］首先对一台电动汽车用内置式永磁同步电机（8极，定子槽数48）的电磁力波公式进行了理论推导，并对各自力波产生的原因进行了分析。最后通过样机测试对理论分析进行了验证。结果表明：对于整数槽永磁同步电机，空间0阶12倍电源频率激励分量主要由一阶齿谐波引起，并且该力波是导致永磁同步电机电磁振动噪音的主要原因。文献［6］对采用分数槽集中绕组的永磁电机（10极，定子槽数12）进行了电磁振动分析。研究发现，将气隙分布电磁力转化到定子齿部的集中力时，高空间阶次的电磁力波可以被调制成低阶次的电磁力波，进而恶化电磁振动噪音。该现象被定义为定子槽的调制效应。

在对永磁同步电机电磁振动机理研究的同时，已有较多改善电机电磁振动噪音的措施被应用于工程实践中，主要包含对电机本体设计和控制器控制策略优化两个方面。文献［7］针对车用永磁同步电机48阶噪音过大的问题进行了不同方案的电机本体优化，包括转子斜极，转子表面开辅助槽，定子绕组树脂灌封和电机壳体增加刚度。经样机验证发现，前两种方案均能有效改善48阶的阶次噪声和噪音总值，车内噪声整体降低约5 dB。文献［8］以一台车用6极36槽永磁同步电机为研究对象，通过在转子表面开两个关于d轴对称的辅助槽的方式削弱气隙磁场齿谐波。并经尺寸参数优化和多物理场仿真，优化后转矩脉动最大降低34%，噪声最大值下降4 dB，最终样机测试结果验证了优化措施的有效性。文献［9］开发了一种在线的电流谐波注入方法对电机的电磁振动进行抑制。该研究不仅详细介绍了电流环和相位补偿的设计方法，还将该理论在一台750 W表贴式永磁同步电机进行验证。结果表明低频偶数阶次的电磁振动在电流谐波注入后得到了明显的下降。文献［10］ 针对控制器由于功率开关管死区和管压降导致的谐波提出在线谐波电流补偿的方法，通过在线提取谐波电流，注入谐波电压来抑制电机运行时的5次、7次谐波电流，改善了转矩脉动和转速波动。

针对内转子式永磁同步电机电磁振动噪声计算时，已有研究多以定子作为振动噪声的激励源，忽略了转子的影响。本文以一台车用8极，48定子槽的永磁同步电机为研究对象，定量分析转子激励对壳体振动的贡献度。首先用麦克斯韦张量法对气隙电磁力的成分进行分析，然后建立电磁振动的动力学模型。在此基础上对研究对象进行电磁场和结构场仿真。将单位力波径向激励和负载工况激励先后单独添加到定子和转子表面，然后经动力学仿真获取壳体表面同一点的振动响应。通过响应结果的对比研究转子激励对壳体振动的影响。最后，将电磁振动仿真结果与样机测试结果进行比较，验证仿真方法的有效性。

1" 电磁激振力及振动模型建立

本节从电磁学和力学角度出发，建立永磁同步电机的电磁振动分析模型。首先根据永磁电机的定转子磁动势与气隙磁导公式可以得到气隙的磁密，然后按照麦克斯韦应力张量法分析径向和切向电磁力的成分。其次建立电磁振动分析模型和动力学方程。

1.1" 电磁激振力

气隙磁密由定子磁场和转子磁场相互作用产生，同时考虑到气隙磁导的调制作用，其大小可以通过下式得到：

B=|F|Λg；

F=Fs+Fr；

Λg=Λ0+∑m=1，2，3，…Λmcos（mZθ）。（1）

式中：|F|表示合成磁动势矢量F的幅值；Λ0和Λm分别为平均磁导和定子开槽调制磁导；m为气隙磁导谐波次数；Z为定子槽数；θ为空间机械角度。对于三相对称定子绕组，基波电流产生的定子磁动势可以表示为

Fs=32∑νFsνcos（vpθ－ωet－φν）。（2）

式中：ν为定子磁动势谐波次数；p为极对数；Fsν为谐波磁动势的幅值；ωe为电流角频率；φν为定子磁动势相位。永磁体在圆周方向均匀分布的转子所产生的磁动势可以表示为

Fr=∑μ=1，3，5，7，…Frμcos（μpθ－μωet－φμ）。（3）

式中：μ为转子磁动势谐波次数；Frμ和φμ分别为转子谐波磁动势的幅值和相位。根据如下的麦克斯韦应力公式可以得到气隙内的径向和切向电磁力：

σn（θ，t）=B2n（θ，t）－B2t（θ，t）2μ0；

σt（θ，t）=Bn（θ，t）Bt（θ，t）μ0。（4）

式中：σn和σt分别代表径向和切向电磁力；Bn和Bt分别代表径向和切向磁密分量；μ0为真空磁导率。由式（1）可知气隙的磁动势矢量由定转子磁动势矢量相加得到。为简化电磁力的推导，忽略定转子磁动势间的相位差（即将定转子磁动势矢量转化为标量）。将式（2）和式（3）代入式（1），并忽略式（4）中的切向磁密，进而可以得到径向电磁力为：

σn=Λ2g2μ0（F2r+F2s+2FrFs）；（5）

FsFr=∑ν∑μFsνFrμcos［（ν±μ）pθ－（1±μ）ωet］。（6）

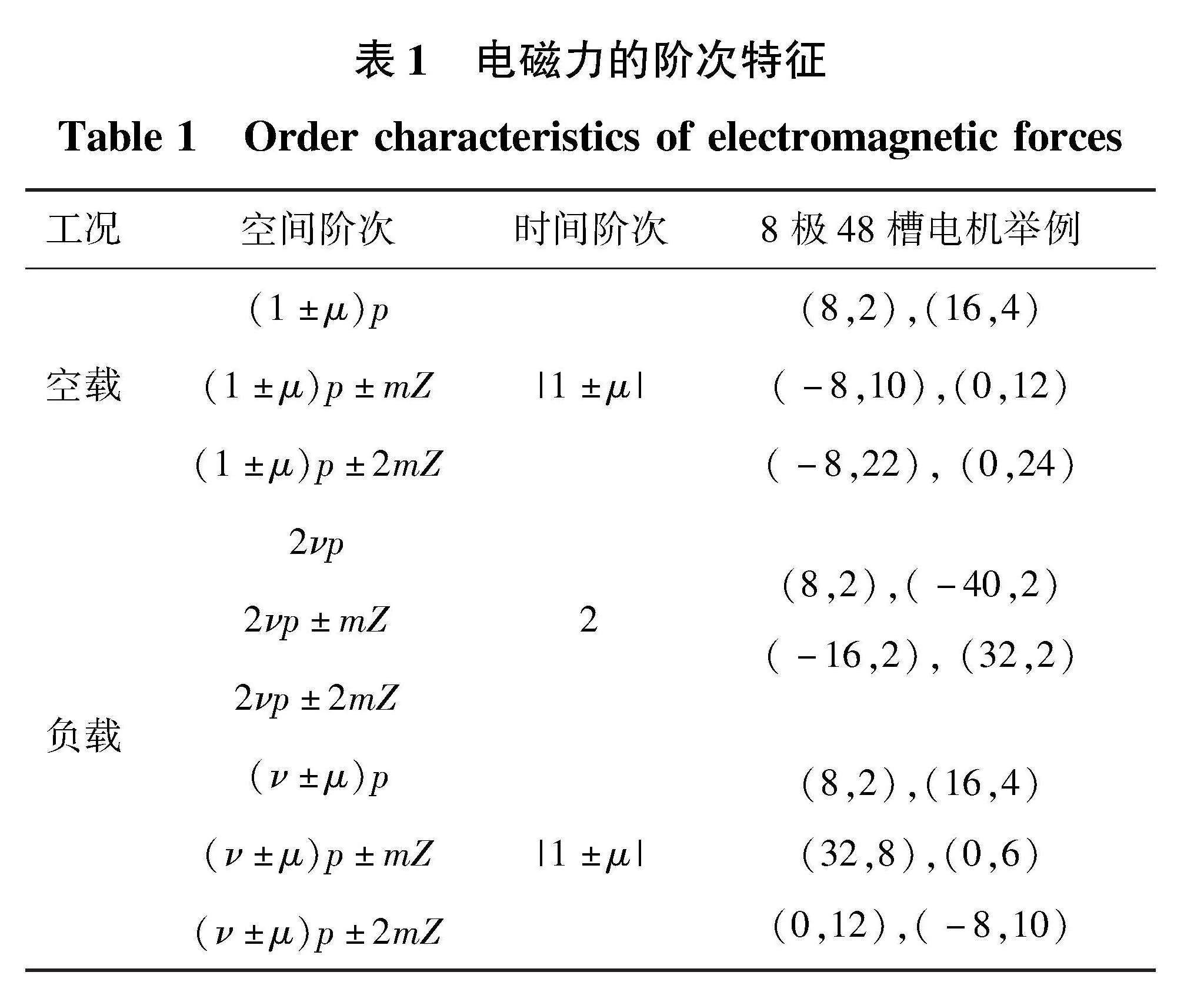
对于空载工况，当定子绕组电流幅值较小时，径向电磁力主要由转子磁动势谐波相互作用产生。负载工况下，除定子或转子各自的磁动势谐波之间相互作用外，还存在定转子磁动势谐波相互作用的情况，如式（6）所示。从式（5）和式（6）可以看出径向电磁力是空间和时间的函数，可分为由平均气隙磁导和开槽磁导调制的两大类电磁力，用表1对此进行归纳。同时以一台定子48槽8极永磁同步电机为对象，对空载和负载工况下的典型电磁力阶次特征举例说明。括号内的第一个数字表示力的空间阶次，第二个数字表示力的时间阶次。根据经典电磁振动理论，低空间阶次的电磁力容易引起电机振动噪音问题。对于电动汽车用永磁同步电机，脉动的空间0阶电磁力是引起呼吸模态共振的主要原因［11］。

1.2" 电磁振动模型

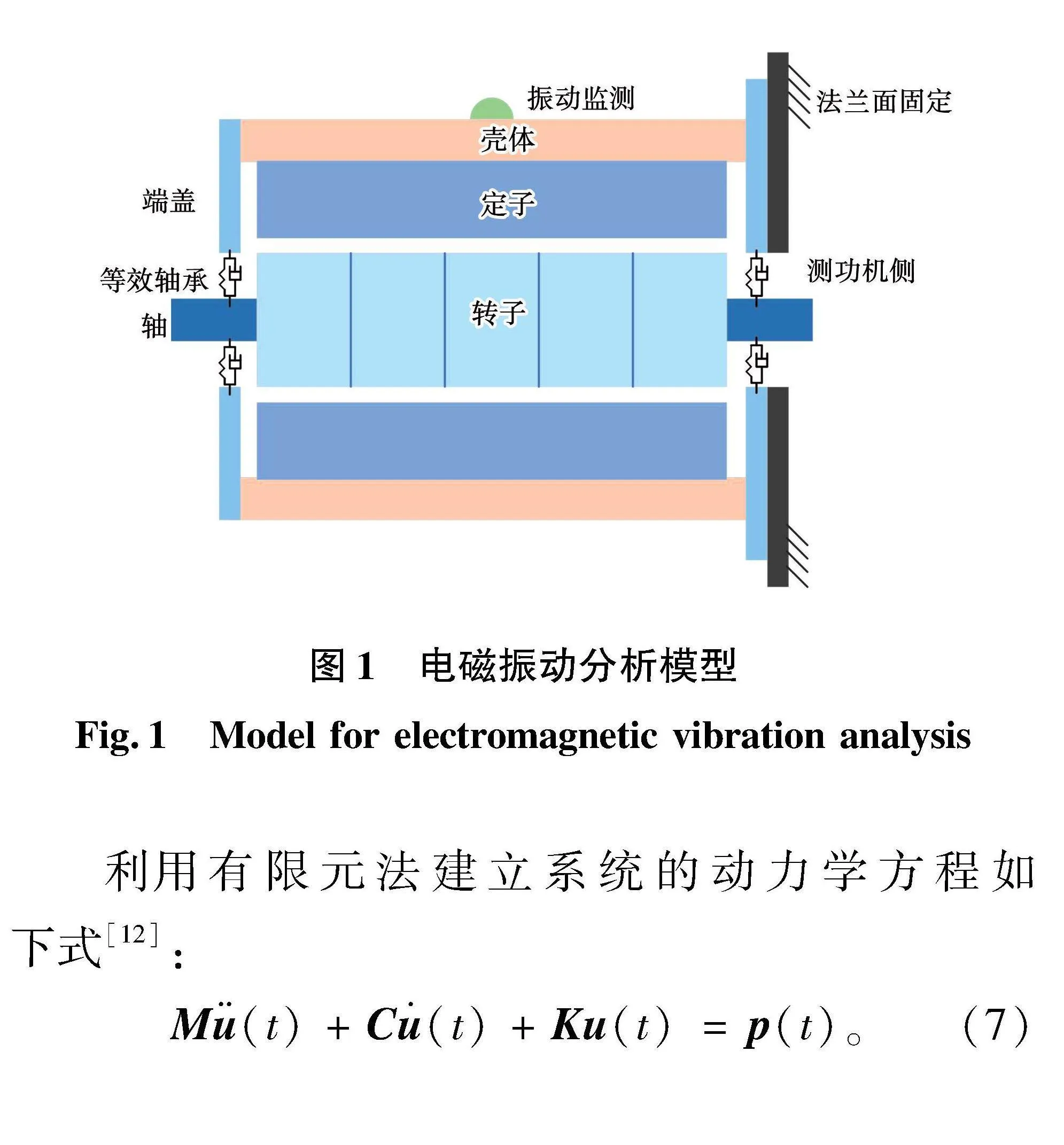
为便于对比分别仅有定子激励和转子激励下的振动响应，首先建立如图1所示的振动模型。其中定子部分包含定子铁心、等效绕组、壳体及端盖，转子部分包含转子铁心和轴。内置式永磁电机的转子通常在轴向被分成多个模块，这样既方便永磁体的插入，还可以根据需要进行斜极以达到改善电机电磁振动噪音的目的。因而转子模型在轴向被分成若干个模块。转子两端分别由滚动轴承支撑，在分析模型中轴承可用包含刚度和阻尼的轴承单元等效替代。

利用有限元法建立系统的动力学方程如下式［12］：

Mu··（t）+Cu·（t）+Ku（t）=p（t）。（7）

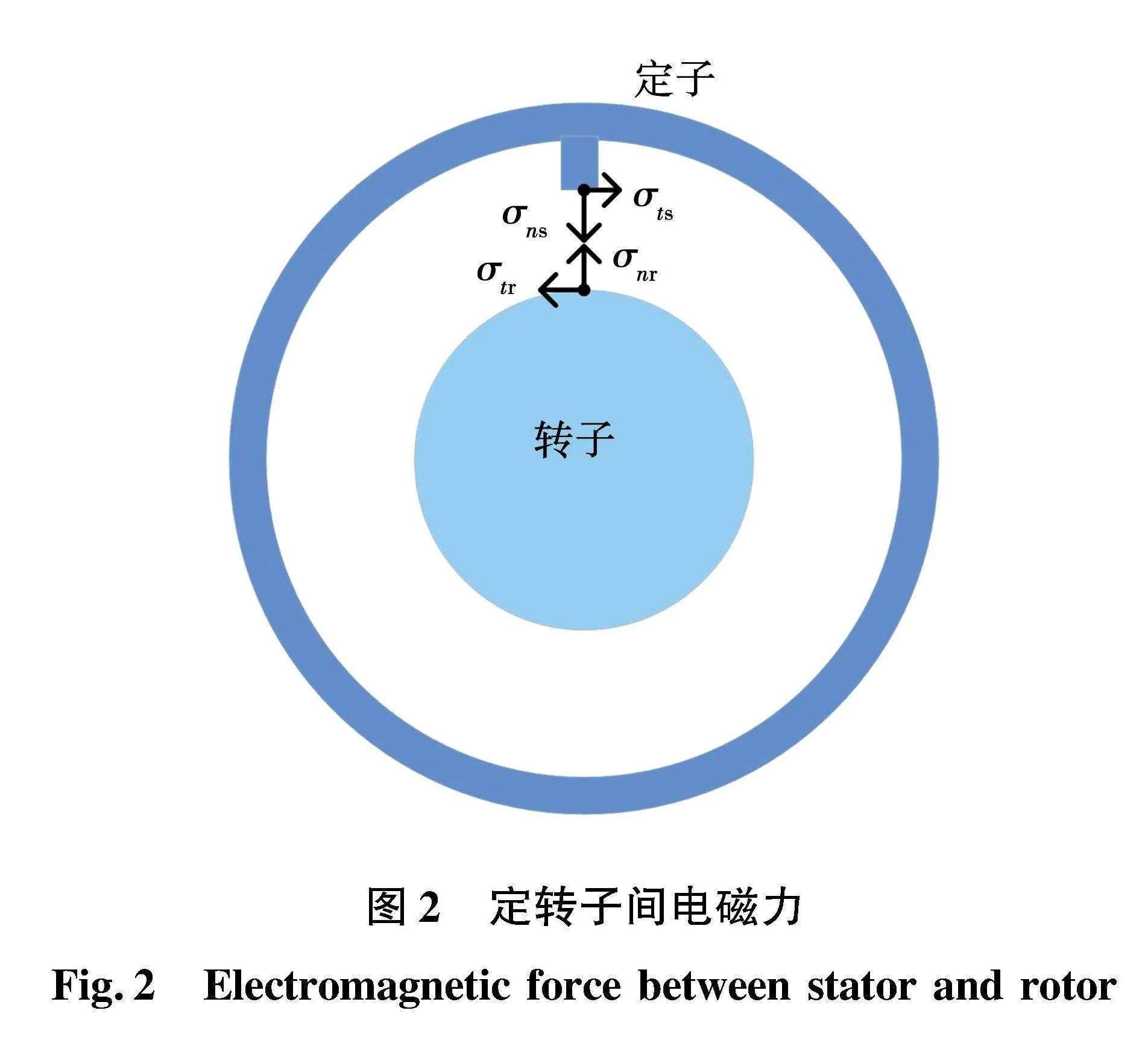
式中：M、C、K分别代表系统的质量矩阵、阻尼矩阵和刚度矩阵；u（t）和p（t）分别代表位移向量和载荷向量。定子与转子间的电磁力可以用图2说明：两者间的径向力和切向力分别大小相等，方向相反。提取壳体表面单点（壳体中间位置）的振动加速度作为分析目标。

2" 电磁振动仿真

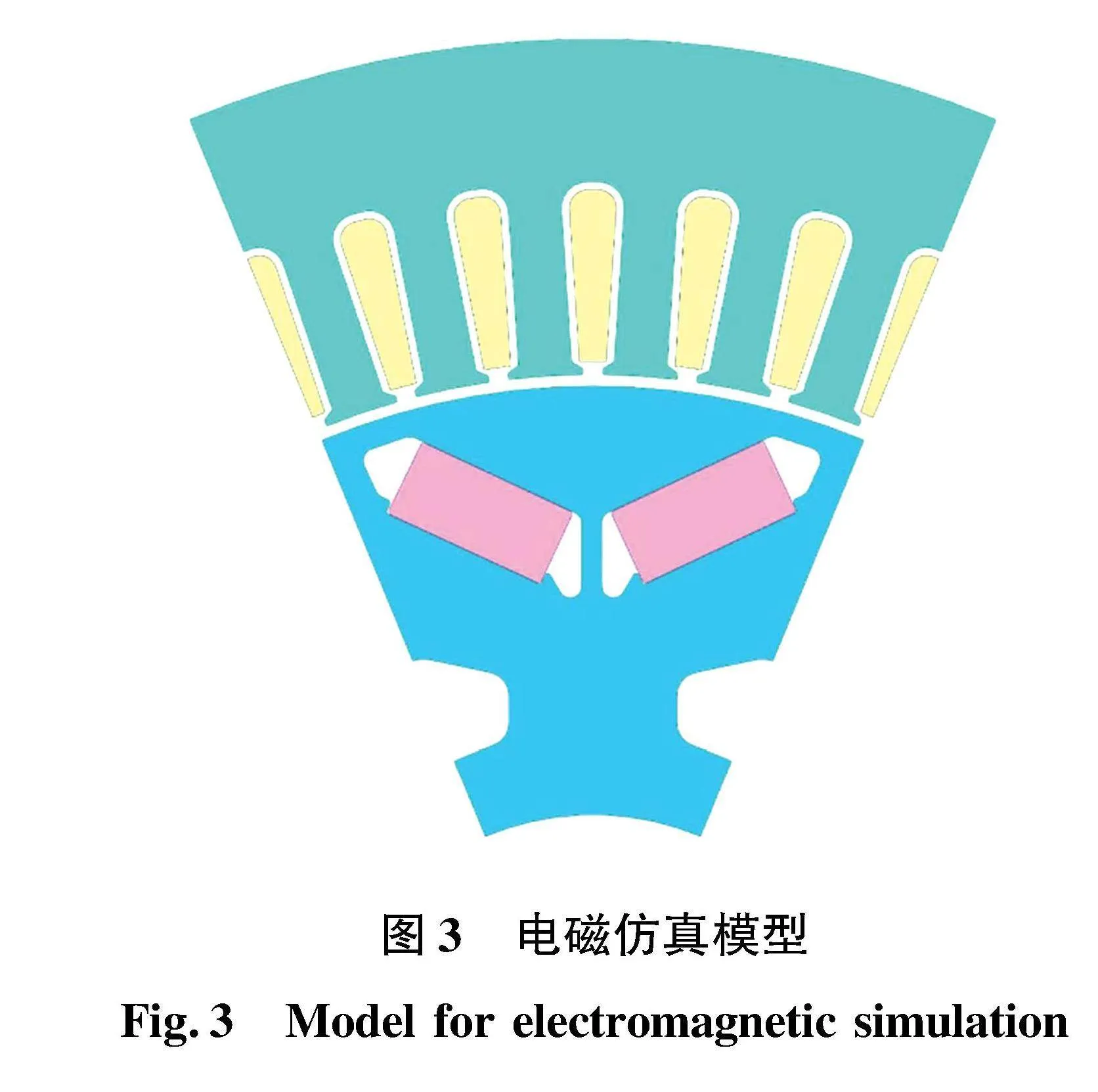
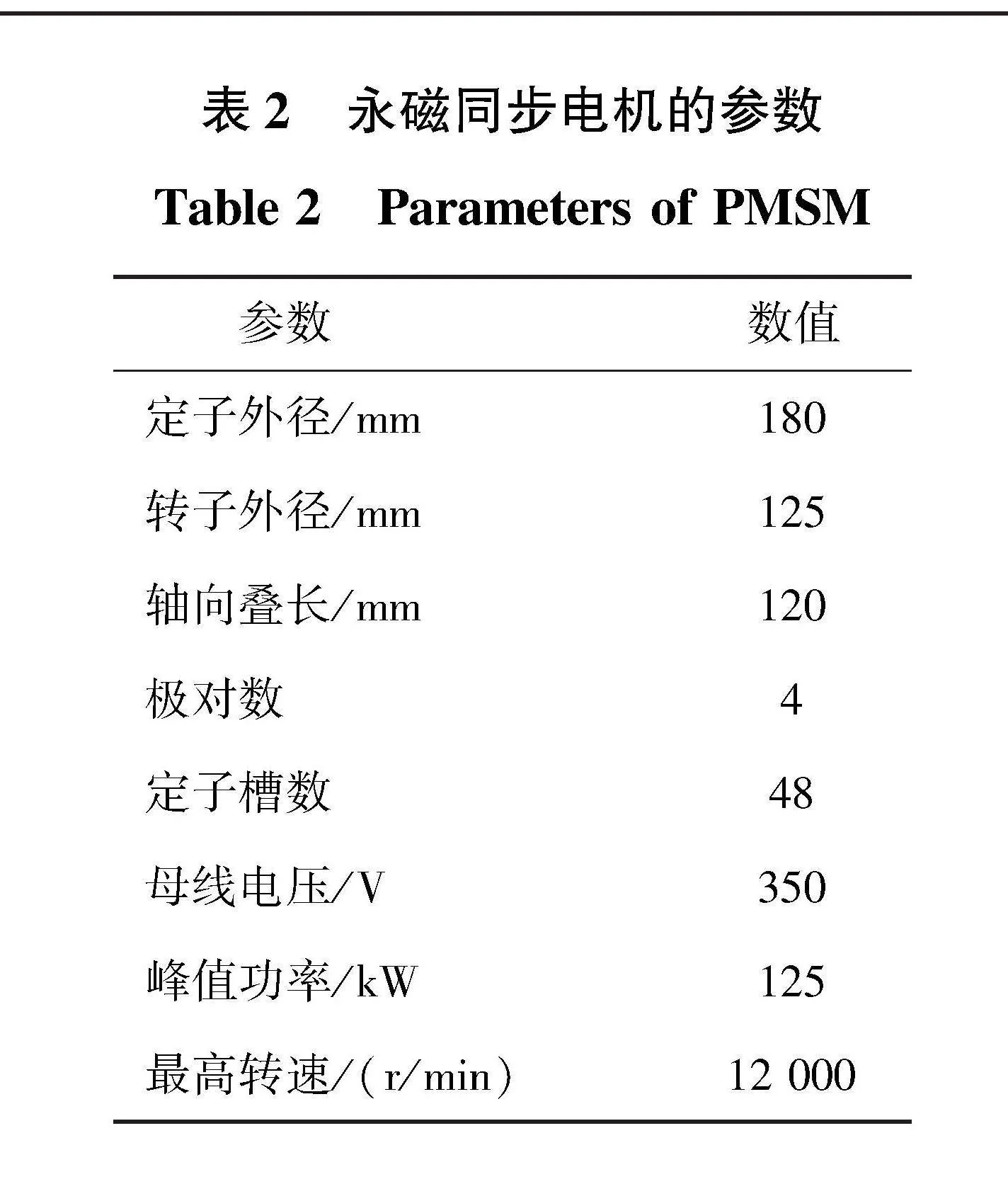
以一台8极定子48槽永磁同步电机作为研究对象，如图3所示，具体参数见表2。首先通过电磁场仿真得到气隙内的电磁力，然后分别对定子和转子进行单独的模态仿真，并结合敲击试验结果对材料属性进行修正，进而得到整机的模态仿真结果。最后，在同一工况下分别对定子和转子施加电磁激振力，并通过模态叠加法得到壳体表面的振动响应。通过对响应的对比可以定量分析转子激励对整体振动响应的贡献度。

2.1" 电磁力仿真

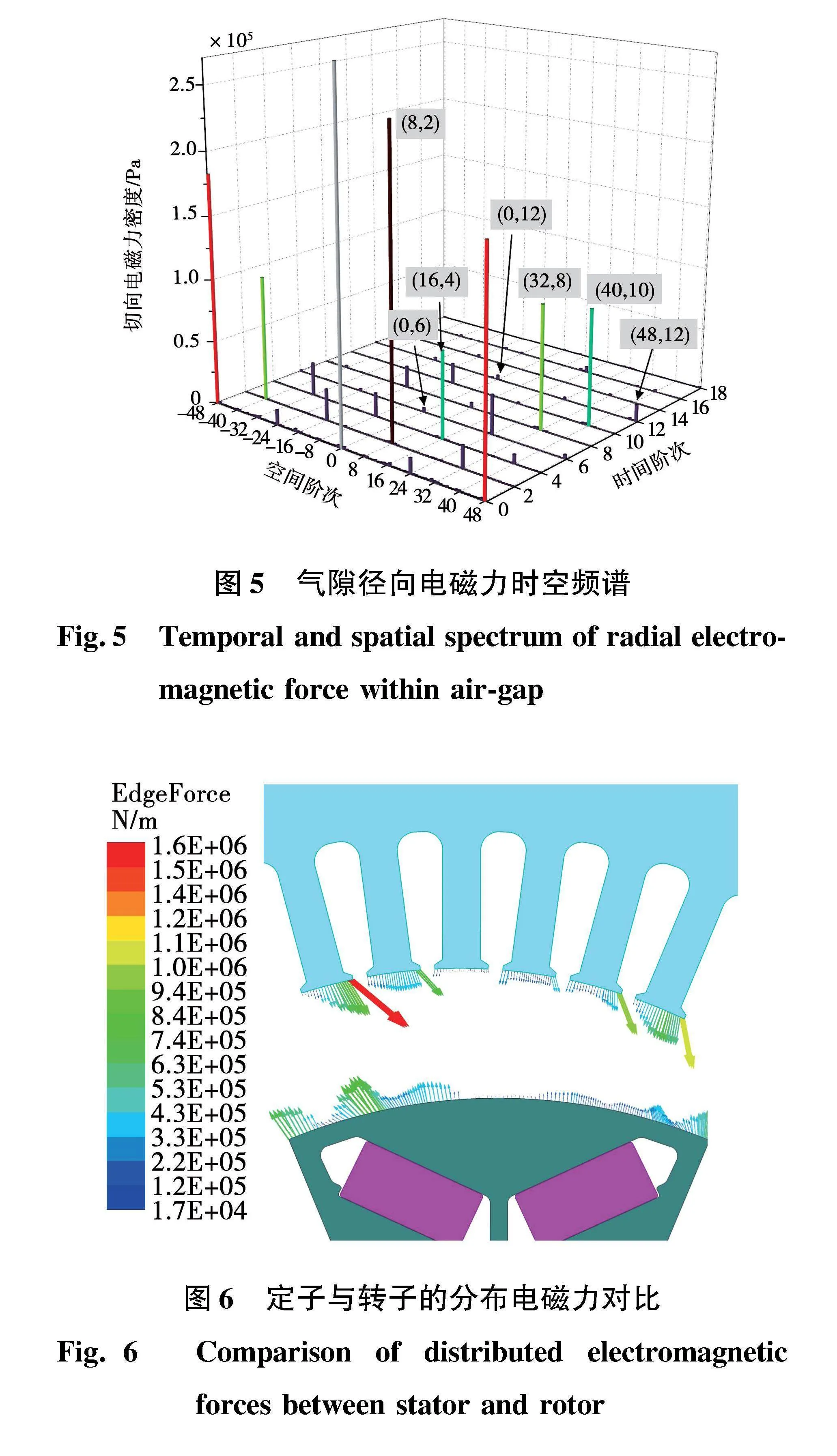
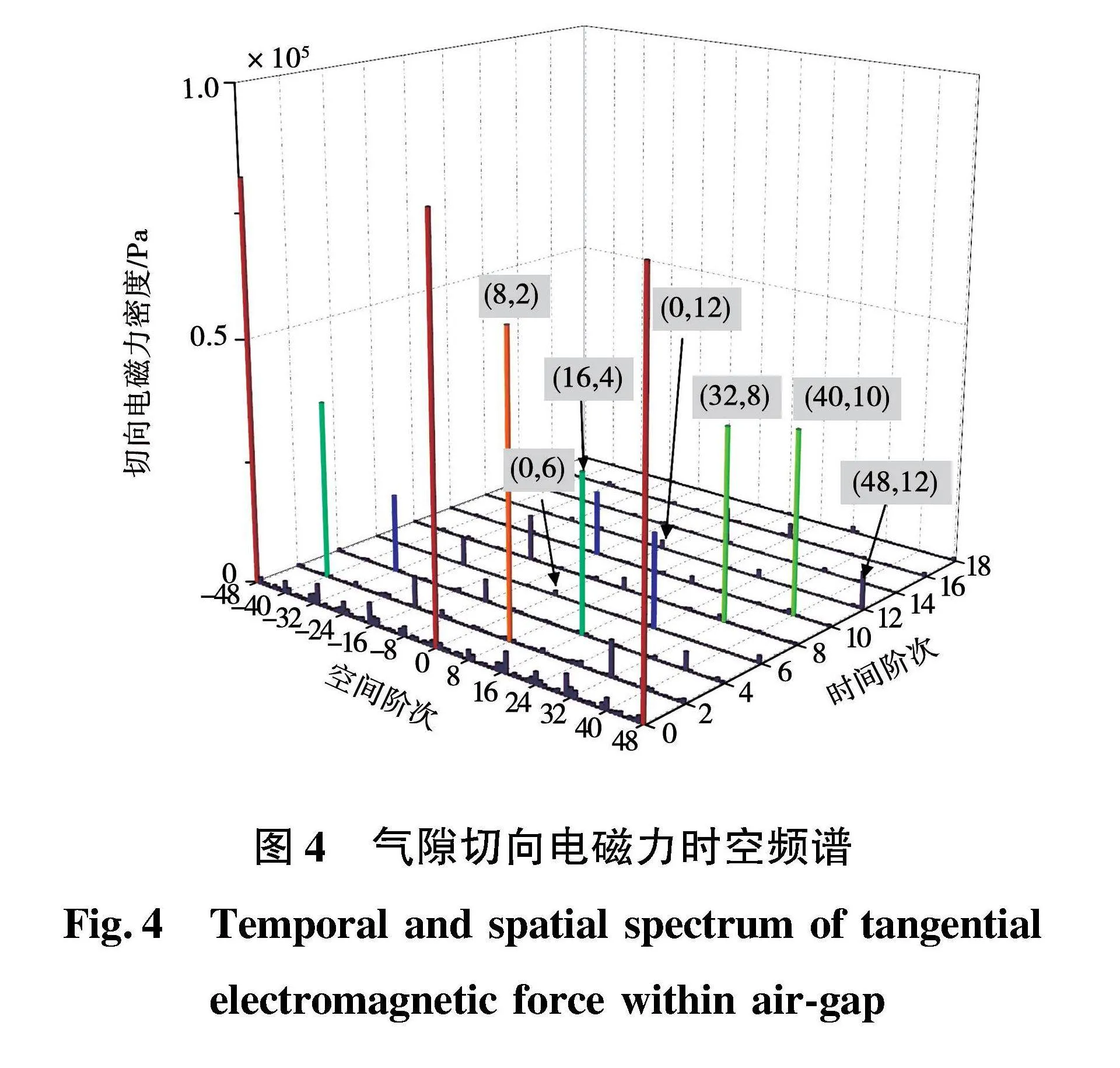
不考虑定转子偏心的情况下，可以采用1/8模型对永磁电机电磁场进行仿真。在工况为转速1 000 r/min，峰值转矩225 N·m的情况下，利用式（4）沿气隙中间线提取一个电周期内各不同空间角度的气隙电磁力，然后对其做时间和空间的2维傅里叶变换得到包含时间与空间阶次的频谱，如图4和图5所示。其中（8，2）表示空间阶次是8，时间阶次是2倍电源频率的基波激励。通过对比图4和图5的电磁力频谱可知，径向和切向电磁力的时空阶次一致，但径向力幅值要远大于切向力。将其与表1的电磁力阶次进行对比，可发现仿真的主要阶次特征与理论分析保持一致。将麦克斯韦应力分别向定子齿部与转子表面进行线积分，进而得到其边线的力密度。图6表示在上述工况同一时刻下定子与转子表面的电磁力分布，并由此可见两者的作用力方向相反。

2.2" 模态仿真

用模态叠加法对系统进行振动响应仿真时须先对图1所示的系统进行模态分析。而该系统又包含不同的子模块，如嵌线定子和插入磁钢的转子，故在装配系统模态分析前分别对定子和转子进行单独的模态分析。

定子铁心由薄硅钢片叠压而成，其整体属性可以用正交各向异性材料等效，故需要确定9个材料参数（3个方向的杨氏模量，泊松比及剪切弹性模量）。对于无取向硅钢，当忽略轧制方向和垂直于轧制方向的力学性能差异时，可以进一步简化为横向各向同性材料，此时仅需要确定5个材料参数。

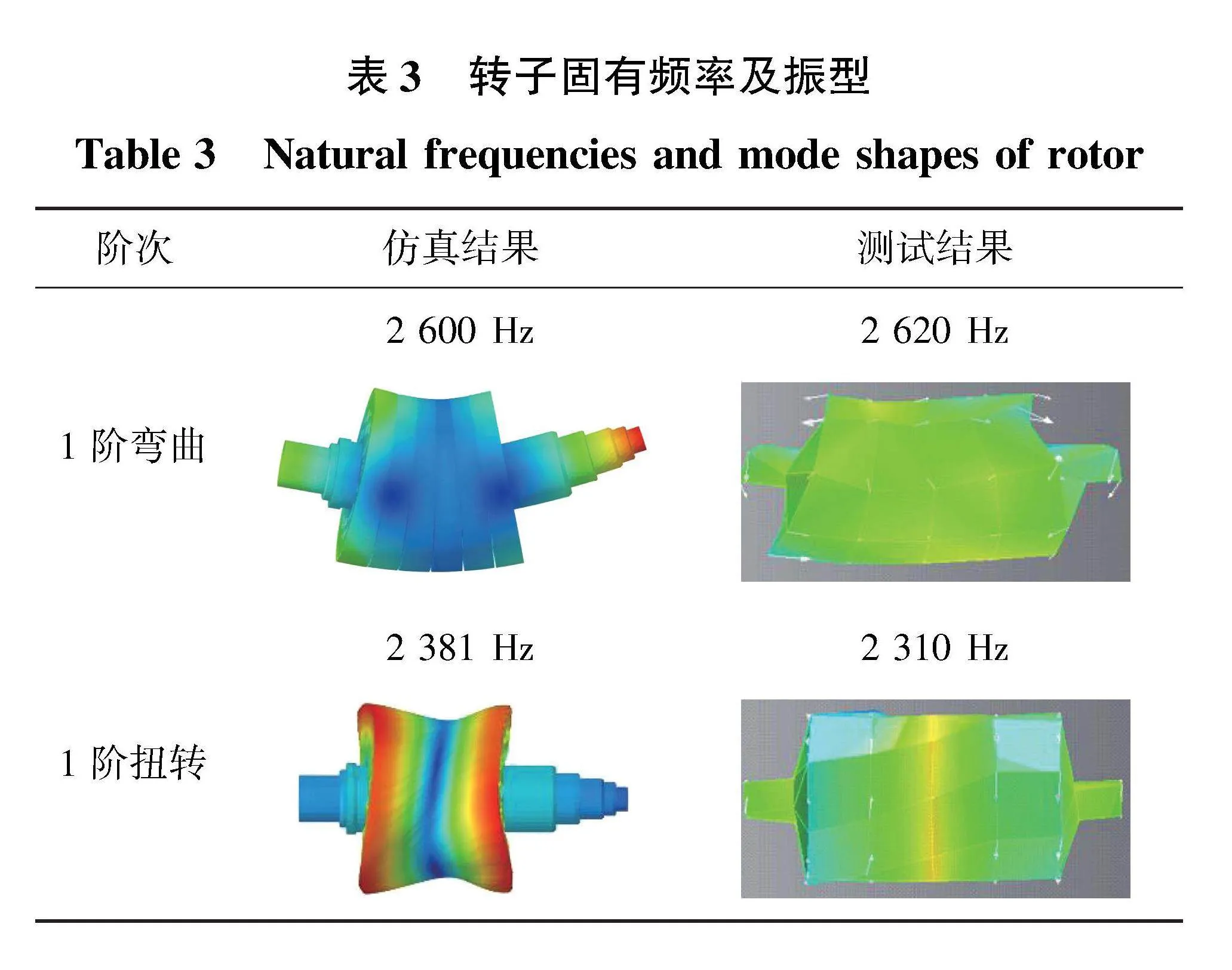
单个转子铁心模块通常是由多个硅钢片铆接而成，将多个模块穿入轴后一般可通过锁紧螺母，压环或螺栓施加轴向预紧力。尽管定子和转子由相同的硅钢片材料组成，但由于其尺寸，轴向预紧力以及相互间联接方式的差异，会导致二者呈现不同的材料属性。在仿真阶段通常根据经验设置材料属性的初始值，并在样机阶段结合部件的试验模态分析结果对仿真所用的材料属性进行修正。以转子为例，通过对样机转子进行敲击试验可获得转子自由状态下的第一阶弯曲和扭转固有频率及对应的振型。从表3的对比可以看出，经修正后的转子模态振型及固有频率的仿真结果与测试结果接近。

2.3" 转子动力学仿真

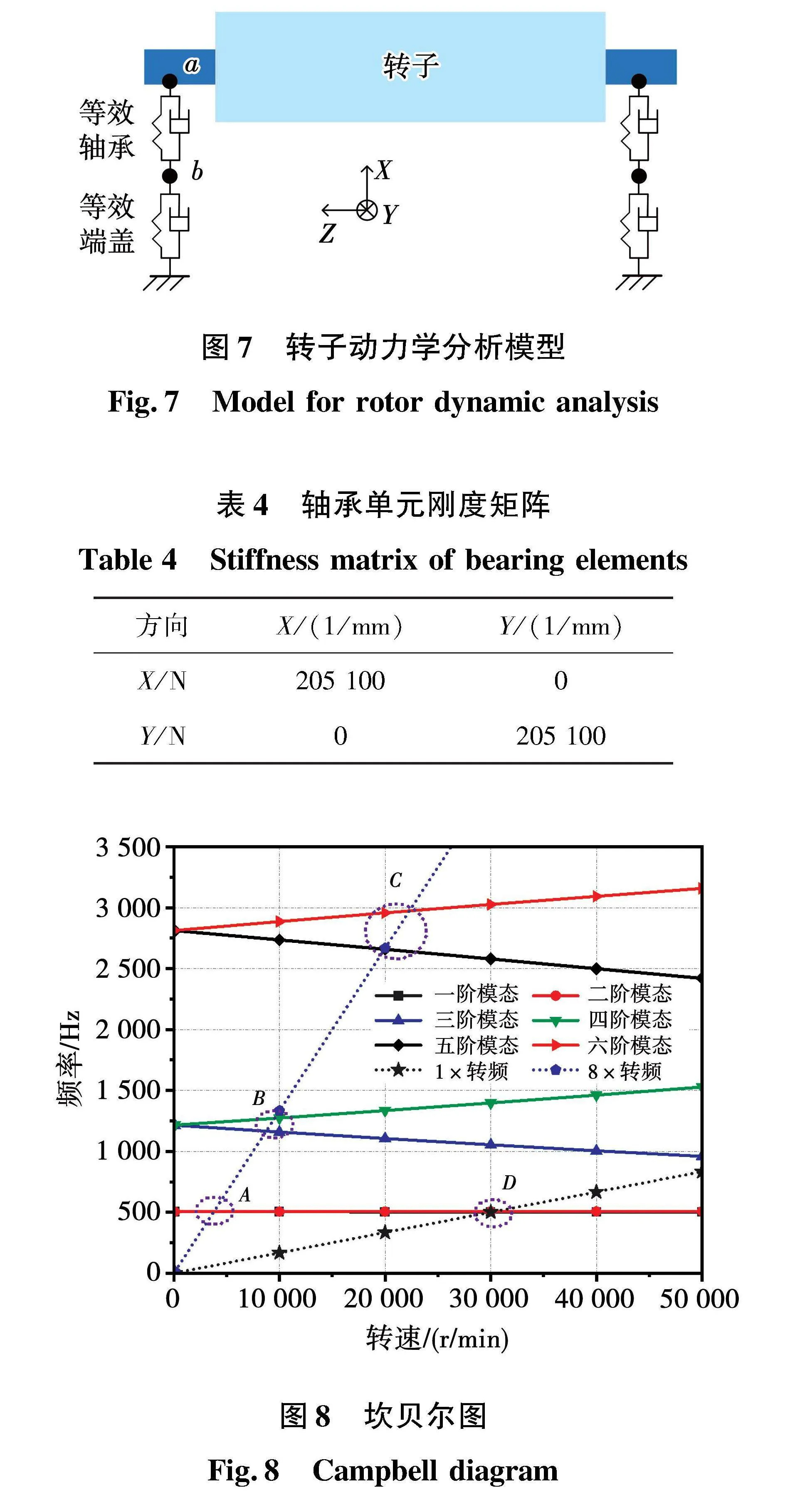
在对转子自由模态进行校正后，可以建立如图7所示的转子动力学分析模型。该系统阻尼较小且对固有频率的影响可以忽略，因而主要关注支撑刚度，其中包含滚动轴承和端盖两部分。滚动轴承的刚度由滚动体与滚道的接触刚度和油膜刚度串联而成，其大小与轴承尺寸参数，预紧力，载荷等有关系［13］。为便于分析，仅考虑与旋转轴线垂直的平面内的支撑刚度（即X和Y两个方向），并忽略2个支撑方向的耦合作用，经计算得到的轴承刚度矩阵如表4所示。端盖的等效支撑刚度可以通过仿真或者试验得到。利用上述参数可以对转子系统进行动力学仿真，模态结果如图8所示。由于陀螺效应的影响，转子的固有频率随转速变化而变化。其中相邻阶次的模态分别对应正反进动两种状态。转子系统第一，第三和第五阶模态振型及轴心的涡动轨迹如图9所示。可以看出，转轴在第一阶和第三阶的弯曲变形相对于第5阶较小。永磁同步电机的转子激励包含机械和电磁两部分。机械激励主要由转子动不平衡引起，通常以一倍转频为特征频率。电磁激励则可能由于偏心，磁路不对称，或转子斜极等引起。由图5可知（8，2）阶电磁激励具有最大的激励幅值，故选取与其对应的转频8阶（转频8阶除以极对数4，即2倍电源频率）作为电磁激励频率。因而可以确定4个临界转速（A，B，C，D）。与一倍转频相关的临界转速D约30 000 r/min，远高于最高转速12 000 r/min，所以在整个允许的运行转速范围内不存在机械激励引起的共振。与8倍转频相关的临界转速C约20 000 r/min，也高于12 000 r/min。而临界转速A和B分别在5 000 r/min和10 000 r/min附近，因而在电机升至最高转速的过程中，可在转速A和B产生转子系统的共振。

影响轴承与端盖串联支撑刚度的因素较多，如电机固定方式，轴承外圈与轴承座的间隙，轴承类型等，因而对临界转速关于支撑刚度的敏感性进行分析。如图10所示，临界转速A和B随支撑刚度变化的范围较小，而临界转速D对支撑刚度的敏感性较高。结合图9（a）中一阶模态振型可知，轴承位置的相对位移较大，加之高转速下陀螺效应影响增大，故与1阶转频相关的临界转速更易受支撑刚度的影响。

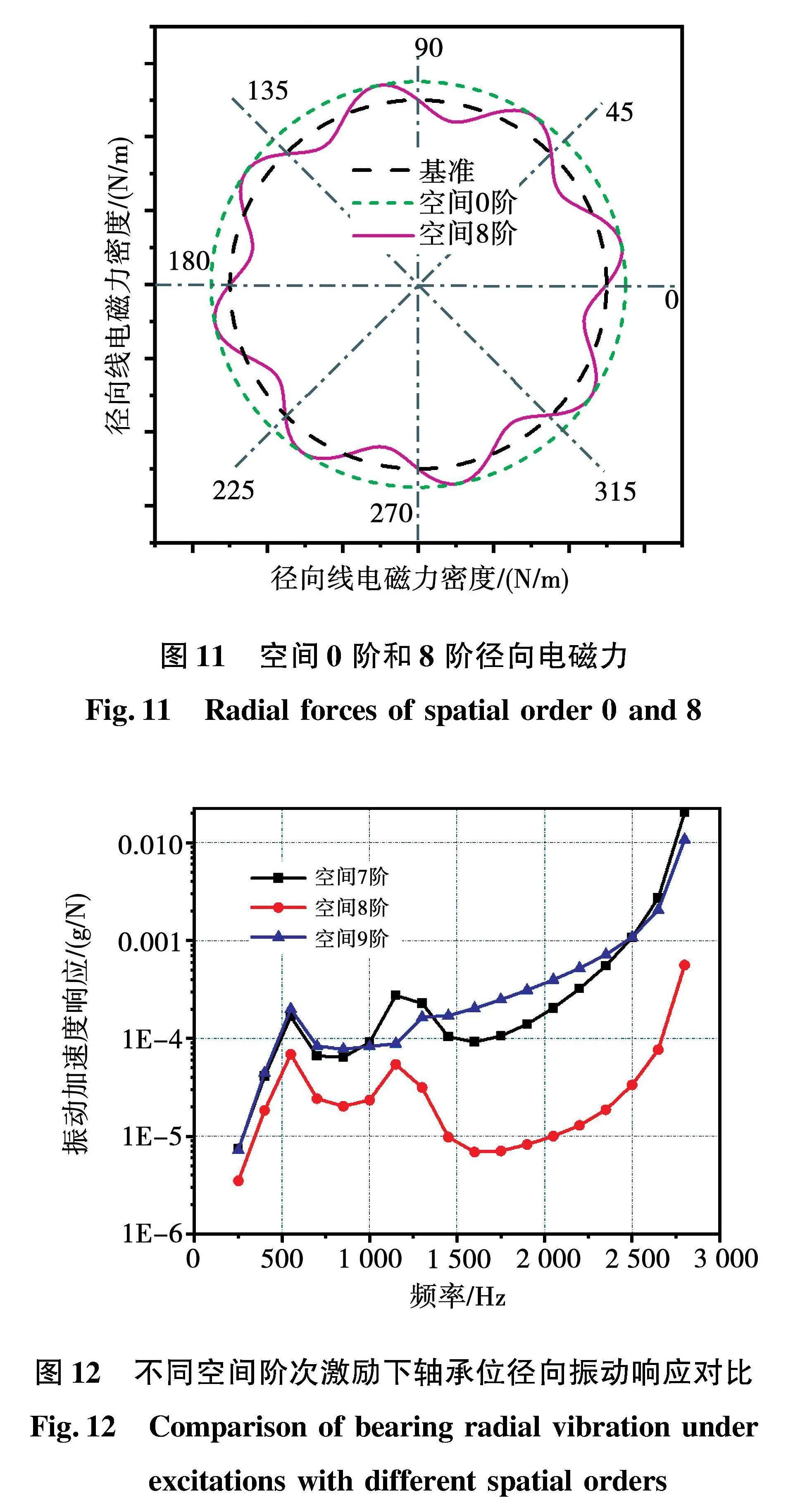
理想情况下对于整数槽永磁同步电机，电磁激励的空间阶次仅含0阶和极数的整数倍阶次，故8极电机所对应的空间阶次为0、8、16和24等，如图11所示。当存在转子静态和动态偏心时，电磁激励会在原有空间阶次基础上产生±1阶边频［14］。以8极永磁同步电机为例，在偏心作用下会产生空间7阶和9阶电磁激励，受不平衡电磁力的影响，振动响应会增大。对转子表面施加不同空间阶次的单位激励，并提取轴承位的径向振动响应做进一步对比，结果如图12所示。可以看出，空间7阶与9阶的响应幅值高于空间8阶，并且响应峰值所对应的频率验证了图8的固有频率分析结果。同时证实不平衡的电磁激励会引起转子系统的共振。

2.4" 整机电磁振动仿真

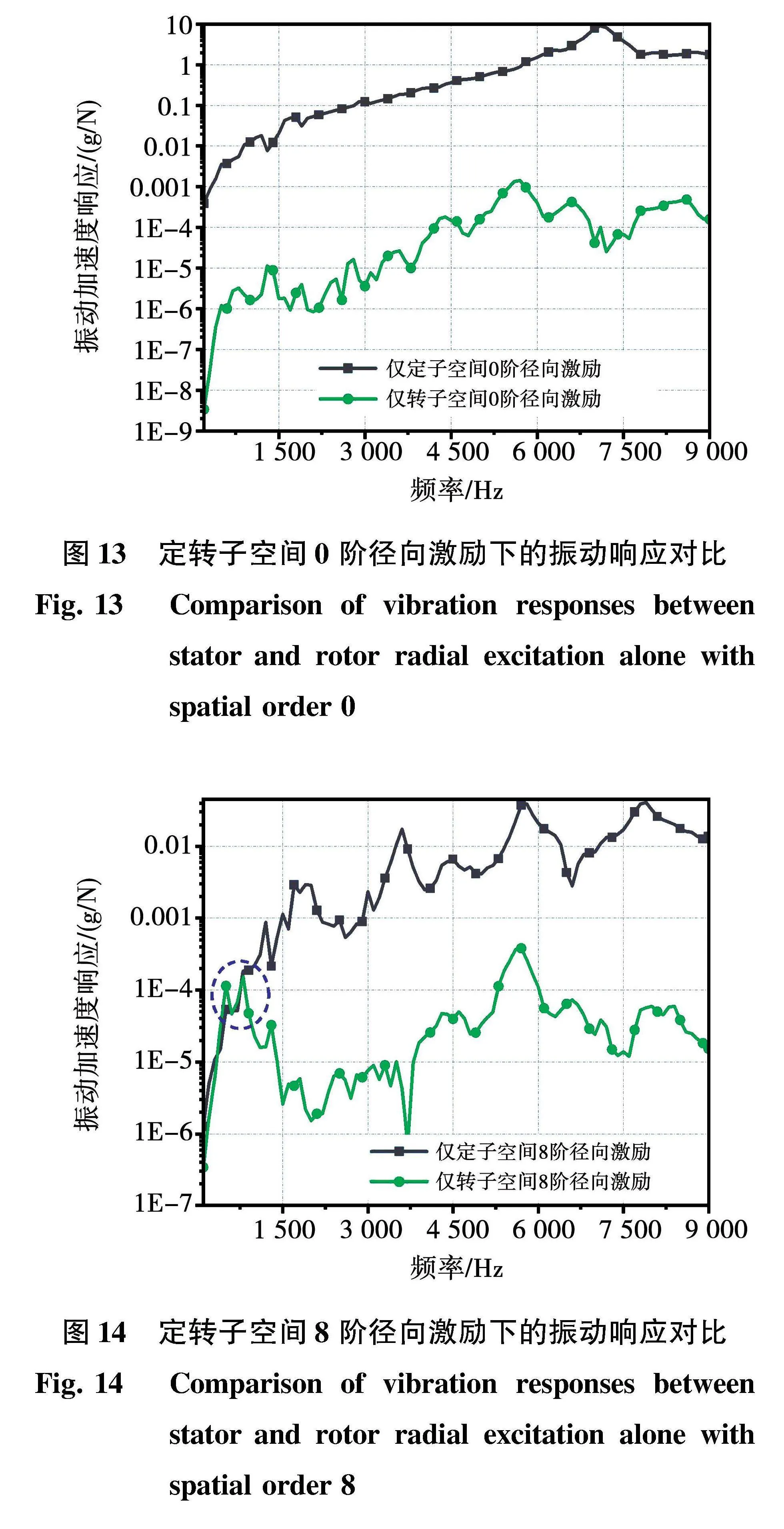
由式（5）和图5可知，气隙中的电磁激励可以分解成多个具有空间和时间阶次的分量。为比较定子和转子单独激励下的振动响应，首先从结构传递函数角度进行仿真，其次对选定工况进行多物理场耦合振动仿真。如图11所示，在单位激励下空间0阶和8阶的电磁力幅值相同。将同一空间阶次的电磁激励单独添加到定子或转子表面，然后通过模态叠加法可获得振动监测点的径向振动响应频谱。从图13可以看出，对于空间0阶电磁力，在仅有转子激励时，在整个响应频率范围内壳体表面的振动响应远低于定子激励引起的振动响应。从图14可以看出，对于空间8阶电磁力，在频率低于1 500 Hz的范围内（如图中紫色圆圈所示）定转子单独激励引起的壳体表面振动响应幅值接近。结合上一节的转子动力学分析结果，可以判断这是由于转子系统共振引起的。这表明在计算低频下的电磁振动响应时，转子激励与定子激励具有同等的重要性。

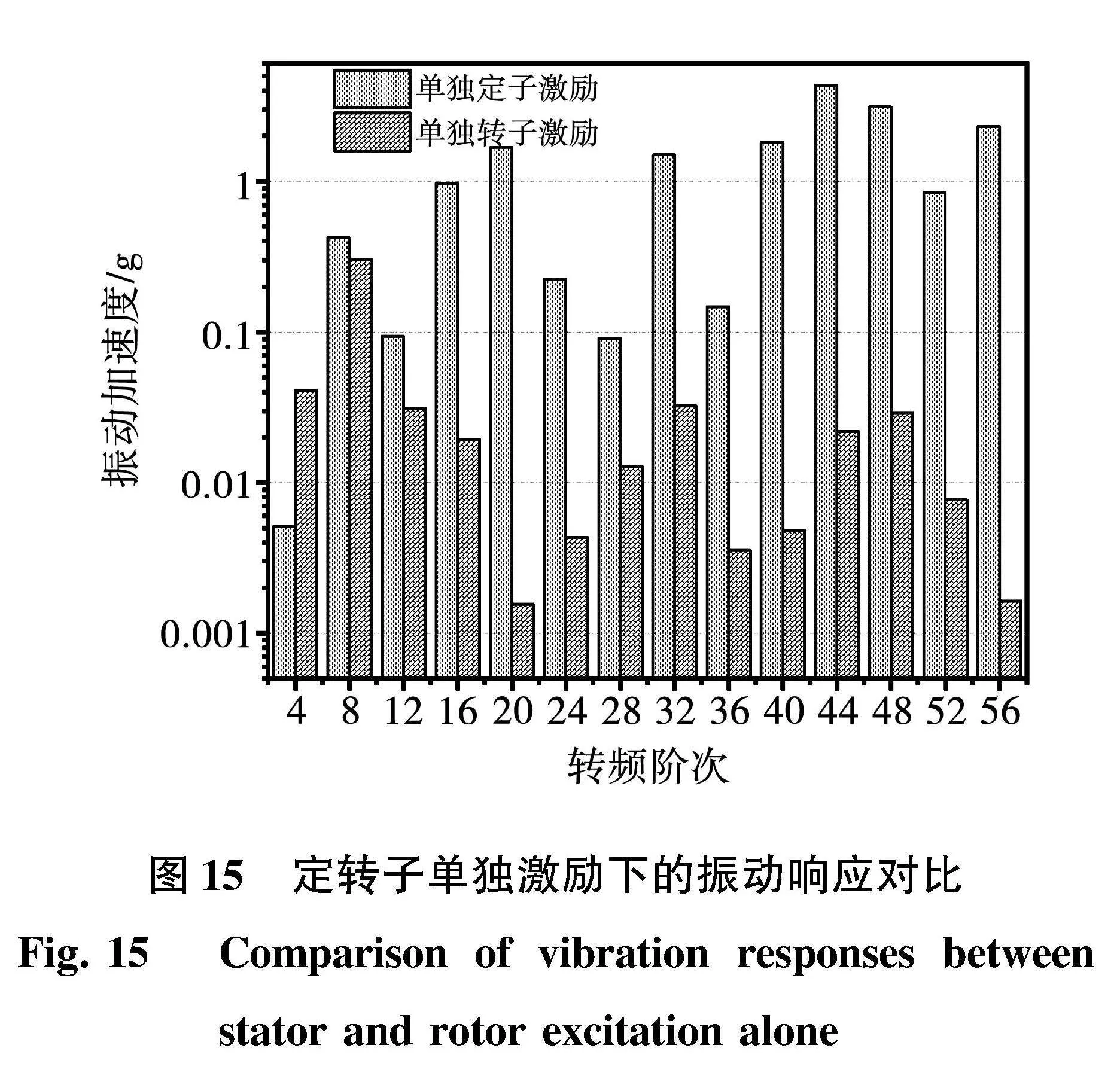
在转速为4 800 r/min，转矩225 N·m，转子静态偏心率20%的工况下对电机进行电磁场仿真，分别提取定子和转子表面的电磁力，并通过网格映射将激励传递到结构场，然后进行动力学仿真可以得到定子和转子单独激励时振动监测点的响应，如图15所示。通过对比可以看出，低频段（12阶转频及以下）定转子单独激励引起的响应幅值接近。进一步验证了上述动力学分析的结论。

3" 试" 验

以上述研究对象进行了样机的制作，并主要进行了两方面的试验：零部件的试验模态测试与整机的振动噪声测试。其中试验模态分析采用西门子Test.Lab设备分别对自由状态下的嵌线定子和转子进行了敲击测试，如图16所示。首先在软件中建立多个节点的几何模型，在校正频响函数后，采用移动力锤法进行模态测试。最后通过软件后处理对多个频响函数进行拟合得到各阶固有频率及振型。转子的模态测试结果如表3所示。从测试结果可知，部件的主要振型与仿真结果相似度很高，且固有频率的绝对误差在可接受范围内。

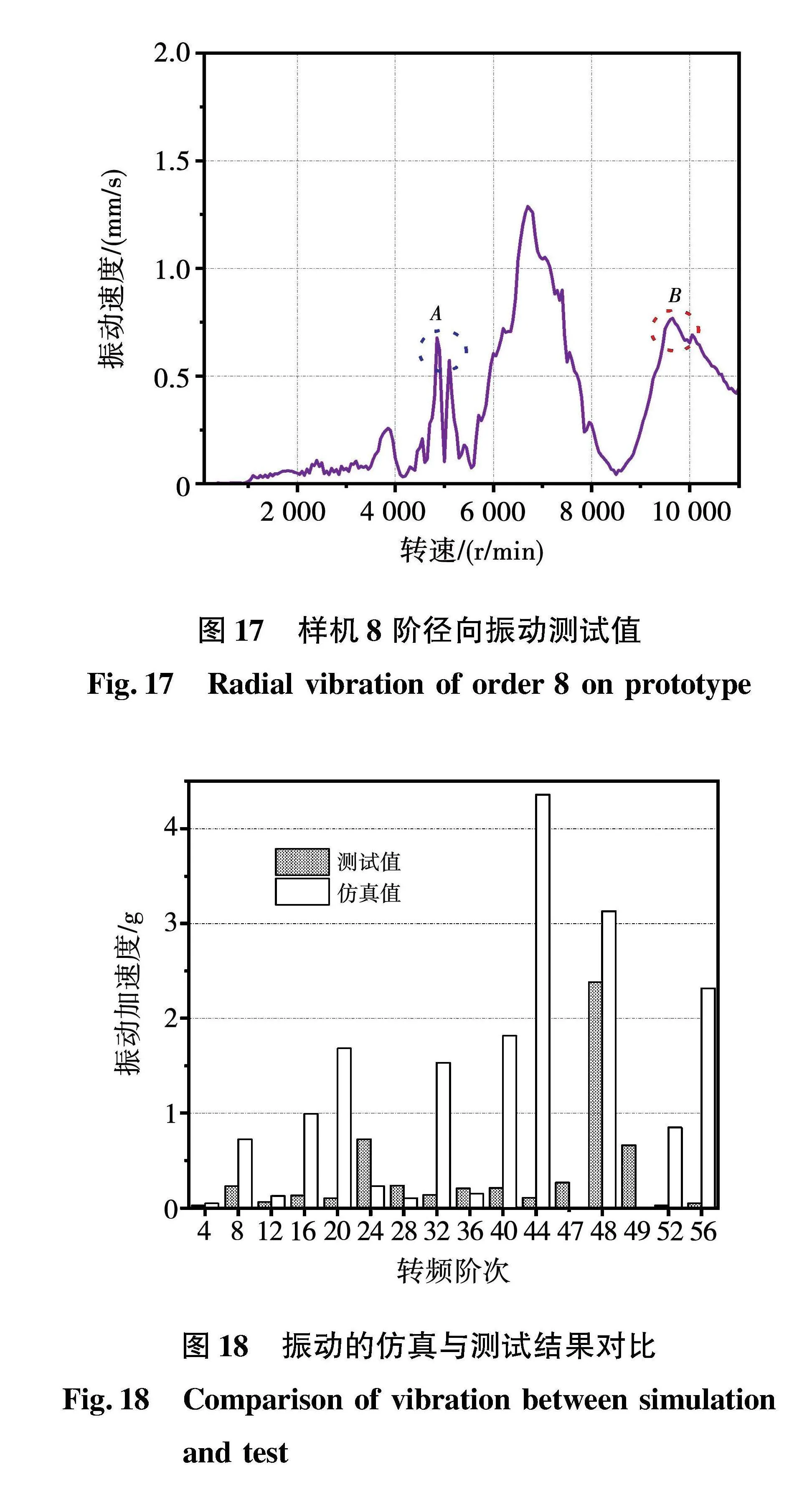
在完成电机标定后依据转矩外特性进行了电机振动噪声测试。将三向振动加速度传感器布置在壳体正下方的外表面，麦克风布置在距离壳体表面约20 cm处。通过Test.Lab软件对升速过程中的振动和声压进行了记录。由于测试空间存在背景噪音和回音，故仅对电机的振动测试结果做分析。如图17所示，提取不同转速下电机的8阶径向振动速度。将图中峰值对应的转速A和B与图8和图10的临界转速仿真结果进行对比（分别在5 000 r/min和10 000 r/min附近），可以发现两者非常接近，因此验证了上述分析的合理性。同时注意到在7 000 r/min下存在另外一个峰值，结合定子的模态及谐响应分析结果，可以判断该处峰值响应主要由定子的低阶模态共振引起。提取A点附近4 800 r/min下的振动频谱，并和图15的振动仿真结果进行对比，如图18所示。可以看出，低频段（12阶以下）二者具有较好的对应关系。

在高频段，测试结果的48阶附近出现边频47和49，这主要由转子动态偏心引起，而仿真中仅考虑了静态偏心，导致仿真结果的阶次出现差异。除此外，整体的振动仿真结果大于测试结果，这主要由于仿真时设置的静态偏心率（20%）高于实际样机的真实偏心率（正常约10%附近），导致电磁激励较大。

5" 结" 论

本文首先推导了内置式永磁同步电机的气隙电磁力公式，进而以一台8极定子48槽内转子式永磁电机为研究对象，通过转子动力学和整机电磁振动仿真定量分析了转子激励对电机电磁振动的影响。结果表明：1）不平衡电磁激励引起的转子临界转速低于最高运行转速，在升速阶段可以引起转子系统的共振；2）对整机进行电磁振动仿真时，在低频段转子激励与定子激励具有同等的重要性，不能被忽略。通过样机测试结果与仿真结果的对比，上述结论得到了验证。

参 考 文 献：

［1］" FANG Yuan， ZHANG Tong. Sound quality investigation and improvement of an electric powertrain for electric vehicles［J］.IEEE Transactions on Industry Electronics，2018，65（2）：1149.

［2］" MEHRGOU M， GARCIA De Madinabeitia I， GRAF B，et al. NVH aspects of electric drive integration of electric machine gearbox and inverter［J］.SAE Technical Paper，2018：2018-01-1556.

［3］" 张磊， 温旭辉. 车用永磁同步电机径向电磁振动特性［J］.电机与控制学报，2012，16（5）：33.

ZHANG Lei，WEN Xuhui. Radial electromagnetic vibration model characteristics of PMSMs for electric vehicles［J］.Electric Machines and Control，2012，16（5）：33.

［4］" HOFMANN A， QI Fang， LANGE T，et al. The breathing mode-shape 0： is it the main acoustic issue in the PMSMs of today’s electric vehicles［C］//Proceedings of the 17th International Conference on Electrical Machines and Systems， October 22-25， 2014， Hangzhou， China. 2014： 3067-3073.

［5］" 李晓华， 刘成健， 梅柏杉，等.电动汽车IPMSM宽范围调速振动噪声源分析［J］.中国电机工程学报，2018，38（17）：5219.

LI Xiaohua，LIU Chengjian，MEI Boshan，et al. Vibration and noise sources analysis of IPMSM for electric vehicles in a wide-speed range［J］.Proceedings of the CSEE，2018，38（17）：5219.

［6］" FANG Haiyang， LI Dawei， QU Ronghai，et al.Modulation effect of slotted structure on vibration response in electrical machines［J］.IEEE Transactions on Industrial Electronics，2019，66（4）：2998.

［7］" 姚学松， 陶文勇.某款电动汽车驱动用永磁同步电机噪声分析［J］.电子产品世界， 2019， 26（12）：74.

YAO Xuesong，TAO Wenyong. Noise analysis of a permanent magnet synchronous motor driven by an electric vehicle［J］.Electronic Engineering and Product World， 2019， 26（12）：74.

［8］" 刘皖秋， 代颖， 叶飞，等.基于转子辅助槽的车用永磁同步电机振动噪声优化［J］.电机与控制应用，2020，47（6）：76.

LIU Wanqiu，DAI Ying，YE Fei，et al.Optimization of vibration and noise of vehicle permanent magnet synchronous motor based on auxiliary slot of rotor［J］.Electric Machines and Control Application，2020，47（6）：76.

［9］" KANG Le， XIA Jiakuan， SU Han，et al. Online control strategy for radial vibration suppression of PMSM by multiharmonic current injection method［J］.IEEE Transactions on Industrial Electronics，2022，69（9）：8692.

［10］" 廖勇，甄帅，刘刃，等.用谐波注入抑制永磁同步电机转矩脉动［J］.中国电机工程学报，2011，31（21）：119.

LIAO Yong，ZHEN Shuai，LIU Ren，et al.Torque ripple suppression of permanent magnet synchronous motor by the harmonic injection［J］.Proceedings of the CSEE， 2011，31（21）：119.

［11］" DAJAKU G， GERLING D. The influence of permeance effect on the magnetic radial forces of permanent magnet synchronous machines［J］.IEEE Transactions on Magnetics，2013，49（6）：2953.

［12］" 闻邦椿，刘树英，张纯宇.机械振动学［M］.北京：冶金工业出版社，2011.

［13］" 闻邦椿，顾家柳，夏松波，等.高等转子动力学［M］.北京：机械工业出版社，1999.

［14］" LIN Fu， ZUO Shuguang， DENG Wenzhe. Impact of rotor eccentricity on electromagnetic vibration and noise of permanent magnet synchronous motor［J］.Journal of Vibroengineering，2018，20（2）：923.

（编辑：刘琳琳）