基于改进零脉冲插入法的永磁同步电机相电流重构策略

摘" 要：

直流母线单电流采样永磁同步电机系统存在相电流重构盲区，导致电流采样失真，提出一种改进零脉冲插入法，实现相电流重构。首先，分析传统固定零脉冲插入法的缺点，由于各相插入零脉冲作用时间相同，未能发挥“双开关PWM”模式抑制电流纹波的优势；其次，通过各相PWM占空比调整零脉冲时间，延长电流采样窗口，提出改进零脉冲插入法重构策略，消除重构盲区，并针对该方法重构盲区出现其他扇区有效电压矢量的情况，分析其空间电压矢量合成关系，证明参考电压矢量合成的准确性；最后，基于戴维南电路法，提出不同电压矢量作用时的电路简化模型，对比两种方法的电流纹波幅值，并搭建永磁同步电机实验平台进行实验。结果表明，改进零脉冲插入法的电流重构误差低于3%，相比传统方法，电流纹波抑制效果达到50%，相电流畸变率从12.72%下降到6.87%。

关键词：单电流传感；直流母线采样；相电流重构；重构盲区；永磁同步电机；零脉冲插入法

DOI：10.15938/j.emc.2024.06.003

中图分类号：TM341

文献标志码：A

文章编号：1007-449X（2024）06-0025-11

收稿日期： 2024-01-31

基金项目：国家自然科学基金（52207037）；电磁能技术全国重点实验室资助课题（61422172220203）

作者简介：陈思宇（1999—），男，硕士研究生，研究方向为永磁同步电机控制；

向学位（1993—），男，博士，副研究员，研究方向为特种电机设计、高性能电驱系统设计与控制等；

李" 辉（1973—），男，博士，教授，博士生导师，研究方向为电力电子器件应用与可靠性、风力发电技术、特种电机设计与控制；

周" 豪（1997—），男，博士研究生，研究方向为永磁同步电机控制；

蒋" 鹏（1997—），男，博士研究生，研究方向为特种电机设计。

通信作者：向学位

Phase current reconstruction strategy of PMSM based on improved zero pulse insertion method

CHEN Siyu，" XIANG Xuewei，" LI Hui，" ZHOU Hao，" JIANG Peng

（State Key Laboratory of Power Transmission Equipment amp; System Security and New Technology， Chongqing University， Chongqing 400044， China）

Abstract：

Aiming at current sampling distortion caused by dead-zone of phase current reconstruction in DC bus single current sampling permanent magnet synchronous motor system， improved zero pulse insertion method （IZPIM） was proposed to realize phase current reconstruction. Firstly， the disadvantages of traditional fixed zero pulse insertion method （FZPIM） was analyzed： because the zero-pulse insertion time of each phase is the same， the advantage of “double-switch PWM” mode to suppress current ripple is not played. Secondly， the IZPIM reconstruction strategy was proposed to eliminate the reconstruction blind area by adjusting the zero-pulse time and extending the current sampling window through the PWM duty ratio of each phase. The spatial voltage vector synthesis relationship was analyzed to prove the accuracy of the reference voltage vector synthesis when other sectors of effective voltage vectors appear in the IZPIM reconstruction dead-zone. Finally， based on the Devenin circuit method， a simplified circuit model with different voltage vectors was proposed， the current grain amplitude of FZPIM and IZPIM was compared， and the experimental platform of permanent magnet synchronous motor was built for experimental verification. The results show that the current reconstruction error of IZPIM is less than 3%. Compared with the traditional method， the current ripple suppression effect reaches 50%， and the phase current distortion rate decreases from 12.72% to 6.87%.

Keywords：single current sensor； DC bus sampling; phase current reconstruction； reconstruction dead-zone； permanent magnet synchronous motor； zero pulse insertion method

0" 引" 言

永磁同步电机（permanent magnet synchronous motor，PMSM）因其效率高、体积小、结构简单、功率密度大等优点，被广泛应用于电动汽车、新能源发电、航空航天等领域［1-3］。在传统的永磁同步电机控制系统中，需要三相电流信息完成闭环控制，考虑到多传感器会增加控制器的体积、成本以及不同传感器的采样偏差会降低系统控制性能等问题［4-5］，许多学者提出了基于单电流传感器的相电流重构技术，然而该技术由于受到电流最小采样时间的限制，当参考电压矢量位于低调制区和扇区边界时会不可避免地出现重构盲区［6-10］，导致电流采样失真。因此，开展相电流重构技术研究，解决电流重构盲区，对于提高系统控制系能具有重要意义。

在永磁同步电机相电流重构研究方面，文献［11-13］针对变频器交流调速系统，提出了一种脉冲移相法，在每个PWM周期，通过对每相PWM进行移相，延长有效电压矢量作用时间以完成采样，这种方法原理简单，但改变了传统SVPWM的对称性，会引入额外的谐波；文献［14-16］针对永磁同步电机，提出了一种测量脉冲插入法，通过在PWM周期内插入测量脉冲完成采样，并提出了相应的补偿策略，降低了重构误差，这种方法同样改变了SVPWM对称性，也可能引入高频谐波，且控制算法比较复杂，不适用于高开关频率场景；文献［17］提出了基于互补非零矢量的相电流重构算法，通过在中调制区添加互补非零矢量，消除了重构盲区，但这种方法允许不相邻电压矢量的相互切换，会导致线电压极性的快速跳变，产生电机侧过电压和共模电压尖峰。文献［18］针对直流母线采样电机控制系统，通过插入测量矢量和补偿矢量完成相电流重构，但由于每相PWM开关次数不同，各相插入的死区时间不同，可能会对输出电压造成影响。传统固定零脉冲插入法［19］（fixed zero pulse insertion method，FZPIM）是在各相PWM信号中间插入作用时间固定的零脉冲，当参考电压矢量处于重构盲区时，增加某一相零脉冲作用时间，延长有效电压矢量作用时间以完成电流采样，实现相电流重构。

除了直流母线采样技术，近年来，一些学者通过改变电流传感器的位置，提出了一种新型相电流重构策略［20-22］。文献［20］提出了一种基于单支路采样法的相电流重构策略；文献［22］提出了一种同时测量支路电流和相电流之和的重构策略，在载波顶点和底点各采样一次，便可获得三相电流信息，完成相电流重构。然而，以上方法需要更改拓扑，增加硬件成本，难以直接适用于直流母线电流采样。

传统固定零脉冲插入法保证了传统SVPWM的对称性，不会引起电流畸变，控制算法易实现，但其“双开关PWM”模式未达到双倍开关频率抑制电流纹波的效果。本文基于传统固定零脉冲插入法，分析其电流纹波特点，提出一种改进零脉冲插入法（improved zero pulse insertion method，IZPIM），实现低调制区和扇区交界处的相电流重构，同时，针对重构盲区出现其他扇区有效电压矢量的情况，验证其空间参考电压矢量合成关系。最后，基于戴维南电路法，提出不同电压矢量作用时的简化电路模型，进行两种方法下电流纹波幅值的对比，并搭建实验平台进行验证。

1" 基于直流母线电阻采样的相电流重构算法

1.1" 直流母线采样基本原理

基于直流母线采样的相电流重构技术的基本原理是在一个PWM周期内，通过在不同的有效电压矢量作用时间内，对直流母线电流进行多次采样，根据直流母线电流与相电流的关系获得两相电流信息，并通过基尔霍夫电流定律获取第三相电流，实现相电流的重构。

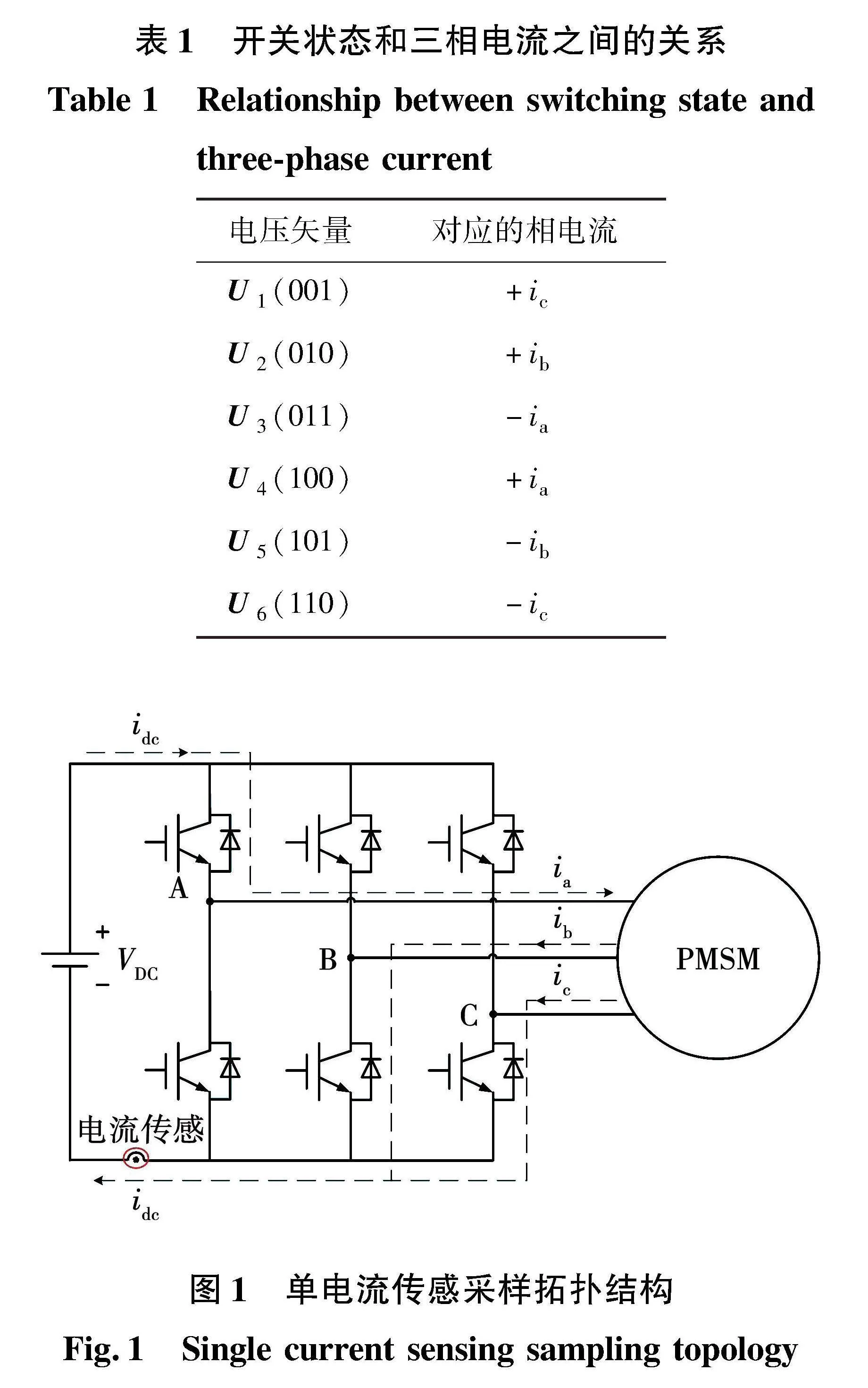
三相逆变器一共有8种开关状态，产生8种基本电压矢量，包括6种非零有效电压矢量U1～U6和2种零电压矢量U0和U7。各电压矢量和三相电流之间的关系如表1所示，单电流传感采样拓扑如图1所示。

在实际情况中，电流采样必须考虑到系统的A/D转换时间Tad、死区时间Td、直流侧电流稳定时间Tset等因素的影响，因此有效电压矢量作用时间必须大于最小采样时间Tmin，以完成电流的准确采样，即

Tmin=Tad+Td+Tset。（1）

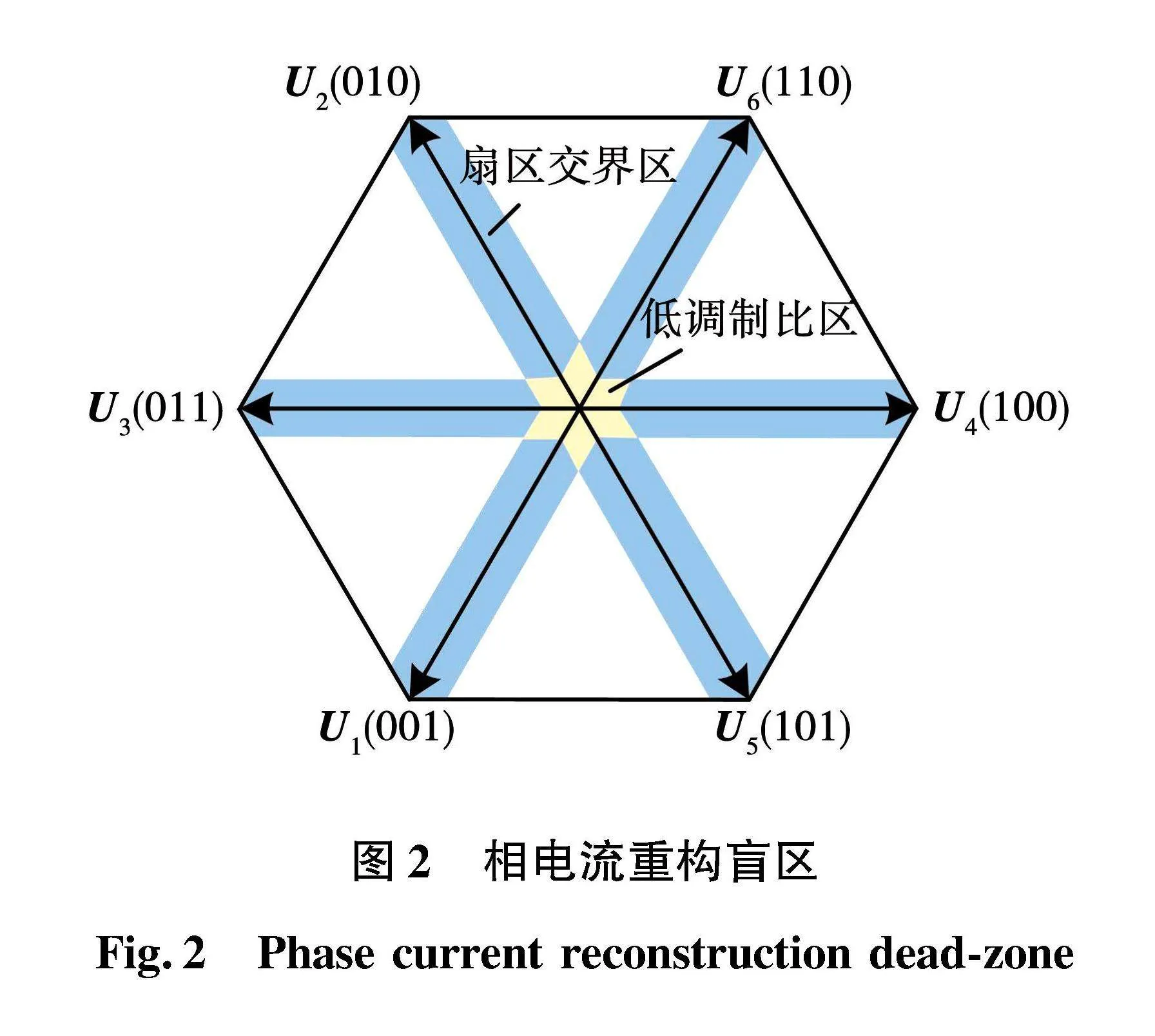
当参考电压矢量在扇区边界和低调制区时，有效电压矢量作用时间小于最小采样时间，不足以完成电流采样，以上情况为电流重构盲区。如图2所示，此时重构电流和实际电流存在很大误差，无法完成电流的精准重构。

1.2" 传统固定零脉冲插入法

固定零脉冲插入法是在每相PWM周期的中间插入一段作用时间固定的零脉冲，并将两部分PWM信号分开，分开前后不能改变其占空比（即所谓的“双开关PWM”）。

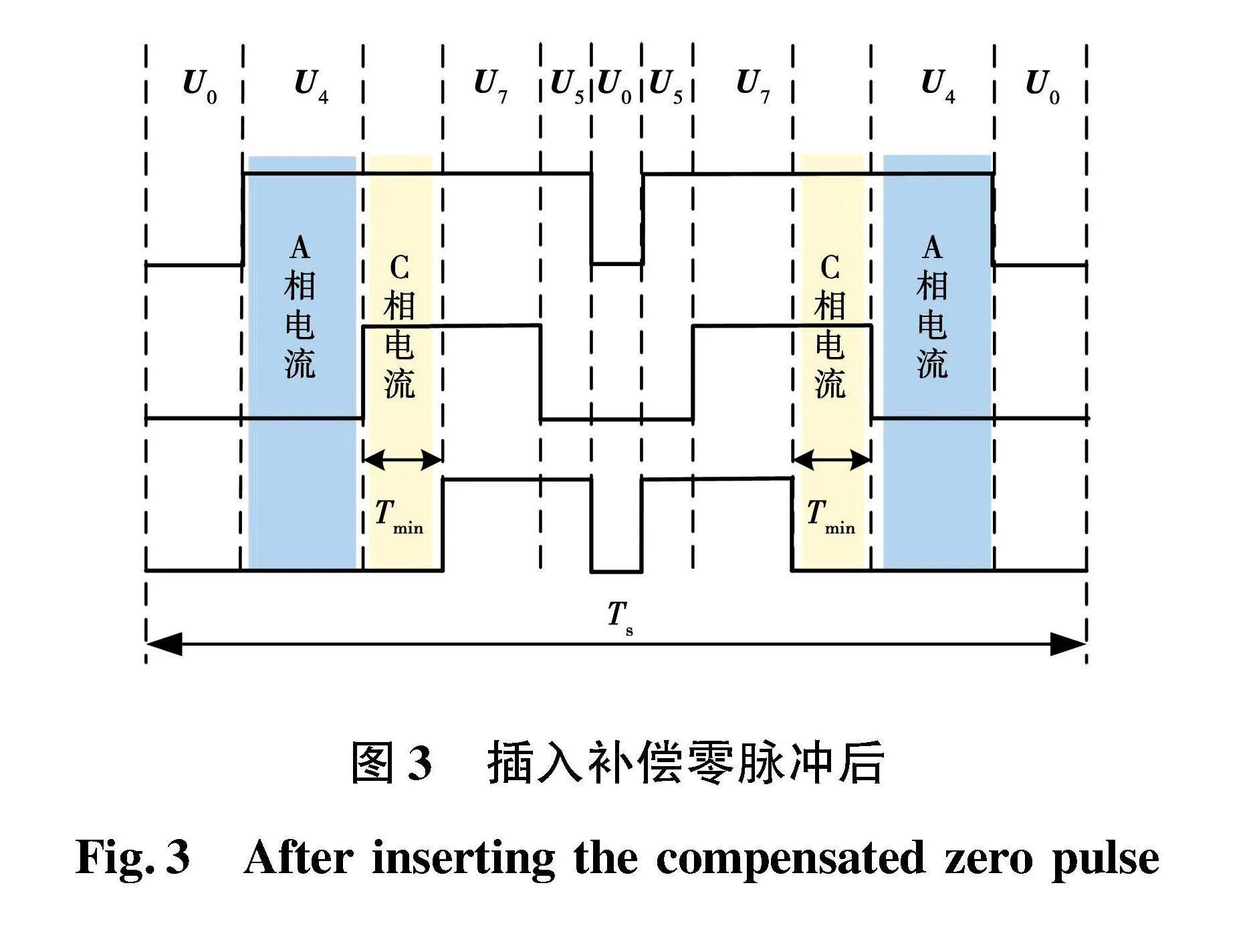
当参考电压矢量位于扇区交界处时，其中一个有效电压矢量作用时间不足以完成采样，需要延长占空比更高一相的零脉冲作用时间。为保证采样的准确性，插入零脉冲后有效电压基本矢量的持续时间必须满足最小采样时间Tmin的要求。以第一扇区为例，当参考电压矢量位于U4（100）附近，补偿零脉冲插入后PWM波形如图3所示。

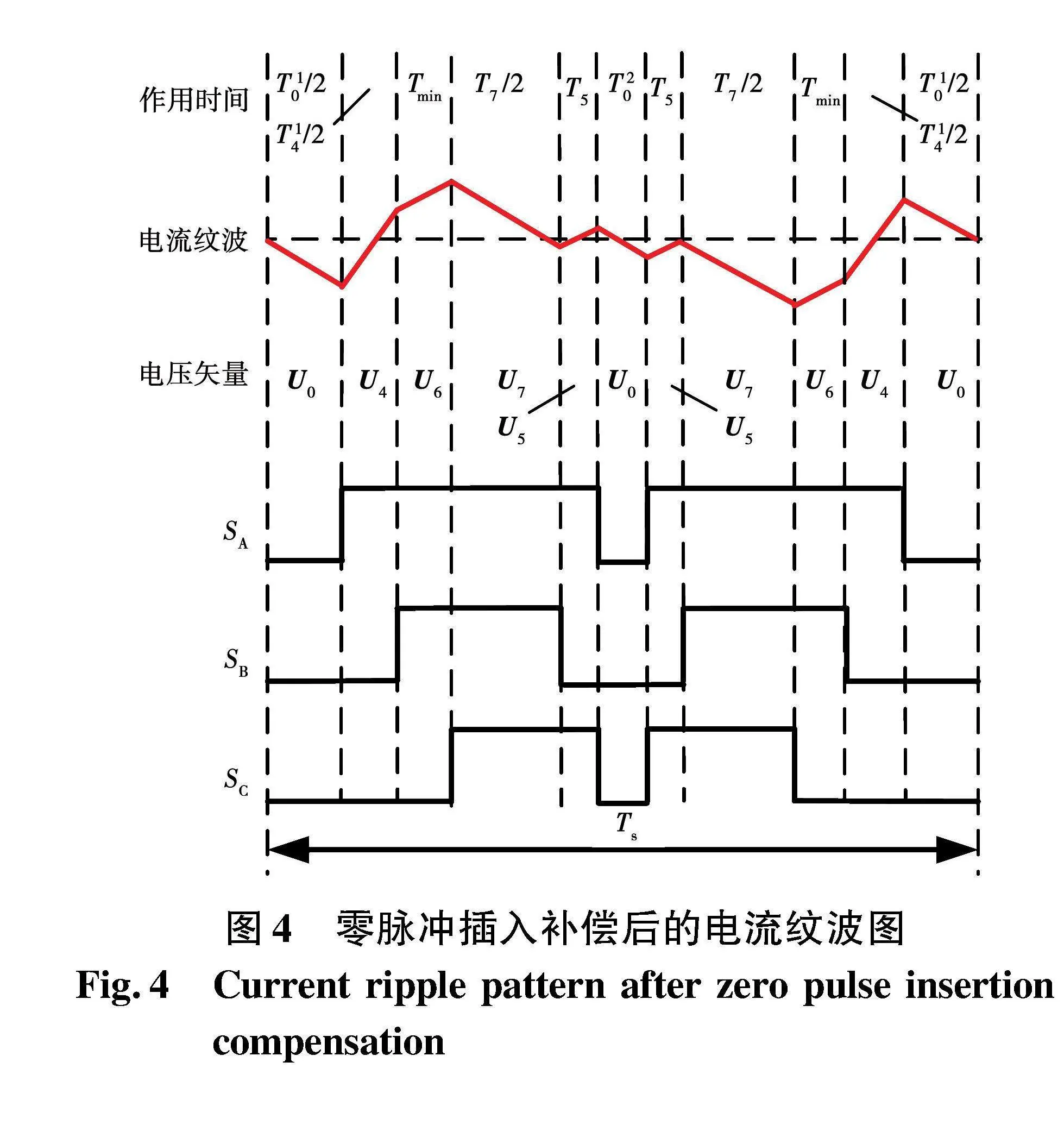
改进零脉冲插入法可以有效地解决直流母线采样技术引入的重构盲区问题，但是也存在缺点：在插入零脉冲后，开关频率提高一倍，但由于各相插入的零脉冲作用时间几乎相同，电流纹波幅值几乎与插入零脉冲前一样，并未发挥“双开关PWM”模式抑制电流纹波的优势，如图4所示。图中：Ui为各电压矢量；Ti为各电压矢量的作用时；Tmin为最小采样时间。

2" 改进零脉冲插入法

2.1" 改进零脉冲插入法基本原理

针对传统固定零脉冲插入法存在的问题，提出一种改进零脉冲插入法。与传统方法不同，在三相PWM信号中间插入的零脉冲作用时间不再固定，与各相PWM占空比相关，使各相两个对称信号之间的零脉冲持续时间与PWM周期开始和末尾的零脉冲持续时间之和相等，并且分开前后同样不改变PWM占空比。

当参考电压矢量位于重构盲区时，保持占空比最大一相的插入零脉冲作用时间不变，对占空比较小的各相的插入零脉冲作用时间进行调整，使有效电压矢量的作用时间满足采样要求。

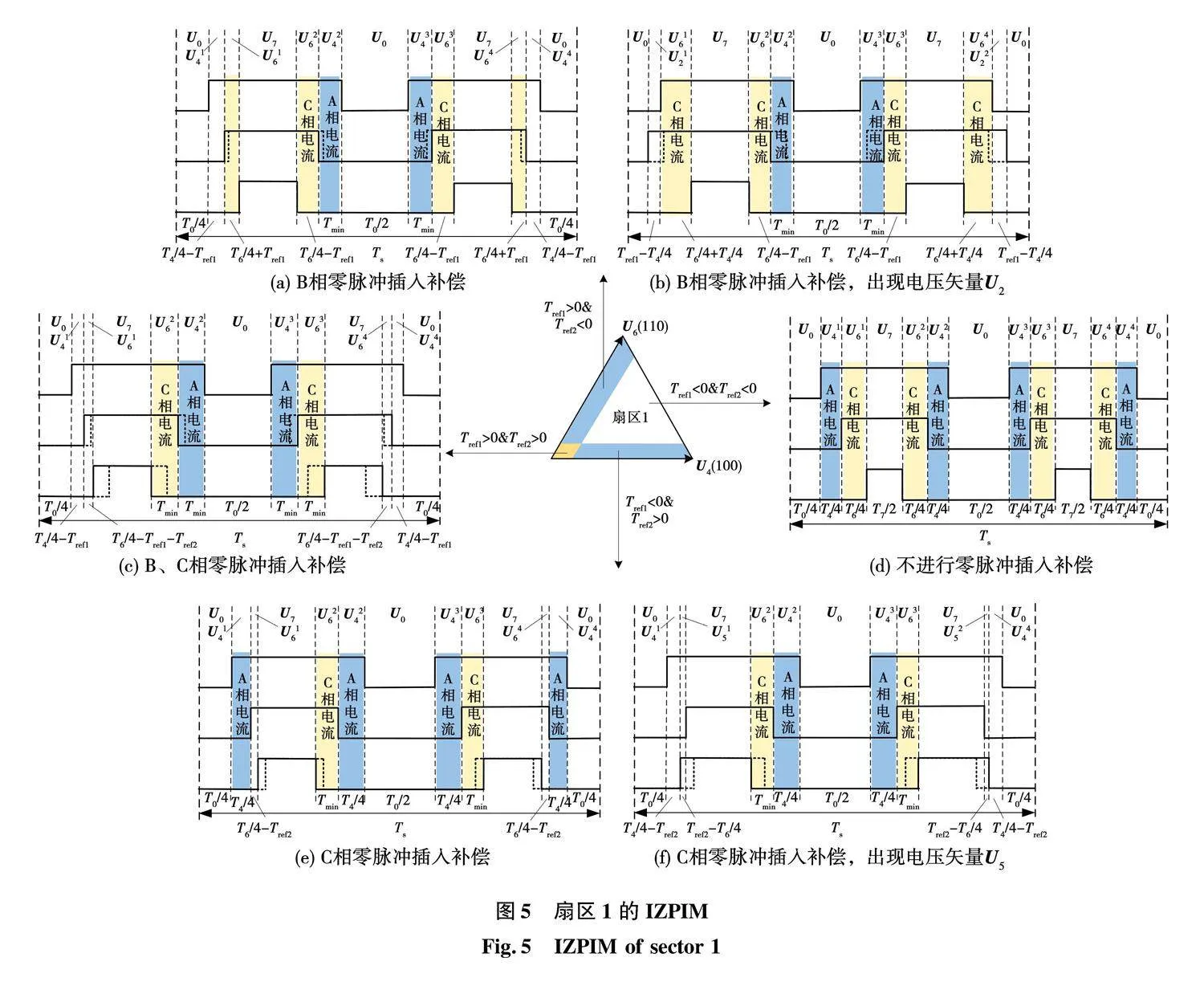
以第一扇区为例，定义Tref1=Tmin-T4/4，Tref2=Tmin-T6/4，当Tref1、Tref2均小于0时表明参考电压矢量位于非重构盲区，不需要进行0脉冲插入补偿。此时一个PWM周期有4个电流采样窗口，每相电流信息均可多次采样求平均值，减小分时采样带来的误差，如图5（d）所示。

当Tref1、Tref2均大于0时，参考电压矢量位于低调制区，2个有效电压矢量作用时间U4（100）、U6（110）均不满足最小采样时间，因此需要对B、C相进行零脉冲插入补偿，使U24、U34、U26、U36的作用时间等于Tmin，如图5（c）所示，此时U14、U44、U16、U46的作用时间不满足最小采样要求，各相电流采样窗口减少为PWM周期中间的2个电压矢量。当Tref1gt;0、Tref2lt;0时，参考电压矢量位于靠近U6（110）的扇区边界，此时需要对B相进行零脉冲插入补偿，使U24、U34的作用时间等于Tmin，如图5（a）、图5（b）所示。当Tref1lt;0、Tref2gt;0时，参考电压矢量位于靠近U4（100）的扇区边界，此时需要对C相进行零脉冲插入补偿，使U26、U36的作用时间等于Tmin，如图5（e）、图5（f）所示。

2.2" 空间电压矢量合成分析

为使有效矢量持续时间达到最小采样时间的要求，在进行零脉冲插入补偿后，可能会导致其他非本扇区的有效电压矢量出现。

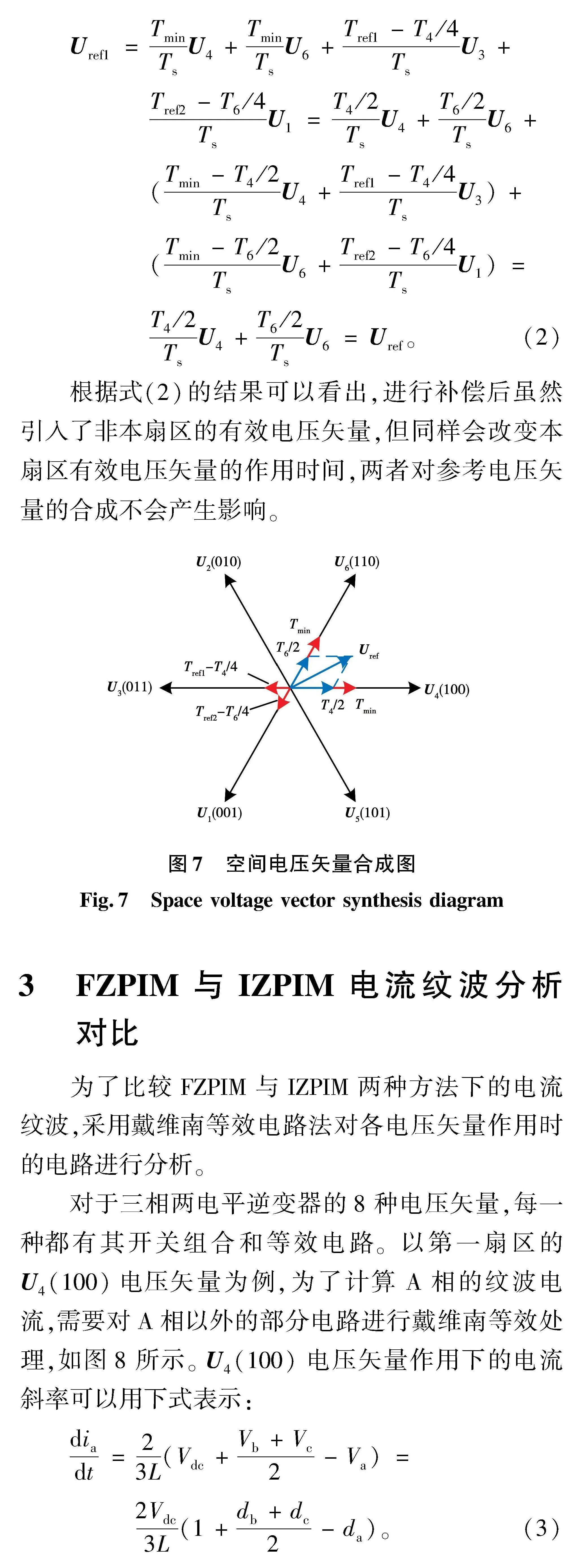
图6为参考电压矢量位于扇区1的低调制区时的PWM示意图，此时有效电压矢量U4（100）、U6（110）的持续时间均小于最小采样时间。为保证U24、U26、U34、U36的作用时间达到最小采样要求Tmin，进行零脉冲插入补偿后，由于B、C两相插入的零脉冲持续时间较长，电压矢量U11、U13、U21、U23会替代原来的U14、U16、U44、U46，此时电压矢量U11、U21的作用时间为Tref2-T6/4，U21、U23的作用时间为Tref1-T4/4。由于PWM半周期对称，因此对前半期周期的PWM进行分析，其空间电压矢量合成关系如图7所示。

进行零脉冲插入补偿后，PWM前半周期的参考电压矢量合成公式为

Uref1=TminTsU4+TminTsU6+Tref1－T4/4TsU3+

Tref2－T6/4TsU1=T4/2TsU4+T6/2TsU6+

（Tmin－T4/2TsU4+Tref1－T4/4TsU3）+

（Tmin－T6/2TsU6+Tref2－T6/4TsU1）=

T4/2TsU4+T6/2TsU6=Uref。（2）

根据式（2）的结果可以看出，进行补偿后虽然引入了非本扇区的有效电压矢量，但同样会改变本扇区有效电压矢量的作用时间，两者对参考电压矢量的合成不会产生影响。

3" FZPIM与IZPIM电流纹波分析对比

为了比较FZPIM与IZPIM两种方法下的电流纹波，采用戴维南等效电路法对各电压矢量作用时的电路进行分析。

对于三相两电平逆变器的8种电压矢量，每一种都有其开关组合和等效电路。以第一扇区的U4（100）电压矢量为例，为了计算A相的纹波电流，需要对A相以外的部分电路进行戴维南等效处理，如图8所示。U4（100）电压矢量作用下的电流斜率可以用下式表示：

diadt=23L（Vdc+Vb+Vc2－Va）=

2Vdc3L（1+db+dc2－da）。（3）

其中Va、Vb、Vc为三相反电动势，由直流母线电压Vdc和三相占空比da、db、dc（范围为0～1）决定。

同理，为得到8种电压矢量作用下的A相电流纹波斜率，可对每种电压矢量作用下的电路都进行戴维南等效，不同电压矢量所对应的电流纹波斜率如表2所示。B、C相的电流纹波可以用相同的方法分析。

3.1" 非重构盲区时电流纹波对比

传统的零脉冲插入法在PWM周期中间插入U0（000）矢量，而传统SVPWM法在PWM周期中间插入U1（111）矢量，由表2可知，U0（000）矢量与U1（111）矢量的电流纹波斜率相等，因此不会改变电流纹波的波形和幅值。

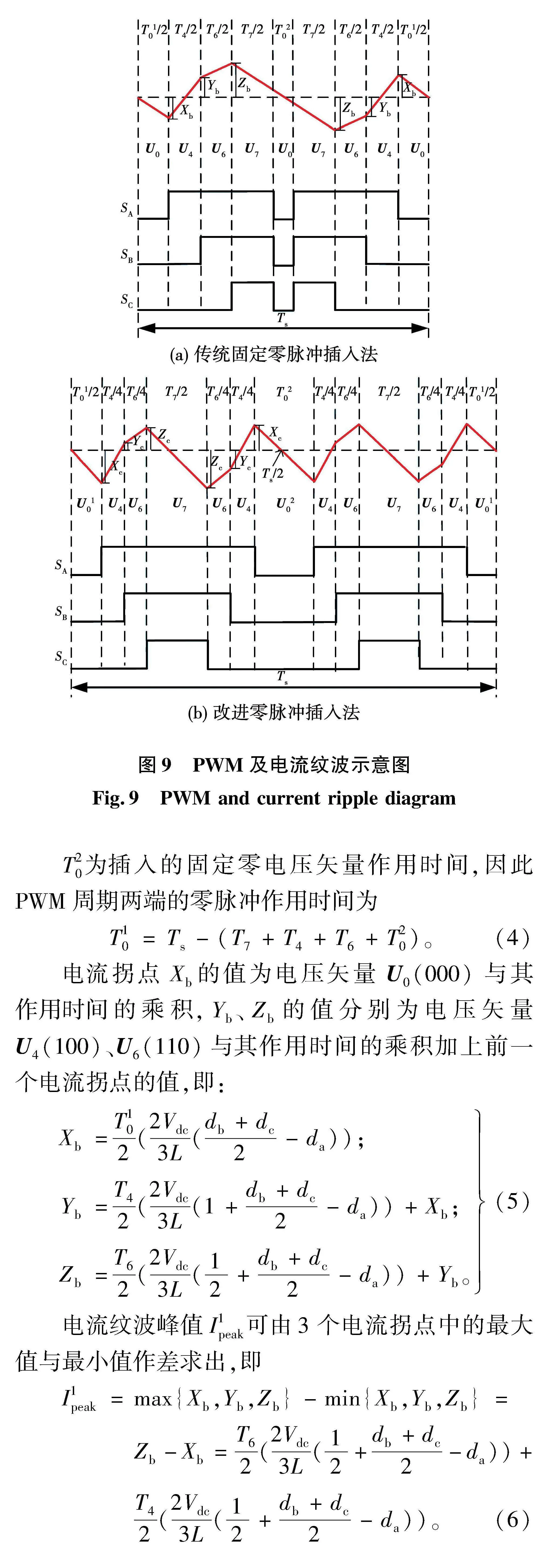
由于在PWM周期内脉冲电压逼近平均电压，因此电流纹波的起点和终点均可当作电流基波值。在改进零脉冲插入法中，电流纹波在PWM周期的起点、终点以及Ts/2处均为电流基波值。以第一扇区为例，SVPWM示意图及电流纹波如图9所示。

在图9（a）中，一个PWM周期内共有7段线性区域，每段线性区域的作用时间由每相占空比决定。因此，结合表2中的电流纹波斜率以及各段线性区域的作用时间，即可求出电流拐点Xb、Yb、Zb的值。

T20为插入的固定零电压矢量作用时间，因此PWM周期两端的零脉冲作用时间为

T10=Ts－（T7+T4+T6+T20）。（4）

电流拐点Xb的值为电压矢量U0（000）与其作用时间的乘积，Yb、Zb的值分别为电压矢量U4（100）、U6（110）与其作用时间的乘积加上前一个电流拐点的值，即：

Xb=T102（2Vdc3L（db+dc2－da））;

Yb=T42（2Vdc3L（1+db+dc2－da））+Xb;

Zb=T62（2Vdc3L（12+db+dc2－da））+Yb。（5）

电流纹波峰值I1peak可由3个电流拐点中的最大值与最小值作差求出，即

I1peak=max{Xb，Yb，Zb}－min{Xb，Yb，Zb}=

Zb－Xb=T62（2Vdc3L（12+db+dc2－da））+

T42（2Vdc3L（12+db+dc2－da））。（6）

在改进零脉冲插入法中，由于每相PWM都被均分两部分，并且每一部分都在半个PWM周期内关于Ts/4对称，前后周期PWM信号相同，因此仅分析前四分之一周期的电流纹波即可。

如图9（b）所示，由于各相插入的零脉冲作用时间不同，PWM周期中间的电压矢量U20（000）仅由三相中占空比最大的A相决定，且PWM周期两边的电压矢量U10（000）与U20（000）作用时间相等，即

T20=T10=（Ts－（T7+T4+T6））/2。（7）

电流拐点的Xc、Yc、Zc的表达式为：

Xc=T104（2Vdc3L（db+dc2－da））；

Yc=T44（2Vdc3L（1+db+dc2－da））+Xc；

Zc=T64（2Vdc3L（12+db+dc2－da））+Yc。（8）

同理可得电流纹波峰值I2peak为

I2peak=max{Xc，Yc，Zc}－min{Xc，Yc，Zc}=

Zc－Xc=T64（2Vdc3L（12+db+dc2－da））+

T44（2Vdc3L（1+db+dc2－da））。（9）

由式（6）与式（9）可得，当参考电压矢量位于非重构盲区时，改进零脉冲插入法相比传统零脉冲插入法电流纹波幅值下降50%。

3.2" 重构盲区时电流纹波对比

当参考电压矢量处于重构盲区时，假设B、C相占空比接近，因此在传统的零脉冲插入法中需要在B相进行零脉冲插入补偿，在改进零脉冲插入法中需要在C相补偿。

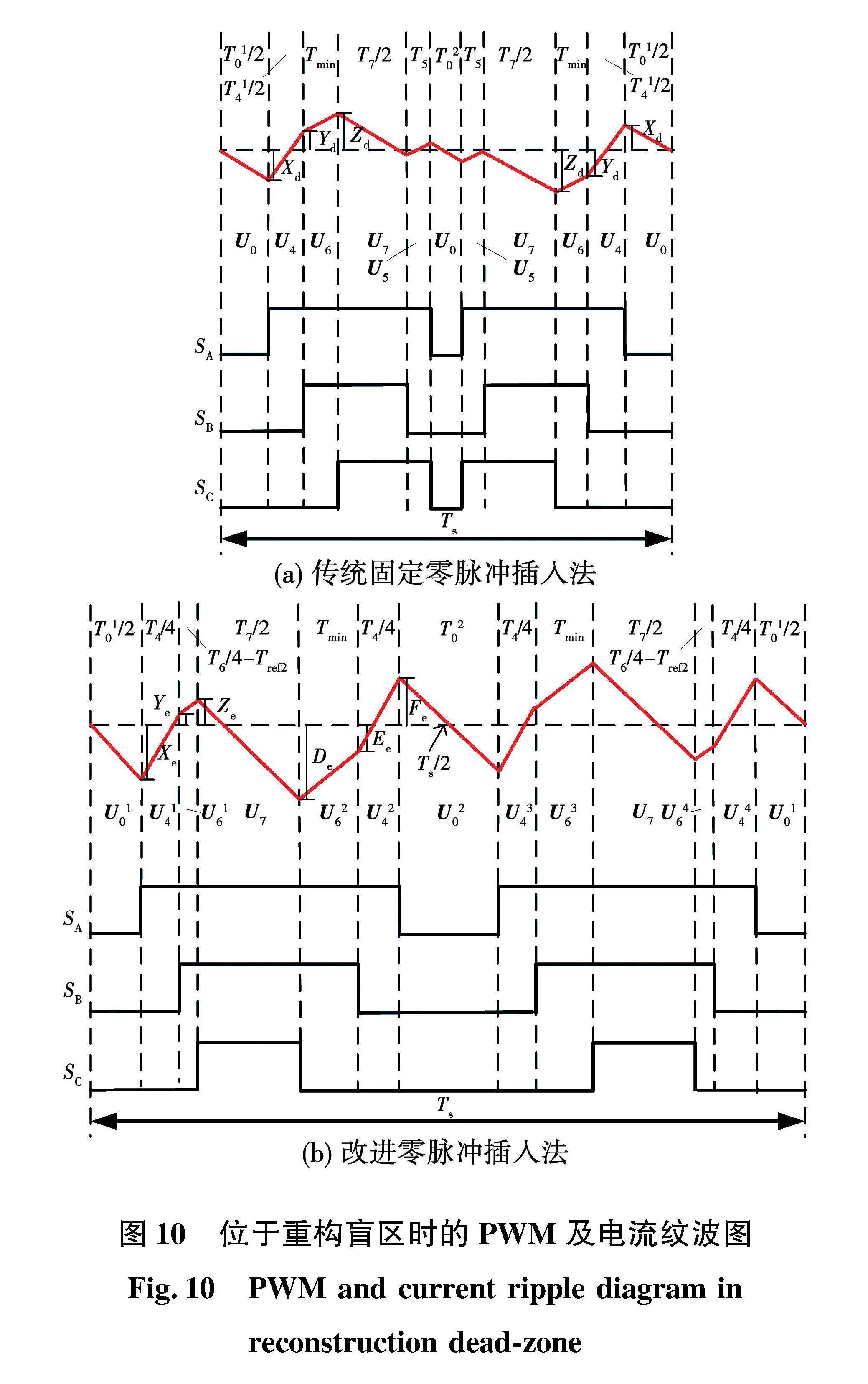
B相进行零脉冲插入补偿后并未改变PWM对称性，如图10（a）所示，因此可对前3个电流拐点进行分析，即：

Xd=T102（2Vdc3L（db+dc2－da））；

Yd=T142（2Vdc3L（1+db+dc2－da））+Xb；

Zd=Tmin（2Vdc3L（12+db+dc2－da））+Yb。（10）

其中：Tmin为最小采样时间，其值等于T5与未补偿前电压矢量U6（110）作用时间T6/2之和；T14为补偿后电压矢量U4（100）的作用时间。电流纹波峰值I3peak的表达式为

I3peak=max{Xd，Yd，Zd}－min{Xd，Yd，Zd}=

Zd－Xd= Tmin（2Vdc3L（12+db+dc2－da））+

T142（2Vdc3L（1+db+dc2－da））。（11）

由于PWM周期中间进行零脉冲插入补偿，半周期内的电流纹波发生改变，PWM信号关于Ts/4不具备对称性，如图10（b）所示，因此需对半周期内的6个电流拐点进行分析，电流拐点的表达式为：

Xe=T102（2Vdc3L（db+dc2－da））；

Ye=T44（2Vdc3L（1+db+dc2－da））+Xd；

Ze=（T64－Tref2）（2Vdc3L（12+db+dc2－da））+Yd；

De=T72（2Vdc3L（db+dc2－da））+Zd；

Ee=Tmin（2Vdc3L（12+db+dc2－da））+Dd；

Fe=T44（2Vdc3L（1+db+dc2－da））+Ed。（12）

图10（b）所示的PWM前半周期中，在C相进行零脉冲插入补偿后，U16（110）电压矢量作用时间缩短，U26（110）电压矢量作用时间延长，因此电流拐点极大、极小值在De、Ee、Fe中出现，电流纹波峰值I4peak表达式为

I4peak=max{De，Ee，Fe}－min{De，Ee，Fe}=

Fe－De= T44（2Vdc3L（1+db+dc2－da））+

Tmin（2Vdc3L（12+db+dc2－da））。（13）

由式（11）与式（13）可得，当参考电压矢量位于重构盲区时，由于进行了零脉冲插入补偿，IZPIM相比FZPIM的电流纹波抑制效果取决于最小采样时间Tmin的选取，Tmin越小，其值越接近50%。

4" 实验验证

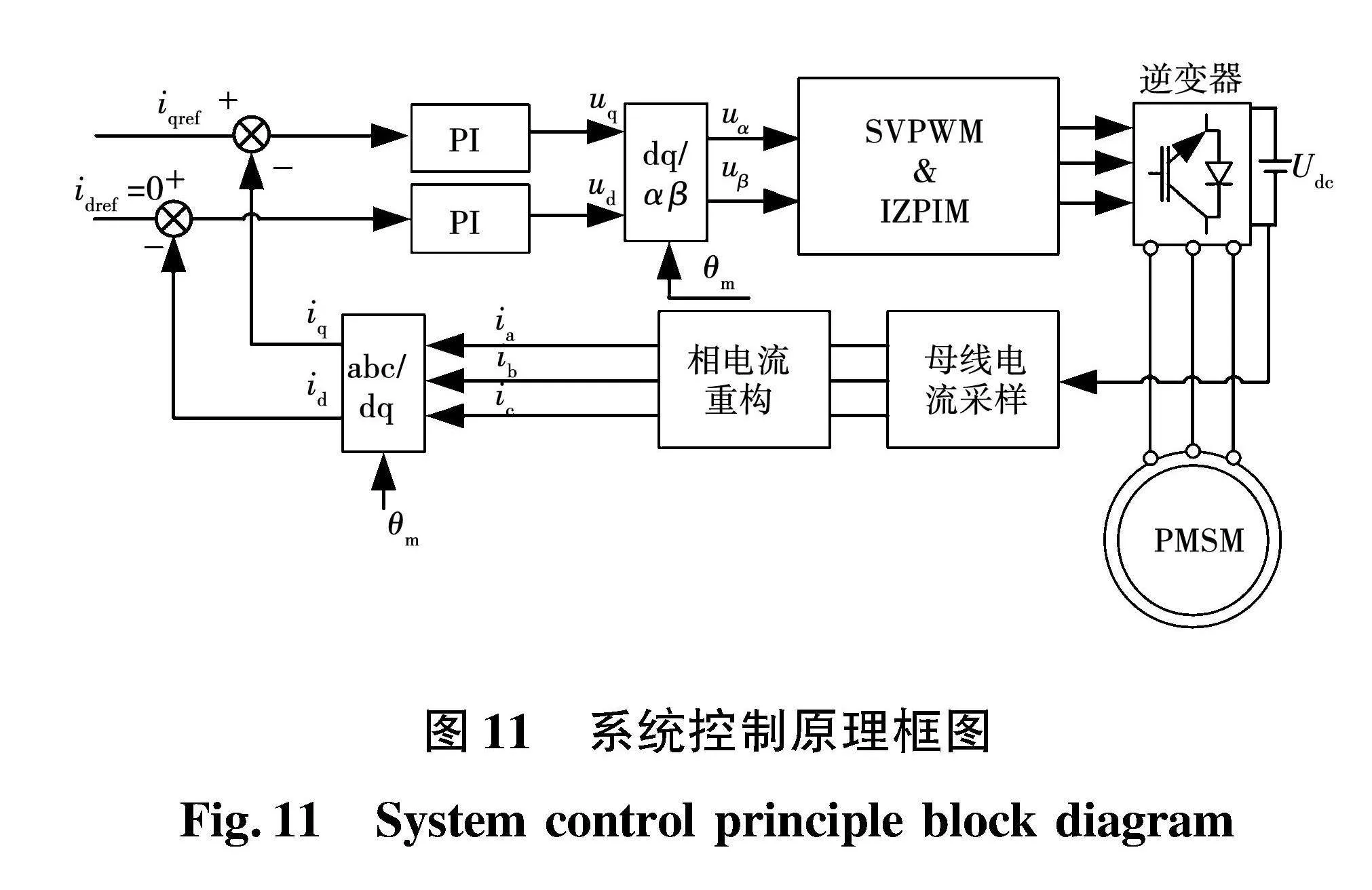
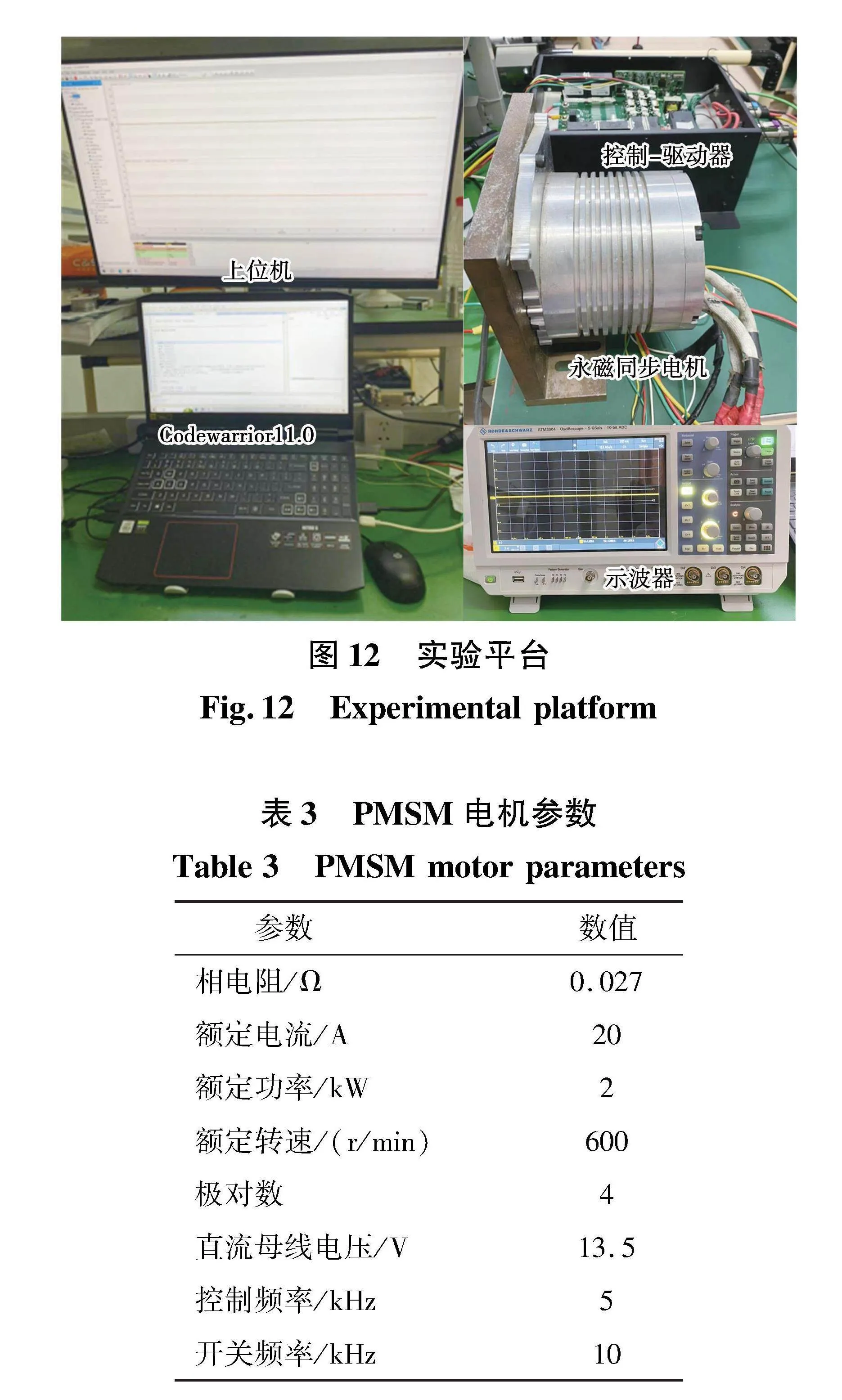
基于IZPIM的永磁同步电机系统控制原理框图如图11所示，搭建的实验平台如图12所示。实验采用NXPS12ZVM型数字信号处理器。系统控制频率为5 kHz，由于一个控制周期内PWM要进行2次开断，因此开关频率应为系统控制频率的2倍，即10 kHz。为了排除速度环对于电流重构的影响，实验采用电流环开环控制，PMSM参数如表3所示。

4.1" 稳态工况实验

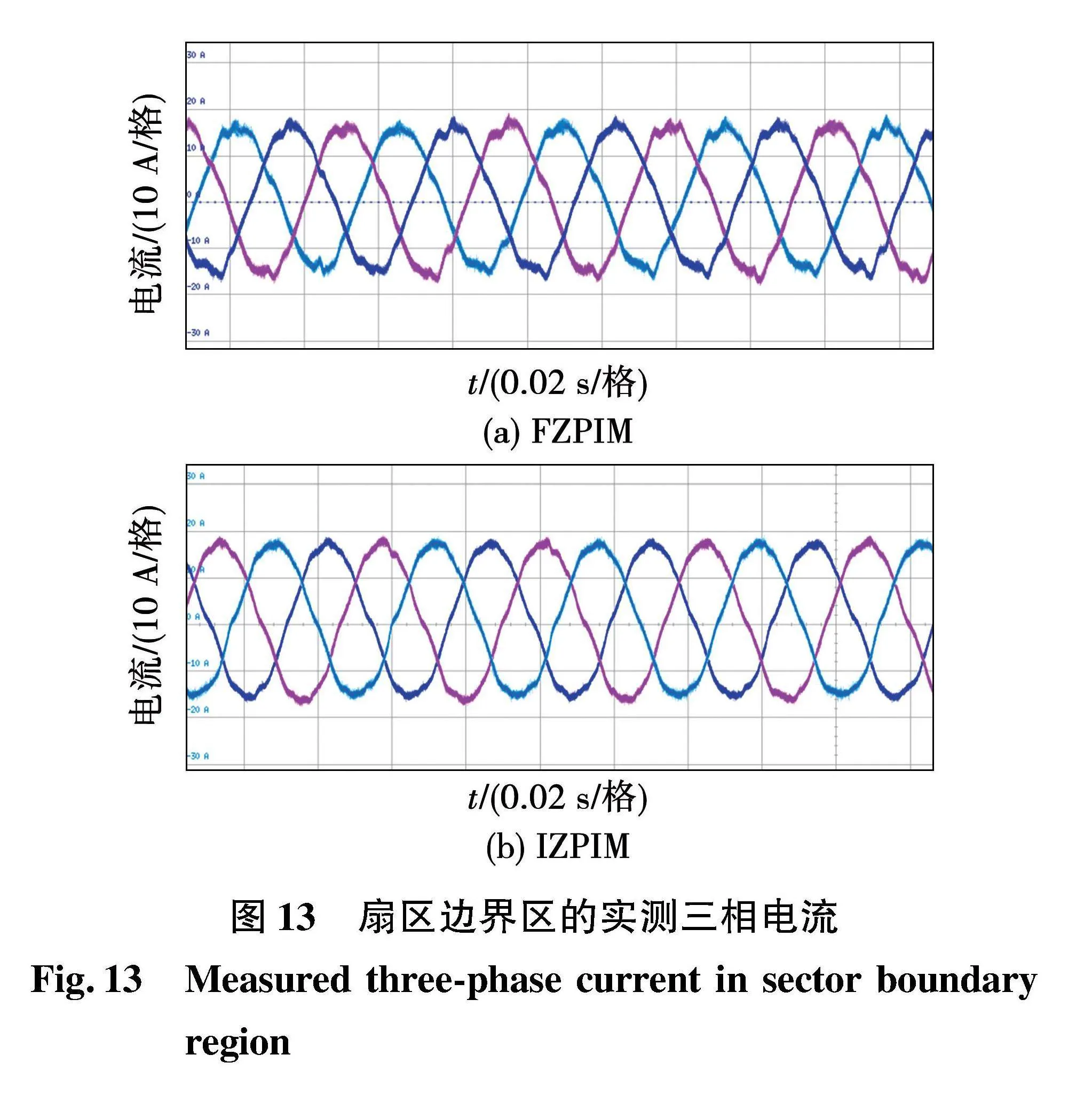
图13为电机运行在扇区边界区，分别使用FZPIM和IZPIM两种重构策略时的相电流波形，可见前者的实际三相电流会有一定畸变，后者的实际三相电流正弦性较好。实验中，电频率为22.6 Hz，转速340 r/min。

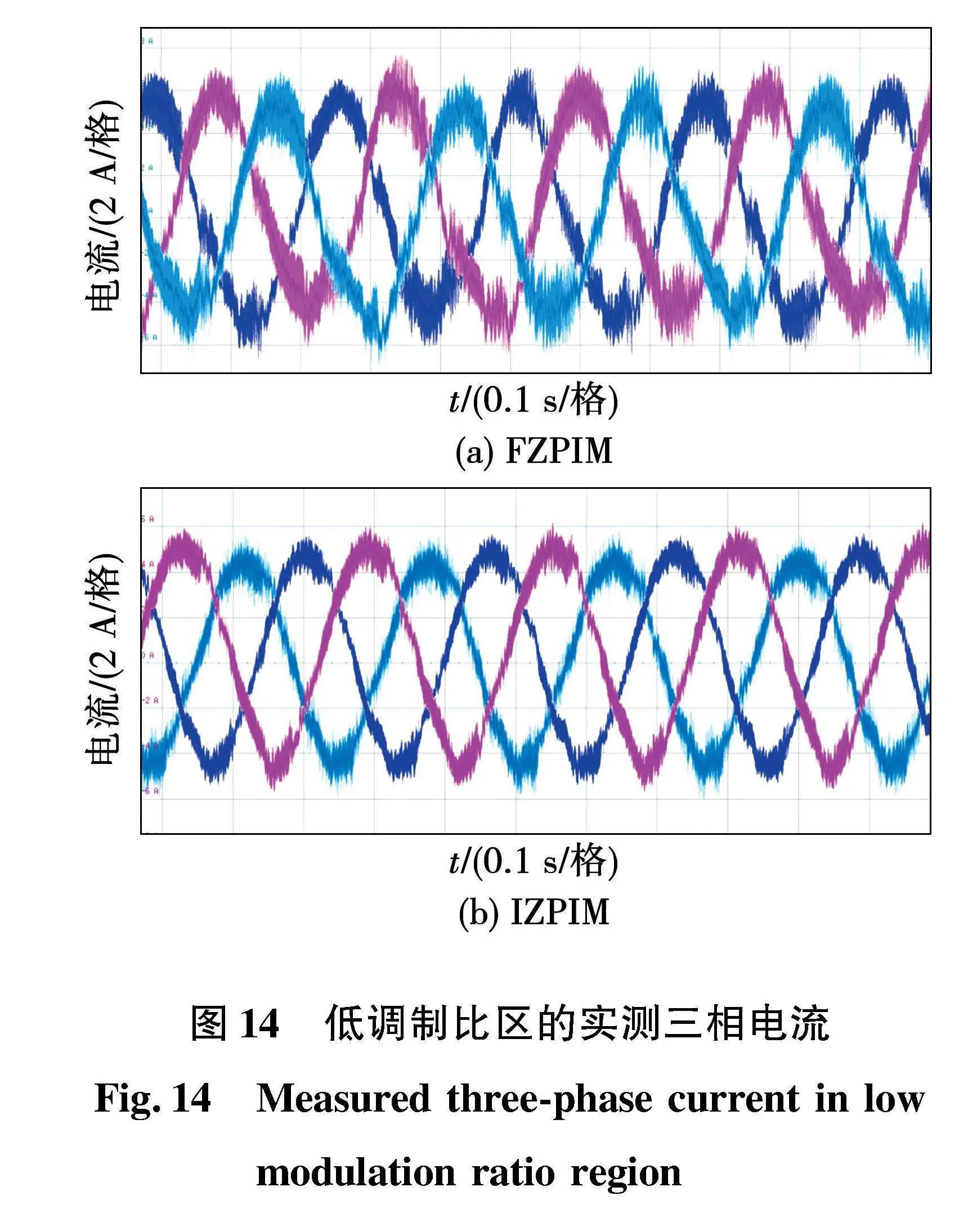
图14为电机运行在低调制比区，分别使用FZPIM和IZPIM两种重构策略时的三相电流波形。此时设定电机目标转速为50 r/min，可以看出，在使用IZPIM时，电机三相电流保持了较好的正弦性。

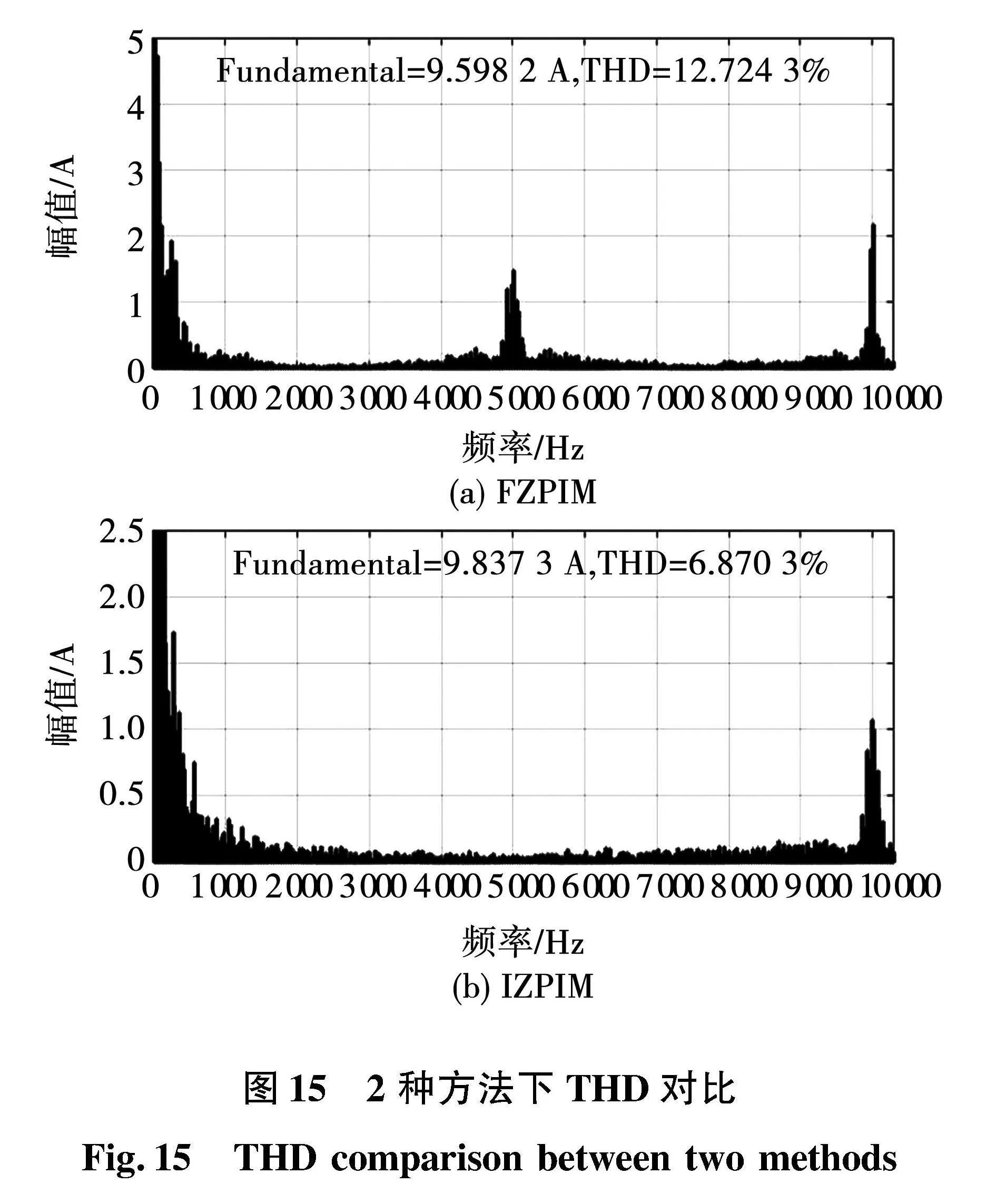
图15分别为采用FZPIM和IZPIM策略运行时的实际电流谐波畸变率分析。

系统的控制频率为5 kHz，开关频率为10 kHz。从图中可以看出采用FZPIM时，电流开关次谐波频率主要集中在5 kHz与10 kHz，幅值最大在2 A左右；采用IZPIM时，电流开关次谐波频率主要集中在10 kHz，电流纹波幅值最大在1 A左右，较FZPIM下降了大约50%，高次谐波频率与开关频率相符合，电流THD从12.73%下降到6.87%。实验结果证实了所提出方法对于电流纹波幅值抑制的正确性与有效性。

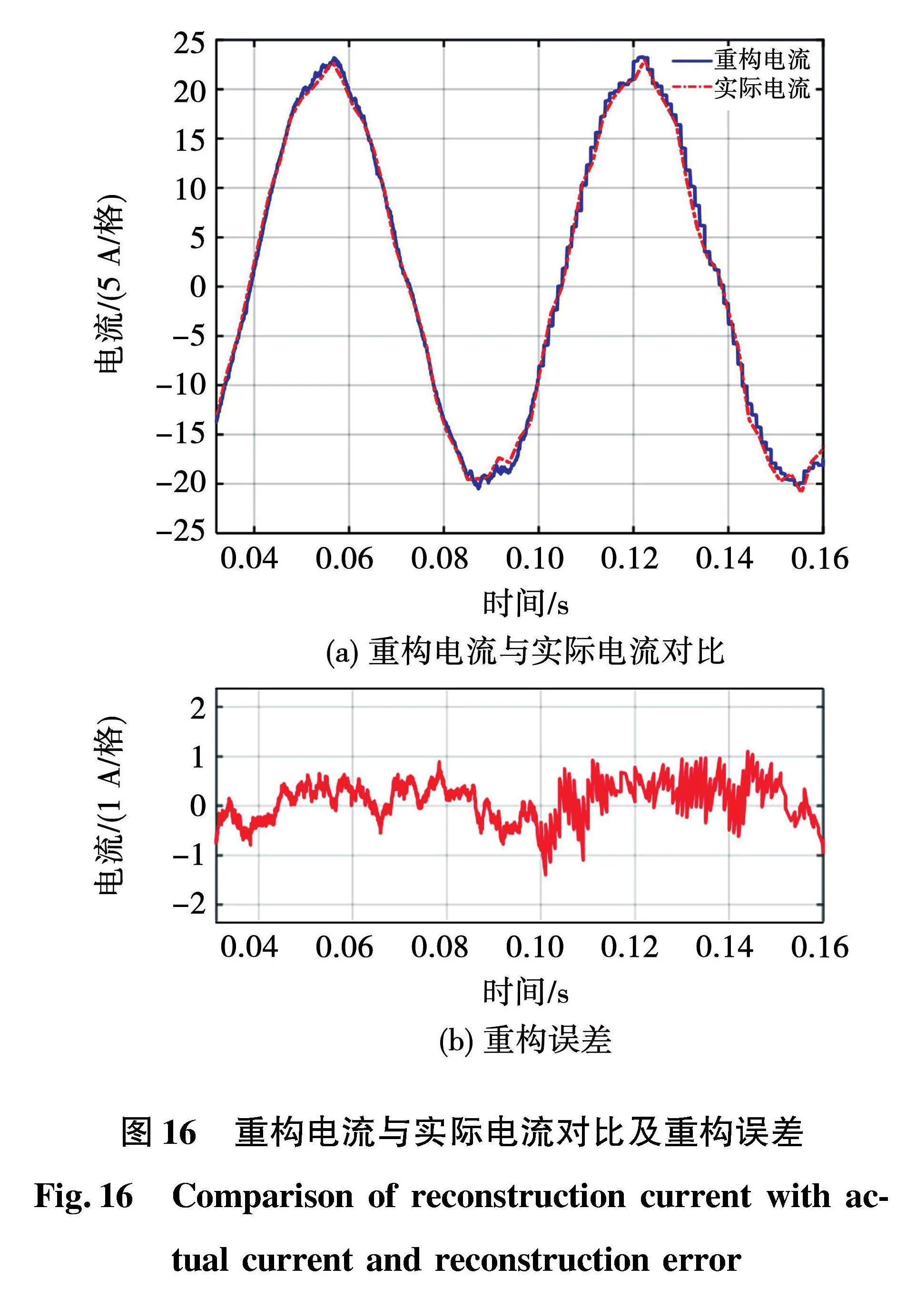
IZPIM的重构电流和实际电流的对比与重构误差如图16所示。两者波形对比为上位机和示波器数据导出后由MATLAB工具做出，图16（a）中可以看出重构电流与实际电流重合性较好。图16（b）为重构误差曲线，可以看出此时的电流重构误差很小，在-0.5～0.5 A之间波动，电流重构误差保持在2.5%以下。

4.2" 动态工况实验

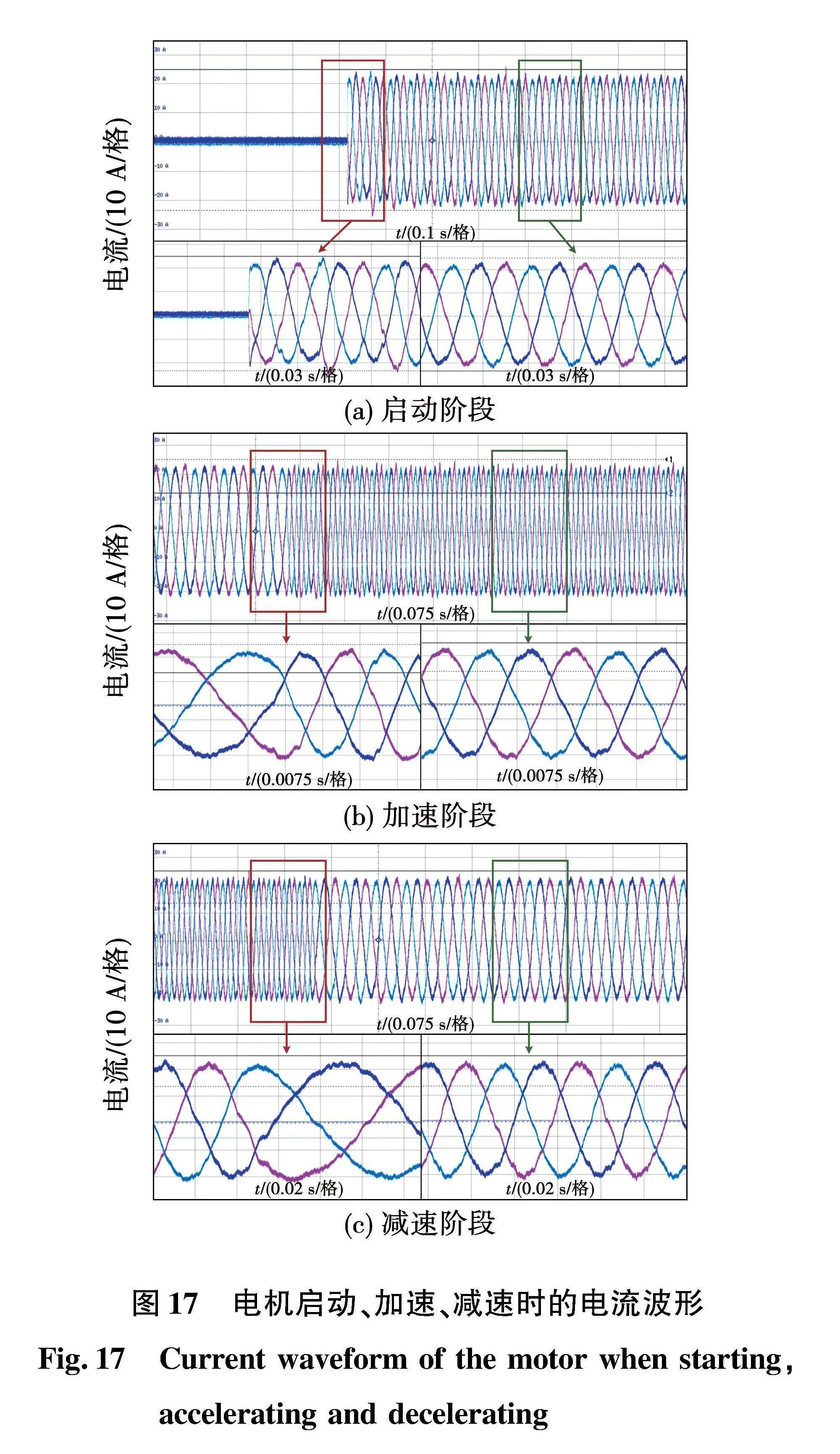
为了进一步验证所提出方法在电机运行于动态工况时的有效性，分别在电机启动、加速与减速的时候进行了实验。图17为电机在动态工况下的三相电流波形，图17（a）所示的启动阶段，电机能从静止迅速达到目标转速300 r/min，在电机转速突变后的短时间内，存在一定的电流波动，但经过电流环调节后，电流逐渐趋于稳定，满足电机闭环控制要求；在图17（b）的加速阶段，电机从300 r/min加速到600 r/min，可以看出电机在转速突增前、过渡阶段、转速突增后，均保持了较好的正弦性；在图17（c）的减速阶段，电机从600 r/min减速到300 r/min，可以看出电机在转速突减前、过度阶段、转速突减后也均未出现电流波动，三相电流保持了较好的正弦性。

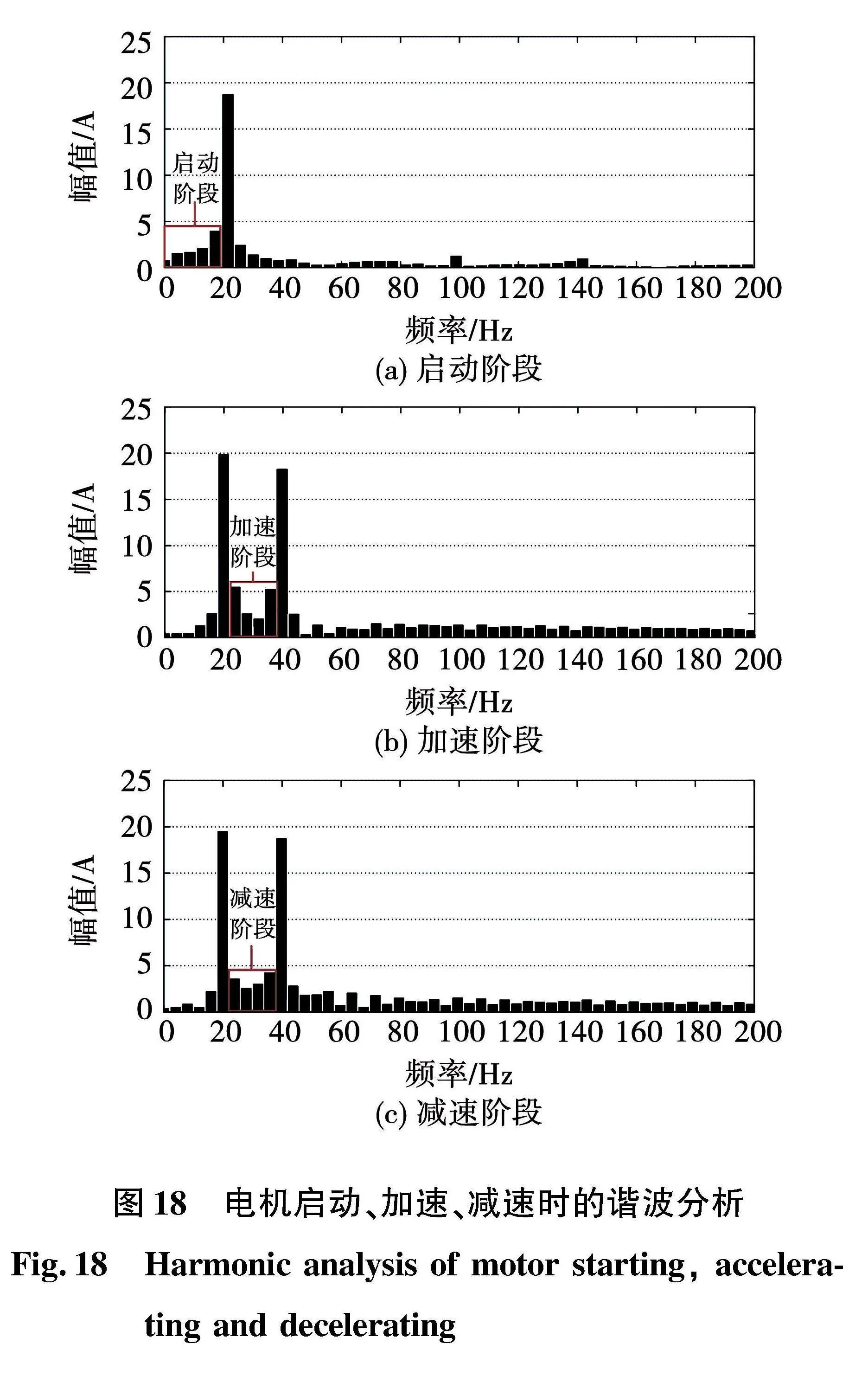
对图17各动态阶段的电流进行谐波分析，结果如图18所示。图18（a）为电机启动阶段的电流谐波分布，可以看出各频率电流分量主要集中在20 Hz及以下，即电机启动后稳态阶段，和启动时动态阶段的电流基频。图18（b）、图18（c）为电机加速、减速阶段的电流谐波分布，各频率电流分量主要集中在20、40 Hz及2个频率之间，即电机加减速前后的稳态阶段，加减速过程中动态阶段的电流基频。其他频次的电流谐波含量低，证明电机动态阶段的电流正弦性较好。

5" 结" 论

针对直流母线单电流采样技术存在的重构盲区的问题，本文提出了一种改进零脉冲插入法，实现了低调制比区和扇区边界区的相电流重构。通过理论推导和实验验证，主要结论如下：

1）通过戴维南电路法，提出不同电压矢量作用时的电路简化模型，证明了IZPIM对比FZPIM的电流纹波抑制效果达到50%。

2）与FZPIM相比，IZPIM在扇区边界区与低调制比区的电流正弦性较好，THD从12.72%下降到6.87%。IZPIM电流重构误差保持在3%以下。

3）通过永磁同步电机稳态工况与动态工况实验验证，IZPIM方法下三相电流均保持较好的正弦性。

参 考 文 献：

［1］" 王宇， 张成糕， 郝雯娟.永磁电机及其驱动系统容错技术综述［J］.中国电机工程学报，2022，42（1）：351.

WANG Yu， ZHANG Chenggao， HAO Wenjuan. Overview of fault-tolerant technologies of permanent magnet brushless machine and its control system［J］．Proceedings of the CSEE，2022，42（1）：351.

［2］" 申永鹏，王前程，王延峰，等.直流母线单电流传感器零点漂移误差自校正策略［J］.电机与控制学报，2023，27（7）：133.

SHEN Yongpeng， WANG Qiancheng，WANG Yanfeng，et al.Self-correction strategy of zero-point drift error of DC bus single current sensor［J］. Electric Machines and Control， 2023，27（7）：133.

［3］" 程明， 姜云磊， 王伟， 等．线电压调制的PWM逆变器相电流重构策略［J］．电机与控制学报，2018，22（2）： 9．

CHENG Ming，JIANG Yunlei，WANG Wei，et al． Phase current reconstruction strategy for PWM inverter based on line voltage modulation［J］． Electric Machines and Control，2018，22（2）： 9．

［4］" SARITHA B， JANAKIRAMAN P A. Sinusoidal three-phase current reconstruction and control using a DC-link current sensor and a curve-fitting observer［J］. IEEE Transactions on Industrial Electronics， 2007， 54（5）： 2657.

［5］" WANG G. Current reconstruction considering time-sharing sampling errors for single DC-link shunt motor drives［J］. IEEE Transactions on Power Electronics， 2021， 36（5）： 5760.

［6］" HA J I. Current prediction in vector-controlled PWM inverters using single DC-link current sensor［J］. IEEE Transactions on Industrial Electronics， 2010， 57（2）： 716.

［7］" LEE D C， LIM D S. AC voltage and current sensorless control of three-phase PWM rectifiers［J］. IEEE Transactions on Power Electronics， 2002， 17（6）： 883.

［8］" LU J， ZHANG X， HU Y. Independent phase current reconstruction strategy for IPMSM sensorless control without using 1 switching states［J］. IEEE Transactions on Industrial Electronics， 2018，65（6）： 4492.

［9］" LU J， HU Y， LIU J， et al. Position sensor fault detection of IPMSM using single DC-bus current sensor with accuracy uncertainty［J］. IEEE/ASME Transactions on Mechatronics， 2019， 24（2）： 753.

［10］" SONG S， XIA Z， FANG G， et al. Phase current reconstruction and control of three-phase switched reluctance machine with modular power converter using single DC-link current sensor［J］. IEEE Transactions on Power Electronics， 2018， 33（10）： 8637.

［11］" 储剑波，胡育文，黄文新，等.一种变频器相电流采样重构技术［J］.电工技术学报， 2010， 25（1）：111.

CHU Jianbo， HU Yuwen， HUANG Wenxin， et al. Phase current sampling reconstruction for inverter［J］. Transactions of China Electrotechnical Society， 2010，25（1）：111.

［12］" ZHU Jiahui， CHENG Qiang， YANG Bin， et al. Experimental research on dynamic voltage sag compensation using 2G HTS SMES［J］. IEEE Transactions on Applied Superconductivity， 2011， 21（3）： 2126.

［13］" GU Yikun， NI Fengli， YANG Dapeng， et al. Switching state phase shift method for three-phase-current reconstruction with a single DC-link current sensor［J］. IEEE Transactions on Industrial Electronics， 2011， 58（11）： 5186.

［14］" HA J I.Voltage injection method for three-phase current reconstruction in PWM inverters using a single sensor［J］.IEEE Transactions on Power Electronics， 2009， 24（3）：767.

［15］" KIM H， JAHNS T M. Phase current reconstruction for AC motor drives using a DC link single current sensor and measurement voltage vectors［J］. IEEE Transactions on Power Electronics，2006， 21（5）： 1413.

［16］" XU Yongxiang， YAN Hao， ZOU Jibin， et al. Zero voltage vector sampling method for PMSM three phase current reconstruction using single current sensor［J］. IEEE Transactions on Power Electronics， 2017， 32（5）： 3797.

［17］" 申永鹏，武克轩，吴成中，等.互补非零矢量单传感器相电流重构策略［J］.电工技术学报， 2023， 38（8）：2126.

SHEN Yongpeng， WU Kexuan， WU Chengzhong， et al.Complementary non-zero vector current reconstruction strategy with single sensor［J］. Transactions of China Electrotechnical Society， 2023，38（8）：2126.

［18］" 申永鹏，郑竹风，杨小亮，等.直流母线电流采样电压空间矢量脉冲宽度调制［J］.电工技术学报，2021，36（8）：1617.

SHEN Yongpeng， ZHENG Zhufeng， YANG Xiaoliang， et al. A compatible SVPWM method for DC bus current sampling［J］.Transactions of China Electrotechnical Society，2021，36（8）：1617.

［19］" NXP.AN5327：3-phase sensorless single-shunt current-sensing PMSM motor control kit with magniv MC9S12ZVM ［EB/OL］.［2016-08］.https：//nxp.com.cn.

［20］" 王文杰，闫浩，邹继斌，等.基于混合脉宽调制技术的永磁同步电机过调制区域相电流重构策略［J］.中国电机工程学报， 2021， 41（17）：6050.

WANG Wenjie， YAN Hao， ZOU Jibin， et al. Phase current reconstruction strategy of PMSM under overmodulation mode based on a hybrid space vector pulse width modulation technique［J］. Proceedings of the CSEE， 2021，41（17）：6050.

［21］" CHO Y， LABELLA T， LAI J S. A three-phase current reconstruction strategy with online current offset compensation using a single current sensor［J］. IEEE Transactions on Industrial Electronics，2012， 56（7）： 2924.

［22］" XIAO Shuxin， SHI Tingna， LI Xinmin， et al．Single-current-sensor control for PMSM driven by quasi-z-source inverter［J］．IEEE Transactions on Power Electronics， 2019， 34（7）：7013.

（编辑：刘琳琳）