基于扩张状态观测器的并联直流变换器增强控制策略

摘" 要：

为进一步改善并联直流变换器在多种内外部扰动下的动态性能，提出一种基于双闭环扩张状态观测器（ESO）的增强控制策略。该策略将比例调节器与ESO相结合，然后分别应用于公共电压外环和各个电流内环，实现各功率单元的动态均流，也强化对输入电压扰动的抑制能力，且无需额外传感器。首先，根据并联变换器的状态方程，推导内环电流ESO控制的表达式。然后，根据电流闭环极点的分布情况，从理论上分析ESO型电流内环在输入电压扰动抑制方面强于比例积分型电流内环的原因。此外，借助伯德图，给出ESO型电流内环对电感失配的鲁棒性更强并能有效消除动态电流偏差的理论依据。最后，使用三相buck变换器进行不同方案的对比验证，实验结果证明了所提策略在改进动态性能方面的有效性和先进性。

关键词：并联直流变换器；扩张状态观测器；双闭环控制；参数鲁棒性；扰动抑制；动态均流

DOI：10.15938/j.emc.2024.06.001

中图分类号：TM46

文献标志码：A

文章编号：1007-449X（2024）06-0001-12

收稿日期： 2023-10-31

基金项目：黑龙江省博士后科研启动基金（LBH-Q20020）；国家自然科学基金（52177211）

作者简介：段鸣航（1990—），男，博士研究生，研究方向为功率变换与电力储能；

段建东（1985—），男，博士，教授，研究方向为新能源发电与电储能、微网能量变换与协调控制；

王露霄（1996—），男，博士研究生，研究方向为电储能系统能量管理；

孙" 力（1960—），男，博士，教授，博士生导师，研究方向为储能技术与微电网的功率控制、电驱动与电推进。

通信作者：段建东

Enhanced control strategy for parallel DC-DC converters based on extended state observer

DUAN Minghang，" DUAN Jiandong，" WANG Luxiao，" SUN Li

（School of Electrical Engineering and Automation， Harbin Institute of Technology， Harbin 150001， China）

Abstract：

To further improve the dynamic performance of parallel DC-DC converters under various inner and outer disturbances， an enhanced control strategy based on dual-loop extended state observer （ESO） was proposed. In this strategy， the proportional regulators were combined with ESOs， and then applied to common outer voltage loop and each inner current loop respectively. In no need of extra sensors， the dynamic current sharing among power units was realized and the ability of input voltage disturbance rejection was also strengthened. Firstly， the expressions of ESO-based inner-loop current control were deduced based on the state equations of parallel converter. After that， according to the poles distribution of closed current loop， the reason why the ESO-based current loop performed better than the proportional-integral-based current loop in terms of input-voltage disturbance rejection was analyzed in theory. Besides， with the help of bode plots， the theoretical evidence that the ESO-based current loop had stronger robustness against mismatched inductances and could effectively remove the dynamic current deviations was given. Finally， a three-phase buck converter was used to conduct the comparative validations of different schemes. The experimental results verify effectiveness and advancement of the proposed strategy in terms of dynamic performance improvement.

Keywords：parallel DC-DC converter; extended state observer; dual-loop control; parameter robustness; disturbance rejection; dynamic current sharing

0" 引" 言

相比于隔离型变换器［1-2］，非隔离直流变换器具有结构简单，效率高，可靠性高的优点，使其近年来在工业民用场合取得广泛应用，如电动汽车［3］、直流微电网［4］、燃料电池［5］、电力储能［6］等。良好的暂态过程需要保证尽量小的超调量和尽量短的调节时间，但实际运行中的外部扰动及内部不确定性对变换器控制提出了严峻挑战。为改善动态响应，负载电流经过前馈通道［7］被引入闭环控制，减小了负载切换引起的电压跌落并缩短了恢复时间。文献［8］在负载电流前馈的基础上，根据电感及电容中储存的暂态功率校正内环给定值，获得了更佳的动态性能。文献［9］提出适用于降压和升压的一致性输入电压前馈策略，增强了升降压变换器对输入电压扰动的抑制性能。文献［10］将文献［9］中的输入电压前馈移至电流内环，对输入侧扰动的鲁棒性进一步提高。然而，文献［7-10］涉及的策略只能抑制单一扰动，同时均引入额外的传感器。

相对而言，观测器既可以估计扰动，也能辨识不便测量的参数摄动，而且不需要额外的传感器，更具优势和应用前景。扩张状态观测器（extended state observer，ESO）是实现自抗扰控制的核心环节［11］，最早由韩京清教授提出，后由学者高志强引入带宽概念［12］，简化为线性ESO，方便了理论分析及工程应用。该观测器可将系统外部扰动及未建模动态整合为总和扰动，并在控制环路加以消除。原理简单、便于实现的特点使得 ESO具有较高的理论与工程价值，已在诸多领域得到应用，包括电机驱动［13-16］、脉宽调制（pulse width modulation， PWM）整流器［17］、风力发电［18-19］、伺服系统［20］、磁悬浮系统［21］、微电网［4］、机器人［22］等。为实现更好的动静态效果，ESO常常与滑模［17，22-23］、模型预测［24］、反步［4］、有限时间［15］、数据驱动［25］等非线性理论相结合，构成复合控制。借助于ESO，系统对外部条件变化和内部参数偏差的敏感性得以降低，但复合控制中较多的控制参数也增加了实现难度。此外，上述复合控制通常采用单闭环框架，快速响应和过流保护难以兼顾。相比之下，比例调节与ESO相结合的控制方式可在较低复杂度下实现无静差跟随，且便于在双闭环框架中使用。目前，该方法已应用于buck和boost变换器的外环电压控制［3，5］。与比例积分（proportional-integral，PI）控制相比，其改善了负载扰动及给定电压阶跃时的暂态性能。

近年来，关于ESO的研究已在不同方面取得进展，强化了观测和抗扰性能。文献［1］将电流应力的优化求解与ESO相融合，提高电能转换效率的同时也兼顾了良好的动态特性。文献［26-30］从自适应调整关键参数方面展开探索。具体而言，文献［26］使用二阶状态变量组合的形式来描述总和扰动，提高了系统对目标信号的跟踪性能，但仅采用单电压闭环控制，难以对各相电感电流实现有效限制。文献［27］根据负载电流反馈值与预设电流临界值的实时比较结果，对控制器带宽进行自适应调整，加快了输出电压响应速度，但需要额外的电流传感器。文献［28］分析了脉冲负载条件下电流谐波含量与控制器截止频率的定性关系，设计出控制带宽在其上下限范围内的指数型变化律，缓解了低谐波含量与高响应速度的矛盾，但该文献未对二阶导数过零点和过渡斜率值作详细说明，选取依赖于经验。文献［29］借助模糊逻辑规则在线调整电压外环的控制带宽，改善了系统鲁棒性，但额外的放大系数同样需要合理选取。文献［30］借助人工神经网络，以超调量及调节时间作为评估指标，自适应整定自抗扰控制中的关键参数，避免了繁琐的调试过程，但其依赖于全工况的测试仿真数据，前期工作量巨大。

通过改进ESO结构，文献［31］在电压外环中引入串联校正环节，缩小稳态误差的同时，也提高了外部扰动的抑制性能，但实现复杂度有所增加。文献［32］通过串联多个不同带宽的ESO，有效弱化了高频测量噪声对估计及控制性能的负面影响，但应用到多相变换器会存在计算负担明显增加的问题。文献［33］引入谐振阻尼，增强了系统对时变扰动的抑制性能。文献［34］在常规ESO中引入校正函数和参考信号的微分前馈，改善了观测器的收敛速度和准确度，但微分环节降低了系统对高频噪声的鲁棒性。

为满足大容量的应用需求，直流变换器通常采用多重模块化形式，以降低单个功率单元的电流容量要求，但各单元的电路参数由于生产工艺偏差，老化程度不一致等因素，往往难以实现电流和热应力的平均分配，所以精准可靠的均流一直是并联变换器的研究热点之一。文献［2，35-36］从硬件电路角度寻求电流偏差的抑制。文献［2］通过优化选取谐振网络参数，实现并联谐振变换器的近似电流平衡，但固有的内阻偏差使得不平衡度无法彻底消除。为方便分析暂态电流的分配，文献［35］建立了基于耦合电感的寄生网络模型，通过改善元器件布局，缓解了动态电流不一致的问题，但均流精确度严重依赖于寄生参数的测量精确度。文献［36］则通过优化阻容缓冲电路的连接位置来实现并联开关管的动态均流，但文中仅以两开关并联情况进行分析和验证，且未对缓冲电路元件的取值作具体介绍。经典的主从控制需采样各相电流，然后分别进行闭环控制，可实现各相稳态电流的均匀分配，但随着并联相数的增加，传感器成本明显增加而且不利于系统的可靠运行。适用于多相buck和boost变换器的无传感器均流方案［37-38］可根据各相等效内阻失配造成的电流不平衡程度，对各相占空比加以校正，实现原理简单，但依赖于电路的先验知识。针对两相变换器，文献［39］使用巧妙的二倍频率电流采样方法实时获取两相电流平均值，电流传感器数量得以减半，但相数为奇数时，该方法面临较大的局限性。针对非线性电感型的并联变换器，文献［40］利用单个电流传感器交替采集各相电流峰值来实现均流，但要选取大量程传感器方可测量总和电流，因而传感器成本的下降未必明显。下垂类均流策略具有高可靠性，高冗余性的优点，适合于微电网应用，但压降问题需要额外的补偿环节方可解决。文献［6］引入线路阻抗的主动检测，提高了下垂均流精确度，但也对电压及电流变化量的采样精确度提出严苛的要求。自适应下垂法［41］可以动态调整各下垂系数使各相的输出阻抗近似相等，但互联通信的使用削弱了原有下垂控制的可靠性。计及母线电压偏差，均流偏差和系统效率的多目标优化，文献［42］提出的改进下垂方案可减小均流误差，但引入多个参数，增加了微处理器的运算量。文献［43］提出电流-电压型下垂方案，此时的系统极点与虚轴的距离比采用经典电压-电流型下垂时更远，可在减小电流偏差的同时改善系统动态性能，但使用比例电压调节器，导致稳态电压误差不能消除。文献［44］将鲁棒H无穷理论应用于外环均流控制器，通过实时修正两相参考电压，实现动态均流，但电流内环的缺少增加了过流风险。目前，方便实现的均流算法往往易受电路参数准确度的影响，如文献［2，35-38］。而为提高均流精确度，改善动态性能，通常要引入较多的传感器［6，41］，附加的控制参数［42］或复杂理论［44］，不利于工程应用。

由于推导复杂，不便于简化，各相电感参数的不匹配对动态均流的影响常被忽视，而受生产工艺水平的限制，实际电感量往往在其名义值上下20%浮动，当长期频繁使用后，各相电感参数的偏差可能进一步扩大，需要对此类内部扰动造成的不良效应加以抑制。另外，储能系统通常应具有良好的瞬态特性，特别是文献［8］所涉及的压降恢复型储能系统面临多种扰动的考验，有必要寻求一种先进的变换器控制策略，使系统遭遇多种内外部扰动时呈现良好的动态响应。同时，应尽量避免增加传感器，这样可保证系统的高性价比，又可避免潜在的传感器故障以及测量误差对控制产生不利影响。

为满足上述期望，提出一种基于双闭环ESO的增强控制方法，旨在解决潜在的电感参数失配所导致的动态电流不平衡和电流尖峰问题，同时进一步提升变换器对输入电压的鲁棒性。所作贡献包括：1）推导ESO应用于电流内环时的扰动观测表达式；2）根据极点分布情况，从理论上分析对输入电压扰动的抑制性能被增强的原因；3）基于伯德图，给出电感参数失配时动态电流一致性被改善的理论依据。

1" 基于双闭环ESO的增强控制策略

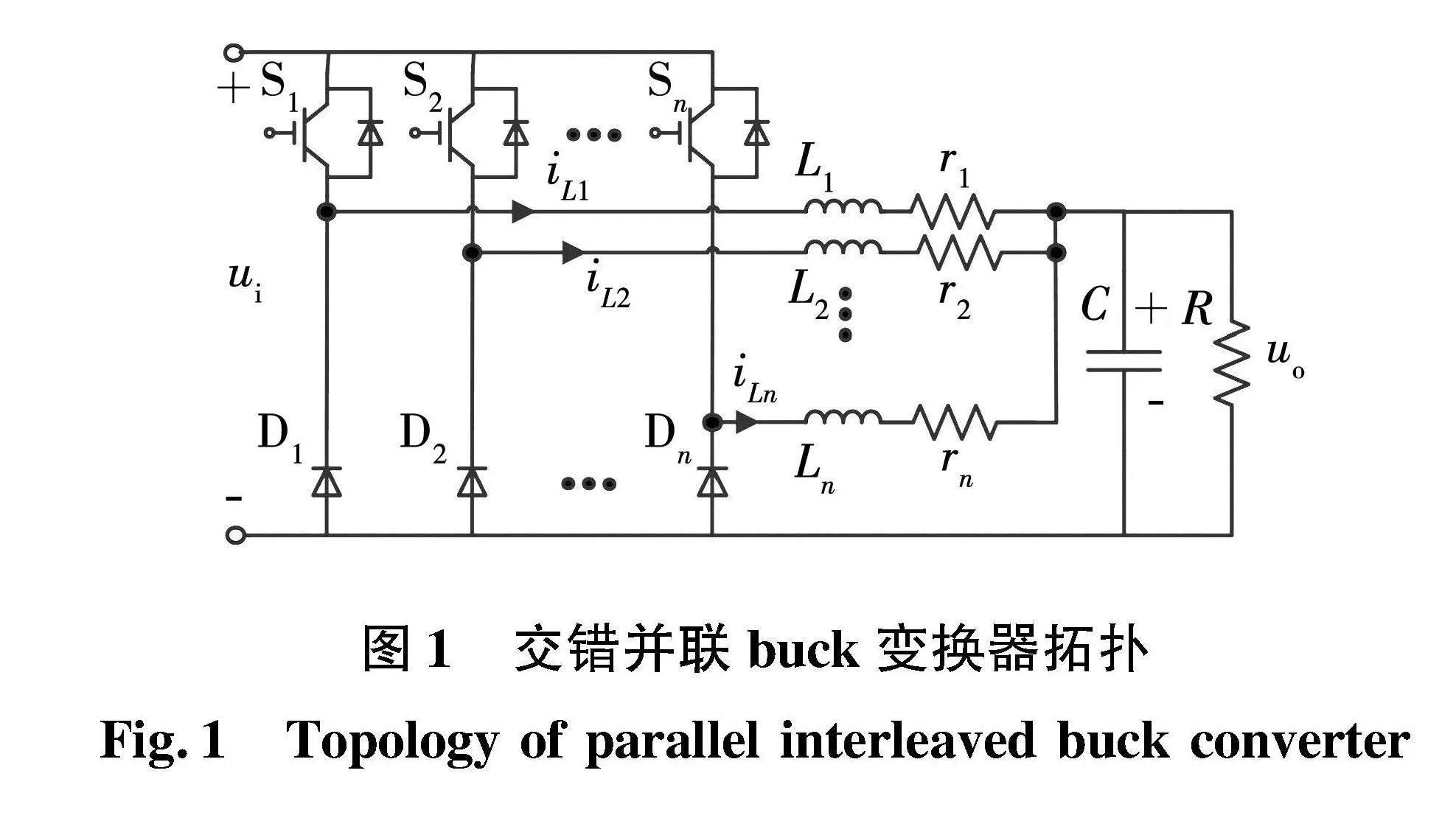
以交错并联buck变换器为研究对象，其电路拓扑如图1所示。其中：ui和uo为变换器的输入和输出电压；C和R是输出侧滤波电容和阻性负载；Sk、Dk、Lk和rk分别是各相的开关管、二极管、电感和等效内阻，k=1，2，…，n，其中n为相数。

基于双闭环ESO的增强控制方案如图2所示，电压外环和多个电流内环均采用ESO调节。其中：uref、iLref 分别是电压环、电流环给定值；iLk、dk分别是各相电流及各相占空比；kpev、bv是电压环的控制增益；kpei、bi则是电流环的控制增益；zv和zik是电压环和第k个电流环的扰动观测量。

以uo和iLk为状态变量，n重化buck变换器的模型为：

Cduo/dt=∑n1iLk－uo/R；（1）

LkdiLk/dt=dkui－uo－rkiLk。（2）

将扰动fk引入式（2），其可重写为

diLk/dt=bidk+fk。（3）

其中：扰动fk=（ui/Lk－ui0/L）dk－（uo+rkiLk）/Lk，ui0和L分别是ui和Lk的额定值。bi的取值可以调整，其初值bi0=ui0/L。fk可视作由ui扰动，电感参数变化等构成的总和扰动。使用ESO将fk扩张为新的状态量，并对电流内环进行观测，具体表示为：

dxik/dt=bidk+zik－g1（xik－iLk）；

dzik/dt=－g2（xik－iLk）。（4）

其中：xik和zik分别是iLk和fk的估计量；g1和g2是电流环ESO的观测器增益。设电流调节器的输出为v， 满足

dk=（v－zik）/bi。（5）

结合式（3），假设fk可被准确观测，即fk≈zik，可得

diLk/dt≈v。（6）

即从电流调节器输出v到电感电流iLk可等效为积分环节，使用比例调节器即可实现电流无静差控制。此时，电流闭环传递函数可写为

iLk/iLref=kpei/（s+kpei）。（7）

因而，比例系数kpei即是电流闭环的控制带宽。

假设iLk可以准确跟随iLref，式（1）可改写为

duo/dt=bviLref+fv。（8）

其中fv=－uo/（RC），可对uo突变和负载变化进行实时观测。根据性能要求，bv的取值可作调整，其初值bv0=n/C。对式（8）应用ESO，可表示为：

dxv/dt=bviLref+zv－h1（xv－uo）；

dzv/dt=－h2（xv－uo）。（9）

其中h1和h2是电压环ESO的观测器增益。同理，从电压调节器输出到uo可等效为积分环节，电压环采用简单的比例控制便可无稳态误差。据此，电压闭环的传递函数可推导为

uo/uref=kpev/（s+kpev）。（10）

此时的比例系数kpev便是电压闭环的控制带宽。

根据带宽参数化原则［12］，将观测器增益赋值为：

g1=2woi，g2=w2oi；

h1=2wov，h2=w2ov。（11）

其中woi和wov分别为内外环的观测器带宽。后文将比例调节与ESO相结合的控制简称为ESO控制。

所提策略的先进性体现为：1）增强系统对输入电压扰动的鲁棒性；2）在各相电感参数失配时，有效抑制各相电流的暂态偏差，实现动态均流；3）实现原理简单，且无需额外传感器。

2" 动态性能的对比分析

着眼于电流内环，对式（4）进行拉式变换得到：

xik=Ki1iLk+Ki2dk；

zik=Ki3iLk+Ki4dk。（12）

其中：

Ki1=（g1s+g2）/［s2+g1s+g2］；

Ki2=bis/［s2+g1s+g2］；

Ki3=g2s/［s2+g1s+g2］；

Ki4=－g2bi/［s2+g1s+g2］。

根据图2的电流内环控制流程，满足

kpeiiLref－（kpei+Ki3）iLk－Ki4dk=bidk。（13）

化简上式，得到电流ESO控制时的控制律

dk=Gie（HiiLref－iLk）。（14）

其中：

Hi=kpei（s2+g1s+g2）/［kpei（s2+g1s+g2）+g2s］；

Gie=［kpei（s2+g1s+g2）+g2s］/［bis（s+g1）］。

而采用PI电流调节器时，其表达式可写为

dk=Gipi（iLref－iLk）=（kpi+kii/s）（iLref－iLk）。（15）

其中kpi和kii是PI电流调节器的比例和积分系数。

2.1" 输入电压扰动的抑制性能分析

为分析不同控制下的ui扰动抑制能力，以系统极点分布情况作为参考。取n=3，并假设各相电感参数匹配，即L1=L2=L3=L，r1=r2=r3=r。于是，从占空比到电流的传递函数可推导为

Gid=ui（Cs+1/R）LCs2+（L/R+Cr）s+n+r/R。（16）

根据式（16）， PI控制时的电流闭环特征方程为

Q1（s）=N3s3+N2s2+N1s+N0。（17）

其中：

N3=LC，N0=uikii/R；

N2=L/R+Cr+Cuikpi；

N1=n+r/R+ui（kpi/R+Ckii）。

当采用电流ESO控制时，其电流特征方程为

Q2（s）=M4s4+M3s3+M2s2+M1s+M0。（18）

其中：

M4=biLC，M0=uikpeig2/R；

M3=bi（L/R+Cr）+biLCg1+Cuikpei；

M2=bi（n+r/R）+big1（L/R+Cr）+

Cui（kpeig1+g2）+uikpei/R；

M1=big1（n+r/R）+Cuikpeig2+

ui（kpeig1+g2）/R。

在开关频率2 kHz下，考虑采样噪声及控制延时，ωoi不宜过大。为保证电流环良好的跟随性能，kpei的值应大一些，取kpei=0.4ωoi。同时，为减少内外环的相互影响，取kpev=kpei/16。另外，为保证电压环较高的观测精确度，取ωov=8kpev。至此，双闭环ESO控制的内外环参数选取如下：kpei=800 rad/s，ωoi=2 000 rad/s，bi=5 000，kpev=50 rad/s，ωov=400 rad/s，bv=454.5。

为作对比，以ui0=30 V，uo=10 V，R=0.5 Ω作为额定工作点来选取相应的PI控制参数。首先，保证PI调节器与ESO控制的比例系数作用相同［5］，需满足kpei/bi=kpi， kpev/bv=kpv。然后，尽可能提高kii且保证起动和阶跃过程中不出现超调量，kiv的选取类似，以先内环再外环的顺序整定PI调节器的积分系数。双环PI和电压ESO控制的电流环参数是：kpi=0.16，kii=30，而电压环参数为：比例系数kpv=0.11，积分系数kiv=12。电压ESO控制与双环PI的内环相同，而与双闭环ESO控制共用电压外环。

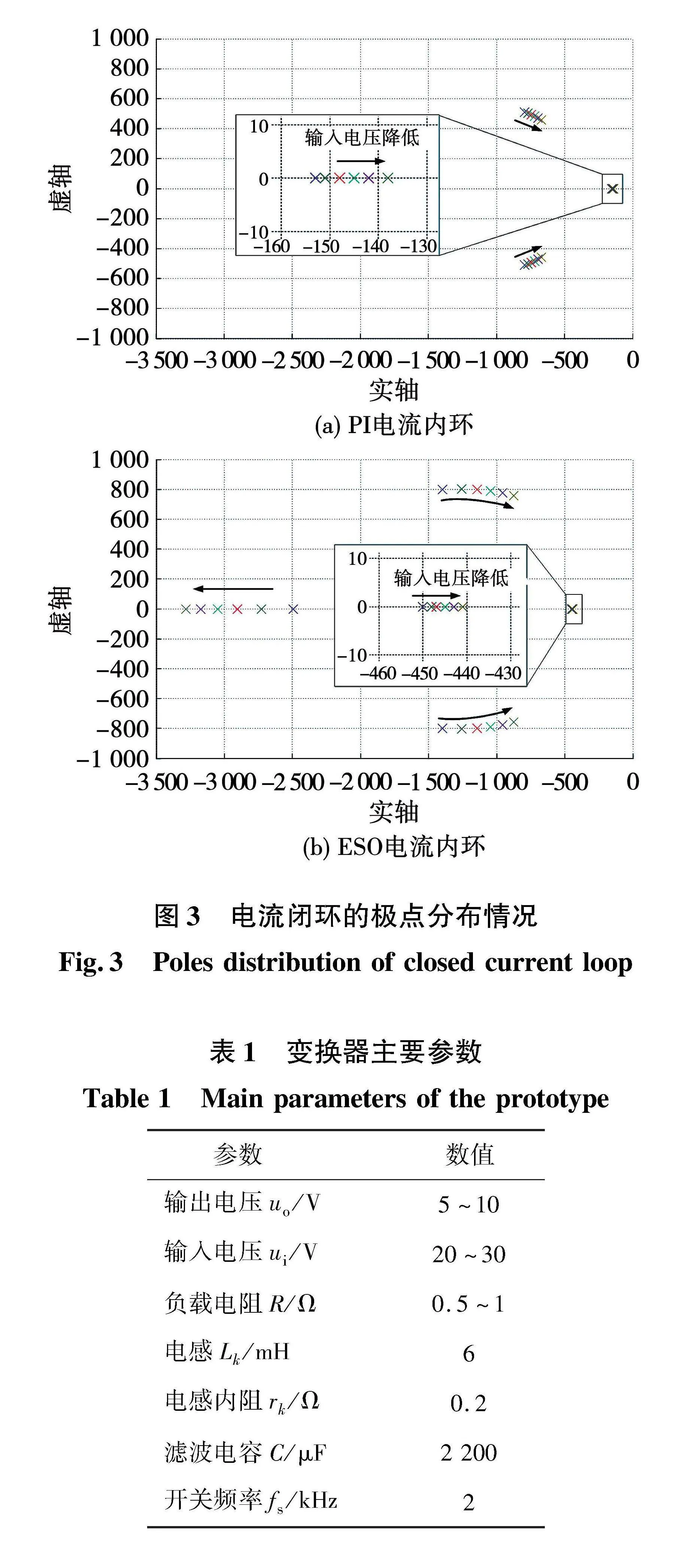
结合表1中的电路参数，当ui从30 V逐步下降至20 V，得到电流闭环的极点分布及变化趋势如图3所示。PI控制电流环的3个极点逐渐接近虚轴，但始终处在左半平面，保证系统稳定运行，其中主导极点保持在-190 rad/s附近。ESO控制电流环的4个极点一直位于左半平面，保证了控制的稳定性，有1个逐渐远离虚轴，而另外3个逐渐靠近虚轴，其中主导极点位于-445 rad/s附近。系统的暂态过程取决于主导极点，就电流环主导极点与虚轴的距离而言，ESO控制时始终大于PI控制时，说明遭遇输入电压扰动时，ESO控制能改善系统的动态特性。

2.2" 动态电流偏差的抑制性能分析

当电感失配时，拉式变换后的式（1）和式（2）可写为：

（sLk+rk）iLk=dkui－uo；（19）

（Cs+1/R）uo=∑n1iLk。（20）

为方便，取n=2。联立式（19）和式（20），可得到

iL1=A11d1+A12d2，iL2=A21d1+A22d2。（21）

其中：

A11=

ui［（Cs+1/R）（sL2+r2）+1］（Cs+1/R）（sL2+r2）（sL1+r1）+sL2+r2+sL1+r1；

A12=A21=

－ui（Cs+1/R）（sL2+r2）（sL1+r1）+sL2+r2+sL1+r1；

A22=

ui［（Cs+1/R）（sL1+r1）+1］（Cs+1/R）（sL2+r2）（sL1+r1）+sL2+r2+sL1+r1。

此时的iLk将由dk和其他相的占空比共同决定。当使用电流ESO控制时，联立式（14）和式（21），可得到：

（GieA11+1）iL1+GieA12iL2=GieHi（A11+A12）iLref；

GieA21iL1+（GieA22+1）iL2=GieHi（A21+A22）iLref。（22）

结合A12=A21，求解式（22），得到关于iL1和iL2的表达式为

iLkiLref=GieHi（A11A22Gie-A212Gie+Akk+A12）A11A22G2ie－A212G2ie+A11Gie+A22Gie+1。（23）

同理，可求得PI控制的电流闭环传递函数为

iLkiLref=Gipi（A11A22Gipi-A212Gipi+Akk+A12）A11A22G2ipi－A212G2ipi+A11Gipi+A22Gipi+1。（24）

各相电流传递函数的区别仅在于分子，为分析其差异部分对整个电流闭环的影响，定义如下：

Ek=［（A11A22－A212）G+A12］/Akk，k=1，2。（25）

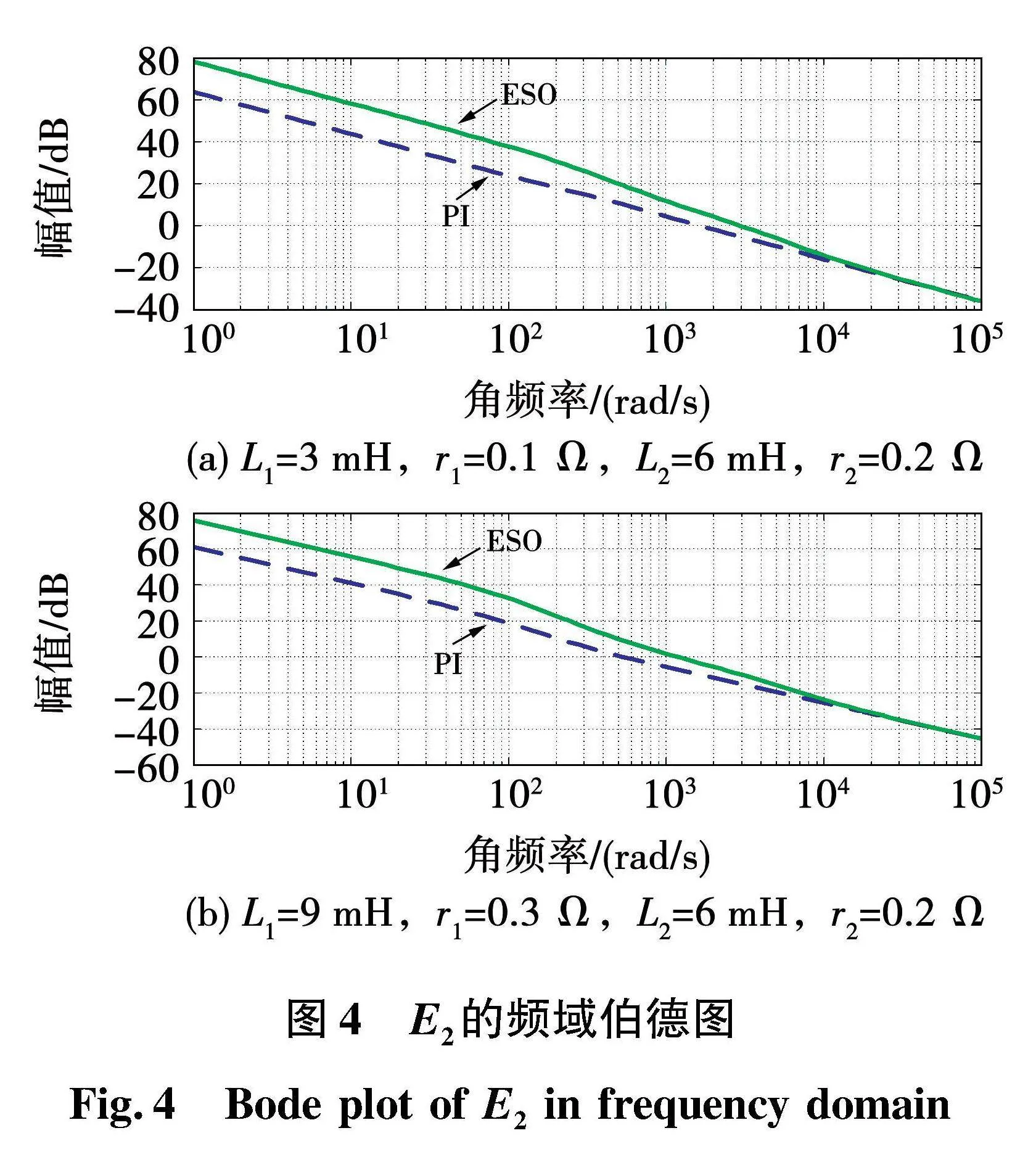
其中G=Gipi或Gie。为分析Ek的频率特性，以E2为例，采用2.1节的电流环参数绘制其伯德图，如图4所示。由于外部扰动的频率往往不高［9］，可重点关注图3的中低频段特性。无论两相电感参数Lk，rk的相互大小关系， ESO控制下的E2幅值均高于PI控制，在中低频段幅值差异保持在14.5 dB左右，共同部分对差异部分的幅值之比明显更大，表明分子差异部分对整个电流传函的影响越小，所以ESO控制对动态电流分配不均有更强的抑制效果。用类似方法分析E1，可得到一致的结论：在中低频段，ESO控制时的E1幅值明显高于PI控制。

3" 实验验证与分析

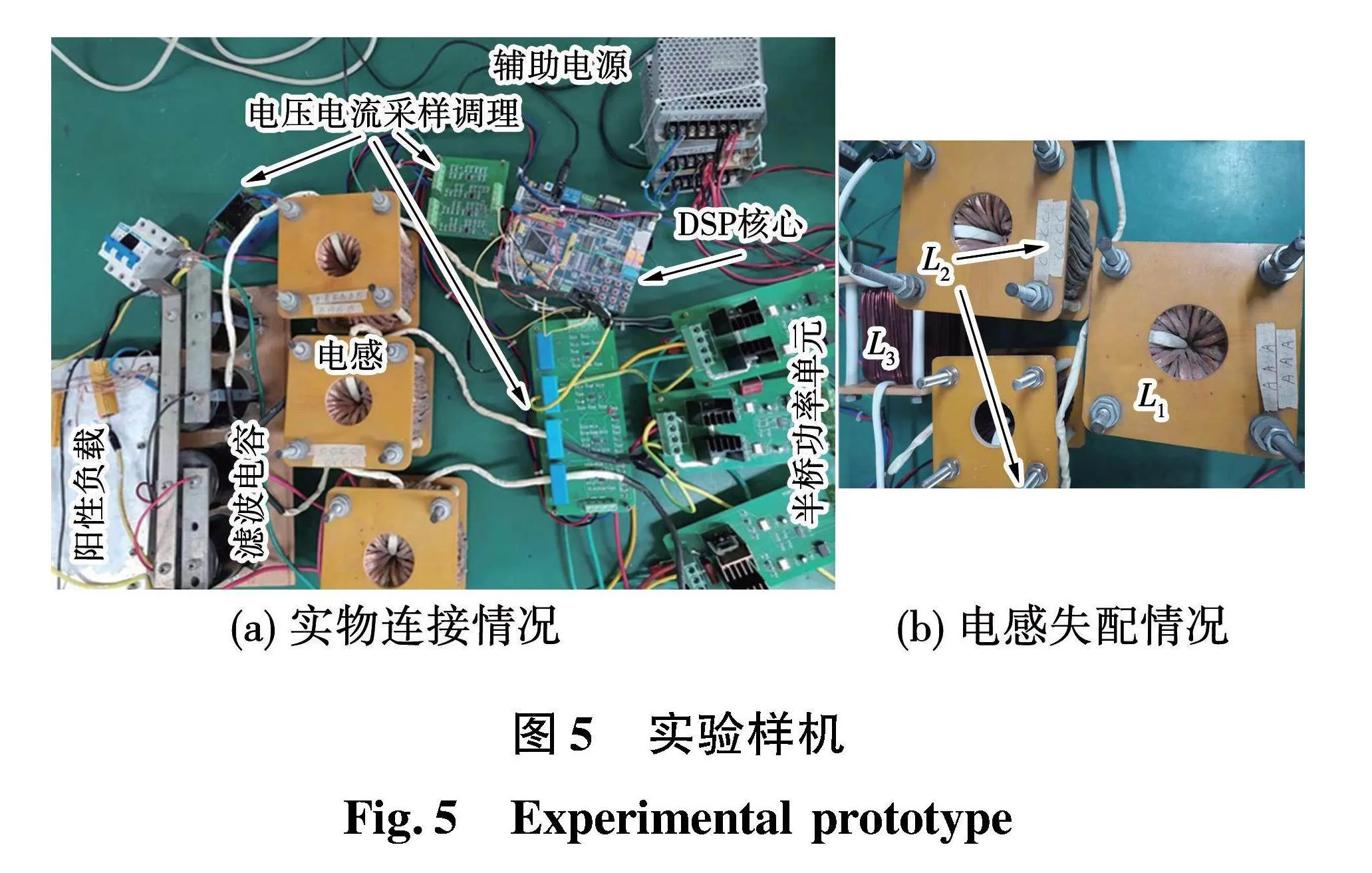
为验证控制策略的有效性，搭建额定功率200 W的三重化buck变换器，主要参数如表1所示，实物情况如图5（a）所示。以PWM驱动半桥单元的上桥臂，并借助下桥臂续流功能，可实现降压斩波输出。

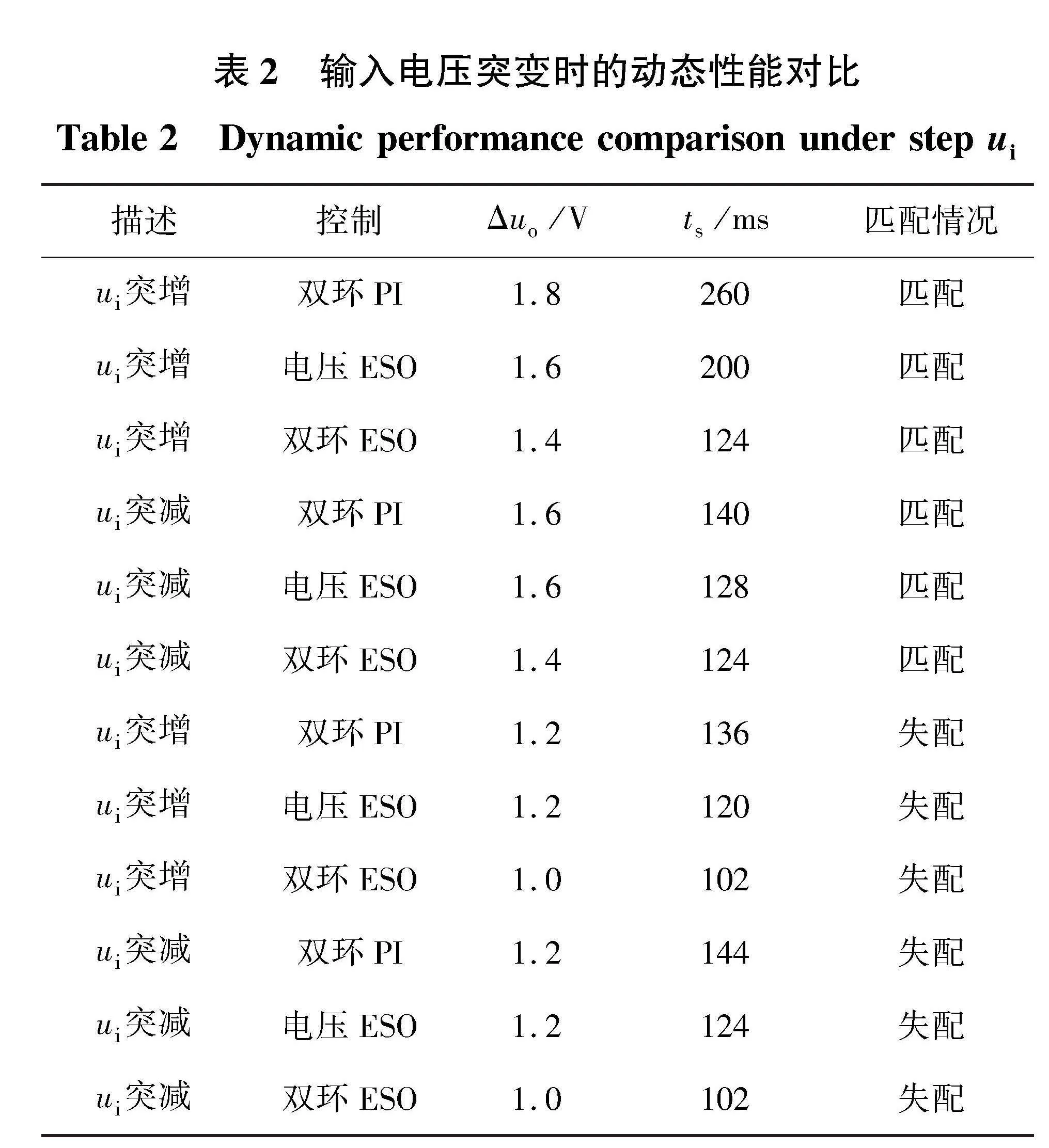
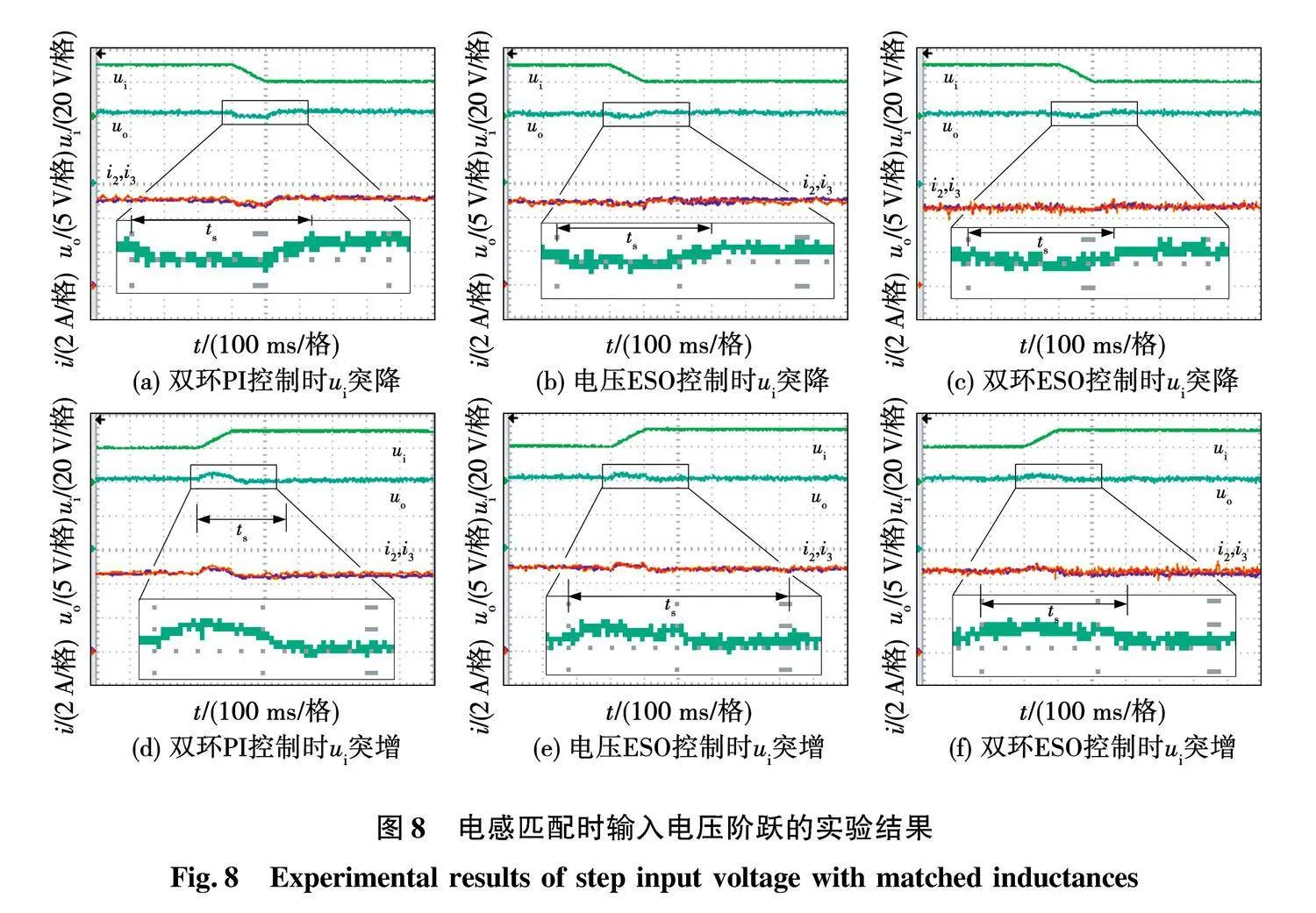
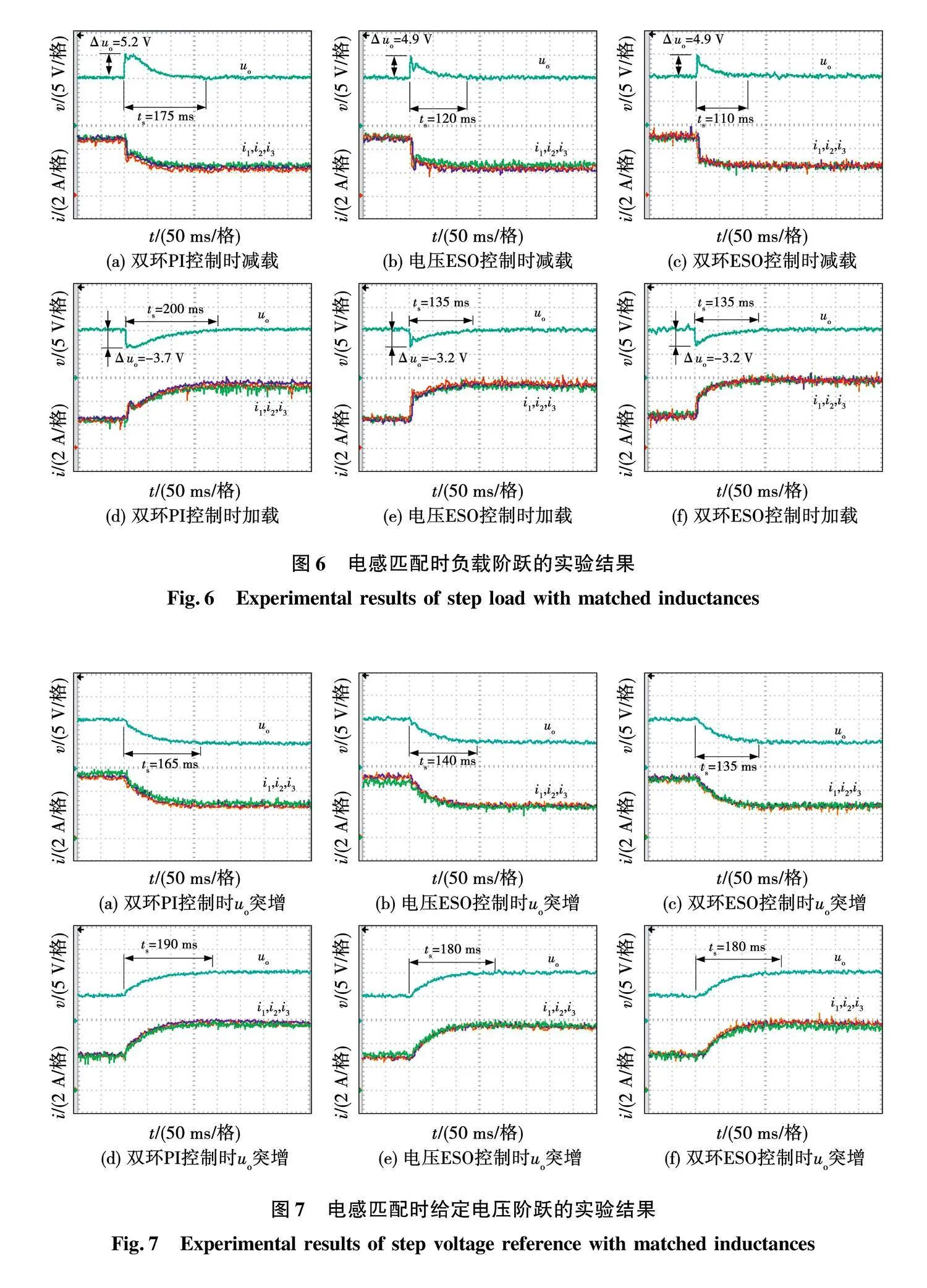
首先，使用2.1节的控制参数，进行电感参数匹配时的相关实验。采用双闭环PI，电压ESO及双闭环ESO控制时负载阶跃，给定电压变化及输入电压突变的暂态实验波形分别如图6、图7和图8所示。当ui突变时，将变换器的动态指标汇总，如表2所示，其中：Δuo代表uo最大变化量；ts代表调节时间。当负载和给定电压变化时，电压ESO与双闭环ESO两种方案下的暂态过程近似，效果相比双环PI有所改进。而遭遇ui变化时，各相电感电流平均值不变，所以引起的uo变化都不大。通过观察各波形下部局部放大图中的像素点数量来确定暂态过程中的Δuo和ts，其中每个像素点对应纵向刻度0.2 V，横向刻度4 ms。所提出的ESO电流内环扰动量中包含ui的信息，借助ESO的高观测带宽特性，相比于PI电流控制的积分型观测，可以加快观测器的收敛，继而闭环系统对输入电压的鲁棒性被进一步增强。如图8所示，双闭环ESO控制对ui扰动的抑制效果比电压ESO控制更强，可实现更小的Δuo及更短的ts。在ui突增时，Δuo减少0.2 V，ts减小76 ms，而ui突减时，Δuo减少0.2 V，ts减小4 ms。另外，由于各相电感参数匹配，所以在上述暂态过程中，三相电流相互之间差别不大，总和电感电流近似被动态均分。

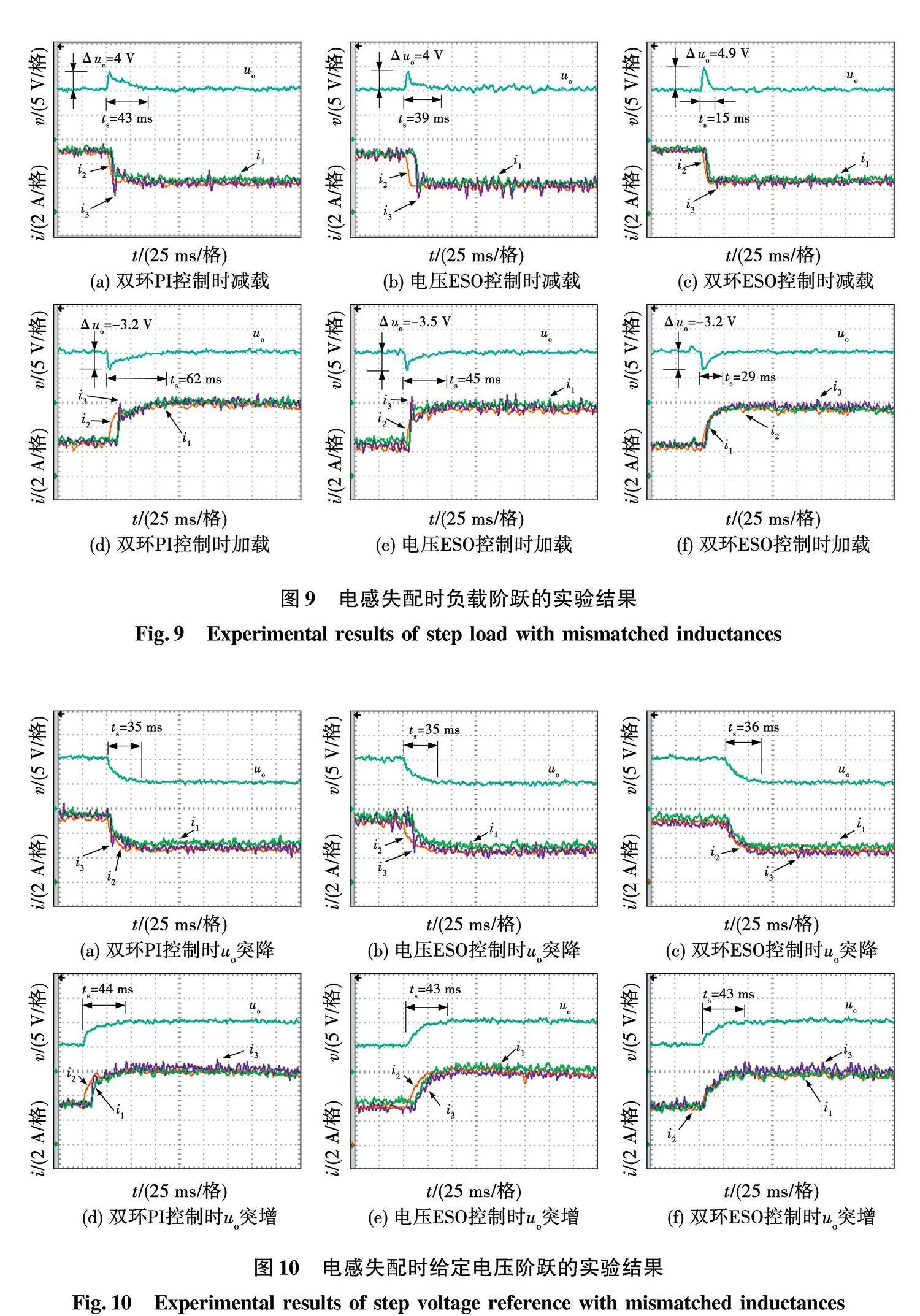
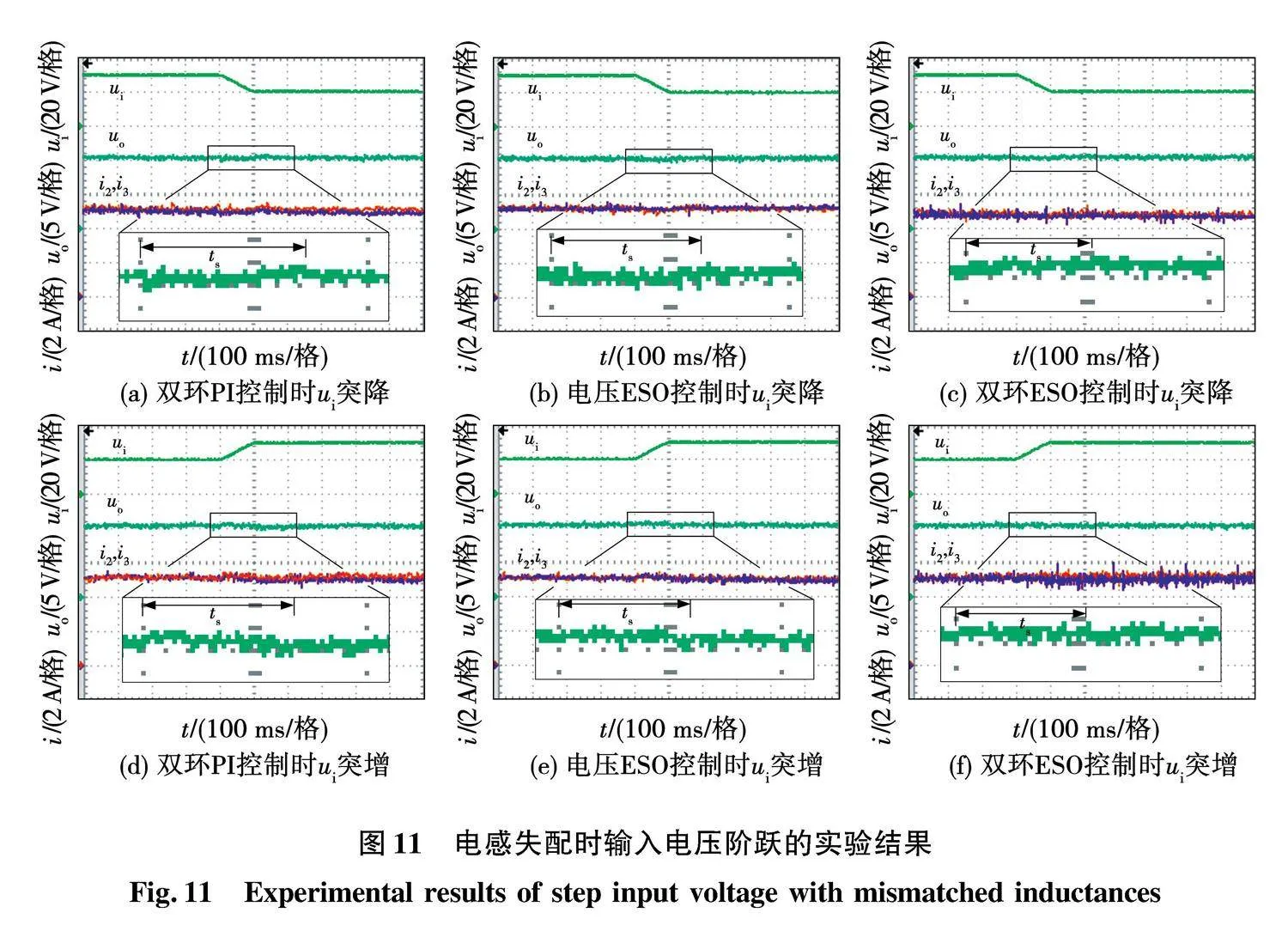
然后，进行电感失配时的相关实验，用6 mH和3 mH的2个电感串联组成新的L2，用3 mH电感替换原来6 mH电感作为新的L3，同时L1不变。以此来模拟电感失配的情况，如图5（b）所示。由于参数匹配时的控制参数选取以尽量避免超调量为参考，暂态过程不易出现电流尖峰，而为彰显 ESO型电流内环改善动态电流一致性的效果，适宜将其应用在有电流尖峰的场景。为此，缩小内外环带宽的差距，降低电流跟随性能。具体做法是：等倍数增大kpev和kpv以提高电压环带宽，同时也等倍数减小kpei和kpi以降低电流环带宽。PI积分系数的调整依旧遵循无超调的前提下尽量大。据此，调整后的电压环参数为：kpv=0.44，kiv=50，kpev=200 rad/s，ωov=400 rad/s。调整后的电流环参数为：kpi=0.04，kii=15，kpei=200 rad/s，ωoi=1 000 rad/s。3种控制方案的负载阶跃，给定电压变化及输入电压突变的暂态实验波形分别如图9、图10和图11所示。随着电压环控制带宽的提高，各控制方式下的电压动态性能均得到提升，ts明显减小，但内外环控制带宽的接近也造成彼此的影响加剧，一定程度恶化了电压和电流的调节质量，波动量有所增加。

当给定电压变化时，采用电压ESO与双闭环ESO时的暂态过程相近。由于外环扰动的观测器带宽明显高于电压环控制带宽，可以更快消除电压给定变化造成的影响，因而2种方案下输出电压的调节时间均稍短于双环PI。在暂态电流方面，各并联电路参数的不一致导致各电流内环的传递函数有所不同，而双环PI和电压ESO控制都采用PI电流调节器，对电路参数的敏感性高，因而在突变瞬间，三相电流便出现一定偏差，随后才逐渐趋于一致。而本研究采用ESO电流内环，电路参数失配带来的各电流内环扰动可被较高带宽的观测器分别且快速地估计出来，并通过各内环的比例调节器消除，所以各相电流在动态过程都保持良好的一致性。

当负载突减时，观测器的峰值现象导致uo的超调量有所增加，但也明显缩短了调节时间，而负载突增时，双环ESO控制下的uo跌落量并未增加，同时恢复时间有所缩短。电流方面，PI电流调节器应对参数失配的能力有限，导致双环PI和电压ESO控制的各相电流在负载增加和减少时均有较大偏差。相同条件下，电感量最小相的电流闭环主导极点距离虚轴最近，受扰动影响最大。因而该相所对应的i3，其变化最为剧烈，加载时最大峰值电流达6.5 A，造成电流尖峰，减载时电流最低下降至0.6 A，不利于变换器的可靠运行，而双环ESO控制可对电感失配情况进行实时观测，并通过比例调节器消除，有效抑制了参数偏差对电流模型的影响，动态均流效果较好，无明显超调。

当ui变化时，其引起的内环扰动量被高增益的电流环ESO快速观测出来，并在内环控制中消除。在外环调节器相同时，输入电压对变换器的影响被进一步弱化。具体说来，双环ESO控制的Δuo相比另两种方案均减小0.2 V。在ui突增和突减时的恢复时间方面，相比电压ESO控制，双闭环ESO控制的ts分别缩短了18 ms和22 ms。而与双环PI控制时相比，ts分别了缩短34 ms和42 ms，改进效果更加明显。与其他2种方案相比，双环ESO策略对ui扰动的抑制效果仍然最优。

相较于PI控制，所提策略也有控制参数增加和计算负担增加的不足。但实际上，通过将控制增益赋予初值，然后专注于调整控制带宽和观测带宽，控制复杂度的增加并不明显。另外，现今工业场合所用的微处理器通常性能强大，且具有较大的内存和闪存空间，大多情况下能够完成多相变换器内外闭环的实时计算任务，影响不很大。

4" 结" 论

为改善并联直流变换器在多干扰工况下的动态性能，本文提出了一种基于ESO的增强控制策略，优化了变换器的暂态性能。基于理论分析和实验波形，得出如下结论：

1）电流闭环主导极点与虚轴的距离，相比于PI电流控制时更远，提升了系统对输入电压的鲁棒性。而在电感参数失配时，减小了电流闭环传递函数的差异部分在中低频段对整个传递函数的影响，降低了各功率单元对电感参数失配的敏感度，继而改善了动态电流一致性。

2）PI电流控制以积分形式来观测内环扰动，观测误差的收敛速度较慢。而本文借助ESO高观测带宽的特点，缩短了扰动估计所需的收敛时间。在遭遇输入电压变化时，加速了输出电压的恢复过程，同时减小了暂态电压波动量。而在电感参数失配时，所提策略可快速估计各功率单元偏离额定工作点和名义电路参数的扰动情况，并通过各自的比例调节器及时消除，有效减少了动态电流偏差，抑制了电流尖峰。

3）所提策略具备一定的通用性，可推广至其他经典直流变换器，且未引入额外传感器，实现原理简单，具有较好的经济性和一定的工程应用价值。

参 考 文 献：

［1］" 王武，雷文浩，蔡逢煌，等. 结合电流应力优化的双有源全桥DC-DC变换器自抗扰控制［J］.电工技术学报， 2022， 37（12）：3073.

WANG Wu， LEI Wenhao， CAI Fenghuang， et al. Active disturbance rejection control of dual-active-bridge DC-DC converter with current stress optimization ［J］. Transactions of China Electrotechnical Society， 2022， 37（12）： 3073.

［2］" 李加明，任小永，周治成，等. 基于谐振网络优化的双向LLC-DCX多模块并联系统均流优化研究［J］.电工技术学报， 2023， 38（10）：2720.

LI Jiaming， REN Xiaoyong， ZHOU Zhicheng， et al. Research on current sharing optimization of bidirectional LLC-DCX multi-module parallel system based on resonant network optimization［J］.Transactions of China Electrotechnical Society，2023，38（10）：2720.

［3］" LU J， SAVAGHEBI M， GUAN Y， et al. A reduced-order enhanced state observer control of DC-DC buck converter ［J］. IEEE Access， 2018，6：56184.

［4］" 吴忠强，王云青，赵德隆，等. 基于ESO-Backstepping的直流微电网母线电压稳定控制［J］.电力系统保护与控制， 2020， 48（8）：112.

WU Zhongqiang， WANG Yunqing， ZHAO Delong， et al. Research on bus voltage stability control of DC microgrid based on ESO-backstepping ［J］. Power System Protection and Control， 2020， 48（8）：112.

［5］" ZHUO S， GAILLARD A， XU L， et al. Extended state observer-based control of DC-DC converters for fuel cell application ［J］. IEEE Transactions on Power Electronics， 2020， 35（9）： 9923.

［6］" 徐炅渊，赵晋斌，屈克庆，等. 计及线路阻抗匹配的混合储能系统均流控制［J］.电力电子技术， 2021， 55（8）：129.

XU Jiongyuan， ZHAO Jinbin， QU Keqing， et al. Current-sharing control of hybrid energy storage system considering line impedance matching ［J］. Power Electronics， 2021， 55（8）：129.

［7］" 李剑林，田联房，王孝洪，等. PWM整流器负载电流前馈控制策略研究［J］.电力电子技术， 2011， 45（11）：58.

LI Jianlin， TIAN Lianfang， WANG Xiaohong， et al. Study on load current feedforward control strategy for PWM rectifier［J］. Power Electronics， 2011， 45（11）：58.

［8］" 陈晔. 基于多相交错并联Buck电路的DVR控制技术研究［D］.哈尔滨：哈尔滨工业大学， 2019.

［9］" 姚川，阮新波，曹伟杰，等. 双管Buck-Boost变换器的输入电压前馈控制策略［J］.中国电机工程学报， 2013， 33（21）：36.

YAO Chuan， RUAN Xinbo， CAO Weijie， et al. An input voltage feedforward control strategy for two-switch buck-boost DC-DC converters ［J］. Proceedings of the CSEE， 2013， 33（21）：36.

［10］" 颜湘武，王杨，葛小凤，等. 双管Buck-Boost变换器的带输入电压前馈双闭环控制策略［J］.电力自动化设备， 2016， 36（10）：65.

YAN Xiangwu， WANG Yang， GE Xiaofeng， et al. Dual-loop control with input voltage feedforward for dual-switch buck-boost converter ［J］. Electric Power Automation Equipment， 2016， 36（10）：65.

［11］" 韩京清. 自抗扰控制器及其应用［J］.控制与决策，1998， 13（1）：19.

HAN Jingqing. Auto-disturbance rejection control and its applications［J］. Control and Decision， 1998， 13（1）：19.

［12］" GAO Zhiqiang. Scaling and bandwidth-parameterization based on control tuning［C］ // Proceedings of the 2004 American Control Conference， June 4-6， 2003， Denver， CO， USA. 2003： 4989-4996.

［13］" QU L， QIAO W， QU L. An enhanced linear active disturbance rejection rotor position sensorless control for permanent magnet synchronous motors ［J］. IEEE Transactions on Power Electronics， 2020， 35（6）：175.

［14］" 毛海杰，李炜，蒋栋年，等. 基于线性扩张状态观测器的永磁同步电机状态估计与性能分析［J］.电工技术学报， 2019， 34（10）：2155.

MAO Haijie， LI Wei， JIANG Dongnian， et al. State estimation and performance analysis based on linear extended state observer for permanent magnet synchronous motor ［J］. Transactions of China Electrotechnical Society， 2019， 34（10）：2155.

［15］" 孙振兴，李世华，张兴华. 基于扩张状态观测器和有限时间控制的感应电机直接转矩控制［J］.控制理论与应用， 2014， 31（6）：748.

SUN Zhenxing， LI Shihua， ZHANG Xinghua. Direct torque control of induction motor based on extended state observer and finite time control scheme ［J］. Control Theory amp; Applications， 2014， 31（6）：748.

［16］" 康尔良，吴炳道，禹聪. 基于LADRC控制的永磁同步电机无位置传感器研究［J］.电机与控制学报， 2023， 27（2）：69.

KANG Erliang， WU Bingdao， YU Cong. Research on sensorless of permanent magnet synchronous motor based on LADRC control ［J］. Electric Machines and Control， 2023， 27（2）：69.

［17］" LIU J， YIN Y， LUO W， et al. Sliding mode control of a three-phase AC/DC voltage source converter under unknown load conditions： industry applications ［J］. IEEE Transactions on Systems， Man， and Cybernetics： Systems， 2018， 48（10）：1771.

［18］" SUN D， SUN L， WU F， et al. Frequency inertia response control of SCESS-DFIG under fluctuating wind speeds based on extended state observers［J］. Energies， 2018， 11（4）：830.

［19］" 刘志坚，余成骏，梁宁，等. 基于扩张状态观测的双馈风机次同步振荡阻尼控制策略［J］.电机与控制学报，2023，27（7）：143.

LIU Zhijian， YU Chengjun， LIANG Ning， et al. Sub-synchronous oscillation damping control of DFIG based on expansion state observation ［J］. Electric Machines and Control， 2023， 27（7）：143.

［20］" 吴春，王超，郑露华. 基于PLL型扩张状态观测器的双惯量弹性伺服系统机械谐振抑制方法［J/OL］. 电工技术学报（2023-12-11）.https：//doi.org/10.19595/j.cnki.1000-6753.tces.231093.

WU Chun， WANG Chao， ZHENG Luhua. A mechanical resonance suppression strategy for two-inertia elastic servo systems based on PLL-type extended state observe ［J/OL］. Transactions of China Electrotechnical Society（2023-12-11）.https：//doi.org/10.19595/j.cnki.1000-6753.tces.231093.

［21］" 胡余生，李立毅，郭伟林，等. 磁悬浮制冷离心压缩机停机气流冲击抑制研究［J］.电机与控制学报，2022，26（1）：24.

HU Yusheng， LI Liyi， GUO Weilin， et al. Study on suppression of airflow impact during shutdown of magnetic suspension refrigeration centrifugal compressor ［J］. Electric Machines and Control， 2022， 26（1）：24.

［22］" RSETAM Kamal， CAO Zhenwei， MAN Zhihong. Cascaded-extended-state-observer-based sliding-mode control for underactuated flexible joint robot ［J］. IEEE Transactions on Industrial Electronics， 2020， 67（12）：10822.

［23］" 王军晓，戎佳艺，俞立. 直流降压变换器的降阶扩张状态观测器与滑模控制设计与实现［J］.控制理论与应用， 2019， 36（9）：1486.

WANG Junxiao， RONG Jiayi， YU Li. Design and implementation of reduced-order extended state observer and sliding mode control for DC-DC buck converter ［J］. Control Theory amp; Applications， 2019， 36（9）：1486.

［24］" BABAYOMI O， ZHANG Z. Model-free predictive control of power converters with cascade-parallel extended state observers［J］.IEEE Transactions on Industrial Electronics，2023，70（10）：10215.

［25］" 惠宇，池荣虎. 基于迭代扩张状态观测器的数据驱动最优迭代学习控制［J］.控制理论与应用， 2018， 35（11）：1672.

HUI Yu， CHI Ronghu. Iterative extended state observer based data driven optimal iterative learning control ［J］. Control Theory amp; Applications， 2018， 35（11）：1672.

［26］" 周雪松，王博，马幼捷，等. 含二阶扰动补偿的交错并联变换器自抗扰控制［J］.电机与控制学报， 2023， 27（12）：159.

ZHOU Xuesong， WANG Bo， MA Youjie， et al. Active disturbance rejection control of interleaving parallel converter with second-order disturbance compensation ［J］. Electric Machines and Control， 2023， 27（12）：159.

［27］" 孟建辉，吴小龙，张自力，等. 三相隔离型AC-DC-DC电源自适应线性自抗扰控制方法及纹波抑制补偿策略［J］.电工技术学报， 2023， 38（14）：3898.

MENG Jianhui， WU Xiaolong， ZHANG Zili， et al. Adaptive linear active disturbance rejection control method and ripple suppression compensation strategy for three-phase isolated AC-DC-DC power supply ［J］. Transactions of China Electrotechnical Society， 2023， 38（14）：3898.

［28］" 高崇禧，颜景斌，李学东，等. 脉冲负载下PWM整流器自适应线性自抗扰控制［J］.电机与控制学报， 2023， 27（1）：55.

GAO Chongxi， YAN Jingbin， LI Xuedong， et al. Adaptive active disturbance rejection control method of PWM rectifier under pulse load ［J］. Electric Machines and Control， 2023， 27（1）：55.

［29］" 陶珑，王萍，王议锋，等. 微电网低压接口变换器的参数寻优自抗扰控制［J］.电工技术学报， 2022， 37（16）：4202.

TAO Long， WANG Ping， WANG Yifeng， et al. Active disturbance rejection control with automatic optimization for low-voltage interface converter in microgird ［J］. Transactions of China Electrotechnical Society， 2022， 37（16）：4202.

［30］" ZENG Y， MASWOOD Ali， POU Josep， et al. Active disturbance rejection control using artificial neural network for dual-active-bridge-based energy storage system［J］.IEEE Journal of Emerging and Selected Topics in Power Electronics，2023，11（1）：301.

［31］" WANG Y， TAO L， WANG P， et al. Improved linear ADRC for hybrid energy storage microgrid output-side converter ［J］. IEEE Transactions on Industrial Electronics， 2022， 69（9）：9111.

［32］" LAKOMY K， MADONSKI R， DAI B， et al. Active disturbance rejection control design with suppression of sensor noise effects in application to DC-DC buck power converter ［J］. IEEE Transactions on Industrial Electronics， 2022， 69（1）： 816.

［33］" LU Y， XIAO W， LU D D C. Enhanced voltage regulation for PV power conversion using quasi-proportional resonant extended state observer ［J］. IEEE Journal of Emerging and Selected Topics in Industrial Electronics， 2023， 4（1）：70.

［34］" TAO L， WANG P， MA X， et al. Robustness optimization through modified linear active disturbance rejection control for high-voltage load interface in microgrid ［J］. IEEE Transactions on Industrial Electronics， 2023， 70（4）：3909.

［35］" GE Y， WANG Z， YANG Y， et al. Layout-dominated dynamic current balancing analysis of multichip SiC power modules based on coupled parasitic network model ［J］. IEEE Transactions on Power Electronics， 2023， 38（2）：2240.

［36］" L J， CHEN C， LIU B， et al. A dynamic current balancing method for paralleled SiC MOSFETs using monolithic Si-RC snubber based on a dynamic current sharing model ［J］. IEEE Transactions on Power Electronics， 2022， 37（11）： 13368.

［37］" 李山，赵瑜，郭强，等. 三相交错并联双向直流变换器无电流传感器均流控制［J］.高电压技术，2021，47（3）：894.

LI Shan， ZHAO Yu， GUO Qiang， et al. Sensorless current sharing control of three-phase interleaved bidirectional DC converter［J］. High Voltage Engineering， 2021， 47（3）：894.

［38］" DUAN M， DUAN J， SUN L. Sensorless current-sharing scheme for multiphase DC-DC boost converters ［J］. IEEE Transactions on Power Electronics， 2023， 38（2）： 1398.

［39］" 樊启高，卢禹卓，毕恺韬，等. 基于倍频采样的两相交错并联三电平双向直流变换器功率均衡解耦控制策略［J］.电工技术学报， 2022， 37（14）：3654.

FAN Qigao， LU Yuzhuo， BI Kaitao， et al. Decoupled power-balancing control strategy for two-phase interleaved parallel bidirectional DC converter based on frequency-doubling sampling ［J］. Transactions of China Electrotechnical Society， 2022， 37（14）：3654.

［40］" YAO Z， LAN Haogang， HE Xinyu， et al. Nonlinear inductor-based single sensor current balancing method for interleaved DC-DC converters ［J］. IEEE Transactions on Power Electronics， 2024， 39（4）：3996.

［41］" 黄桂根，王腾飞，王慧馨，等. 基于低带宽通信直流微网变换器自适应下垂均流技术研究［J］.机电工程，2016，33（5）：620.

HUANG Guigen， WANG Tengfei， WANG Huixin， et al. Research of adaptive droop current-sharing technique for DC micro-grid converters based on low-bandwidth communication［J］.Journal of Mechanical amp; Electrical Engineering，2016，33（5）：620.

［42］" THANH V， SU W. Improving current sharing and voltage regulation for DC microgrids：a decentralized demand response approach［J］.IEEE Transactions on Smart Grid，2023，14（4）：2508.

［43］" WANG H， HAN M， HAN R， et al. A decentralized current-sharing controller endows fast transient response to parallel DC-DC converters ［J］. IEEE Transactions on Power Electronics， 2018， 33（5）：4362.

［44］" 游江，孟繁荣，张敬南. 基于回路成形的并联DC/DC变换器均流控制器设计［J］.中国电机工程学报， 2019， 39（2）：585.

YOU Jiang， MENG Fanrong， ZHANG Jingnan. Loop-shaping based current sharing controller design for parallel DC/DC converters ［J］. Proceedings of the CSEE， 2019， 39（2）：585.

（编辑：刘琳琳）