基于蒙特卡洛树搜索的五子棋对弈算法研究

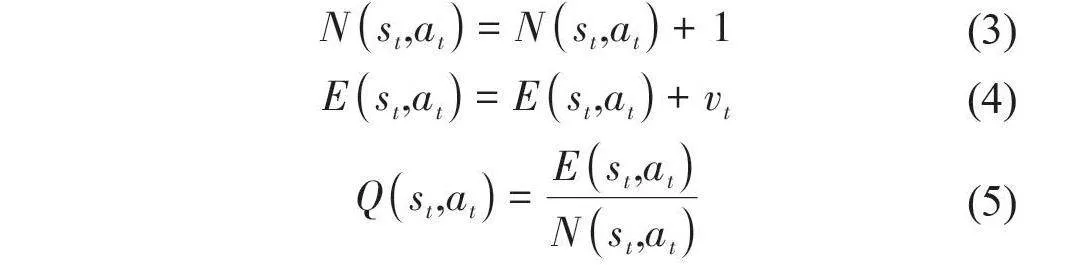
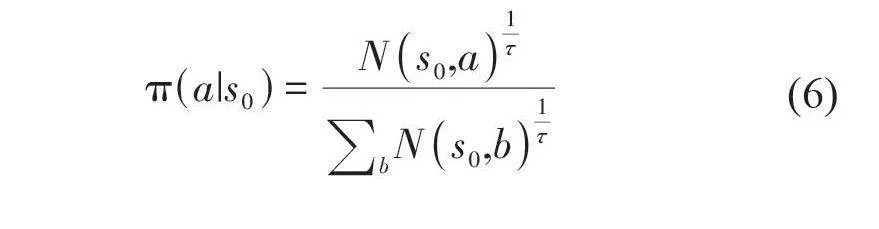
关键词：蒙特卡洛树搜索；策略价值网络；强化学习；五子棋；计算机博弈

中图分类号：TP389.1 文献标识码：A

文章编号：1009-3044（2024）18-0015-04

0 引言

人工智能（Artificial Intelligence，简称AI） 作为一门多领域交叉的学科，不仅对人类社会产生了深远的影响，同时也成为现代科学技术发展的重要方向之一。随着计算机算力的不断提高和机器学习技术的迅猛发展，AI在各个领域展现出了惊人的应用能力。其中，游戏博弈问题一直是人工智能研究的重要方向，各种经典游戏的AI算法发展也得到了广泛的关注和研究。

游戏博弈问题是在多方参与、基于策略决策的情境中，通过制定合理的行动策略来获取最优结果的一类问题。其研究核心是如何利用计算机在合理的时间内搜索到最佳策略，并将其应用于实际的游戏过程中[1]。AI在棋类游戏领域的研究颇具代表性，其中五子棋作为一种简单却又具有一定复杂性的游戏，一直是AI研究者关注的对象之一。通过研究五子棋的AI 算法，可以深入分析游戏规则，从而提高AI在其他复杂博弈问题上的应用能力。

蒙特卡洛树搜索（Monte Carlo Tree Search，简称MCTS） 是近年来在游戏博弈问题中备受瞩目的一种基于模拟的搜索算法。相较于传统的搜索方法，MCTS不依赖于先验信息，通过建立搜索树并通过模拟对树节点进行扩展和评估，从而找到最佳路径。由于其强大的扩展能力和对不完全信息的适应性，MCTS在各种博弈游戏中都取得了较好的效果，成为当前五子棋AI算法的主要研究方法之一。

1 相关工作与技术背景

1.1 传统游戏算法及其局限性

传统的游戏算法主要采用搜索树或博弈树的方法来解决游戏博弈问题。其中，最简单的是枚举法，即将所有可能的下法都进行尝试，并选择能够获得最优结果的下法。然而，随着游戏状态的复杂度增加，枚举法需要耗费大量的计算资源和时间。而且，枚举法只能处理局面较小的情况，在复杂的游戏中无法应对。

为了解决复杂游戏中的问题，一种常见的思路是使用启发式搜索算法。这些算法通过评估当前游戏状态的好坏来选择下一步的行动，如最大最小值搜索（Minimax） 和Alpha-Beta剪枝。然而，这些算法在面对复杂游戏时依然存在一定局限性。由于游戏树的复杂度指数级增长，搜索空间很难完全覆盖。此外，传统算法对于不完全信息的处理也存在困难，无法应对隐蔽的对手策略。

1.2 基于深度学习的游戏算法

近年来，深度学习技术在AI领域取得了巨大的突破，对游戏博弈问题也产生了重要影响。基于深度学习的游戏算法通过训练神经网络来学习游戏规则和策略，能够从大量的游戏数据中提取特征，并自动调整策略。

在围棋领域，基于深度学习的算法已经取得了一些重要突破。例如，AlphaGo算法通过深度卷积神经网络和强化学习相结合的方式，战胜了多次世界冠军，并向全世界展示了人工智能在复杂游戏中的强大实力。然而，基于深度学习的算法依赖于大量的训练数据和高算力的计算资源，对训练过程中的数据获取和计算效率要求较高。

1.3 蒙特卡洛树搜索与其他算法在五子棋领域的对比

蒙特卡洛树搜索（MCTS） 是一种基于模拟的搜索方法，通过建立搜索树并模拟对树节点进行扩展和评估，从而找到最佳路径[2]。与传统搜索算法相比，MCTS 具有更好的扩展能力和对不完全信息的适应性。

在棋类领域，基于蒙特卡洛树搜索的算法已经取得了显著成果。AlphaGo中的MCTS算法就是其中的一种典型应用。该算法通过对游戏状态进行模拟和评估来选择最优的落子位置。与其他算法相比，MCTS并不依赖于先验知识，具有更好的适应性和鲁棒性。

然而，MCTS仍然存在一些挑战和限制，例如对游戏状态的搜索效率和时间成本较高，以及对搜索深度的选择问题。此外，在具体问题中，不同的参数选择和策略变化可能会导致不同的结果。因此，深入研究和分析MCTS算法在五子棋领域的应用，优化算法参数和策略选择，对于提升AI五子棋算法的性能至关重要。

2 系统设计过程

2.1 蒙特卡洛树搜索设计

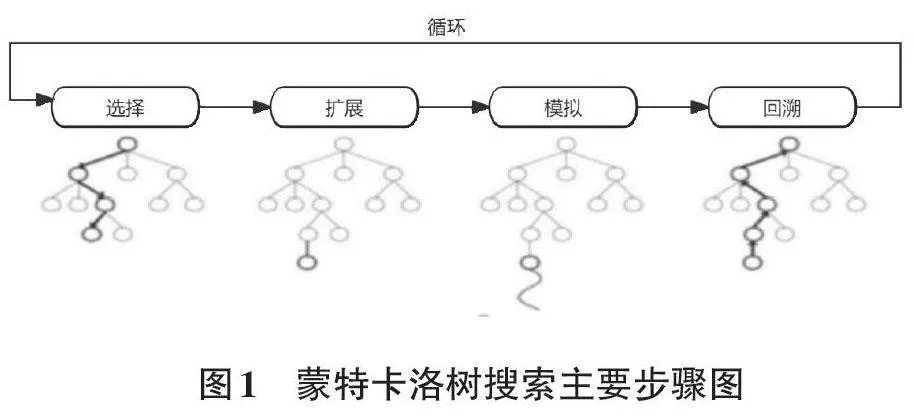
蒙特卡洛树搜索（MCTS） 是一种在不完全信息游戏中寻找最优决策的算法，通过大量随机模拟来估算动作的价值。MCTS如图1所示，包含4个主要步骤：选择（Selection） 、扩展（Expansion） 、模拟（Simulation） 和回溯（Backpropagation） 。

2.1.1 选择阶段

流程图如图2 所示，对于MCTS内部已经出现过的局面，我们会选择由公式（1） 得出的基于当前状态棋盘状态s 下的Q + U 值最大的a 作为下一步要执行的落子动作[3]。其中Q 为当前节点的评估值，称为开发组件，即当前节点的平均行为价值，是一个0到1之间的值，简单地说，这就是动作a 在从状态s开始执行游戏（模拟步骤）并首先选择该动作时的胜率估计。U则是探索组件，它由公式（2） 得出，其中c 为超参数，用来决定探索程度及其权重，搜索树会在这个值较大时趋向于向未模拟过的落子点探索，在其较小时则会快速收敛。P 为深度神经网络策略输出的对应动作a的先验概率，N （s，b）为根节点的访问次数，N （s，a）为当前访问的叶节点的访问次数。

这种搜索方式最初会倾向于选择先验概率P 较大以及访问次数N（s，a）较小的节点。经过多次选择之后，将逐渐倾向于选择平均行为价值Q 较高的点。通过一直选择动作a 直至棋局结束，如果到达的节点是尚未结束的蒙特卡洛搜索树叶子节点，则进行下一阶段的操作。

2.1.2 展开与评估阶段

对于第一次访问到的叶子节点，通过深度神经网络预测来输出当前叶子节点下所有合法走子动作a 以及其先验概率p，并将这些可能的新节点加入蒙特卡洛搜索树中。同时，初始化这些访问次数N、累计行动价值E、平均行动价值Q 以及先验概率值等信息。

2.1.3 回传阶段

在评估完成后将新叶子节点分支的信息依次向根节点回溯，并更新每一层祖先节点分支上的访问次数N、累计行动价值E、平均行动价值Q，具体的更新公式如下：

2.1.4 执行阶段

在蒙特卡洛树搜索结束后，模型就可以根据公式（6） 计算根节点S下的落子概率分布。其中，τ参数用于调节探索程度，在（0，1]区间内变化。当τ接近1时，采样行为趋向于模拟蒙特卡洛树搜索（MCTS） 的原始采样；而当τ接近0时，采样行为更偏向贪心策略，即优先选择拥有最多访问次数N的动作。为防止在τ值较低时直接计算N的τ次方根可能引发的数值问题，计算动作概率前，我们先对访问次数N进行微调（增加一个极小值1e-10） ，然后取其对数并与1/τ相乘，最后通过一个经过简化的softmax函数转换成概率值。这样处理在数学上与原公式有着相似的效果。

2.2 神经网络设计

AlphaGo Zero 使用了庞大的卷积神经网络，通过20 到 40 个残差网络模块处理棋盘状态，随后分别通过两层或三层网络产生策略和价值输出，使得整个网络的层数达到 40 层乃至超过80层[4]。这样的设计既需要大量的计算资源，也十分耗时。因此，本研究根据五子棋算法的需求，大幅简化了其网络结构。

2.2.1 网络结构设计

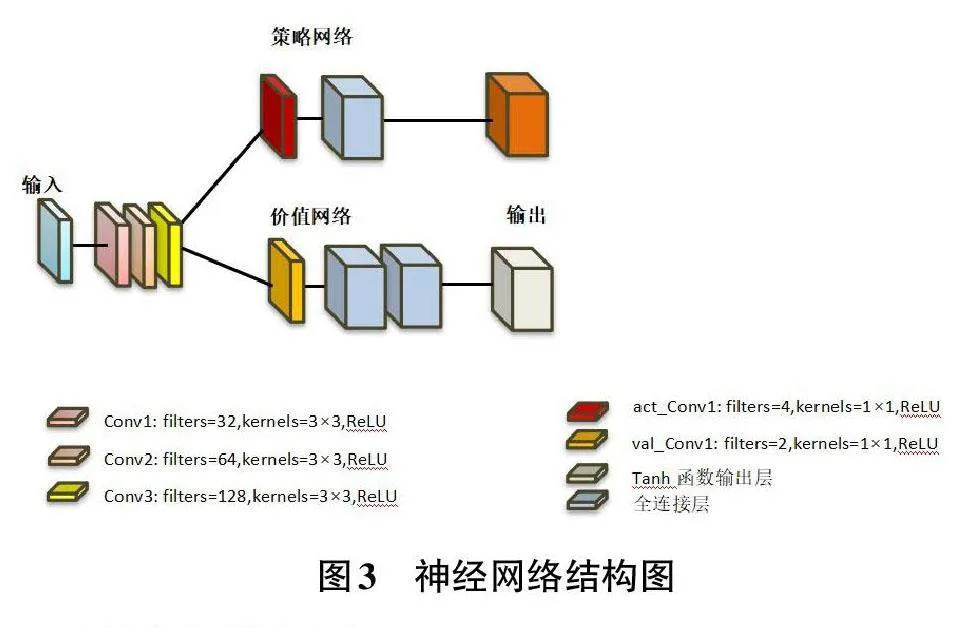
网络结构设计如图3所示。输入是一个具有四个通道的棋盘状态，每个通道代表不同的信息（当前玩家的棋子位置、对手的棋子位置、对手最后落子位置和一个表示当前玩家的指示层）。首先，通过三个卷积层（conv1、conv2、conv3） 处理输入。这些层用于提取棋局状态的特征。每层卷积后接一个 ReLU 激活函数，用于增加非线性。

第一个卷积层将输入的四个通道转换为 32 个特征映射。

第二个卷积层将 32 个特征映射转换为 64 个。

第三个卷积层将 64 个特征映射转换为 128 个。

然后将网络分为策略网络层和价值网络层两个输出：

在策略网络层这端，首先使用含有4个1×1 卷积核的卷积层act_Conv1进行降维，从共享特征中提取与行动策略相关的特征。然后接一个全连接层act_fc1，将策略卷积层的输出转换为棋盘上每个位置的行动概率的对数形式。使用softmax函数进行激活，确保输出的概率分布。

在价值网络层这端，首先通过含有2个1×1卷积核的卷积层val_Conv1进行降维，从共享特征中提取与棋局价值相关的特征。接下来，两个全连接层val_fc1 和 val_fc2 将价值卷积层的输出逐步转换成一个标量值，这个值通过 tanh 激活函数进行缩放，以表示当前棋局状态对于当前玩家胜利的概率估计。这个值的范围是 [-1， 1]，其中 1表示当前玩家肯定胜利，-1表示肯定失败。

2.2.2 损失函数组成

损失函数由价值损失（Value Loss） 以及策略损失（Policy Loss） 两部分组成。价值损失（Value Loss） 使用均方误差（Mean Squared Error， MSE） 损失来评估网络预测的棋局价值（x_val） 与真实棋局价值（win⁃ner_batch） 之间的差异。价值损失旨在使网络能够准确预测当前棋局状态的胜负情况。公式表示为：

Value Loss = MSE （x_val，winner_batch） （7）

策略损失（Policy Loss） 使用交叉熵损失来评估网络预测的行动概率分布（log_act_probs） 与通过蒙特卡洛树搜索得到的目标行动概率分布（mcts_probs） 之间的差异。策略损失旨在优化网络的策略输出，使其更接近最优策略。公式表示为：

Policy Loss =-mean（sum（mcts_probs×log_act_probs，axis = 1）） （8）

总损失是价值损失和策略损失之和，可表示为：

Total Loss=Value Loss+Policy Loss （9）

2.2.3 损失函数优化

使用Adam优化器来最小化组合损失。在优化过程中还引入了L2 正则化项[5]，用于减少过拟合的风险。L2正则化项会惩罚权重参数的平方，促使模型学习到更平滑的权重，从而提高模型的泛化能力。通过这种方式，模型在训练过程中通过不断调整网络参数来减少总损失，从而学习到预测棋局价值和选择最佳行动策略的能力。

3 算法实现与运行效果

3.1 设置游戏规则进行自我对弈

在本研究中，设置了一个9×9的棋盘进行五子棋比赛，每次下棋前执行 400 次蒙特卡洛树搜索。实验设计了两种智能体：最佳玩家（best-player） 和当前玩家（current-player） 。最佳玩家通过自我对弈来积累经验数据，并利用目前为止表现最好的神经网络模型。而当前玩家则在最佳玩家积累的经验基础上，对其神经网络进行再训练，并挑战最佳玩家。如果当前玩家赢了，最佳玩家会采用当前玩家的神经网络，为下一轮迭代做准备。

实验初期，利用蒙特卡洛树搜索策略进行自我对弈，以收集初始的棋盘数据。在初期五子棋的自我对弈中，由于缺乏神经网络的引导，下棋策略完全是随机选择，导致这批收集到的数据在棋技方面相对较弱。

3.2 训练神经网络生成模型

在第一阶段中，通过自我对弈收集的棋局数据被用作神经网络的训练材料。对于棋盘状态的表示，采用矩阵形式，其中如果轮到黑方下棋，黑棋位置标记为 1，其余位置（包含白棋和空位）标记为 0；若轮到白方下棋，则白棋位置标记为 1，其余位置（包含黑棋和空位）标记为 0。利用这种转换方法可以有效地将棋盘状态转化为神经网络可处理的输入格式。为了提高模型的泛化能力，还采用了数据增强技术（如旋转和翻转棋盘），这样可以从不同的视角学习相同的游戏局面。

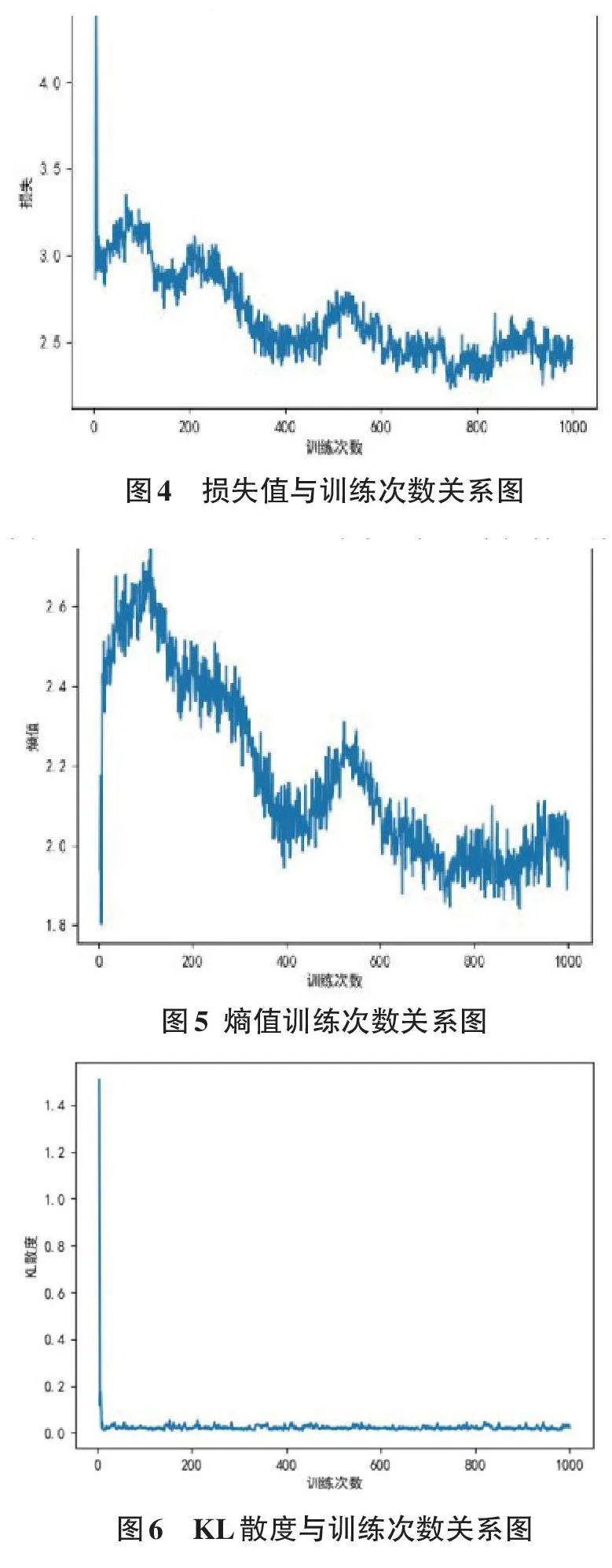
使用经过初步训练的神经网络模型，最佳玩家（best-player） 继续进行自我对弈，以收集更多棋局数据。训练过程中，网络的参数会根据损失函数进行调整，损失函数用来衡量模型预测与实际结果之间的差异。损失值随训练次数的变化如图4所示。损失值包括策略损失和价值损失两部分。策略损失用来衡量网络输出的动作概率分布与蒙特卡洛树搜索得到的概率分布之间的差异；而价值损失用来衡量网络预测的游戏结果与实际游戏结果之间的差异[6]。

除了损失函数，训练过程中的另外两个重要参数是熵值（entropy） 和 KL 散度（KL divergence） 。熵值表示模型输出分布的不确定性或混乱度。高熵值表明模型输出的概率分布较为均匀，而低熵值则表示模型输出倾向于某几个确定的结果。图5显示了熵值与训练次数的关系。从图5中可以看出，随着训练次数的增加，模型越来越倾向于输出某几个胜率高的落子动作。

KL散度衡量的是策略更新前后输出分布之间的差异。数值越小，表示更新后的策略与更新前的策略更为接近。图6显示了 KL散度与训练次数的关系。

在这一迭代过程中，神经网络的学习目标是不断调整其参数，使得网络输出的落子概率分布和实际的胜利策略更为接近，同时确保对局结果的估计值与实际胜方的对应误差最小化。这通过最大化策略向量与搜索概率的匹配度以及减少估计值与真实赢家之间的误差来实现。

3.3 评估神经网络模型

如图4所示，每隔一定训练批次评估经过最新训练的策略价值网络的表现，确定是否采用这个新策略作为当前最佳策略。评估通过比赛形式实现，让当前玩家（current_player） 与拥有最优神经网络模型的最佳玩家（best_player） 进行10局五子棋对决，每赢一局得1分。累计双方的得分，若current_player 的总分超过best_player，则将best_player 的神经网络模型更新为current_player的模型，进而开始新一轮的迭代过程。整个流程通过循环执行上述步骤，AI 在自我对弈的基础上不断学习和进步，同时通过持续的评估确保了学习过程的有效性和方向的正确性，最终训练出一个强大的五子棋 AI 玩家。

3.4 博弈水平检测

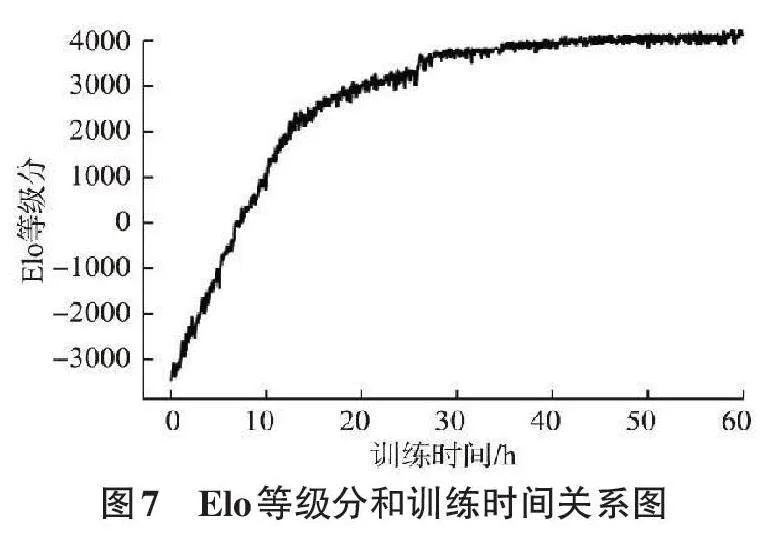
在本次研究中，我们采用了 Elo等级分制度来衡量五子棋算法的技术水平[7]。图7展示了训练时长与Elo评分之间的关系。结果显示，经过大约40小时的训练后，该算法的 Elo 评分达到约4000分，明显超越了一般人类玩家的水平。

4 总结

本研究基于蒙特卡洛树搜索（MCTS） 与策略价值网络相结合的方法，设计并实现了一种五子棋对弈算法。通过深度学习技术和自我对弈的方式，算法能够不断学习和优化，实现了较高水平的棋局策略和决策能力。实验结果表明，该算法在五子棋对弈中表现出了较强的竞争力和适应性，能够与人类玩家进行高水平的对弈。

在设计过程中，策略价值网络的引入为蒙特卡洛树搜索提供了更准确的先验知识，使得搜索过程更加高效和目标明确。通过不断的自我对弈和学习，网络能够逐渐提升其对棋局的理解和预测能力，从而提高了对弈算法的整体表现。此外，本研究还探讨了不同的网络结构、搜索策略和训练方法对算法性能的影响，为未来相关研究提供了有价值的参考。

5 展望

尽管本研究取得了一定的成果，但仍有许多潜在的改进空间和研究方向。未来的研究可以从以下几个方面进行深入：

1）网络结构和训练方法的优化。通过探索更先进的神经网络结构和训练技术，进一步提升策略价值网络的性能和效率，例如利用卷积神经网络（CNN） 的深层特征提取能力和循环神经网络（RNN） 处理序列数据的优势。

2）搜索策略的改进。对蒙特卡洛树搜索算法进行优化，如采用更高效的剪枝技术和探索/利用平衡策略，以提高搜索的精度和速度。

3）多样化训练数据。通过引入更多样化的训练数据和对弈场景，提升模型的泛化能力和适应不同对手的能力。

4）算法的泛化与应用。探索算法在其他棋类游戏或决策制定领域的应用，验证其泛化能力和实用价值。