浅层模型剪枝对准确率及计算量变化探究

关键词：剪枝；浅层网络；粒度控制；模型准确率；模型计算量

中图分类号：TP183 文献标识码：A

文章编号：1009-3044（2024）18-0011-04

近年来，深度学习在多个领域相较于传统算法展现了巨大的性能提升，广泛应用于计算机视觉领域[1-3]。然而，由于深度学习具有参数量庞大、计算复杂的特点，它在嵌入式环境中的应用受到阻碍。为降低深度神经网络进行推理所需的运算量，研究者提出了多种算法，其中剪枝算法因其显著减少参数量和运算量的特性而备受关注。

剪枝算法首先对神经网络参数或连接的重要程度进行评估，然后删除其中最不重要的参数或连接，使其不参与最终的运算。最基本的两种剪枝方式是非结构化剪枝[4-7]和结构化剪枝。非结构化剪枝只考虑单个参数的影响，不考虑修剪对整个网络结构的影响，文献[4-7]就是典型的非结构化剪枝。这种剪枝类型着眼于剪枝粒度控制，聚焦于更精细化的剪枝，在相同稀疏性下往往可以得到更好的准确率。随后的剪枝研究常聚焦于与硬件的协同设计，注重约束控制，实际推理能力有所提升，但在相近稀疏性下的准确率表现往往不如传统非结构化剪枝。因此，该文以准确率变动为主要评价因素之一，选择传统的非结构化剪枝作为比对对象。

同时，在剪枝算法的研究中，由于浅层网络的剪枝可能会导致准确率的大幅下降，一些剪枝算法在剪枝时会经验性地忽视浅层网络的剪枝或对浅层模型的剪枝做特殊处理。例如，文献[8]中，作者将剪枝后的恢复训练过程分为两段：第一段训练除了第一层以外的所有层，不对第一层网络进行处理；第二段则单独训练第一层，以获得更高的准确率。又如文献[9] 中，作者直接将第一层的参数剔除出实际的剪枝序列，以减少准确率的下降。然而，这些文章对浅层处理都是基于经验性的判断，虽然指出了对浅层网络剪枝会带来准确率的显著下降，并对其做了特殊处理或将浅层网络剔除出剪枝序列，但并未分析浅层网络剪枝导致准确率下降的原因。

此外，它们忽视了浅层网络剪枝对降低模型运算量的益处。在相同剪枝率的条件下，进行浅层网络剪枝的模型能够降低更多的运算量，而剪枝前后模型计算量减少量也是剪枝算法的重要评判指标。该文通过对浅层剪枝率的人工调整，可在有限范围内寻求准确率下降和计算量减少之间的平衡，以取得更好的实际效果，更贴合实际需求。

通过这两种基于传统剪枝算法的pzZXxlGfTqCQlaan/ruBqw==理念变化，针对不同的实际任务需求，本文提出的算法可以从浅层网络的剪枝粒度控制方向选择更优的算法，而不再仅仅在稀疏度方向寻求任务需求的契合。

该文接下来的结构如下：第1章分析了浅层网络剪枝敏感性的成因和浅层网络剪枝对计算量减少的影响，并据此分别提出了忽略浅层网络剪枝和提高浅层网络剪枝率的剪枝算法。而注重浅层剪枝、不对浅层剪枝做特殊处理、忽视浅层剪枝这三种思路的总体比较则在第2章中展示和分析。最后，第3章对全文进行了总结与展望。

据此，该文的主要贡献总结为以下三点：

1） 探究了浅层网络剪枝对准确率的影响。详细分析了浅层网络对剪枝敏感的原因，从而可以在剪枝前预见性地判断出哪些卷积层的剪枝会对网络模型准确率产生重要影响。据此研究，可以事先推断出剪枝序列中哪些层应当被忽视，以达到更优的准确率，并事先决定具体的剪枝策略，而无须依赖经验性的数据来决定将哪些层的参数剔除出剪枝序列。

2） 探究了浅层网络剪枝对计算量的影响。阐释了为什么在相同剪枝率下，浅层网络剪枝能够降低更多运算量的原因。基于此研究，本文提出了一种人工增大浅层网络剪枝率以降低模型运算量的算法，并对算法成效进行了验证。

3） 基于不同任务需求的剪枝策略选择。通过这两种不同的算法，可以从浅层网络剪枝的粒度控制领域，针对不同的任务需求合理选择适合的算法与模型。如果任务需求较高的准确率，则可以采取忽视浅层网络剪枝的策略；如果任务需求较低的计算量，则可以采取增大浅层网络剪枝率的策略。

1 浅层网络剪枝研究

1.1 忽略浅层网络的剪枝研究

在计算机视觉领域，浅层网络的主要作用是对图像进行最初的特征提取，即对经过预处理的图像数据进行初次处理。浅层网络的运算结果直接影响了后续的特征提取环节，因此对浅层网络的权重进行剪枝会对后续网络中所有依赖于该权重数据的特征提取环节产生影响。

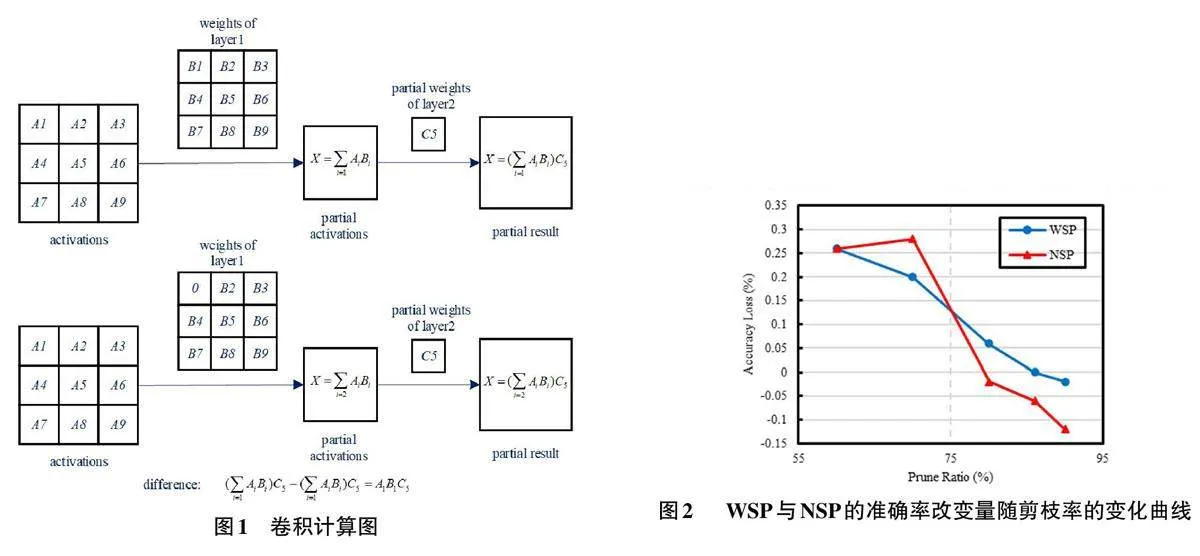
具体到卷积神经网络（CNN） 的运算机制，浅层网络中的数据变动会影响其后相应的深层网络的运算结果，其影响范围通常大于深层网络数据变动的范围。如图1所示，上一层单个权重B1的变动会使得下一层的运算结果产生difference的幅度变化。随着网络深度的增加，浅层权重带来的变动对整个网络的影响也会随之累积并放大，其影响范围会远大于深层网络的权重变动。

在卷积层进行卷积运算时，浅层网络的单个权重参与的运算次数高于深层网络。以VGG16为例，其卷积层运算不会缩小特征图的尺寸，这一功能由池化层提供。因此，输入特征图的尺寸从浅层到深层呈不严格递减关系。第一层池化层前的卷积层处理的输入特征图具有最大的尺寸，卷积核需要进行滑动运算的次数也最多。因此，尽管浅层网络的权重量往往较少，但单层的总运算量与深层网络相比并不低，而且浅层一个权重的操作所影响的数据量大于深层权重的操作量。假设输入VGG16模型的图像初始尺寸为224×224像素，那么第一层卷积层中的一个卷积核需要进行224×224次滑动运算，而最后一层卷积层的一个卷积核仅需进行较少次数的滑动运算。

鉴于上述两点原因，网络模型的浅层表现出更大的剪枝敏感性。换句话说，模型剪枝敏感性高的成因并不是浅层网络本身导致的，而是由于浅层网络的权重数据往往参与了大量的运算，并且对后续数据运算有很大的影响。

具体到模型而言，以VGG16为例，其前两层（即第一个block） 是剪枝敏感性最大的两层卷积层，这两层处理的输入特征图的尺寸最大，且影响后续所有深层网络的运算。基于此，通过将这两层的权重数据剔除出剪枝序列，可以在剪枝后提高模型的准确率。

本文从ImageNet数据集中任意选择了100类作为数据集，采用标准的带有BN层的VGG16网络模型，根据两种剪枝策略进行剪枝并进行仿真分析。图2展示了随剪枝率变化时，正常的非结构化剪枝与忽视前两层的浅层剪枝这两种剪枝策略对应的模型准确率变化曲线。本文将传统的非结构化剪枝简写为NSP（No-Structuring-Pruning） ，将忽视浅层的剪枝称为WSP（Without-Shallow-Pruning） 。在图中，横轴代表模型的剪枝率，即有多少权重被剪枝不参与实际运算，而纵轴代表剪枝后模型的准确率与剪枝前模型的准确率的差值。

关于在稀疏性较低的情况下，准确率反而上升的一种解释是剪枝找到了正确的网络容量节点，从而减少了过拟合。因此，主要观测曲线的后半段，即当准确率出现明显下降时，两种剪枝策略所造成的影响。图中的曲线表明：在具有较高稀疏性的情况下（模型准确率变动明显时），在相近的剪枝率下，经NSP剪枝后的模型准确率低于经WSP剪枝后的模型准确率。

仿真结果表明了研究的正确性，即根据事先对模型结构的观测，可以预见性地确认不同层的剪枝敏感性，并根据哪些层剪枝敏感性更高的信息，将这些层的权重数据剔除出剪枝序列，从而直接避免这些层参与剪枝流程，更好地贴合部分任务对更高准确率的需求。

1.2 增大浅层剪枝率的剪枝研究

在1.1节中，该文说明了在单个权重的运算量方面，浅层网络的单权重运算量显著高于深层网络的单权重运算量。同样以VGG16为例，假设输入特征图的尺寸为224×224像素，图3展示了各层的总运算量对比，图4展示了各卷积层的单个权重所参与的运算次数对比。

统计结果表明，在一个剪枝程序中，人为地增大浅层网络权重的修剪比例，同时降低深层网络权重的修剪比例，使程序聚焦于浅层网络的修剪，可以在相近的全局剪枝率条件下减少更多的计算量。在该例中，减去一个权重，如果该权重位于Conv1，它能减少50 176次的运算量；但如果该权重位于Conv6，它仅能减少144次的运算量。

因此，剪枝时可以通过增大浅层剪枝率而降低深层剪枝率的策略，使得模型在相近的剪枝率下能够减少更多的运算量。本文提出一种可行的剪枝率选择策略如下：

通过这种方式，可以人工保证剪枝率变动前后，模型的全局剪枝率相近。此处剪枝率与各层的参数量相乘可能并非整数值，因此实际剪枝时需进行相应取整操作，使全局剪枝率趋近但不一定完全相等。

在该例中，选择采取增大前四层的修剪比例的策略的理论支撑是图5中得到的数据。如果需要更换网络模型结构，增大修剪比例的层的选择策略应根据相应的单权重运算量统计图表进行变动。

通过这种算法，可以得到任意剪枝率的增大浅层网络剪枝率的模型，本文将该算法称为SAP（Shallow-Attention-Pruning） 。

同样以ImageNet中选取的100类数据作为数据集，模型超参数与1.1保持一致。图5展示了WSP与SAP算法减少的计算量比例随剪枝率的变化曲线。从图中可以看出，采用SAP的方法可以在相近的剪枝率下减少更多的计算量。

浅层网络是否参与剪枝及其剪枝程度实际上取决于每一项任务的需求。如果一项任务的主要需求是在同等剪枝率下保持高准确率，那么应将浅层网络权重数据排除在剪枝序列之外；如果一项任务的主要需求是在同等剪枝率下降低计算量，则应在条件允许的范围内（如允许的准确率下降范围内）加大浅层网络权重数据的剪枝率。

2 实验结果及算法性能分析

上文提出了两项对于浅层剪枝的研究，并根据研究结果提出了两种剪枝算法：WSP和SAP，分别代表忽视浅层网络权重剪枝和着重浅层网络权重剪枝的两种策略。本文还分析了这两种剪枝算法对准确率和计算量的影响及其成因。在图6和图7中，综合展示了NSP、WSP、SAP三种算法对准确率和计算量的影响。

图中表明，采取WSP剪枝策略允许模型在高剪枝率情况下有更小的准确率损失，而采用SAP剪枝策略的模型在高剪枝率情况下则会伴随更大的计算量减少。例如，在图6中，在稀疏性近90%（即非零参数量降低近90%） 的剪枝后模型中，采用WSP算法剪枝的模型相较于不剪枝的模型几乎没有性能损失，而采用传统的非结构化剪枝会有约0.1%的性能衰减，采用SAP算法的剪枝模型的性能衰减率达到0.2%。从图7 中可以发现，采用SAP算法的剪枝模型在相近的稀疏性下能减少的计算量也是最多的。

由此可见，采用不同的剪枝方式可以实现不同的剪枝目标：在高稀疏性的情况下，如果对准确率有较高要求且对计算量要求较低，则可以考虑采用WSP算法；如果对计算量的减少需求较高，则可以采用SAP 算法；如对计算量和准确率均有相应需求，则可以考虑不做特殊处理，即采用NSP算法。

3 总结与展望

本文探讨了两种不同于传统非结构化剪枝（NSP 算法）的剪枝策略，这两种策略着眼于是否对浅层网络权重进行剪枝。浅层网络在此定义为处理输入特征图尺寸较大的卷积层。WSP算法将浅层网络的数据剔除出剪枝序列，在相近全局剪枝率的条件下具有最高的准确率；SAP算法则专注于浅层网络的剪枝，致力于增大浅层网络的剪枝率，在相近全局剪枝率的条件下减少了更多的计算量。本文还对经过三种剪枝策略后的模型进行了综合分析，说明了针对不同的任务需求，剪枝策略的选取方法。

本文后续的工作将主要围绕在具体的硬件平台上执行研究。此外，将该研究应用在结构化剪枝上也是下一步需要重点研究的方向。