关于数形结合思想在初中数学解题中的应用探究

【摘要】数形结合思想是一种常见的数学思想方法，是指将数学问题中的数量关系与几何图形相结合［1］，它在初中数学解题中应用十分广泛.本文结合实例探究数形结合思想在初中数学问题中的解题思路，与读者交流探讨.

【关键词】初中数学；数形结合；解题应用

初中学生的数学思维还不够成熟，对抽象的数学问题理解起来较为困难.数字与图形的结合可以帮助学生快速理解，得出答案［2］.因此，初中数学教师应重视引导学生数学思想的形成，在解题教学中潜移默化地向学生灌输数形结合思想，切实提高学生的数学分析能力和解题能力，为学生应对中考提供有利的保障.

1 数形结合思想在函数中的应用

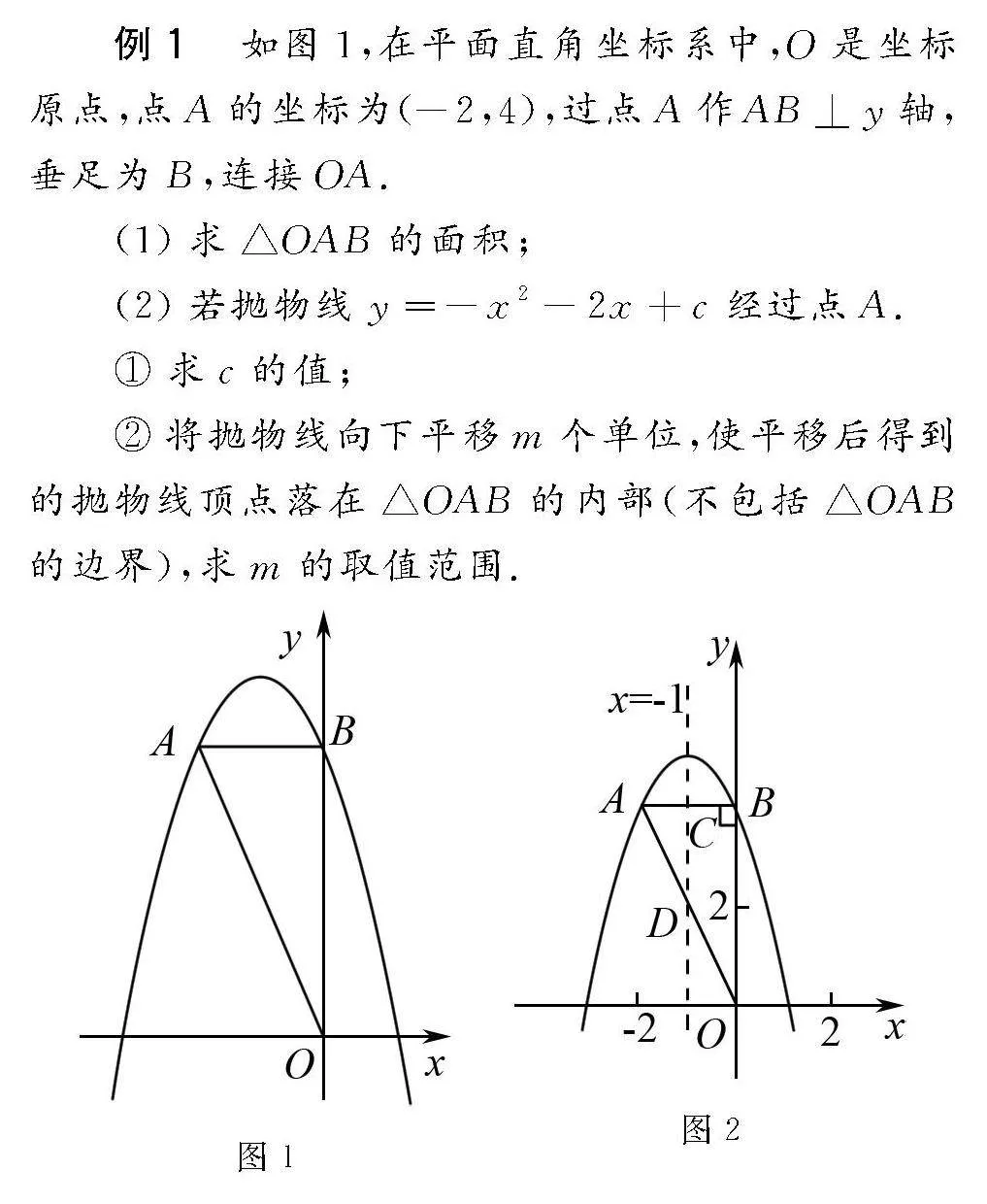
例1 如图1，在平面直角坐标系中，O是坐标原点，点A的坐标为（-2，4），过点A作AB⊥y轴，垂足为B，连接OA.

（1）求△OAB的面积；

（2）若抛物线y=－x2－2x+c经过点A.

①求c的值；

②将抛物线向下平移m个单位，使平移后得到的抛物线顶点落在△OAB的内部（不包括△OAB的边界），求m的取值范围.

图2

思路分析 第一问，根据点A的坐标确定AB、OB的长度，即可求出三角形的面积；第二问，第一小问，根据题意求出抛物线中的未知常数项c，第二小问，需先求出抛物线的顶点坐标，然后向下平移抛物线，确定需要求的点的坐标，进而得出m的取值范围.

解析 （1）因为点A的坐标为（-2，4），

AB⊥y轴，

所以AB=2，OB=4，

所以S△OAB=12×AB×OB=12×2×4=4.

（2）①因为抛物线y=－x2－2x+c经过点A，

把点A代入y=－x2－2x+c中，

得4=－（－2）2－2×（－2）+c，

所以c=4.

②由①得出，y=－x2－2x+4.

因为y=－x2－2x+4=－（x+1）2+5，所以抛物线y的顶点坐标为（-1，5）.

结合图形，开始向下移动抛物线，可以得出当抛物线顶点位于AB的中点时，它在△OAB的边界，继续向下移动抛物线，开始落在△OAB的内部；当移动到OA的中点时，抛物线顶点位于△OAB的边界，继续向下移动抛物线，不再满足落在△OAB内部的条件，如图2.所以求出AB的中点坐标、OA的中点坐标即可求出m的取值范围.

经计算AB的中点坐标为（－1，4），OA的中点坐标为（－1，2），

所以m的取值范围为1＜m＜3.

评析 本题主要考查二次函数的综合应用以及数形结合思想，是中考试题中一种常考的题型，学生要重点掌握，注意细节.

2 数形结合思想在不等式中的应用

例2 如果x=1，y=2是关于x、y的方程（ax+by－12）2+ax－by+8=0的解，求不等式组x-a＞13x+14bax-3＜x+3的解集.

思路分析 解题时，应先将方程的解代入方程，然后利用非负数的性质求出常数的值，最后代入不等式组求解集即可.

解析 因为x=1，y=2是关于x、y的方程（ax+by－12）2+ax－by+8=0的解，

所以（a+2b－12）2+a－2b+8=0，

由非负数的性质可知，a+2b－12=0，

且a－2b+8=0，

联立上式a+2b-12=0a-2b+8=0，

解得a=2b=5，

将a=2b=5代入不等式组得

x-2＞13x+1452x-3＜x+3

化简得8x＜－24x＜6，

解第一个不等式得x<－3，

解第二个不等式得x<6，画出数轴（如图3），

所以不等式的组得解集为x<－3.

评析 这道题考查了方程解的定义、非负数的性质以及不等式组的解法等知识点，难度中等，在中考中很常见，学生要掌握其解题方法和步骤，利用数形结合的思想，求解不等式或不等式组的解集.

图4

3 数形结合思想在几何中的应用

例3 如图4，在Rt△ABC中，斜边AB的长为35厘米，边长为12厘米的正方形CDEF内接于△ABC，求△ABC的周长为多少厘米？

思路分析 此题文字表述少，考查学生的知识储备情况.解此题的关键是利用相似三角形和勾股定理分别得到一个等式，组合得到一元二次方程组，最后，解一元二次方程组即可.

解析 设BC=a，AC=b，

在Rt△ABC中，AB=35cm，

根据勾股定理得出，a2+b2=352=1225 ①.

由题意知，正方形CDEF内接于△ABC，

所以∠AFE=∠ACB，∠A=∠A，

所以Rt△AEF∽Rt△ABC，

所以EFBC=AFAC，即12a=b－12b，

经化简得到12b=a（b－12），

即12（a+b）=ab ②，

联合①②，得出a2+b2=1225，12（a+b）=ab，，

结合计算可得到（a+b）2=1225+24（a+b），

将a+b看成一个整体，

利用十字相乘法解一元二次方程可得

［（a+b）－49］［（a+b）+25］=0，

解得a+b=49或a+b=－25（舍去），

所以△ABC的周长为a+b+35=49+35=84（厘米）.

评析 这道题考查了相似三角形的判定、勾股定理以及解一元二次方程的方法等知识，是一道综合性很强的题.解题时要注意应用数形结合的思想，方便理解和整理思路.

4 结语

数形结合思想是初中数学学习中最重要的数学思想之一，它是从数量和图形两个方面来解决数学问题.本文主要研究数形结合思想在函数、不等式以及几何这些数学问题中的应用，实践表明，在初中数学解题过程中，教师要重视学生数学思想的培养，尤其是数形结合思想，它可以帮助学生快速且准确的解决数学问题，提高解题效率，为学生养成良好的思维习惯奠定基础，为中考提供有利的保障［3］.

参考文献：

［1］王丽娟.初中数学教学中渗透数形结合思想的策略［J］.家长，2023（26）：22-24.

［2］辛艳，高丽.初中数学教学中如何渗透数形结合思想［J］.新智慧，2023（21）：80-82.

［3］刘媛.核心素养视域下初中数学渗透数形结合思想的策略［J］.试题与研究，2023（21）：97-99.