数形结合：可视化演绎“数与运算”的一致性

作者简介：单广红，江苏省淮安市浦东实验小学特级教师，正高级教师。

课题项目：本文系江苏省教育科学“十四五”规划2021年度课题“基于‘童化’视域的小学数学镶嵌式学习研究”的阶段性研究成果。课题编号：D/2021/02/324。

摘要：“数与运算”的一致性主要包括数概念的一致性、运算意义的一致性、算理算法的一致性。在课堂教学中落实“数与运算”的一致性，需要教师在一定的学习时段灵活、统筹安排。在第二学段学习完整数除法单元内容后，教师可以设计“整数四则运算再认识”一课的教学，引导学生理解整数四则运算在算理和算法上的一致性。

关键词：数形结合；数与运算；一致性；算理；算法

《义务教育数学课程标准（2022年版）》（以下通称“新课标”）指出：“数的运算教学应注重对整数、小数和分数四则运算的统筹，让学生进一步感悟运算的一致性。”“数与代数”领域包括“数与运算”和“数量关系”两大学习主题。“数与运算”是一个较为庞大的话题体系，包括三个方面：数概念的一致性、运算意义的一致性、算理算法的一致性。整数、小数、分数等数概念及其运算学习内容零散分布在各学段，跨度较大，需要教师灵活统整教学内容，让学生打通“数概念”与“数运算”内部之间的“隔断”，自主迁移经验。在第二学段学习完整数除法单元后，教师可以设计“整数四则运算zu4JickG1GQkUYjrLCevJ1T7dJ9ZaaxuT8q+AJixBJc=再认识”一课的教学，引导学生理解整数四则运算在算理和算法上的一致性。

一、感受加减法相同计数单位的简单线性增减

加法是将不同两部分或几部分合并在一起的运算。减法、乘法、除法都是由加法衍生而来的。整数加法是四则运算的基础，需要学生理解透彻其算理和算法，然后类比迁移到其他运算中。

（一）整数计数：建构计数直观模型的十进制原理

数是对数量的抽象，认数的目的是解决计算问题。计数本身就是加法运算，如238是由2个百、3个十和8个一组成的，其实就是200 + 30 + 8 = 238，相邻计数单位之间因存在“十进制”的特殊关系而产生了特定的“位值”。

<E：＼2023田田＼7-20＼辽宁教育·教研版202407＼LJ24-13-1.psd>

计数：2个百、3个十和8个一合起来是238。

计算：200 + 30 + 8 = 238。

为了数数方便，由“一个一个地数”到“一群一群地数”，整数计数便成为关于计数单位的加法运算。因此，对数概念的学习基础直接影响到数运算的算法算理理解。整数的计数单位有个、十、百、千、万等，每个计数单位都对应着一个数学模型。常用的数学模型有小棒、小正方体、小方块、计数器等，在小学阶段呈现的最大的可视化计数单位数学模型是由小正方体拼成的“万”，更大的单位则需要依据基本的计数单位去抽象推理。为了方便沟通“数与运算”的一致性，本文均选用平面方块图作为图例。

（二）整数加法：掌握启蒙计算图式的可视化表达

小学阶段的学生对算理理解的表象水平一般用三种图式表示：实物图式、半抽象图式和符号图式。在教学中，教师要给足时间让学生对算理进行可视化表达，使其能准确进行互译解读。例如，在“整数四则运算再认识”的课始，教师可以唤醒学生的加法算理。

师：请用你喜欢的方式表示“371 + 54”的计算过程。

生：我用估算，371 ≈ 380，54 ≈ 50，它们的和大约是四百。

生：我是用口算计算的，1 + 4 = 5，70 + 50 = 120，300 + 120 + 5 = （300 + 100） + 20 + 5 = 425。

生：我是通过贴方块图来计算的。

<E：＼2023田田＼7-20＼辽宁教育·教研版202407＼LJ24-13-12.psd>[4][2][5]

生：我画了数位图。

<E：＼2023田田＼7-20＼辽宁教育·教研版202407＼LJ24-13-13.psd>

生：我是用竖式计算的，[ 3 7 1+ 1 5 4 4 2 5]。

师：仔细观察，你有什么发现？

生：相同计数单位上的数相加。

生：哪一位满“十”，就要向前一位进“1”。

生：通过方块图和数位图可以清楚地看出，十位满十向百位进“1”的过程。

师：整数加法是把相同计数单位上的数相加。这个过程可以写成371 + 54 = 3（百） + 7（十） + 1（一） + 5（十） + 4（一） = 3（百） + （7 + 5）（十） + （1 + 4）（一） = 3（百） + 1（百） + 2（十） + 5（一） = 425。

加法算理是最基础的算理，是四则运算以及其他所有运算的启蒙，对加法算理的理解在学生的整个运算中起着至关重要的作用。很多教师在教学中对计数比较重视，突出讲解，但在计算中却弱化了对计数单位的关注。在教学“数概念”与“数运算”两个内容时，很多教师存在“脱节”现象，多数计算教学会停留在运算技能上，采用竖式，按计算法则一位一位地相加，最后导致一部分学生只能快速计算出结果，却不清楚算理。因此，在阶段整理复习时，教师可以进行梳理，引导学生发现多位数加法和计数道理一样，仍然先计算分别有多少个计数单位，再通过“十进制”的计数原理得出结果。这既是对学习经验的激活，又是对前期存在的短板进行弥补。

（三）整数减法：关注逆向思维逻辑的进阶式生长

减法是加法的逆运算，教师可以引导学生把研究整数加法的方法结构迁移运用到整数减法算理学习中。数学学习不仅要把每一类的学习方法研究透，还要把各种方法之间的关联之处提炼出来。

师：计算“371 - 54”，用多种方式表示思考过程。

生：我用了四种方法（见下页图）。

师：观察这几种方法，你又有什么发现？

生：只有相同数位计数单位相同，才可以相减。

生：不够减时要从前一位退“1”，然后在本位加10后再减。

师：和加法相比，它们有什么共同点？

生：也是只有相同的计数单位才能计算。

师：计算过程可以写成371 - 54 = 3（百） + 7（十） + 1（一） - 5（十） - 4（一） = 3（百） + （6 - 5）（十） + （11 - 4）（一） = 3（百） + 1（十） + 7（一） = 317。

教师引导学生用可视化的方法表达加、减法的算理：相同的计数单位相加减。抽象的计数单位如实物一样有“形”可依，学生在计算过程中只有在脑中抽象出每个计数单位对应的数学模型，才能克服“数”与“运算”的割裂现象，有效实现“数”与“运算”的一致性。在多种图式的表达中，教师要引导学生特别重视方块图的掌握与应用。通过方块图，学生能从视觉“形”上感受到“单位相同”，不同计数单位有大小之分，是“一类”的才能相加，同时也是后续小数与分数算理研究的关键数学模型，便于演绎整数、小数、分数之间算f01d5d342a0d93baad4a55100fe93418理和算法的一致性。数位图类似于计数器，但优于计数器，计数器每位受10颗珠的限制，数位图可以任意画○的个数，借助方块图，沟通数位图和竖式之间的联系，最后形成规范的竖式，进行抽象的数学符号表达。

二、探究乘法计算与乘积计数单位的二维变化规律

乘法是加法的简便运算。整数乘法的算理，在教材中一般是通过实物情境进行研究的，用数学模型来解释的例子较少。因为教材中没有样例，所以教师教学时操作起来很困难，容易忽略对乘法算理的探究，直接教给学生计算步骤。如果要体现与整数加、减法算理的一致性，教师不妨也引导学生借助方块图表达算理思路，感受其比数位图有明显的优势。

（一）多位数乘法算理分享与图谱模型构建

教师要引导学生在计算中对照实物与图形，归纳出具有代表性的乘法数学模型。下面以“三位数乘两位数”为例来阐述。

师：请大家计算“12 × 128”，并用自己喜欢的方式表达思考过程。

生：我用口算128×10 = 1280，128 × 2 = 256，1280 + 256 = 1536。

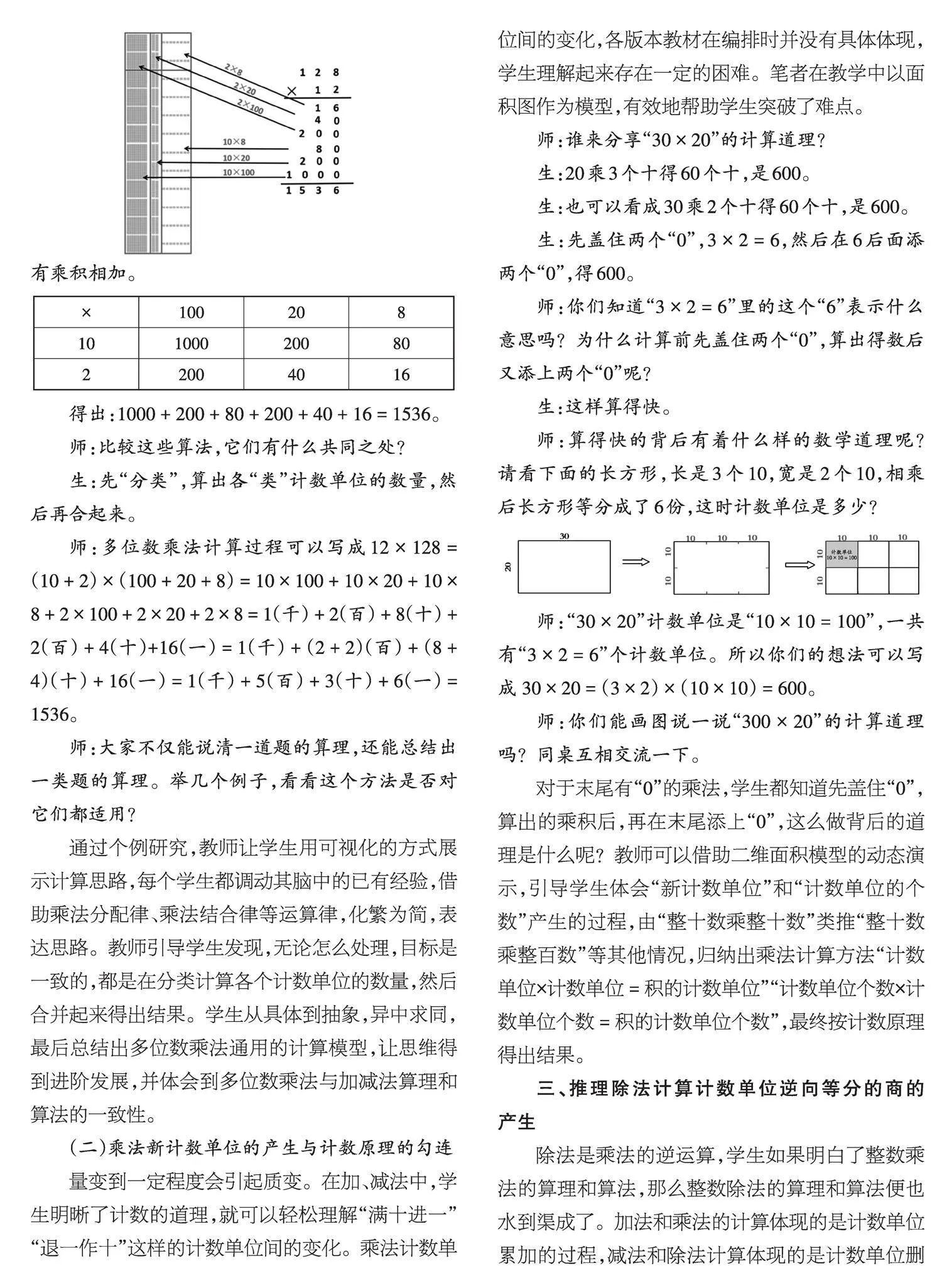
生：个位“8”乘12得96个一；十位“2”乘12得24个十；百位“1”乘12得12个百；最后三积相加得1536。

<E：＼2023田田＼7-20＼辽宁教育·教研版202407＼LJ24-13-18.psd>

生：我是用三位数乘两位数，这样更简便。个位“2”乘128得256个一；十位“1”乘128得128个十；然后两积相加结果也是1536。

<E：＼2023田田＼7-20＼辽宁教育·教研版202407＼LJ24-13-19.psd>

生：把这两个分步过程叠放在一起，可以看出每一步的计算过程。

<E：＼2023田田＼7-20＼辽宁教育·教研版202407＼LJ24-13-20.psd>

师：他的方法还可以做成“面图谱”。

生：还可以用表格表示出任意的两个多位整数相乘的方法，把两个乘数分别按计数单位拆分，列成表格，把两两相乘的积记录在相交的格里，最后把所有乘积相加。

[× 100 20 8 10 1000 200 80 2 200 40 16 ]

得出：1000 + 200 + 80 + 200 + 40 + 16 = 1536。

师：比较这些算法，它们有什么共同之处？

生：先“分类”，算出各“类”计数单位的数量，然后再合起来。

师：多位数乘法计算过程可以写成12 × 128 = （10 + 2） × （100 + 20 + 8） = 10 × 100 + 10 × 20 + 10 × 8 + 2 × 100 + 2 × 20 + 2 × 8 = 1（千） + 2（百） + 8（十） + 2（百） + 4（十）+16（一） = 1（千） + （2 + 2）（百） + （8 + 4）（十） + 16（一） = 1（千） + 5（百） + 3（十） + 6（一） = 1536。

师：大家不仅能说清一道题的算理，还能总结出一类题的算理。举几个例子，看看这个方法是否对它们都适用？

通过个例研究，教师让学生用可视化的方式展示计算思路，每个学生都调动其脑中的已有经验，借助乘法分配律、乘法结合律等运算律，化繁为简，表达思路。教师引导学生发现，无论怎么处理，目标是一致的，都是在分类计算各个计数单位的数量，然后合并起来得出结果。学生从具体到抽象，异中求同，最后总结出多位数乘法通用的计算模型，让思维得到进阶发展，并体会到多位数乘法与加减法算理和算法的一致性。

（二）乘法新计数单位的产生与计数原理的勾连

量变到一定程度会引起质变。在加、减法中，学生明晰了计数的道理，就可以轻松理解“满十进一”“退一作十”这样的计数单位间的变化。乘法计数单位间的变化，各版本教材在编排时并没有具体体现，学生理解起来存在一定的困难。笔者在教学中以面积图作为模型，有效地帮助学生突破了难点。

师：谁来分享“30 × 20”的计算道理？

生：20乘3个十得60个十，是600。

生：也可以看成30乘2个十得60个十，是600。

生：先盖住两个“0”，3 × 2 = 6，然后在6后面添两个“0”，得600。

师：你们知道“3 × 2 = 6”里的这个“6”表示什么意思吗？为什么计算前先盖住两个“0”，算出得数后又添上两个“0”呢？

生：这样算得快。

师：算得快的背后有着什么样的数学道理呢？请看下面的长方形，长是3个10，宽是2个10，相乘后长方形等分成了6份，这时计数单位是多少？

<E：＼2023田田＼7-20＼辽宁教育·教研版202407＼LJ24-13-2.psd>[计数单位

10 × 10 = 100]

师：“30 × 20”计数单位是“10 × 10 = 100”，一共有“3 × 2 = 6”个计数单位。所以你们的想法可以写成 30 × 20 = （3 × 2） × （10 × 10） = 600。

师：你们能画图说一说“300 × 20”的计算道理吗？同桌互相交流一下。

对于末尾有“0”的乘法，学生都知道先盖住“0”，算出的乘积后，再在末尾添上“0”，这么做背后的道理是什么呢？教师可以借助二维面积模型的动态演示，引导学生体会“新计数单位”和“计数单位的个数”产生的过程，由“整十数乘整十数”类推“整十数乘整百数”等其他情况，归纳出乘法计算方法“计数单位×计数单位 = 积的计数单位”“计数单位个数×计数单位个数 = 积的计数单位个数”，最终按计数原理得出结果。

三、推理除法计算计数单位逆向等分的商的产生

除法是乘法的逆运算，学生如果明白了整数乘法的算理和算法，那么整数除法的算理和算法便也水到渠成了。加法和乘法的计算体现的是计数单位累加的过程，减法和除法计算体现的是计数单位删减的过程。

（一）三位数除以一位数算理探究

例如，有437本课外书平均分给3个班，每个班能分到多少本？还多出几本？

师：谁来说一说你的思考过程？

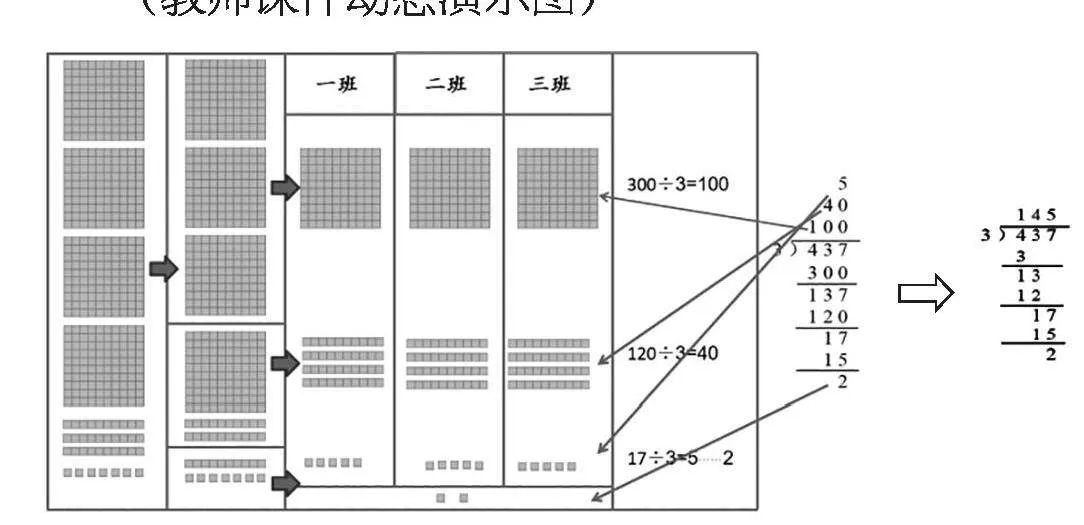
生：我用口算的方法，因为300 ÷ 3 = 100，120 ÷ 3 = 40，15 ÷ 3 = 5，17 - 15 = 2，所以437 ÷ 3 = 145……2。

生：我用分小方块图的方法来计算。

（教师课件动态演示图）

<E：＼2023田田＼7-20＼辽宁教育·教研版202407＼LJ24-13-22.psd><E：＼2023田田＼7-20＼辽宁教育·教研版202407＼LJ24-13-23.psd>

师：这个过程可以用这样的竖式表示出来。会简写这个竖式吗？请对照图说说理由。

生：因为3个百除以3得1个百，商1写在百位上表示的就是1个百，后面2个0可以省略不写。

生：分哪个计数单位，商就写在哪一位上面，不会乱。

生：12个十除以3得4个十，十位商4，个位0也可以省略。

师：现在理解为什么“除到哪一位，商就写在哪一位的上面”了吧。每个数位的数都有相应的“位值”，竖式中每次商与除数的乘积，末尾的“0”都可以省略不写。

师：除法计算，就是在等分计算单位。请把这个过程用算式表示出来。

生：437 ÷ 3 = 4（百）3（十）7（一） ÷ 3 = 3（百） ÷ 3 + 12（十） ÷ 3 + 17（一） ÷ 3 = 145……2。

（二）除法新计数单位的产生与计数原理的勾连

除法中新计数单位的产生是学生最难理解的一个知识点，教师仍可以引导学生借助面积模型，在乘法的基础上进行倒推。结合班级的学情，学生若能基于nWCjMWva/X3JGHStfLVnhg==乘法算理完成推理，教师可放手让其自主探究分享；若有难度，教师可用课件演示，以便把此推理逻辑运用到小数和分数的算理和算法一致性研究中。

师：谁来分享一下“12000 ÷ 30”的思考过程？

生：被除数12000可以看成长方形的面积，除数30可以看成长方形的宽，12000 ÷ 30是求长方形的长。“30”里有3个10，把宽等分成3份，每份长方形面积是4000；4000里有4个千，把它等分成4份，每份小长形的面积是1000；聚焦每个小长方形，宽是10，则长为1000 ÷ 10 = 100，是长的计数单位；长为4个百，即400。

生：刚才这个过程可以用算式表示为12000 ÷ 30 = （12 ÷ 3） × （1000 ÷ 10） = 4 × 100 = 400。

生：我发现“计数单位 ÷ 计数单位 = 商的计数单位”“计数单位个数 ÷ 计数单位个数 = 商的计数单位个数”，然后“新的计数单位 × 计数单位个数 = 商”。

学生在操作均分小方块时，能不断强化各种计数单位的数学模型，让抽象的计数单位和生活中的物品一样“有形可依”，让复杂的计算过程“有理可讲”。通过推理，学生发现除法的最终计算方法也是在计算各有多少个计数单位，最后再合并。

综上所述，整数的加、减、乘、除的算法是一致的：计数单位的个数 × 计数单位；算理也是一致的：通过运算律可以推理出算理。加法是四则运算的核心，减法是加法的逆运算，乘法是加法的简便运算，除法是乘法的逆运算，是减法的简便运算。学生亲历操作，结合课件的动态演示，“数”“形”结合，成功打通“数概念”与“数运算”之间的“隔断墙”，深刻体会整数四则运算的一致性。

参考文献：

［1］于玲.打通“隔断墙”，落实“数的运算”的一致性［J］.小学数学教师，2023（7～8）.

［2］巩子坤，史宁中，张丹.义务教育数学课程标准修订的新视角：数的概念与运算的一致性［J］.课程·教材·教法，2023（7）.

（责任编辑：杨强）