基于运算一致性的《分数除以整数》教学改进

许雅婷 李雨佩

《义务教育数学课程标准（2022年版）》教学建议指出，要从数学意义、原理及法则之间的联系出发，强化学生对数学知识本质的理解。教师帮助学生厘清知识背后的道理，既是体现数学知识本质的教学需要，也是发展学生数学核心素养的育人要求。组稿聚焦分数除法，探讨如何在计算教学中引导学生深入理解算理、掌握算法，并逐步趋向知识本质，领悟整数除法、小数除法和分数除法的一致性。

在以往的教学中，教师习惯用直观图帮助学生理解分数除法的算理，进而建立分数除法与分数乘法的联系。笔者认为，《分数除以整数》作为单元起始课和小学阶段四则运算板块的终止内容，不能仅仅以教会分数除法的算理算法为目标，还应引导学生整体建构知识，沟通整数除法、小数除法、分数除法的算理，感悟除法运算的一致性，理解数的运算本质是统一计数单位后计数单位个数的运算。下面笔者通过对这节课两次教学情况的对比，阐释教学改进的原因及策略。

一、改进复习导入方式，让已有经验相互关联

第一次教学时，教师提问：“我们之前学习过哪些除法运算？”学生举例后，教师追问：“这些除法算式可以分成几类？”学生根据不同的标准进行分类。这种复习导入方式看似引导学生回忆了整数除法和小数除法，但学生的理解只停留在几种除法“型”上的区别，并未触及本质，不利于学生后续理解整数除法、小数除法、分数除法运算的一致性。基于此，在集体教研之后，教师做了如下改进。

第二次教学伊始，教师出示问题：①40张纸平均分成2份，每份有多少张？怎样列式？为什么用除法？②0.4张纸平均分成2份，每份有多少张？怎样列式？学生列出除法算式后，发现：虽然两道题中“4”的意义不同，但两个算式都将计数单位的个数平均分。学生据此推断：只要把一个物体平均分成几份，求其中的一份，就可以用除法解决。教师点拨：分数除以整数与已经学习的整数除以整数、小数除以整数的意义相同。

改进后的教学，教师借助问题情境引导学生复习整数除法、小数除法的算理，而后引出分数除法，唤醒学生探究分数除法算理的知识储备，为后面沟通整数除法、小数除法和分数除法算理的联系做了铺垫。

二、改进算法优化方式，让探究过程更加丰满

第一次教学时，教师呈现问题：“把一张纸的[45]平均分成2份。每份是这张纸的几分之几？先列式计算，再说一说这样算的道理。”有的学生用“[45]÷2=0.8÷2=0.4=[25]”进行计算，教师点拨“将分数转化成小数是探究新知的一个好方法”。有的学生用“[45]÷2=[4÷25]=[25]”进行计算，教师点拨“这是将计数单位的个数（4个[15]）平均分成两份”。还有的学生用“[45]÷2=[45]×[12]=[25]”进行计算，并说明把[45]平均分成2份，求每份是多少，就是求[45]的[12]是多少，所以[45]÷2=[45]×[12]，计算结果为[25]。教师点拨：“看来分数除以整数和我们前面学习的分数乘法之间是有联系的。”基于以上分析，教师直接给出优化算法——分数除以整数就是用分数乘这个整数的倒数。

集体教研时，组内教师提出：过早优化算法，学生对除法运算的理解不够，导致知其然而不知其所以然，不利于达到“感悟四则运算算理的一致性”目标，不利于学生形成完整的知识体系，养成善于探索、追求本质的学习观，反而让学生不自觉地将分数除法与整数除法、小数除法的算理割裂开来，在后面的探究过程中毫不犹豫地选择“乘倒数”这种最简便的计算方法，而不愿意探索细化分数单位的算理。因此，将分数单位细化之后再进行平均分这一看似不简便的方法，才是沟通整数除法、小数除法、分数除法的桥梁。

第二次教学时，为更好引导学生理解除法运算的一致性，教师没有急于给出优化的算法，而是给出新问题，继续引导学生思考：“把一张纸的[45]平均分成3份，每份是这张纸的几分之几？怎样列式？”有的学生用“[45]÷3=[1215]÷3=[12÷315]=[415]”进行计算，并说明“把5份中的每1份继续平均分成3份，相当于把这张纸平均分成了15份，而这样的4份就是每人分到的纸张”。教师追问：“为什么要把5份中的每1份继续平均分成3份呢？”学生回答：“因为4÷3得不到整数结果，而把每1份再平均分成3份，就把这张纸平均分成了15份，然后运用分数的基本性质把[45]变成[1215]，用12÷3就能得到整数结果。”教师点拨：“这里用到了分数的基本性质，在分数大小不变的情况下将计数单位变小了，这样分数单位的个数就会变多，之后再平均分分数单位的个数，就能比较容易地运用整数除法得到结果。”在教师的点拨下，学生结合教材格子图进一步发现：[把45]平均分成3份，求每份是多少，就是求[45]的[13]是多少，所以[45]÷3=[45]×[13]。由此，学生通过自主探究获得了优化算法，更加深入地理解了教材内容。

三、增设算法比较环节，让算理凸显本质联系

在整数除以整数、小数除以整数的运算中，除到不能除时，我们都是将计数单位变小继续除。教学分数除以整数时，教师能否沿用这一方法，引导学生感悟“三类”除法运算的一致性呢？为此，教师基于集体教研的结果在教学中添加了算法对比环节。

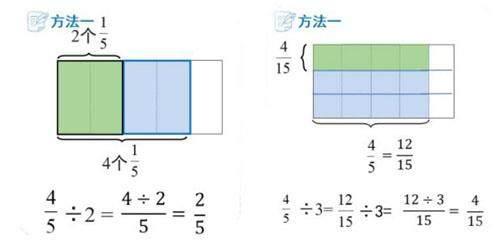
教师出示如下两幅图及计算过程，引导学生先独立思考，再小组讨论计算过程的不同点和相同点。

首先，学生通过对比观察得出：左边的除法能用被除数的分子直接平均分，右边的除法不能用被除数的分子直接平均分。接着，教师让学生探讨遇到不能直接平均分的情况应该怎样解决。学生讨论后得出：可以将计数单位变小后再分。这一教学环节旨在对比、沟通两种不同算法，引导学生感悟“在分子不能直接整除时，需要根据分数的基本性质将分子变成可以整除的情况，这样做，分数单位变小了，分数单位的个数变多了，计算就变得方便了”。两种情况的对比揭示了分数除以整数的本质——将分数单位不断细分。然后，教师顺势引导：“我们以前用过这种方法吗？”学生回忆后发现，在三年级“除数是一位数的除法”、五年级“小数除以整数”的学习过程中，我们都是用细分计数单位的方法进行计算的。最后，教师肯定了学生的回答，并出示三年级、五年级学习的整数除法和小数除法的教材内容，引导学生进一步归纳、概括，认识到“三种”除法的算理都指向计数单位个数的细分。

此外，学生在课上提出的猜想“分数乘整数是用分子乘整数作为分子，分数除以整数能否用分子除以整数作为分子呢？”本不在教师的预设中，但这恰恰证明学生对除法运算的一致性具备感性经验，只是找不到数学道理将这一猜想合理化。其实，除法运算的一致性就体现的计数单位的不断细分：在整数除法中，细分的标志是将下一个数位上的数“落”下来；在小数除法中，细分体现于“添0”的过程；在分数除法中则是分数单位不断变小。整数、小数的计数单位细分有明显标志，而分数除法与之不同，其分数单位细分的过程体现在将除数变成倒数后分母乘分母的过程中。明确了这些，学生就能避免仅仅熟记“乘倒数”的计算方法，却不明白背后道理的问题。

（作者单位：武汉经济技术开发区三角湖小学）