跨章节一题多解，实现知识互联

［摘 要］ 跨章节一题多解，相较于章节内的一题多解，在提升解题能力的同时，借助思维导图又能更好地实现知识互联，以及在一定程度上实现各章节知识融合，从而建立立体化的知识体系.

［关键词］ 一题多解；章节融合；思维导图；知识互联；知识立体化

跨章节一题多解问题的提出

一题多解，顾名思义是指一个问题可以有多种思路和方法来解决. 一题多解的意义在于：培养学生创造性思维；提高学生解决问题的能力；满足不同学生的需求；帮助教师更好地了解学生的思考方式和学习情况，从而更好地指导学生学习.

但是在日常教学过程中，我们所接触的一题多解大多是在同一章节知识体系内展开的不同思路或运算细节的处理，学生的认知结构中，各个章节各个方法相对孤立，缺乏比较和连接，于是不容易建立良好的数学方法结构，也就不容易培养数学理解能力. 相较之下，如果能够提升跨章节一题多解的能力，利用不同章节里的知识从不同角度解决同一个问题，那么这将有利于学生综合能力的提高，从而促进学生再认识已有知识和方法，改进和优化思维过程，使得方法理解向深度和广度拓展，实现知识立体化，获得更深刻、更有广度的数学知识结构体系，最终有效提升数学学科核心素养.

1. 跨章节一题多解的难点

跨章节一题多解的难点如下：

第一，知识面覆盖广. 跨章节一题多解通常需要运用多个知识点，这要求学生掌握广泛的知识，而不仅仅是某一章节的知识.

第二，抽象度较高. 一些跨章节一题多解的问题可能涉及抽象度较高的概念或原理，需要学生有一定的抽象思维能力.

第三，思维更发散. 这需要学生具有创造性思维和发散性思维，能够从不同角度出发寻找解决方法.

第四，综合应用难度高. 跨章节一题多解的问题通常需要学生综合运用多个知识点和技能来解决，这要求学生具有良好的综合应用能力和分析问题的能力.

第五，需要学生具备较强的独立思考和探索能力，这对于一些学生来说比较困难.

因此，要让学生真正掌握跨章节一题多解的能力，需要在教学中注重知识面的广度、抽象思维能力的培养、发散思维和综合应用能力的训练，并且善于鼓励学生独立思考、探索和创造.

2. 思维导图对跨章节一题多解的帮助

思维导图是提高跨章节一题多解能力的有效工具之一，具体表现在以下几个方面.

（1）思维导图可以帮助学生梳理知识点，将知识点按照逻辑关系进行组织，使得学生能够清晰了解知识点之间的关系. 这有助于学生对多个知识点进行整合，并提高学生跨章节一题多解的能力.

（2）思维导图通过分支和节点的形式，展示问题的多个方面和不同的求解思路，可以促进学生发散性思维的发展. 学生可以通过思维导图自由发挥思维能力，提出多种可能的解决方案和思路，培养创造性思维.

（3）思维导图可以帮助学生综合应用知识，提升学生的综合应用能力. 学生可以将不同的知识点在思维导图上进行组合和搭配，以达到解决问题的目的.

（4）思维导图可以帮助学生回顾、总结和反思学习过程，自我检查和评估所掌握的知识和技能，发现自己的不足之处，并不断补充和改进.

案例探究

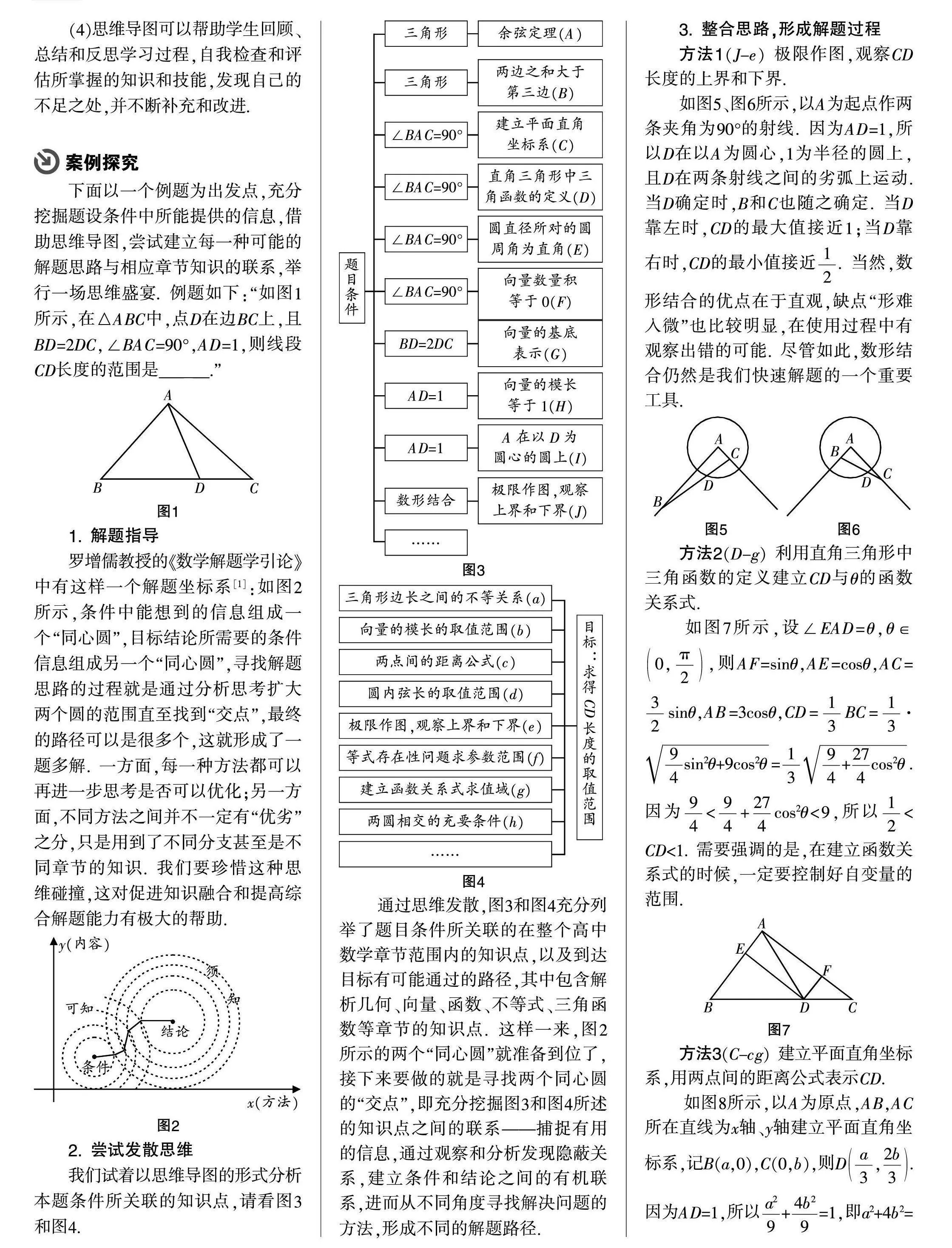
下面以一个例题为出发点，充分挖掘题设条件中所能提供的信息，借助思维导图，尝试建立每一种可能的解题思路与相应章节知识的联系，举行一场思维盛宴. 例题如下：“如图1所示，在△ABC中，点D在边BC上，且BD=2DC，∠BAC=90°，AD=1，则线段CD长度的范围是______.”

1. 解题指导

罗增儒教授的《数学解题学引论》中有这样一个解题坐标系［1］：如图2所示，条件中能想到的信息组成一个“同心圆”，目标结论所需要的条件信息组成另一个“同心圆”，寻找解题思路的过程就是通过分析思考扩大两个圆的范围直至找到“交点”，最终的路径可以是很多个，这就形成了一题多解. 一方面，每一种方法都可以再进一步思考是否可以优化；另一方面，不同方法之间并不一定有“优劣”之分，只是用到了不同分支甚至是不同章节的知识. 我们要珍惜这种思维碰撞，这对促进知识融合和提高综合解题能力有极大的帮助.

2. 尝试发散思维

我们试着以思维导图的形式分析本题条件所关联的知识点，请看图3和图4.

通过思维发散，图3和图4充分列举了题目条件所关联的在整个高中数学章节范围内的知识点，以及到达目标有可能通过的路径，其中包含解析几何、向量、函数、不等式、三角函数等章节的知识点. 这样一来，图2所示的两个“同心圆”就准备到位了，接下来要做的就是寻找两个同心圆的“交点”，即充分挖掘图3和图4所述的知识点之间的联系——捕捉有用的信息，通过观察和分析发现隐蔽关系，建立条件和结论之间的有机联系，进而从不同角度寻找解决问题的方法，形成不同的解题路径.

3. 整合思路，形成解题过程

方法1（J-e） 极限作图，观察CD长度的上界和下界.

如图5、图6所示，以A为起点作两条夹角为90°的射线. 因为AD=1，所以D在以A为圆心，1为半径的圆上，且D在两条射线之间的劣弧上运动. 当D确定时，B和C也随之确定. 当D靠左时，CD的最大值接近1；当D靠右时，CD的最小值接近. 当然，数形结合的优点在于直观，缺点“形难入微”也比较明显，在使用过程中有观察出错的可能. 尽管如此，数形结合仍然是我们快速解题的一个重要工具.

方法2（D-g） 利用直角三角形中三角函数的定义建立CD与θ的函数关系式.

如图7所示，设∠EAD=θ，θ∈

0，

，则AF=sinθ，AE=cosθ，AC=sinθ，AB=3cosθ，CD=BC=·=.因为<+cos2θ<9，所以<CD<1. 需要强调的是，在建立函数关系式的时候，一定要控制好自变量的范围.

方法3（C-cg） 建立平面直角坐标系，用两点间的距离公式表示CD.

如图8所示，以A为原点，AB，AC所在直线为x轴、y轴建立平面直角坐标系，记B（a，0），C（0，b），则D

，

. 因为AD=1，所以+=1，即a2+4b2=9，所以CD==. 由a2>0，

b2>0得0<b2<，所以<CD<1. 需要强调的是，在代入消元时，被消的元的取值范围要传递给新元.

方法4（A-f） 利用余弦定理建立CD与某直观变量之间的等量关系.

如图9所示，设CD=x，则cosC=，cosC=. 根据数学中“算两次”的思想，可得=，整理得3-3x2=AC2. 又0<AC<3x，所以0<3-3x2<9x2，解得<x<1. 需要强调的是，利用等式存在性求其中一个变量的取值范围时，要控制好其他变量的取值范围.

方法5（G-g） 以，为基底表示，从而求模长范围.

如图10所示，记=a，=b，因为BD=2DC，所以=a+b. 因为

=1，所以a2+4b2=9，所以

=（b-a）==. 下同方法3.

方法6（F-f） 借助·=0，建立与已知长度的的等量关系.

如图11所示，记=a，=b，a，b的夹角为θ，CD=

b

=t. 因为·=0，所以（a-2b）（a+b）=0，化简得1-tcosθ-2t2=0，即cosθ=. 注意到θ∈（0，π），则cosθ∈（-1，1），所以-1<<1，解得<t<1.

方法6与方法4类似，利用等式存在性求某个变量的取值范围，需要一定的知识储备，这里汇集了解不等式、求值域和函数零点等知识点. 学生在日常学习中要注重知识的积累和总结，以及对方法的优化和反思. 相关拓展可参考文［2］.

方法7（B-a） 构造三角形，利用两边之和大于第三边的基本关系列不等式.

如图12所示，取BC的中点E，连接AE，设DE=x，则AE==3x. 又AD=1，在三角形ADE中，有x+1>3x，

x+3x>1，

3x+1>x，解得<x<，CD=2x，所以<CD<1.

方法8（EI-h） 点A同时位于两个隐藏的圆上，利用两圆相交的充要条件列不等式.

如图13所示，一方面，点A在以D为圆心，1为半径的圆上；另一方面，点A在以BC为直径的圆上. 借助两圆相交的充要条件可得

1-CD<CD<1+CD，解得<CD<1.

方法9（E-d） 挖掘出一个深度隐藏的圆，在该圆内观察CD长度的范围.

如图14所示，过C作AC的垂线，交AD的延长线于点E，取AE的中点O，则∠ACE=90°. 根据三角形相似可知==，所以DE=. 所以，点C在以AE为直径的圆O上，从而DE<CD<AD，即<CD<1.

在方法8和方法9中，都用到了“隐藏圆”，这需要学生在日常学习中多思考、多发现、多总结、多概括，这些都是思维的基础，丰富的知识模块会带来正向的思维定式，思维的敏捷性和发散性都能得到极大的提高. 与“隐藏圆”相关的拓展可参考文［3］.

结语

要培养学生跨章节一题多解的能力，就要注重培养学生创造性思维、综合应用能力和自主学习能力等. 通过提供多种不同类型的问题、组织跨学科知识梳理、增加可供联想的解题过程，引导学生分析问题本质，从而帮助学生掌握跨章节一题多解的能力，提高学生的综合素质和解题能力.

跨章节一题多解可以帮助实现整个学科知识的互联，再进一步，就是跨学科知识融合，教师可以尝试将不同章节甚至不同学科的知识点组织起来，设计相关问题，引导学生综合分析和解决问题，从而建立立体化的知识体系.

参考文献：

［1］ 罗增儒. 数学解题学引论［M］. 西安：陕西师范大学出版社，2016.

［2］ 李忠良. 从一类含参等式存在性问题看“范围的传递”［J］. 中学数学月刊，2016（04）：39-40 .

［3］ 李忠良. 寻找一些隐藏着的圆［J］. 中学数学教学参考，2017（28）：36-38.