混合动力系统偏好强化学习能量管理策略研究

唐香蕉，满兴家，罗少华，邵杰

摘要： 为实现混合动力系统在电池荷电状态（state of charge，SOC）平衡以及动力性约束下的经济性提升，提出了基于偏好强化学习的混合动力能量管理策略，该策略将能量管理问题建模为马尔科夫决策过程，采用深度神经网络建立输入状态值到最优动作控制输出的函数映射关系。与传统的强化学习控制算法相比，偏好强化学习算法无需设定回报函数，只需对多动作进行偏好判断即可实现网络训练收敛，克服了传统强化学习方法中回报函数加权归一化设计难题。通过仿真试验和硬件在环验证了所提出能量管理策略的有效性和可行性。结果表明，与传统强化学习能量管理策略相比，该策略能够在满足混合动力车辆SOC平衡和动力性约束下，提升经济性4.6%～10.6%。

关键词： 混合动力汽车；能量管理；偏好强化学习；优化控制；电池荷电状态（SOC）；控制策略

DOI： 10.3969/j.issn.1001-2222.2024.03.010

中图分类号：U469.72文献标志码： B文章编号： 1001-２２２２（２０24）０3-００58-０8

混合动力能量管理策略通过对发动机和动力电池功率的调控及分配，可以优化能源利用，提高系统的燃油经济性，是混合动力汽车（hybrid electric vehicle，HEV）的核心关键技术［1-3］。

基于规则的控制是HEV最常用的能量管理策略，该控制方法具有运算量低、易于实现的优点［4］。但其规则及逻辑的设计极度依赖工程经验，且设计出的控制策略通常仅针对某一具体工况（如NEDC/WLTC等），缺乏对实车复杂工况的自适应能力。另外，因为规则控制没有将整车能量管理转化为规范的最优控制问题，策略不具有最优性。

由于HEV的能量管理问题隶属于优化问题范畴，近年来各种优化算法在能量管理策略研究中得到广泛应用，如动态规划算法［5］、粒子群算法［6］、遗传算法［7］、凸优化算法［8］等。但上述优化方法均缺乏自学习能力，一定程度削弱了求解控制策略的最优性和自适应性。近年来，基于强化学习的方法在能量管理领域日益受到重视［9-11］。C.Liu等［12］运用强化学习Q-Learning算法为某一插电式HEV设计了功率分配策略。T.Liu等［13］针对混合动力履带车辆提出了一种基于深度确定性策略梯度（deep deterministic policy gradient，DDPG）强化学习的控制策略，并论证了策略的自适应性、最优性以及学习能力。但上述传统强化学习的控制效果严重依赖于回报函数的设计，而回报函数的设计需要兼顾系统经济性、动力性约束以及动力电池荷电状态（state of charge，SOC）平衡，传统方法需要依赖经验对不同性能函数进行加权，一定程度增大了强化学习回报函数的设计难度。而近年来提出的偏好强化学习［14］不依赖于回报函数的设计，通过在备选动作集合中根据偏好（即控制目标）选择推荐动作，即可对控制参数进行反馈调整，已经在机器人控制［15］、金融管理［16］等领域取得一定成功应用。

基于偏好强化学习已经在控制领域表现出的强大应用潜力，本研究提出一种基于偏好强化学习的混合动力系统能量管理策略，以需求扭矩、车速、动力电池SOC为输入，发动机扭矩为控制输出，通过偏好强化学习调整控制策略参数，建立状态输入到控制输出的最优映射，并通过与传统深度强化学习（Q-Learning和DDPG）算法进行对比，验证算法的有效性。

1混合动力车辆建模

研究对象是一款单轴并联式混合动力客车，其混合动力系统如图1所示，主要硬件组成包括发动机、离合器、电机、动力电池和变速系统。电机直接连接在自动离合器的输出和变速器的输入之间，从而实现了减速时的再生制动和高效的电动机辅助操作。另外，发动机可以通过自动离合器与传动系统分离实现纯电动驱动。表1列出了该车辆的部分关键参数。

下面从需求输出端出发，通过向动力源输入端倒推的方式建立整车驱动力平衡模型。根据车辆动力学，车轮的角速度ωw和车轮处的需求扭矩Tw可以表示为

ωw=vrw，（1）

Tw=rwρ2Afcdv2+frmgcosα+mgsinα+

Jtotrwdvdt。（2）

式中：v为车速；rw为车轮半径；ρ为空气密度；Af为迎风面积；cd为空气阻力系数；fr为滚动阻力系数；m为汽车整备质量；g为重力常数；α为道路坡度；Jtot为车辆总惯性矩。

从车轴倒推至变速箱可得变速箱输入处的角速度ωin和需求扭矩Tin：

ωin=ωwRg，（3）

Tin=Tw+Tloss（ωw，ge）R（ge）η（ge）（Tw+Tloss≥0）

Tw+Tloss（ωw，ge）R（ge）η（ge）（Tw+Tloss<0）。（4）

式中：Tloss为由摩擦引起的额外损失；R（ge）为从变速箱输入到车轮的总传动比；η（ge）为从变速箱输入到车轮处的总传输效率。相应的变速箱挡位ge可以通过如下换挡进程计算：

ge（k+1）=5ge（k）+q（k）>5

1ge（k）+q（k）<1

ge（k）+q（k）otherwise。（5）

式中：q（k）为变速箱挡位控制指令，只能取离散值1，0和-1，分别代表降挡、保持不变和升挡。

根据驱动力平衡条件，可得：

Tin=Te+Tm。（6）

式中：Te和Tm分别表示发动机和电机的扭矩。

另外，由于驱动电机的功率来自于动力电池，因此满足如下功率平衡方程：

Pm=PbηDC/ACsgn（Pm）。（7）

式中：Pm为驱动电机的输入功率；Pb为动力电池的输出功率；ηDC/AC为逆变器的效率；sgn为符号函数，sgn（+）=1，sgn（-）=-1。

1.1发动机模型

发动机模型重点关注发动机的燃油消耗率fuel，如图2所示，发动机燃油消耗率是发动机转速ne和发动机扭矩Te的函数，通过在图2中插值，可以根据发动机的转速和扭矩来计算发动机的瞬时油耗。

1.2电机模型

本研究采用的电机模型如下［17］：

Em=RmIm+LmdImdt+Eb。（8）

式中：Em，Im分别为电机的电压和电流；Eb，Rm，Lm分别为反电动势、电枢电阻和电枢电感，并且

Eb=Kvnm，（9）

Tm=KTIm。（10）

式中：Kv，KT均为电机常数；nm为电机转速；Tm为电机扭矩。

进一步，电机的输入功率Pm可以表示为

Pm=Tmnmη（Tm，nm），驱动状态

TmnmηTm，nm，制动状态。（11）

式中：η为电机效率。电机效率MAP如图3所示，效率可由电机扭矩和转速通过插值获得。

1.3动力电池模型

本研究针对动力电池采用二阶RC等效电路模型［18］，如图4所示。该模型由3个模块组成：开路电压（open circuit voltage，OCV）模块、内部电阻R0模块和RC网络模块，其中Vt为端电压，VOCV为开路电压，V1和V2分别表示RC网络1和RC网络2的电压，I为电流（充电为正，放电为负），R0为欧姆内阻，R1和R2为极化内阻，C1和C2为极化电容。

根据基尔霍夫电压和电流定律，电压V1和V2满足以下规则：

V·i=-ViRiCi+ICi。（12）

端电压Vt如式（13）所示：

Vt=VOCV+R0I+V1+V2。（13）

动力电池的输出功率可表示为

Pb=IVt。（14）

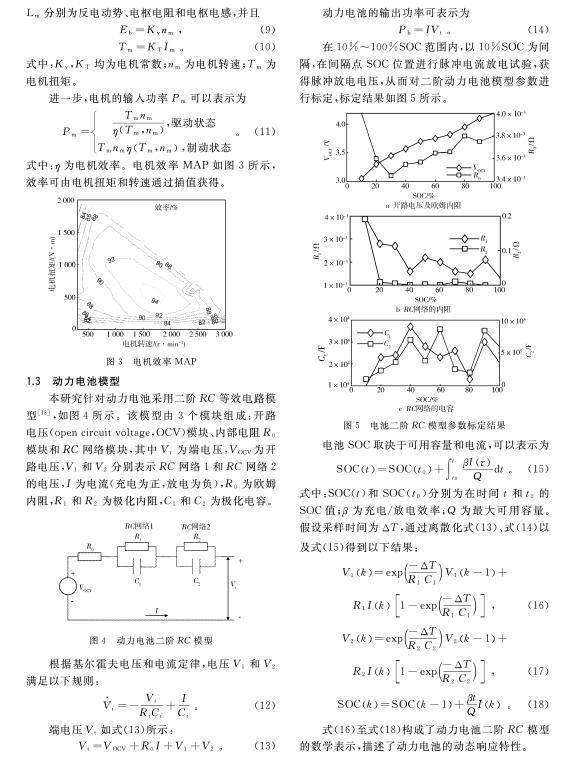
在10%～100%SOC范围内，以10%SOC为间隔，在间隔点SOC位置进行脉冲电流放电试验，获得脉冲放电电压，从而对二阶动力电池模型参数进行标定，标定结果如图5所示。

电池SOC取决于可用容量和电流，可以表示为

SOCt=SOCt0+∫tt0βIτQdt。（15）

式中：SOC（t）和SOC（t0）分别为在时间t和t0的SOC值；β为充电/放电效率；Q为最大可用容量。假设采样时间为ΔT，通过离散化式（13）、式（14）以及式（15）得到以下结果：

V1k=exp-ΔTR1C1V1k-1+

R1Ik1-exp-ΔTR1C1，（16）

V2k=exp-ΔTR2C2V2k-1+

R2Ik1-exp-ΔTR2C2，（17）

SOCk=SOCk-1+βtQIk。（18）

式（16）至式（18）构成了动力电池二阶RC模型的数学表示，描述了动力电池的动态响应特性。

2基于偏好强化学习的能量管理策略设计

偏好强化学习是一种先进的强化学习算法，它使用人类或机器学习模型提供的偏好信息来指导智能体的学习过程。相比于传统的强化学习方法，偏好强化学习可以在复杂的环境下更高效地学习［19］。

偏好强化学习的基本组成包括（S，A，μ，δ，γ，ρ），其中S为状态空间，A为动作空间，μ（S）为初始状态分布，δ为马尔科夫状态概率转移模型δ（s′|s，a），γ为折扣因子，ρ为偏好概率。

偏好强化学习的目标是从一个偏好关系的集合中学习一个最优策略。偏好关系可以表示为一个偏序关系，即一个优于关系（“”），它表示一个状态或行为比另一个状态或行为更受欢迎。在偏好强化学习中，偏序关系可以表示为一个偏好函数。具体地，假设一条采样的轨迹可以表示为

τ=s0，a0，s1，a1，…sn-1，an-1，sn。（19）

ρ（τiτj）定义为给定轨迹（τiτj）下，τiτj的概率，智能体可以接收到一个偏好集合：

ζ=ζi=τi1τi2i=1，2，…N。（20）

并且假设偏好是严格偏好，即有

ρτiτj=1-ρτjτi。（21）

对于强化学习智能体而言，目标是在一个给定的集合ζ中找到一个策略π*，能够最大化偏好选择。因此τ1τ2∈ζ需要满足的条件是：

τ1τ2Prτ1>Prπτ2。（22）

其中：

Prπτ=μs0∏τt=0πat∣stδst+1∣st，at。（23）

基于轨迹的最大化偏好问题可以描述为

τ1τ2π*=

argmaxπPrπτ1-Prπτ2。（24）

可以定义一个最小化偏好损失函数：

Lπ，τ1τ2=-Prπτ1-Prπτ2。（25）

在有多个偏好相互比较的关系下，损失函数可以表示为

Lπ，ζ=Lπ，ζ0，Lπ，ζ1，…Lπ，ζn。（26）

权重加和的方式则为

π，ζ=∑Ni=1αiLπ，ζi。（27）

本研究采用近似策略分布来获得能够最大化轨迹偏好的策略，策略流程如表2所示。

基于偏好强化学习的混合动力能量管理策略框架如图6所示，具体施流程如下。

1） 确定偏好强化学习的状态空间S和动作空间A。本研究以驾驶员处获取的需求扭矩Tw、动力系统状态车速v和动力电池SOC作为强化学习状态变量，构成状态空间S=［Tw，v，SOC］，以发动机扭矩Te作为动作变量，构成动作空间A=Te。

2） 确定偏好强化学习的网络架构。本研究采用深度神经网络构建以系统状态s为输入、以动作变量发动机扭矩Te的概率分布为输出的策略模型。

3） 基于奖励偏好对网络进行训练。系统根据深度神经网络输出的动作变量概率分布，随机采样获得执行动作，将其输入到混合动力系统模型获得下一时刻状态参数，然后通过将采样动作值与动态规划（dynamic programming，DP）确定的最优动作序列（在DP算法中以燃油经济性为目标生成最优动作序列，同时加入SOC终止值与目标平衡SOC相等的约束，保证动力电池工作在最佳SOC区间）进行相似度比较，生成偏好排序，最后将偏好选择反馈给强化学习的策略网络，以实现网络参数的最优化迭代更新。

3仿真验证

模型的正确性是能量管理策略开发的前提条件。为了验证模型的正确性，将采集的车辆实际车速作为目标工况输入建立的混合动力车辆模型进行仿真，比对仿真数据和实际数据以判断模型的准确性。图7示出了车速跟随和动力电池电压的仿真数据与实车数据的对比结果。由图可知在目标工况跟随方面，所建立的车辆模型可以很好地跟随实车速度，平均误差为0.12 km/h，模型精度较高；在动力电池电压跟随方面，由于实车环境存在多种环境噪声影响，且动力电池表现出高动态性特征，仿真数据与实车数据存在一定的误差，但总体的变化趋势相同，平均误差为3.13 V。故所建模型可以作为能量管理策略开发和硬件在环试验的模型基础。

为了验证所提出方法的有效性，根据图7a所示采集的车速工况曲线对偏好强化学习策略网络进行训练。为了保证策略的泛化性能，需要设定不同的SOC初始值。因为本研究的混合动力车辆在训练中加入了SOC终止值与目标平衡SOC（这里取0.6）相等的约束，较少工作在较高SOC和较低SOC区间，所以选择在0.55，0.60和0.65 3种靠近平衡SOC值的情况下进行仿真。为了验证所提出能量管理策略的优越性，将其与传统强化学习Q-Learning和DDPG控制策略进行对比。Q-Learning和DDPG采用和偏好强化学习相同的状态空间、动作空间以及马尔科夫状态概率转移模型，但需要设计回报函数。由于本研究以经济性为目标，因此在Q-Learning和DDPG中采用的回报函数r为

r（st，a（t））=fuelt+φSOCt-SOCsust2。（28）

式中：SOCsust为期望维持的平衡SOC；φ为折算系数，其值通过等效能量法确定，用于将每一时刻SOC与SOCsust的偏离值折算到等效油耗，从而保证动力电池工作在最佳区间。传统强化学习的目标是通过最大化累计回报获得最优策略，即

πEMS=argmaxa（t）∈A∑N-1t=0r（s（t），a（t））Ts。（29）

式中：N为训练工况的总步长；Ts为采样周期（本研究中为1 s）。

表3列出了偏好强化学习与传统强化学习策略的对比结果，其中油耗Fuelc的计算方法如下：

Fuelc=∑N-1t=0fueltTs+φSOCend-SOCsust。（30）

式中：SOCend为测试工况结束时的电池SOC；折算系数φ用于将工况结束时SOC与平衡值的偏移量折算至等效油耗，使不同算法的比较更加公平。

从表3中的等效油耗Fuelc可以看出，偏好强化学习的燃油消耗最少，说明所提出的策略具有良好的节能效果，与另外两种常用的强化学习算法相比，节能率提升4.6%～10.6%。

为了进一步比较不同算法的差异，图8示出了不同初始SOC下，不同算法的SOC变化曲线。由于传统强化学习在回报函数中增加了SOC平衡约束，结束时刻的SOC与平衡值偏离较小。偏好强化学习通过在动态规划算法中考虑SOC的平衡偏好，同样可以实现SOC平衡性约束，并且在结束时刻偏好强化学习的SOC与平衡SOC值偏离更小（从表3可以看出，3种不同初始SOC状态下，结束时刻偏好强化学习的SOC偏离目标平衡值均为0.01，而Q-Learning和DDPG偏离值为0.02～0.03），说明了偏好强化学习训练过程的有效性。

另外，从图8中可以看出，Q-Learning算法与另外两种强化学习算法的SOC变化差异较大，这是由于Q-Learning算法需要对能量管理中的状态量和控制量进行离散化处理，导致引入了离散化精度误差，而偏好强化学习和DDPG通过深度神经网络直接构建从连续状态量到连续控制量的非线性映射，避免了离散化误差，因此优化效果更好。从表3还可以看出，Q-Learning算法在3种初始SOC下的等效油耗均为最高。

为了进一步说明控制策略的最优性，图9示出了DP和偏好强化学习两种策略下发动机的工作点分布（起始SOC为60%）。从图9可以看出，两者的工作点均主要分布在燃油消耗率曲线的最优等高线上，DP和偏好强化学习的平均燃油消耗率分别为221 g/（kW·h）和226 g/（kW·h）。特别地，由于DP获得的是全局最优解，因此DP的工作点均沿着最优等高线分布，偏好强化学习对应的发动机工作点分布主要也沿最优等高线分布，同时也存在部分沿次优等高线分布的情况。

4硬件在环验证

基于混合动力系统的RTLab模型以及MotoTron控制器，建立完整的硬件在环仿真平台，如图10所示。在该硬件在环平台中，采用偏好强化学习策略作为控制策略，MotoTron控制器接受RT-LAB传递的需求扭矩、车速以及电池SOC信号，根据控制策略输出最优发动机扭矩。RT-LAB接受MotoTron控制器发送的发动机扭矩控制信号，同时输出系统状态信号。

图11示出了硬件在环仿真工况下发动机工作点的分布。从图11可以看出，绝大部分发动机工作点仍沿着最优等高线方向的最佳位置分布。计算表明，该工况下的平均燃油消耗为229 g/（kW·h），略高于仿真工况下的结果。

表4对比了硬件在环试验中3种强化学习控制策略的平均燃油消耗，可以看出，偏好强化学习在硬件在环试验中仍然具有最佳的燃油经济性。

5结束语

面向混合动力车辆，提出了基于偏好强化学习的能量管理策略。该策略在保证车辆动力性及SOC平衡的约束范围内，以最小化燃油消耗率为目标，获得了混合动力系统的最佳控制策略。验证表明：在仿真工况下，相比于传统的能量管理控制策略（即DDPG和Q-Learning），所提出的控制策略可以实现4.6%～10.6%经济性的提高；在硬件在环试验中，所提出的控制策略仍然取得了较为理想的性能表现。

参考文献：

［1］杨亚联，石小峰.混联式混合动力汽车工况预测能量管理研究［J］.机械设计与制造，2020，10：276-280.

［2］严陈希，耿文冉，黄明宇，等.基于工况识别的混合动力汽车能量管理策略［J］.机械设计与制造，2022，3：24-29.

［3］Hu B，Li J.A deployment-efficient energy management strategy for connected hybrid electric vehicle based on offline reinforcement learning［J］.IEEE Transactions on Industrial Electronics，2021，69（9）：9644-9654.

［4］罗勇，褚清国，隋毅，等.P0+P3构型插电式混合动力汽车能量管理策略［J］.车用发动机，2023（3）：73-81.

［5］Lee H，Song C，Kim N，et al.Comparative analysis of energy management strategies for HEV：Dynamic programming and reinforcement learning［J］.IEEE Access，2020，8：67112-67123.

［6］Chen S Y，Hung Y H，Wu C H，et al.Optimal energy management of a hybrid electric powertrain system using improved particle swarm optimization［J］.Applied Energy，2015，160：132-145.

［7］Min D，Song Z，Chen H，et al.Genetic algorithm optimized neural network based fuel cell hybrid electric vehicle energy management strategy under start-stop condition［J］.Applied Energy，2022，306：118036.

［8］Hadj-Said S，Colin G，Ketfi-Cherif A，et al.Convex Optimization for Energy Management of Parallel Hybrid Electric Vehicles［J］.Ifac Papersonline，2016，49（11）：271-276.

［9］Cao J，Xiong R.Reinforcement Learning-based Real-time Energy Management for Plug-in Hybrid Electric Vehicle with Hybrid Energy Storage System［J］.Energy Procedia，2017，142：1896-1901.

［10］Zhou J，Xue Y，Xu D，et al.Self-learning energy management strategy for hybrid electric vehicle via curiosity-inspired asynchronous deep reinforcement learning［J］.Energy，2022，242：122548.

［11］Hu D，Zhang Y.Deep Reinforcement Learning Based on Driver Experience Embedding for Energy Management Strategies in Hybrid Electric Vehicles［J］.Energy Technology：Generation，Conversion，Storage，Distribution，2022（6）：10.

［12］Liu C，Murphey Y L.Power management for plug-in hybrid electric vehicles using reinforcement learning with trip information［C］//2014 IEEE Transportation Electrification Conference and Expo.New York：IEEE Computer Society，2014.

［13］Liu T，Hu X，Li S E，et al.Reinforcement learning optimized look-ahead energy management of a parallel hybrid electric vehicle［J］.IEEE/ASME transactions on mechatronics，2017，22（4）：1497-1507.

［14］Liu Y，Datta G，Novoseller E，et al.Efficient Preference-Based Reinforcement Learning Using Learned Dynamics Models［J］.arXiv preprint arXiv：2301.04741，2023.

［15］Lee K，Smith L，Dragan A，et al.B-pref：Benchmarking preference-based reinforcement learning［J］.arXiv preprint arXiv：2111.03026，2021.

［16］Xu N，Kamra N，Liu Y.Treatment recommendation with preference-based reinforcement learning［C］//2021 IEEE international conference on big knowledge （ICBK）.New York：IEEE Computer Society，2021：1-8.

［17］孔泽慧，樊杰.基于深度强化学习的分布式电驱动车辆扭矩分配策略［J］.汽车技术，2022（2）：36-42.

［18］Xie Y，Wang S，Fernandez C，et al.Improved gray wolf particle filtering and high-fidelity second-order autoregressive equivalent modeling for intelligent state of charge prediction of lithium-ion batteries［J］.International journal of energy research，2021，45（13）：19203-19214.

［19］Zhang G，Kashima H.Learning state importance for preference-based reinforcement learning［J］.Machine Learning，2023，113：1885-1901.

Hybrid Power Energy Management Strategy Based on Preferring Reinforcement Learning

TANG Xiangjiao1，MAN Xingjia1，LUO Shaohua2，SHAO Jie1

（1.Shanghai General Motors Wuling，Liuzhou545000，China;2.China Automotive Engineering Research Institute Co.，Ltd.，Chongqing401122，China）

Abstract： To enhance the economy of hybrid power system under SOC balance and power constraints， a hybrid power energy management strategy was proposed based on the preferring reinforcement learning. The strategy treated the energy management problem as a Markov decision process and adopted a deep neural network to learn and build the nonlinear mapping from the input states to the optimal control inputs. Compared with the traditional reinforcement learning algorithm， the preferring reinforcement learning did not require the setting of a reward function and only needed to make preference judgments on multiple actions to achieve the convergence of network training， which overcame the design difficulty of weighting normalization in reward function. The effectiveness and feasibility of the proposed energy management strategy were verified through simulation experiments and hardware-in-the-loop tests. The results show that compared with traditional reinforcement learning energy management strategies， the proposed strategy can improve the economy by 4.6% to 10.6% while maintaining the SOC balance and power constraints of hybrid power vehicle.

Key words： hybrid electric vehicle;energy management;preferring reinforcement learning;optimal control;SOC;control strategy

［编辑： 姜晓博］