数学概念的内涵与外延的教学创设

赵三洪

对于某一数学概念的掌握过程需要从类比与迁移、抽象与概括、拓展与归纳等多思维层面协调认知.以“反比例函数”的概念为例，在教学中要求学生及时准确地找出函数式中自变量和因变量的关系，以及从事例中领悟和总结反比例函数的概念.为此，教师在课堂教学中把认知和建构反比例函数的概念作为难点；通过类比、迁移、形象的观察与实践，亲身经历新概念生成的过程，为学生创造必要的情境分解难点.

1 “导”——创设新概念的外延情境

问题观察下列函数（其中a，b，c为常数）：

（1）y=2 023x+2 024；（2）y=2 0232 024x；（3）y=axb+c（a≠0，b≠0）；（4）y=ax2-c；（5）ax+by=c（a≠0，b≠0）；（6）y=ax3+bx+c（a≠0）.

其中是一次函数的有哪些？

预设结果：（1）（3）和（5）是一次函数，从图象看，它们都是线性关系.

创设目的：课堂伊始创设问题情境是数学概念教学的起点.

创设好的问题情境能为学生提供激活思维活动的平台，引导学生确定新概念的建构方向.这也是数学课堂教学良好的导入新课的环节，以问题探究驱动学生的求知欲望.这样的教学设计以一次函数的概念作为新概念的外延，使学生在反复类比、辨认和分析等活动中可以确定（1）（3）和（5）是一次函数，初步体验在一次函数之外还存在其他函数关系，为下一环节认知反比例函数概念奠定基础.

达成结果：（2）与（3）两个函数的结构非常相似，引导学生类比分析，找出自变量位置的不同.再通过这一变化，说明函数特性的变化，从而自然而然地生成新概念——反比例函数，激发学生对比两个函数的探究兴趣，也让学生成为课堂活动的主角.

2 “悟”——搭建新概念的实践平台

问题我们学校距火车站大约8 km，想一想，从学校有哪些方式到火车站？

预设结果：乘公交车、骑自行车、坐出租车、步行……

电子白板展示：请大家完成表格的填写.

活动1：从杭州到大理全程2 500 km，按照同学们的想法出行，具体速度（单位：km/h）见下表1：

想一想1：能确定一个函数关系吗？自变量和因变量分别是什么？

预设结果：①能，时间是因变量，速度是自变量，因为速度在变化，时间也在变化；②不能，因为对于四种交通工具都有唯一的取值，也只有唯一的时间与之对应……

想一想2：从表中可以发现v和t这两个变量之间存在什么样的关系？

预设结果：①随着v的增大，t逐渐减小.

②两个变量之积是2 500或t=2 500v……

活动2：给你一张21 cm×30 cm（16K型）纸，能设计一个面积为63 cm2的矩形吗？

追问：是不是16K型纸只能设计2个面积为63 cm2的矩形纸片？

想一想1：矩形的宽是长的函数吗？为什么？

预设结果：对于长x的每一个确定值，宽y都有唯一确定的值与之对应.

想一想2：在活动1和活动2的问题中，两个变量之间的关系相同吗？

预设结果：①不相同，活动1中两个变量之积等于2 500，活动2中两个变量之积等于63；②2 500和63都是常量，所以两个变量的关系是相同的.

课堂小结：从学生对上述两个问题的解决情况来看，事件的情境虽然不同，但抽象出来的两个变量之间的关系是相同的，即两个变量之积是常量（数）.因此，我们把其中一个变量称为另一个变量的反比例函数.

出示关系式：y=kx（k≠0）.

创设目的：引导学生亲历新概念的形成过程，让学生逐步理解反比例函数概念是在什么条件下得到的，函数的变化特征是什么，经过与一次函数的分析对比，抽象归纳构建数学新概念的本质内涵.

本环节是通过常见的生活事例促成学生形成新概念.反比例函数概念比较抽象，如果教师一味地在课堂上给出新概念，不利于学生理解和认知.因此，从学情出发，联系实际生活，即可激发学生探究新概念的兴趣.创设的两个情境都是学生熟悉的、涉及反比例函数关系的事例，利用学生熟知的一次函数作外延铺垫，可调动学生参与数学活动的热情，在亲历探讨两个变量之积是常量这一相同的特殊内涵后，能够初步实现反比例函数概念的形成.

备课组交流感悟：通过备课组集体备课发现，“反比例函数”新概念生成环节，除了创设具体的生活事例外，还可以通过物理实验等其他方式来形成概念.将内涵式发展与外延式建构类比，是帮助学生形成数学新概念的有效手段，但对数学新概念的本质进行深刻的内化还需要学生的自主认知，而创设教学实践活动情境是绝佳的途径.

3 “议”——内化新概念的本质特征

议一议1：在下列函数表达式中，x为自变量，请填表2：

预设结果：①反比例函数未选xy+37=0，y=29x-1.

②将反比例函数y=2 02310x的k填成2 023（应为202.3）.

议一议2：小明看到，工人师傅将一根1 000m长的光缆缠绕到固定盘上，固定盘外剩余光缆长度随着时间推移而逐渐减少.小明认为固定盘外剩余光缆长度是时间的反比例函数，这种判断正确吗？

预设结果：判断正确，两个变量中一个增加，另一个减少，二者“成反比”，是反比例函数.

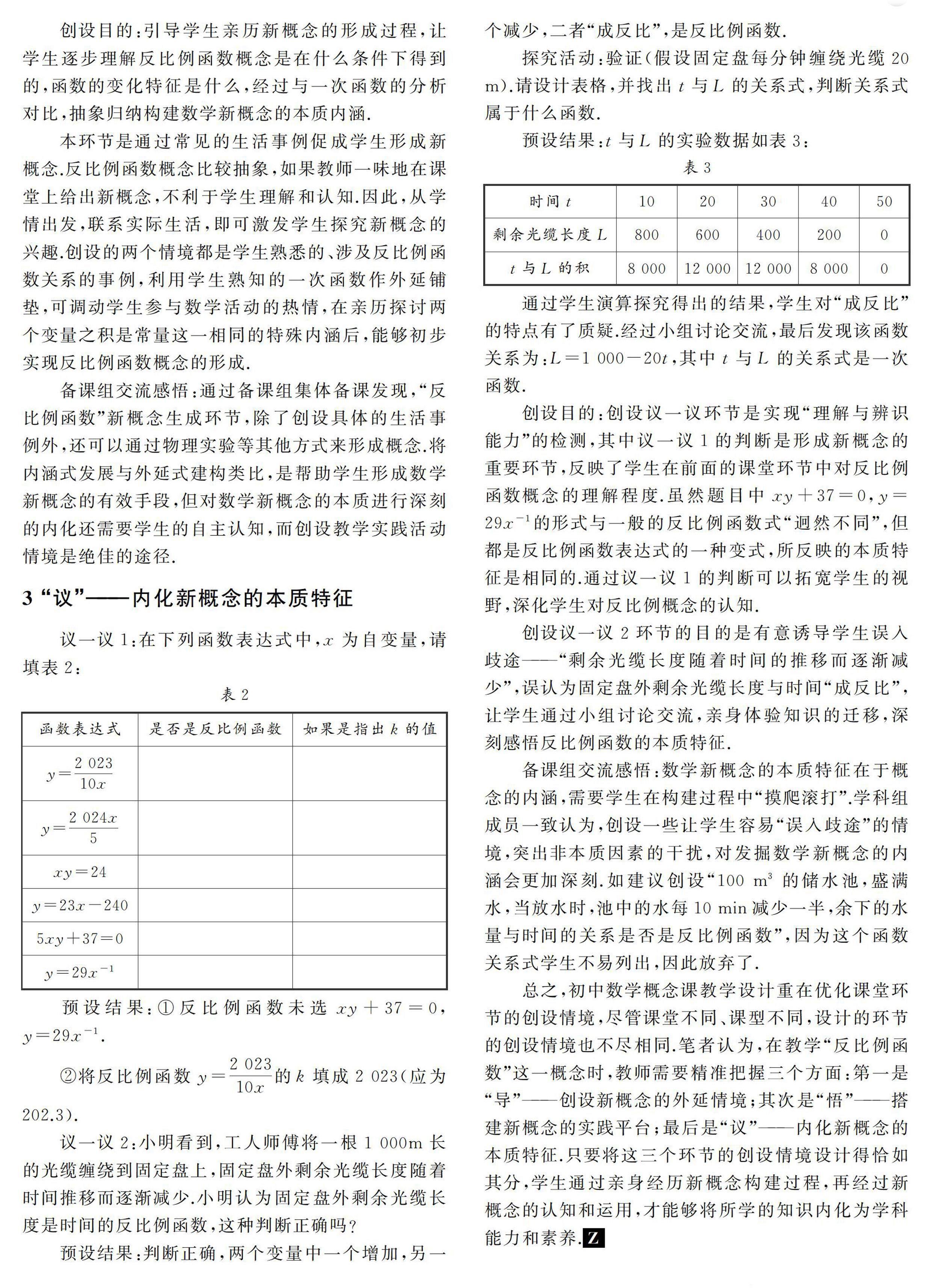
探究活动：验证（假设固定盘每分钟缠绕光缆20 m）.请设计表格，并找出t与L的关系式，判断关系式属于什么函数.

预设结果：t与L的实验数据如表3：

通过学生演算探究得出的结果，学生对“成反比”的特点有了质疑.经过小组讨论交流，最后发现该函数关系为：L=1 000-20t，其中t与L的关系式是一次函数.

创设目的：创设议一议环节是实现“理解与辨识能力”的检测，其中议一议1的判断是形成新概念的重要环节，反映了学生在前面的课堂环节中对反比例函数概念的理解程度.虽然题目中xy+37=0，y=29x-1的形式与一般的反比例函数式“迥然不同”，但都是反比例函数表达式的一种变式，所反映的本质特征是相同的.通过议一议1的判断可以拓宽学生的视野，深化学生对反比例概念的认知.

创设议一议2环节的目的是有意诱导学生误入歧途——“剩余光缆长度随着时间的推移而逐渐减少”，误认为固定盘外剩余光缆长度与时间“成反比”，让学生通过小组讨论交流，亲身体验知识的迁移，深刻感悟反比例函数的本质特征.

备课组交流感悟：数学新概念的本质特征在于概念的内涵，需要学生在构建过程中“摸爬滚打”.学科组成员一致认为，创设一些让学生容易“误入歧途”的情境，突出非本质因素的干扰，对发掘数学新概念的内涵会更加深刻.如建议创设“100 m3的储水池，盛满水，当放水时，池中的水每10 min减少一半，余下的水量与时间的关系是否是反比例函数”，因为这个函数关系式学生不易列出，因此放弃了.

总之，初中数学概念课教学设计重在优化课堂环节的创设情境，尽管课堂不同、课型不同，设计的环节的创设情境也不尽相同.笔者认为，在教学“反比例函数”这一概念时，教师需要精准把握三个方面：第一是“导”——创设新概念的外延情境；其次是“悟”——搭建新概念的实践平台；最后是“议”——内化新概念的本质特征.只要将这三个环节的创设情境设计得恰如其分，学生通过亲身经历新概念构建过程，再经过新概念的认知和运用，才能够将所学的知识内化为学科能力和素养.