认知负荷理论和GeoGebra在教学中的应用

陈佳欣 郑卫峰

摘   要：高中物理的磁场部分内容具有抽象性、复杂性等特点，根据认知负荷理论，对学生在“洛伦兹力”一节的学习中存在的认知负荷进行了分析，并从降低内在认知负荷和外在认知负荷、增加相关认知负荷3个方面分别举例说明了GeoGebra软件在“洛伦兹力”教学中的作用，为利用信息技术手段助力物理课堂教学提供有益的参考。

关键词：认知负荷理论；GeoGebra；洛伦兹力；物理教学

1  认知负荷理论的基本观点

认知负荷是指认知主体利用工作记忆系统对认知任务进行加工和保持过程中所需要承受的负荷总量，认知负荷理论由澳大利亚教育心理学家John Sweller[ 1 ]于1988年首次提出。“洛伦兹力”是高中物理磁场内容的重要组成部分，其知识本身具有抽象性、复杂性等特点，既涉及到运动与相互作用物理观念，又有模型建构、科学推理等素养能力的要求，因此知识本身的认知负荷比较强。而传统的课堂教学中教师以板书的方式呈现教学内容，使学生难以理解磁场力的三维空间位置、洛伦兹力的本质、带电粒子在磁场中的运动等重要内容，即知识呈现的形式不利于降低学生在学习时的认知负荷。

认知负荷包括内在认知负荷、外在认知负荷和相关认知负荷。三种认知负荷具有可加性，若学习过程中的认知负荷超过工作记忆的负载量，就会对学习效果产生负面影响。

物理学习中，内在认知负荷主要源于物理知识本身，如物理概念和规律等。内在认知负荷与学习者的知识经验密切相关，一般而言，学习者具有与学习材料相关的认知经验越多，学习材料带来的认知负荷越低。如洛伦兹力的公式需要运用安培力公式和电流的微观表达式进行推导，但是学生对微观世界缺乏直接经验的感知。因此教学中教师应明确学习任务的难点以及学生的已有认知经验，有意识地将洛伦兹力这一新知识与学生已学习过的安培力建立起联系，从而降低内在认知负荷。

外在认知负荷源于认知任务不恰当的呈现方式和教学设计。不当的教学设计和呈现方式不但对认知活动没有帮助，还会导致学生承受额外的负荷，也称为无效认知负荷。如学生处理“带电粒子在磁场中的运动”这一类问题时需要一定的数理结合能力、作图能力以及空间思维能力，教学中若教师仅靠板书很难将复杂的、三维立体的物理模型清晰地呈现，即学生很难想象带电粒子在磁场中复杂的运动轨迹。因此教学中处理类似的问题时，可利用相关软件将轨迹动态变化的物理图景以动态方式呈现，从而降低外在认知负荷。

相关认知负荷也称为有效认知负荷，能促进有效的认知加工，其产生于图式的建构和自动化的活动，外在表现为有意义的认知过程与结果。因此，唤醒学习者的认知投入能增加有效认知负荷。物理学习中的相关认知负荷主要来源于学习者对所要解决的物理问题的有效认知，比如“带电粒子在有界磁场中运动的临界问题”，在不同初始条件下带电粒子在磁场中的运动规律比较复杂，学生很难想象其复杂的运动轨迹图像和几何关系[ 2 ]。因此在培养学生的问题解决能力时，要为学生提供支架和变异样例有利于图式的建构和迁移，从而增加相关认知负荷，如果能为学生提供带电粒子以不同初始条件在不同磁场边界中运动的样例，并引导学生完成样例的解答，那么可以很好地帮助学生形成对这类问题的有效认知。

2  GeoGebra在认知负荷理论中的运用

GeoGebra软件兼具几何、代数、图形和计算等功能，在其绘图区中，可以显示点、线、向量等几何图形的坐标和函数表达式，还可以添加文字以辅助说明，即轻松实现关联信息的捆绑。因此在物理教学中利用GeoGebra软件能弥补教学中静态图像和文字描述不足的缺点，为学生提供更丰富的感性材料，减少学生在信息加工过程中的负担。GeoGebra的滑动条和复选框功能可以轻松改变物理量参数值，从而实现对物理情境的变异，根据变异任务策略，对学习任务予以变异能够引发学生投入更多的心理努力[ 3 ]，提高问题迁移能力。

根据上述分析，GeoGebra软件能够降低学生在物理学习中产生的认知负荷，尤其是涉及到复杂的物理模型和物理过程时，GeoGebra的优势更是传统教学无法比拟的。而“洛伦兹力”这一节内容涉及到的三维模型、动态变化和临界问题等复杂问题可以借助GeoGebra软件制作课件，辅助课堂教学。因此本文将基于认知负荷理论，介绍GeoGebra软件在“洛伦兹力”教学中的应用，教学思路如图1所示。

3  认知负荷理论下的“洛伦兹力”教学设计

3.1  利用GeoGebra理解“洛伦兹力”的概念，降低内在认知负荷

学习“洛伦兹力”时，学生已经会判断安培力的方向，对磁场和磁场力的空间关系有了一定的知识基础。安培力可视为大量运动电荷受到洛伦兹力的宏观表现，但是从宏观到微观的思维跨度较大，所以教学的关键是基于学生已有的宏观上的认知经验，在宏观和微观运动间建立联系。利用GeoGebra软件构建电流在磁场中的模型，可以实现从安培力到洛伦兹力的衔接，从而循序渐进地引导学生理解洛伦兹力与安培力的关系，加深对洛伦兹力概念的深入理解与掌握。“从安培力到洛伦兹力”教学思路如图2所示。

【教学过程】

任务1：回顾通电导线在磁场中受安培力的作用

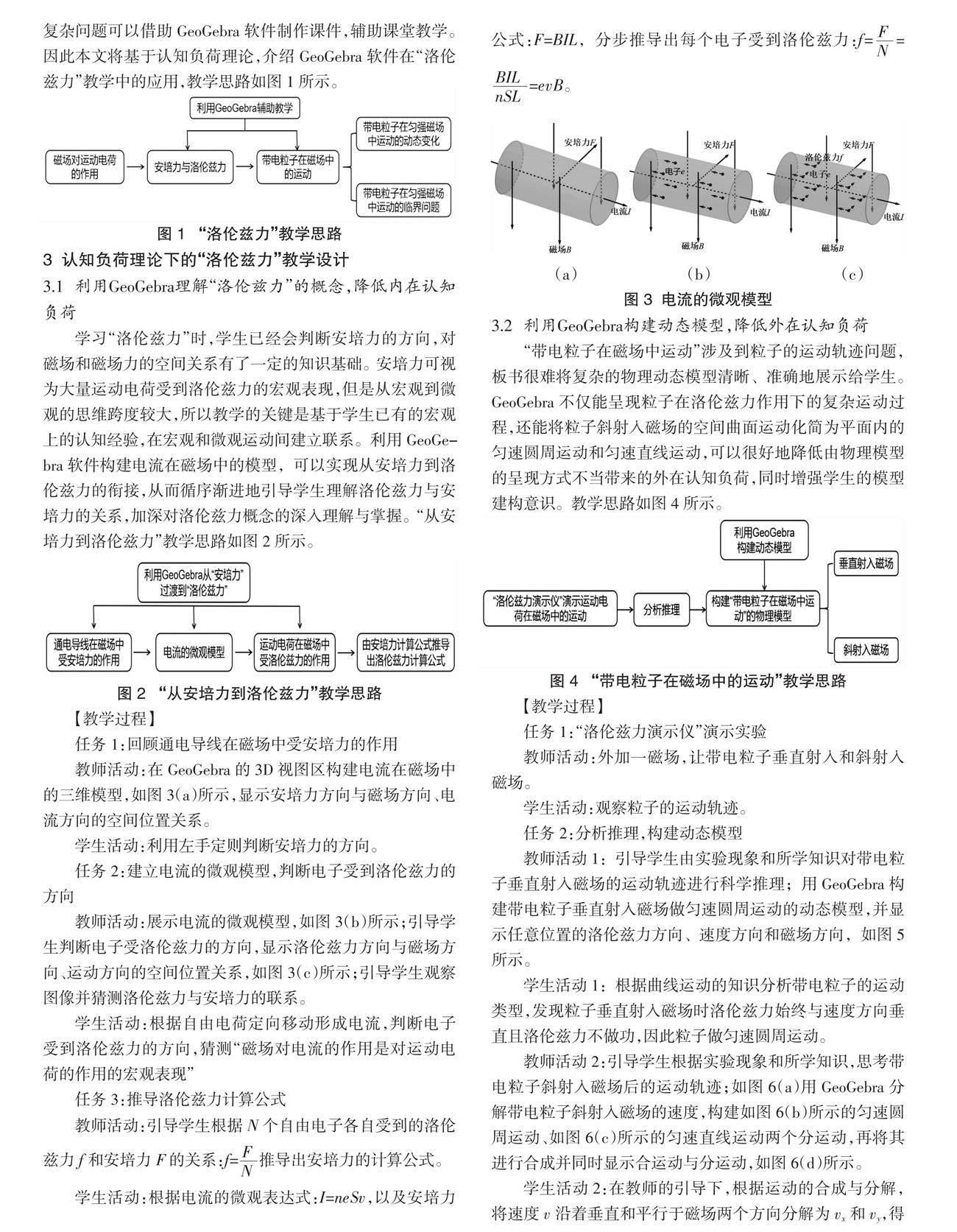
教师活动：在GeoGebra的3D视图区构建电流在磁场中的三维模型，如图3（a）所示，显示安培力方向与磁场方向、电流方向的空间位置关系。

学生活动：利用左手定则判断安培力的方向。

任务2：建立电流的微观模型，判断电子受到洛伦兹力的方向

教师活动：展示电流的微观模型，如图3（b）所示；引导学生判断电子受洛伦兹力的方向，显示洛伦兹力方向与磁场方向、运动方向的空间位置关系，如图3（c）所示；引导学生观察图像并猜测洛伦兹力与安培力的联系。

学生活动：根据自由电荷定向移动形成电流，判断电子受到洛伦兹力的方向，猜测“磁场对电流的作用是对运动电荷的作用的宏观表现”

任务3：推导洛伦兹力计算公式

教师活动：引导学生根据N个自由电子各自受到的洛伦兹力f和安培力F的关系：f=■推导出安培力的计算公式。

学生活动：根据电流的微观表达式：I=neSv，以及安培力公式：F=BIL，分步推导出每个电子受到洛伦兹力：

3.2  利用GeoGebra构建动态模型，降低外在认知负荷

“带电粒子在磁场中运动”涉及到粒子的运动轨迹问题，板书很难将复杂的物理动态模型清晰、准确地展示给学生。GeoGebra不仅能呈现粒子在洛伦兹力作用下的复杂运动过程，还能将粒子斜射入磁场的空间曲面运动化简为平面内的匀速圆周运动和匀速直线运动，可以很好地降低由物理模型的呈现方式不当带来的外在认知负荷，同时增强学生的模型建构意识。教学思路如图4所示。

【教学过程】

任务1：“洛伦兹力演示仪”演示实验

教师活动：外加一磁场，让带电粒子垂直射入和斜射入磁场。

学生活动：观察粒子的运动轨迹。

任务2：分析推理，构建动态模型

教师活动1：引导学生由实验现象和所学知识对带电粒子垂直射入磁场的运动轨迹进行科学推理；用GeoGebra构建带电粒子垂直射入磁场做匀速圆周运动的动态模型，并显示任意位置的洛伦兹力方向、速度方向和磁场方向，如图5所示。

学生活动1：根据曲线运动的知识分析带电粒子的运动类型，发现粒子垂直射入磁场时洛伦兹力始终与速度方向垂直且洛伦兹力不做功，因此粒子做匀速圆周运动。

教师活动2：引导学生根据实验现象和所学知识，思考带电粒子斜射入磁场后的运动轨迹；如图6（a）用GeoGebra分解带电粒子斜射入磁场的速度，构建如图6（b）所示的匀速圆周运动、如图6（c）所示的匀速直线运动两个分运动，再将其进行合成并同时显示合运动与分运动，如图6（d）所示。

学生活动2：在教师的引导下，根据运动的合成与分解，将速度v沿着垂直和平行于磁场两个方向分解为vx和vy，得到两个分运动：以vx的速度作垂直于磁场平面的匀速圆周运动和以vy的速度做沿着磁场方向的匀速直线运动，再尝试画出其合运动的运动轨迹。

3.3  利用GeoGebra改变带电粒子在磁场中的运动情境，增加相关认知负荷

“带电粒子在有界匀强磁场中运动”的动态问题和临界问题可变性和灵活性强[ 4 ]，利用GeoGebra可以逐步呈现问题的解答步骤、还可以改变物理量的大小和物理情境，增加相关认知负荷，有利于提供问题迁移能力。教学思路如图7所示。

【教学过程】

任务1：构建基础模型，提供解答样例。

问题情境：垂直纸面向内的磁场中，有正电粒子水平射入，如何确定其运动轨迹？

教师活动：创设带电粒子射入匀强磁场做匀速圆周运动的情境，引导学生由圆心O的位置和半径r的大小确定运动轨迹；利用GeoGebra构建模型，如图8所示。

学生活动：由洛伦兹力过圆心确定圆心所在直线，根据洛伦兹力提供向心力qvB=确定轨迹圆半径r=。

任务2：改变初始条件，介绍“放缩圆”模型

问题情境：改变上述粒子入射速度的大小，其运动轨迹有何特点？

教师活动：创设情境，引导学生思考带电粒子从同一入射点和同一方向以不同的速率射入匀强磁场的运动轨迹；利用GeoGebra展示带电粒子以不同的速率在磁场中运动的轨迹圆的动态变化，如图9所示；总结“放缩圆”的特点。

学生活动：分析影响带电粒子在匀强磁场中运动的因素，尝试绘制不同的轨迹圆；观察图像，发现轨迹圆半径大小会随着速率的增加而增大，轨迹圆是“放缩”的关系，且各轨迹圆的圆心共线。

任务3：构建磁场边界，灵活应用模型

问题情境1：相距为d的平行极板间存在垂直纸面向外的匀强磁场，磁感应强度为B，电荷量为q、质量为m的正电粒子入射速度与左边界的夹角为60°，如图10（a）所示，求轨迹从右边界飞出时速度的取值范围。

教师活动：引导学生找出临界轨迹并用几何知识求解，利用GeoGebra逐步呈现解答步骤——确定临界轨迹：改变速度大小，呈现一系列动态圆，正好与边界相切的曲线即为临界轨迹，如图10（b）所示；确定圆心位置：根据洛伦兹力的方向指向圆心作速度的垂线AO，根据弦AE的中垂线过圆心作直线DO，AO与DO的交点O即为圆心，如图10（c）所示；利用几何关系求解：如图10（d）作辅助线AO、CO、DO，由几何关系可知R+Rsin30°=d，由洛伦兹力提供向心力qvB=，解得R=d，v=，所以要从右边界飞出磁场，速度的取值范围为v＞。

学生活动：分析带电粒子以不同速率在磁场中运动的轨迹，找到恰好与右边界相切的临界轨迹，并尝试用几何知识得到临界速度。

问题情境2：改变入射角为30°，将右边界改为上边界，其他条件不变，求轨迹从上边界飞出时速度的取值范围。

教师活动：引导学生独立思考，利用GeoGebra逐步呈现解答步骤，如图11所示。

学生活动：根据上述步骤确定临界轨迹，由几何关系确定临界速度。

4  小结

GeoGebra软件的动态交互性能对物理过程进行动态模拟，增强情境的真实性[ 5 ]，对物理概念、物理规律、物理模型、物理过程等都可进行可视化的展示。在认知负荷理论的指导下，分析学生学习“洛伦兹力”时存在的认知负荷，将课堂教学与GeoGebra软件相结合，能够实现对三种认知负荷的合理调控，提高教学的有效性。因此，在教学过程中应当根据学生已有认知和教学内容合理进行教学设计，以降低内在、外在认知负荷，增加相关认知负荷，提高学生学习的有效性，进而提升学生的物理学科核心素养。

参考文献：

［1］ Sweller J.Cognitive load during problem solving： Effects on learning[J].Cognitive Science，1988，12（2）：257-285.

［2］ 陈林，桑芝芳.基于GeoGebra软件的磁场动态圆问题的可视化分析：以一道带电粒子在磁场中运动的多解问题为例[J].物理教学，2020，42（9）：26-28．

［3］ 汪明，曹道平.基于认知负荷理论的有效教学设计研究[J].现代教育技术，2013，23（5）：16-19．

［4］ 初乐香，杨艳.带电粒子在有界匀强磁场中运动的临界问题探讨[J].中学物理教学参考， 2022， 51（18）：54-57．

［5］ 刘健智，程婷.GeoGebra软件在物理可视化教学中的应用[J].物理教师，2021，41（6）：70-73．