有机给体-受体结构光诱导过程的非绝热动力学模拟:方法与应用

刘向洋 刘莎莎

摘要：有机太阳能电池的核心组成是有机给体-受体（donor-acceptor，D-A）结构.探究有机给体-受体结构的光激发后的动力学过程对设计新型有机太阳能电池非常重要.非绝热动力学模拟是研究该过程的重要理论方法.然而，相比于小分子体系，有机给体-受体结构通常较为复杂，计算量大，难以采用高精度的非绝热动力学模拟方法.为了克服这一困难，介绍了课题组所发展基于线性响应-含时密度泛函（LR-TDDFT）理论的非绝热动力学模拟方法，通过结合多种分析方法，可以有效的探究有机给体-受体结构光诱导的动力学过程，如电荷转移过程，能量转移过程，激子动力学等.该方法不仅可以用于解释现有的实验结果，还可以为后续设计新型有机给体-受体结构提供帮助.

关键词：有机太阳能电池; 给体-受体复合物; 光化学与光物理; 非绝热动力学; 含时密度泛函理论

中图分类号：O644.12  文献标志码：A  文章编号：1001-8395（2024）05-0638-12

doi：10.3969/j.issn.1001-8395.2024.

随着能源危机与环境污染问题日益严峻，寻找清洁且可再生的新型能源从而替代传统的化石燃料迫在眉睫.在诸多清洁能源中，太阳能因其取之不尽用之不竭的特性得到了人们的广泛关注.人们利用太阳能最原始的方式是通过将光能转换为热能，然而，采用这一方法的太阳能利用率较低.因此，需要找到更加有效的方式去吸收，转换，存储丰富的太阳能资源.目前，有效利用太阳能的方式主要有2种：一种是采用太阳能电池利用光伏效应将太阳能转换为电能[1-5]，另外一种则是利用光催化材料将太阳能转换为化学能，如光催化还原二氧化碳，光解水制备氢气等[6-10].

对于太阳能电池，提高其效率的关键在于寻找合适的材料，使得可以有效的吸收太阳光，并且生成的电荷可以发生高效的分离，生成载流子.目前，常见的太阳能电池材料根据其组成可以大致分为全无机太阳能电池，如传统的硅基太阳能电池，有机-无机混合的太阳能电池，如近几年关注度较高的钙钛矿太阳能电池，以及完全由有机小分子或聚合物组成的有机太阳能电池.在这几类太阳能电池中，尽管有机太阳能电池的光电转换效率并不是最优的，该类太阳能电池因其廉价，无毒，柔性高以及易改性等特点得到了广泛的关注[11-14].然而，相比于无机材料，有机材料通常激子结合能高达300 meV，远大于室温下热能kBT[11].这使得基于同质结的有机太阳能电池电荷分离效率极差.为了有效的分离激子并促进电荷转移过程，有着不同电化学势的有机分子或者聚合物可以被结合在一起形成异质结.通常，具有较低电离势（IP）的材料被称作电子给体，而具有高的电子亲和势（EA）的材料被称作电子受体，两者结合形成的结构成为有机给体-受体结构[11-14].有机给体和受体结构可以通过范德华力或者共价键进行结合，并且，通过对给体和受体的结构进行化学改性，可以方便地调控有机给体-受体的结构性质.除了有机太阳能电池以外，有机给体-受体结构在有机发光二极管，有机场效应晶体管等领域都有着潜在的应用前景.因此，发展不同的有机给体-受体结构来满足不同的应用需求在近些年是研究的热点之一.

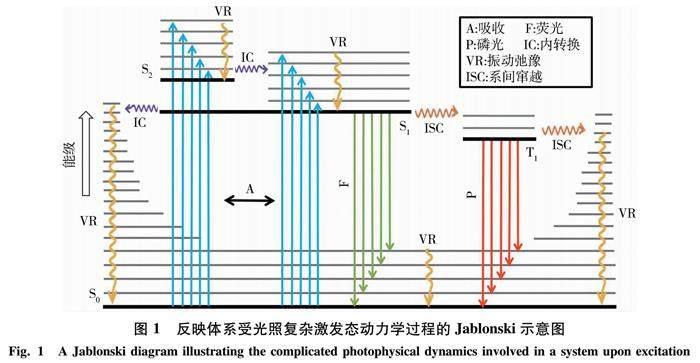
由于有机给体-受体的应用与其光诱导动力学过程密切相关，阐明其相关的微观机制是合理设计新型有机-给体受体结构的必由之路.然而，探究这些过程无论在理论还是实验上都具有极大的挑战性.首先，相关的过程往往涉及到多个电子激发态，能量高，寿命短，难以用常规的理论或实验手段进行研究;其次，这些过程往往涉及多个失活通道之间复杂的竞争过程，如图1所示，既包含荧光，磷光等辐射跃迁过程，也包含内转换，系间窜越等非辐射跃迁过程.最后，相比于气相小分子的光化学，有机给体-受体结构通常电子态更加密集，使得相关的光物理和光化学过程愈加复杂.理论上，非绝热动力学模拟（NAMD）是探究这些复杂的光诱导动力学过程[15-20].

原则上说，无论是电子还是原子核都属于微观粒子，都应当采用量子力学的方法来进行处理.然而，全量子动力学模拟的代价高昂，目前主要仍用于研究小分子或模型体系中.而目前在研究复杂体系中应用最广泛的一类非绝热动力学模拟方法称作混合量子-经典非绝热动力学模拟方法（MQC-NAMD）[21-22].在这类方法中，由于原子核的质量远大于电子质量，可以近似采用经典力学的方法来处理原子核的运动，而采用量子力学的方法研究电子运动.常见的MQC-NAMD方法有Erenfest平均场方法（EMF）[23-25]，轨线面跳跃方法（TSH）[26-27]以及量子轨迹平均场方法（QTMF）等[28-29]，其中TSH方法因其物理图景清晰，程序易于实现等优点应用最为广泛.TSH方法的核心在于认为体系在任意时刻只在单一势能面上运动，但是同时可以在不同的势能面之间发生跳跃.根据跳跃方法的不同衍生出了许多变体，如最少面跳跃方法（FSSH）[26-27]，Zhu-Nakamura面跳跃方法（ZNSH）[30-31]，退相干诱导面跳跃方法（DISH）等[32].尽管对有机给体-受体结构进行MQC-NAMD模拟的方法原则上与模拟气相小分子类似，但由于体系较大，许多适用于研究小分子的高精度电子结构计算方法无法用于计算有机给体-受体结构的激发态.因此，在从头算级别下，探究该类体系激发态性质最常用的电子结构计算方法是线性响应-含时密度泛函理论（LR-TDDFT）[33-34].然而，相关的非绝热动力学模拟方法仍比较少.

在这样的背景下，本课题组近期发展了基于LR-TDDFT的非绝热动力学模拟方法，通过将该方法与多种分析方法相结合，可以有效研究有机给体-受体结构超快的光诱导动力学过程，包括光诱导电荷转移，光诱导能量转移，以及激子动力学等过程.本文接下来将按照下面的顺序展开内容.首先，在第1部分介绍所发展的理论方法以及分析方法;随后，在第2部分通过几个具体的例子来说明该方法的应用;最后，在第3部分进行总结与展望.

1 方法

1.1 最少面跳跃方法（FSSH）

如前所述，TSH方法是最常用的混合量子-经典非绝热动力学模拟方法，存在多种不同的变体.在诸多TSH变体中，最经典的是Tully等[26]提出的最少面跳跃方法（FSSH），也是他们[27]在研究有机给体-受体结构光诱导动力学过程中采用的主要方法.因此，本部分对该方法以及相关的关键问题进行简要介绍.将核坐标R（t）作为参量，可以将含时Schrdinger方程写作

ih2πtΨ（r，R（t），t）=0（r，R（t））Ψ（r，R（t），t），（1）

其中，0是电子的零级哈密顿量，r表示电子坐标.含时电子波函数可以表达为绝热电子波函数的线性组合

Ψ（r，R（t），t）=∑Ni=1Ci（t）Ψi（r，R（t）），（2）

其中，Ψi为0在核坐标R（t）下的本征函数.通过将（2）式代入（1）式，左乘Ψ*j并对电子坐标积分，可以得到

ih2πtCj=CjEj-ih2π∑NiCiΛji，（3）

其中，Ej是绝热电子态j本征值，Λji=〈Ψj|tΨi〉是不同电子态之间的非绝热耦合项，并且该项还可以被写作核速度v与非绝热耦合矢量dji的点积，即Λji=v·dji.在Tully等[26]提出的最少面跳跃方法中，在t时刻从电子态i跃迁到j，Pij（t）可以写作

Pij（t）=max[0，2Re（C*iCjΛij）C*iCiΔt]，（4）

其中，Δt是积分（3）式时采用的时间间隔.在FSSH算法中，只有当2个条件同时满足时，从电子态i到电子态j的跃迁才可能发生.第一个条件是

∑j-1k=1Pik（t）

其中，rnd（t）是t时刻0到1之间的随机数.第二个条件则需要避免能量禁阻的跳跃过程，使得跳跃前后能量守恒.（3）式表明为了得到各个绝热特定时刻的电子态系数Cj，需要得到各个电子态的能量Ej以及不同电子态之间的非绝热耦合项Λji.此外，还需要得到特定结构下原子核的梯度或受力使得原子核坐标R可以根据牛顿运动方程进行演化.这些数据可以通过特定的电子结构计算方法得到，随着计算方法或采用的近似不同，计算量可能差异巨大.我们的工作主要采用LR-TDDFT进行电子结构计算，并且采用了经典轨迹近似来减少计算量.

此外，为了进行基于TSH的非绝热动力学模拟，我们还需要决定初始条件，包括初始坐标，速度以及特定波长光激发后到达的电子态等.可以通过Wigner取样和分子动力学模拟的方式来得到初始坐标和速度，前者由于需要计算频率，计算量较大，更适用于小分子体系;后者则可以用于分子，材料和生物体系，因此，在复杂体系的非绝热动力学模拟中应用更多.而对于初始电子态的选取，需要满足2个条件.首先，该电子态的垂直激发能需要接近实验所用的光子能量;第二，该电子态应该有足够大的振子强度.初始电子态既可以一次性赋予所有的初始结构，也可以通过计算每个结构的垂直激发独立选取.

最后，需要强调的是，常见的MQC-NAMD方法如EMF，TSH存在的一个问题是并未考虑量子退相干效应，可能会在一些情况下得到有问题的结果[35-37].因此，在轨迹演化过程中有必要进行退相干校正.目前进行退相干校正的方法有许多，我们主要是采用Zhu等[38]提出的，由Granucci等[39]拓展到TSH算法中的基于能量的退相干校正（EDC）方法.

1.2 LR-TDDFT级别下计算非绝热耦合项的高效算法

从上一小节可知FSSH动力学模拟的关键在于求解（3）式中的电子态系数，而求解电子态系数的关键在于得到各个电子态的能量以及不同电子态之间的非绝热耦合项.电子态的能量通常可以由电子结构计算软件直接给出，而非绝热耦合项的计算较为复杂.对于有机给体-受体结构，我们所采用的电子结构计算方法是LR-TDDFT，尽管可以通过解析的方法算出非绝热耦合矢量dji，然后利用与速度的点积得到非绝热耦合项Λji.但是由于Λji随着电子态数目的增多急剧增加，对于有机给体-受体结构，通过计算非绝热耦合矢量来得到非绝热耦合项的计算量巨大，难以用于实际体系的模拟.因此，我们所采用的是用数值方法计算Λji.而利用数值方法计算Λji的方式主要有2种：一种是基于Slater行列式的方法[40]，一种是基于分子轨道的方法[41].由于后者的计算效率远高于前者，我们在程序中主要采用的是后者来进行计算.下面对该方法进行简要介绍.依照惯例，下面的公式中下标{a，b，c}代表空轨道，{i，j，k}代表占据轨道，而{p，q，r}代表任意类型的轨道.

在LR-TDDFT中，任意激发态K的电子波函数ΨK可以近似写作单激发Slater行列式的线性组合

ΨK=∑occi∑unoccawKiaψai，（6）

其中，wKia未单激发Slater行列式ψai对应的组态系数，可以通过基态波函数构造得到.因此，非绝热耦合项ΛKJ=〈ΨK|tΨJ〉可以写作

ΛKJ=∑ijab（wK*iatwJjb〈ψai|ψbj〉+wK*iawJjb〈ψai|tψbj〉），（7）

其中，第一项可以根据分子轨道的正交归一性〈p|q〉=δpq简化为∑iawK*iatwJia，而第二项中ψbj对时间求导得到

tψbj=∑k≠jψbj{k}′+ψb′j，（8）

其中，ψqp{r}′表示该组态对应的行列式类似于ψqp，但是分子轨道r（r≠p）需要用tr来替换，而ψq′p表示该组态对应的行列式类似于ψqp，但是分子轨道p需要用tq来替换.因此，（7）式中的第二项可以写作

〈ψai|tψbj〉=∑k≠j〈ψai|ψbj{k}′〉+〈ψai|ψb′j〉，（9）

其中的第二项受正交条件〈j|tp〉=0以及〈p|q〉=δpq的影响可以进一步简化为δij〈a|tb〉，于是得到

〈ψai|tψbj〉=δij〈a|tb〉-Pijδab〈j|ti〉，（10）

其中，Pij是一个跟程序中Slater行列式构造方式相关的符号项.

最终，LR-TDDFT下非绝热耦合项可以表达为

ΛKJ=∑iawKiatwJia+∑iabwKiawJib〈a|tb〉-∑ijaPijwKiawJja〈j|ti〉，（11）

其中，分子轨道对时间的导数可以通过有限差分的方式进行计算

〈p|tq〉≈〈p（t）|q（t+Δt）〉2Δt-〈p（t+Δt）|q（t）〉2Δt，（12）

其中，p（t）和q（t+Δt）分别对应t和t+Δt时刻的分子轨道.

1.3 常用分析方法

除了传统TSH模拟中分析结构变化和态布居随时间变化的情况外，对于有机给体-受体结构，还可以结合多种基于LR-TDDFT的激发态电子结构分析方法，如电子-空穴密度，单电子跃迁密度矩阵，激子大小，光谱模拟等方法对该体系的激发态动力学进行更加全面的分析.在本节将对这些分析方法进行简要介绍.

（a） 半经典吸收光谱模拟.

吸收光谱可以通过Barbatti等[42-43]提出的半经典的方法进行模拟.基于N个基态结构Rk的集合，可以使用一阶含时微扰理论计算吸光横截面积.

σ（E）=πe22mcε0∑l≠i[1N∑Nkfil（Rk）×g（E-ΔEil（Rk），δ）]，（13）

其中，ε0为真空介电常数，c为光速，e和m对应电子电荷与质量，fil（Rk）和ΔEil（Rk）则为Rk坐标下从初始态i到末态l对应的振子强度和跃迁能量，g（E-ΔEil（Rk），δ）为以ΔEil（Rk）为中心，以常数δ作展宽的函数.实际应用中，常用的由2种展宽函数，分别是Gaussian型函数

gGauss（E-ΔEil，δ）=（2π）1/2h2πδexp（-2（E-ΔEil）2δ2），（14）

以及Lorentz型函数

gLorentz（E-ΔEil，δ）=hδ4π2[（E-ΔEil）2+（δ2）2]-1，（15）

其中，h是普朗克常数.主要采用Gaussian型函数来模拟初始态为基态，末态为激发态的吸收光谱.

（b） 基于片段的激子分析.

在多种分析有机给体-受体结构电子结构的方法中，有一种基于单电子跃迁密度矩阵的方法可以分析电荷转移过程.该方法可以在不同的原子轨道基上实现，如非正交的原子轨道（AO）或者Lwdin正交化原子轨道（LO）[44-45].我们采用的方法是用LO轨道进行研究.在该方法中，单电子跃迁密度矩阵TLO可以写作

TLO=（SAO）1/2TAO（SAO）1/2=（SAO）1/2（CTMOCT）（SAO）1/2，（16）

其中，C和SAO为分子轨道系数和非正交原子轨道重叠矩阵，而TAO和TMO代表AO和MO表示中的跃迁密度矩阵.由于Lwdin原子轨道的正交性，从a到b的跃迁变为

Dab=∑i∈a，j∈b（TLO）2ij，（17）

其中，i和j分别为原子轨道序号，a和b则为原子编号.因此，从片段D到片段A的跃迁密度可以写作

ΩDA=∑a∈D，b∈ADab，（18）

D=A和D≠A则分别表示D片段的局域激发态（LE）和从D到A的电荷转移激发态（CT）.据此，绝热激发态的LE和CT成分的贡献可以定量得到.ΩDA也可以视作不同的基于片段的局域激子和电荷转移激子的线性组合.此外，片段上的电子和空穴也可以计算得到.片段D上的空穴定义为

hD=∑a∈DDab=∑AΩDA，（19）

而片段A上的电子定义为

eA=∑b∈ADab=∑DΩDA.（20）

（c） 激子大小.

激子大小可以反映电子空穴之间的平均距离，对于研究电荷分离过程非常有用.我们采用下面的公式[46]计算激子大小

aΕ= ∑DMNa2MN，（21）

其中，DMN与由（17）式求得，而aMN为原子M和N之间的距离.

（d） 电子-空穴密度与D指数.

电子激发可以得到许多的电子-空穴对，对这些电子-空穴密度的分析非常有用[47-48].在该方法中，电子和空穴密度可以写作

ρhole（r）=ρholeloc（r）+ρholecross（r）=∑i→a（wia）2i（r）i（r）+∑i→a∑j≠i→awiawjai（r）j（r），（22）

ρele（r）=ρeleloc（r）+ρelecross（r）=∑i→a（wia）2a（r）a（r）+∑i→a∑i→b≠awiawiba（r）b（r），（23）

其中

∑i→a≡∑occi∑vira，∑i→a∑j≠i→a≡∑occi∑occj≠i∑vira;

而wia为单激发Slater行列式ψai对应的组态系数.i（r）和j（r）为空穴对应的分子轨道;a（r）和b（r）则为电子对应的轨道.根据电子-空穴密度，还可以定义一些有用的参数，比如电子和空穴之间的质心距离.

基于电子-空穴密度，可以计算得到电子在X，Y和Z方向上的质心位置

Xele=∫xρele（r）dr，（24）

Yele=∫yρele（r）dr，（25）

Zele=∫zρele（r）dr，（26）

空穴的质心可以用同样的方法得到.基于电子和空穴质心，可以计算3个方向上电子和空穴的质心距离，定义为

Dx=|Xele-Xhole|， Dy=|Yele-Yhole|，Dz=|Zele-Zhole|.（27）

最后，衡量电子和空穴质心距离的D指数定义为

DIndex=（Dx）2+（Dy）2+（Dz）2，（28）

该指数可以衡量电子和空穴分离的程度.

2 应用

2.1 ZnPc-C60结构的光诱导电荷转移与能量转移过程

一类代表性的给体-受体结构是由酞菁锌（ZnPc）和富勒烯（C60）组成的，其中酞菁锌作为电子给体，而富勒烯为电子受体.两者可以通过共价键或非共价键方式结合在一起[49-56].实验工作表明，当它们以非共价键的方式结合在一起时，光伏效率与其空间相对位置密切相关[52].简而言之，face-on的取向比edge-on的取向有更高的光电转换效率.此外，时间分辨光谱表明从ZnPc到C60的电荷转移过程可以在150 fs以内发生[56].然而，原子级别相关的微观机制还不清楚.为此，我们构造了face-on和edge-on的ZnPc/C60模型（图2（a）），并采用电子结构计算结合非绝热动力学模拟来研究其光激发后动力学过程的微观机制[57].计算结果表明，无论是哪种取向，吸收谱中的光谱明态都对应ZnPc的局域激发（LE）态.换言之，在光照后，电子和空穴初始时都局域在ZnPc分子上.然而，不同的取向却会导致不同电子态的能量发生变化.具体说来，在face-on取向中，从ZnPc到C60最低的电荷转移激发态能量低于ZnPc局域激发态的能量（图2（b）），表明光诱导电子转移过程在能量上是有利的.而在edge-on取向中，情况完全不同，最低的S1和S2态均为ZnPc的局域激发态，而电荷转移态（ZnPc→C60）则对应能量较高的S3和S4态（图2（b））.这说明在edge-on取向下，ZnPc局域激发后，从ZnPc到C60的电子转移过程在能量上并不是有利的.这些电子结构计算的结果进一步被非绝热动力学模拟所证实.如图2（c）中所示，初始布居的ZnPc局域激子|C60ZnPc〉可以在100 fs之内转换为电荷转移激子.该过程中还伴随着从ZnPc到C60的电荷转移过程，电子-空穴质心距离（D指数）增加的过程等.而在edge-on取向被激发后，没有发生复杂的动力学过程，电子和空穴在模拟时间尺度内始终位于ZnPc上.两者不同的激发态动力学过程可能是造成不同光电转换效率的主要原因之一.

除了上述通过非共价键结合在一起的ZnPc/C60体系外，两者通过共价键结合在一起的不同方式也可能对其激发态性质产生重要影响.如图3（a）所示，构造了2个以氧原子作为连接原子以共价键连接的ZnPc/C60复合物[58].根据不同的成键方式，一个结构称作56-bonding的结构，另外一个称为66-bonding的结构.采用类似的方法，首先计算了不同结构下最低的5个激发单重态，发现ZnPc的局域激发态在2个结构中仍为光谱明态.尽管该局域激发态的能量与非共价键形成的结构非常接近，该给体-受体的激发态性质确实与它们的成键类型密切相关，如图3（b）所示.在56-bonding结构中，ZnPc的局域激发态对应S3，S4，而S2为电荷转移态（ZnPc→C60）.此外，上面的未成键结构相比较，56-bonding结构下的S1对应C60的局域激发态.后续的非绝热动力学模拟则进一步表明ZnPc的局域激子首先转换为ZnPc→C60的电荷转移激子，而后转换为C60的局域激子.因此，整个过程可以被视作电荷转移态辅助的光诱导能量转移过程.与此同时，66-bonding结构中ZnPc的局域激发态对应最低的S1和S2态.在模拟过程中，电子和空穴始终局域在ZnPc片段，并未发生电荷和能量转移过程.这些结果说明，除了通过取向调整以外，化学键连接方式也可以作为一种调控有机给体-受体结构的有效手段.这对于调控有机给体-受体结构的光诱导能量和电子转移效率有非常重要的意义.

2.2 非富勒烯给体-受体结构PTB7-PDI的激发态动力学

上面讨论了富勒烯及其各种衍生物因其出色的电子迁移性作为受体的应用.然而，基于富勒烯的受体存在一些缺点，包括在紫外-可见光区吸收较弱、通过简单的化学修饰难以调节电子/光学性质以及光稳定性差等，这严重制约了它们在有机太阳能电池中的进一步发展.具体来说，由于光的吸收较弱，在基于富勒烯受体的有机太阳能电池中只存在一个电荷生成通道，即只有给体能够高效吸收光，光诱导的电子在激发后从给体传递到受体.这种电荷生成途径也被称为通道I电荷生成机制.然而，如果受体也能充分吸收光，光诱导的空穴从受体到给体的传递也可能参与电荷分离过程，即所谓的通道II电荷生成机制.为了充分利用这2个通道来提高有机太阳能电池的光电转换效率，在过去十年里，人们致力于开发基于非富勒烯受体（NFA）的有机太阳能电池.在各种非富勒烯受体中，基于苝二酰亚胺（PDI）的受体因其出色的光学性能和光稳定性而备受关注.

在2014年，Zhong等[59]通过周环反应设计并合成了螺旋状的PDI二聚体受体，如图4（a）所示.采用易得的聚合物PTB7或PBDTT-TT作为电子给体，相应有机太阳能电池的光电转换效率提高到6.0%以上.根据瞬态吸收光谱结果，他们提出在高能激发下2个通道都有望在电荷生成过程中发挥关键作用，这可能是其较高光电转换效率的原因.然而，这种非富勒烯给体-受体界面电荷生成的微观机制仍有待阐明.为此，我们构建了简化的PTB7/PDI模型，如图4（a）所示[60].考虑到计算量，我们只使用了3个结构单元来模拟聚合物PTB7，并简化了PTB7和PDI的所有烷基侧链.使用该模型得到的吸收光谱与实验定性一致，验证了简化模型和所选择的电子结构计算方法的可靠性.接下来，我们研究了PTB7/PDI模型系统的激发态动力学.根据模拟结果，我们发现在不同波长的激发下会发生不同的电荷生成过程.在591 nm处的激发主要生成局域激发激子|PTB7〉，而CT激子|PTB7+PDI-〉也有一些贡献（图4（b））.随着时间的推移，通道I电荷生成过程即从PTB7到PDI的电子转移在1 ps内完成，对应LE激子|PTB7〉到电荷转移激子|PTB7+PDI-〉的激子转换.在这个过程中，局域激发激子|PDI〉和电荷转移激子|PTB7-PDI+〉不参与其中.相比之下，在487 nm处激发时情况变得更加复杂（图5（c））.最初的激发将产生包括局域激发激子|PDI〉、|PTB7〉以及电荷转移激子|PTB7+PDI-〉在内的3种类型的激子.随后，在最初的250 fs内，电子首先从PDI转移到PTB7，然后在随后的模拟时间内又转移到PDI.与此同时，空穴在1 ps内从PDI单调地转移到PTB7.因此，在487 nm的激发下，通道I和通道II电荷生成过程在1 ps内超快进行.尽管存在这些差异，但在2种情况下都观察到了对可见光的吸收和超快电荷生成过程，这可能是改善此类有机太阳能的光电转换效率的原因.

2.3 分子聚集体PBQ激子动力学研究

除了上述电荷和能量转移动力学外，我们发展的方法还可以用于探索分子聚集体中的激子动力学.2018年，实验研究人员设计并合成了一种新型的苝双亚胺二聚体Bis-PBI，它可以自组装成苝双亚胺四聚体（PBQ）（图5（a））[61].借助广谱荧光上转换光谱（FLUPS）的帮助，他们提出了PBQ在激发后，有超快Frenkel激子弛豫和激基复合物形成过程.在激发后的50 fs内，最初相干的Frenkel激子态先离域化到整个四聚体上，随后在约200 fs内发生激子定域化.然而，这些结果是通过分析时间分辨光谱得到的，原子层面上的机制仍不明确.非绝热动力学模拟表明，光激发后，PBQ被激发到S6～S10态，这些绝热电子态可以看作来自4个PBI基团的局域激发激子和电荷转移激子的组合.随后，激发的PBQ在500 fs内经历了超快的弛豫，达到最低的激发态S1，并伴随着复杂的激子转换以及激子定域/离域动力学，如图5（b）和（c）所示[62].简而言之，最初产生的混合局域激发激子和电荷转移激子转变为B/C和A/D的局域激发激子，其中B/C的局域激发激子贡献最大（0.44），而A/D的局域激发激子也有较小的贡献（0.21），表明形成了局部激基复合物（图5（b））.这里使用的A/B/C/D标记表示PBQ中垂直于PBI分子平面方向上的4个PBI片段（图5（a））.此外，通过定义电子和空穴沿3个笛卡尔坐标方向的均方根偏差（RMSD），我们还可以以定量方式研究激子的定域/离域动力学（图5（c））.我们的模拟结果表明，PBQ的光诱导电子和空穴表现出超快的定域（约10 fs）→离域（约60 fs）→定域（约200 fs）的动力学，其中局域激发激子和电荷转移激子都发挥着不可或缺的作用.我们当前工作得到的结果与先前的实验研究一致，并提供了相关过程的更多细节.这样的见解可能有助于设计高性能的基于PBI的光电子器件.

3 总结与展望

本文介绍本课题组近期发展的适用于模拟有机给体-受体结构复杂激发态动力学的非绝热动力学模拟方法，包括具体的公式细节，以及其在探究一些典型的有机给体-受体结构中的具体应用.研究结果表明，我们所发展的方法不仅可以用于成功的解释实验结果，还可以提供更多的理论细节，为后续设计新型有机给体-受体结构提供非常有力的工具.

尽管取得了一定的成功，我们所发展的方法仍可以进一步进行改进.首先，尽管目前主要用的激发态电子结构方法是LR-TDDFT方法，相关的理论方法可以方便地被拓展到更高精度的单参考态电子结构计算方法.其次，原始的方法中只包含了相同自旋态之间的内转换过程，还可以通过自旋绝热或者自旋透热的方式将自旋-轨道耦合效应加以考虑，从而模拟包含不同自旋态之间系间窜越的过程;此外，该方法还可以与最优化调控范围分离泛函（OT-RSH）相结合，在不增加计算量的情况下可以进一步提高计算精度;通过与隐式连续极化溶剂模型（PCM）相结合，可以研究环境效应对这类结构光诱导动力学过程的影响;最后，目前的方法主要采用了经典轨迹近似，为考虑激发态对核运动的影响，后续发展实时的非绝热动力学模拟方法也是我们重要的目标之一.

参考文献

[1] HEDLEY G J， RUSECKAS A， SAMUEL I D W. Light harvesting for organic photovoltaics[J]. Chem Rev，2017，117（2）：796-837.

[2] ZHANG G， ZHAO J， CHOW P C Y， et al. Nonfullerene acceptor molecules for bulk heterojunction organic solar cells[J]. Chem Rev，2018，118（7）：3447-3507.

[3] CHENG P， LI G， ZHAN X， et al. Next-generation organic photovoltaics based on non-fullerene acceptors[J]. Nat Photonics，2018，12（3）：131-142.

[4] INGANS O. Organic photovoltaics over three decades[J]. Adv Mater，2018，30（35）：1800388.

[5] HODES G. Perovskite-based solar cells[J]. Science，2013，342（6156）：317-318.

[6] ASAHI R， MORIKAWA T， OHWAKI T， et al. Visible-light photocatalysis in nitrogen-doped titanium oxides[J]. Science，2001，293（5528）：269-271.

[7] THOMPSON T L， YATES J T. Surface science studies of the photoactivation of TiO2-new photochemical processes[J]. Chem Rev，2006，106（10）：4428-4453.

[8] HABISREUTINGER S N， SCHMIDT-MENDE L， STOLARCZYK J K. Photocatalytic reduction of CO2 on TiO2 and other semiconductors[J]. Angew Chem Int Ed，2013，52（29）：7372-7408.

[9] KONDRATENKO E V， MUL G， BALTRUSAITIS J， et al. Status and perspectives of CO2 conversion into fuels and chemicals by catalytic， photocatalytic and electrocatalytic processes[J]. Energy Environ Sci，2013，6（11）：3112-3135.

[10] CHEN J G， CROOKS R M， SEEFELDT L C， et al. Beyond fossil fuel-driven nitrogen transformations[J]. Science，2018，360（6391）：eaar6611.

[11] STOLTZFUS D M， DONAGHEY J E， ARMIN A， et al. Charge generation pathways in organic solar cells： assessing the contribution from the electron acceptor[J]. Chem Rev，2016，116（21）：12920-12955.

[12] WANG W， LUO L， SHENG P， et al. Multifunctional features of organic charge-transfer complexes： advances and perspectives[J]. Chem Eur J，2021，27（2）：464-490.

[13] 赵可清. 噻吩盘状液晶研究进展[J]. 四川师范大学学报（自然科学版），2019，42（3）：285-300.

[14] 张云峰，刘涛，薛慧玲，等. 染料敏化太阳能电池的研究进展[J]. 四川师范大学学报（自然科学版），2014，37（6）：929-941.

[15] ZHENG Q J， CHU W B， ZHAO C Y， et al. Ab initio nonadiabatic molecular dynamics investigations on the excited carriers in condensed matter systems[J]. Wires Comput Mol Sci，2019，9（6）：e1411.

[16] NELSON T R， WHITE A J， BJORGAARD J A， et al. Non-adiabatic excited-state molecular dynamics： theory and applications for modeling photophysics in extended molecular materials[J]. Chem Rev，2020，120（4）：2215-2287.

[17] BREDAS J L， NORTON J E， CORNIL J， et al. Molecular understanding of organic solar cells： the challenges[J]. Acc Chem Res，2009，42（11）：1691-1699.

[18] XIE B B， JIA P K， WANG K X， et al. Generalized Ab initio nonadiabatic dynamics simulation methods from molecular to extended systems[J]. J Phys Chem A，2022，126（11）：1789-1804.

[19] ZOBEL J P， HEINDL M， PLASSER F， et al. Surface hopping dynamics on vibronic coupling models[J]. Acc Chem Res，2021，54（20）：3760-3771.

[20] MALHADO J P， BEARPARK M J， HYNES J T. Non-adiabatic dynamics close to conical intersections and the surface hopping perspective[J]. Front Chem，2014，2：97.

[21] CRESPO-OTERO R， BARBATTI M. Recent advances and perspectives on nonadiabatic mixed quantum-classical dynamics[J]. Chem Rev，2018，118（15）：7026-7068.

[22] GAO L H， XIE B B， FANG W H. Theories and applications of mixed quantum-classical non-adiabatic dynamics[J]. Chinese J Chem Phys，2018，31（1）：12-26.

[23] BILLING G D. On the use of Ehrenfests theorem in molecular scattering[J]. Chem Phys Lett，1983，100（6）：535-539.

[24] NEGELE J W. The mean-field theory of nuclear structure and dynamics[J]. Rev Mod Phys，1982，54（4）：913-1015.

[25] DOLTSINIS N L， MARX D. First principles molecular dynamics involving excited states and nonadiabatic transitions[J]. J Theor Comput Chem，2002，1（2）：319-349.

[26] TULLY J C， PRESTON R K. Trajectory surface hopping approach to nonadiabatic molecular collisions： reaction of H+ with D2[J]. J Chem Phys，1971，55（2）：562-572.

[27] HAMMES-SCHIFFER S， TULLY J C. Proton transfer in solution： molecular dynamics with quantum transitions[J]. J Chem Phys，1994，101（6）：4657-4667.

[28] XIE B B， LIU L H， CUI G L， et al. Ab initio implementation of quantum trajectory mean-field approach and dynamical simulation of the N2CO photodissociation[J]. J Chem Phys，2015，143（19）：194107.

[29] SHEN L， TANG D D， XIE B B， et al. Quantum trajectory mean-field method for nonadiabatic dynamics in photochemistry[J]. J Phys Chem A，2019，123（34）：7337-7350.

[30] YU L， XU C， LEI Y， et al. Trajectory-based nonadiabatic molecular dynamics without calculating nonadiabatic coupling in the avoided crossing case： transcis photoisomerization in azobenzene[J]. Phys Chem Chem Phys，2014，16（47）：25883-25895.

[31] YU L， XU C， ZHU C. Probing the π-〉π* photoisomerization mechanism of cis-azobenzene by multi-state Ab initio on-the-fly trajectory dynamics simulation[J]. Phys Chem Chem Phys，2015，17（27）：17646-17660.

[32] JAEGER H M， FISCHER S， PREZHDO O V. Decoherence-induced surface hopping[J]. J Chem Phys，2012，137（22）：22A545.

[33] CASIDA M E. Time-dependent density-functional theory for molecules and molecular solids[J]. J Mol Struct：Theo Chem，2009，914（1/2/3）：3-18.

[34] MARQUES M A L， ULLRICH C A， NOGUEIRA F， et al. Time-dependent density functional theory[M]. Berlin：Springer，2006.

[35] SHU Y A， TRUHLAR D G. Decoherence and its role in electronically nonadiabatic dynamics[J]. J Chem Theory Comput，2023，19（2）：380-395.

[36] TRUHLAR D G. Decoherence in combined quantum mechanical and classical mechanical methods for dynamics as illustrated for non-born-oppenheimer trajectories[M]. Berlin：Springer，2007.

[37] SUBOTNIK J E， JAIN A， LANDRY B， et al. Understanding the surface hopping view of electronic transitions and decoherence[J]. Annu Rev Phys Chem，2016，67（1）：387-417.

[38] ZHU C Y， NANGIA S， JASPER A W， et al. Coherent switching with decay of mixing： an improved treatment of electronic coherence for non-born-oppenheimer trajectories[J]. J Chem Phys，2004，121（16）：7658-7670.

[39] GRANUCCI G， PERSICO M. Critical appraisal of the fewest switches algorithm for surface hopping[J]. J Chem Phys，2007，126（13）：134114.

[40] PITTNER J， LISCHKA H， BARBATTI M. Optimization of mixed quantum-classical dynamics： time-derivative coupling terms and selected couplings[J]. Chem Phys，2009，356（1/2/3）：147-152.

[41] RYABINKIN I G， NAGESH J， IZMAYLOV A F. Fast numerical evaluation of time-derivative nonadiabatic couplings for mixed quantum-classical methods[J]. J Phys Chem Lett，2015，6（21）：4200-4203.

[42] BARBATTI M， AQUINO A J A， LISCHKA H. The UV absorption of nucleobases： semi-classical Ab initio spectra simulations[J]. Phys Chem Chem Phys，2010，12（19）：4959-4967.

[43] CRESPO-OTERO R， BARBATTI M. Spectrum simulation and decomposition with nuclear ensemble： formal derivation and application to benzene， furan and 2-phenylfuran[J]. Theor Chem Acc，2012，131（6）：1237.

[44] PLASSER F， LISCHKA H. Analysis of excitonic and charge transfer interactions from quantum chemical calculations[J]. J Chem Theory Comput，2012，8（8）：2777-2789.

[45] HUANG J， DU L， HU D， et al. Theoretical analysis of excited states and energy transfer mechanism in conjugated dendrimers[J]. J Comput Chem，2015，36（3）：151-163.

[46] KRANER S， SCHOLZ R， PLASSER F， et al. Exciton size and binding energy limitations in one-dimensional organic materials[J]. J Chem Phys，2015，143（24）：244905.

[47] LU T， CHEN F. Multiwfn： a multifunctional wavefunction analyzer[J]. J Comput Chem，2012，33（5）：580-592.

[48] LIU Z Y， LU T， CHEN Q X. An sp-hybridized all-carboatomic ring， cyclo[18] carbon： electronic structure， electronic spectrum， and optical nonlinearity[J]. Carbon，2020，165：461-467.

[49] GULDI D M， GOULOUMIS A， VZQUEZ P， et al. Charge-transfer states in strongly coupled phthalocyanine fullerene ensembles[J]. Chem Commun，2002（18）：2056-2057.

[50] PARK S H， JEONG J G， KIM H J， et al. The electronic structure of C60/ZnPc interface for organic photovoltaic device with blended layer architecture[J]. Appl Phys Lett，2010，96（1）：013302.

[51] LANE P A， CUNNINGHAM P D， MELINGER J S， et al. Photoexcitation dynamics in films of C60 and Zn phthalocyanine with a layered nanostructure[J]. Phys Rev Lett，2012，108（7）：077402.

[52] RAND B P， CHEYNS D， VASSEUR K， et al. The impact of molecular orientation on the photovoltaic properties of a phthalocyanine/fullerene heterojunction[J]. Adv Funct Mater，2012，22（14）：2987-2995.

[53] BURTONE L， FISCHER J， LEO K， et al. Trap states in ZnPc∶C60 small-molecule organic solar cells[J]. Phys Rev B，2013，87（4）：045432.

[54] MNCH T， GUTTMANN P， MURAWSKI J， et al. Investigating local（photo-） current and structure of ZnPc∶C60 bulk-heterojunctions[J]. Org Electron，2013，14（11）：2777-2788.

[55] GAUL C， HUTSCH S， SCHWARZE M， et al. Insight into doping efficiency of organic semiconductors from the analysis of the density of states in N-doped C60 and ZnPc[J]. Nat Mater，2018，17（5）：439-444.

[56] WANG T， KAFLE T R， KATTEL B， et al. A multidimensional view of charge transfer excitons at organic donor-acceptor interfaces[J]. J Am Chem Soc，2017，139（11）：4098-4106.

[57] LIU X Y， LI Z W， FANG W H， et al. Nonadiabatic exciton and charge separation dynamics at interfaces of zinc phthalocyanine and fullerene： orientation does matter[J]. J Phys Chem A，2020，124（37）：7388-7398.

[58] LI Z W， YANG J J， LIU X Y， et al. Chemical bonding as a new avenue for controlling excited-state properties and excitation energy-transfer processes in zinc phthalocyanine-fullerene dyads[J]. Chem Eur J，2021，27（12）：4159-4167.

[59] ZHONG Y， TRINH M T， CHEN R， et al. Efficient organic solar cells with helical perylene diimide electron acceptors[J]. J Am Chem Soc，2014，136（43）：15215-15221.

[60] XU D H， CHEN Y， ZHANG S Y， et al. Excitation wavelength-dependent charge generation dynamics in a nonfullerene organic solar cell interface[J]. Sol RRL，2021，5（3）：2000719.

[61] KAUFMANN C， KIM W， NOWAK-KRL A， et al. Ultrafast exciton delocalization， localization， and excimer formation dynamics in a highly defined perylene bisimide quadruple π-stack[J]. J Am Chem Soc，2018，140（12）：4253-4258.

[62] ZHANG S， ZENG Y P， WAN X J， et al. Ultrafast exciton delocalization and localization dynamics of a perylene bisimide quadruple π-stack： a nonadiabatic dynamics simulation[J]. Phys Chem Chem Phys，2022，24（12）：7293-7302.

Nonadiabatic Dynamics Simulations on the Photoinduced Dynamics

of Organic Donor-Acceptor Compounds： Methods and Applications

LIU Xiangyang， LIU Shasha

（College of Chemistry and Material Science， Sichuan Normal University， Chengdu 610066， Sichuan）

Abstract：Investigating the photoinduced dynamics in organic donor-acceptor （D-A） structures， one of the key components for organic solar cells， is crucial for designing novel organic solar cells. Nonadiabatic dynamics simulations are important theoretical methods for studying these processes. However， compared to small molecular systems， organic D-A structures are often more complex， computationally demanding， and challenging to employ high-level nonadiabatic dynamics simulation methods. To overcome this challenge， this paper introduces a nonadiabatic dynamics simulation method developed by our group based on linear-response time-dependent density functional theory （LR-TDDFT）. By combining various analysis methods， this approach effectively explores the photoinduced dynamics in organic D-A structures， such as charge transfer processes， energy transfer processes， and exciton dynamics. This method can not only be used to elucidate available experimental results but also assist in the subsequent design of new organic D-A structures.

Keywords：organic solar cell; donor-acceptor compound; photochemistry and photophysics; nonadiabatic dynamics simulations; linear-response time-dependent density functional theory

（编辑 周 俊）

基金项目：四川省科技厅科技计划项目（2020YJ0161）

第一作者简介：刘向洋（1993—），男，副研究员，博士，博士生导师，主要从事复杂分子、生物和材料体系光物理和光化学过程理论的研究，E-mail：xiangyangliu@sicnu.edu.cn

引用格式：刘向洋，刘莎莎. 有机给体-受体结构光诱导过程的非绝热动力学模拟：方法与应用[J]. 四川师范大学学报（自然科学版），2024，47（5）：638-649.