多配送中心的末端物流配送研究

王扬　张文浩

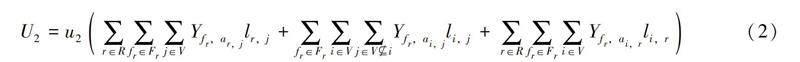
关键词：车辆路径问题；末端物流配送；深度强化学习

中图分类号：F252文献标识码：A文章编号：2096-7934（2024）04-0078-10

一、引言

物流是一个复合型产业，主要由发货方、收货方以及将二者联系在一起的快递公司组成，其中又涉及到了仓储、运输、配送、信息共享等多个方面，是集多方面于一体的综合性服务产业，对国家经济的发展起到了不可忽视的作用［1］。随着社会分工的不断细化，各个地区的经济往来不断密切，经济结构和产业结构的调整是必然的进程，对我国当前的产业结构进行分析，可以得出第三产业已经成为我国经济支柱产业的结论，而物流行业正是属于第三产业的服务业，因此，对物流的发展进行研究有助于我国经济的发展和社会的进步［2］。1978年“物流”这一概念第一次引入我国，随后物流产业不断发展，四十余年后的今天，我国已经成为全球物流总额最大的国家［3］，形成了一个完备的物流体系。我国物流总额不断增加的情况，既体现出了物流行业高速发展的大环境，同时也在一定程度上体现出物流行业中庞大的成本，如果能在当前的基础上节约成本，无疑是对物流行业的正向激励，对我国经济的发展也有不可忽视的作用。

小批量、多批次是目前城市末端配送的两大特点，现有的城市物流管理体系未对末端的配送进行统一规划，导致参与末端配送的配送主体混杂，服务质量参差不齐，物流资源浪费严重，大量的物流配送车辆一定程度上也加剧了城市的拥堵，影响城市的交通效率［4］。如果可以对配送车辆的行驶路径进行优化，无疑可以提高配送效率。

车辆路径问题（Vehicle Routing Problem， 以下简称“VRP”）最早在1959 年被丹齐格（Dantzig）和拉姆瑟（Ramser）提出［5］，并提出了基于线性规划的求解过程，之后受到了众多学者的关注，在随后的几十年里，VRP问题得到不断的扩充和发展。

自车辆路径问题被提出后，利纳斯（Linus）（1981），博丁（Bodin）和戈尔登（Golden）（1981），阿萨德（Assad）（1988），德罗谢尔（Desrochers）（1990）等许多学者从不同视角，按不同标准对该问题进行了分类［6］。

其中，按车辆类型可分为单车型问题和多车型问题，单车型问题指所有车辆的容量都给定同一值，多车型问题指所有车辆的容量都给定不同值；按配送中心（车场）数目可分为单配送中心（车场）问题和多配送中心（车场）问题；按有需求点有无时间窗要求，可分为无时间窗问题、硬时间窗问题、软时间窗问题。硬时间窗问题指车辆必须在时间窗内到达，早到则等待，晚到则拒收。软时间窗问题指车辆不一定要在时间窗内到达，但是在时间窗外到达必须受到惩罚。

多车型车辆路径问题是车辆路径问题的一种扩展。根据车辆的型号是否相同，可将车辆路径问题分为单车型问题（Homogeneous Vehicle Routing Problem，以下简称“VRP”）和多车型问题（Heterogeneous Vehicle Routing Problem，HVRP）［7］。戈尔登（Golden）等人于1984年首次对不同的车辆类型建立了假设，并以此假设为约束，提出了多车型的车辆路径问题，之后通过启发式算法进行了计算［8］。之后汉达（Handa）对多车型车辆路径的数学模型进行了拓展，并提出了一个新的下界［9］。刘（Liu）针对多车型车辆路径问题的两个延伸问题进行了研究：一个是仅具有可变成本的多车型车辆路径问题，另一个在前者的基础上添加了固定成本，并设计了一种能够同时求解这两个变体问题的混合种群启发式算法［10］。

多车场车辆路径问题（Multi-Depot Vehicle Routing Problem，以下简称“MDVRP”）是基本车辆路径问题的扩展，指的是有数个车场同时对多个用户进行服务，要求对各车场的车辆和行驶路线进行适当的安排，在保证满足各用户需求的前提下，使总的运输成本最低。MDVRP 最早由蒂尔曼（Tillman）于1969年采用节约算法进行求解［11］。随后，蒂尔曼（Tillman）等人在1972年对先前采用的节约算法进行了改进，再次对MDVRP进行了更加高效的求解［12］。之后雷恩（Wren）等人通过扫描算法对先前的求解过程进行了改进，使得多车场的路径规划问题可求解规模扩大到5个配送中心［13］。近年来汤雅连等人通过改进蚁群算法对多车场的车辆路径问题进行了求解，其依靠3-opt策略来提高算法的局部搜索能力，将提出的算法应用在3个随机产生的实例中，使得精确度得以提高［14］。叶勇等人针对动态的多车场模型，建立最小化车辆行驶里程的数学模型，并运用狼群算法对其进行求解［15］。李（Li）等人以收益最大化、成本最小化、时间最小化和碳排放最小化为目标，设计了改进的蚁群算法对该问题进行求解，算法使用了一种新的方法来更新信息素，获得了更优的解决方案［16］。布兰度（Brando）研究了开放多车场车辆路径问题，车辆在向客户交付货物后不返回原车场，即路线的终点不是起点，提出了一种迭代局部搜索算法来求解该问题［17］。凡（Fan）等人考虑了车辆的速度、负载和道路的坡度对燃油消耗的影响，建立了车辆的固定成本、时间惩罚成本以及运输成本总和最小的整数规划数学模型。

带时间窗的车辆路径问题（the vehicle routing problem with time windows，以下简称“VRPTW”）是指若干车辆从配送中心出发，给周边客户进行配送货物。每个客户都有接受服务的时间范围，配送服务必须在相应的时间窗内进行［18］。陈（Chen）等人提出一种结合了和声搜素算法和可变邻域下降算法求解带时间窗的动态车辆路径问题［19］。尼（Ni）等人建立一种带软时间窗约束的模糊需求车辆路径模型，采用改进的遗传算法求解该模型，得到了最优配送路径［20］。哈勒（Khale）等人提出了一种硬时间窗约束条件下车辆路径问题的精确求解方法，该算法以一种紧凑的方式形成标签，将资源需求松弛信息整合到其中［21］。

深度强化学习（Deep reinforcement learning，以下简称“DRL”）作为一种近年来应用较多的求解方法，在处理连续问题时取得了较多的成果。其特点在于训练时间较长，测试时间较短，如果能够将训练好的模型应用到现实车辆路径规划问题中，便可以提高配送效率，降低配送成本。

温亚尔斯（Vinyals）首次将指针网络与VRP问题相结合，使得在输入维度时，不会因为维度限制模型的架构，但是该研究主要是用以解决小规模的车辆路径决策问题［22］。李（Li）提出了一种利用DRL解决多目标优化问题的想法，即将一个总的优化目标分解成多个子目标，通过建立一个端到端的模型框架求解问题［23］。福克纳（Falkner）等人提出了一种双向的搜索模型，该模型的双向编码器会分别学习节点和位置特征的嵌入，一次提高DRL在求解VRP问题时的速度和精准度［24］。哈利勒（Khalil）等人提出了一种将强化学习与图嵌入神经网络相结合的框架，然后通过Q-Learning来学习贪婪策略的想法，以此扩大求解范围［25］。

综合来看，用深度强化学习来求解车辆路径问题，其所使用的算法在求解时的策略更新幅度较大，在这种情况下，往往需要花费较多的时间找到最优解。因此，本文在现有研究的基础上，建立一个多配送中心的数学模型，利用近端策略优化算法中以新旧策略变化幅度来控制状态更新的特点，求解多配送中心的末端物流配送模型。

二、多配送中心末端物流配送模型

（一）问题描述

有多个配送中心，不同配送中心有隶属于各自配送中心的车辆，车辆首先在各自的配送中心装载快递包裹，包裹分配结束后，各车辆出发，按照所装载快递包裹的需求点依次进行配送，在将所有的快递包裹配送完成后，车辆返回各自的配送中心，具体描述如下。

1.配送中心分配货物

在配送中心接收到需要进行末端配送的货物后，需根据不同快递包裹目的地，将不同的包裹分配给不同的配送人员进行配送。为了保证分配过程的合理性和精确性，对每个包裹分别进行决策，选择最合适的配送人员完成后续配送过程。

2.配送车辆配送货物

不同配送中心有不同的配送车辆，其配送过程可以大致分为由配送中心到第一个快递柜以及第一个快递柜到后续快递柜（返回配送中心）两个过程。在完成一个地点的配送工作后，配送人员需要对下一个配送目的地进行决策，以保证选择出的路径最合理，所有包裹配送完成后，各配送车辆返回各自的配送中心。

（二）模型假设

①配送中心和配送终点的坐标位置已知。②不考虑包裹重量和体积的影响。③不考虑道路状况、天气条件、车辆行驶距离的影响。④所有车辆的型号都相同，配送人员的业务水平都相同。

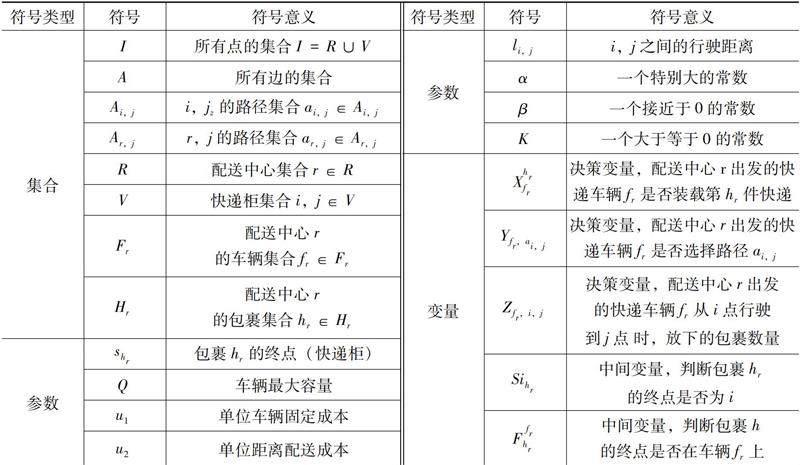
（三）符号定义

（四）目标函数

该模型的目标函数为配送总成本最小，配送成本包括固定成本与可变成本。

表1 多配送中心模型符号定义

1.固定成本

固定成本是指与车辆的使用或者配送过程中固定的成本，不论行驶的距离或货物的数量如何变化，其成本不变。包括车辆购买或租赁成本、车辆保养和维护成本、保险费用、车辆存储和停车费用以及管理成本。本次研究模型的固定成本仅与参与配送的车辆数目有关。

式（1）表示所有参与配送车辆的总固定成本。

2.可变成本

可变成本是指随着配送过程而变化的成本，包括燃料成本、车辆损耗成本等。本次研究模型的可变成本仅与车辆的行驶距离有关。

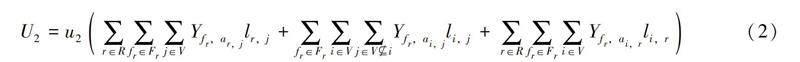
式（2）表示所有参与配送车辆的可变成本。

（五）数学模型

1.目标函数

2.约束条件

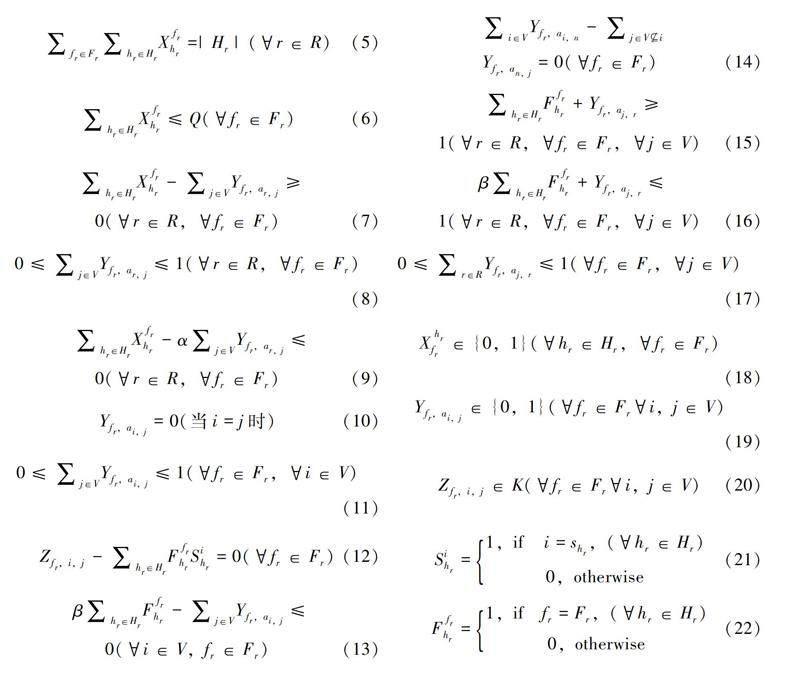
3.模型解释

式（3）为目标函数，表示配送总成本最小。目标函数分为两个部分，一个是固定成本，由配送车辆的数量决定，另一个是可变成本，由所有车辆行驶的总距离决定；式（4）表示在配送中心进行快递包裹分配时，对于任何一件包裹，只能且必须放在某个配送中心的某一辆车上；式（5）表示某一配送中心所有配送车辆在完成整个分配过程后，所有车辆总计装载的包裹数量等于该配送中心的包裹总量；式（6）表示任意配送中心任意车辆的初始装载量都要小于车辆的最大容量限制；式（7）表示车辆发车约束，当车辆没有装载快递时，该车辆不能参与配送；式（8）表示从任意配送中心出发的车辆，只能选择一个快递柜作为初始目的地；式（9）表示当车辆装载快递时，该车辆必须发车，参与后续配送过程；式（10）表示排除某辆车决策到同一个快递柜的情况，即避免决策出的下一目的地仍为此配送点；式（11）表示任意车辆由快递柜i到j时，只有一个方向可以选择；式（12）表示车辆在i放下的包裹数量为该车携带的以i点为终点的包裹数量；式（13）表示车辆在装载货物时，必须前往下一个快递柜处；式（14）表示路径连续性约束，其中n为某个快递柜的索引且n≠i，j ；式（15）表示车辆在配送结束后需返回原配送中心；式（16）表示从任意配送中心出发的车辆在完成某次配送后，若还存在包裹，车辆继续配送；式（17）表示在车辆返回配送中心时，只有一个方向可以选择；式（18）至式（22）为变量约束。

三、算法设计

由于常规的启发式算法在解决规模较大的问题时，难以适应环境的变化，求解准确度可能存在一些问题，而深度强化学习DRL能够从与环境的交互中学习，并不断优化其决策策略。DRL通过试错学习并逐步改进策略，特别适用于那些难以为人类直觉所理解的高维或连续动作空间问题。因此本次研究考虑通过深度强化学习对问题进行求解。

在深度强化学习中，环境和策略是两个核心概念，它们共同定义了学习过程的动态和目标。环境在深度强化学习中扮演着至关重要的角色。它是智能体进行学习和交互的外部世界的抽象表示。环境的特征包括状态、动作以及反馈机制。环境的设计需要平衡现实性和计算效率。过于复杂的环境可能会增加学习的难度和计算成本，而过于简单的环境可能会导致无法抓住现实问题的关键点。

策略是智能体在给定状态下采取动作的规则。在深度强化学习中，策略通常由深度神经网络表示，能够处理高维的输入并输出相应的动作。策略可以分为确定性策略和随机性策略，确定性策略是指对于给定的状态，某一策略总是产生相同的动作。这种策略适用于环境动态较为确定的情况。随机性策略是指在某些状态下，某一策略会根据概率分布选择动作。这种策略有助于探索环境，防止策略陷入局部最优解之中。

（一）环境设置

为了求解此次研究的问题，需要首先建立环境以此模拟场景。建立的环境里有若干个配送中心和若干个配送终点。每个配送中心有一定数量的车辆，这些车辆需要将包裹送达不同的配送终点。具体来看，这个环境包含以下五点内容。

1.状态空间

状态空间定义了智能体可以感知的所有可能环境状态。在深度强化学习中，状态通常是高维的，可能包括图像、传感器数据或其他形式的观测信息。状态空间的大小和复杂性决定了问题的难度。例如，在棋盘游戏中，状态空间包括棋盘上所有可能的棋子排列；在自动驾驶车辆中，状态空间可能包括周围环境的高维传感器数据。

在此次研究内容中，状态表示当前的配送情况。它包括每个配送终点已经配送完成的快递包裹数量，还未配送的快递包裹数量，当前配送车辆的位置，配送车辆已装载的快递包裹数量等信息。

2.动作空间

动作空间是强化学习中的一个关键概念，它定义了在特定环境下智能体可以执行的所有可能的动作。动作空间的设计对于强化学习算法的性能有着重要的影响，因为决定了智能体如何与环境互动以及如何学习完成特定任务的策略。

此次研究中设置的动作主要由两部分组成，分别是选择的配送终点和在配送终点放下的包裹数量。这两个部分使得建立的模型能够决定某一配送车辆下一个要访问的位置和该车辆在某一配送点需要放下包裹的数量。

3.奖励机制

奖励机制是强化学习的核心，它定义了智能体接收奖励（或惩罚）的条件。奖励通常是一个数值信号，指导智能体学习如何改进其行为以最大化总奖励。设计有效的奖励机制是成功应用深度强化学习的关键，其决定了智能体的学习目标和优化方向。

在此次研究中，奖励的优劣主要基于是否能有效减少车辆的行驶距离以及能否在某个配送点尽可能放下更多的快递包裹。如果配送车辆选择了合适的配送终点并成功放下了较多数量的包裹，那么此次动作就会得到正奖励；如果选择了一个配送终点，但在该位置没有包裹需要被放下，或者车辆行驶距离相对较远，那么此次动作可能会得到负奖励。

4.环境动态

车辆在完成一个动作后，环境的状态也会发生变化，因此，需要把这个变化结果表示出来。如更新配送车辆的位置，计算移动到新配送终点的距离，更新各配送终点完成与未完成的包裹数量等。

5.结束条件

根据模型中设置的约束条件，当所有包裹都被送达后结束。

（二）策略设置

由于车辆可以选择的配送点较多，且每个配送点的货物需求量有有所不同，因此环境中所涉及的状态较多，在这种情况下，求解所需的时间可能较长，因此为了尽可能缩小求解时间，需要避免在探索最优解时所产生的波动，基于这种特点，本文考虑通过使用PPO算法来解决问题。

近端策略优化（Proximal Policy Optimization，以下简称“PPO”）是一种用于深度强化学习的优化算法。PPO算法由OpenAI的研究人员于2017年提出，具有较易实现，并且在多种环境中表现出良好的性能的特点。设计此类算法的初衷是解决策略梯度方法中的一些问题，例如难以稳定和调整的训练过程，防止出现波动较大而结果难以收敛的情况。

PPO之所以更稳定，是因为其核心思想是在每次更新策略时，尽量减少从旧策略到新策略的变化，从而避免在学习过程中出现大的波动。故在构建目标函数时，为了体现出新旧策略的变化，通过KL散度来表示两种策略的差异性。

四、案例求解

本章针对O1公司、O2公司、O3公司2023年某日的实际订单数据进行求解，分别选取3家公司各1个配送中心。

（一）案例数据

表2 包裹配送数据

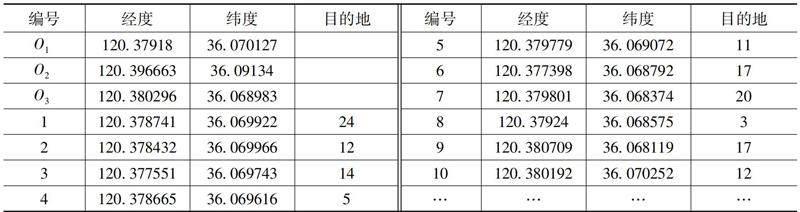
（二）参数设置

设置如下参数：固定费用，单位为元/次，取值为30；单位运费，单位为元/公里，取值为1.5。

（三）求解结果

经过深度强化学习求解，得到的不同配送中心的车辆配送路径如图1至图3所示。其配送总成本1397.88，调动车辆24辆，总行驶距离451.92公里。

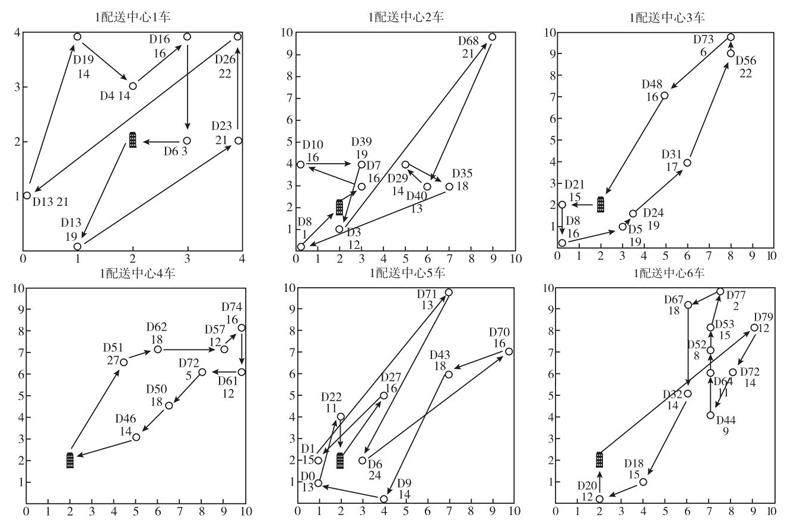
图1 多配送中心S公司求解路径

图2 多配送中心Y公司求解路径

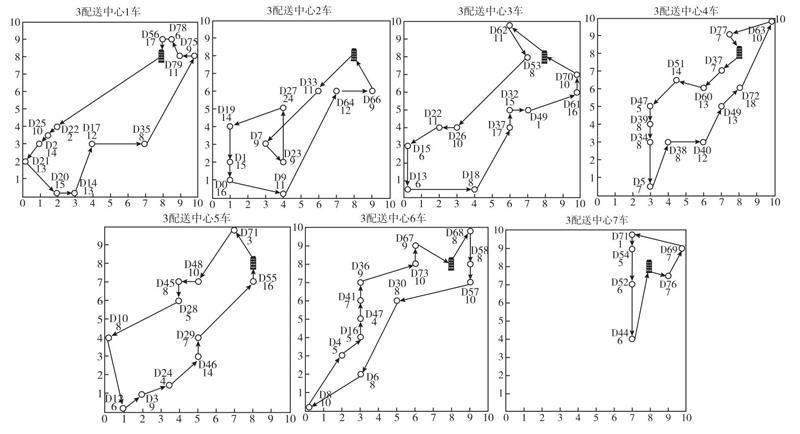
图3 多配送中心J公司求解路径

（四）结果分析

在配送中心位置、配送点位置以及配送点需求量已知的情况下，本次研究通过建立车辆配送的数学模型，进而将数学模型转化为深度强化学习的求解模型，实现了对多配送中心车辆配送问题的求解。

由以上车辆配送路径图中可以看出，在求解出的路径中，配送点之间间隔距离较小时，能够保证车辆可以通过较少的配送距离完成较多快递包裹的配送任务；同时线路交叉情况较少，在这种情况下提高了避免了配送车辆走重复的路线的可能，减少了车辆的行驶距离。车辆的配送路径也较为合理，所规划的路径连续性强，基本避免了配送车辆出现大距离折返的情况。

同时也可以发现，在某些配送点，车辆配送的快递包裹数量较少，为了配送少量包裹而行驶较远的距离，例如，1配送中心的7车前往D74配送点进行配送时，仅完成了5个快递包裹的配送任务以及2配送中心的2车在前往D78配送点进行配送时，仅仅为了完成7个包裹的配送任务，就付出了较大的距离成本，这种配送方式显然“性价比”不高，无疑提高了配送成本。

五、结论与启示

本文基于多配送中心的车辆路径问题，建立了以包裹状态为研究对象的数学模型，设计了深度强化学习中的环境状态，并以PPO为策略网络对案例进行求解，最终求解结果表明，以深度强化学习结合不同包裹的配送状态对问题进行求解这一思路具有可行性，所求解出的车辆配送路径较为合理，基本没有出现车辆绕路行驶的情况。另外针对某些配送点配送包裹数量较少的问题，后续还需针对此方向进行扩展研究。

参考文献：

［1］赵林度.中国物流研究现状及发展趋势［J］.物流研究，2020（1）：1-10.

［2］王珊珊.制度变迁视角下中国物流行业发展政策演变研究［D］.北京：北京邮电大学，2021.

［3］魏际刚.中国物流业发展的现状、问题与趋势［J］.北京交通大学学报（社会科学版），2019，18（1）：1-9.

［4］邢少伟.考虑同时取送货的电动无人车末端协同配送研究［D］.重庆：重庆邮电大学，2021.

［5］DANTZIG G B， RAMSER J H.The truck dispatching problem.［J］.Management science 2020，6（1），80-89.

［6］李军，郭耀煌.物流配送车辆优化调度理论与方法［M］.北京：中国物资出版社，2001.

［7］陈君兰，叶春明.物流配送车辆调度问题算法综述［J］.物流科技，2012，35（3）：8-12.

［8］史春燕，黄辉.车辆路径问题：研究综述及展望［J］.物流科技，2014，37（12）：75-77.

［9］GOLDEN B， ASSAD A， LEVY L， et al.The fleet size and mix vehicle routing problem［J］.Pergamon， 1984， 11（1）：49-66.

［10］HANDE Y.Formulations and alid inequalities for the heterogeneous vehicle routing problem［J］.Mathematical programming，2006，106（2）：365-390.

［11］TILLMAN F A.The multipl terminal delivery problem with probabilistic demands［J］.Transportation science，1969，3（3）：192-204.

［12］TILLMAN F A， CAIN T M.An upperbound algorithm for the single and multiple terminal delivery problem［J］.Management science，1972，18（11）：664-682.

［13］GOLDEN B L， MAGNANTI T L， NGUYEN H Q.Implementing vehicle routing algorithms［J］.Networks，1977，7（2）：113-148.

［14］汤雅连， 蔡延光， 杨期江.求解带软时间窗多车场多车型车辆路径问题的一种改进蚁群算法（英文）［J］.Journal of southeast university（English Edition），2015，31（1）：94-99.

［15］叶勇，张惠珍.多配送中心车辆路径问题的狼群算法［J］.计算机应用研究，2017，34（9）：2590-2593.

［16］LI Y， SOLEIMANI H， ZOHAL M.An improved ant colony optimization algorithm forthe multi-depot green vehicle routing problem with multiple objectives［J］.Journal of cleaner production，2019，227：1161-1172.

［17］BRANDO J.A memory-based iterated local search algorithm for the multi-depotopen vehicle routing problem［J］.European journal of operational research，2020，284（2）：559-571.

［18］FAN H， ZHANG Y， TIAN P， et al.Time-dependent multi-depot green vehiclerouting problem with time windows considering temporal-spatial distance［J］.Computersand operations research，2021：105211.

［19］OLOMON M M.Algorithms for the vehicle routing and scheduling problems with time window constraints［M］.Informs，1987.

［20］CHEN S F， CHEN R， GAO J， et al.A modified harmony search algorithm for solving the dynamic vehicle routing problem with time windows［J］.Scientific programming，2017.

［21］NI S Q.Fuzz demand vehicle routin problem with soft time window based on genetic algorithm［J］.Management sciencean engineering，2018，12（3）.

［22］SILVER D， HUANG A， MADDISON C J， et al.Mastering the game of go with deep neural networks and tree search［J］.Nature，2016，529（7587）：484-489.

［23］VINALYS O，FORTUNATO M，JAITLY N.Pointer net-works［J］.Advances in neural information processing systems，2015.

［24］LI K， ZHANG T， WANG R.Deep reinforcement learning for multi-objective optimization［J］.IEEE transactions on cybernetics，2020，51（6）：3103-3114.

［25］FALKNER J K，THYSSENS D，SCHMIDT T L.Large neighborhood search based on neural construction heuristics［J］.Computer science，2022，2.

Research on Terminal Logistics Distributionwith Multiple Distribution Centers

WANG Yang，ZHANG Wen-hao

（Beijing University of Technology， Beijing 100124）

Abstract：The terminal logistics distribution process is the most complex one for the participating parties， and its distribution cost and efficiency are closely related to the logistics company and customers.This paper focuses on the logistics distribution situation of multiple distribution centers， with the goal of minimizing distribution costs， and establishes a logistics distribution mathematical model.Then， by designing deep reinforcement learning algorithms， a learning environment is established， and the case is solved to obtain the driving path of distribution vehicles.The results show that using deep reinforcement learning to solve the vehicle routing problem is highly feasible.

Keywords：vehicle routing problem;terminal logistics distribution;deep reinforcement learning