精选学习素材 提升思维含量

王之忠

摘   要：教师在教学时要精选学习素材，提升思维含量。以人教版小学数学三年级下册“两位数乘两位数整理与复习”一课为例，帮助学生在口算中理解运算一致性，秉承“温故知新”原则，让学生在复习中获得新的认识，让数学知识转变成解决问题的能力。使学生通过学习，在笔算中经历推理过程，在计算中解决实际问题。教师要合理选择学习素材，提高学习动力与效果，避免浪费时间。

关键词：小学数学；单元复习；数学思维；计算推理

中图分类号：G623.5   文献标识码：A   文章编号：1009-010X（2024）16-0017-03

“两位数乘两位数”是人教版三年级下册第四单元的教学内容，这个单元的主要内容是10乘两位数和整十数乘整十数的口算、两位数乘两位数的估算、两位数乘两位数的笔算、两步连乘计算的实际问题等。教师在教学“两位数乘两位数整理与复习”时，秉承着“温故知新”的原则，“温故”就是要帮助学生复习和巩固这个单元中的知识，对薄弱的知识进行查漏补缺；“知新”就是要让学生在复习中获得新的认识，让数学知识转变成解决问题的能力。

教师要精选学习素材，科学设计学习任务，确定复习课的教学目标：1.通过整理和复习，找出本单元主要学习哪些知识点，查漏补缺，建立清晰全面的知识结构，将所学知识条理化和系统化；2.进一步理解和掌握两位数乘两位数的算理和算法，沟通笔算乘法的关系，渗透转化的数学思想；进一步理解乘法运算的变化，灵活运用各种方法解决问题；3.在解决问题中，提高学生综合分析、信息处理和灵活选择解决策略的能力，培养学生自主学习、自主归纳、自主整理的意识。

一、在口算中理解运算一致性

《义务教育数学课程标准（2022年版）》（以下简称《课标》）中指出，感悟数的运算以及运算之间的关系，体会数的运算本质上的一致性，形成运算能力和推理意识。乘法的运算一致性主要表现在计数单位与计数单位相乘，计数单位上的数字与计数单位上的数字相乘。因此，教师精心挑选了六道计算题，其中包括整十数乘整十数、两位数乘两位数、三位数乘一位数、两位数乘一位数等，让学生选择哪些类型更加适合口算。

师：同学们，这节课我们来复习两位数乘两位数的乘法。（出示：48×43=336）这道题目的结果是错误的，你是怎么看出来的？

生1：48×43，我们可以用竖式计算，先算48×3=144，再算48×40=1920，最后144+1920=2064。

生2：我把48看成50，把43看成40，50乘40等于2000，所以48乘43约等于2000。但是2000和336相差很大，所以是错误的。

师：第一位同学是借助笔算，第二位同学是用估算，一眼就判断出这道题是错误的，口算、估算和笔算是这个单元主要学习的内容。（出示：①23×50，②28×33，③290×3，④17×44，⑤50×40，⑥38×23，⑦31×4，⑧49×12）同学们，请你看一看哪几题可以不计算直接口算？

生3：①、③、⑤、⑦。

师：你能说一说你是怎么口算的？

生3：23×50，先算三五十五，再算二五一十，所以得数是1150。290×3，先算三九二十七，再算二三得六，所以得数是870。50×40，四五二十，所以得数是2000。31×4……

师：在这四道口算题中，50×40在计算过程中只用了一句乘法口诀，两个乘数末尾只有两个0，但是乘数的积却有三个0？

生3：四五二十，产生了一个0；10乘10等于100，产生了两个0，所以一共有三个0。

师：也就是原来的计数单位相乘产生了一个新的计数单位……

在这个教学片段中，教师引导学生挑选出口算题，在口算中帮助学生巩固口算的方法，引导学生用不同的策略去理解算理，用自己的语言表达计算过程。同时，教师挑选出最特别的一道整数乘整数，让学生结合计数单位和计算单位的个数来阐述运算的一致性。

二、在笔算中经历推理过程

在小学阶段中，数形结合是重要的数学思想方法之一，推理意识也是重要的核心素养之一。在巩固笔算乘法过程中，教师让学生经历了两个层次：第一层次是掌握两位数乘两位数笔算乘法的算理和算法，能正确解释两部分积的含义；第二层次是教师将两位数乘两位数的笔算乘法与比较大小结合在一起，引导学生在观察、猜想、验证等推理过程，得到正确的结论。

师：同学们，剩下的四道题我们可以用笔算，边做边想两位数乘两位数的笔算要注意什么。

生1：竖式计算时横式不要漏写，计算不能算错。

（教师带领学生校对两位数乘两位数的笔算。）

师：我们来看17×44这个竖式，发现这个竖式里有两个68，这两个68的意思一样吗？

生2：第一个68表示68个一，第二个68表示68个十。

师：你知道这两个68是怎么得到的么？

生2：第一个是17乘4个一等于68个一，第二个是17乘4个十等于68个十。

师：（出示点子图）同学们，你能在点子图上找到68个一和68个十？（学生在点子图中指出。）你能说一说刚才是怎么笔算两位数乘两位数？

生3：两位数先乘另一个两位数的个位，再乘另一个两位数的十位，最后把这两部分加起来。

师：这位同学说得非常完整了。刚才我们笔算了四道计算题，（出示：28×33=644，17×44=748，38×23=874，49×12=588）请你分别算出每道算式两个乘数的和与两个乘数的差，比较这四道算式得数的大小，把你的发现记录在学习单上。

（学生的发现1：两个乘数的和都是61，两个乘数的差越大，两个乘数的积越小。学生的发现2：两个乘数的和都相等，两个乘数的差越小，两个乘数的积越大。）

师：这两位同学虽然表达得不完全一样，只是他们观察角度的方向不同，意思其实是一样的。那这个结论只是我们的猜测，我们还要进行验证。请你在后面写一个这样符合要求的两位数乘两位数算式，再笔算这道算式看看是否也有这样的规律。

生4：我写了16×45=720，与原来的17×44=748相比，两个乘数的和相等，两个乘数的差变小，两个乘数的积变大。

师：这样的例子我们写不完，我们来看看点子图，如果每行的点子数和行数的和不变，随着每行的点子数变小，行数再变多，点子的总个数越来越少。

在这个教学片段中，教师有目的地选择28×33、17×44、38×23和49×12这样四道两位数乘两位数乘法，学生在计算时看似是无意的组合，其实为后面的推理过程埋下了很好的铺垫，有利于学生在计算教学中经历推理的过程，发现一组乘法算式中的规律。

三、在计算中解决实际问题

计算是解决问题的基础，解决问题是学习的最终归宿。解决问题都少不了计算，还需要学生根据情境合理地选择用估算解决问题还是用精确计算解决问题，根据计算中的数据合理地选择口算或笔算等多种形式。

师：同学们，刚才我们用乘法算式探索规律，还可以用乘法来解决问题。（出示题目：①号篮球的价格是48元/个，②号篮球的价格是38元/个，③号篮球的价格是28元/个。张老师买19个同样的篮球，付给营业员800元。他买的是哪种篮球？张老师买篮球一共要用多少元？应找回多少元？）同学们，请你先在学习单上做一做，再与同桌说一说你是怎么做的。

生1：张老师买19个同样的篮球付给营业员800元，我就想（   ）×19≈800，我把19看作20，计算得到（   ）里可以是40，所以②号篮球的价格38元/个最接近40。接着计算张老师买篮球一共要用38×19=722（元），应找回800-722=78（元）。

师：在解决这道题目时我们先用估算判断张老师要买哪种篮球，再用精确计算得到篮球的总价和应找回多少元。（出示题目：一辆载重2000千克的卡车，装了52桶油，每桶油连桶重43千克。这辆卡车超载吗？）同学们，请你在学习单上做一做。

生2：我是这样做的，52×43=2236（千克），22362000，所以超载了。

生3：我是用估算做的，把52看成50，把43看成40，50乘40已经是2000了，所以52乘43肯定要比2000多了，超载了。

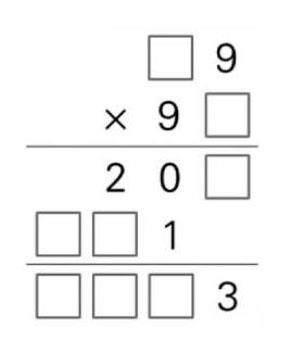
师：这道题用精确计算和估算都可以，但是我们发现估算要稍微简单些。（出示题目如图）同学们，请你在方框里填空，使竖式成立。

生4：我先根据得数个位上的3，推测9的乘法口诀中末尾是3的，有“七九六十三”，确定一个乘数是97……

在这个教学片段中，教师在选择学习素材时考虑了综合性、层次性、多变性的练习，帮助学生巩固两位数乘两位数的估算和精确计算，提高学生综合应用知识的能力。第一题给予学生多个条件，要学生从复杂的条件中合理地选择所需要的条件进行解决问题，运用两位数乘两位数的估算和精确计算解决购物问题。第二题是让学生判断这辆汽车是否超载，学生可以选择估算或精确计算解决问题。第三题是两位数乘两位数的数字谜，学生在解决数字谜时要善于自己观察，根据数字特征寻找突破口，从而确定方框中的数到底是多少，最后还要进行检查和验算。这三道练习不仅包括了这个单元的教学重难点，还让学生思考怎样灵活地选择解题策略。

总之，精选学习素材是根据学生学习过程中的学习目标和需求，有针对性地筛选和提供优质学习资源。教师要善于利用教科书、教辅等资料，通过对学习素材的筛选和验证，为学生提供高质量的学习资源，并帮助学生学会如何高效地获取和利用学习资源，这样才能满足每个学生的学习需求和兴趣爱好，可以使他们更加主动、积极地参与学习，提高学习的动力和效果，避免在琐碎和无用的内容上浪费时间。