对数正态多层贝叶斯混合模型的参数估计

摘要：用传统的正态多层贝叶斯混合模型在对具有均值异质性和方差异质性的偏态分布数据进行统计推断时效果不佳.针对这一问题，本文对数正态多层先验分布的构造与贝叶斯定理相结合，并引入到混合模型中，从而建立了对数正态多层贝叶斯混合模型.在混合模型的混合个数（k）已知的情况下，利用Gibbs抽样算法对各未知参数进行贝叶斯估计，并对使用Gibbs算法所生成的迭代链进行收敛性诊断.随机模拟结果显示，在相对误差、均方误差（MSE）准则下，贝叶斯估计的效果较似然估计更优.最后，通过实证分析证明了所建立的模型是切实可行的.

关键词：混合模型;正态多层贝叶斯混合模型;对数正态多层贝叶斯混合模型;贝叶斯估计;Gibbs算法

中图分类号：O212.8文献标志码：A

Parameter Estimation of Lognormal Multilayer Bayesian Model

WANG Zhikai， HUANG Jiewu

（School of Data Science and Information Engineering， Guizhou Minzu University， Guiyang 550025， China）

Abstract： In view of the fact that the traditional normal multi-layer Bayesian mixture model is not effective in the statistical inference of skewed distribution data with mean heterogeneity and variance heterogeneity， this paper combines the construction of log-normal multi-layer prior distribution with Bayesian theorem and introduces it into the mixture model， so as to establish a log-normal multi-layer Bayesian mixture model. In the case of known mixing number （k） of the mixture model， the Bayesian estimation of unknown parameters is performed by applying the Gibbs sampling algorithm， and the convergence of the iterative chain generated by the Gibbs algorithm is diagnosed. Random simulation results show that the effect of Bayesian estimation is better than that of likelihood estimation under the relative error and mean square error （MSE） criteria. Finally， the empirical analysis proves that the established model is feasible.

Key words： hybrid model; normal multilayer bayesian mixture model; lognormal multilayer bayesian mixture model; bayesian estimation; gibbs algorithm

混合模型是一种基于有限混合分布的统计模型，它能够有效地捕捉真实数据的多模态、偏度、峰度以及未观测到的异质性等特征.通过建立混合模型，可以解决复杂统计问题，并避免因过多模型而引起的过拟合问题.其应用非常广泛，特别是在生物学、经济学、医学等领域.

在现实生活中，对于具有不同组间异质性（呈双峰或多峰）的正态分布数据，若再使用单个正态单层贝叶斯模型来拟合这些数据时，可能会出现过多的参数和模型导致过拟合的问题.因此，Robert［1］为了解决参数和模型个数过拟合的问题，首次提出正态多层贝叶斯混合模型，并在模型个数已知的情况下讨论了均值、方差和模型权重这些参数的先验分布选择问题.此外，国内外学者还进一步对正态多层贝叶斯混合模型进行了很多研究.例如，Green［2］基于模型的混合个数未知的情况下，讨论了模型混合个数的先验分布选择问题，并提出了一种可逆马尔可夫链采样器来计算模型混合个数的后验概率，最后将后验概率最大的作为模型的混合个数;Green［3］为了实现对混合模型中不同维数参数子空间之间进行跳跃式抽样，提出了完全贝叶斯混合分析的RJMCMC算法;Jasra等［4］针对于Green所提出的可逆马尔可夫链采样器不能准确识别模型个数和选择模型的问题，提出了模型转换问题的解决方案，并讨论了模型混合个数的后验推断对先验规范的敏感性;针对不同组间存在相同均值的情况，导致 RJMCMC算法无法精确给出模型混合成分个数的问题，Papastamoulis等［5］提出了一种结合加权均值、标准的拆分-合并和产生-消亡移动过程的方法来更新模型的混合成分个数; Liu［6］考虑在模型混合个数未知的情况下，提出了一种将混合模型按非减均值排列的方法来解决模型之间切换困难的问题;当数据存在缺失时，Shiow-Lan等［7］提出了一种考虑数据分类特征的参数化方法实现对原始数据的缺失信息进行填补，再分别使用贝叶斯方法与极大似然方法对模型参数的进行估计;McLachlan等［8］除了对有限正态多层贝叶斯混合模型应用的理论进行研究之外，还探讨了矩量法、极大似然估计、E-M算法、贝叶斯分析在有限正态多层贝叶斯混合模型应用的最新情况；Zhang等［9］使用RJMCMC算法对多元正态多层贝叶斯混合模型进行了全贝叶斯统计推断;刘金山等［10］建立了一种对先验弱依赖的正态多层贝叶斯混合模型，采用RJMCMC 算法对模型参数估计;刘鹤飞等［11］在混合个数未知的情况下，研究了多元正态混合模型的贝叶斯推断.上面提到的研究都是具有异质性的数据在服从正态分布的假设下进行讨论的，而实际的数据呈现严格对称分布的情况非常的少，特别是经济学、气候科学和生态学等领域中的实际数据常常会呈现偏态分布.此时，如果我们再继续基于正态假设下用这些数据作统计推断，可能会获得不合理甚至错误的结论.

因此，为了更好的捕捉到这些具有异质性的偏态数据的特征，进而提高统计推断的精确度，本文将对数正态多层先验分布的构造方法与贝叶斯定理相结合，并引入混合模型中，建立了对数正态多层贝叶斯混合模型.在混合模型的混合个数（k）已知的情况下，利用Gibbs算法对对数正态多层贝叶斯混合模型的参数进行估计，并使用图像法和方差比法分别对随机模拟和实证分析中Gibbs算法所生成的迭代链进行收敛性检验.该检验验证了基于Gibbs算法求得的模型各参数贝叶斯估计值的可靠性，同时也说明了该模型能更好地对具有异质性的偏态分布数据进行统计推断.

1对数正态多层贝叶斯混合模型

为了解决实际中一些具均值异质性和方差异质性的偏态分布数据不适用于正态多层贝叶斯混合模型的问题，本文将对数正态多层先验分布的构造方法与贝叶斯定理相结合并引入混合模型中，建立如下所示的对数正态多层贝叶斯混合模型.

假定一个分层混合数据集Y=Y1，Y2，…，Yk是来自k个相互独立对数正态分布的混合样本，其中Yj=xj1，xj2，…，xjnj，（j=1，2，…，k）.假设该分层混合数据集满足以下的多层贝叶斯混合模型：

xji～∑kj=1wjLN（μj，σ2j），j=1，…，k，i=1，…，nj;μj～N（θ，τ2），σ2j～IG（γ，β），j=1，…，k;θ～N（μ0，σ20），τ2～IG（α1，λ1），β～G（g，h）;σ20～IG（α2，λ2），wj～D（η，…，η）.（1）

则称该模型为对数正态多层贝叶斯混合模型.其中，k是模型的混合个数（表示模型是由k个独立的对数正态分布混合而成）且kgt;1，IGαi，λi表示参数为αi，λi的逆伽马（IGamma）分布，G（g，h）表示参数为（g，h）的伽玛（Gamma）分布，D（η，…，η）表示参数为η的狄利克雷分布，wj是第j个混合成分的权重，μj，σj2，θ，τ2，σ20，β是未知的参数，μ0，γ，g，h，η，α1，α2，λ1，λ2是给定的超参数.

2模型的参数估计

2.1对数正态多层贝叶斯混合模型参数的极大似然估计

设Y=Y1，Y2，…，Yk是来自模型（1）的观测数据，则有似然函数为：

L（Y|μ，σ2，θ，τ2，β，σ20，w）∝1σj2nj/2+γ+1wjnj+η-1exp{-12σj2∑nj，ki=1，j=1（lnxji-μj）2}·1τ2k/2+α1+1

·exp{-12τ2∑kj=1（μj-θ）2}·1σ201/2+α2+1exp{-12σ20（θ-μ0）2}·exp{-λ1τ2}

·exp{-λ2σ20}·βg-1·exp{-β（∑kj=1σj-2+h）}，i=1，…，nj，j=1，…，k.（2）

其中，Yj=xj1，xj2，…，xjnj，μ=（μ1，μ2，…，μj），σ2=（σ21，σ22，…，σ2j），w=（w1，w2，…，wk）.

进而对μj，σ2j，θ，τ2，σ20，β，wj求极大似然估计，得：

μ^j=（∑ni，ki，j=1lnxji-θ）/（nj+1），σ^j2=（12∑nj，ki，j=1（lnxji-μ^j）2+kβ）/（nj2+γ+1），（3）

θ^=（∑kj=1μ^j+μ0）/（k+1），τ^2=（12∑kj=1（μ^j-θ^）2+λ1）/（k2+α1+1）（4）

σ^02=（12（θ^-μ0）2+λ2）/（12+α2+1），β^=（kγ+g）/（∑kj=1σ^j-2+h），w^j=wj/∑kj=1wj（5）

其中，i=1，…，nj，j=1，…，k.

2.2对数正态多层贝叶斯混合模型参数的贝叶斯估计

由模型（1）可知，设Y=（Y1，Y2，…，Yk）是来自模型（1）的观测数据，其中μ=（μ1，μ2，…，μk），σ2=（σ21，σ22，…，σ2k），Yj=xj1，xj2，…，xjnj，（j=1，…，k）.此观测数据的联合密度函数为：

p（Y|μ，σ2，θ，τ2，β，σ20，w）∝∏kj=11σj2nj/2wjnjexp{-12σj2∑nj，ki，j=1（lnxji-μj）2}（6）

其中，i=1，…，nj，j=1，…，k.

则得到该对数正态多层贝叶斯混合模型各未知参数的联合后验分布为：

π（μ，σ2，θ，τ2，β，σ20，w|Y）∝p（Y|μ，σ2，θ，τ2，β，σ20，w）π（μj|θ，τ2）π（σj2|β）π（τ2）π（θ|σ20）π（σ20）π（β）π（wj）.由上述各未知参数的联合后验分布，进而推导得到参数μj，σ2j，θ，τ2，σ20，β，wj的条件后验分布分别为：π（μj|σ2，θ，τ2，β，σ20，w，Y）～N（σj2njτ2+σj2θ+njτ2+σj2njτ2+σj2Yj，τ2σj2njτ2+σj2），

j=1，…，k;π（σj2|μ，θ，τ2，β，σ20，w，Y）～IG（nj2+γ，12∑nj，ki，j=1（lnxji-μj）2+β），

π（θ|μ，σ2，τ2，β，σ20，w，Y）～N（τ2kσ20+τ2μ0+kσ20kσ20+τ2μ-，σ20τ2kσ20+τ2）;π（τ2|μ，σ2，θ，β，σ20，w，Y）～IG（k2+α1，12∑kj=1（μj-θ）2+λ1）;π（σ20|μ，σ2，θ，τ2，β，w，Y）～IG（12+α2，12·（θ-μ0）2+λ2）;π（β|μ，σ2，θ，τ2，σ20，w，Y）～G（kγ+g，∑kj=1σj-2+h）;π（wj|μ，σ2，θ，τ2，β，σ20，Y）～D（η+n1，…，η+nj）.其中Yj=1nj∑nj，ki，j=1lnxji，μ-=1k∑kj=1μj.

由于所得到的各未知参数的条件后验分布为标准分布，可直接用Gibbs抽样进行抽样得到每个未知参数条件后验分布的平稳分布.Gibbs抽样是MCMC方法里最简单且应用最广泛的抽样方法，Gibbs抽样算法的具体步骤如下：

（1）给定目标平稳分布π（μj，σj2，θ，τ2，σ20，β，wj）（j=1，2，…，k），假设需要进行N次迭代得到Gibbs样本量为N，在第A次迭代时的Gibbs抽样开始收敛;

（2）给定初始值为μj（0），σj2（0），θ（0），τ2（0），σ2（0）0，β（0），wj（0），j=1，2，…，k；

（3）对于t=1，2，…，A，…，N，假设第t-1次迭代的估计值为（μj（t-1），σj2（t-1），θ（t-1），τ2（t-1），σ02（t-1），β（t-1），wj（t-1）），则第t次迭代的步骤为：（a） 从条件后验分布π（μj|σj2（t-1），θ（t-1），τ2（t-1），σ02（t-1），β（t-1），wj（t-1），Y）随机抽取μj（t），用μj（t）更新μj;（b） 从条件后验分布π（σj2|μj（t），θ（t-1），τ2（t-1），σ02（t-1），β（t-1），wj（t-1），Y）随机抽取σj

2（t），用σj2（t）更新σj2;（c） 从条件后验分布π（θ|μj（t），σj2（t），τ2（t-1），σ02（t-1），β（t-1），wj（t-1），Y）随机抽取θ（t），用θ（t）更新θ;（d） 从条件后验分布π（τ2|μj（t），σj2（t），θ（t），

σ02（t-1），β（t-1），wj（t-1），Y）随机抽取τ2（t），用τ2（t）更新τ2;（e） 从条件后验分布π（σ20|μj（t），σj2（t），θ（t），τ2（t），β（t-1），wj（t-1），Y）随机抽取σ02（t），用σ02（t）更新σ20;（f） 从条件后验分布π（β|μj（t），σj2（t），θ（t），τ2（t），σ02（t），wj（t-1），Y）随机抽取β（t），用β（t）更新β;（g） 从条件后验分布π（wj|μj（t），σj2（t），θ（t），τ2（t），σ02（t），β（t），Y）随机抽取wj（t），用wj（t）更新wj;

（4） 重复（3）过程，迭代N次，得到{（μj（1），σj2（1），θ（1），τ2（1），σ02（1），β（1），wj（1）），（μj（2），σj2（2），θ（2），τ2（2），σ02（2），β（2），wj（2）），…，（μj（A），σj2（A），θ（A），τ2（A），σ02（A），β（A），wj（A）），…，（μj（N），σj2（N），θ（N），τ2（N），σ02（N），β（N），wj（N））}j=1，…，k，即为根据Gibbs抽样获得的样本集.

假设得到各参数的Gibbs样本容量为N，且在第A次迭代时开始收敛，则把后面N-A个样本的均值作为各未知参数的贝叶斯估计值，即：

μ^j=1N-A∑Nt=A+1μj（t），σ^j2=1N-A∑Nt=A+1σj2（t），θ^=1N-A∑Nt=A+1θ（t），τ^2=1N-A∑Nt=A+1τ2（t），

σ^20=1N-A∑Nt=A+1σ02（t），β^=1N-A∑Nt=A+1β（t），w^j=1N-A∑Nt=A+1wj（t）

其中，j=1，2，…，k.

3模拟研究

基于上述对对数正态多层贝叶斯混合模型参数的贝叶斯估计的理论研究，本文主要考虑在混合模型的混合个数（k）已知且kgt;1的情况下，利用R软件对混合模型的各未知参数进行模拟研究.

假设当混合模型的混合个数k=3时，以权重w=（0.2，0.5，0.3），均值μ=（0.5，1.2，1.8），方差σ2=（0.3，0.1，0.2）分别产生总样本量为500、1 000的混合对数正态随机数作为模拟的观测数据，这两组不同样本量的模拟数据分布如图1和图2所示.

从上述两组观测样本量的模拟数据分布图可知，每一组的观测样本都是存在分层结构，说明这两组观测样本组间都是存在均值和方差的异质性，模拟数据结构满足模型（1）.

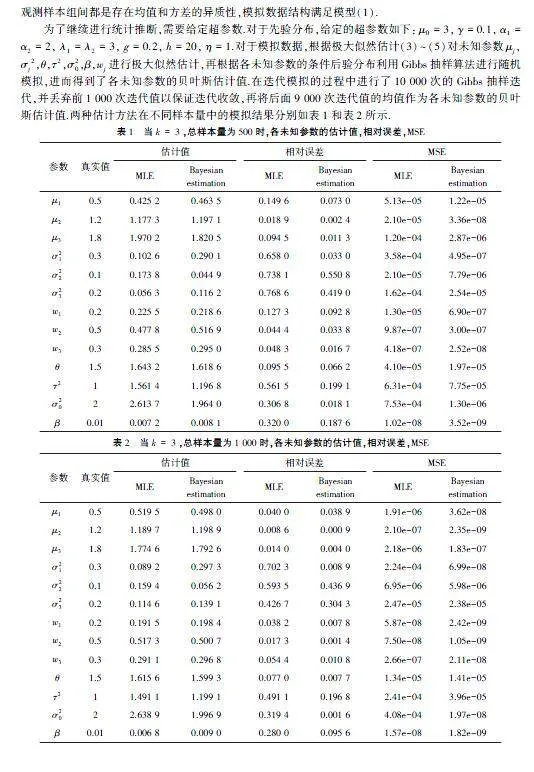
为了继续进行统计推断，需要给定超参数.对于先验分布，给定的超参数如下：μ0=3，γ=0.1，α1=α2=2，λ1=λ2=3，g=0.2，h=20，η=1.对于模拟数据，根据极大似然估计（3）～（5）对未知参数μj，σj2，θ，τ2，σ20，β，wj进行极大似然估计，再根据各未知参数的条件后验分布利用Gibbs抽样算法进行随机模拟，进而得到了各未知参数的贝叶斯估计值.在迭代模拟的过程中进行了10 000次的Gibbs抽样迭代，并丢弃前1 000次迭代值以保证迭代收敛，再将后面9 000次迭代值的均值作为各未知参数的贝叶斯估计值.两种估计方法在不同样本量中的模拟结果分别如表1和表2所示.

表1和表2给出了在不同样本量下，用两种估计方法得到的各未知参数估计值.要证明所得模型中各个未知参数的贝叶斯估计值的可靠性，需要确保使用Gibbs算法生成的迭代链能够收敛.因此，可以利用图像法对Gibbs抽样生成的迭代链进行收敛性诊断.在样本量不同的情况下，对该模型中各未知参数的Gibbs抽样所生成的迭代链进行模拟轨迹图，如图3和图4所示.

从图3和图4可知，通过观察所有未知参数的Gibbs抽样迭代轨迹图发现没有明显的周期性和趋势性.这表明在不同样本量的情况下，模型中各个未知参数通过Gibbs抽样生成的所有迭代链都是收敛的.因此，可以证明所得模型中各个未知参数的贝叶斯估计值是可靠的，则将后面9 000次迭代值的均值作为各未知参数的贝叶斯估计值是合理的.

综上可知，针对不同总样本量，对数正态多层贝叶斯混合模型中各个未知参数通过Gibbs抽样生成的所有迭代链都是收敛的，即证明了表1和表2所给出的各个未知参数的估计值是可靠的.而从表1和表2的模拟结果可知，当总样本量相同时，各未知参数的贝叶斯估计值都比极大似然估计值更接近于真实值.在相对误差准则下，贝叶斯估计的相对误差均不超过10%，极大似然估计的相对误差均不超过15%，说明了贝叶斯估计的精确度高于极大似然估计;在MSE准则下，贝叶斯估计的效果优于极大似然估计，说明了Gibbs抽样得到的迭代值的波动较小，相对稳定.

针对总样本量不同的情况，当总样本量逐渐增大时，各未知参数的相对误差、MSE逐渐减小，说明了随着总样本量的增加，贝叶斯估计的精度越来越高，Gibbs抽样得到的迭代值的波动越小.

4实证分析

本文实证分析所用的数据是来自我国国家统计局官网所统计发布的2013年至2023年每一季度城镇居民人均收入和农村人民人均收入统计数据，根据该统计情况来对我国城镇居民和农村居民的收入差别进行研究，具体数据分别如表3和表4所示.

4.1数据的正态性检验

首先，对上述两组数据分别记城镇居民人均收入为x1、记农村居民人均收入为x2，再对这两组数据分别取对数，最后采用Shapiro-Wilk检验对选取的数据进行正态性检验.假设检验为：H0：这两组数据服从对数正态分布;H1：这两组数据不服从对数正态分布.其中显著性水平取值为0.05.

利用Shapiro-Wilk检验方法进行检验得到的结果如表5所示.由表5可知，两组数据Shapiro-Wilk检验的P值都大于0.05，说明原假设成立，即这两组数据服从对数正态分布.因此，可以用这两组数据来对本文所提出的对数正态多层贝叶斯混合模型中的未知参数进行估计.

4.2模型参数的估计

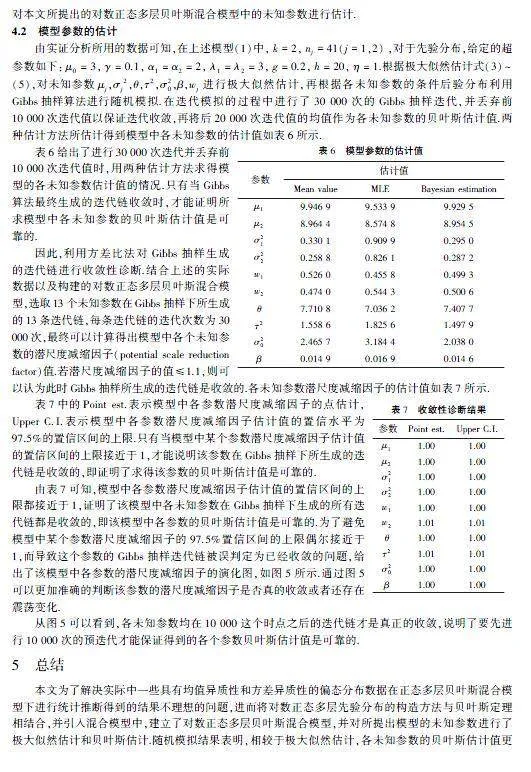
由实证分析所用的数据可知，在上述模型（1）中，k=2，nj=41（j=1，2），对于先验分布，给定的超参数如下：μ0=3，γ=0.1，α1=α2=2，λ1=λ2=3，g=0.2，h=20，η=1.根据极大似然估计式（3）～（5），对未知参数μj，σj2，θ，τ2，σ20，β，wj进行极大似然估计，再根据各未知参数的条件后验分布利用Gibbs抽样算法进行随机模拟.在迭代模拟的过程中进行了30 000次的Gibbs抽样迭代，并丢弃前10 000次迭代值以保证迭代收敛，再将后20 000次迭代值的均值作为各未知参数的贝叶斯估计值.两种估计方法所估计得到模型中各未知参数的估计值如表6所示.

表6给出了进行30 000次迭代并丢弃前10 000次迭代值时，用两种估计方法求得模型的各未知参数估计值的情况.只有当Gibbs算法最终生成的迭代链收敛时，才能证明所求模型中各未知参数的贝叶斯估计值是可靠的.

因此，利用方差比法对Gibbs抽样生成的迭代链进行收敛性诊断.结合上述的实际数据以及构建的对数正态多层贝叶斯混合模型，选取13个未知参数在Gibbs抽样下所生成的13条迭代链，每条迭代链的迭代次数为30 000次，最终可以计算得出模型中各个未知参数的潜尺度减缩因子（potential scale reduction factor）值.若潜尺度减缩因子的值≤1.1，则可以认为此时Gibbs抽样所生成的迭代链是收敛的.各未知参数潜尺度减缩因子的估计值如表7所示.

表7中的Point est.表示模型中各参数潜尺度减缩因子的点估计，Upper C.I.表示模型中各参数潜尺度减缩因子估计值的置信水平为 97.5%的置信区间的上限.只有当模型中某个参数潜尺度减缩因子估计值的置信区间的上限接近于1，才能说明该参数在Gibbs抽样下所生成的迭代链是收敛的，即证明了求得该参数的贝叶斯估计值是可靠的.

由表7可知，模型中各参数潜尺度减缩因子估计值的置信区间的上限都接近于1，证明了该模型中各未知参数在Gibbs抽样下生成的所有迭代链都是收敛的，即该模型中各参数的贝叶斯估计值是可靠的.为了避免模型中某个参数潜尺度减缩因子的97.5%置信区间的上限偶尔接近于1，而导致这个参数的Gibbs抽样迭代链被误判定为已经收敛的问题，给出了该模型中各参数的潜尺度减缩因子的演化图，如图5所示.通过图5可以更加准确的判断该参数的潜尺度减缩因子是否真的收敛或者还存在震荡变化.

从图5可以看到，各未知参数均在10 000这个时点之后的迭代链才是真正的收敛，说明了要先进行10 000次的预迭代才能保证得到的各个参数贝叶斯估计值是可靠的.

5总结

本文为了解决实际中一些具有均值异质性和方差异质性的偏态分布数据在正态多层贝叶斯混合模型下进行统计推断得到的结果不理想的问题，进而将对数正态多层先验分布的构造方法与贝叶斯定理相结合，并引入混合模型中，建立了对数正态多层贝叶斯混合模型，并对所提出模型的未知参数进行了极大似然估计和贝叶斯估计.随机模拟结果表明，相较于极大似然估计，各未知参数的贝叶斯估计值更稳定，也更接近于真实值.最后，通过实证分析证明了所提出的模型是切实可行的.

［参考文献］

［1］ROBERT C P.Estimation of finite mixture distributions through Bayesian sampling［J］.Journal of the Royal Statistical Society，1994，56（2）：363-375.

［2］GREEN，PETER J.Reversible jump Markov chain Monte Carlo computation and Bayesian model determination［J］.Biometrika，1995，82（4）：711-732.

［3］GREEN，PETER J.On Bayesian analysis of mixtures with an unknown number of components［J］.Journal of the Royal Statistical Society Series B （Statistical Methodology），1997，59（4）：758-792.

［4］JASRA D A，HOLMES C C，STEPHENS D A.Markov chain monte carlo methods and the label switching problem in bayesian mixture modeling［J］.Statistical Science，2005，20（1）：50-67.

［5］PAPASTAMOULIS P，ILIOPOULOS G.Reversible Jump MCMC in mixtures of normal distributions with the same component means［J］.Computational Statistics amp; Data Analysis，2009，53（4）：900-911.

［6］LIU Z H.Bayesian Mixture Models［D］.Hamilton：McMaster University，2010.

［7］SHIOW-LAN GAU，JEAN DIEU TAPSOBA，SHEN-MING LEE.Bayesian approach for mixture models with grouped data［J］.Computational Statistics，2014，29（5），1025-1043.

［8］MCLACHLAN G J，LEE S X，RATHNAYAKE S I.Finite mixture models［J］.Annual Review of Statistics and Its Application，2019，06（1）：355-378.

［9］ZHANG Z，CHAN K L，YIMING W U，et al.Learning a multivariate Gaussian mixture model with the reversible jump MCMC algorithm［J］.Statistics amp; Computing，2004，14（4）：343-355.

［10］刘金山，陈镇坤，黄来华.基于贝叶斯分层混合模型的大脑 FMRI 图像分割［J］.数理统计与管理，2015，34（4）：603-611.

［11］刘鹤飞，王坤，宗凤喜.混合个数未知的多元正态混合模型的贝叶斯推断［J］.统计与决策，2019，35（02）：26-29.

［责任编辑王光］